Progress in Simulation Modeling Based on the Finite Element Method for Electrical Discharge Machining
Abstract
:1. Introduction
2. Single-Spark Simulations
2.1. Material Removal Rate
2.2. Surface Roughness
2.3. Tool Wear Ratio
2.4. Recast Layer Thickness
2.5. Summary
3. Multi-Spark Simulations
3.1. Material Removal Rate
3.2. Surface Roughness
3.3. Tool Wear Ratio
3.4. Recast Layer Thickness
3.5. Summary
4. Hybrid Machining Simulations
4.1. Material Removal Rate
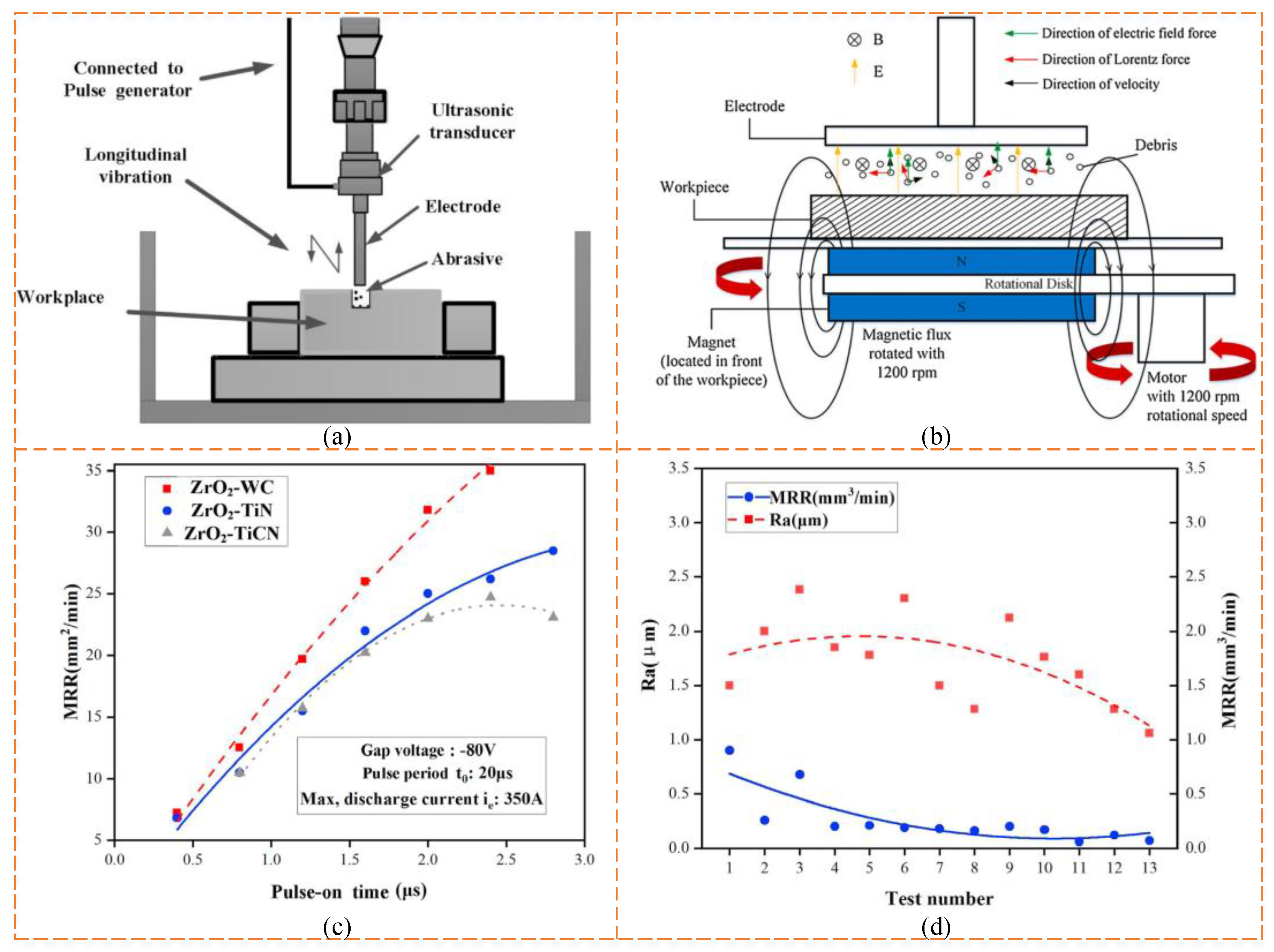
4.2. Surface Roughness
4.3. Tool Wear Ratio
4.4. Recast Layer Thickness
4.5. Summary
5. Outlooks
Author Contributions
Funding
Conflicts of Interest
References
- Tilghman, B.C. Cutting Metal by Electricity. U.S. Patent 416,873, 10 December 1889. [Google Scholar]
- Strobel, K. Electric Arc Cutting Machine. U.S. Patent 2007225, 7 September 1936. [Google Scholar]
- Ho, K.H.; Newman, S.T. State of the Art Electrical Discharge Machining (EDM). Int. J. Mach. Tools Manuf. 2003, 43, 1287–1300. [Google Scholar] [CrossRef]
- Das, S.; Klotz, M.; Klocke, F. EDM Simulation: Finite Element-Based Calculation of Deformation, Microstructure and Residual Stresses. J. Mater. Process. Technol. 2003, 142, 434–451. [Google Scholar] [CrossRef]
- Mahajan, A.; Devgan, S.; Kalyanasundaram, D. Electrical Discharge Machining- a Futuristic Technique for Surface Engineering of Biomedical Alloys: A Concise Review. Surf. Topogr. Metrol. Prop. 2022, 10, 043001. [Google Scholar] [CrossRef]
- Lu, Y.; Sun, P.; Yang, X.; Guo, X.; Li, X.; Ming, W. Review of Research Progress in Nontraditional Machining of Ultrahigh-Temperature Ceramic Matrix Composites. Coatings 2023, 13, 187. [Google Scholar] [CrossRef]
- Liu, K.; Lauwers, B.; Reynaerts, D. Process Capabilities of Micro-EDM and Its Applications. Int. J. Adv. Manuf. Technol. 2010, 47, 11–19. [Google Scholar] [CrossRef]
- Kumar, D.; Porwal, R.K. Recent Advances in Machining of Composite Materials by Electrical Discharge Machine. Key Eng. Mater. 2023, 965, 3–20. [Google Scholar] [CrossRef]
- Pandey, A.K.; Anas, M. Sustainability and Recent Trends in Micro-Electric Discharge Machining (μ-EDM): A State-of-the-Art Review. Mater. Today Proc. 2022, 57, 2049–2055. [Google Scholar] [CrossRef]
- Die Sinking and Wire Cutting Edm Market Size, Trends and Growth Opportunity, by Service, by Type, by Hole Size, by Price Range by Application, by Industry Vertical, by Region and Forecast to 2030. Available online: https://www.researchandmarkets.com/reports/5783625/global-die-sinking-wire-cutting-edm-market-size (accessed on 4 May 2023).
- Ming, W.; Xie, Z.; Ma, J.; Du, J.; Zhang, G.; Cao, C.; Zhang, Y. Critical Review on Sustainable Techniques in Electrical Discharge Machining. J. Manuf. Process. 2021, 72, 375–399. [Google Scholar] [CrossRef]
- Guo, X.; Tan, L.; Xie, Z.; Zhang, L.; Zhang, G.; Ming, W. Simulation and Experimentation of Renewable Dielectric Gap Flow Fields in EDM. Int. J. Adv. Manuf. Technol. 2023, 170. [Google Scholar] [CrossRef]
- Ming, W.; Zhang, S.; Zhang, G.; Du, J.; Ma, J.; He, W.; Cao, C.; Liu, K. Progress in Modeling of Electrical Discharge Machining Process. Int. J. Heat Mass Transf. 2022, 187, 122563. [Google Scholar] [CrossRef]
- Joshi, S.N.; Pande, S.S. Development of an Intelligent Process Model for EDM. Int. J. Adv. Manuf. Technol. 2009, 45, 300–317. [Google Scholar] [CrossRef]
- Descoeudres, A.; Hollenstein, C.; Waelder, G.; Demellayer, R.; Perez, R. Time- and Spatially-Resolved Characterization of Electrical Discharge Machining Plasma. Plasma Sources Sci. Technol. 2008, 17, 024008. [Google Scholar] [CrossRef]
- He, W.; Wang, D.; Ming, W.; Ma, J.; Liu, K.; Du, J. Research Progress on Cutting Machining Simulation Technology of Metallic Glasses. Int. J. Adv. Manuf. Technol. 2022, 122, 1167–1193. [Google Scholar] [CrossRef]
- Unses, E.; Cogun, C. Improvement of Electric Discharge Machining (EDM) Performance of Ti6Al4V Alloy with Added Graphite Powder to Dielectric. Stroj. Vestn.-J. Mech. Eng. 2015, 61, 409–418. [Google Scholar] [CrossRef]
- Yu, Z.; Li, D.; Yang, J.; Zeng, Z.; Yang, X.; Li, J. Fabrication of Micro Punching Mold for Micro Complex Shape Part by Micro EDM. Int. J. Adv. Manuf. Technol. 2019, 100, 743–749. [Google Scholar] [CrossRef]
- Bindya Devi, M.; Kumar Birru, A.; Kumar Bannaravuri, P. The Recent Trends of EDM Applications and Its Relevance in the Machining of Aluminium MMCs: A Comprehensive Review. Mater. Today Proc. 2021, 47, 6870–6873. [Google Scholar] [CrossRef]
- Chekuri, R.B.R.; Eshwar, D.; Kotteda, T.K.; Srikanth Varma, R.S. Experimental and Thermal Investigation on Die-Sinking EDM Using FEM and Multi-Objective Optimization Using WOA-CS. Sustain. Energy Technol. Assess. 2022, 50, 101860. [Google Scholar] [CrossRef]
- Yue, X.; Yang, X. Molecular Dynamics Simulation of Machining Properties of Polycrystalline Copper in Electrical Discharge Machining. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2019, 233, 371–380. [Google Scholar] [CrossRef]
- Zhang, W. Research on the Influence of the Discharge Breakdown Process on the Crater Formation during EDM. Multidiscip. Model. Mater. Struct. 2021, 17, 841–860. [Google Scholar] [CrossRef]
- Chen, Z.; Hu, S.; Zhang, S.; Zhang, Q.; Zhang, Z.; Ming, W. Simulation and Experimental Study on the Precision Molding of Irregular Vehicle Glass Components. Micromachines 2023, 14, 1974. [Google Scholar] [CrossRef]
- Ming, W.; Zhang, Z.; Wang, S.; Huang, H.; Zhang, Y.; Zhang, Y.; Shen, D. Investigating the Energy Distribution of Workpiece and Optimizing Process Parameters during the EDM of Al6061, Inconel718, and SKD11. Int. J. Adv. Manuf. Technol. 2017, 92, 4039–4056. [Google Scholar] [CrossRef]
- Singh, H. Experimental Study of Distribution of Energy during EDM Process for Utilization in Thermal Models. Int. J. Heat Mass Transf. 2012, 55, 5053–5064. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y.; Shen, Y.; Li, Z.; Ji, R.; Cai, B. A Novel Method of Determining Energy Distribution and Plasma Diameter of EDM. Int. J. Heat Mass Transf. 2014, 75, 425–432. [Google Scholar] [CrossRef]
- Li, Q.; Yang, X. Study on Arc Plasma Movement and Its Effect on Crater Morphology during Single-Pulse Discharge in EDM. Int. J. Adv. Manuf. Technol. 2020, 106, 5033–5047. [Google Scholar] [CrossRef]
- Ghiculescu, D.; Marinescu, N.I.; Nanu, S. Modelling Aspects of Removal Mechanism at Ultrasonic Aided Electrodischarge Machining. Int. J. Mater. Form. 2009, 2, 685–688. [Google Scholar] [CrossRef]
- Khatri, B.C.; Rathod, P.; Valaki, J.B. Ultrasonic Vibration–Assisted Electric Discharge Machining: A Research Review. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2016, 230, 319–330. [Google Scholar] [CrossRef]
- Mansoor, S.M.; Raj, S.O.N.; Pal, V.K.; Roy, S. Finite Element Analysis of Magnetic Field Assisted Wire Electric Discharge Machine. IOP Conf. Ser. Mater. Sci. Eng. 2018, 402, 012051. [Google Scholar] [CrossRef]
- Ming, W.; Zhang, Z.; Wang, S.; Zhang, Y.; Shen, F.; Zhang, G. Comparative Study of Energy Efficiency and Environmental Impact in Magnetic Field Assisted and Conventional Electrical Discharge Machining. J. Clean. Prod. 2019, 214, 12–28. [Google Scholar] [CrossRef]
- Jithin, S.; Raut, A.; Bhandarkar, U.V.; Joshi, S.S. FE Modeling for Single Spark in EDM Considering Plasma Flushing Efficiency. Procedia Manuf. 2018, 26, 617–628. [Google Scholar] [CrossRef]
- Chen, Y.; Hu, S.; Li, A.; Cao, Y.; Zhao, Y.; Ming, W. Parameters Optimization of Electrical Discharge Machining Process Using Swarm Intelligence: A Review. Metals 2023, 13, 839. [Google Scholar] [CrossRef]
- Chao, Z.; Mingbo, Q.; Jing, Y.; Yunxiao, H.; Jiongbo, F. Influence of Electrode Temperature on Electric Erosion Pit Morphology during Cool Electrode EDM. Int. J. Adv. Manuf. Technol. 2017, 93, 2173–2181. [Google Scholar] [CrossRef]
- Tariq Jilani, S.; Pandey, P.C. Analysis and Modelling of Edm Parameters. Precis. Eng. 1982, 4, 215–221. [Google Scholar] [CrossRef]
- Tariq Jilani, S.; Pandey, P.C. An Analysis of Surface Erosion in Electrical Discharge Machining. Wear 1983, 84, 275–284. [Google Scholar] [CrossRef]
- DiBitonto, D.D.; Eubank, P.T.; Patel, M.R.; Barrufet, M.A. Theoretical Models of the Electrical Discharge Machining Process. I. A Simple Cathode Erosion Model. J. Appl. Phys. 1989, 66, 4095–4103. [Google Scholar] [CrossRef]
- Patel, M.R.; Barrufet, M.A.; Eubank, P.T.; DiBitonto, D.D. Theoretical Models of the Electrical Discharge Machining Process. II. The Anode Erosion Model. J. Appl. Phys. 1989, 66, 4104–4111. [Google Scholar] [CrossRef]
- Salonitis, K.; Stournaras, A.; Stavropoulos, P.; Chryssolouris, G. Thermal Modeling of the Material Removal Rate and Surface Roughness for Die-Sinking EDM. Int. J. Adv. Manuf. Technol. 2009, 40, 316–323. [Google Scholar] [CrossRef]
- Eubank, P.T.; Patel, M.R.; Barrufet, M.A.; Bozkurt, B. Theoretical Models of the Electrical Discharge Machining Process. III. The Variable Mass, Cylindrical Plasma Model. J. Appl. Phys. 1993, 73, 7900–7909. [Google Scholar] [CrossRef]
- Joshi, S.N.; Pande, S.S. Thermo-Physical Modeling of Die-Sinking EDM Process. J. Manuf. Process. 2010, 12, 45–56. [Google Scholar] [CrossRef]
- Ming, W.; Zhang, G.; Li, H.; Guo, J.; Zhang, Z.; Huang, Y.; Chen, Z. A Hybrid Process Model for EDM Based on Finite-Element Method and Gaussian Process Regression. Int. J. Adv. Manuf. Technol. 2014, 74, 1197–1211. [Google Scholar] [CrossRef]
- Yeo, S.H.; Kurnia, W.; Tan, P.C. Electro-Thermal Modelling of Anode and Cathode in Micro-EDM. J. Phys.-Appl. Phys. 2007, 40, 2513–2521. [Google Scholar] [CrossRef]
- Kansal, H.K.; Singh, S.; Kumar, P. Numerical Simulation of Powder Mixed Electric Discharge Machining (PMEDM) Using Finite Element Method. Math. Comput. Model. 2008, 47, 1217–1237. [Google Scholar] [CrossRef]
- Singh, M.; Sharma, S.; Ramkumar, J. Numerical Simulation of Melt-Pool Hydrodynamics in μ-EDM Process. Procedia CIRP 2020, 95, 226–231. [Google Scholar] [CrossRef]
- Wang, Z.L.; Xie, B.C.; Wang, Y.K.; Zhao, W.S. Numerical Simulation of Cathode Erosion in EDM Process. Adv. Mater. Res. 2012, 462, 109–115. [Google Scholar] [CrossRef]
- Kuriachen, B.; Varghese, A.; Somashekhar, K.P.; Panda, S.; Mathew, J. Three-Dimensional Numerical Simulation of Microelectric Discharge Machining of Ti6Al4V. Int. J. Adv. Manuf. Technol. 2015, 79, 147–160. [Google Scholar] [CrossRef]
- Gadelmawla, E.S.; Koura, M.M.; Maksoud, T.M.A.; Elewa, I.M.; Soliman, H.H. Roughness Parameters. J. Mater. Process. Technol. 2002, 123, 133–145. [Google Scholar] [CrossRef]
- Marafona, J.; Chousal, J.A.G. A Finite Element Model of EDM Based on the Joule Effect. Int. J. Mach. Tools Manuf. 2006, 46, 595–602. [Google Scholar] [CrossRef]
- Wandra, R. Finite Element Analysis of Powder Mixed Electric Discharge Machining on Ti-Alloy. Mater. Today Proc. 2022, 50, 593–599. [Google Scholar] [CrossRef]
- Chen, Z.; Xie, J.; Zhu, X. Experimental Study on Surface Physical Behaviour and Integrity of Polycrystalline Diamond (PCD) in Micron-Scale Abrasive Flow Assisted Impulse-Discharge Machining. Int. J. Refract. Met. Hard Mater. 2023, 116, 106330. [Google Scholar] [CrossRef]
- Algodi, S.J.; Clare, A.T.; Brown, P.D. Modelling of Single Spark Interactions during Electrical Discharge Coating. J. Mater. Process. Technol. 2018, 252, 760–772. [Google Scholar] [CrossRef]
- Assarzadeh, S.; Ghoreishi, M. Prediction of Root Mean Square Surface Roughness in Low Discharge Energy Die-Sinking EDM Process Considering the Effects of Successive Discharges and Plasma Flushing Efficiency. J. Manuf. Process. 2017, 30, 502–515. [Google Scholar] [CrossRef]
- Philip, J.T.; Mathew, J.; Kuriachen, B. Numerical Simulation of the Effect of Crater Morphology for the Prediction of Surface Roughness on Electrical Discharge Textured Ti6Al4V. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 248. [Google Scholar] [CrossRef]
- George, J.; Mathew, J.; Manu, R. Determination of Crater Morphology and 3D Surface Roughness in Wire Electrical Discharge Turning of Inconel 825. Arab. J. Sci. Eng. 2020, 45, 5109–5127. [Google Scholar] [CrossRef]
- Li, Z.; Liu, Y.; Cao, B.; Li, W. Modeling of Material Removal Morphology and Prediction of Surface Roughness Based on WEDM Successive Discharges. Int. J. Adv. Manuf. Technol. 2022, 120, 2015–2029. [Google Scholar] [CrossRef]
- Joudivand Sarand, M.; Shabgard, M.; Jodari Saghaie, M.; Joudivand Sarand, L. Tool Wear Estimating Model Considering Modeling Improvement Factors in Electrical Discharge Machining Process Based on Physical Properties of Tool Electrodes. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2017, 231, 850–866. [Google Scholar] [CrossRef]
- Papazoglou, E.L.; Karmiris-Obratański, P.; Leszczyńska-Madej, B.; Markopoulos, A.P. A Study on Electrical Discharge Machining of Titanium Grade2 with Experimental and Theoretical Analysis. Sci. Rep. 2021, 11, 8971. [Google Scholar] [CrossRef] [PubMed]
- Vignesh, M.; Ramanujam, R. Numerical Modelling and Experimental Validation of Crater Formation in WEDM Hybrid Turning of Ti6Al4V Alloy. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2021, 235, 392–404. [Google Scholar] [CrossRef]
- Pandey, P.C.; Jilani, S.T. Plasma Channel Growth and the Resolidified Layer in Edm. Precis. Eng. 1986, 8, 104–110. [Google Scholar] [CrossRef]
- Shabgard, M.R.; Gholipoor, A.; Mohammadpourfard, M. Investigating the Effects of External Magnetic Field on Machining Characteristics of Electrical Discharge Machining Process, Numerically and Experimentally. Int. J. Adv. Manuf. Technol. 2019, 102, 55–65. [Google Scholar] [CrossRef]
- George, J.; Philip, J.T.; Mathew, J.; Manu, R. Prediction and Analysis of Material Removal Rate and White Layer Thickness during Wire Electrical Discharge Turning (WEDT) Process. CIRP J. Manuf. Sci. Technol. 2022, 39, 210–222. [Google Scholar] [CrossRef]
- Zhang, G.; Huang, H.; Zhang, Z.; Zhang, Y. Study on the Effect of Three Dimensional Wire Vibration on WEDM Based on a Novel Thermophysical Model. Int. J. Adv. Manuf. Technol. 2019, 100, 2089–2101. [Google Scholar] [CrossRef]
- Gholipoor, A.; Shabgard, M.R.; Mohammadpourfard, M. A Novel Approach to Plasma Channel Radius Determination and Numerical Modeling of Electrical Discharge Machining Process. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 185. [Google Scholar] [CrossRef]
- Shahane, S.; Pande, S.S. Development of a Thermo-Physical Model for Multi-Spark Wire EDM Process. Procedia Manuf. 2016, 5, 205–219. [Google Scholar] [CrossRef]
- Banerjee, S.; Prasad, B. Numerical Evaluation of Transient Thermal Loads on a WEDM Wire Electrode under Spatially Random Multiple Discharge Conditions with and without Clustering of Sparks. Int. J. Adv. Manuf. Technol. 2010, 48, 571–580. [Google Scholar] [CrossRef]
- Erdem, O.; Cogun, C.; Uslan, I.; Erbas, M. Thermo-Fluid Multi-Physics Modeling and Experimental Verification of Volumetric Workpiece Material Removal by a Discharge Pulse in Electric Discharge Machining Process. J. Phys. D Appl. Phys. 2020, 53, 395501. [Google Scholar] [CrossRef]
- Hinduja, S.; Kunieda, M. Modelling of ECM and EDM Processes. CIRP Ann. 2013, 62, 775–797. [Google Scholar] [CrossRef]
- Izquierdo, B.; Sánchez, J.A.; Plaza, S.; Pombo, I.; Ortega, N. A Numerical Model of the EDM Process Considering the Effect of Multiple Discharges. Int. J. Mach. Tools Manuf. 2009, 49, 220–229. [Google Scholar] [CrossRef]
- Philip, J.T.; Kuriachen, B.; Mathew, J. Numerical Modelling and Simulation of Single and Multi-spark Impacts in Electrical Discharge Machining. In Advances in Simulation, Product Design and Development: Proceedings of AIMTDR 2018; Springer: Singapore, 2019; pp. 479–488. [Google Scholar]
- Saikiran, H.; Kaushal, I.V.; Chandra, M.A. Experimental and numerical analysis of metal removal rate and surface finish on orvar supreme. In Proceedings of the 38th IRF International Conference, Chennai, India, 20 March 2016. [Google Scholar]
- Almacinha, J.A.; Lopes, A.M.; Rosa, P.; Marafona, J.D. How Hydrogen Dielectric Strength Forces the Work Voltage in the Electric Discharge Machining. Micromachines 2018, 9, 240. [Google Scholar] [CrossRef] [PubMed]
- Razeghiyadaki, A.; Molardi, C.; Talamona, D.; Perveen, A. Modeling of Material Removal Rate and Surface Roughness Generated during Electro-Discharge Machining. Machines 2019, 7, 47. [Google Scholar] [CrossRef]
- Yildiz, Y. Prediction of White Layer Thickness and Material Removal Rate in Electrical Discharge Machining by Thermal Analyses. J. Manuf. Process. 2016, 23, 47–53. [Google Scholar] [CrossRef]
- Kurnia, W.; Tan, P.C.; Yeo, S.H.; Tan, Q.P. Surface Roughness Model for Micro Electrical Discharge Machining. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2009, 223, 279–287. [Google Scholar] [CrossRef]
- Jithin, S.; Raut, A.; Bhandarkar, U.V.; Joshi, S.S. Finite Element Model for Topography Prediction of Electrical Discharge Textured Surfaces Considering Multi-Discharge Phenomenon. Int. J. Mech. Sci. 2020, 177, 105604. [Google Scholar] [CrossRef]
- Abed, F.N.; Ramesh, V.; Fadhil Jwaid, M.; Agarwal, N.; Koundal, D.; Mohamed Ibrahim, A. Enhancement Modelling Based on Electrical Discharge Machining Successive Discharges. Adv. Mater. Sci. Eng. 2022, 2022, e8017375. [Google Scholar] [CrossRef]
- Jamunkar, T.; Sundaram, M. Prediction of Surface Roughness on Electrical Discharge Machined Surfaces. Manuf. Lett. 2022, 33, 143–152. [Google Scholar] [CrossRef]
- Jithin, S.; Bhandarkar, U.V.; Joshi, S.S. Multi-Spark Model for Predicting Surface Roughness of Electrical Discharge Textured Surfaces. Int. J. Adv. Manuf. Technol. 2020, 106, 3741–3758. [Google Scholar] [CrossRef]
- Puertas, I.; Luis, C.J.; Álvarez, L. Analysis of the Influence of EDM Parameters on Surface Quality, MRR and EW of WC–Co. J. Mater. Process. Technol. 2004, 153–154, 1026–1032. [Google Scholar] [CrossRef]
- Kim, D.; Chen, X.; Allen, P. Micro-Electro Discharge Drilling Characteristics on Molybdenum Aperture Fabrication. Int. J. Mach. Mach. Mater. 2010, 7, 161–175. [Google Scholar] [CrossRef]
- Barenji, R.V.; Pourasl, H.H.; Khojastehnezhad, V.M. Electrical Discharge Machining of the AISI D6 Tool Steel: Prediction and Modeling of the Material Removal Rate and Tool Wear Ratio. Precis. Eng. 2016, 45, 435–444. [Google Scholar] [CrossRef]
- Bellotti, M.; Wu, M.; Qian, J.; Reynaerts, D. Tool Wear and Material Removal Predictions in Micro-EDM Drilling: Advantages of Data-Driven Approaches. Appl. Sci. 2020, 10, 6357. [Google Scholar] [CrossRef]
- Ramasawmy, H.; Blunt, L.; Rajurkar, K.P. Investigation of the Relationship between the White Layer Thickness and 3D Surface Texture Parameters in the Die Sinking EDM Process. Precis. Eng. 2005, 29, 479–490. [Google Scholar] [CrossRef]
- Tan, P.C.; Yeo, S.H. Modeling of Recast Layer in Micro-Electrical Discharge Machining. J. Manuf. Sci. Eng. 2010, 132, 031001. [Google Scholar] [CrossRef]
- Shabgard, M.; Oliaei, S.N.B.; Seyedzavvar, M.; Najadebrahimi, A. Experimental Investigation and 3D Finite Element Prediction of the White Layer Thickness, Heat Affected Zone, and Surface Roughness in EDM Process. J. Mech. Sci. Technol. 2011, 25, 3173–3183. [Google Scholar] [CrossRef]
- Yadav, K.; Pradhan, S.K. Analysis of Recast Layer Thickness and Martensitic Layer Thickness in Wire Electrical Discharge Machining. Mater. Today Proc. 2021, 46, 10799–10805. [Google Scholar] [CrossRef]
- Rajurkar, K.P.; Pandit, S.M. Quantitative Expressions for Some Aspects of Surface Integrity of Electro Discharge Machined Components. J. Eng. Ind. 1984, 106, 171–177. [Google Scholar] [CrossRef]
- Cao, M.R.; Yang, S.Q.; Li, W.H.; Yang, S.C. Chip-Ejection Mechanism and Experimental Study of Water Dispersant Dielectric Fluid on Small-Hole EDM. Adv. Mater. Res. 2010, 97–101, 4111–4115. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.; Ming, W.; Zhang, Y.; Cao, C.; Zhang, G. A Review on Magnetic Field Assisted Electrical Discharge Machining. J. Manuf. Process. 2021, 64, 694–722. [Google Scholar] [CrossRef]
- Zhang, Z.; Wei, S.; Wang, P.; Qiu, W.; Zhang, G. Progress in Applications of Laser Induced Cavitation on Surface Processing. Opt. Laser Technol. 2024, 170, 110212. [Google Scholar] [CrossRef]
- Ming, W.; Jia, H.; Zhang, H.; Zhang, Z.; Liu, K.; Du, J.; Shen, F.; Zhang, G. A Comprehensive Review of Electric Discharge Machining of Advanced Ceramics. Ceram. Int. 2020, 46, 21813–21838. [Google Scholar] [CrossRef]
- Jatti, V.S.; Khedkar, N.K.; Jatti, A.V.; Jatti, V.S. Finite Element Simulation of Electric Discharge Machining Process during Machining of NiTi, NiCu and BeCu Alloys. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Shen, D.; Ming, W.; Ren, X.; Xie, Z.; Liu, X. Progress in Non-Traditional Processing for Fabricating Superhydrophobic Surfaces. Micromachines 2021, 12, 1003. [Google Scholar] [CrossRef]
- Bonny, K.; De Baets, P.; Vleugels, J.; Salehi, A.; Van der Biest, O.; Lauwers, B.; Liu, W. Influence of Secondary Electro-Conductive Phases on the Electrical Discharge Machinability and Frictional Behavior of ZrO2-Based Ceramic Composites. J. Mater. Process. Technol. 2008, 208, 423–430. [Google Scholar] [CrossRef]
- Clijsters, S.; Liu, K.; Reynaerts, D.; Lauwers, B. EDM Technology and Strategy Development for the Manufacturing of Complex Parts in SiSiC. J. Mater. Process. Technol. 2010, 210, 631–641. [Google Scholar] [CrossRef]
- Gupta, A.; Joshi, S.S. Modelling Effect of Magnetic Field on Material Removal in Dry Electrical Discharge Machining. Plasma Sci. Technol. 2017, 19, 025505. [Google Scholar] [CrossRef]
- Beravala, H.; Pandey, P.M. Modelling of Material Removal Rate in the Magnetic Field and Air-Assisted Electrical Discharge Machining. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 1286–1297. [Google Scholar] [CrossRef]
- Shabgard, M.R.; Sadizadeh, B.; Amini, K.; Pourziaie, H. Comparative Study and Mathematical Modeling of Machining Parameters in Ultrasonic-Assisted EDM of AISI H13 Tool Steel by the Application of Workpiece Vibration. Adv. Mater. Res. 2011, 154–155, 1604–1613. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, H.; Ming, W.; Xu, Z.; Huang, Y.; Zhang, G. Study on Machining Characteristics of WEDM with Ultrasonic Vibration and Magnetic Field Assisted Techniques. J. Mater. Process. Technol. 2016, 234, 342–352. [Google Scholar] [CrossRef]
- Praneetpongrung, C.; Fukuzawa, Y.; Nagasawa, S.; Yamashita, K. Effects of the Edm Combined Ultrasonic Vibration on the Machining Properties of Si3N4. Mater. Trans. 2010, 51, 2113–2120. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Lee, H.-S. Machining Characteristics of Magnetic Force-Assisted EDM. Int. J. Mach. Tools Manuf. 2008, 48, 1179–1186. [Google Scholar] [CrossRef]
- Ming, W.; Shen, F.; Zhang, G.; Liu, G.; Du, J.; Chen, Z. Green Machining: A Framework for Optimization of Cutting Parameters to Minimize Energy Consumption and Exhaust Emissions during Electrical Discharge Machining of Al 6061 and SKD 11. J. Clean. Prod. 2021, 285, 124889. [Google Scholar] [CrossRef]
- Ma, J.; Yin, C.; Li, X.; Han, X.; Ming, W.; Chen, S.; Cao, Y.; Liu, K. Optimization of EDM Process Parameters Based on Variable-Fidelity Surrogate Model. Int. J. Adv. Manuf. Technol. 2022, 122, 2031–2041. [Google Scholar] [CrossRef]
- Ming, W.; Xie, Z.; Cao, C.; Liu, M.; Zhang, F.; Yang, Y.; Zhang, S.; Sun, P.; Guo, X. Research on EDM Performance of Renewable Dielectrics under Different Electrodes for Machining SKD11. Crystals 2022, 12, 291. [Google Scholar] [CrossRef]
- Ming, W.; Shen, F.; Zhang, Z.; Huang, H.; Du, J.; Wu, J. A Comparative Investigation on Magnetic Field–Assisted EDM of Magnetic and Non-Magnetic Materials. Int. J. Adv. Manuf. Technol. 2020, 109, 1103–1116. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.; Shi, J.; Dong, Y.; Yang, S.; Zhang, X.; Lin, B. Analysis of Material Removal and Surface Generation Mechanism of Ultrasonic Vibration–Assisted EDM. Int. J. Adv. Manuf. Technol. 2020, 110, 177–189. [Google Scholar] [CrossRef]
- Pupaza, C.; Ghiculescu, D.; Opran, C.G. A Model Regarding Material Removal Using FEM at Ultrasonic Aided EDM of Metal Matrix Composites. Appl. Mech. Mater. 2015, 760, 557–562. [Google Scholar] [CrossRef]
- Tang, L.; Ji, Y.; Ren, L.; Zhai, K.G.; Huang, T.Q.; Fan, Q.M.; Zhang, J.J.; Liu, J. Thermo-Electrical Coupling Simulation of Powder Mixed EDM SiC/Al Functionally Graded Materials. Int. J. Adv. Manuf. Technol. 2019, 105, 2615–2628. [Google Scholar] [CrossRef]
- Du, J.; Tian, B.; Duan, L.; Ming, W.; Liu, K.; He, W. Traditional and Non-Traditional Machining Technology of Metallic Glass. Int. J. Adv. Manuf. Technol. 2022, 120, 2879–2902. [Google Scholar] [CrossRef]
- Chen, Y.; Guo, X.; Zhang, G.; Cao, Y.; Shen, D.; Li, X.; Zhang, S.; Ming, W. Development of a Hybrid Intelligent Process Model for Micro-Electro Discharge Machining Using the TTM-MDS and Gaussian Process Regression. Micromachines 2022, 13, 845. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Zhang, Y.; Lin, L.; Wu, J.; Yu, H.; Pan, X.; Li, G.; Wu, J.; Xue, T. Study on Productivity and Aerosol Emissions of Magnetic Field-Assisted EDM Process of SiCp/Al Composite with High Volume Fractions. J. Clean. Prod. 2021, 292, 126018. [Google Scholar] [CrossRef]
- Namboodiri, V.N.J.; Pazhamannil, R.V.; Govindan, P. Finite Element Based Numerical Modelling of Near-Dry EDM with Glycerin-Air Dielectric Mixture. IOP Conf. Ser. Mater. Sci. Eng. 2022, 1248, 012019. [Google Scholar] [CrossRef]
- Nadda, R.; Nirala, C.K. Thermal Modeling of Single Discharge in Prospect of Tool Wear Compensation in μEDM. Int. J. Adv. Manuf. Technol. 2020, 107, 4573–4595. [Google Scholar] [CrossRef]
- Allen, P.; Chen, X. Process Simulation of Micro Electro-Discharge Machining on Molybdenum. J. Mater. Process. Technol. 2007, 186, 346–355. [Google Scholar] [CrossRef]
- Shabgard, M.R.; Gholipoor, A.; Mohammadpourfard, M. Numerical and Experimental Study of the Effects of Ultrasonic Vibrations of Tool on Machining Characteristics of EDM Process. Int. J. Adv. Manuf. Technol. 2018, 96, 2657–2669. [Google Scholar] [CrossRef]
- Tan, P.C.; Yeo, S.H. Simulation of Surface Integrity for Nanopowder-Mixed Dielectric in Micro Electrical Discharge Machining. Met. Mater. Trans. B 2013, 44, 711–721. [Google Scholar] [CrossRef]
- Liu, J.F.; Guo, Y.B. Modeling of White Layer Formation in Electric Discharge Machining (EDM) by Incorporating Massive Random Discharge Characteristics. Procedia CIRP 2016, 42, 697–702. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, S.; Zhang, Z.; Huang, H.; Li, W.; Zhang, G.; Huang, Y. Simulation and Experimental Investigations of Complex Thermal Deformation Behavior of Wire Electrical Discharge Machining of the Thin-Walled Component of Inconel 718. J. Mater. Process. Technol. 2019, 270, 306–322. [Google Scholar] [CrossRef]
- Chen, X.; Wu, Y.; He, X.; Ming, W. A Comprehensive Review of Deep Learning-Based PCB Defect Detection. IEEE Access 2023, 11, 139017–139038. [Google Scholar] [CrossRef]



| Heat Source type | Purposes | Authors, Year | Findings | Remarks |
|---|---|---|---|---|
| Non-Gaussian heat source | MRR | Tariq Jilan and Pandey [35], 1982 | As the diameter of the heat source increased, the pulse power density decreased and the MRR decreased. | The removal of metal in EDM is due not only to melting but also to evaporation, thus greatly reducing the amount of heat available for conduction. |
| Tariq Jilan and Pandey [36], 1982 | From the point of view of relative electrode wear, the optimum pulse shape for pulse durations of 50 and 100 µs was an initial current of about 50% of its value at the end of the pulse duration. | The effects of evaporation and re-solidification can be incorporated into the EDM model. | ||
| Dibitonto et al. [37], 1989 | In the confirmed experiments, the predicted Rmax matched the experimental values at low discharge energies (<100 mJ), while the predicted MRR, at high discharge energies (≥100 mJ), was close to the experimental values. | Finite element modeling at high discharge energies should be further investigated. | ||
| Salonitis et al. [39], 2009 | The average deviation between the experimental average MRR and the theoretical predictions of the model was about 8.2%. | These deviations are due to neglecting the formation of the recast layer and assuming that the idling time is insignificant compared to the discharge time. | ||
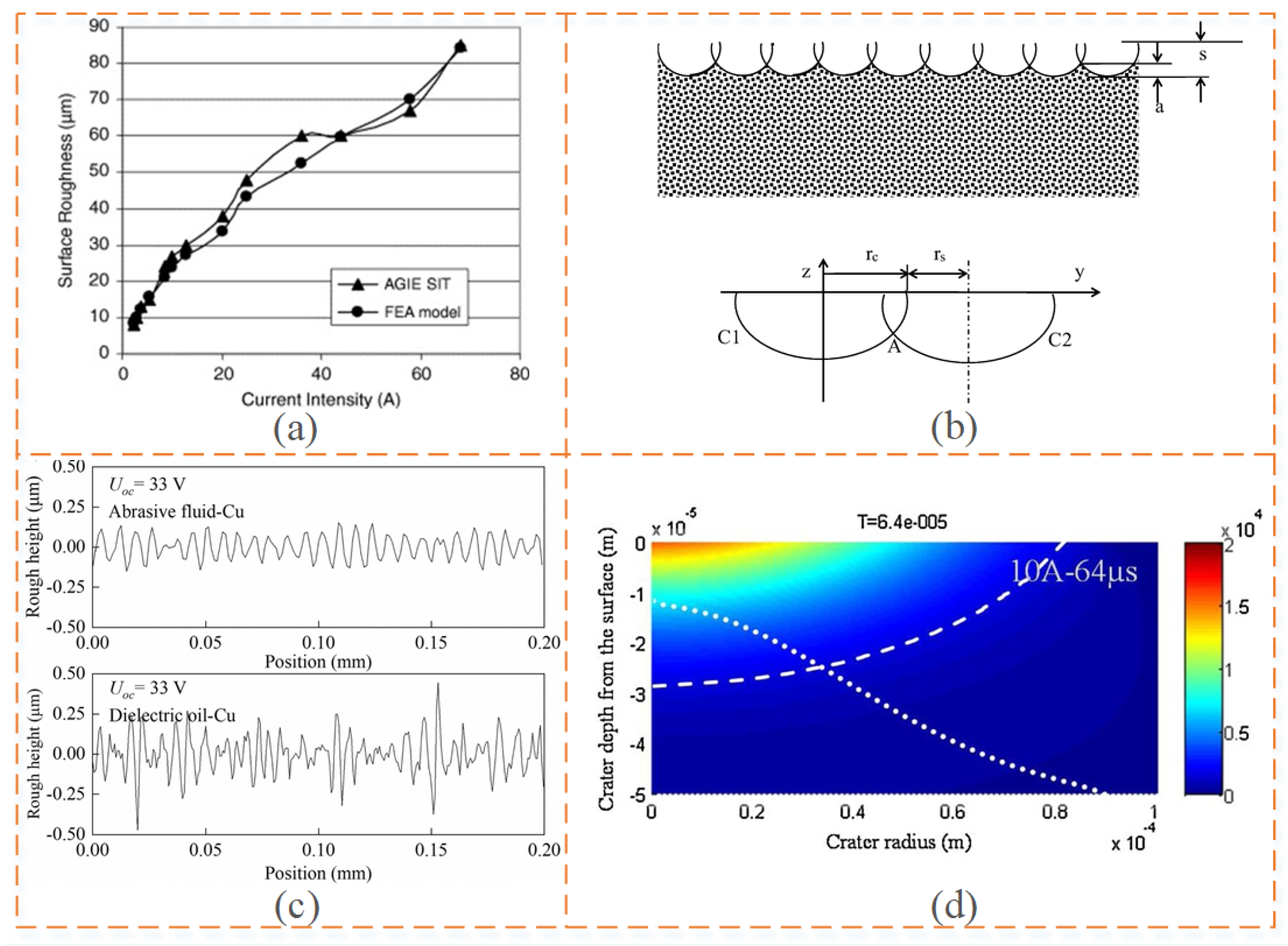
| Ra | Marafona et al. [49], 2006 | The predicted SR agrees well with the experimental results. | Two-dimensional axisymmetric finite elements have simpler formulations than three-dimensional finite elements. | |
| Salonitis et al. [39], 2009 | The average deviation between the experimental average SR and the theoretical prediction of the model was about 6.1%. | The error may arise because the formation of the recast layer is enhanced when dealing with larger peak currents. | ||
| RLT | Pandey and Jilani. [60], 1986 | The heat source model can calculate the thickness of the heat-affected zone caused by a single spark more accurately, and there was a good correlation between the predicted and experimental values. | This heat source model can more accurately calculate the thickness of the heat-affected zone caused by single sparks. | |
| Shabgard et al. [61], 2019 | The maximum error between the RLT obtained by the numerical and experimental methods was 8.8%. | The application of an external magnetic field during EDM has a positive effect on increasing the PFE and reducing the RLT. | ||
| Gaussian heat source | MRR | Eubank et al. [40], 1993 | An anode model, a cathode model, and a cylindrical plasma model were developed using a Gaussian heat source. | Gaussian heat sources can more accurately simulate the heat distribution during machining than disc heat sources. |
| Joshi et al. [14], 2009 | The optimal network architecture 4–8–12–4 has a prediction error of 1.53% for the MRR. | The ANN-based process model can be used to select optimum process conditions to improve EDM’s process productivity and finishing capability. | ||
| Joshi and Pande [41], 2010 | The results show that the trends of the simulation analysis are consistent with the experimental results. | This thermophysical model can be used to perform a wide range of parametric studies. | ||
| Singh, H. [25], 2012 | For different machining parameters the results of the MRR match very well. | It is possible to study the effect of different material properties and machining parameters on the proportion of energy transferred to the workpiece. | ||
| Wang et al. [46], 2012 | The temperature distribution at the cathode discharge point during a single discharge in the EDM process was predicted. | The mechanism of material removal during EDM is better explained. | ||
| Ming et al. [42], 2014 | The validation experiments show that the mean error of the MRR is 14.75%. | Through the GPR model, it is found that the responses of the EDM process can be accurately predicted for the chosen process conditions. | ||
| Kuriachen et al. [47], 2015 | The model calculations were in good agreement with the experimental results. | Combining different spark radii with the effects of capacitance and voltage, plasma pressure, and the enthalpy of the material results in a better simulation model. | ||
| Singh et al. [45], 2020 | The prediction errors for the diameter and depth of the discharge crater were 12% and 13%, respectively. | Material removal is mainly evaporation and melt discharge caused by recoil pressure, which determines the size of the discharge crater. | ||
| Ra | Ming et al. [42], 2014 | The mean error of Ra was 20.74%. | This model can be used to select optimal process conditions to improve EDM performance. | |
| Philip et al. [54], 2020 | The model employed a Gaussian heat source, and the observed minimum-to-maximum error between the predicted Ra and the actual roughness Ra values ranges from about 8 to 25%. | The formation of radially enlarged craters is the main cause of highly rough surfaces. | ||
| George et al. [55], 2020 | The average absolute error of the forecast was 10.05%. | This study allows for the online monitoring of the surface quality of difficult-to-machine materials. | ||
| Ming et al. [13], 2022 | The predicted Rmax error was found to be lower at low discharge energies (<100 mJ) and higher at high discharge energies (≥100 mJ). | The accuracy of the predictions needs to be further improved, especially for EDM processes. | ||
| Li et al. [56], 2022 | The error in the prediction of the SR was 8.26% for the continuous discharge material removal model of wire-cutting EDM. | This study contributes to a better understanding of the principles of the wire-cutting process and the formation of single-spark discharge craters. | ||
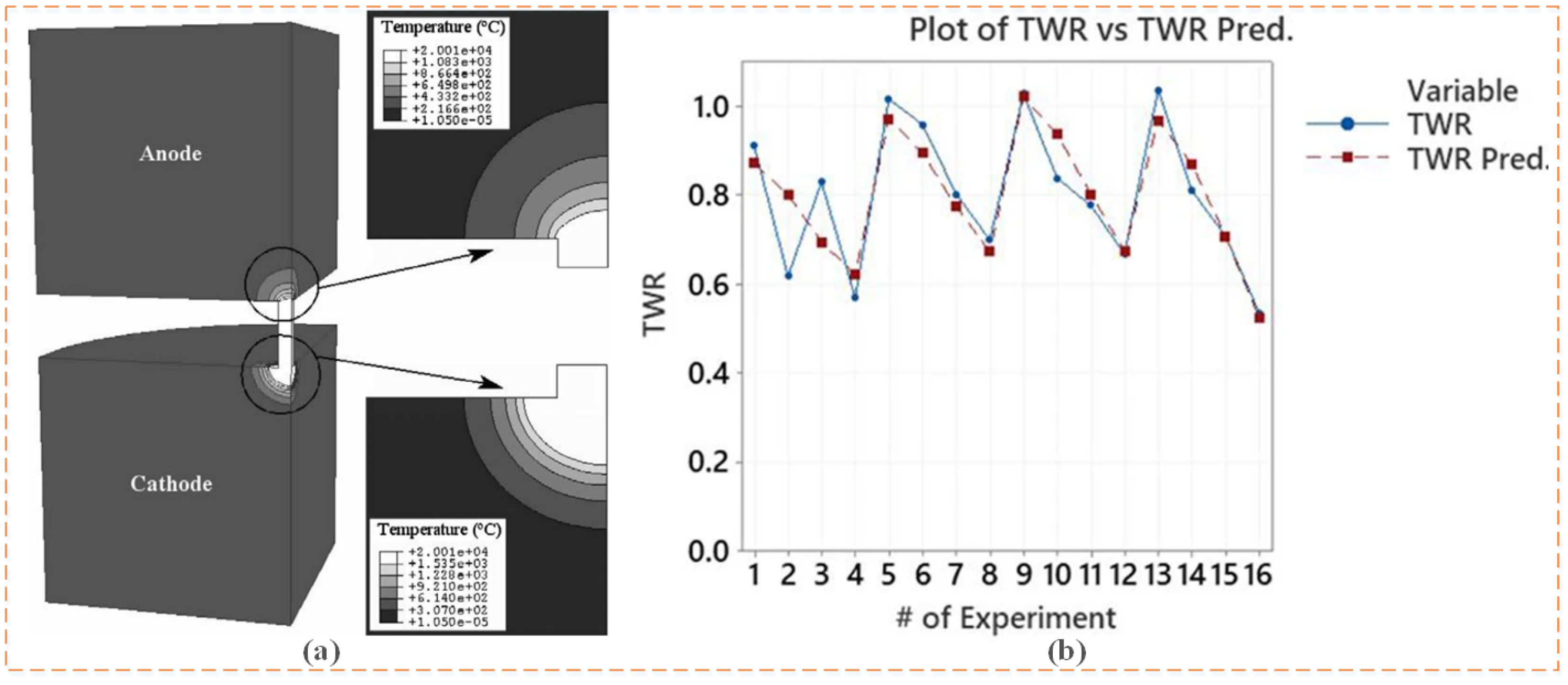
| TWR | Marafona et al. [49], 2006 | The TWR results are fairly consistent with the values the researchers found for the AGIE SIT table itself. | Two-dimensional axisymmetric finite elements have simpler formulations than three-dimensional finite elements and can reduce CPU time with very similar results. | |
| Joshi and Pande [14], 2009 | The prediction accuracy of this model artificial neural network’s optimal network architecture, 4–8–12–4, for the TWR was 17.34%. | Artificial neural network-based process modeling can be used to select optimal process conditions to improve the productivity and finishing capabilities of EDM machining. | ||
| Joudivand Sarand et al. [57], 2017 | The average error in predicting tool wear was 4.83%. | This study considers the direct and interactive effects of thermal, electrical, and physical variables on the EDM process, with accurate predictions. | ||
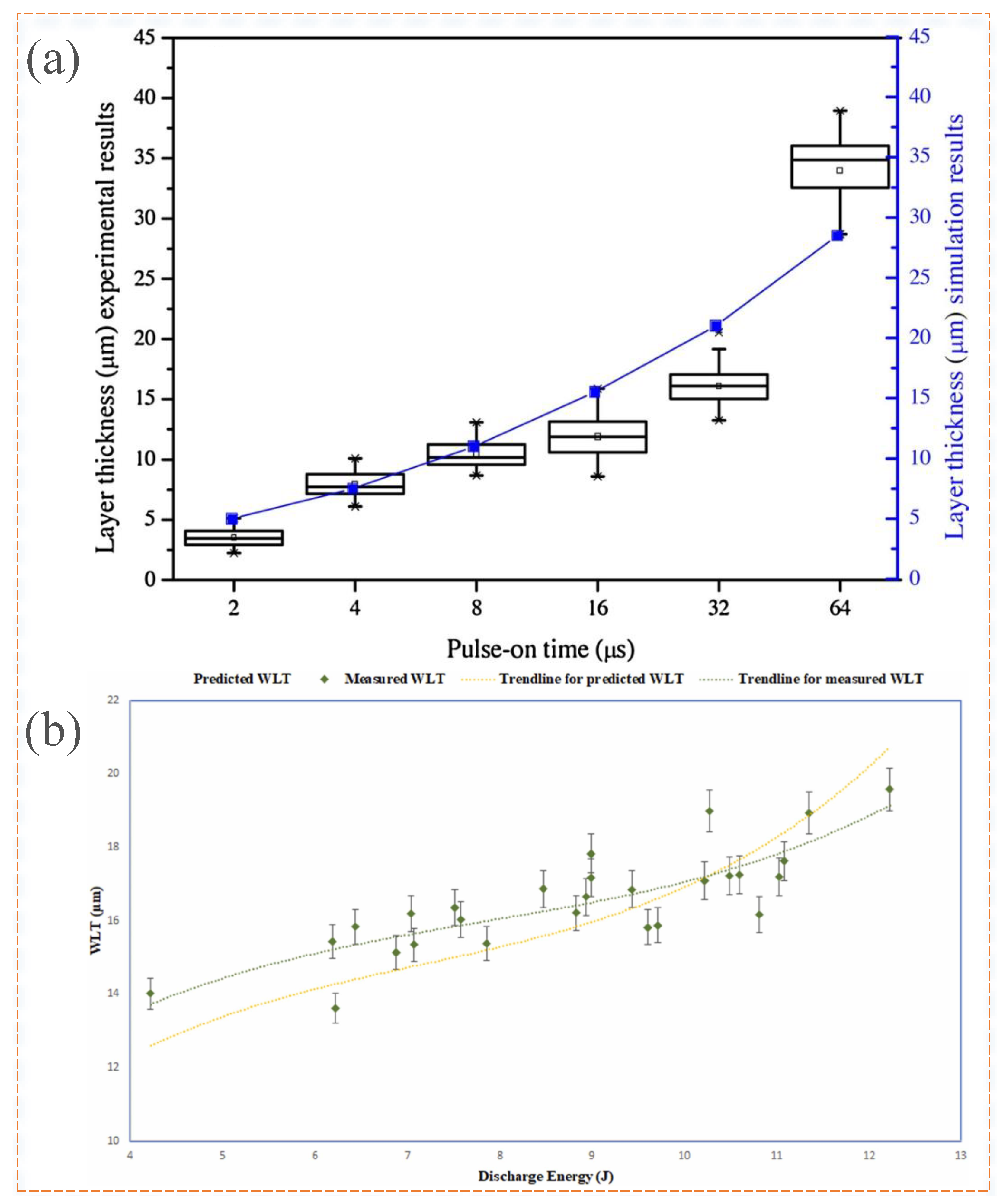
| Papazoglou et al. [58], 2021 | The TWR was mainly dependent on the pulse-on time, and an increase in pulse duration led to a decrease in that ratio. | Optimal processing schedules can be achieved on a case-by-case basis using recommended MRR, TWR, and average white layer thickness correlations. | ||
| RLT | Joudivand Sarand et al. [57], 2017 | The average error in the estimation of the RLT was 3.96%. | Pulse current, pulse on-time, and the thermal diffusion coefficient have a significant effect on the thickness of the recast layer. | |
| Zhang et al. [63], 2019 | Upon comparison with the experimental results, the relative error of the RLT was found to be less than 20%. | Controlling wire vibration helps improve EDM’s wire-cutting performance. | ||
| Gholipoo-r et al. [64], 2020 | The increase in pulse duration decreased the PFE and increased the thickness of the recast layer. | Above a certain value of pulse current, the increase in the PFE is counterbalanced by the depth of thermal penetration and the volume of molten material, and the RLT decreases. | ||
| George et al. [62], 2022 | The model predicted the RLT better, with an average absolute error of 5.12%. | The RLT tends to increase with increasing discharge energy. |
| Purposes | Authors, Year | Findings | Remarks |
|---|---|---|---|
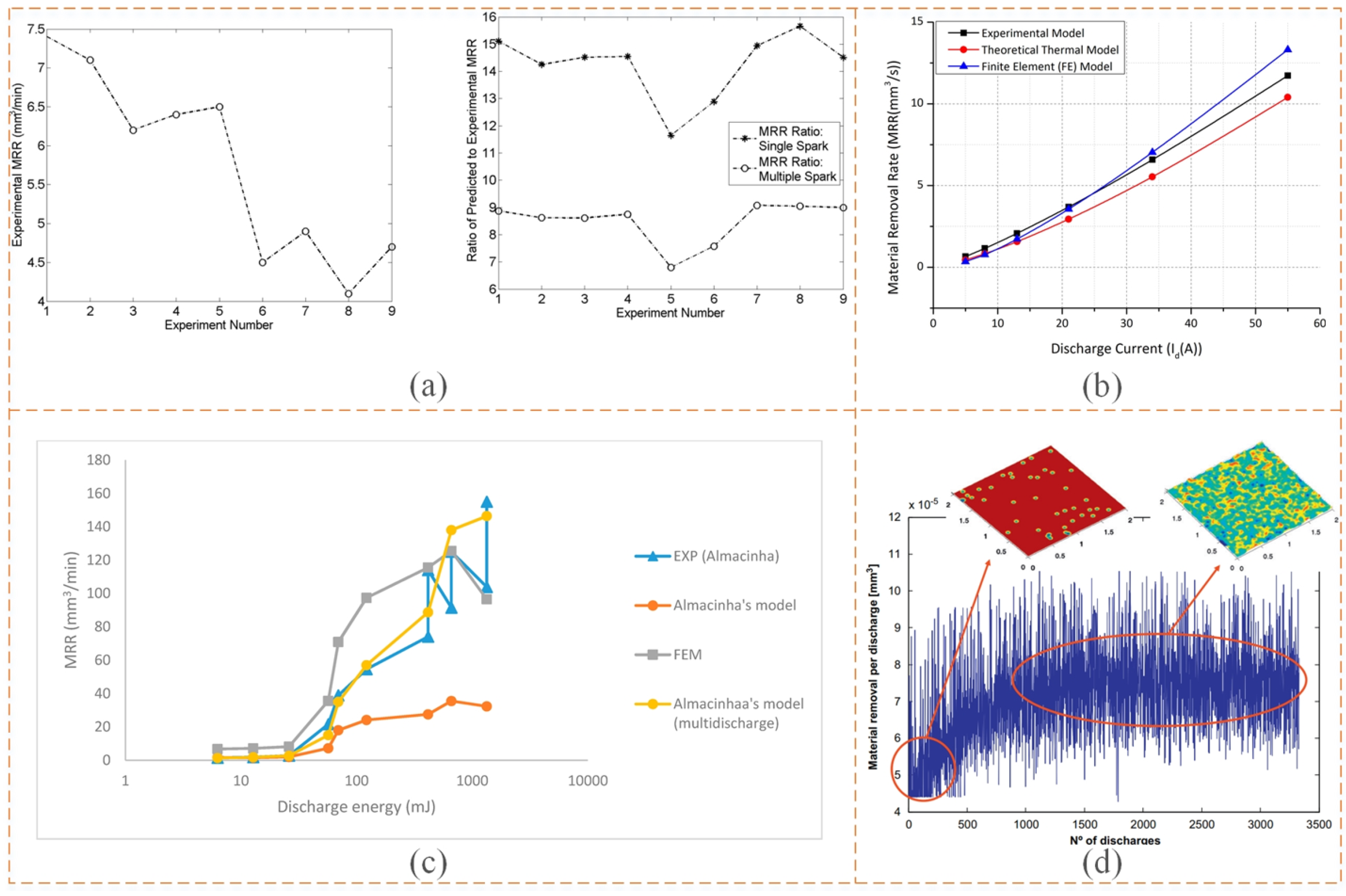
| MRR | Izquierdo et al. [69], 2009 | The finite difference method was used and the MRR prediction error was less than 3%. | The inverse discrimination method can be used to estimate the discharge characteristics for a particular operation. |
| Yakup Yildiz [74], 2016 | The average error in predicting the MRR using the FEM was 3.34%. | The effect of additional parameters on the measurement of the properties of different types of materials can be studied in the same way. | |
| Shahane and Pande [65], 2016 | The results predicted by the multi-spark model were closer to the experimental values by about 50%. | The multi-spark model can be further used for extensive parametric studies, which can be used to predict the MRR by varying the input process parameters. | |
| H.SAIKIRAN et al. [71], 2016 | An axisymmetric model was used for the MRR modeling of the Orvar Supreme H-13 EDM process, and the MRR was calculated by counting the number of pulses in multi-discharge machining. The experimental results were in good agreement with the analytical results. | This model can be used to obtain the residual stress distribution, and to enhance the thermal stress distribution of the particle rupture phenomenon. | |
| Razeghiyadaki et al. [73], 2019 | Compared to the standard finite element model, the finite element model considering transient evaporation showed a 1.5% better agreement with the experimental values. | Consideration can be given to the study of EDM in non-conductive ceramic materials. | |
| Ra | Kurnia et al. [75], 2009 | The theoretical results produced by the model had an average error of 6.5% in Ra when compared to the respective experimental results. | This surface roughness prediction model can be applied to other workpiece materials. |
| Izquierdo et al. [69], 2009 | A numerical model of the EDM process considering the effect of multiple discharges was developed with an SR prediction error of less than 6%. | It is possible to generate surfaces comparable to those obtained by the actual EDM process and, after adjusting the model parameters, the predicted results are in good agreement with the measured results. | |
| Jithin et al. [76], 2020 | The results show that the predicted values are in good agreement with the measured values and the prediction error is between 6~17.5%. | This model takes into account the expansion of the discharge column at the critical time and the dependence of the spark radius on the discharge power and discharge duration. | |
| Jithin et al. [79], 2020 | A multi-spark discharge model was developed to reduce the average prediction error of Ra to 11.5%. | In each simulation of the multi-spark model, the position, size, and shape of the individual peaks and valleys of the sparks vary due to their random distribution. | |
| Jamunkar and Sundaram [78], 2022 | The model gives a normal distribution of SR values for any given EDM process parameter. The maximum deviation between the predicted and measured values is 0.76 µm. | Finite element analysis and online EDM monitoring techniques were used to create a simulated EDM surface. | |
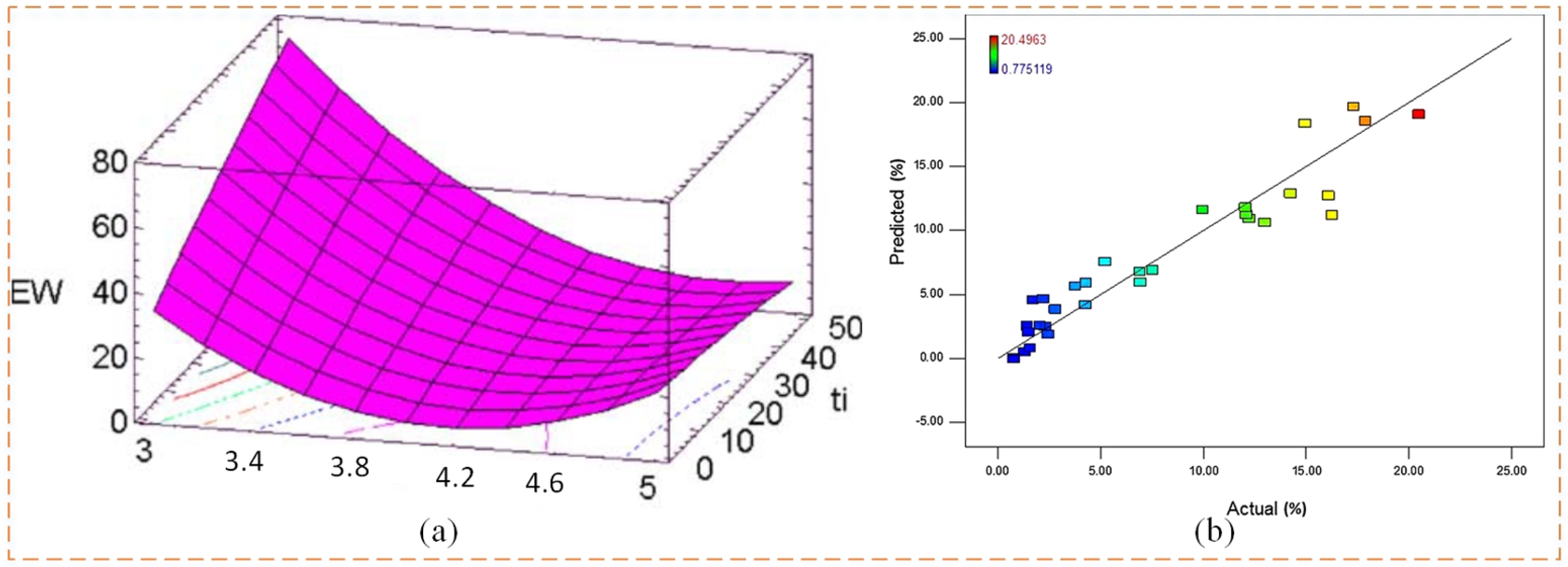
| TWR | Puertas et al. [80], 2004 | To be able to obtain low electrode wear values, an intensity factor value close to the electrode’s center value (i.e., I = 4), or slightly higher, should be used, along with a low pulse duration value, for the operating interval under consideration. | The relationship between the TWR, SR, MRR, and design factors was investigated. |
| Kim et al. [81], 2010 | The relative TWR increased significantly when the pulse duration was greater than 2 µs, and the combination of large voltages and large pulse durations produced significant tool wear. | Tool wear is the main cause of chip formation. | |
| Reza Vatankhah Barenji et al. [82], 2016 | The TWR was minimized when the pulse-on time, pulse current, and input voltage were 40 µs, 14 A, and 150 V, respectively. | Increasing the pulse current increases the TWR. The higher the input voltage, the lower the TWR. | |
| Bellotti et al. [83], 2020 | By using process monitoring data as inputs to the regression model, the errors in predicting the TWR were reduced by approximately 85%. | Expanding the dataset with higher aspect ratio holes could be considered in the future to investigate the applicability of data-driven regression modeling to a wider range of industrial applications of the MEMS process. | |
| RLT | Tan and Yeo [85], 2010 | The model has a peak discharge current of 1.45 A, a pulse on-time of 166 ns to 606 ns, and a predicted thickness of the recast layer ranging between 1.0 µm and 1.82 µm. | The model developed using the multiple discharge method is suitable for the estimation of the RLT in microfabricated EDM. |
| Shabgard et al. [86], 2011 | An axisymmetric 3D finite element model was developed and the average deviation between its predicted and actual values was 9.65%. | The increase in pulse current resulted in a slight decrease in the thickness of the recast layer and the depth of the heat-affected zone, but with a rougher surface. | |
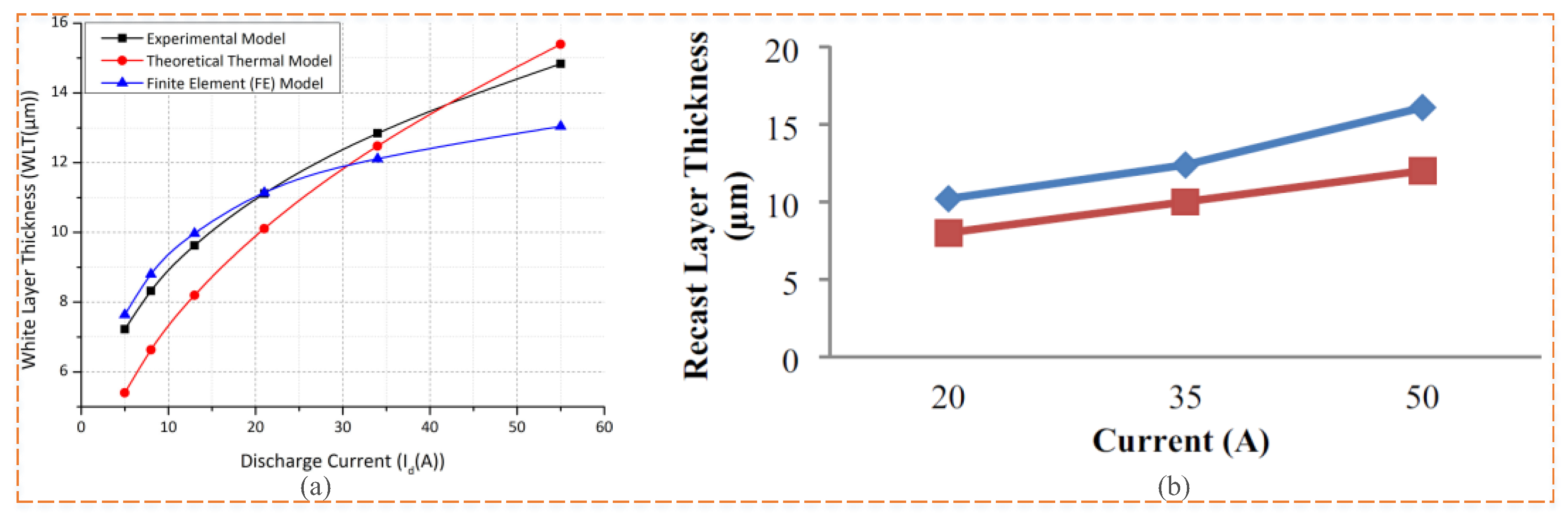
| Yakup Yildiz [74], 2016 | The average error in predicting the thickness of the recast layer via the FEM was 1.98%. | This study conveniently relates the discharge current to white layer thickness and the MRR in EDM machining. | |
| Yadav and Pradhan [87], 2021 | Numerical simulations predicted a value of 10.2 µm for the thickness of the recast layer, which is in good agreement with previous experimental results. | This method can be used for the RLT prediction for different materials and boundary conditions. |
| Purposes | Authors, Year | Findings | Remarks |
|---|---|---|---|
| MRR | H.K. Kansal et al. [44], 2008 | In theory and experiment, the MRR values obtained by PMEDM were always higher than those of conventional EDM. | This model can be used to predict the evolution of temperatures, stresses, strains, and cracks that may occur on the surface of a PMEDM-machined workpiece. |
| Shabgard et al. [99], 2011 | The application of ultrasonic vibration to the workpiece had a significant effect on the MRR of the finishing method, increasing it three-fold. | The ultrasonic vibration of the workpiece changes the pressure in the gap, resulting in better flushing and improved machining stability. | |
| Zhang et al. [100], 2016 | The hybrid technology of USV-MF-assisted EDM wire-cutting still offers significant advantages in balancing machining efficiency and surface quality. | The hybrid EDM-WEDM process has enormous advantages and application potential in the field of practical machining and manufacturing. | |
| Gupta and Joshi [97], | At moderate energy levels, the error in the predicted value of the mean diameter of the single-spark discharge crater was 10%, while the error in the mean depth was 9%. | This model neglects the effect of the self-magnetic field. | |
| Beravala and Pandey [98], 2020 | The model developed predicts an MRR error of less than 10%. | The prediction error of this model is mainly caused by the assumed conditions and uncontrollable experimental errors. | |
| Ra | Ming et al. [31], 2009 | Simulation and experimental studies showed that the machining performance of MF-EDM was significantly better than that of EDM, especially in terms of surface integrity and discharge stability. | MF-EDM offers greater potential and advantages than conventional methods in improving machinability and surface quality. |
| Ming et al. [106], 2020 | When machining the SKD11 material, the SR increased when the servo voltage was increased excessively. However, when machining the Ti6Al4V material, when the servo voltage was 71V, the SR was satisfactory. | The energy efficiency of magnetic materials was significantly improved compared to that of non-magnetic materials. | |
| Ghiculescu et al. [28], 2009 | Cumulative micro-jet flow almost eliminated the material melted by discharge, resulting in a 500% increase in the machining rate. SR was improved by up to 50%. | Future research will focus on synchronizing EDM and US generators and improving the flexibility of EDM+US technology. | |
| Pupaza et al. [108], 2015 | A lower SR can be obtained by using lower values of pulse time and longer values of pause time. | Low pulse time values and high pause time values can be used to increase the machining rate. | |
| Wang et al. [107], 2020 | Ultrasonic vibration caused more adjacent melting pits to overlap, resulting in a smaller area of carbon buildup and a smoother surface, and the introduction of ultrasound reduced the SR by 15.8–29.1%. | Crater depth and surface residual height decrease with increasing ultrasonic amplitude. | |
| Tang et al. [109], 2019 | Compared with conventional EDM, PMEDM’s machining efficiency increased by 16.34% and SR decreased by 29.42%. | This research provides a new way to improve efficiency in high-performance material processing and related fields. | |
| TWR | Ming et al. [31], 2009 | Used to calculate the energy flow and temperature distribution of the workpiece, tool electrode, and discharge channel under single/continuous-spark conditions with good predictions. | The application of magnetic field-assisted technology in EDM also reduces the negative impact on the health of the operator. |
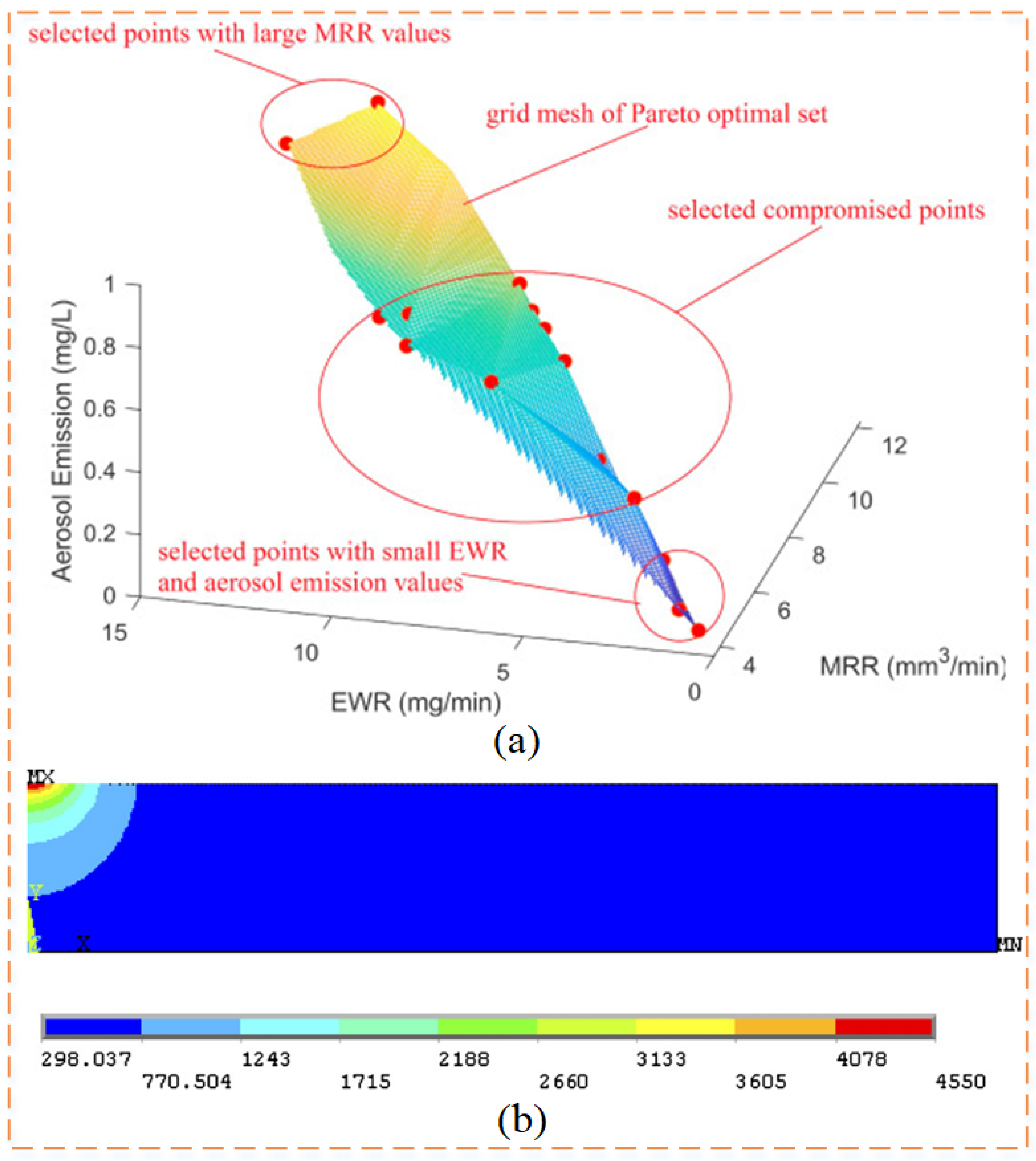
| Zhang et al. [112], 2021 | For 65% SiCp/Al, the average best solution for EWR and aerosol emissions was reduced by about 5.7% and 10%, respectively, while MRR increased by 5.5%. | MF-EDM outperforms conventional EDM in terms of energy efficiency and environmental impact. | |
| Joudivand Sarand et al. [57], 2017 | Parameters such as the heat diffusion coefficient of the tool electrode, the pulse current, and the pulse duration had a significant effect on the degree of tool wear. | The strong dependence of this model improvement factor on the thermo-physical variables of the EDM process dramatically alters the numerical methods for accurately predicting the amount of tool wear. | |
| Nadda and Nirala [114], 2020 | A finite element simulation of the Gaussian heat flow density distribution of a single discharge micro-EDM was performed, and a thermal modeling-based tool wear compensation technique was proposed. | This research can be used to establish a real-time tool wear monitoring and compensation system based on thermal modeling. | |
| Allen and Chen [115], 2007 | The model estimated that the TWR decreased with increased pulse duration and was much higher for molybdenum than for steel under the same machining conditions. | Tensile residual stresses remaining on the workpiece may superimpose after several spark cycles, leading to surface damage such as microcracks. | |
| RLT | Shabgard et al. [116], 2018 | At all pulse currents and durations, ultrasonic vibration reduces the thickness of the recast layers produced on machined surfaces. | This study simulates the US-EDM process from an electrothermal perspective. |
| Shabgard et al. [61], 2019 | The numerical results of the RLT were in good agreement with the experimental results, with a maximum error of 8.8%. | Applying a magnetic field near the EDM gap increases the PFE while reducing the height of the RLT generated in all pulse currents and pulse-on time. | |
| Tan and Yeo [117], 2013 | To validate the model, the simulated R max and RLT values were compared with their corresponding measured values. The trends of the simulated and measured results are approximately the same. | The process model takes into account the effect of powder particles on the plasma channel size and the proportion of heat flux distributed to the workpiece. | |
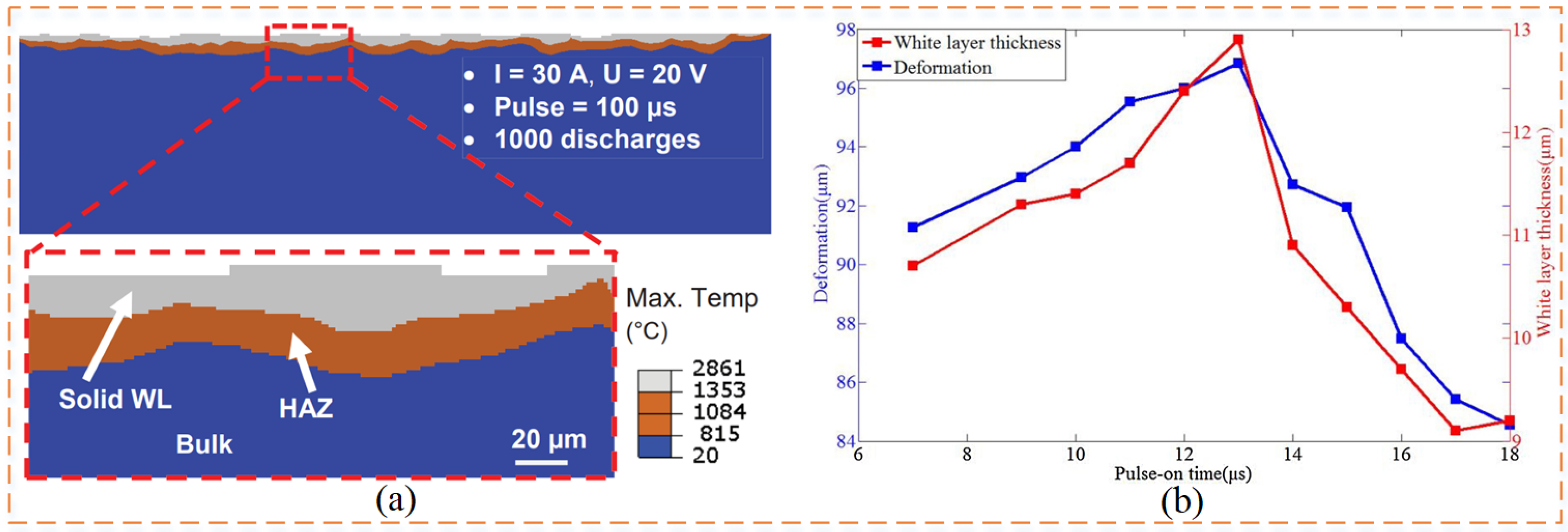
| Shabgard et al. [86], 2011 | The increase in pulse current resulted in a slight decrease in the white layer thickness and heat-affected zone depth. | Each increase in discharge duration results in more heat being distributed into the workpiece, so more of the underlying material is exposed to high temperatures. | |
| Liu and Guo [118], 2016 | The predicted WL and HAZ transformations of martensite match the experimental data with reasonable accuracy. | This provides us with the ability to predict macro-scale cumulative thermal damage during EDM processes. | |
| Zhang et al. [119], 2019 | A thermophysical model was established, and by studying the surface characteristics of the deformed specimens, the changes in the thickness of the recast layer were consistent with the changes in their thermal deformation. | The change in the thickness of the recast layer almost corresponds to the change in its thermal deformation. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Sun, S.; Xing, W.; Zhang, Y.; Wu, Y.; Xu, Y.; Wang, H.; Zhang, G.; Luo, G. Progress in Simulation Modeling Based on the Finite Element Method for Electrical Discharge Machining. Metals 2024, 14, 14. https://doi.org/10.3390/met14010014
Li L, Sun S, Xing W, Zhang Y, Wu Y, Xu Y, Wang H, Zhang G, Luo G. Progress in Simulation Modeling Based on the Finite Element Method for Electrical Discharge Machining. Metals. 2024; 14(1):14. https://doi.org/10.3390/met14010014
Chicago/Turabian StyleLi, Liwei, Shuo Sun, Wenbo Xing, Yuyan Zhang, Yonglei Wu, Yingjie Xu, Hongyan Wang, Guojun Zhang, and Guofu Luo. 2024. "Progress in Simulation Modeling Based on the Finite Element Method for Electrical Discharge Machining" Metals 14, no. 1: 14. https://doi.org/10.3390/met14010014
APA StyleLi, L., Sun, S., Xing, W., Zhang, Y., Wu, Y., Xu, Y., Wang, H., Zhang, G., & Luo, G. (2024). Progress in Simulation Modeling Based on the Finite Element Method for Electrical Discharge Machining. Metals, 14(1), 14. https://doi.org/10.3390/met14010014






