Predictive Modeling of Hardness Values and Phase Fraction Percentages in Micro-Alloyed Steel during Heat Treatment Using AI
Abstract
:1. Introduction
- Curate a comprehensive steel database from the CCT diagrams in the steel atlas [12]. This database will encompass an exhaustive set of temperature-time cooling profiles of a variety of steels with various alloying element combinations and the corresponding phase fractions and hardness values obtained from the thermomechanical processing of the steel.
- Develop a neural network model capable of simultaneously predicting the hardness values of steel and microstructure phase fractions, given its composition and continuous cooling transformation profile.
- Demonstrate the practical utility of this model and conduct a sensitivity analysis on the model to understand the impact of key input variables on the predicted output, providing further insight into the relationships between steel composition as well as heat treatment processes, and the resulting properties.
2. Literature Review
3. Methods
3.1. Database Creation
3.2. Description of the Cooling Profile
3.2.1. Lagrange Interpolating Polynomial
3.2.2. Least Squares Approximation
3.2.3. Directly Using All Temperature–Time Pairs
3.3. Neural Network Architecture for Hardness
3.4. Neural Network Architecture for Phase Fractions
3.5. Neural Network Architecture for Phase Fractions
3.6. MLP Training
3.7. Termination Criteria of the Training Algorithm
- The number of epochs reached 1000.
- The MSE cost was below 1 × 10−3.
- The MSE cost did not improve over the previous 40 epochs.
4. Results and Discussion
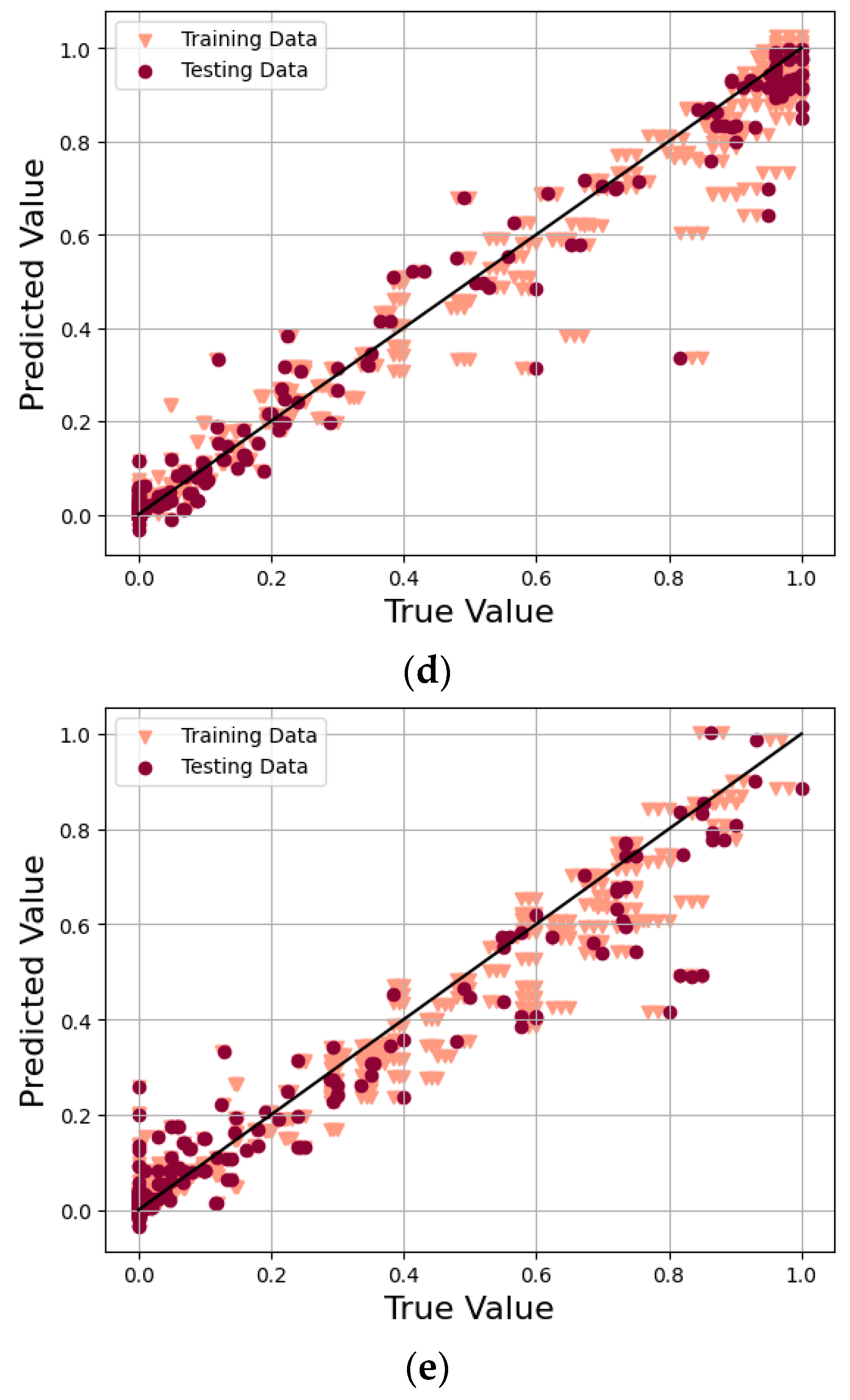
4.1. Evaluation of the Neural Network
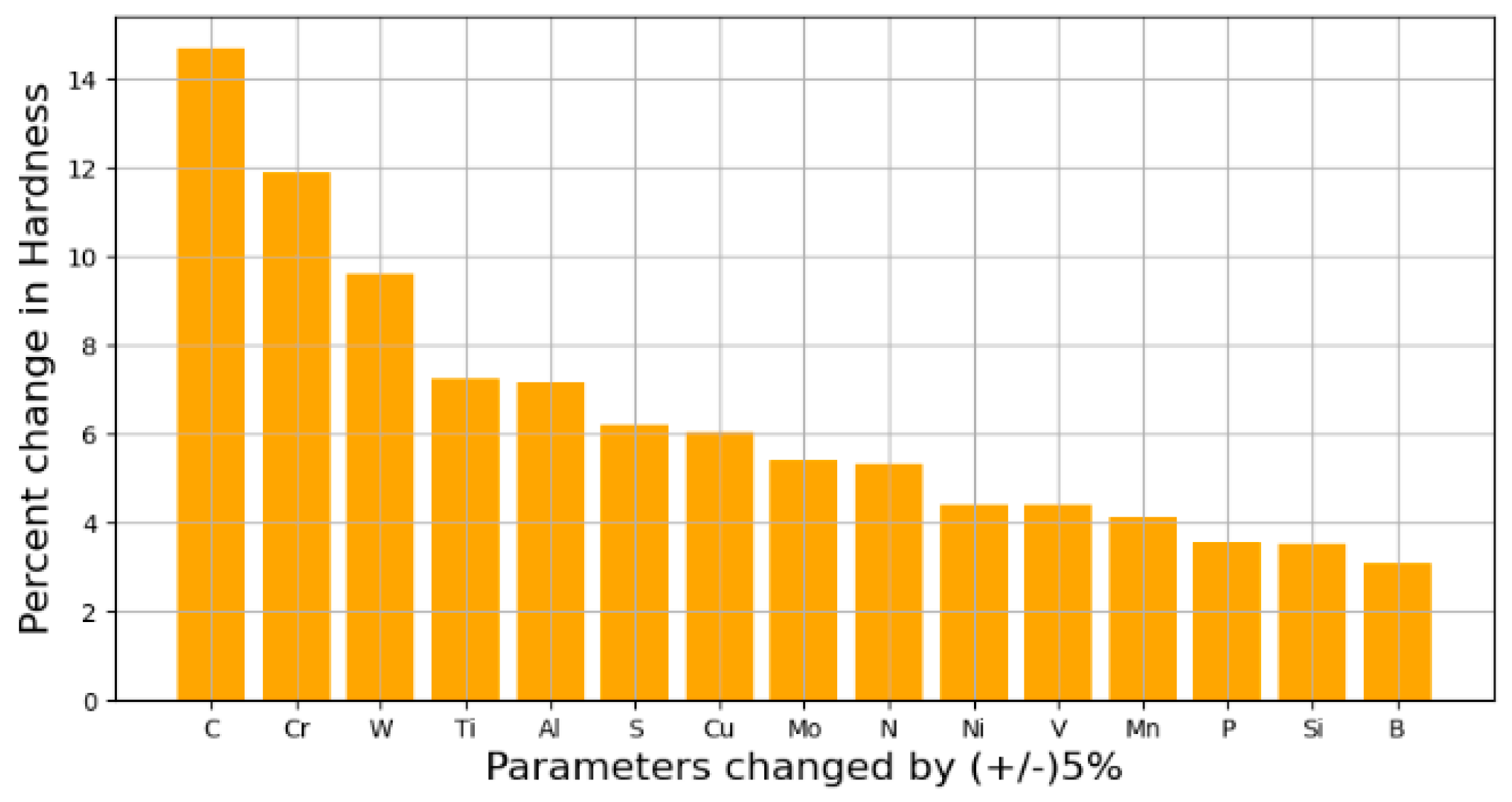
4.2. Sensitivity Analysis
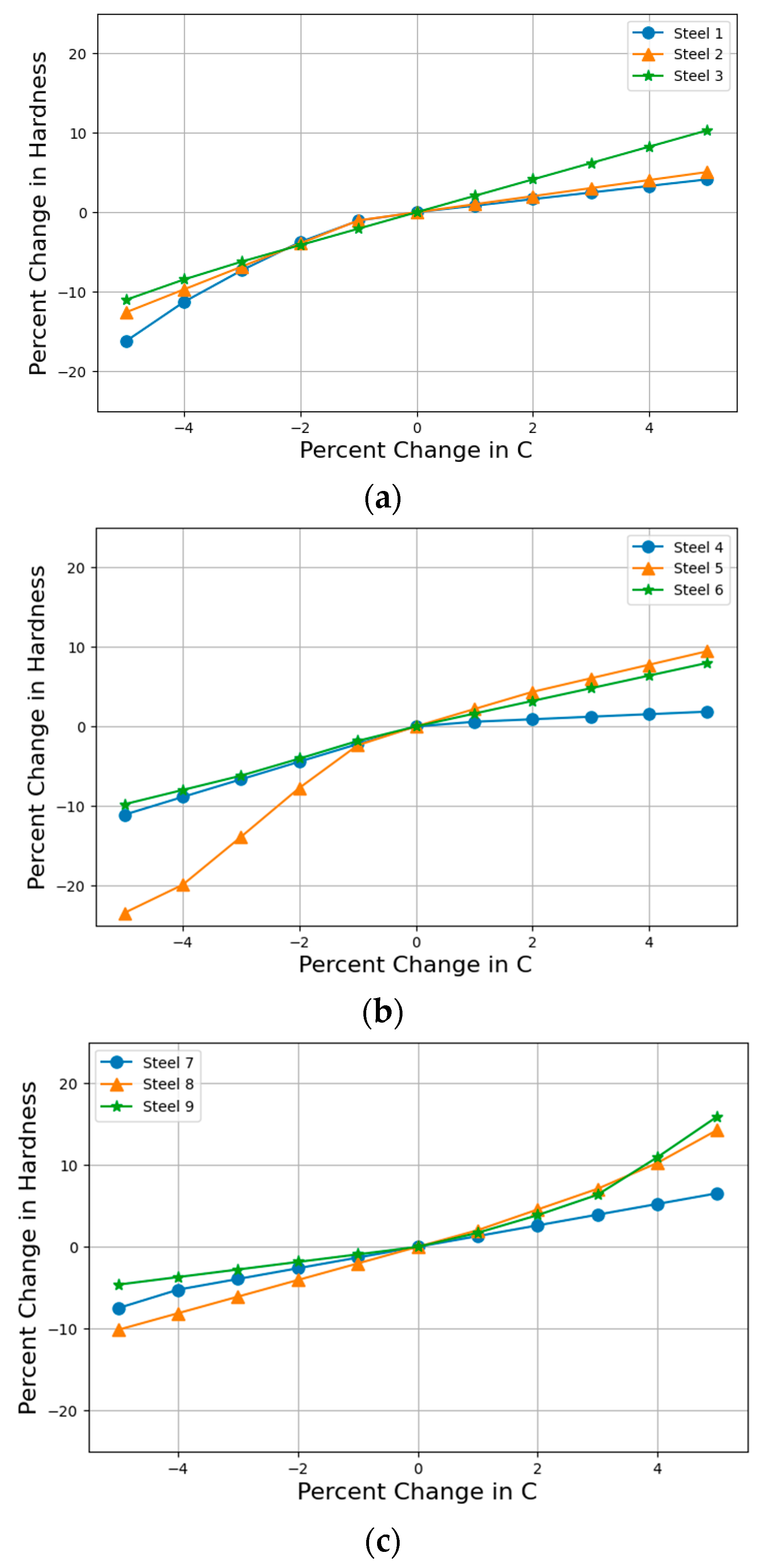
4.2.1. Analysis of the Impact of Carbon Content on the Hardness of Steel
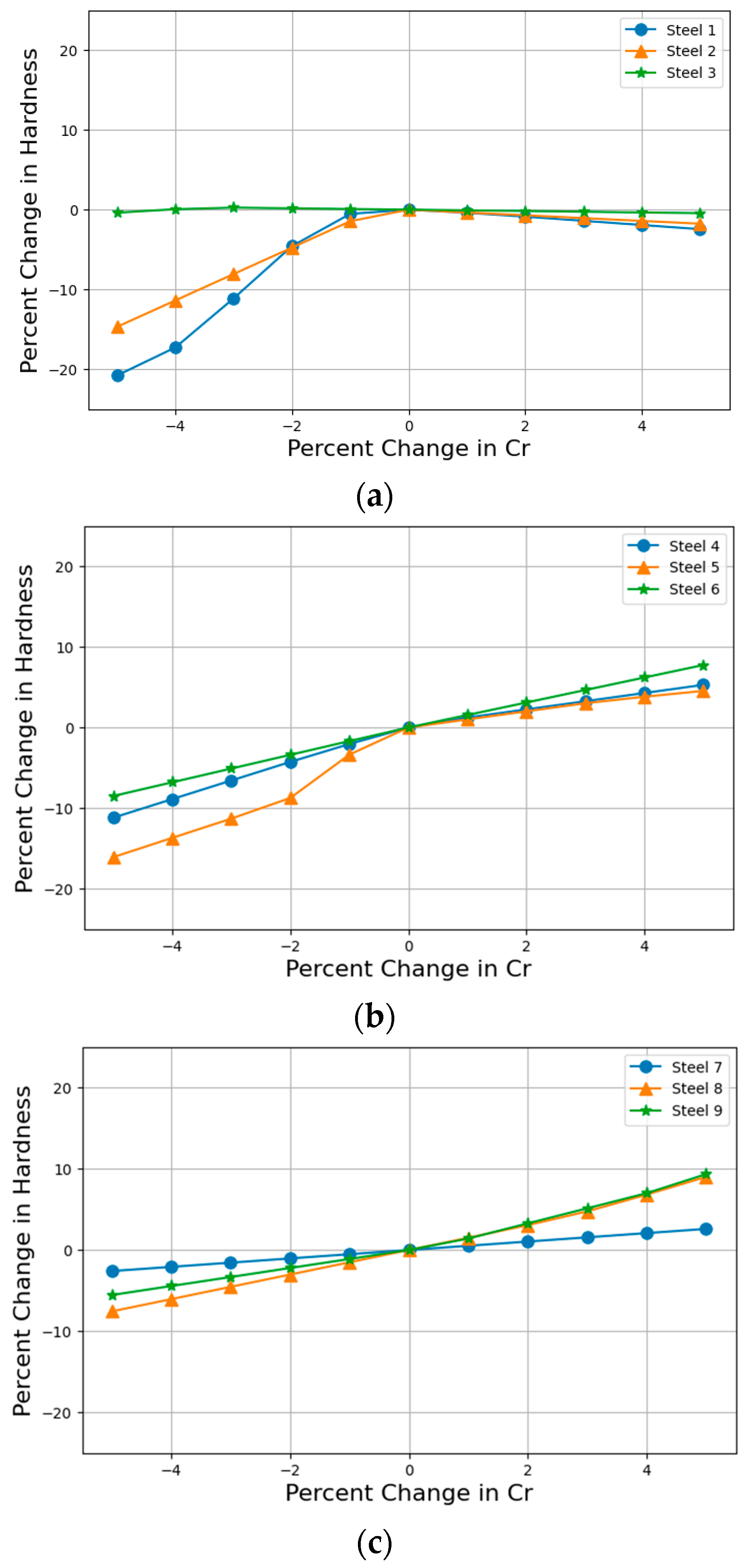
4.2.2. Analysis of the Impact of Chromium Content on the Hardness of Steel
4.2.3. Analysis of Other Alloying Elements
5. Limitations of This Study
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Celada-Casero, C.; Huang, B.M.; Yang, J.R.; San-Martin, D. Microstructural mechanisms controlling the mechanical behaviour of ultrafine grained martensite/austenite microstructures in a metastable stainless steel. Mater. Des. 2019, 181, 107922. [Google Scholar] [CrossRef]
- Yin, W.; Peyton, A.J.; Strangwood, M.; Davis, C.L. Exploring the relationship between ferrite fraction and morphology and the electromagnetic properties of steel. J. Mater. Sci. 2007, 42, 6854–6861. [Google Scholar] [CrossRef]
- Shi, B.L.; Zhang, C.; Tang, Y.W.; Wei, G.J.; Li, Y.; He, C.; Xu, K. Investigation on the Microstructure and Mechanical Properties of T23 Steel during High Temperature Aging. Mater. Sci. Forum 2020, 993, 575–584. [Google Scholar] [CrossRef]
- Jung, I.D.; Shin, D.S.; Kim, D.; Lee, J.; Lee, M.S.; Son, H.J.; Reddy, N.; Kim, M.; Moon, S.K.; Kim, K.T.; et al. Artificial intelligence for the prediction of tensile properties by using microstructural parameters in high strength steels. Materialia 2020, 11, 100699. [Google Scholar] [CrossRef]
- Bok, H.H.; Kim, S.N.; Suh, D.W.; Barlat, F.; Lee, M.G. Non-isothermal kinetics model to predict accurate phase transformation and hardness of 22MnB5 boron steel. Mater. Sci. Eng. A 2015, 626, 67–73. [Google Scholar] [CrossRef]
- Van Bohemen, S.M.C. Exploring the correlation between the austenite yield strength and the bainite lath thickness. Mater. Sci. Eng. A 2018, 731, 119–123. [Google Scholar] [CrossRef]
- Huang, C.C.; Chen, Y.T.; Chen, Y.J.; Chang, C.Y.; Huang, H.C.; Hwang, R.C. The Neural Network Estimator for Mechanical Property of Rolled Steel Bar. In Proceedings of the 2009 Fourth International Conference on Innovative Computing, Information and Control (ICICIC), Kaohsiung, Taiwan, 7–9 December 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1216–1219. [Google Scholar]
- Monajati, H.; Asefi, D.; Parsapour, A.; Abbasi, S. Analysis of the effects of processing parameters on mechanical properties and formability of cold rolled low Carbon steel sheets using neural networks. Comput. Mater. Sci. 2010, 49, 876–881. [Google Scholar] [CrossRef]
- Sterjovski, Z.; Nolan, D.; Carpenter, K.R.; Dunne, D.P.; Norrish, J. Artificial neural networks for modelling the mechanical proper-ties of steels in various applications. J. Mater. Process. Technol. 2005, 170, 536–544. [Google Scholar] [CrossRef]
- Sidhu, G.; Bhole, S.D.; Chen, D.L.; Essadiqi, E. Determination of volume fraction of bainite in low Carbon steels using artificial neural networks. Comput. Mater. Sci. 2011, 50, 3377–3384. [Google Scholar] [CrossRef]
- Sidhu, G.; Bhole, S.D.; Chen, D.L.; Essadiqi, E. Development and experimental validation of a neural network model for predic-tion and analysis of the strength of bainitic steels. Mater. Des. 2012, 41, 99–107. [Google Scholar] [CrossRef]
- Voort, G.F.V. Atlas of Time-Temperature Diagrams for Irons and Steels; ASM International: Detroit, MI, USA, 1991. [Google Scholar]
- Sidhu, G.; Srinivasan, S.; Bhole, S. An algorithm for optimal design and thermomechanical processing of high Carbon bainitic steels. Int. J. Aerodyn. 2018, 6, 176. [Google Scholar] [CrossRef]
- Huang, X.; Wang, H.; Xue, W.; Xiang, S.; Huang, H.; Meng, L.; Ma, G.; Ullah, A.; Zhang, G. Study on time-temperature-transformation diagrams of stain-less steel using machine-learning approach. Comput. Mater. Sci. 2020, 171, 109282. [Google Scholar] [CrossRef]
- Geng, X.; Wang, H.; Xue, W.; Xiang, S.; Huang, H.; Meng, L.; Ma, G. Modeling of CCT diagrams for tool steels using different machine learning techniques. Comput. Mater. Sci. 2020, 171, 109235. [Google Scholar] [CrossRef]
- Zein, H.; Tran, V.; Abdelmotaleb Ghazy, A.; Mohammed, A.T.; Ahmed, A.; Iraqi, A.; Huy, N.T. How to Extract Data from Graphs using Plot Digitizer or Getdata Graph Digitizer. 2015. [Google Scholar] [CrossRef]
- Farmer, J. Lagrange’s Interpolat. Formula. Aust. Sr. Math. J. 2018, 32, 8–12. [Google Scholar]
- Pallavi; Joshi, S.; Singh, D.; Kaur, M.; Lee, H.N. Comprehensive Review of Orthogonal Regression and Its Applications in Dif-ferent Domains. Arch. Comput. Methods Eng. 2022, 29, 4027–4047. [Google Scholar] [CrossRef]
- Bhadeshia, H.K.D.H.; Dimitriu, R.C.; Forsik, S.; Pak, J.H.; Ryu, J.H. Performance of neural networks in materials science. Mater. Sci. Technol. 2009, 25, 504–510. [Google Scholar] [CrossRef]
- Rojas, R. Neural Networks; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Geng, X.; Mao, X.; Wu, H.H.; Wang, S.; Xue, W.; Zhang, G.; Ullah, A.; Wang, H. A hybrid machine learning model for predicting continuous cooling transformation diagrams in welding heat-affected zone of low alloy steels. J. Mater. Sci. Technol. 2022, 107, 207–215. [Google Scholar] [CrossRef]
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the International Conference on Learning Representations. Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Wang, X.; Chen, Y.; Wei, S.; Zuo, L.; Mao, F. Effect of Carbon Content on Abrasive Impact Wear Behavior of Cr-Si-Mn Low Alloy Wear Resistant Cast Steels. Front. Mater. 2019, 6, 153. [Google Scholar] [CrossRef]
- Sotoodeh, K. Corrosion study and material selection for cryogenic valves in an LNG plant. In Cryogenic Valves for Lique-Fied Natural Gas Plants; Elsevier: Amsterdam, The Netherlands, 2022; pp. 175–211. [Google Scholar]
- de la Concepción, V.L.; Lorusso, H.N.; Svoboda, H.G. Effect of Carbon Content on Microstructure and Mechanical Properties of Dual Phase Steels. Procedia Mater. Sci. 2015, 8, 1047–1056. [Google Scholar] [CrossRef]
- Khanh, P.M.; Nam, N.D.; Chieu, L.T.; Quyen, H.T.N. Effects of Chromium Content and Impact Load on Microstructures and Properties of High Manganese Steel. Mater. Sci. Forum 2014, 804, 297–300. [Google Scholar] [CrossRef]
- Tian, Y.; Ju, J.; Fu, H.; Ma, S.; Lin, J.; Lei, Y. Effect of Chromium Content on Microstructure, Hardness, and Wear Resistance ofAs-Cast Fe-Cr-B Alloy. J. Mater. Eng. Perform. 2019, 28, 6428–6437. [Google Scholar] [CrossRef]
- Mahlami, C.S.; Pan, X. An Overview on high manganese steel casting. In Proceedings of the 71st World Foundry Congress, Bilbao, Spain, 19–21 May 2014. [Google Scholar]





| Input Parameter | Range |
|---|---|
| C (wt%) | 0.1–2.19 |
| Si (wt%) | 0–1.05 |
| Ni (wt%) | 0–3.03 |
| Mn (wt%) | 0.2–1.98 |
| Mo (wt%) | 0–0.56 |
| Cr (wt%) | 0–13.12 |
| V (wt%) | 0–0.31 |
| Cu (wt%) | 0–0.91 |
| Al (wt%) | 0–0.063 |
| N (wt%) | 0–0.003 |
| P (wt%) | 0–0.44 |
| S (wt%) | 0–0.29 |
| B (wt%) | 0–0.05 |
| W (wt%) | 0–1.15 |
| Ti (wt%) | 0–0.18 |
| T (C) | 140.48–1774.62 |
| t (s) | 0.100122–188,000 |
| Output | Range (%) |
|---|---|
| Austenite | 0–30 |
| Ferrite | 0–92 |
| Bainite | 0–100 |
| Martensite | 0–100 |
| Pearlite | 0–100 |
| Lagrange Interpolation MRE | Least Squares Approximation MRE | |
|---|---|---|
| Mode | 82.0975 | 12.9347 |
| Mean | 5.6517 | 2.26397 |
| Median | 2.7776 | 1.4660 |
| Parameters | Value |
|---|---|
| Hidden layers | [1–3] |
| Neurons in each hidden layer | [0–20] |
| Optimizer | SGD, Adam |
| Activation function | RELU, Sigmoid |
| Batch size | 64, 128, 256 |
| Epochs | 100, 200, 500, 1000 |
| Dropout | [0.1–0.4] |
| Parameters | Value |
|---|---|
| Hidden layers | 2 |
| Neurons in each layer | (32, 20, 20, 1) |
| Optimizer | Adam |
| Activation function | RELU |
| Batch size | 128 |
| Epochs | 1000 |
| Dropout | 0.1 |
| MLP Model | R2 for Testing | R2 for Training and Testing Data |
|---|---|---|
| Hardness | 0.99 | 0.99 |
| Ferrite | 0.99 | 0.99 |
| Martensite | 0.98 | 0.99 |
| Pearlite | 0.98 | 0.99 |
| Bainite | 0.96 | 0.98 |
| Element | Steel 1 | Steel 2 | Steel 3 | Steel 4 | Steel 5 | Steel 6 | Steel 7 | Steel 8 | Steel 9 |
|---|---|---|---|---|---|---|---|---|---|
| High Carbon | Medium Carbon | Low Carbon | |||||||
| C | 1.04 | 1.03 | 0.98 | 0.44 | 0.41 | 0.39 | 0.3 | 0.22 | 0.16 |
| Mn | 0.33 | 0.97 | 1.84 | 0.2 | 0.66 | 1.56 | 0.51 | 0.64 | 0.5 |
| P | 0.23 | 0.016 | 0.023 | 0.025 | 0.008 | 0.01 | 0.011 | 0.01 | 0.013 |
| S | 0.006 | 0.018 | 0.011 | 0.01 | 0.024 | 0.024 | 0.007 | 0.011 | 0.14 |
| Si | 0.26 | 0.28 | 0.08 | 0.3 | 0.25 | 0.21 | 0.32 | 0.25 | 0.31 |
| Ni | 0.31 | 0.13 | 0 | 0.31 | 0.31 | 0 | 3.03 | 0.33 | 2.02 |
| Cr | 1.53 | 1.05 | 0 | 13.12 | 1.03 | 0 | 0.07 | 0.97 | 1.95 |
| Mo | 0.01 | 0.03 | 0 | 0.01 | 0.17 | 0 | 0 | 0.23 | 0.03 |
| Cu | 0.2 | 0.25 | 0 | 0.09 | 0.28 | 0 | 0 | 0.16 | 0 |
| Al | 0 | 0 | 0 | 0 | 0 | 0 | 0.032 | 0 | 0.03 |
| V | 0.01 | 0 | 0 | 0.02 | 0.01 | 0 | 0 | 0.01 | 0.01 |
| Ti | 0 | 0 | 0 | 0 | 0 | 0 | 0.01 | 0 | 0 |
| W | 0 | 1.15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| HV | 890 | 885 | 633 | 525 | 640 | 264 | 205 | 294 | 339 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bassi, A.; Bodas, S.T.; Hasan, S.S.; Sidhu, G.; Srinivasan, S. Predictive Modeling of Hardness Values and Phase Fraction Percentages in Micro-Alloyed Steel during Heat Treatment Using AI. Metals 2024, 14, 49. https://doi.org/10.3390/met14010049
Bassi A, Bodas ST, Hasan SS, Sidhu G, Srinivasan S. Predictive Modeling of Hardness Values and Phase Fraction Percentages in Micro-Alloyed Steel during Heat Treatment Using AI. Metals. 2024; 14(1):49. https://doi.org/10.3390/met14010049
Chicago/Turabian StyleBassi, Ankur, Soham Tushar Bodas, Syed Shuja Hasan, Gaganpreet Sidhu, and Seshasai Srinivasan. 2024. "Predictive Modeling of Hardness Values and Phase Fraction Percentages in Micro-Alloyed Steel during Heat Treatment Using AI" Metals 14, no. 1: 49. https://doi.org/10.3390/met14010049
APA StyleBassi, A., Bodas, S. T., Hasan, S. S., Sidhu, G., & Srinivasan, S. (2024). Predictive Modeling of Hardness Values and Phase Fraction Percentages in Micro-Alloyed Steel during Heat Treatment Using AI. Metals, 14(1), 49. https://doi.org/10.3390/met14010049






