Research on the Temperature and Thermal Stress of the Roll Quenching Process of Thin Plates
Abstract
1. Introduction
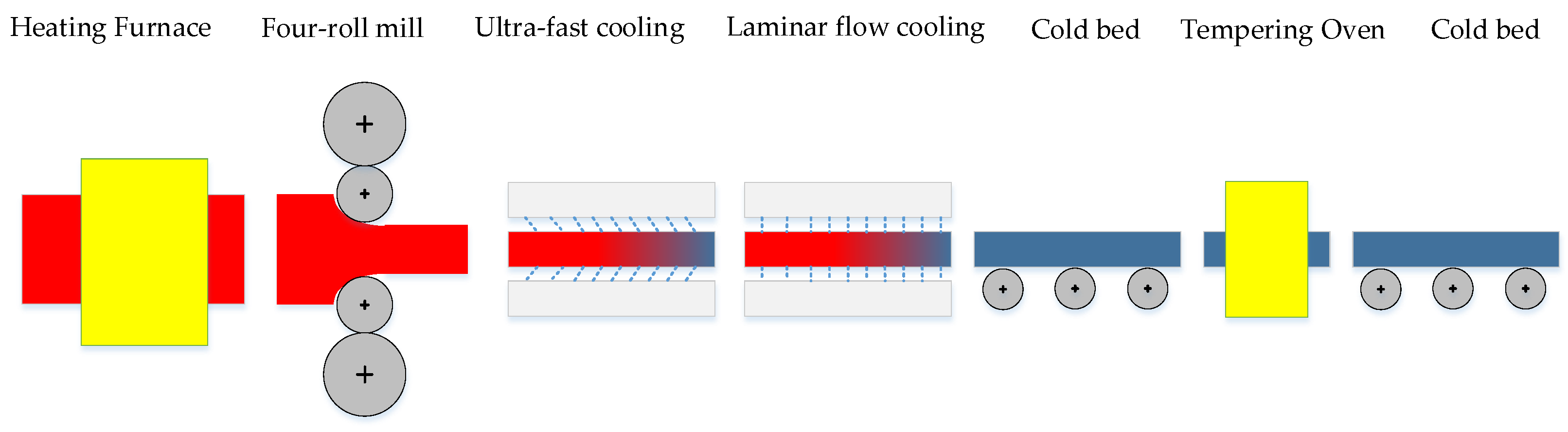
2. Roll Quenching Cooling Mechanism Analysis
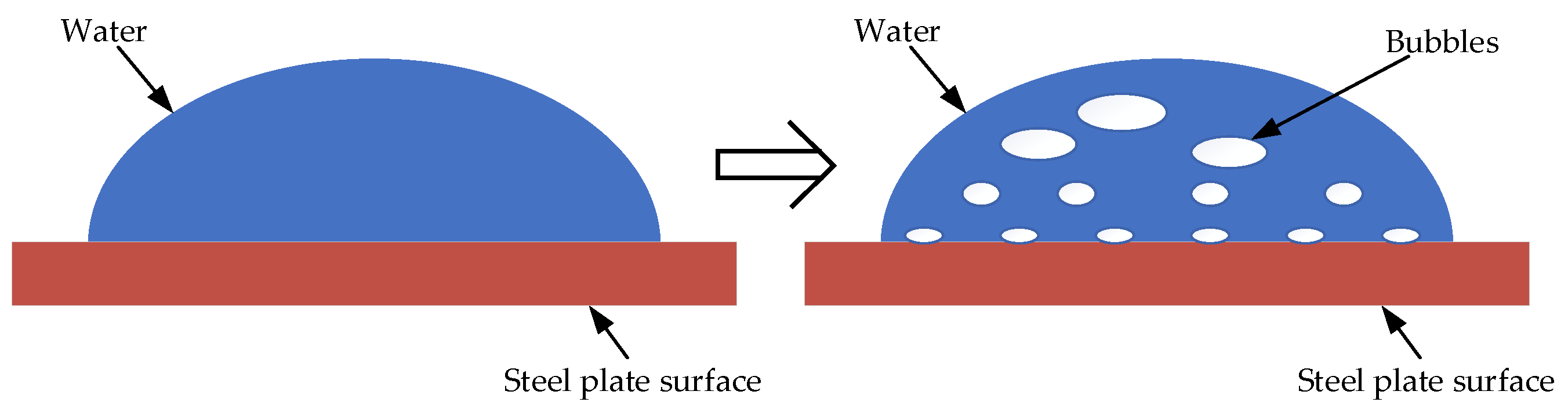
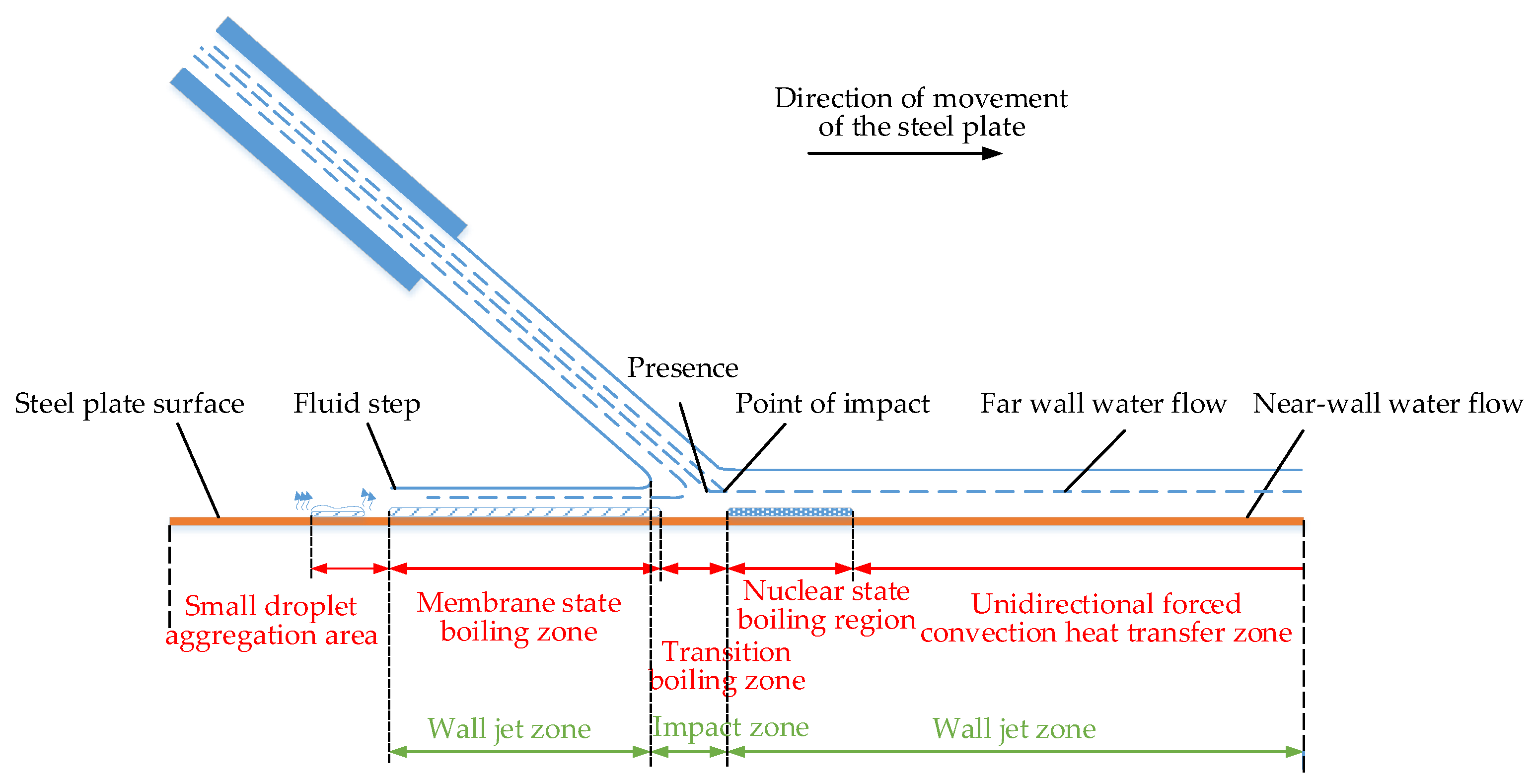
2.1. Modeling of Segmented Convective Heat Transfer Coefficients
2.2. Modeling of the Temperature Field of the Quenching Process
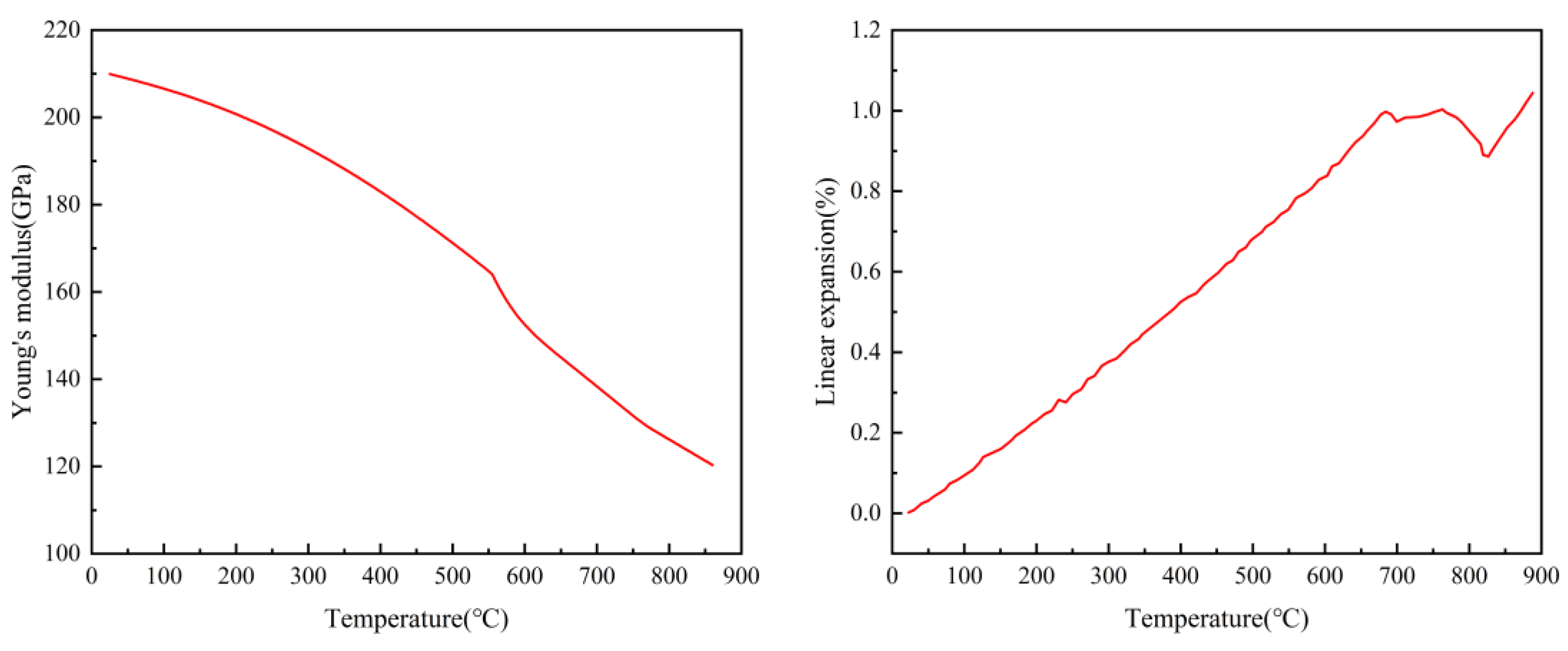
2.3. Modeling of the Thermal Stress Field during Quenching Process
3. Results and Discussion
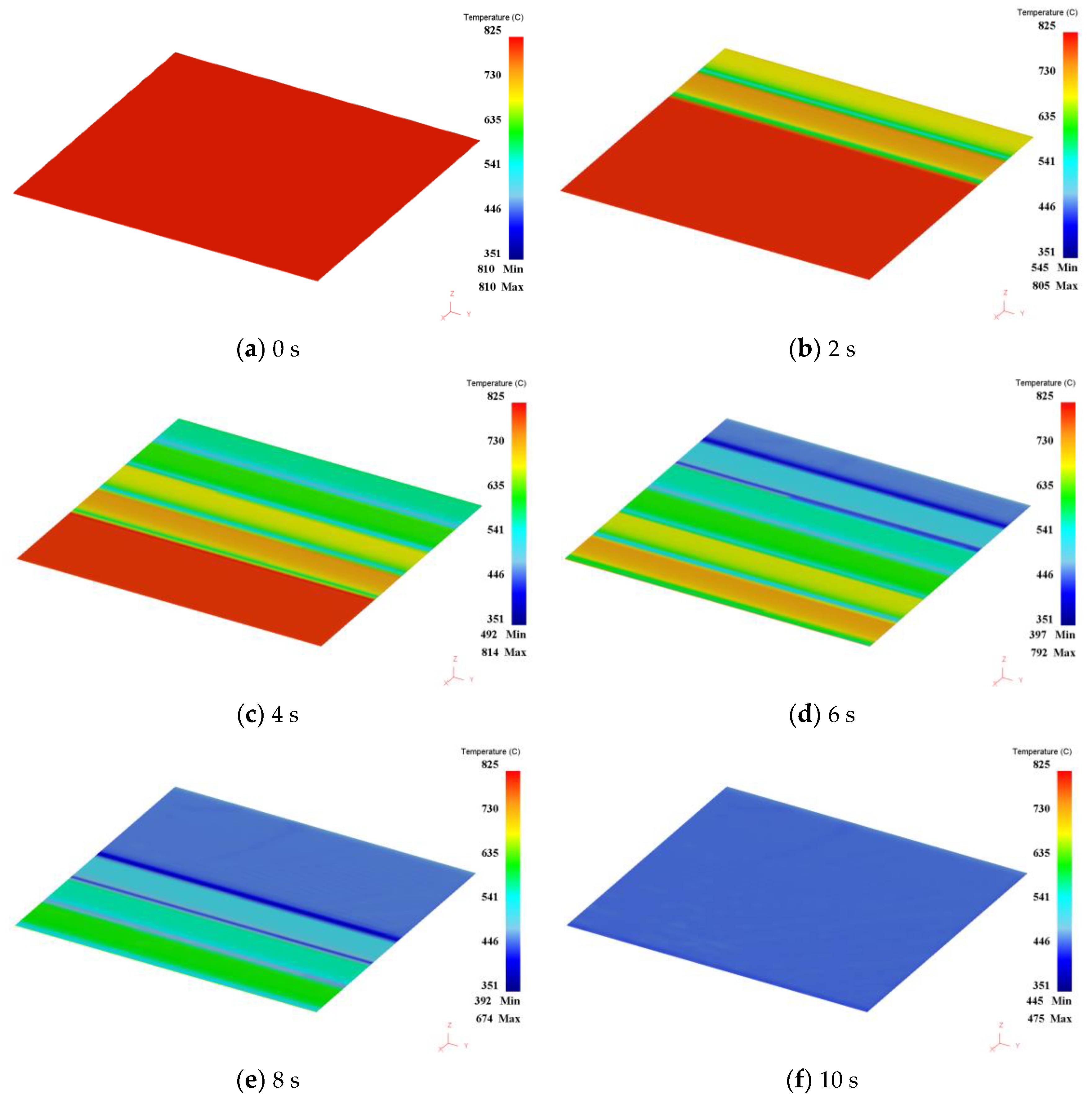
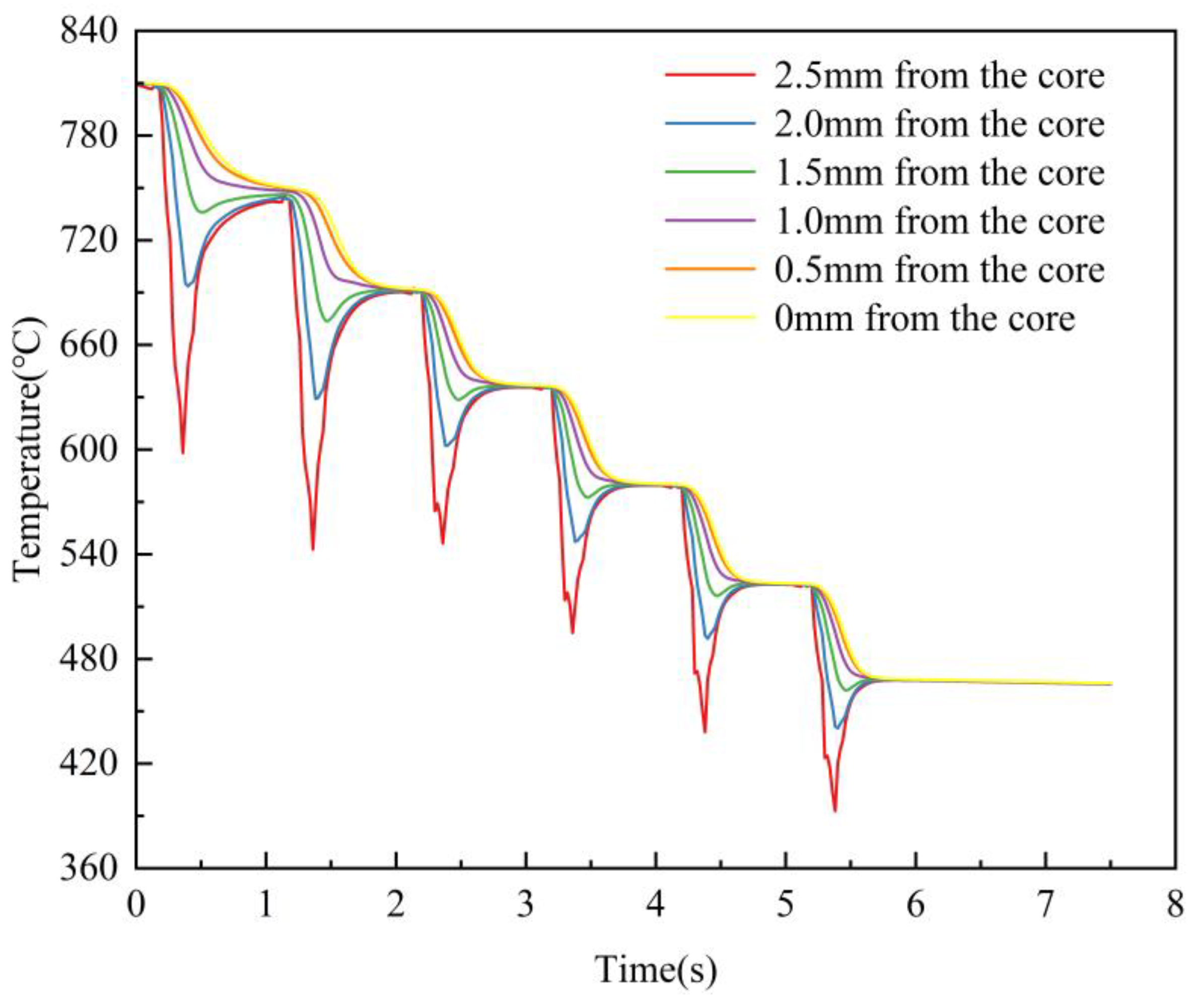
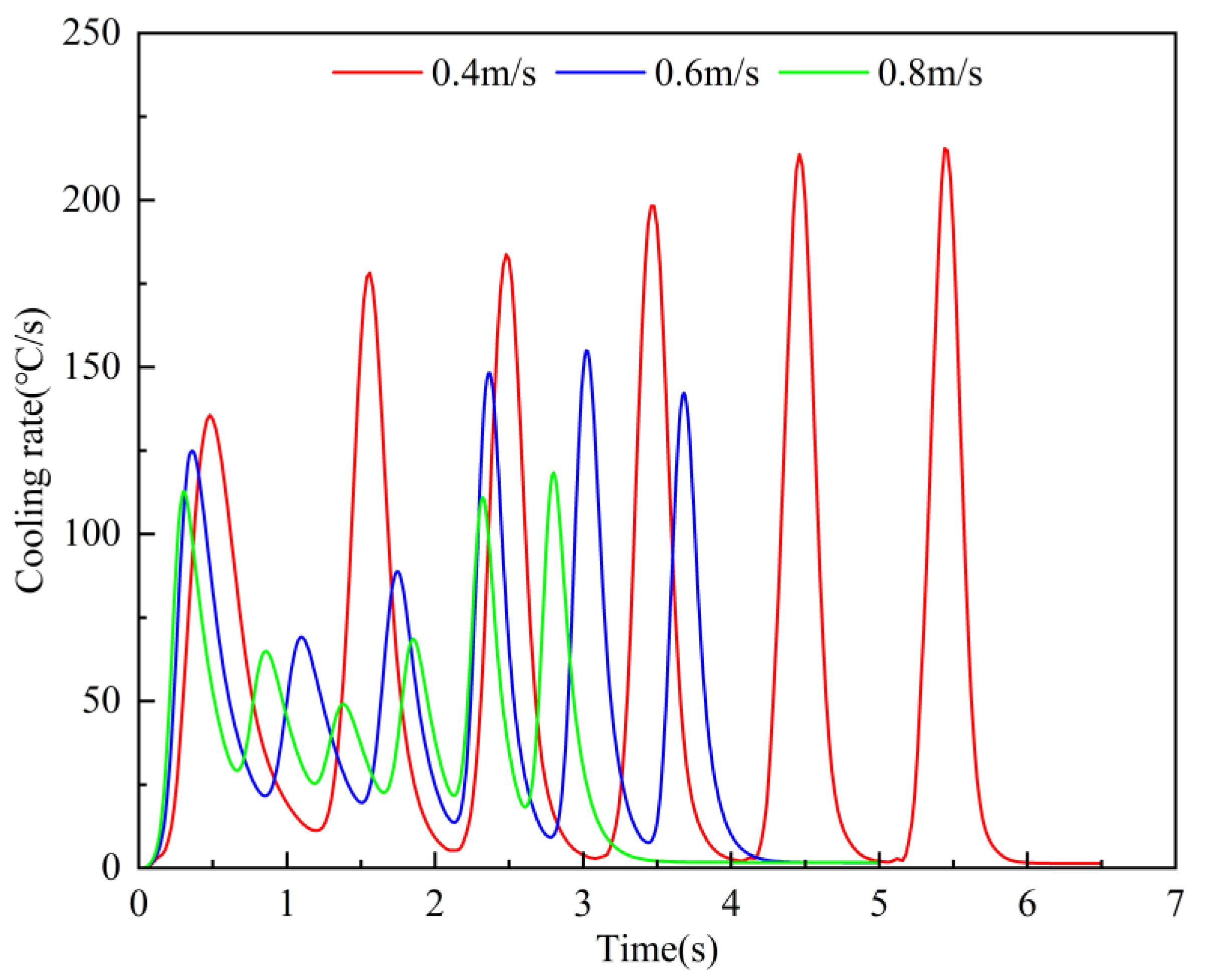
3.1. Steel Plate Temperature Field Results and Analysis
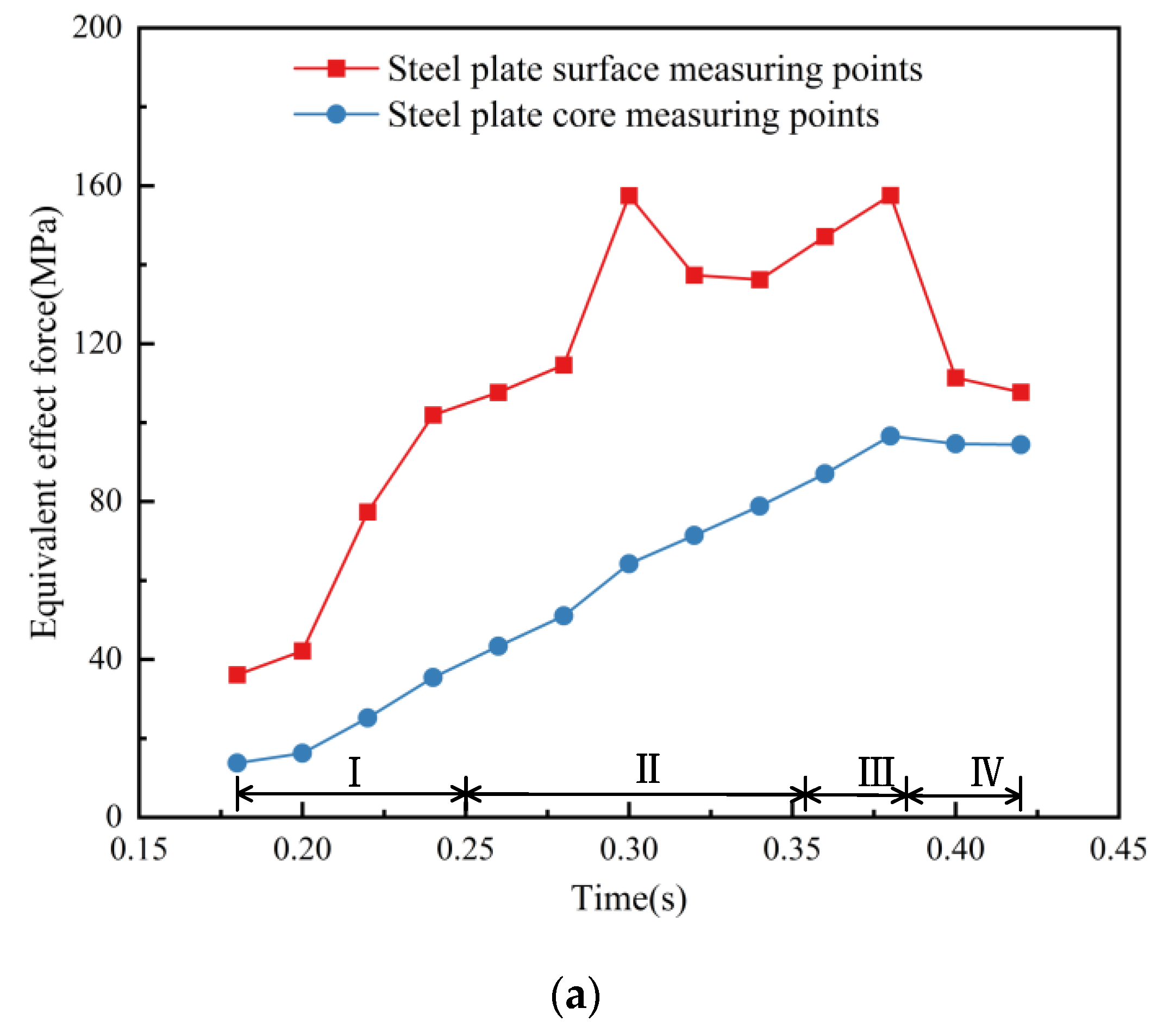
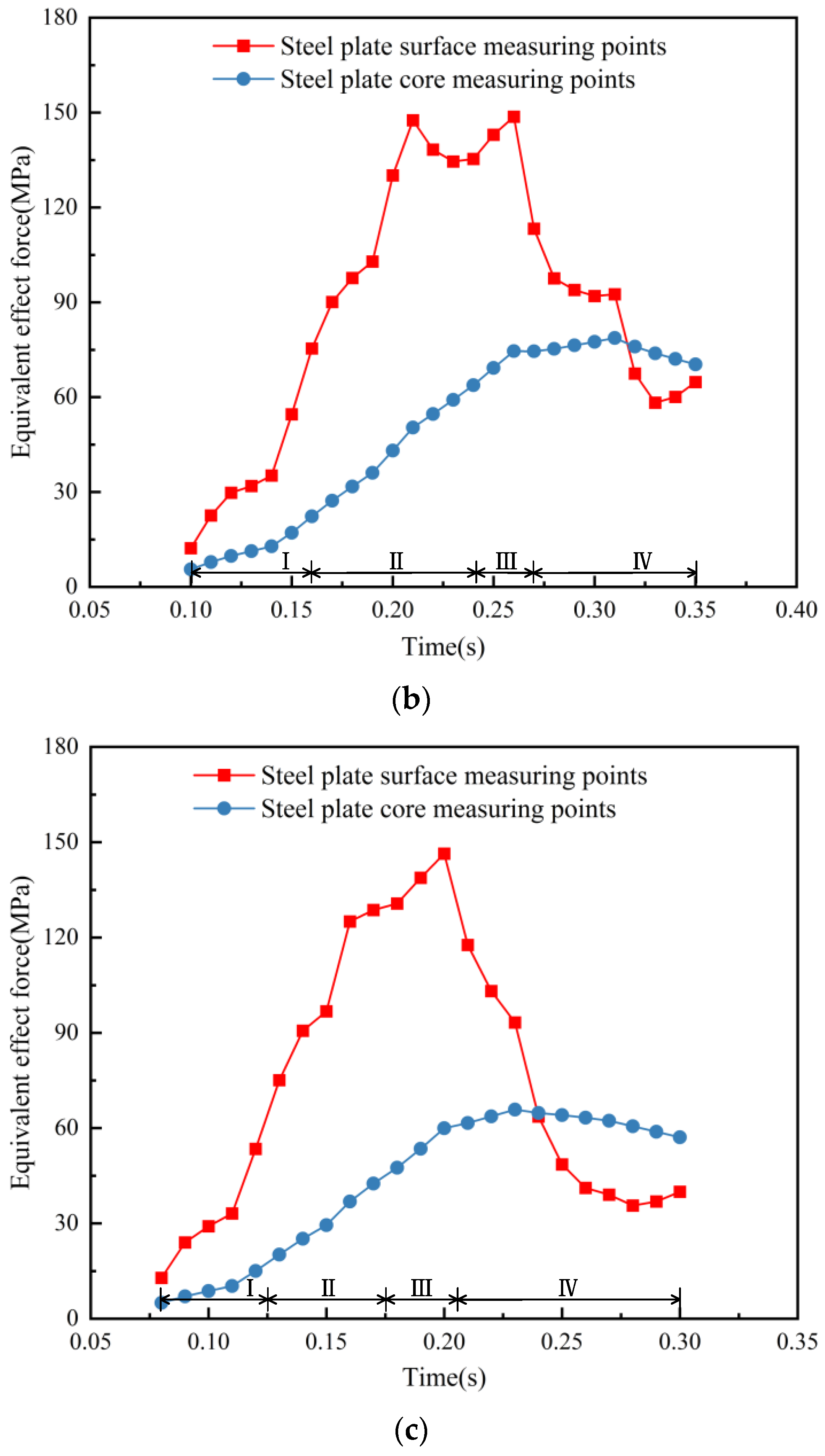
3.2. Steel Plate Stress Field Results and Analysis
4. Application of Research Results
5. Conclusions
- (1)
- Based on the calculated equivalent force generated when passing through each nozzle region during the quenching process of the steel plate, it is concluded that the maximum equivalent force occurs during the quenching process with a hysteresis. When in the nozzle area, the equivalent force is always increasing, but not immediately after leaving the quenching area; it will continue to increase, and after a certain period of time, the equivalent force will gradually decrease again. The farther away from the surface, the more obvious the hysteresis effect.
- (2)
- When the roller conveyor speed is too small, the steel plate quenching area is cooled faster, and the temperature difference between the longitudinal direction and the thick direction is larger. Therefore, the steel plate core and surface equivalent force difference are larger and more prone to warping. When the roller speed is too large, the cooling speed of the steel plate is significantly reduced, and the longitudinal plate shape is better at this time. When the roller gap setting value is too small, the steel plate quenching plastic deforms and generates greater stress. At this time, the steel plate is prone to jamming and side waves. When the roller gap setting value is too large, the roller cannot play the full role of pressure. The steel plate appeared to have a serious edge wave, and the overall shape of the plate was warping. In summary, the quenching machine roll gap is closer to the incoming material thickness, and the quenching plate shape is significantly improved.
- (3)
- Under the premise of adjusting the relevant parameters of the quenching machine to ensure uniformity of quenching, what affects the shape of the plate after quenching is the value of the open-cooling temperature, roll speed, and roll gap. Among them, the speed of the roller conveyor directly affects the temperature drop and stress distribution of the steel plate. In this paper, based on the results of simulation calculations and on-site applications, the quenching section of the roll provides solution ideas and key parameters to ensure that the plate shape is good while improving the quenching speed as much as possible, shortening the production cycle, and improving efficiency.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yuan, G.; Sun, J. Innovative practice of rolling technology under the development trend of high quality and greening. Wuhan Eng. Vocat. Tech. Coll. 2021, 38, 1–9. [Google Scholar]
- Fu, T.L.; Han, Y.; Deng, W.T. Development progress and application of new technology of roll quenching for high-grade steel plates. Steel Roll. 2022, 39, 60–66. [Google Scholar]
- Wang, Z.D.; Li, J.D.; Fu, T.L. Development and application of continuous heat treatment equipment for ultra-wide special steel plate. Steel Roll. 2019, 36, 1–5+13. [Google Scholar]
- Qiao, X.Y.F.; Liu, Y. Plate shape control during quenching of thin gauge steel plates. J. Iron Steel Res. 2011, 23, 159–162. [Google Scholar]
- Zhang, W.; Wu, M.; Du, S. Plate shape recognition based on Gaussian function and particle swarm optimization for roller quenching process. J. Process Control 2022, 119, 115–127. [Google Scholar] [CrossRef]
- Wu, Q.; He, S.; Hu, P. Effect of finish rolling temperature on microstructure and mechanical properties of X80 pipeline steel by on-line quenching. Mater. Sci. Eng. A 2023, 862, 144496. [Google Scholar] [CrossRef]
- Chen, Y.; Sun, S.; Zhang, T. Effects of post-weld heat treatment on the microstructure and mechanical properties of laser-welded NiTi/304SS joint with Ni filler. Mater. Sci. Eng. A 2020, 771, 138545. [Google Scholar] [CrossRef]
- Ramesh Babu, S.; Nyyssönen, T.; Jaskari, M. Observations on the relationship between crystal orientation and the level of auto-tempering in an as-quenched martensitic steel. Metals 2019, 9, 1255. [Google Scholar] [CrossRef]
- Tian, S.; Liu, Z.; Fu, R. Effect of Organizational Evolution on the Stress Corrosion Cracking of the Cr-Co-Ni-Mo Series of Ultra-High Strength Stainless Steel. Materials 2022, 15, 497. [Google Scholar] [CrossRef]
- Peng, X.; Zhang, P.; Hu, K. Simultaneous Improvement in Mechanical Properties and Fatigue Crack Propagation Resistance of Low Carbon Offshore Structural Steel EH36 by Cu–Cr Microalloying. Metals 2021, 11, 1880. [Google Scholar] [CrossRef]
- Shi, J.; Jiang, L.Y.; Yuan, G. Influence of ultra-fast cooling water volume ratio on the surface heat transfer of strip steel. Trans. Mater. Heat Treat. 2015, 36, 245–249. [Google Scholar]
- Shi, J.; Yuan, G.; Jiang, L. Numerical analysis of heat transfer intensity from twin slot vertical jet impingement on strip surface after hot rolling. J. Cent. South Univ. 2015, 22, 2816–2824. [Google Scholar] [CrossRef]
- Lei, K.; Gang, Z.; Ni, T. Computation of synthetic surface heat transfer coefficient of 7B50 ultra-high-strength aluminum alloy during spray quenching. Trans. Nonferrous Met. Soc. China 2018, 28, 989–997. [Google Scholar]
- Shi, L.; Zhu, X.; Du, Z. Experimental investigation on convective heat transfer of inclined jets impinging on the rotating cylindrical surface in the confined space. Int. J. Heat Mass Transfer. 2023, 202, 123744. [Google Scholar] [CrossRef]
- Yuan, G.; Zhang, R.; Zhang, Y. Heat Transfer Characteristics of a Hot-Rolled Seamless Steel Tube During a Controlled Cooling Process. Steel Res. Int. 2023, 94, 2200150. [Google Scholar] [CrossRef]
- Fu, Z.L.; Liu, A.Y.; Xiao, Y.L. Experimental study on heat transfer characteristics between particle flow and wall. Exp. Heat Transfer. 2023, 1–17. [Google Scholar] [CrossRef]
- Liu, S.; Mu, X.; Shen, S. Experimental study on the distribution of local heat transfer coefficient of falling film heat transfer outside horizontal tube. Int. J. Heat Mass Transf. 2021, 170, 121031. [Google Scholar] [CrossRef]
- Lobasov, A.S.; Minakov, A.V.; Rudyak, V.Y. The investigation of the velocity slip and the temperature jump effect on the heat transfer characteristics in a microchannel. Case Stud. Therm. Eng. 2022, 31, 101791. [Google Scholar] [CrossRef]
- Agrawal, C.; Kumar, R.; Gupta, A. Effect of jet diameter on the maximum surface heat flux during quenching of hot surface. Nucl. Eng. Des. 2013, 265, 727–736. [Google Scholar] [CrossRef]
- Wikström, P.; Blasiak, W.; Berntsson, F. Estimation of the transient surface temperature, heat flux and effective heat transfer coefficient of a slab in an industrial reheating furnace by using an inverse method. Steel Res. Int. 2007, 78, 63–70. [Google Scholar] [CrossRef]
- Zhang, Z.M.; Yu, W.; Cai, Q.W. Determination of heat transfer coefficient for roll quenching of medium-thick plate. Trans. Mater. Heat Treat. 2013, 34, 170–175. [Google Scholar]
- Xu, J.; Chen, G.; Bao, X. A Study on the Heat Transfer Characteristics of Steel Plate in the Matrix Laminar Cooling Process. Materials 2021, 14, 5680. [Google Scholar] [CrossRef] [PubMed]
- Malinowski, Z.; Telejko, T.; Hadała, B. Dedicated three dimensional numerical models for the inverse determination of the heat flux and heat transfer coefficient distributions over the metal plate surface cooled by water. Int. J. Heat Mass Transfer. 2014, 75, 347–361. [Google Scholar] [CrossRef]
- Karwa, N.; Gambaryan-Roisman, T.; Stephan, P. Experimental investigation of circular free-surface jet impingement quenching: Transient hydrodynamics and heat transfer. Exp. Therm. Fluid Sci. 2011, 35, 1435–1443. [Google Scholar] [CrossRef]
- Zou, L.; Ning, L.; Wang, X. Evaluation of interfacial heat transfer coefficient based on the experiment and numerical simulation in the air-cooling process. Heat Mass Transf. 2022, 58, 337–354. [Google Scholar] [CrossRef]
- Zhang, Z.M.; Yu, W.; Cai, Q.W. Control Basis for Cooling Rate of Plates during Roller Quenching in High-Pressure Zone. Adv. Mater. Res. 2012, 538, 2090–2094. [Google Scholar] [CrossRef]
- Yuan, G.; Han, Y.; Wang, C. Cooling mechanism of quenching process of roll quenching machine for medium-thick plate. Trans. Mater. Heat Treat. 2010, 31, 148–152. [Google Scholar]
- Wang, C.; Wang, Z.; Yuan, G. Heat transfer during quenching by plate roller quenching machine. J. Iron Steel Res. Int. 2013, 20, 1–5. [Google Scholar] [CrossRef]
- Zhang, J.K.; Zhang, R.M.; Chen, Y.Y. Temperature field simulation of quenching and cooling process of roll quenching machine. Heat Treat. Met. 2011, 36, 85–88. [Google Scholar]
- Wang, X.Y.; Su, H.; Pan, T. ANSYS finite element simulation of the effect of surface cooling velocity on the temperature field of ultra-thick plate section. Mater. Sci. Technol. 2013, 21, 49–54. [Google Scholar]
- Cui, D.; Liang, H. Numerical simulation on quenching temperature field of 40Cr steel. Adv. Mater. Res. 2011, 154, 417–420. [Google Scholar] [CrossRef]
- Carlone, P.; Palazzo, G.S.; Pasquino, R. Finite element analysis of the steel quenching process: Temperature field and solid–solid phase change. Comput. Math. Appl. 2010, 59, 585–594. [Google Scholar] [CrossRef]
- Xie, Q.; Wang, Y.; Li, X. Two-dimensional transient heat transfer model of moving quenching jet based on machine learning. Int. J. Heat Mass Transf. 2022, 191, 122765. [Google Scholar] [CrossRef]
- Li, C.; Yu, H.; Deng, G. Numerical simulation of temperature field and thermal stress field of work roll during hot strip rolling. J. Iron Steel Res. Int. 2007, 14, 18–21. [Google Scholar] [CrossRef]
- Yuan, G.; Wang, G.D.; Wang, L.J. Temperature field analysis of quenching process in roll quenching machine for medium-thick plate. J. Northeast. Univ. (Nat. Sci.) 2010, 31, 527–530+538. [Google Scholar]
- Agrawal, C. Surface quenching by jet impingement—A review. Steel Res. Int. 2019, 90, 1800285. [Google Scholar] [CrossRef]
- Tong, C.N.; Gao, Y.D. A practical method for modeling heat transfer coefficients of water-cooled processes in steel plates. Iron Steel 2011, 46, 50–55. [Google Scholar]

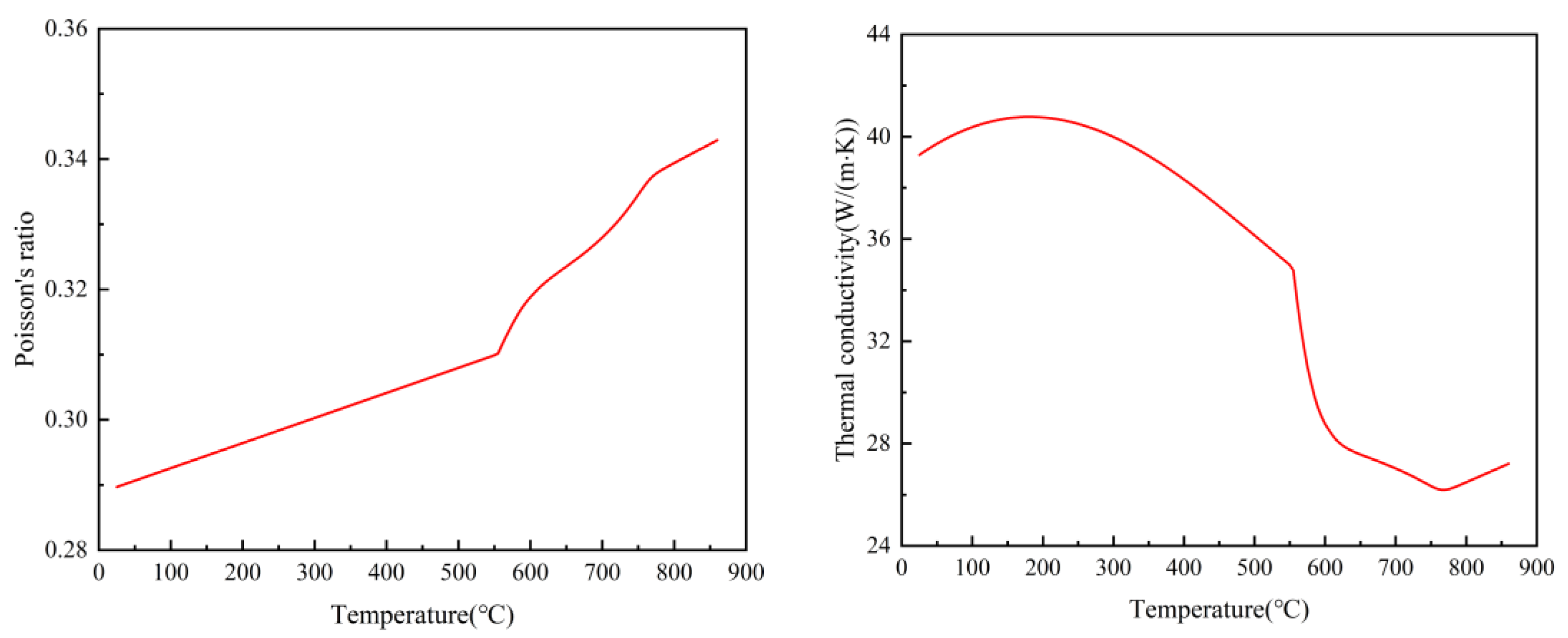
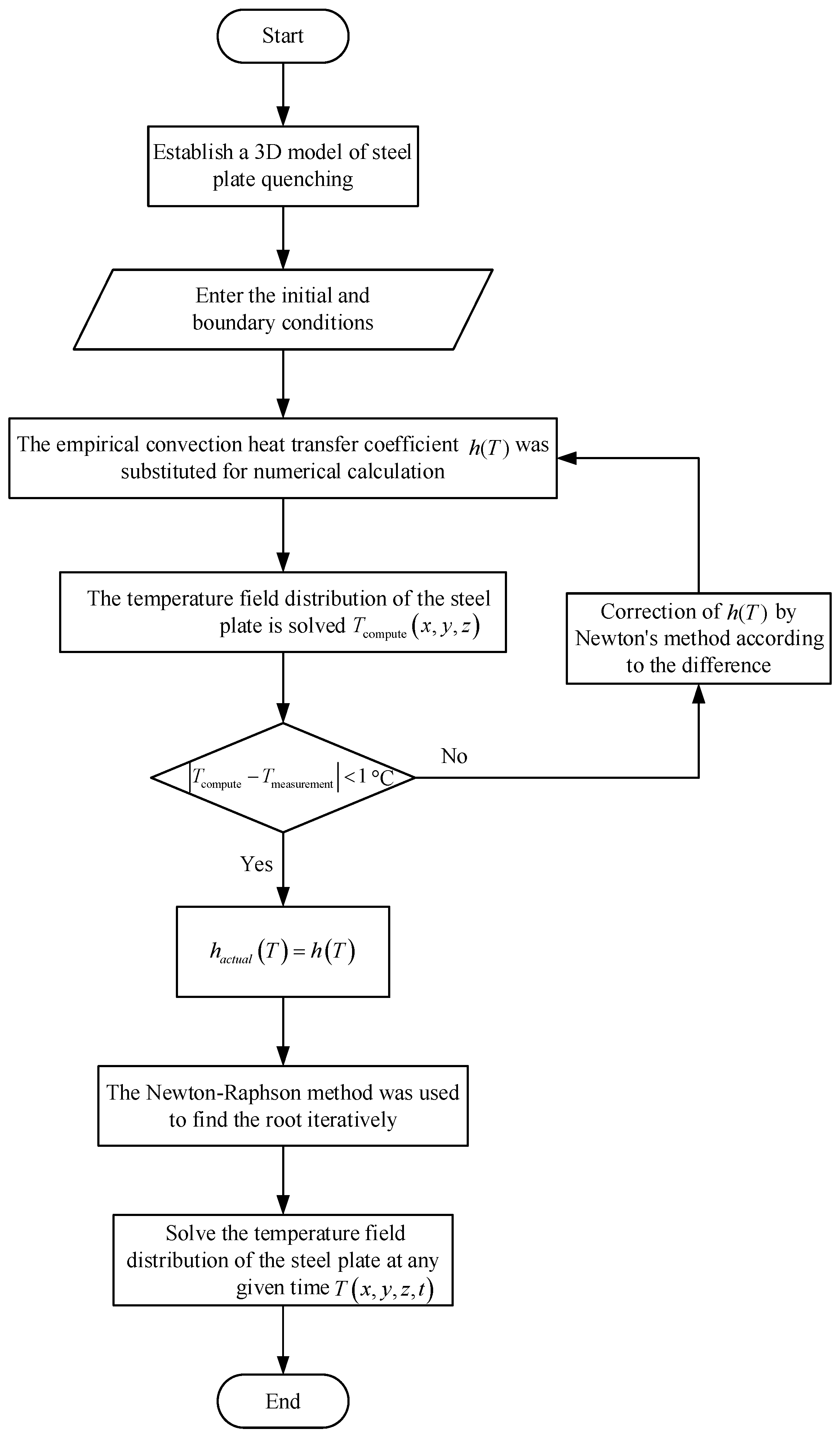

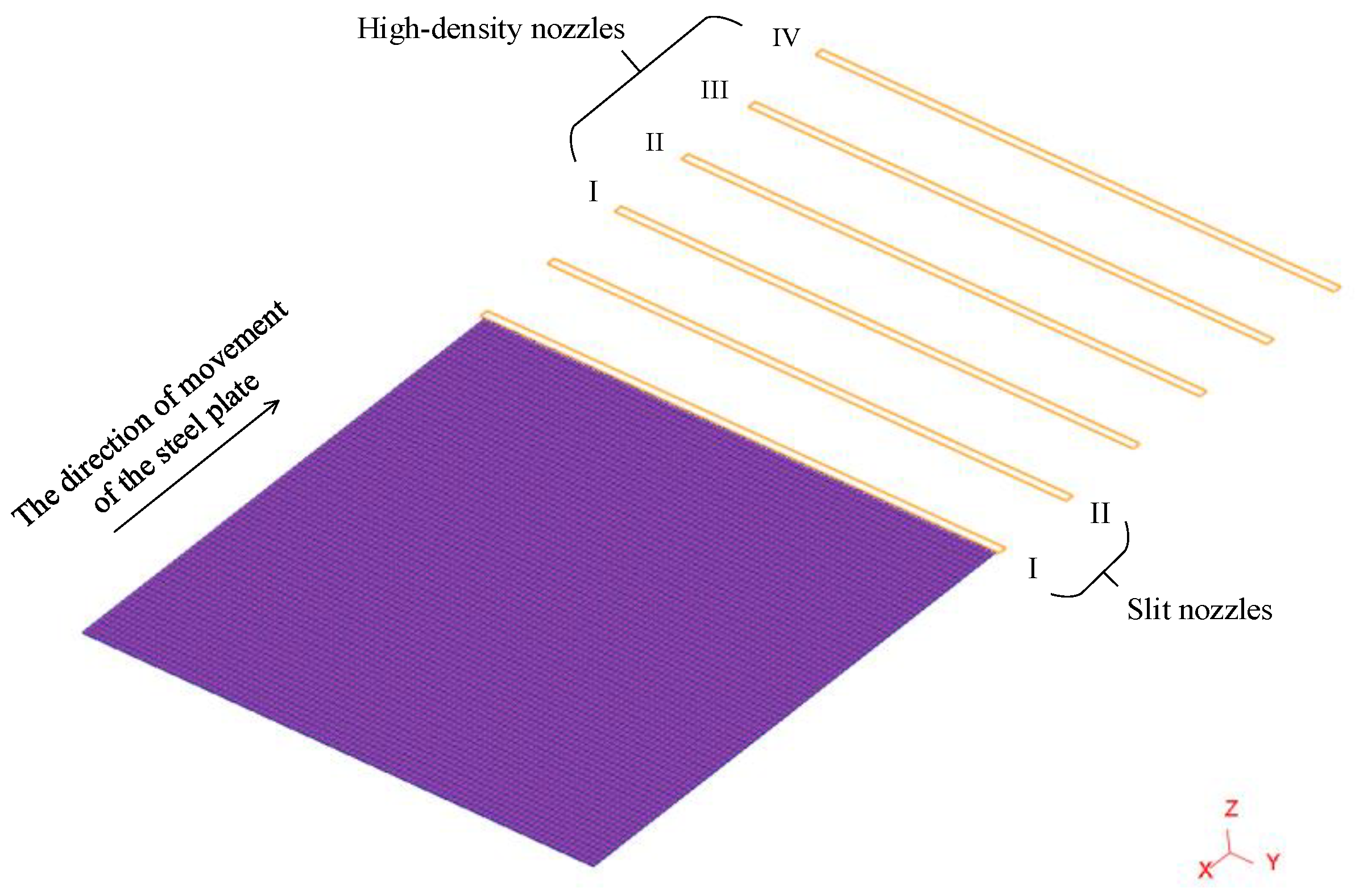
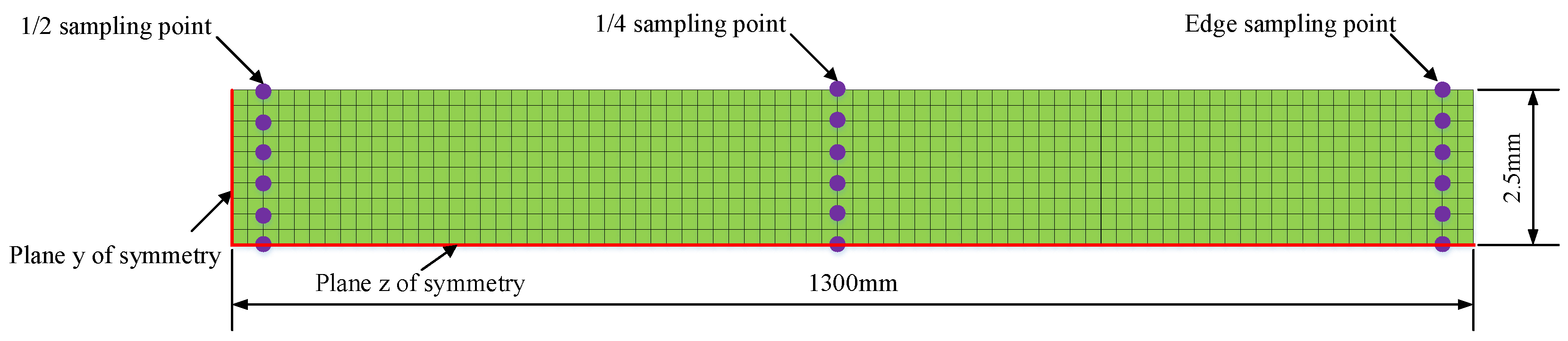



| Elemental | C | Si | Mn | P | S | Ti | Cu | Ni | Cr | Fe |
|---|---|---|---|---|---|---|---|---|---|---|
| mass percent % | 0.145 | 0.299 | 1.424 | 0.009 | 0.00035 | 0.015 | 0.0159 | 0.0117 | 0.694 | bal |
| Steel Plate Parameters | Cooling Process Parameters | Roller Conveyor Speed (m/s) | ||
|---|---|---|---|---|
| Thicknesses/mm | 5 | Cooling water temperature/°C | 22 | 0.4 |
| Width/mm | 2600 | Jet pressure/MPa | 0.8 | 0.6 |
| Minimum grid size/mm | 0.25 | Open-cooling temperature/°C | 810 | 0.8 |
| Steel Plate and Roller Conveyor Information | Key Cooling Information | ||
|---|---|---|---|
| Thickness/mm | 5 | Slit nozzle flow/(m3/h) | 500 |
| Width/mm | 2600 | High-density nozzle flow/(m3/h) | 160 |
| Open cold temperature/°C | 810 | Cooling water temperature/°C | 22 |
| Roll seam setting/mm | 5.05 | Jet pressure/MPa | 0.8 |
| Roller conveyor speed/(m/s) | 0.8 | Upper and lower water ratio settings | 1.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Li, X.; Yi, K.; Elmi, S.A. Research on the Temperature and Thermal Stress of the Roll Quenching Process of Thin Plates. Metals 2024, 14, 83. https://doi.org/10.3390/met14010083
Wang J, Li X, Yi K, Elmi SA. Research on the Temperature and Thermal Stress of the Roll Quenching Process of Thin Plates. Metals. 2024; 14(1):83. https://doi.org/10.3390/met14010083
Chicago/Turabian StyleWang, Jianhui, Xuetong Li, Kesong Yi, and Sahal Ahmed Elmi. 2024. "Research on the Temperature and Thermal Stress of the Roll Quenching Process of Thin Plates" Metals 14, no. 1: 83. https://doi.org/10.3390/met14010083
APA StyleWang, J., Li, X., Yi, K., & Elmi, S. A. (2024). Research on the Temperature and Thermal Stress of the Roll Quenching Process of Thin Plates. Metals, 14(1), 83. https://doi.org/10.3390/met14010083






