Miniature Tensile and Small Punch Testing: Mechanical Performance and Application in Hydrogen Embrittlement Analysis
Abstract
:1. Introduction
2. Experimental Procedures
3. Finite Element Models and Material Parameters
4. Results and Discussions
4.1. Experimental Results
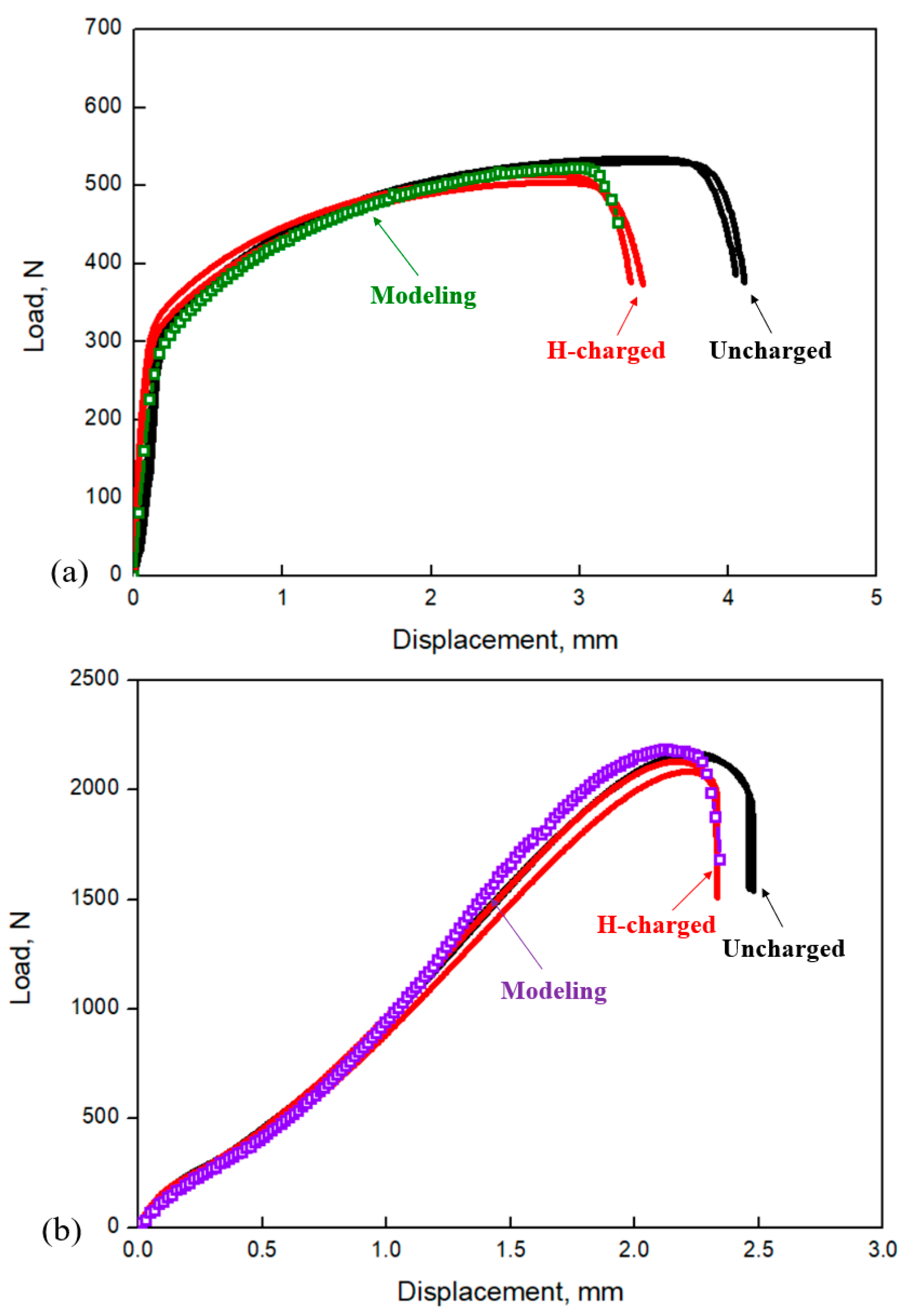
4.2. Finite Element Results
4.3. Application in Hydrogen Embrittlement Sensitivity Analysis
5. Conclusions
- (1)
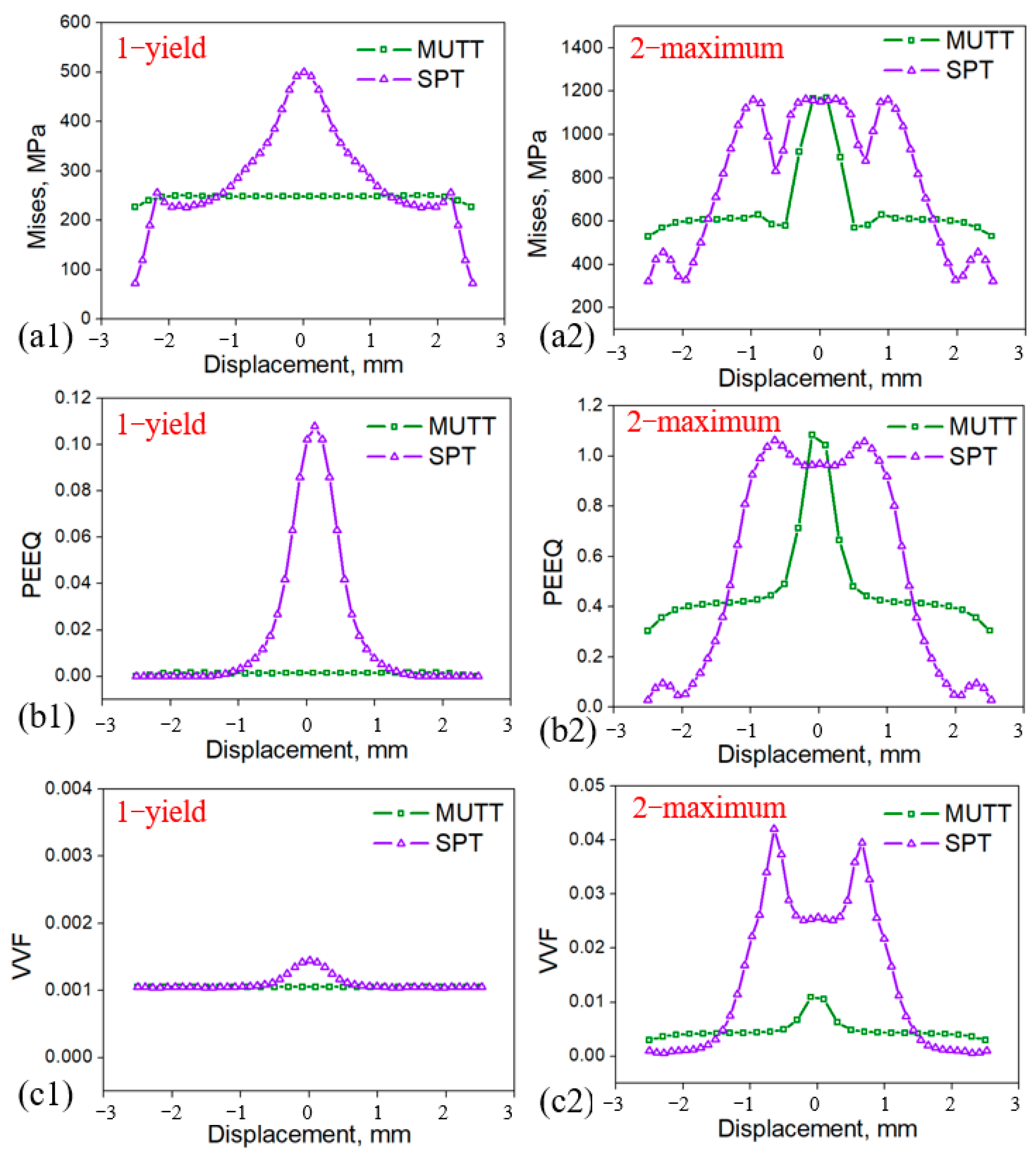
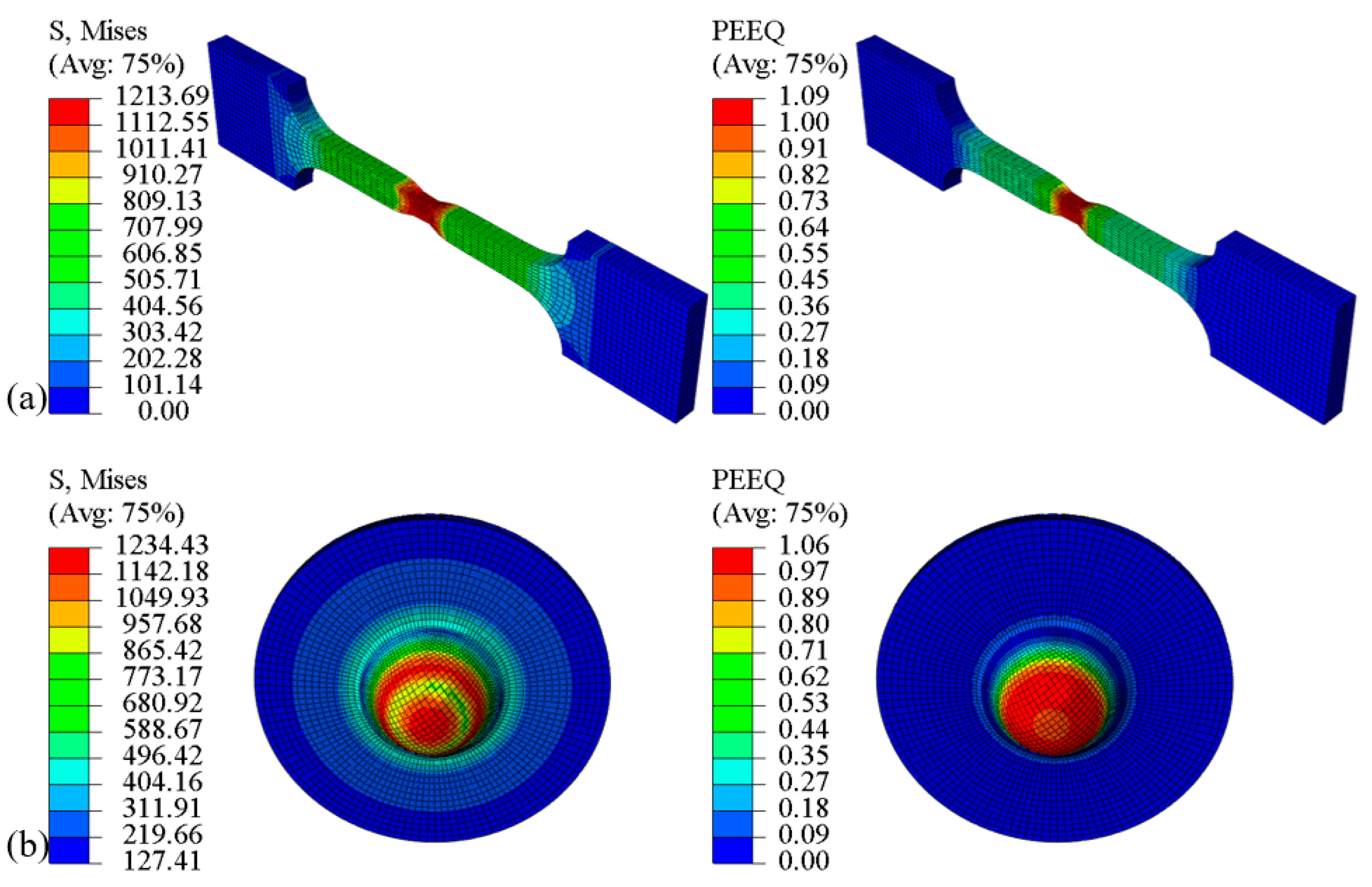
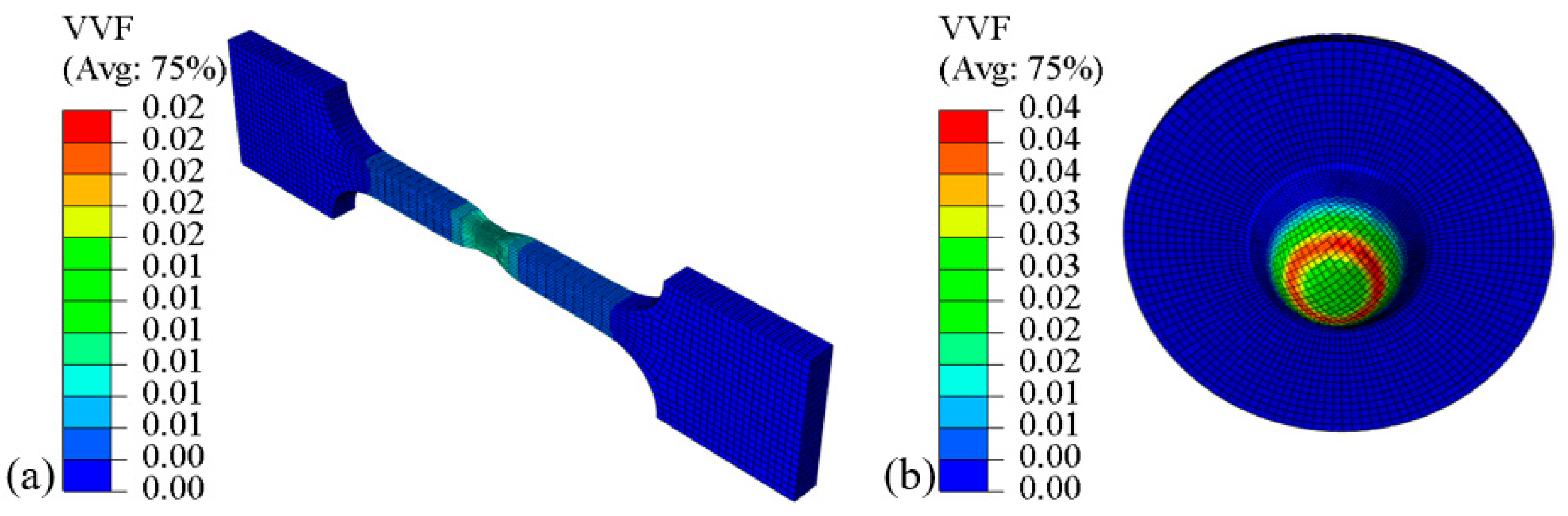
- The stress–strain distributions of the miniature tensile test and small punch test are different due to their distinct deformation processes. The maximum stress–strain points of the miniature tensile test specimen are located at the gauge length center, whereas those of the small punch specimen are concentrated on the circular contact surface with the punch ball. Before the failure stage, the achieved maximum Mises stress and equivalent plastic strain values of the miniature tensile test and small punch test were very close, but the areas reaching the maximum damage of the small punch specimen are relatively large. During damage evolution, the maximum void volume fraction values of the small punch test () are twice that of the miniature uniaxial tensile test ().
- (2)
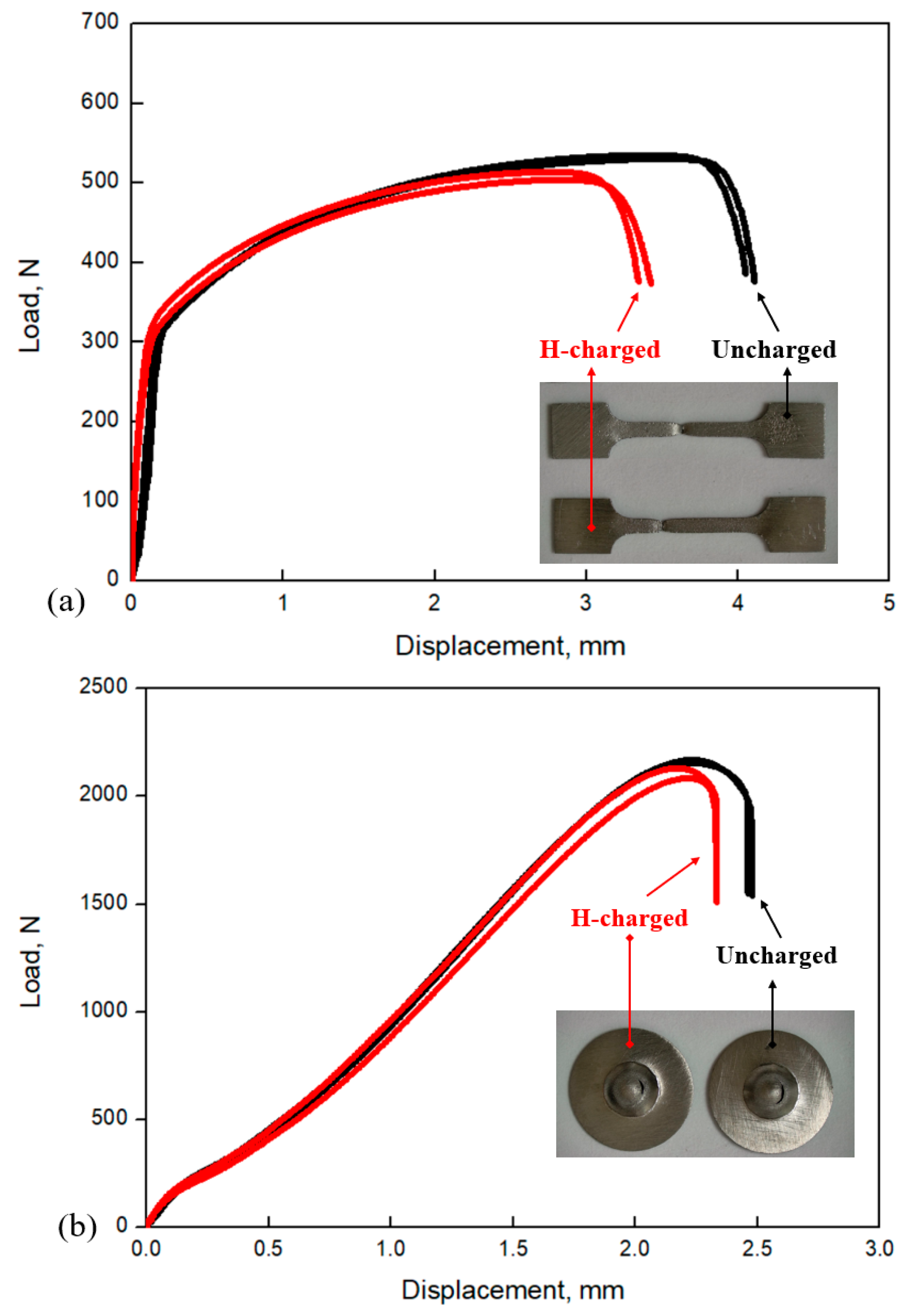
- The hydrogen embrittlement sensitivity of 316L stainless steel was characterized through miniature tensile test and small punch test. The GTN damage parameters of hydrogen-charged miniature tensile specimen and small punch specimen were determined based on the inverse finite element analysis. The hydrogen-induced ductility loss is mainly related to the parameters of nucleation strain , volume fraction of the nucleated voids and critical void volume fraction . Among them, the difference in critical void volume fraction is the most obvious. The value of the hydrogen-charged miniature tensile specimen was reduced from 0.025 to 0.0055, which is about a quarter smaller than that of the hydrogen-charged small punch specimen ().
- (3)
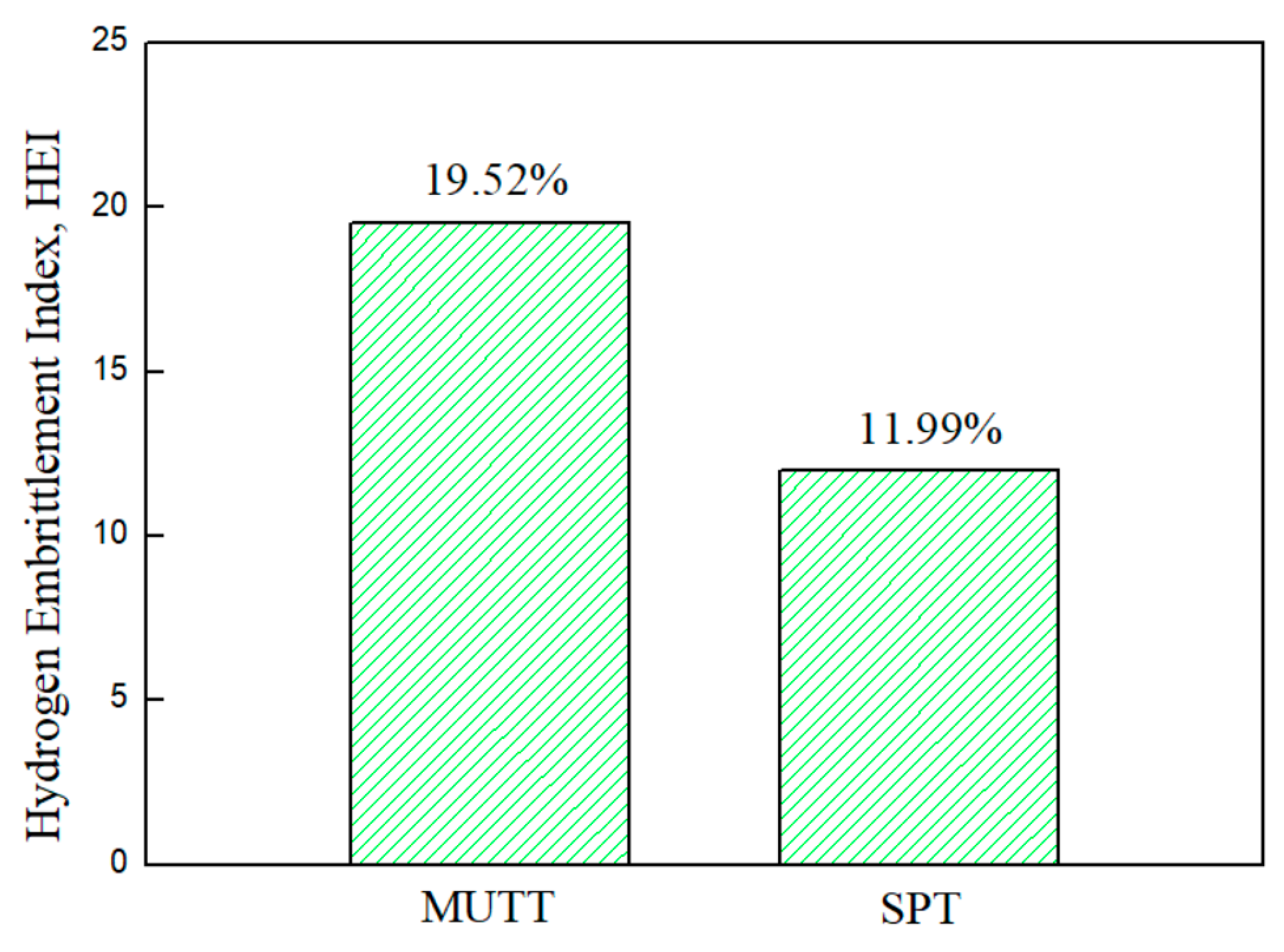
- Under the same hydrogen charging environment and displacement rate, the determined hydrogen embrittlement index based on the loss of fracture energy of miniature tensile test () is higher than that of the small punch test , which is consistent with the determined embrittlement indexes based on the elongation, area reduction and thickness reduction. The calculations and correlations of hydrogen embrittlement sensitivity under different sizes of specimens need to be focused on. This research can provide a reference for the comparison of multi-scale combined testing and its application performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Baik, J.M.; Buck, O.; Kameda, J. Small punch test evaluation of intergranular embrittlement of an alloy steel. Scr. Metall. 1983, 17, 1443–1447. [Google Scholar] [CrossRef]
- Misawa, T.; Adachi, T.; Saito, M.; Hamaguchi, Y. Small punch tests for evaluating ductile-brittle transition behavior of irradiated ferritic steels. J. Nucl. Mater. 1987, 150, 194–202. [Google Scholar] [CrossRef]
- Bruchhausen, M.; Holmström, S.; Simonovski, I.; Austin, T.; Lapetite, J.M.; Ripplinger, S.; De Haan, F. Recent developments in small punch testing: Tensile properties and DBTT. Theor. Appl. Fract. Mech. 2016, 86, 2–10. [Google Scholar] [CrossRef]
- Wang, J.; Zheng, Y.; Ling, X. Damage analysis of in-service ethylene cracking furnace tubes using small punch test. Eng. Fail. Anal. 2023, 152, 107438. [Google Scholar] [CrossRef]
- Seo, K.W.; Kim, Y.J.; Kim, K.S. Quantification of pre-strain effect on ductile fracture and application to irradiation embrittlement problems. Eng. Fract. Mech. 2024, 300, 109986. [Google Scholar] [CrossRef]
- Kodaira, Y.; Takano, Y.; Yonezu, A. Characterization of creep deformation behavior of porous polymer membrane under Small-Punch test. Eng. Fail. Anal. 2022, 135, 106149. [Google Scholar] [CrossRef]
- Geng, X.; Peng, J.; Jiang, L.; Liu, X.; Tu, Y.; Xue, Z. Experimental study of mechanical properties and fracture modes in different regions of the nickel-based welding joint based on small punch test. Weld. World 2023, 67, 637–650. [Google Scholar] [CrossRef]
- Singh, S.; Santana Pérez, O.; Rodríguez González, M.C.; Oksman, K.; Maspoch, M.L. Mechanical behaviour of poly (lactic acid)/cellulose nanocrystal nanocomposites: A comparative study between conventional tensile test and small punch test. Express Polym. Lett. 2020, 14, 1127–1136. [Google Scholar] [CrossRef]
- Reggente, M.; Angeloni, L.; Passeri, D.; Chevallier, P.; Turgeon, S.; Mantovani, D.; Rossi, M. Mechanical characterization of methanol plasma treated fluorocarbon ultrathin films through atomic force microscopy. Front. Mater. 2020, 6, 338. [Google Scholar] [CrossRef]
- Lucon, E.; Benzing, J.T.; Derimow, N.; Hrabe, N. Small punch testing to estimate the tensile and fracture properties of additively manufactured Ti-6Al-4V. J. Mater. Eng. Perform. 2021, 30, 5039–5049. [Google Scholar] [CrossRef]
- Torres, J.; Gordon, A.P. Mechanics of the small punch test: A review and qualification of additive manufacturing materials. J. Mater. Sci. 2021, 56, 10707–10744. [Google Scholar] [CrossRef]
- García-Blanco, I.; García, T.E.; Cabezas, J.G.; González, R.; Álvarez, G.; Rodríguez, C. Use of the small punch test for mechanical characterization of co– based laser cladding joint. Eng. Fail. Anal. 2024, 159, 108129. [Google Scholar] [CrossRef]
- Depover, T.; Wan, D.; Wang, D.; Barnoush, A.; Verbeken, K. The effect of hydrogen on the crack initiation site of TRIP-assisted steels during in-situ hydrogen plasma micro-tensile testing: Leading to an improved ductility? Mater. Charact. 2020, 167, 110493. [Google Scholar] [CrossRef]
- Álvarez, G.; Arniella, V.; Belzunce, F.J.; Rodríguez, C. Study of the influence of current density and displacement rate on hydrogen embrittlement using small punch tests. Theor. Appl. Fract. Mech. 2023, 125, 103838. [Google Scholar] [CrossRef]
- Bae, K.O.; Shin, H.S.; Baek, U.B. Quantitative evaluation of hydrogen embrittlement susceptibility in various steels for energy use using an in-situ small punch test. Int. J. Hydrogen Energy 2021, 46, 20107–20118. [Google Scholar] [CrossRef]
- Arroyo, B.; Andrea, L.; Gutiérrez-Solana, F.; Álvarez, J.A. Time optimization of the step loading technique in hydrogen embrittlement small punch tests. Theor. Appl. Fract. Mech. 2022, 117, 103206. [Google Scholar] [CrossRef]
- Gussev, M.N.; Howard, R.H.; Terrani, K.A.; Field, K.G. Sub-size tensile specimen design for in-reactor irradiation and post-irradiation testing. Nucl. Eng. Des. 2017, 320, 298–308. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, T.; Zhang, J.; Ding, H.; Xiao, S.; Lu, L.; Yang, B.; Yang, G.; Liu, Y. A review of selected small specimen test techniques for identifying deformation and failure properties of metallic materials. J. Mater. Sci. 2023, 58, 63–100. [Google Scholar] [CrossRef]
- Liu, H.; Chen, R.; Wen, M.; Zhang, L.; Shen, Y. Optimizing parallel section length for small tensile specimen with fabrication non-uniformity in thickness. Fusion Eng. Des. 2019, 147, 111244. [Google Scholar] [CrossRef]
- GB/T 29459-2012; Test Method for Small Punch Testing of Metallic Materials for in-Service Pressurized Equipment. China National Standardization Management Committee: Beijing, China, 2012.
- ASTM E3205-2020; Standard Test Method for Small Punch Testing of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2020.
- BS EN 10371-2021; Metallic Materials—Small Punch Test Method. British Standards Institution: London, UK, 2021.
- Cao, Y.; Ren, C.; Zu, Y.; Zhen, Y. Quantitative Characterization of Strength Properties of Girth Welded Joints Based on Small Punch Test. J. Mater. Eng. Perform. 2023, 1–12. [Google Scholar] [CrossRef]
- Bruchhausen, M.; Holmström, S.; Lapetite, J.M.; Ripplinger, S. On the determination of the ductile to brittle transition temperature from small punch tests on Grade 91 ferritic-martensitic steel. Int. J. Press. Vessel. Pip. 2017, 155, 27–34. [Google Scholar] [CrossRef]
- Álvarez, G.; Rodríguez, C.; Belzunce, F.J.; García, T.E. Use of notched small punch test specimens for the determination of fracture properties in structural steels. Theor. Appl. Fract. Mech. 2020, 106, 102442. [Google Scholar] [CrossRef]
- Lai, H.S.; Jiang, X. Determination of fracture toughness through small punch test of notched-tube specimen. Eng. Fract. Mech. 2023, 279, 109059. [Google Scholar] [CrossRef]
- Wen, C.; Xu, T.; Guan, K. Correlation factor study of small punch creep test and its life prediction. Materials 2016, 9, 796. [Google Scholar] [CrossRef]
- Peng, J.; Gao, M.; Zhang, H.; Geng, X.; Liu, X.; Pan, H. Small punch creep test reveals the differences of high-temperature creep behaviours for laser powder bed fusion and Rolled Inconel 718 alloys. Mater. Sci. Eng. A 2023, 886, 145698. [Google Scholar] [CrossRef]
- ASTM E8/E8M-15a; Standard Test Methods for Tension Testing of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2015.
- Gussev, M.; Busby, J.; Field, K.; Sokolov, M.; Gray, S. Role of scale factor during tensile testing of small specimens. In Small Specimen Test Techniques: 6th Volume; ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar]
- Zheng, P.; Chen, R.; Liu, H.; Chen, J.; Zhang, Z.; Liu, X.; Shen, Y. On the standards and practices for miniaturized tensile test—A review. Fusion Eng. Des. 2020, 161, 112006. [Google Scholar] [CrossRef]
- Gurson, A.L. Continuum theory of ductile rupture by void nucleation and growth: Part I—Yield criteria and flow rules for porous ductile media. J. Eng. Mater. Technol. 1977, 99, 2–15. [Google Scholar] [CrossRef]
- Tvergaard, V. Influence of voids on shear band instabilities under plane strain conditions. Int. J. Fract. 1981, 17, 389–407. [Google Scholar] [CrossRef]
- Peng, J.; Li, K.; Dai, Q.; Gao, G.; Zhang, Y.; Cao, W. Estimation of mechanical strength for pre-strained 316L austenitic stainless steel by small punch test. Vacuum 2019, 160, 37–53. [Google Scholar] [CrossRef]
- Shin, H.S.; Custodio, N.A.; Baek, U.B. Numerical analysis for characterizing hydrogen embrittlement behaviors induced in STS316L stainless steel using an in-situ small-punch test. Theor. Appl. Fract. Mech. 2021, 116, 103139. [Google Scholar] [CrossRef]

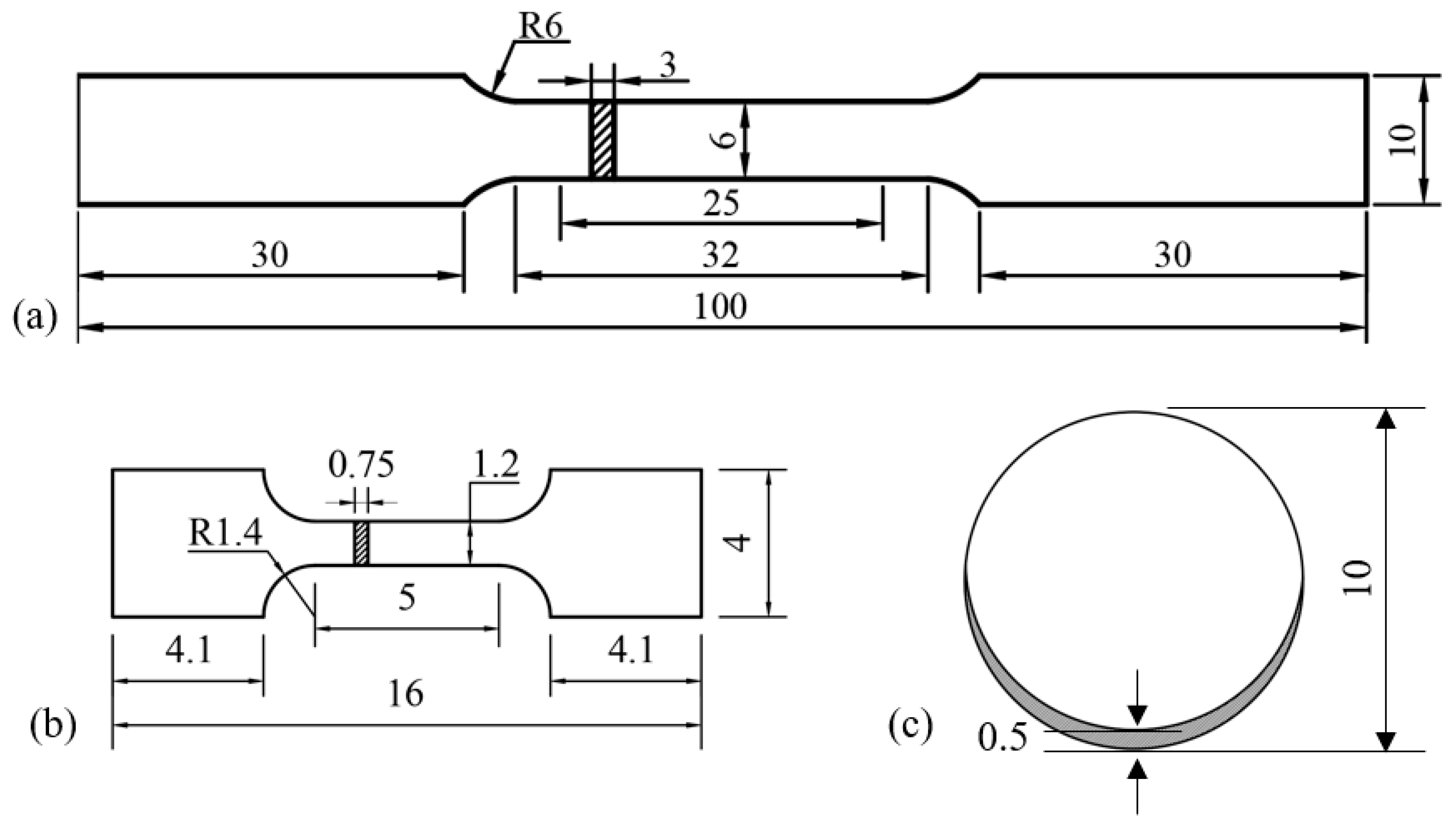
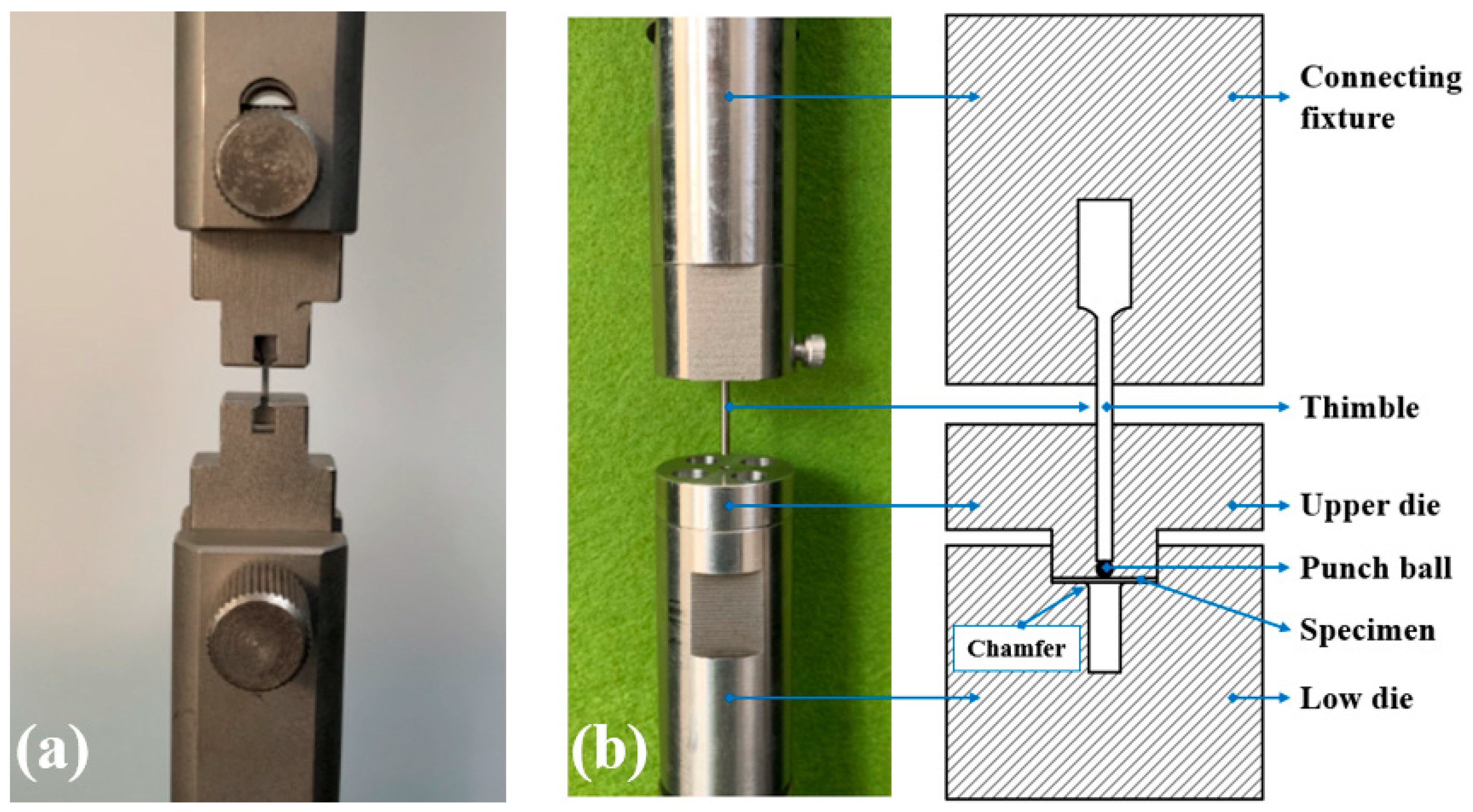
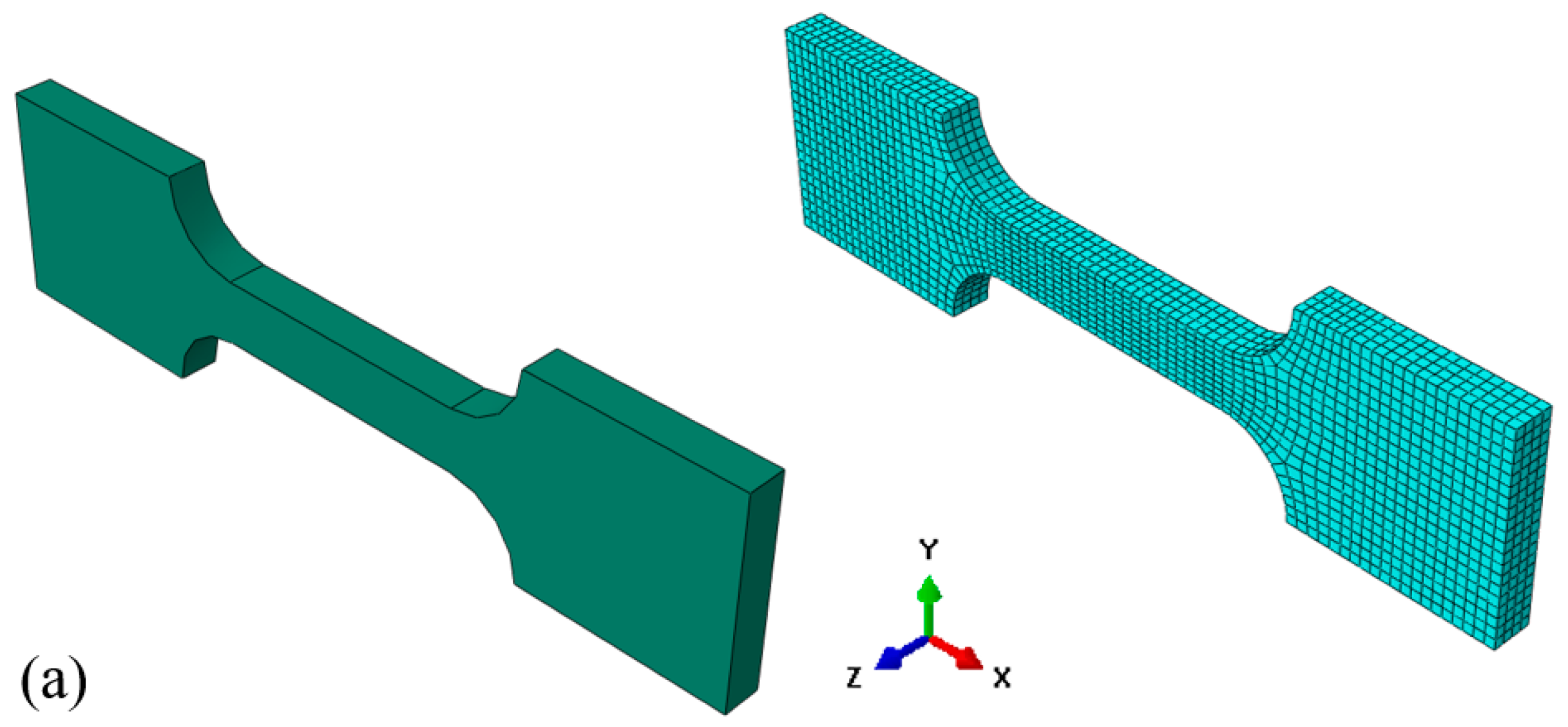
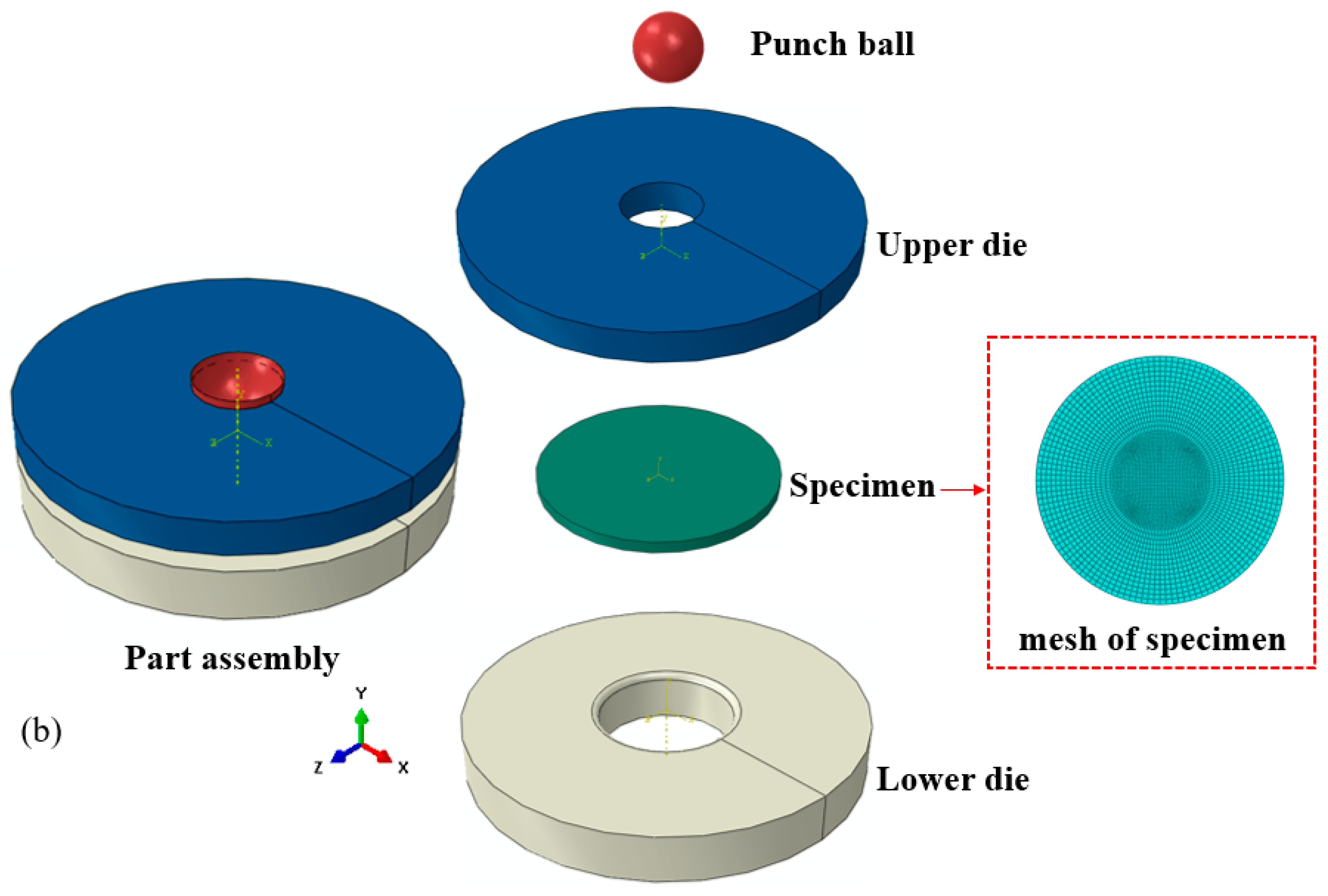
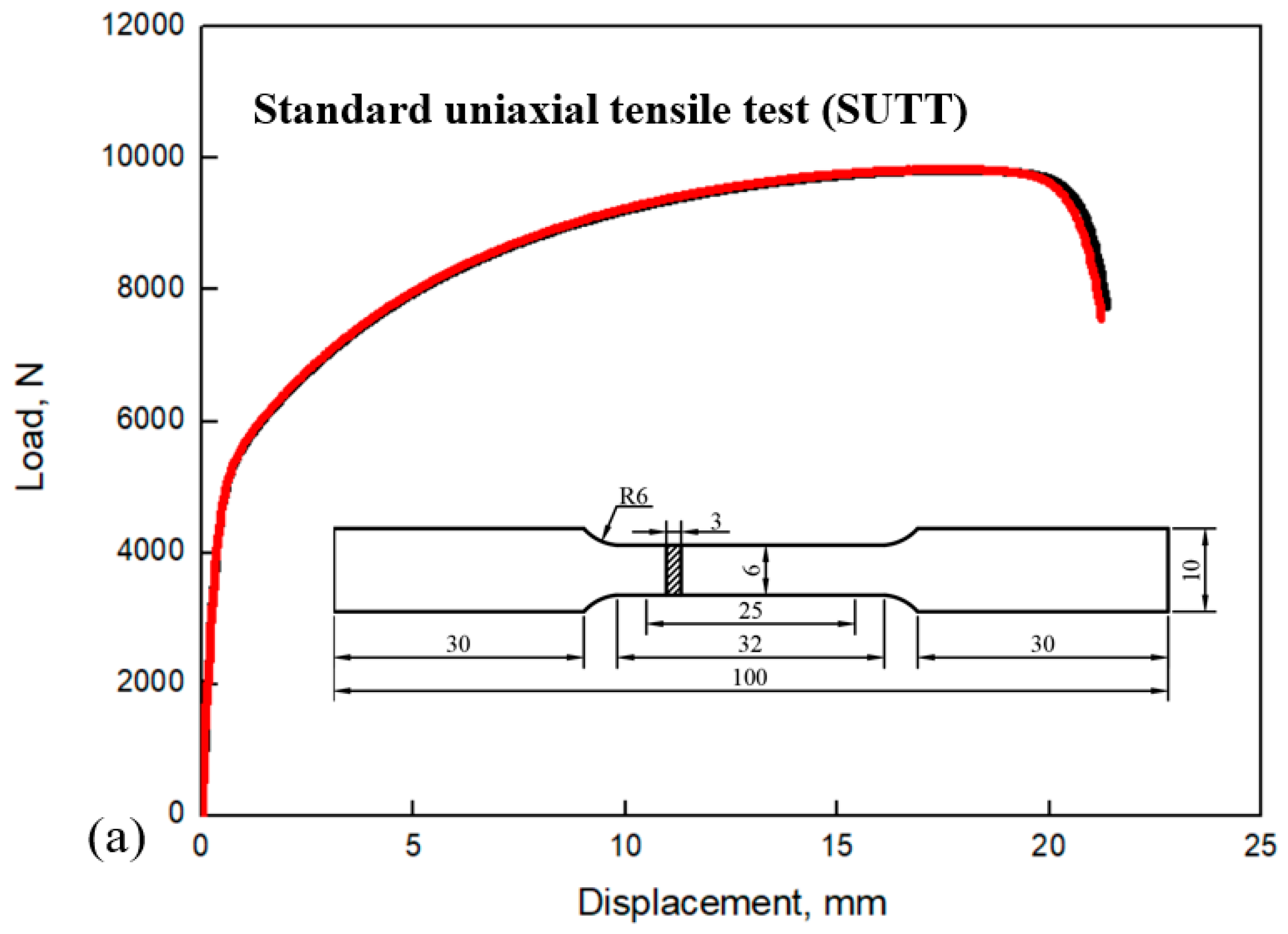



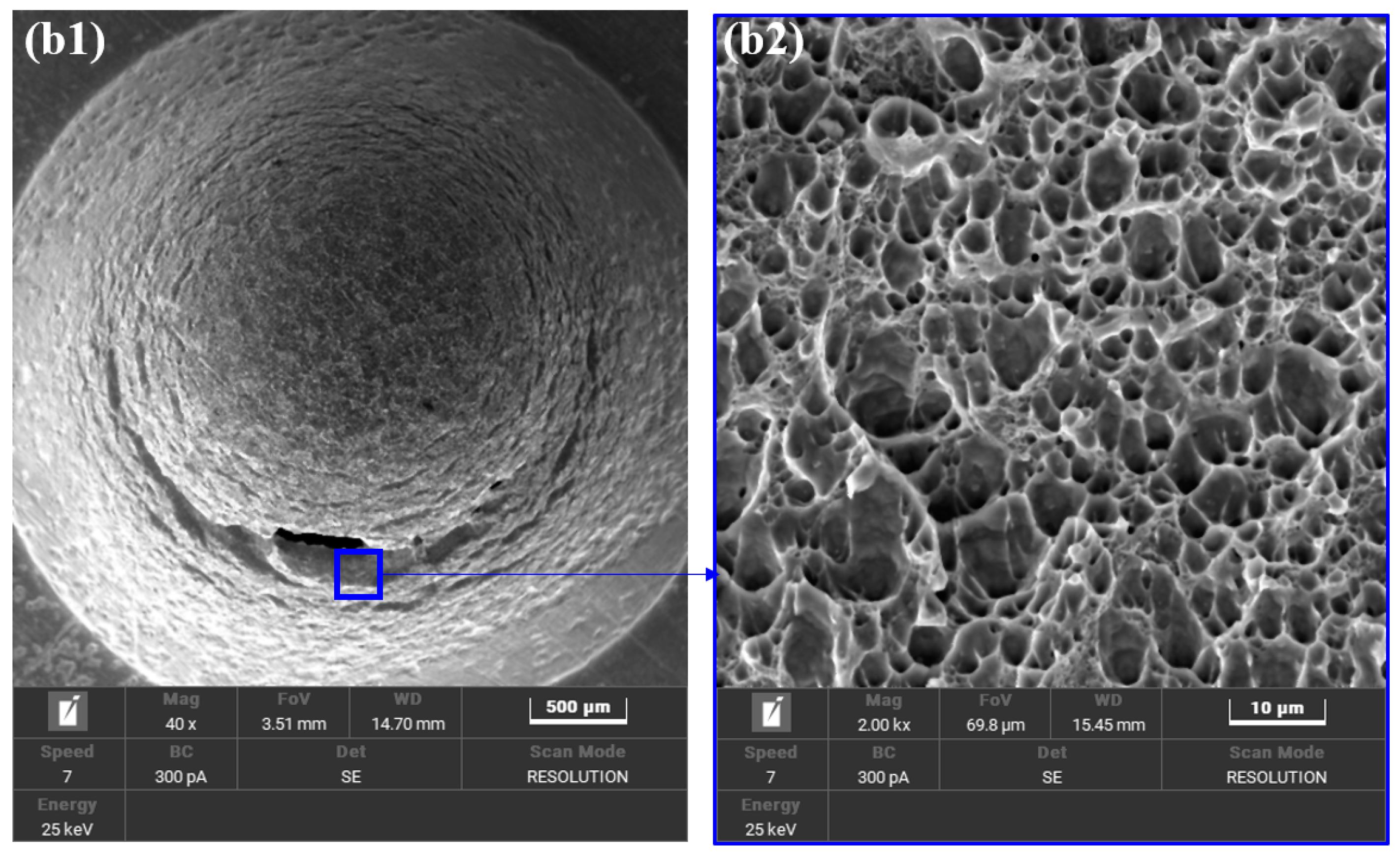
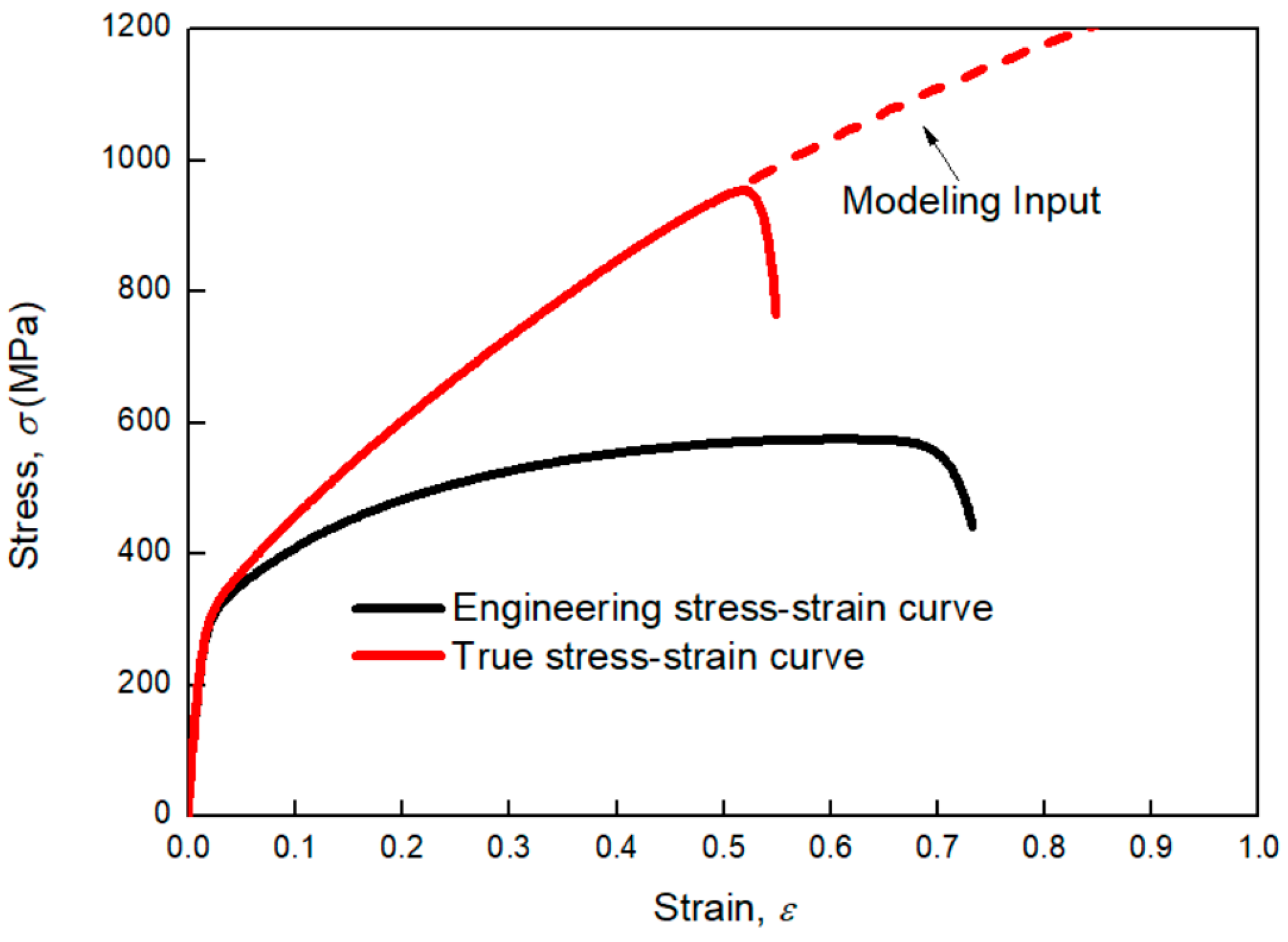

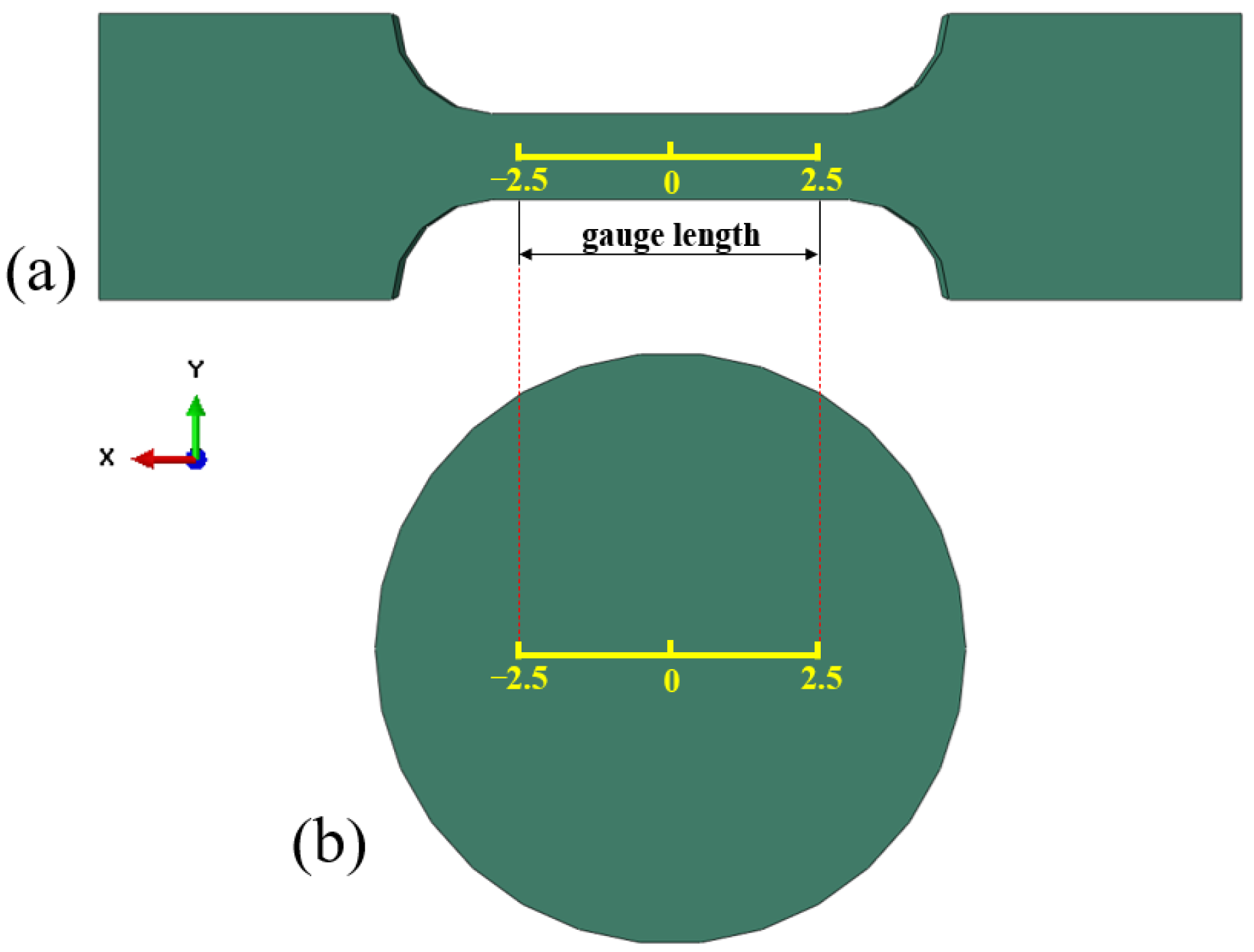


| C | Si | Mn | P | S | Ni | Cr | Mo | Fe |
|---|---|---|---|---|---|---|---|---|
| 0.02 | 0.42 | 1.63 | 0.023 | 0.002 | 12.17 | 17.23 | 2.18 | Bal. |
| Testing Type | (N) | (N) | (MPa) | (MPa) | (N) | (mm) | Fracture Energy (N·mm) |
|---|---|---|---|---|---|---|---|
| SUTT | 4102.58 | 9889.90 | 272.05 | 578.02 | 7911.92 | 21.31 | 183,618.61 |
| MUTT | 260.19 | 534.12 | 289.11 | 593.46 | 427.30 | 4.06 | 1883.66 |
| SPT | 173.65 | 2179.06 | / | 1757.65 | 2.49 | 3179.80 |
| Parameters | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Values | 1.5 | 1 | 2.25 | 0.99895 | 0.3 | 0.1 | 0.0025 | 0.025 | 0.1 |
| Parameters | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Uncharged | 1.5 | 1 | 2.25 | 0.99895 | 0.3 | 0.1 | 0.0025 | 0.025 | 0.1 |
| H-charged MUTT | 1.5 | 1 | 2.25 | 0.99895 | 0.15 | 0.1 | 0.004 | 0.0055 | 0.1 |
| H-charged SPT | 1.5 | 1 | 2.25 | 0.99895 | 0.2 | 0.1 | 0.0025 | 0.02 | 0.1 |
| Uncharged | Hydrogen-Charged | HEI (%) | |
|---|---|---|---|
| Elongation, A (%) | 52.63 | 38.97 | 25.95 |
| Area reduction, Z (%) | 62.98 | 27.54 | 56.27 |
| Uncharged | Hydrogen-Charged | HEI (%) | |
|---|---|---|---|
| Maximum displacement, , (mm) | 2.48 | 2.33 | 6.04 |
| Thickness reduction, ROT (%) | 63.75 | 59.82 | 6.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, P.; Zhou, W.; Miao, X.; Peng, J.; Liu, X. Miniature Tensile and Small Punch Testing: Mechanical Performance and Application in Hydrogen Embrittlement Analysis. Metals 2024, 14, 1104. https://doi.org/10.3390/met14101104
Tao P, Zhou W, Miao X, Peng J, Liu X. Miniature Tensile and Small Punch Testing: Mechanical Performance and Application in Hydrogen Embrittlement Analysis. Metals. 2024; 14(10):1104. https://doi.org/10.3390/met14101104
Chicago/Turabian StyleTao, Ping, Wei Zhou, Xinting Miao, Jian Peng, and Xuedong Liu. 2024. "Miniature Tensile and Small Punch Testing: Mechanical Performance and Application in Hydrogen Embrittlement Analysis" Metals 14, no. 10: 1104. https://doi.org/10.3390/met14101104
APA StyleTao, P., Zhou, W., Miao, X., Peng, J., & Liu, X. (2024). Miniature Tensile and Small Punch Testing: Mechanical Performance and Application in Hydrogen Embrittlement Analysis. Metals, 14(10), 1104. https://doi.org/10.3390/met14101104








