Accelerating Laser Powder Bed Fusion: The Influence of Roller-Spreading Speed on Powder Spreading Performance
Abstract
1. Introduction
2. Methodology
2.1. Mathematical Model
2.2. Numerical Model
2.3. Performance Parameters of the Spreading Process
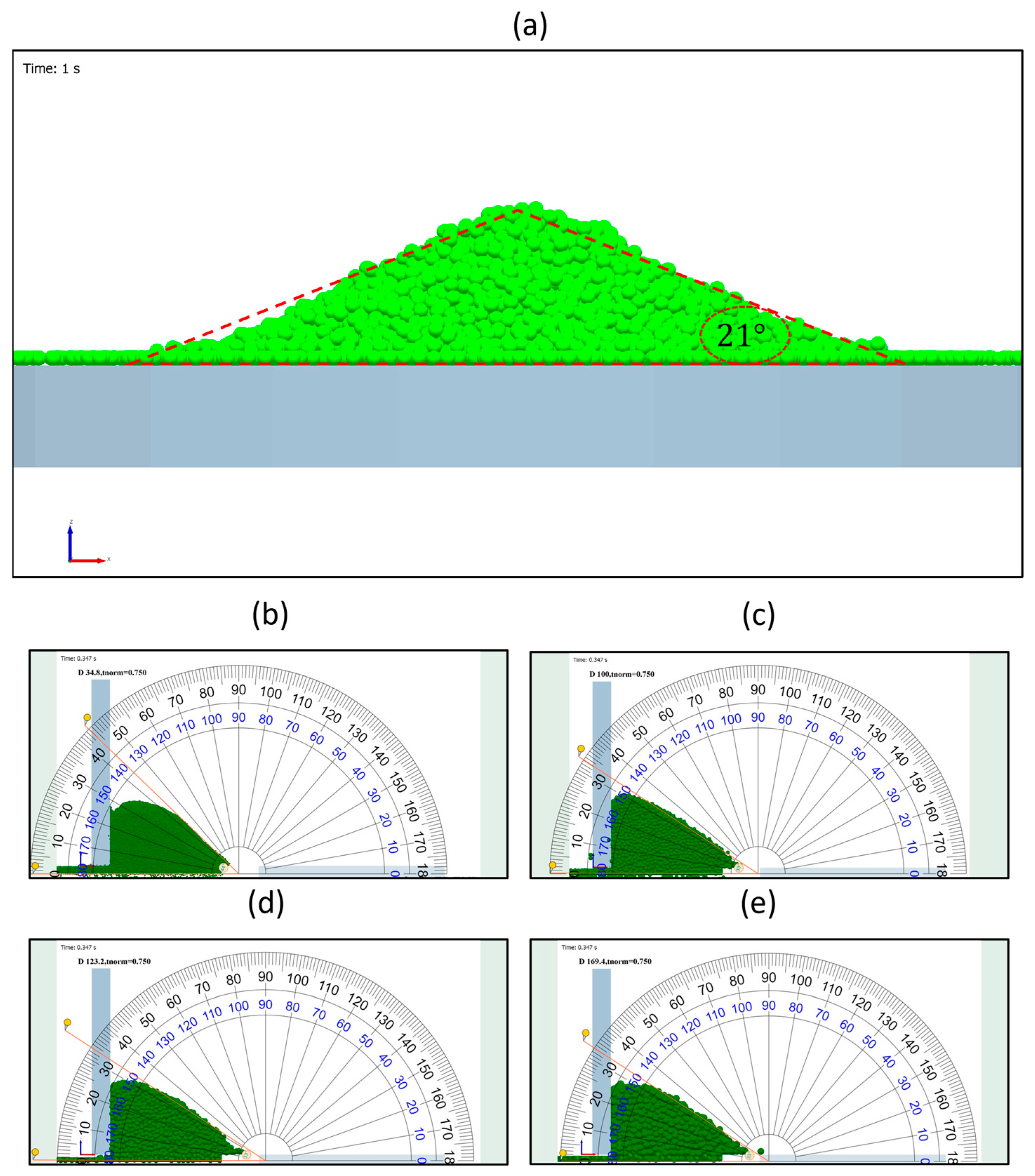
2.4. Material Calibration and Model Verification
2.5. Simulation Conditions
3. Results and Discussion
3.1. Microscopic Analysis
3.1.1. Effect of Spreading Speed on the Non-Rotating Roller
3.1.2. Effect of the Spreading Speed on Counter-Rotating Roller
3.1.3. Effect of the Spreading Speed on Forward-Rotating Roller
Sub-Rolling
Super-Rolling
3.2. Macroscopic Analysis
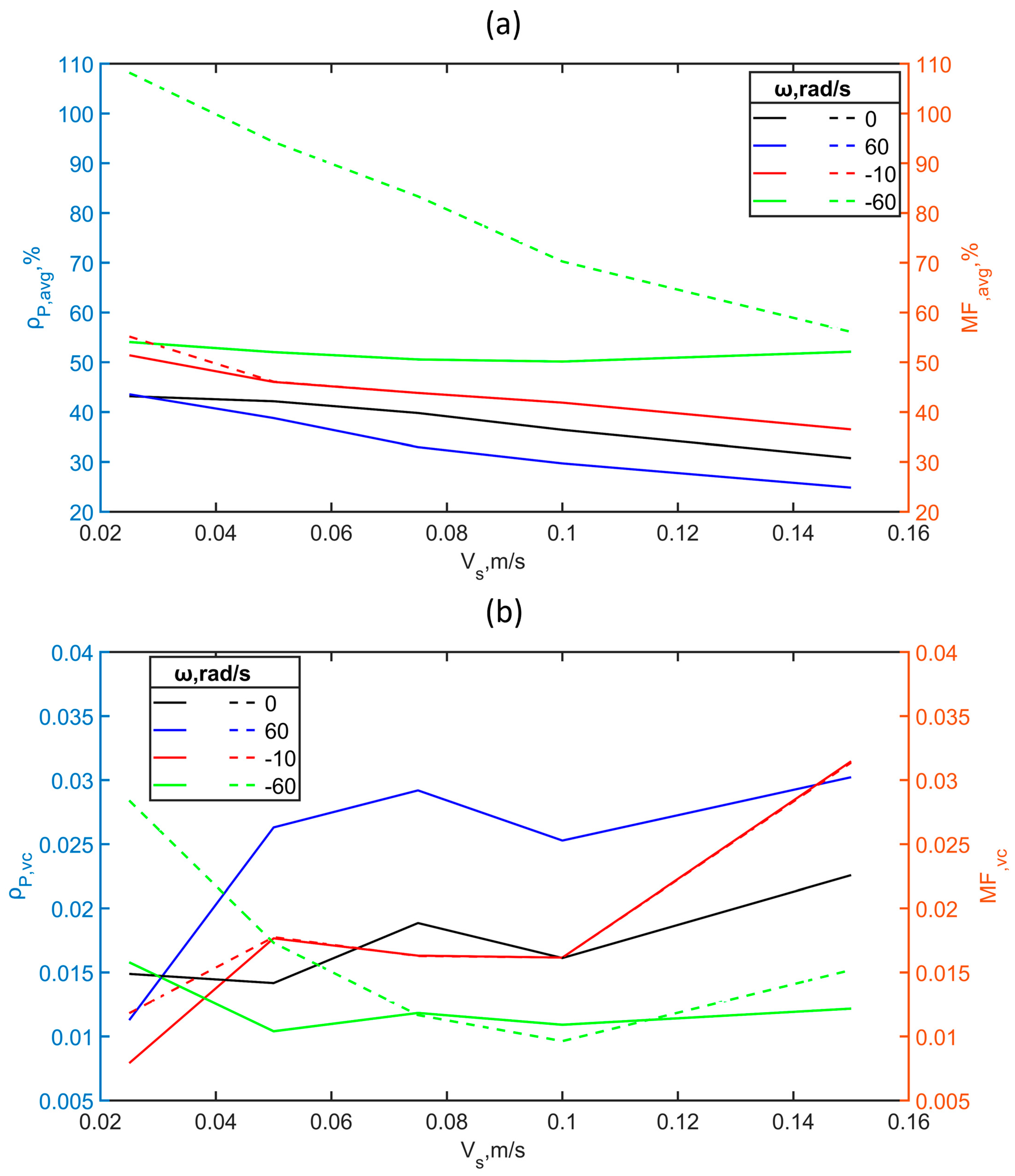
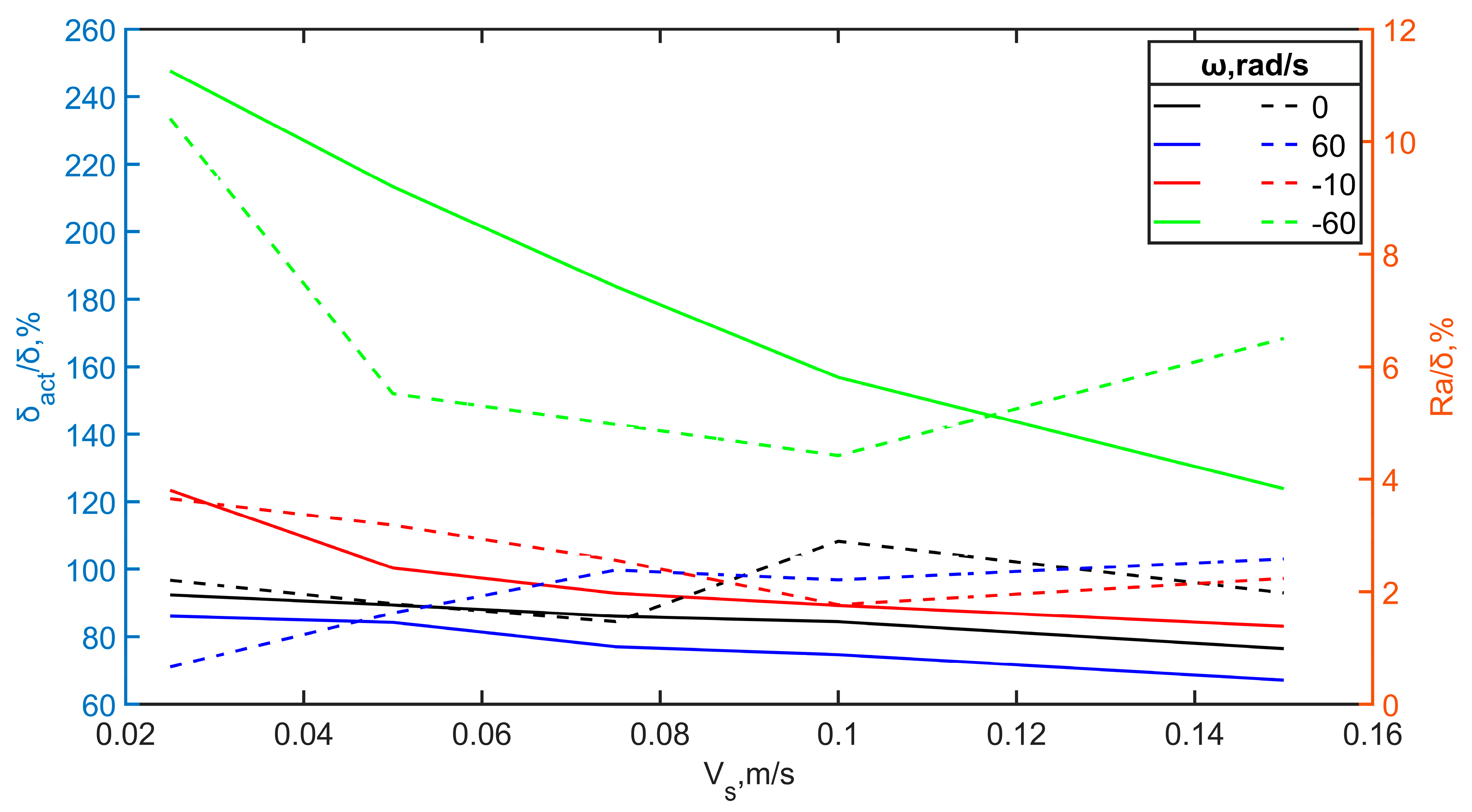
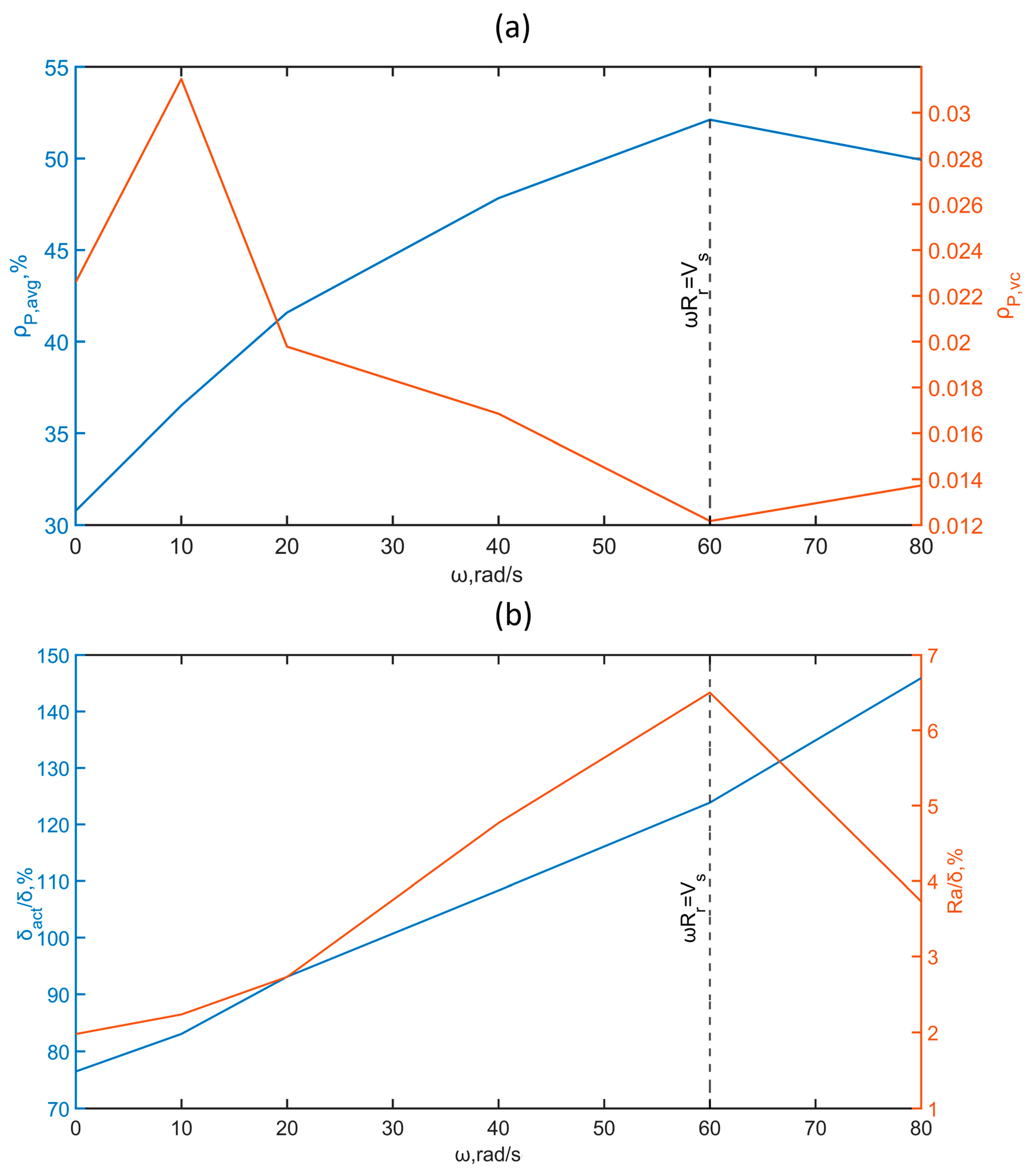
3.2.1. Effects of the Spreading Speed on the Macroscopic Properties
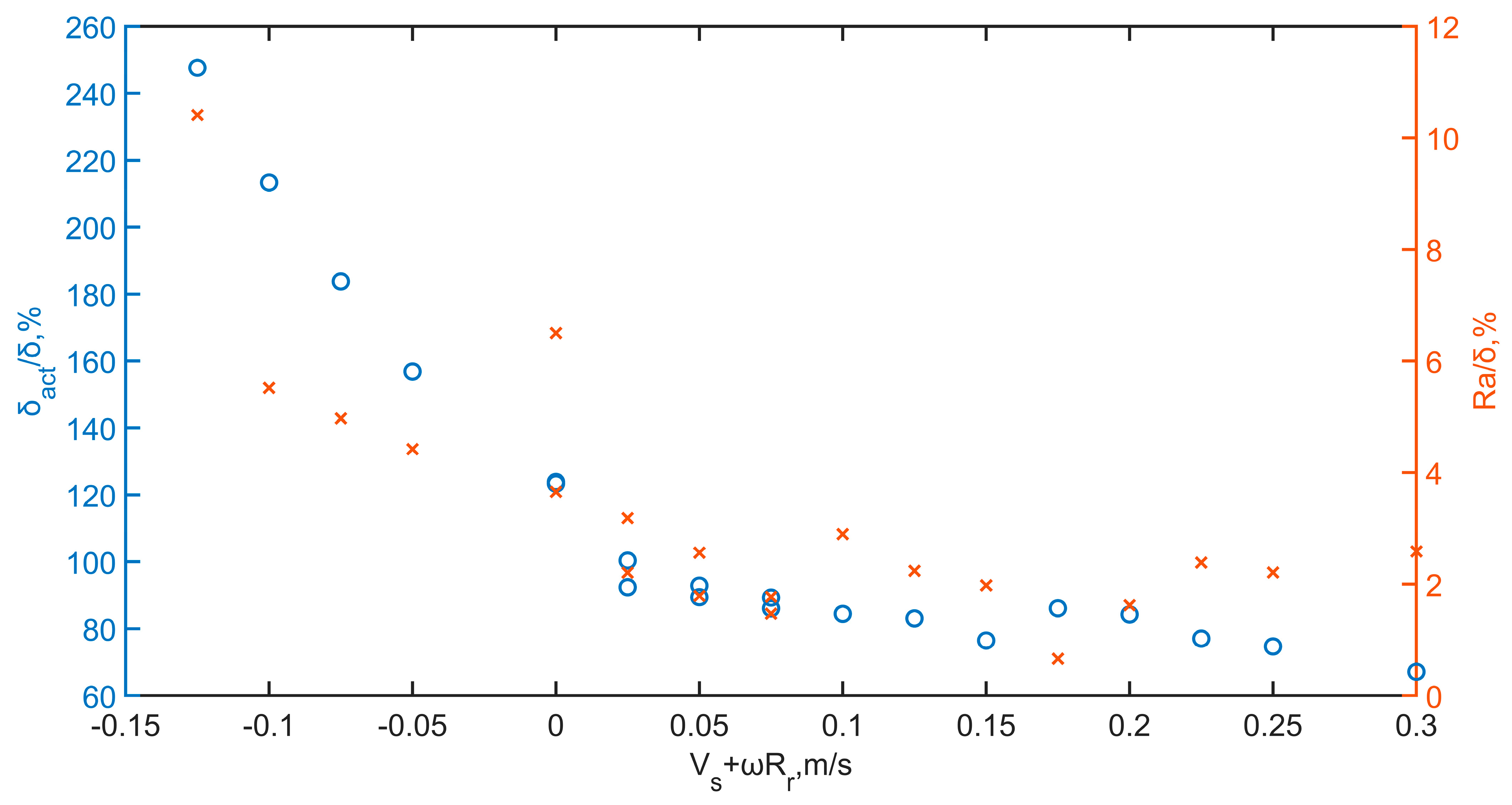
3.2.2. Effect of the Resultant Speed
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yakout, M.; Elbestawi, M.A.; Veldhuis, S.C. On the Characterization of Stainless Steel 316L Parts Produced by Selective Laser Melting. Int. J. Adv. Manuf. Technol. 2018, 95, 1953–1974. [Google Scholar] [CrossRef]
- Yakout, M.; Cadamuro, A.; Elbestawi, M.A.; Veldhuis, S.C. The Selection of Process Parameters in Additive Manufacturing for Aerospace Alloys. Int. J. Adv. Manuf. Technol. 2017, 92, 2081–2098. [Google Scholar] [CrossRef]
- Fereiduni, E.; Ghasemi, A.; Elbestawi, M. Unique Opportunities for Microstructure Engineering via Trace B4C Addition to Ti-6Al-4V through Laser Powder Bed Fusion Process: As-Built and Heat-Treated Scenarios. Addit. Manuf. 2022, 50, 102557. [Google Scholar] [CrossRef]
- Chen, H.; Chen, Y.; Liu, Y.; Wei, Q.; Shi, Y.; Yan, W. Packing Quality of Powder Layer during Counter-Rolling-Type Powder Spreading Process in Additive Manufacturing. Int. J. Mach. Tools Manuf. 2020, 153, 103553. [Google Scholar] [CrossRef]
- Zhang, J.; Tan, Y.; Xiao, X.; Jiang, S. Comparison of Roller-Spreading and Blade-Spreading Processes in Powder-Bed Additive Manufacturing by DEM Simulations. Particuology 2022, 66, 48–58. [Google Scholar] [CrossRef]
- Zhang, J.; Tan, Y.; Bao, T.; Xu, Y.; Xiao, X.; Jiang, S. Discrete Element Simulation of the Effect of Roller-Spreading Parameters on Powder-Bed Density in Additive Manufacturing. Materials 2020, 13, 2285. [Google Scholar] [CrossRef]
- Lee, Y.; Gurnon, A.K.; Bodner, D.; Simunovic, S. Effect of Particle Spreading Dynamics on Powder Bed Quality in Metal Additive Manufacturing. Integr. Mater. Manuf. Innov. 2020, 9, 410–422. [Google Scholar] [CrossRef]
- Yao, D.; An, X.; Fu, H.; Zhang, H.; Yang, X.; Zou, Q.; Dong, K. Dynamic Investigation on the Powder Spreading during Selective Laser Melting Additive Manufacturing. Addit. Manuf. 2021, 37, 101707. [Google Scholar] [CrossRef]
- Ribeiro, I.; Matos, F.; Jacinto, C.; Salman, H.; Cardeal, G.; Carvalho, H.; Godina, R.; Peças, P. Framework for Life Cycle Sustainability Assessment of Additive Manufacturing. Sustainability 2020, 12, 929. [Google Scholar] [CrossRef]
- Taddese, G.; Durieux, S.; Duc, E. Sustainability Performance Indicators for Additive Manufacturing: A Literature Review Based on Product Life Cycle Studies. Int. J. Adv. Manuf. Technol. 2020, 107, 3109–3134. [Google Scholar] [CrossRef]
- Fouda, Y.M.; Bayly, A.E. A DEM Study of Powder Spreading in Additive Layer Manufacturing. Granul. Matter 2020, 22, 10. [Google Scholar] [CrossRef]
- Meier, C.; Weissbach, R.; Weinberg, J.; Wall, W.A.; Hart, A.J. Critical Influences of Particle Size and Adhesion on the Powder Layer Uniformity in Metal Additive Manufacturing. J. Mater. Process. Technol. 2019, 266, 484–501. [Google Scholar] [CrossRef]
- Shaheen, M.Y.; Thornton, A.R.; Luding, S.; Weinhart, T. The Influence of Material and Process Parameters on Powder Spreading in Additive Manufacturing. Powder Technol. 2021, 383, 564–583. [Google Scholar] [CrossRef]
- Si, L.; Zhang, T.; Zhou, M.; Li, M.; Zhang, Y.; Zhou, H. Numerical Simulation of the Flow Behavior and Powder Spreading Mechanism in Powder Bed-Based Additive Manufacturing. Powder Technol. 2021, 394, 1004–1016. [Google Scholar] [CrossRef]
- Yao, D.; Liu, X.; Wang, J.; Fan, W.; Li, M.; Fu, H.; Zhang, H.; Yang, X.; Zou, Q.; An, X. Numerical Insights on the Spreading of Practical 316 L Stainless Steel Powder in SLM Additive Manufacturing. Powder Technol. 2021, 390, 197–208. [Google Scholar] [CrossRef]
- Lampitella, V.; Trofa, M.; Astarita, A.; D’Avino, G. Discrete Element Method Analysis of the Spreading Mechanism and Its Influence on Powder Bed Characteristics in Additive Manufacturing. Micromachines 2021, 12, 392. [Google Scholar] [CrossRef]
- Xiang, Z.; Zhang, M.; Yan, R.; Yin, Q.; Zhang, K. Powder-Spreading Dynamics and Packing Quality Improvement for Laser Powder Bed Fusion Additive Manufacturing. Powder Technol. 2021, 389, 278–291. [Google Scholar] [CrossRef]
- Yao, D.; Wang, J.; Li, M.; Zhao, T.; Cai, Y.; An, X.; Zou, R.; Zhang, H.; Fu, H.; Yang, X.; et al. Segregation of 316L Stainless Steel Powder during Spreading in Selective Laser Melting Based Additive Manufacturing. Powder Technol. 2022, 397, 117096. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, Z.; Li, E.; Shen, H.; Yu, A. Powder Deposition Mechanism during Powder Spreading with Different Spreader Geometries in Powder Bed Fusion Additive Manufacturing. Powder Technol. 2022, 395, 802–810. [Google Scholar] [CrossRef]
- Phua, A.; Doblin, C.; Owen, P.; Davies, C.H.J.; Delaney, G.W. The Effect of Recoater Geometry and Speed on Granular Convection and Size Segregation in Powder Bed Fusion. Powder Technol. 2021, 394, 632–644. [Google Scholar] [CrossRef]
- Wu, Q.; Qiao, C.; Wang, J.; Yao, D.; Wu, Y.; Fan, W.; Li, M.; An, X. Adaptability Investigations on Bottom Modified Blade in Powder Spreading Process of Additive Manufacturing. Addit. Manuf. 2022, 49, 102477. [Google Scholar] [CrossRef]
- Haeri, S.; Wang, Y.; Ghita, O.; Sun, J. Discrete Element Simulation and Experimental Study of Powder Spreading Process in Additive Manufacturing. Powder Technol. 2016, 306, 45–54. [Google Scholar] [CrossRef]
- Haeri, S. Optimisation of Blade Type Spreaders for Powder Bed Preparation in Additive Manufacturing Using DEM Simulations. Powder Technol. 2017, 321, 94–104. [Google Scholar] [CrossRef]
- Parteli, E.J.R.; Pöschel, T. Particle-Based Simulation of Powder Application in Additive Manufacturing. Powder Technol. 2016, 288, 96–102. [Google Scholar] [CrossRef]
- Seluga, K.J. Three Dimensional Printing by Vector Printing of Fine Metal Powders. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2001. [Google Scholar]
- Tang, M.; Guo, Y.; Zhang, W.; Ma, H.; Yang, L.; Wei, W.; Wang, L.; Fan, S.; Zhang, Q. On Recoated Powder Quality with a Forward Rotating Flexible Roller in Laser Powder Bed Fusion of 30 wt% 5 μm SiCp/AlSi10Mg Composites. Mater. Des. 2023, 225, 111489. [Google Scholar] [CrossRef]
- Niino, T.; Sato, K. Effect of Powder Compaction in Plastic Laser Sintering Fabrication. In Proceedings of the Solid Freeform Fabrication Symposium 2009, Austin, TX, USA, 3–5 August 2009. [Google Scholar]
- Ziaee, M.; Hershman, R.; Mahmood, A.; Crane, N.B. Fabrication of Demineralized Bone Matrix/Polycaprolactone Composites Using Large Area Projection Sintering (LAPS). J. Manuf. Mater. Process. 2019, 3, 30. [Google Scholar] [CrossRef]
- Gan, J.Q.; Yu, A.B.; Zhou, Z.Y. DEM Simulation on the Packing of Fine Ellipsoids. Chem. Eng. Sci. 2016, 156, 64–76. [Google Scholar] [CrossRef]
- Zhu, H.P.; Zhou, Z.Y.; Yang, R.Y.; Yu, A.B. Discrete Particle Simulation of Particulate Systems: A Review of Major Applications and Findings. Chem. Eng. Sci. 2008, 63, 5728–5770. [Google Scholar] [CrossRef]
- Burman, B.C.; Cundall, P.A.; Strack, O.D.L. A Discrete Numerical Model for Granular Assemblies. Geotechnique 1980, 30, 331–336. [Google Scholar] [CrossRef]
- Mindlin, R.D.; Deresiewicz, H. Elastic Spheres in Contact Under Varying Oblique Forces. J. Appl. Mech. 2021, 20, 327–344. [Google Scholar] [CrossRef]
- Johnson, K.L.; Kendall, K.; Roberts, A.D. Surface Energy and the Contact of Elastic Solids. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1971, 324, 301–313. [Google Scholar] [CrossRef]
- Altair EDEM, 2021.1; Altair Engineering Inc.: Troy, MI, USA, 2021.
- Alizadeh, M.; Asachi, M.; Ghadiri, M.; Bayly, A.; Hassanpour, A. A Methodology for Calibration of DEM Input Parameters in Simulation of Segregation of Powder Mixtures, a Special Focus on Adhesion. Powder Technol. 2018, 339, 789–800. [Google Scholar] [CrossRef]
- Roessler, T.; Katterfeld, A. Scaling of the Angle of Repose Test and Its Influence on the Calibration of DEM Parameters Using Upscaled Particles. Powder Technol. 2018, 330, 58–66. [Google Scholar] [CrossRef]
- Chen, H.; Wei, Q.; Wen, S.; Li, Z.; Shi, Y. Flow Behavior of Powder Particles in Layering Process of Selective Laser Melting: Numerical Modeling and Experimental Verification Based on Discrete Element Method. Int. J. Mach. Tools Manuf. 2017, 123, 146–159. [Google Scholar] [CrossRef]
- Gu, D.; Xia, M.; Dai, D. On the Role of Powder Flow Behavior in Fluid Thermodynamics and Laser Processability of Ni-Based Composites by Selective Laser Melting. Int. J. Mach. Tools Manuf. 2019, 137, 67–78. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| 0.3 | |
| 7800 kg/m3 | |
| Young’s modulus, E | 22 GPa |
| Coefficient of restitution, e | 0.64 |
| 0.6 | |
| 0.085 | |
| Powder Size (D), µm | Dynamic Angle of Repose (Deg) | ||
|---|---|---|---|
| Experimental Value | Yao Simulation | Current Simulation | |
| 34.8 | 45.9° | 44.0° | 44° |
| 100 | 30.4° | 31.9° | 33° |
| 123.2 | 30.1° | 32.2° | 33° |
| 169.4 | 32.3° | 32.5° | 33° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salim, M.A.; Tullis, S.; Elbestawi, M. Accelerating Laser Powder Bed Fusion: The Influence of Roller-Spreading Speed on Powder Spreading Performance. Metals 2024, 14, 1137. https://doi.org/10.3390/met14101137
Salim MA, Tullis S, Elbestawi M. Accelerating Laser Powder Bed Fusion: The Influence of Roller-Spreading Speed on Powder Spreading Performance. Metals. 2024; 14(10):1137. https://doi.org/10.3390/met14101137
Chicago/Turabian StyleSalim, Mohamed Awad, Stephen Tullis, and Mohamed Elbestawi. 2024. "Accelerating Laser Powder Bed Fusion: The Influence of Roller-Spreading Speed on Powder Spreading Performance" Metals 14, no. 10: 1137. https://doi.org/10.3390/met14101137
APA StyleSalim, M. A., Tullis, S., & Elbestawi, M. (2024). Accelerating Laser Powder Bed Fusion: The Influence of Roller-Spreading Speed on Powder Spreading Performance. Metals, 14(10), 1137. https://doi.org/10.3390/met14101137







