Predictive Modeling and Optimization of Hot Forging Parameters for AISI 1045 Ball Joints Using Taguchi Methodology and Finite Element Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Microstructure Characterization
2.3. Microstructure Evolution Model
2.4. Design of Experiment
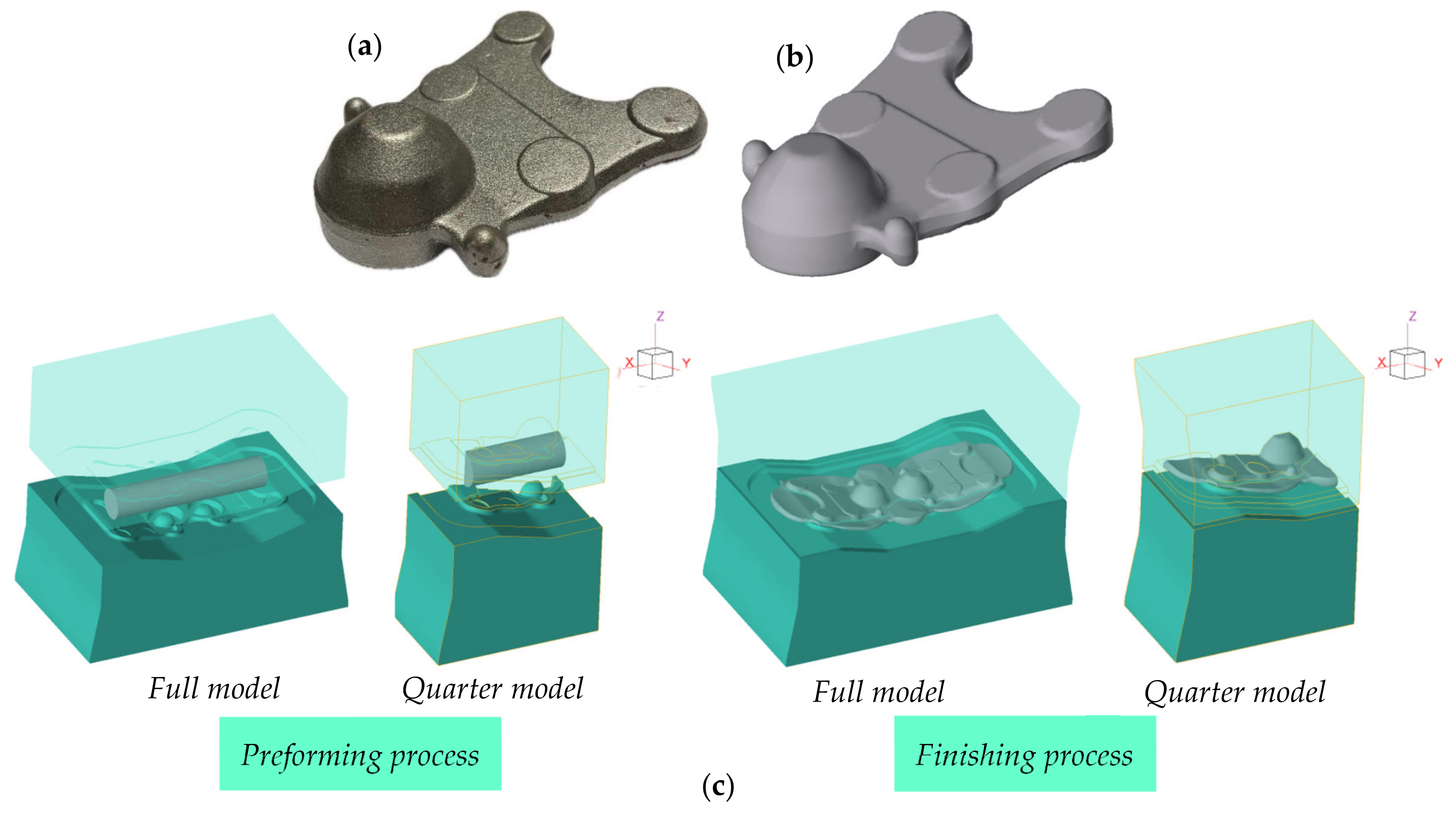
2.5. FE Simulation of Ball Joint
3. Results
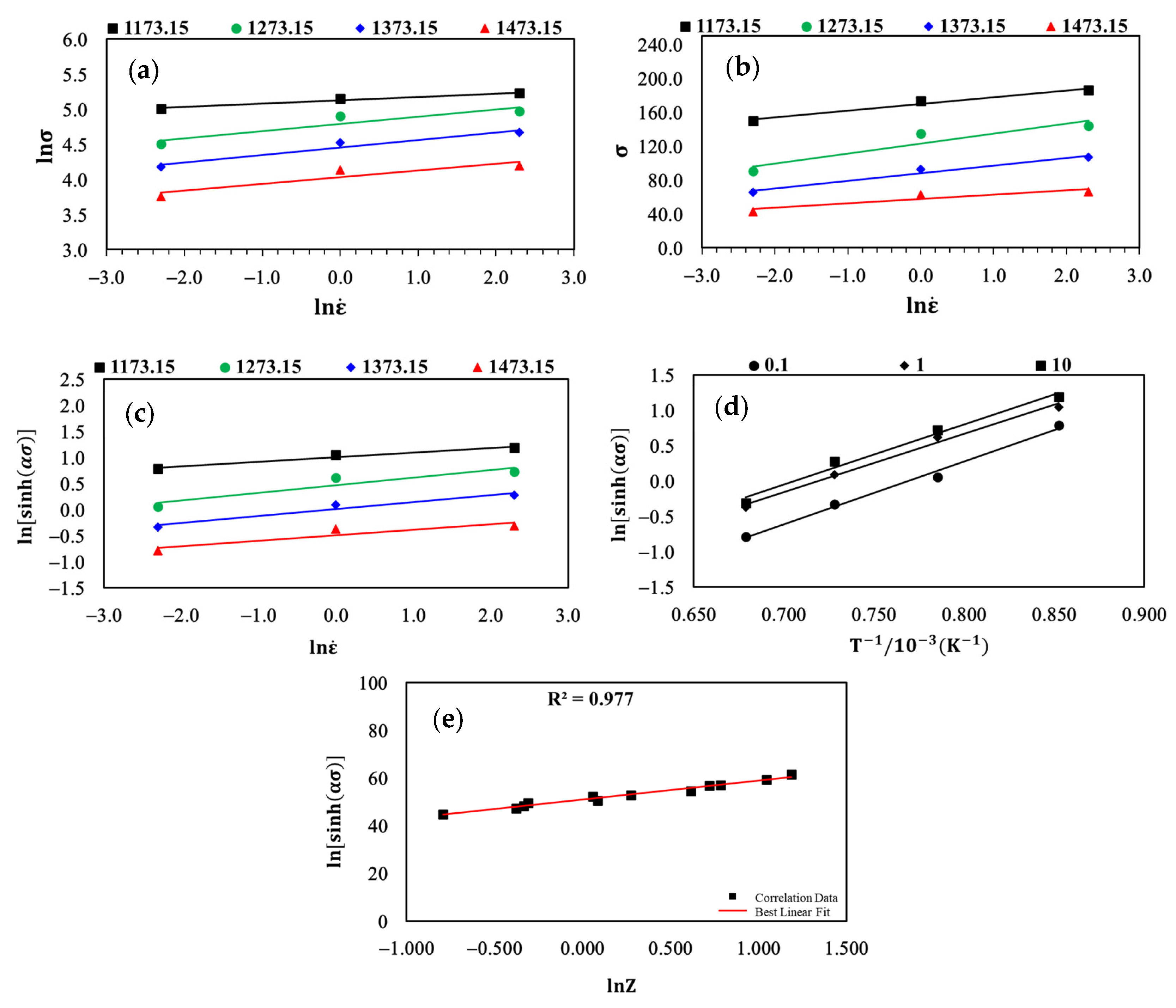
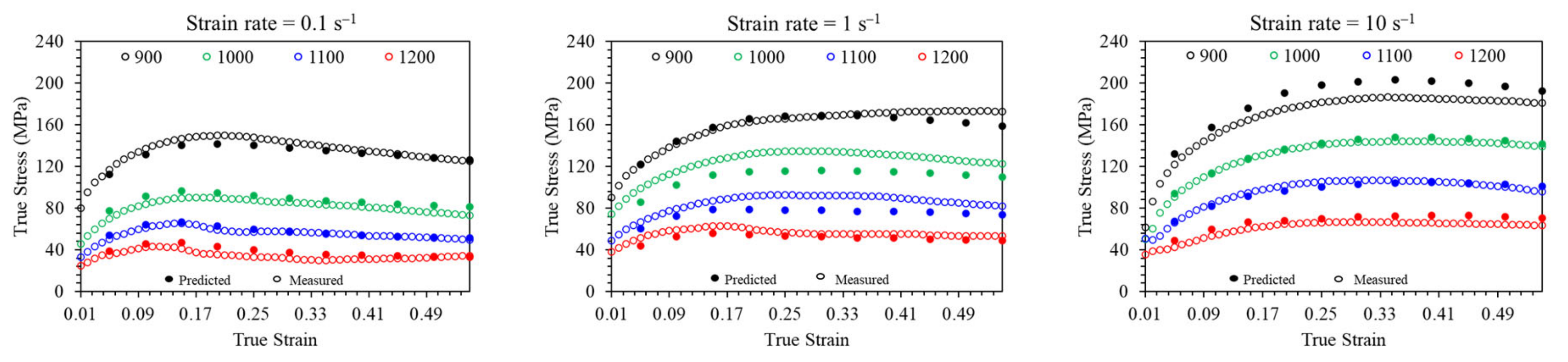
3.1. Modeling the Arrhenius-Based Constitutive Equation
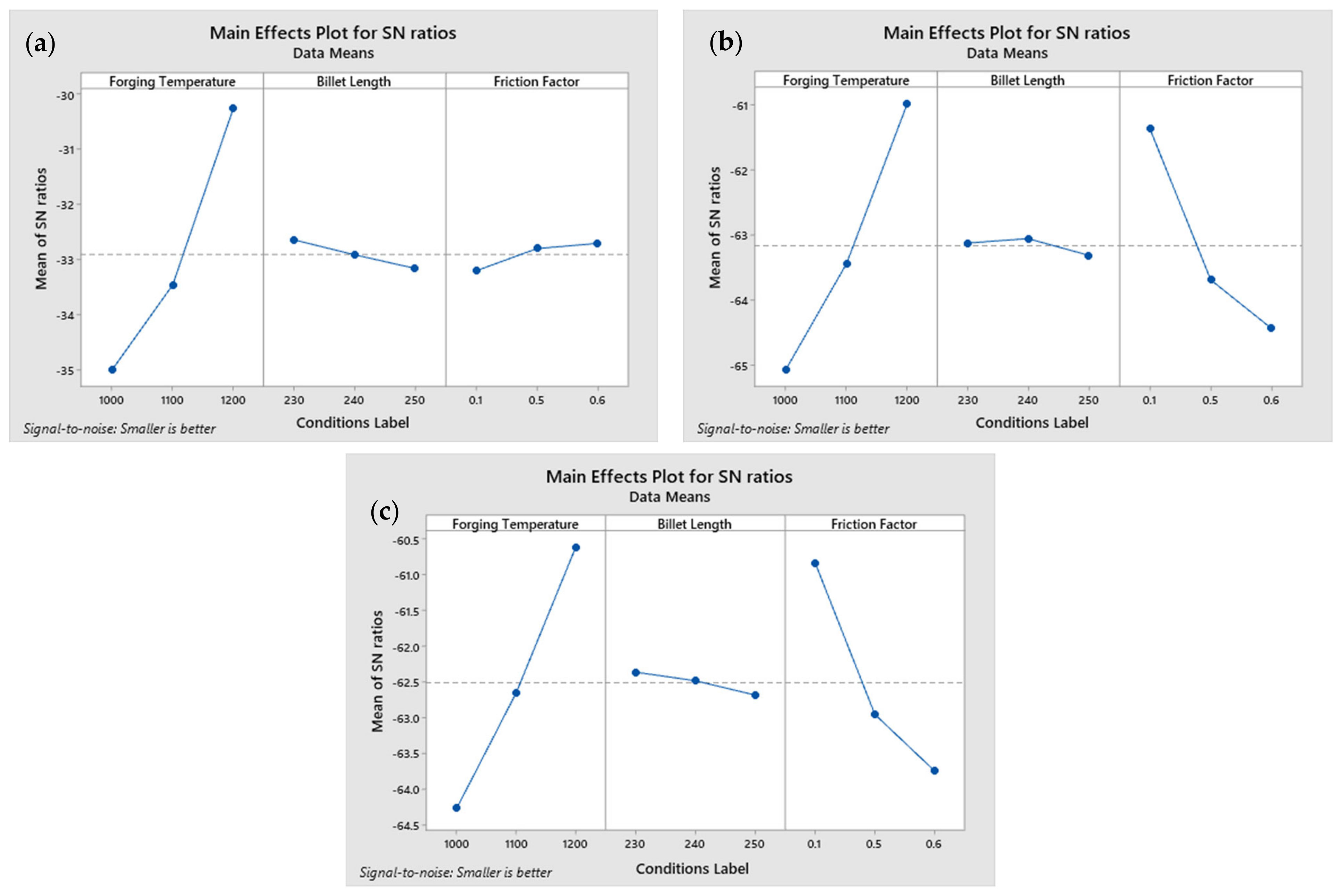
3.2. S/N Ratio Analysis
3.3. Analysis of Variance (ANOVA)
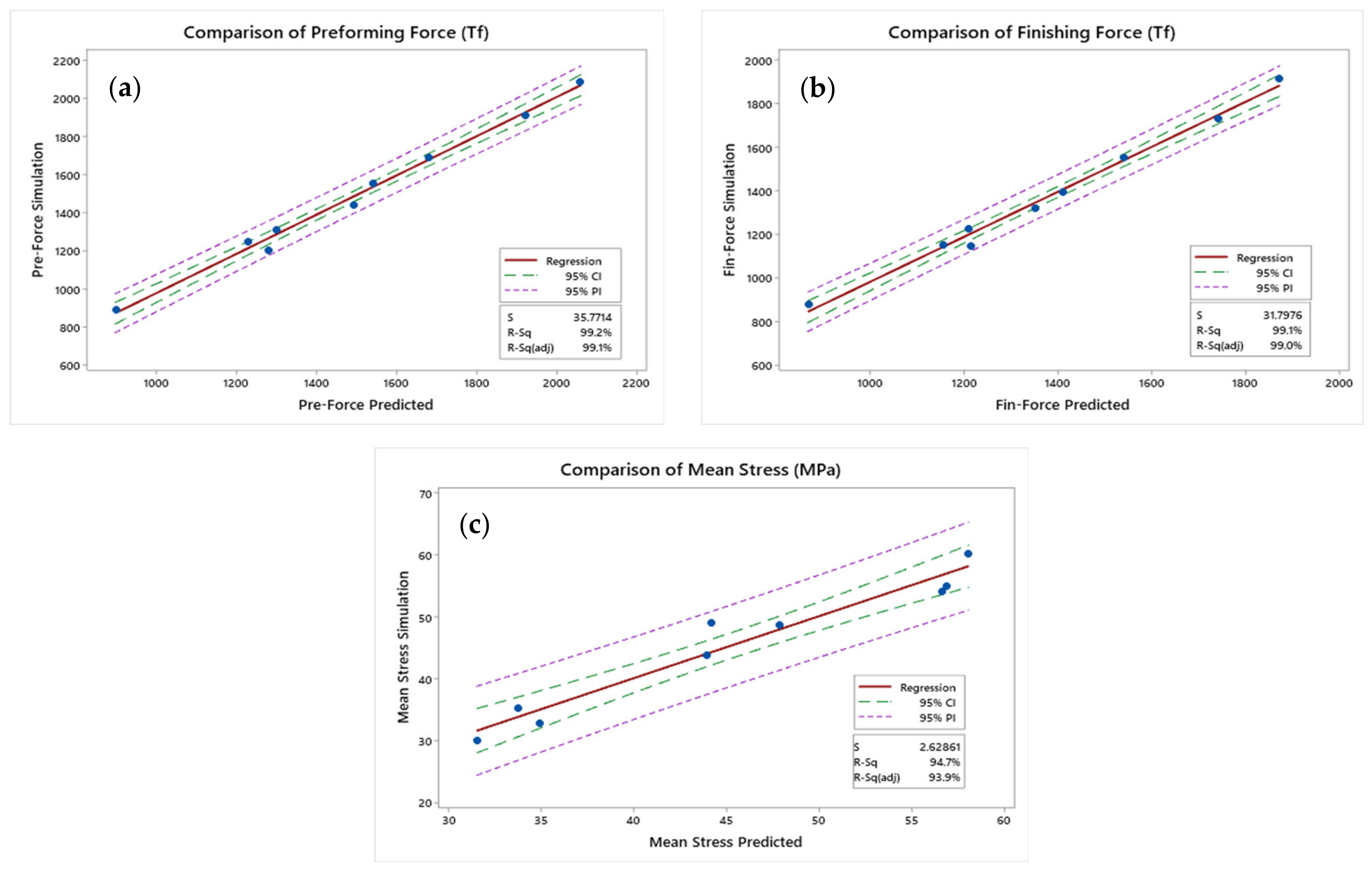
3.4. Regression Analysis
3.5. Verification Results of FEM
4. Conclusions
- The Arrhenius constitutive model accurately predicted the flow stress under various strain rates and temperatures based on the Zener–Hollomon parameter. With an R2 of 0.968 and an AARE of 7.079, the model showed a high precision in its predictions. These constants have effectively optimized the manufacturing processes for AISI 1045 ball joints. Integrating these models into finite element software has proven valuable for improving process conditions.
- The Taguchi method and FE simulations identified the optimal forging parameters—a billet temperature of 1200 °C, a billet length of 230 mm, and a friction factor of 0.1. The ANOVA showed that the billet temperature significantly affected the preforming force (62.30%), finishing force (59.50%), and mean stress (94.20%), while the friction factor impacted the preforming (36.19%) and finishing forces (38.28%). The regression analyses, with high R2 values, validated the predictive accuracy of these parameters. Overall, the billet temperature and friction factor were crucial for optimizing the forging efficiency, with less impact from the billet size.
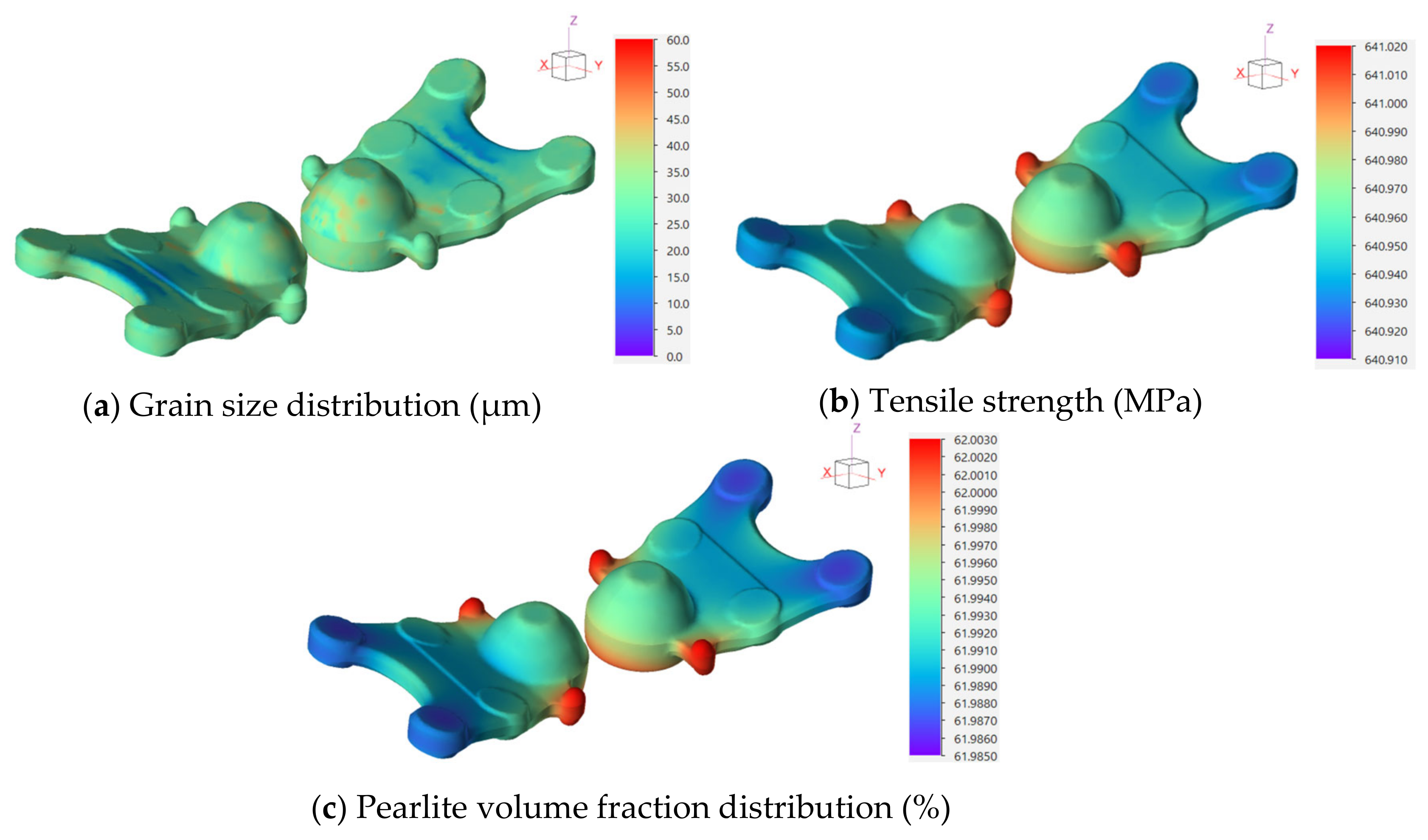
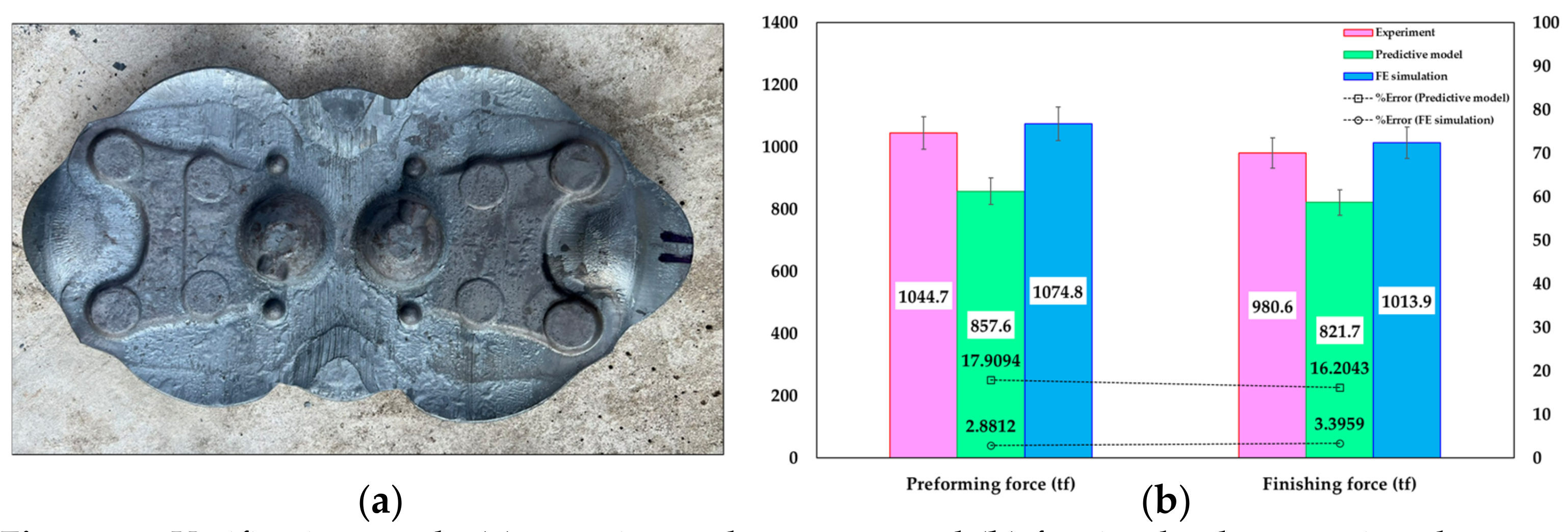
- Verifying the optimal forging parameters through a simulation and practical experiments confirmed the effectiveness of these parameters, resulting in defect-free components and accurate production outcomes in Figure 13a. The FE simulation showed minimal discrepancies in the forging forces compared to predictive models, with percentage errors of 2.88% for the preforming force and 3.40% for the finishing force, indicating a high accuracy (Figure 13b). Additionally, the FE simulation visualizations provided insights into the stress distribution and temperature changes, enhancing the understanding and design of the forging process.
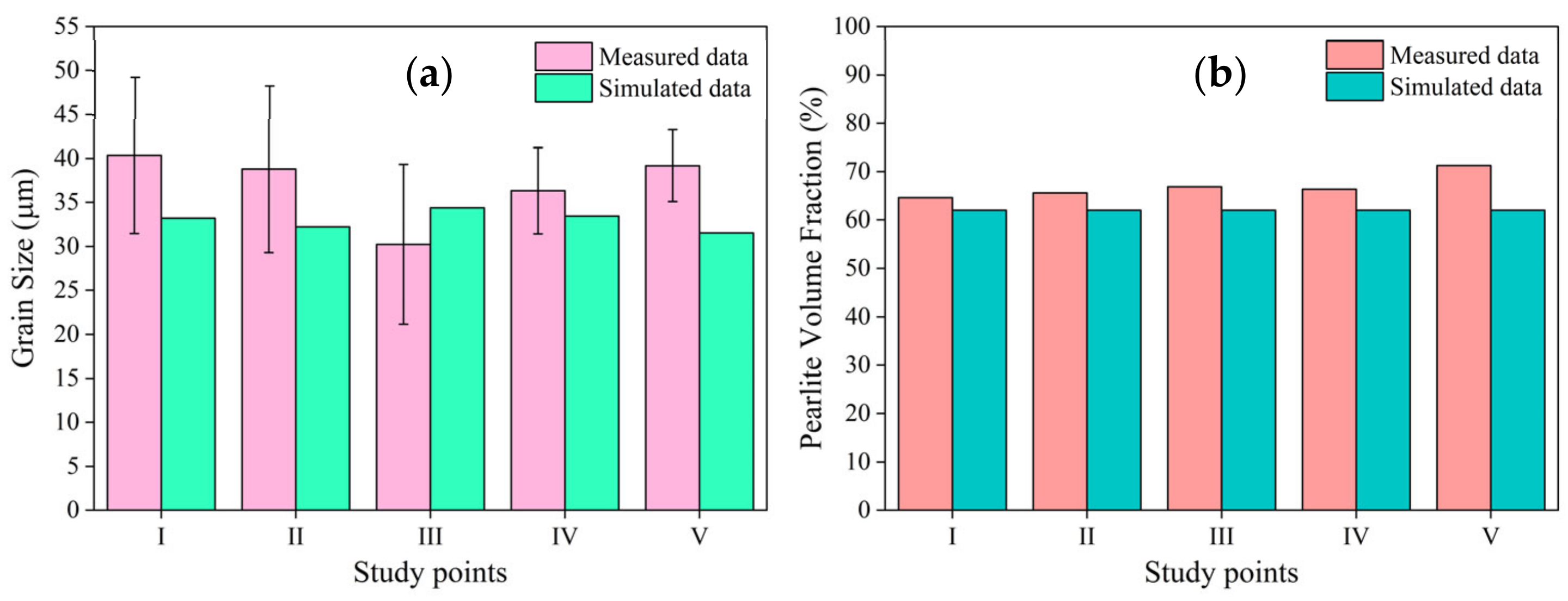
- The study also investigated microstructure evolution modeling to predict the grain size distribution and microstructural changes in AISI 1045 medium carbon steel post-forging. The FE simulations estimated grain sizes between 6.762 μm and 45.405 μm, with the actual measurements revealing an average grain size of 36.982 μm and an average error of 15.159% compared to the simulations. The model accurately predicted the pearlite volume fraction, with a minimal error of 7.3016%, confirming its effectiveness in forecasting the key microstructural outcomes in forged components.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Altan, T. Cold and Hot Forging: Fundamentals and Applications; Gracious Ngaile, G.S., Ed.; ASM International: Materials Park, OH, USA, 2005; p. 341. [Google Scholar]
- Huang, S.-Q.; Yi, Y.-P.; Zhang, Y.-X. Simulation of 7050 Wrought Aluminum Alloy Wheel Die Forging and its Defects Analysis based on DEFORM. In Proceedings of the AIP Conference Proceedings, Pohang, Republic of Korea, 15 June 2010; pp. 638–644. [Google Scholar]
- Bonte, M.H.A.; Fourment, L.; Do, T.-T.; van den Boogaard, A.H.; Huétink, J. Optimization of forging processes using Finite Element simulations. Struct. Multidiscipl. Optim. 2010, 42, 797–810. [Google Scholar] [CrossRef]
- Sukjantha, V.; Aue-u-lan, Y. Determination of Optimal Preform Part for Hot Forging Process of the Manufacture Axle Shaft by Finite Element Method. Appl. Sci. Eng. Prog. 2013, 6, 35–42. [Google Scholar]
- Tenesgen, A.D.; Irfaan, M.; Bhardwaj, B. Improvement of Hot Forging Process by Minimized Die Stress using Finite Element Method. Int. J. Eng. Sci. Technol. 2015, 3, 1316–1329. [Google Scholar]
- Pundir, R.; Chary, G.H.V.C.; Dastidar, M.G. Application of Taguchi method for optimizing the process parameters for the removal of copper and nickel by growing Aspergillus sp. Water Resour. Ind. 2018, 20, 83–92. [Google Scholar] [CrossRef]
- Kivak, T.; Samtaş, G.; Çiçek, A. Taguchi method based optimisation of drilling parameters in drilling of AISI 316 steel with PVD monolayer and multilayer coated HSS drills. Measurement 2012, 45, 1547–1557. [Google Scholar] [CrossRef]
- Chen, X.; Jung, D. Gear hot forging process robust design based on finite element method. J. Mech. Sci. Technol. 2008, 22, 1772–1778. [Google Scholar] [CrossRef]
- Choi, S.K.; Chun, M.S.; Van Tyne, C.J.; Moon, Y.H. Optimization of open die forging of round shapes using FEM analysis. J. Mater. Process. Technol. 2006, 172, 88–95. [Google Scholar] [CrossRef]
- Equbal, I.; Ohdar, R.; Bhat, N.S.; Ahmad, S. Preform Shape Optimization of Connecting Rod Using Finite Element Method and Taguchi Method. Int. J. Mod. Eng. Res. 2012, 2, 4532–4539. [Google Scholar]
- Sanjari, M.; Taheri, A.K.; Movahedi, M.R. An optimization method for radial forging process using ANN and Taguchi method. Int. J. Adv. Manuf. Technol. 2009, 40, 776–784. [Google Scholar] [CrossRef]
- Obiko, J.O.; Mwema, F.M.; Shangwira, H. Forging optimisation process using numerical simulation and Taguchi method. SN Appl. Sci. 2020, 2, 713. [Google Scholar] [CrossRef]
- Riaz, M.; Atiqah, N. A Study on the Mechanical Properties of S45c Medium Type Carbon Steel Specimens under Lathe Machining and Quenching Conditions. Int. J. Res. Eng. Technol. 2014, 3, 121–130. [Google Scholar]
- Gutierrez-Gonzalez, C.F.; Smirnov, A.; Centeno, A.; Fernández, A.; Alonso, B.; Rocha, V.G.; Torrecillas, R.; Zurutuza, A.; Bartolome, J.F. Wear behavior of graphene/alumina composite. Ceram. Int. 2015, 41, 7434–7438. [Google Scholar] [CrossRef]
- Gutiérrez-Mora, F.; Cano-Crespo, R.; Rincón, A.; Moreno, R.; Domínguez-Rodríguez, A. Friction and wear behavior of alumina-based graphene and CNFs composites. J. Eur. Ceram. Soc. 2017, 37, 3805–3812. [Google Scholar] [CrossRef]
- Bharath, K.; Khanra, A.K.; Davidson, M. Hot deformation behavior and dynamic recrystallization constitutive modeling of Al–Cu–Mg powder compacts processed by extrusion at elevated temperatures. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2021, 235, 581–596. [Google Scholar] [CrossRef]
- Sakai, T.; Belyakov, A.; Kaibyshev, R.; Miura, H.; Jonas, J.J. Dynamic and post-dynamic recrystallization under hot, cold and severe plastic deformation conditions. Prog. Mater. Sci. 2014, 60, 130–207. [Google Scholar] [CrossRef]
- Irani, M.; Lim, S.; Joun, M. Experimental and numerical study on the temperature sensitivity of the dynamic recrystallization activation energy and strain rate exponent in the JMAK model. J. Mater. Res. Technol. 2019, 8, 1616–1627. [Google Scholar] [CrossRef]
- Quan, G.-z.; Shi, R.-j.; Zhao, J.; Liu, Q.; Xiong, W.; Qiu, H.-m. Modeling of dynamic recrystallization volume fraction evolution for AlCu4SiMg alloy and its application in FEM. Trans. Nonferrous Met. Soc. China 2019, 29, 1138–1151. [Google Scholar] [CrossRef]
- Ji, H.; Peng, Z.; Huang, X.; Wang, B.; Xiao, W.; Wang, S. Characterization of the Microstructures and Dynamic Recrystallization Behavior of Ti-6Al-4V Titanium Alloy through Experiments and Simulations. J. Mater. Eng. Perform. 2021, 30, 8257–8275. [Google Scholar] [CrossRef]
- Poliak, E.; Jonas, J. Initiation of Dynamic Recrystallization in Constant Strain Rate Hot Deformation. ISIJ Int. 2003, 43, 684–691. [Google Scholar] [CrossRef]
- Siripath, N.; Suranuntchai, S.; Sucharitpwatskul, S. Modeling Dynamic Recrystallization Kinetics in BS 080M46 Medium Carbon Steel: Experimental Verification and Finite Element Simulation. Int. J. Technol. 2024, 15, 1292–1307. [Google Scholar] [CrossRef]
- Kumar, V.; Kumari, N. Modeling and multiple performance optimization of ultrasonic micro-hole machining of PCD using fuzzy logic and taguchi quality loss function. Adv. Mater. Res. 2012, 1, 129–146. [Google Scholar] [CrossRef]
- Wu, D.; Chang, M. Use of Taguchi method to develop a robust design for the magnesium alloy die casting process. Mater. Sci. Eng. A-Struct. Mater. 2004, 379, 366–371. [Google Scholar] [CrossRef]
- Phadke, M.S. Quality Engineering Using Robust Design; Prentice Hall: Upper Saddle River, NJ, USA, 1989. [Google Scholar]
- Jamaluddin, H.; Ghani, J.A.; Deros, B.M.; Rahman, M.N.A.; Ramli, R.B. Quality improvement using Taguchi method in shot blasting process. J. Mech. Eng. Sci. 2016, 10, 2200–2213. [Google Scholar]
- Poungprasert, R.; Siripath, N.; Suranuntchai, S. A Comparative Study of Lubrication Performance for Bs 080M46 Medium Carbon Steel Using Ring Compression Test and Finite Element Simulation. Key Eng. Mater. 2024, 973, 37–44. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Chen, M.-S.; Zhang, J. Modeling of flow stress of 42CrMo steel under hot compression. Mater. Sci. Eng. A 2009, 499, 88–92. [Google Scholar] [CrossRef]
- Sellars, C.M.; McTegart, W.J. On the mechanism of hot deformation. Acta Metall. 1966, 14, 1136–1138. [Google Scholar] [CrossRef]
- Hajari, A.; Morakabati, M.; Abbasi, S.M.; Badri, H. Constitutive Modeling for High-Temperature Flow Behavior of Ti-6242S Alloy. Mater. Sci. Eng. A 2017, 681, 103–113. [Google Scholar] [CrossRef]
- Mirzadeh, H. Constitutive modeling and prediction of hot deformation flow stress under dynamic recrystallization conditions. Mech. Mater. 2015, 85, 66–79. [Google Scholar] [CrossRef]
- Xiao, Z.; Wang, Q.; Huang, Y.; Hu, J.; Li, M. Hot Deformation Characteristics and Processing Parameter Optimization of Al–6.32Zn–2.10Mg Alloy Using Constitutive Equation and Processing Map. Metals 2021, 11, 360. [Google Scholar] [CrossRef]
- Dandekar, T.R.; Khatirkar, R.K.; Gupta, A.; Bibhanshu, N.; Bhadauria, A.; Suwas, S. Strain rate sensitivity behaviour of Fe–21Cr-1.5Ni–5Mn alloy and its constitutive modelling. Mater. Chem. Phys. 2021, 271, 124948. [Google Scholar] [CrossRef]
- Wang, L.; Liu, F.; Zuo, Q.; Chen, C.F. Prediction of Flow Stress for N08028 Alloy under Hot Working Conditions. Mater. Des. 2013, 47, 737–745. [Google Scholar] [CrossRef]
- Hu, M.; Dong, L.; Zhang, Z.; Lei, X.; Yang, R.; Sha, Y. Correction of Flow Curves and Constitutive Modelling of a Ti-6Al-4V Alloy. Metals 2018, 8, 256. [Google Scholar] [CrossRef]
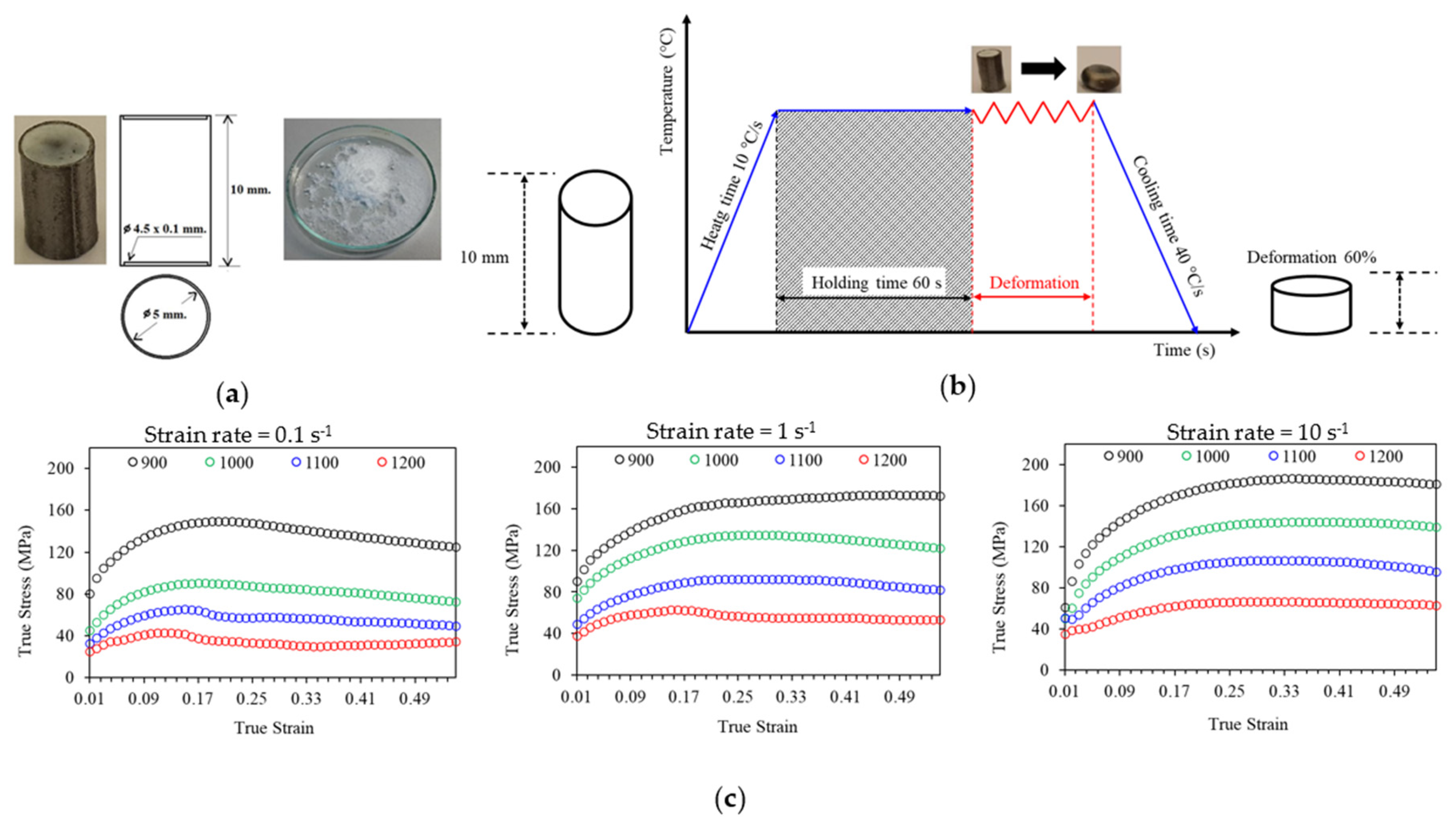





| Element | C | Si | Mn | P | S | Cu | Cr | Ni | Mo | Fe |
|---|---|---|---|---|---|---|---|---|---|---|
| Nominal | 0.42–0.48 | 0.15–0.35 | 0.60–0.90 | Max. 0.03 | Max. 0.035 | Max. 0.3 | Max. 0.2 | Max. 0.2 | - | Bal. |
| Actual | 0.47 | 0.19 | 0.67 | 0.03 | 0.02 | 0.18 | 0.11 | 0.07 | 0.02 | Bal. |
| α | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.012 | 0 | 0.189 | 29,448.700 | 0.478 | 0.040 | 22,058.400 | 0.117 | 5.070 | 2.404 | −67,793.200 | −0.073 | 7082.570 |
| Factor | Units | Symbol | Level 1 | Level 2 | Level 3 |
|---|---|---|---|---|---|
| Forging Temperature | °C | A | 1000 | 1100 | 1200 |
| Billet Size | mm | B | 230 | 240 | 250 |
| Friction Factor | - | C | 0.15 | 0.50 | 0.64 |
| Parameter | Description |
|---|---|
| Element type | Tetrahedral |
| Number of nodes: initial billet | 800 |
| Number of surface elements: initial billet | 1180 |
| Number of volumetric elements: initial billet | 2944 |
| Die’s temperature | 250 °C |
| Forging equipment | Crank press JFP-1350 M/C (Gyeonggi-do, Republic of Korea) |
| Strokes per minute | 85 |
| Stroke length | 240 |
| Crank radius to conrod length ratio | 0.15 |
| n′ | β | α | n | Q | A | |
|---|---|---|---|---|---|---|
| 11.60611 | 0.11840 | 0.01020 | 8.12972 | 577.20710 | 50.87365 | 1.2421 × 1022 |
| Exp. No. | A (°C) | B (mm) | C | Max. Preforming Force (tf) | Max. Finishing Force (tf) | Max. Mean Stress (MPa) | S/N Ratios | ||
|---|---|---|---|---|---|---|---|---|---|
| Max. Preforming Force | Max. Finishing Force | Max. Mean Stress | |||||||
| 1 | 1000 | 230 | 0.100 | 1444.000 | 1321.000 | 60.125 | −63.191 | −62.418 | −35.581 |
| 2 | 1000 | 240 | 0.500 | 1912.000 | 1732.000 | 53.994 | −65.630 | −64.771 | −34.647 |
| 3 | 1000 | 250 | 0.600 | 2093.000 | 1916.000 | 54.965 | −66.415 | −65.648 | −34.802 |
| 4 | 1100 | 230 | 0.500 | 1556.000 | 1398.000 | 43.801 | −63.840 | −62.910 | −32.830 |
| 5 | 1100 | 240 | 0.600 | 1691.000 | 1554.000 | 49.026 | −64.563 | −63.829 | −33.809 |
| 6 | 1100 | 250 | 0.100 | 1248.000 | 1151.000 | 48.716 | −61.924 | −61.222 | −33.754 |
| 7 | 1200 | 230 | 0.600 | 1310.000 | 1226.000 | 29.927 | −62.345 | −61.770 | −29.521 |
| 8 | 1200 | 240 | 0.100 | 889.000 | 877.000 | 32.704 | −58.978 | −58.860 | −30.292 |
| 9 | 1200 | 250 | 0.500 | 1203.000 | 1147.000 | 35.229 | −61.605 | −61.191 | −30.938 |
| Levels | Control Factors | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Maximum Preforming Force (tf) | Maximum Finishing Force (tf) | Maximum Mean Stress (MPa) | |||||||
| A | B | C | A | B | C | A | B | C | |
| 1 | −65.08 | −63.13 | −61.36 | −64.28 | −62.37 | −60.83 | −35.01 | −32.64 | −33.21 |
| 2 | −63.44 | −63.06 | −63.69 | −62.65 | −62.49 | −62.96 | −33.46 | −32.92 | −32.80 |
| 3 | −60.98 | −63.31 | −64.44 | −60.61 | −62.69 | −63.75 | −30.25 | −33.16 | −32.71 |
| Delta | 4.10 | 0.26 | 3.08 | 3.67 | 0.32 | 2.92 | 4.76 | 0.52 | 0.50 |
| Rank | 1 | 3 | 2 | 1 | 3 | 2 | 1 | 2 | 3 |
| Factor | DOF | Sum of Squares | Mean Squares | % Contribution | F-Value | p-Value |
|---|---|---|---|---|---|---|
| Maximum preforming force | ||||||
| A | 2 | 699,442.000 | 349,721.000 | 62.30% | 101.450 | 0.010 |
| B | 2 | 10,065.000 | 5032.000 | 0.90% | 1.460 | 0.407 |
| C | 2 | 406,244.000 | 203,122.000 | 36.19% | 58.930 | 0.017 |
| Error | 2 | 6894.000 | 3447.000 | 0.61% | ||
| Total | 8 | 1,122,645.000 | 100.00% | |||
| Maximum finishing force | ||||||
| A | 2 | 492,503.000 | 246,251.000 | 59.50% | 103.430 | 0.010 |
| B | 2 | 13,610.000 | 6805.000 | 1.64% | 2.860 | 0.259 |
| C | 2 | 316,795.000 | 158,397.000 | 38.28% | 66.530 | 0.015 |
| Error | 2 | 4762.000 | 2381.000 | 0.58% | ||
| Total | 8 | 827,669.000 | 100.00% | |||
| Maximum mean stress | ||||||
| A | 2 | 859.930 | 429.965 | 94.20% | 25.300 | 0.038 |
| B | 2 | 4.360 | 2.180 | 0.48% | 0.130 | 0.886 |
| C | 2 | 14.621 | 7.310 | 1.60% | 0.430 | 0.699 |
| Error | 2 | 33.991 | 16.995 | 3.72% | ||
| Total | 8 | 912.901 | 100.00% | |||
| Forging Force | Experiment | Predictive Model | FE Simulation | %Error (Predictive Model) | %Error (FE Simulation) |
|---|---|---|---|---|---|
| Preforming force (tf) | 1044.70 | 857.60 | 1074.80 | 17.9094 | 2.8812 |
| Finishing force (tf) | 980.60 | 821.70 | 1013.90 | 16.2043 | 3.3959 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jantepa, N.; Siripath, N.; Suranuntchai, S. Predictive Modeling and Optimization of Hot Forging Parameters for AISI 1045 Ball Joints Using Taguchi Methodology and Finite Element Analysis. Metals 2024, 14, 1198. https://doi.org/10.3390/met14101198
Jantepa N, Siripath N, Suranuntchai S. Predictive Modeling and Optimization of Hot Forging Parameters for AISI 1045 Ball Joints Using Taguchi Methodology and Finite Element Analysis. Metals. 2024; 14(10):1198. https://doi.org/10.3390/met14101198
Chicago/Turabian StyleJantepa, Naiyanut, Nattarawee Siripath, and Surasak Suranuntchai. 2024. "Predictive Modeling and Optimization of Hot Forging Parameters for AISI 1045 Ball Joints Using Taguchi Methodology and Finite Element Analysis" Metals 14, no. 10: 1198. https://doi.org/10.3390/met14101198
APA StyleJantepa, N., Siripath, N., & Suranuntchai, S. (2024). Predictive Modeling and Optimization of Hot Forging Parameters for AISI 1045 Ball Joints Using Taguchi Methodology and Finite Element Analysis. Metals, 14(10), 1198. https://doi.org/10.3390/met14101198







