Metallic Metamaterials with Auxetic Properties: Re-Entrant Structures
Abstract
:1. Introduction
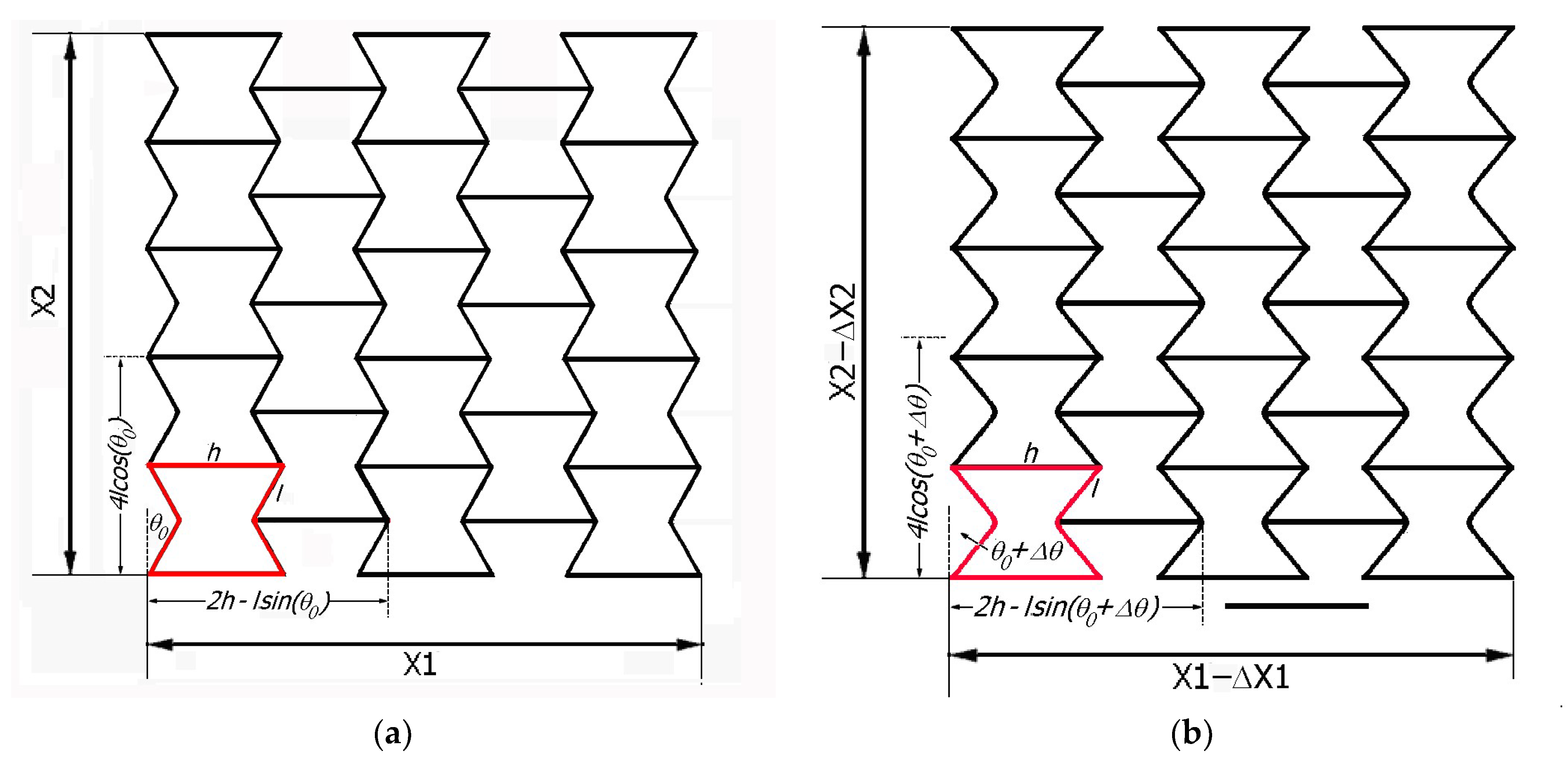
2. Geometric Analysis of an Auxetic Structure of Made of Re-Entrant (Bowtie) Unit Cells
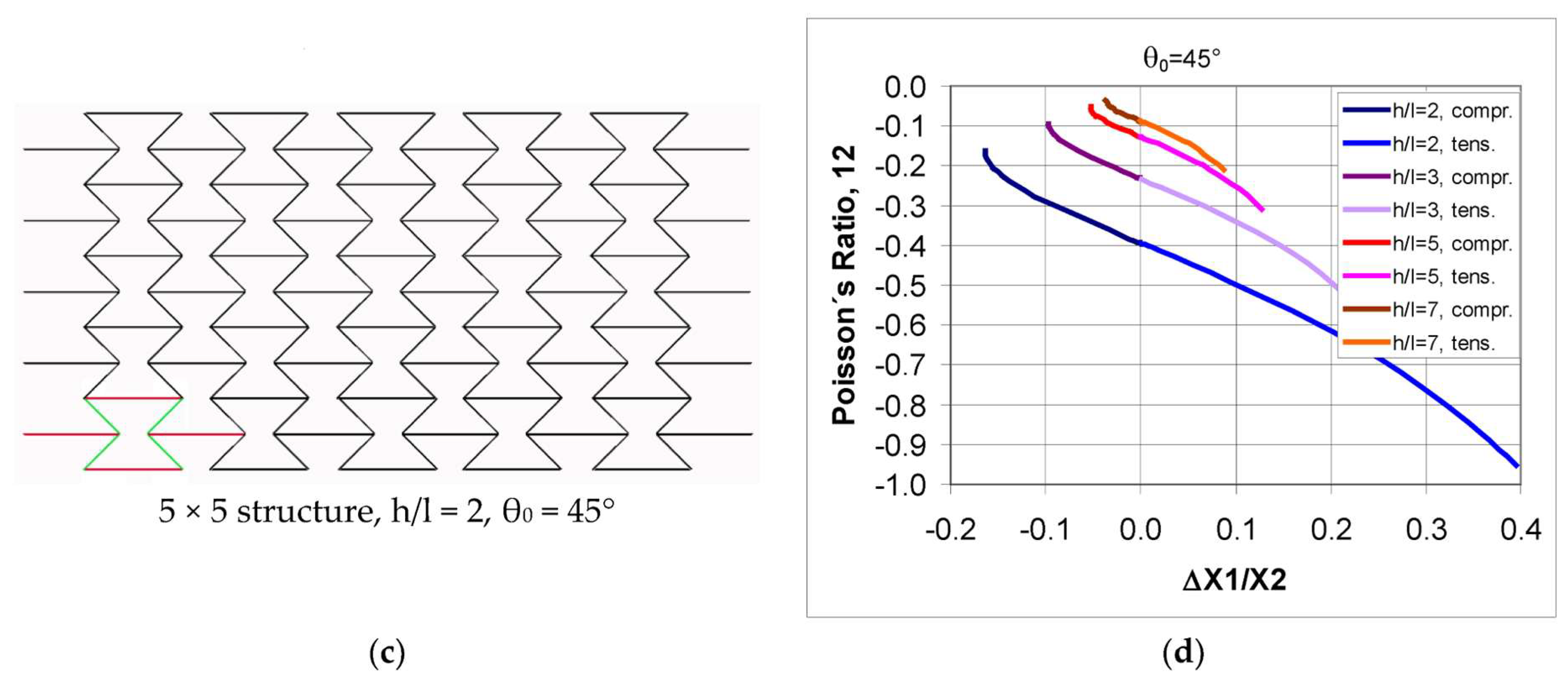
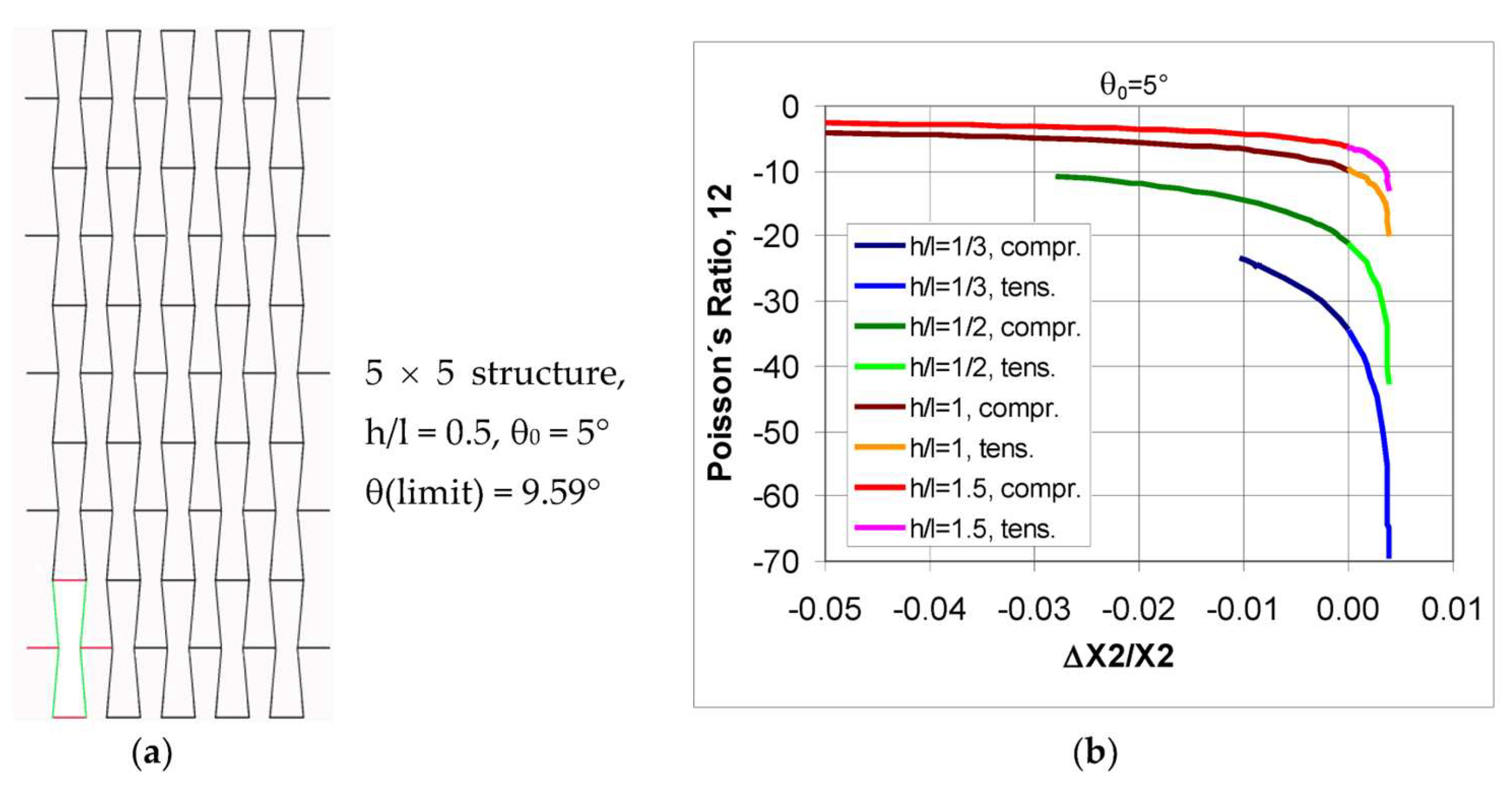
Geometric Analysis of a Structure with Dimensions of 5 × 5 (Figure 1)
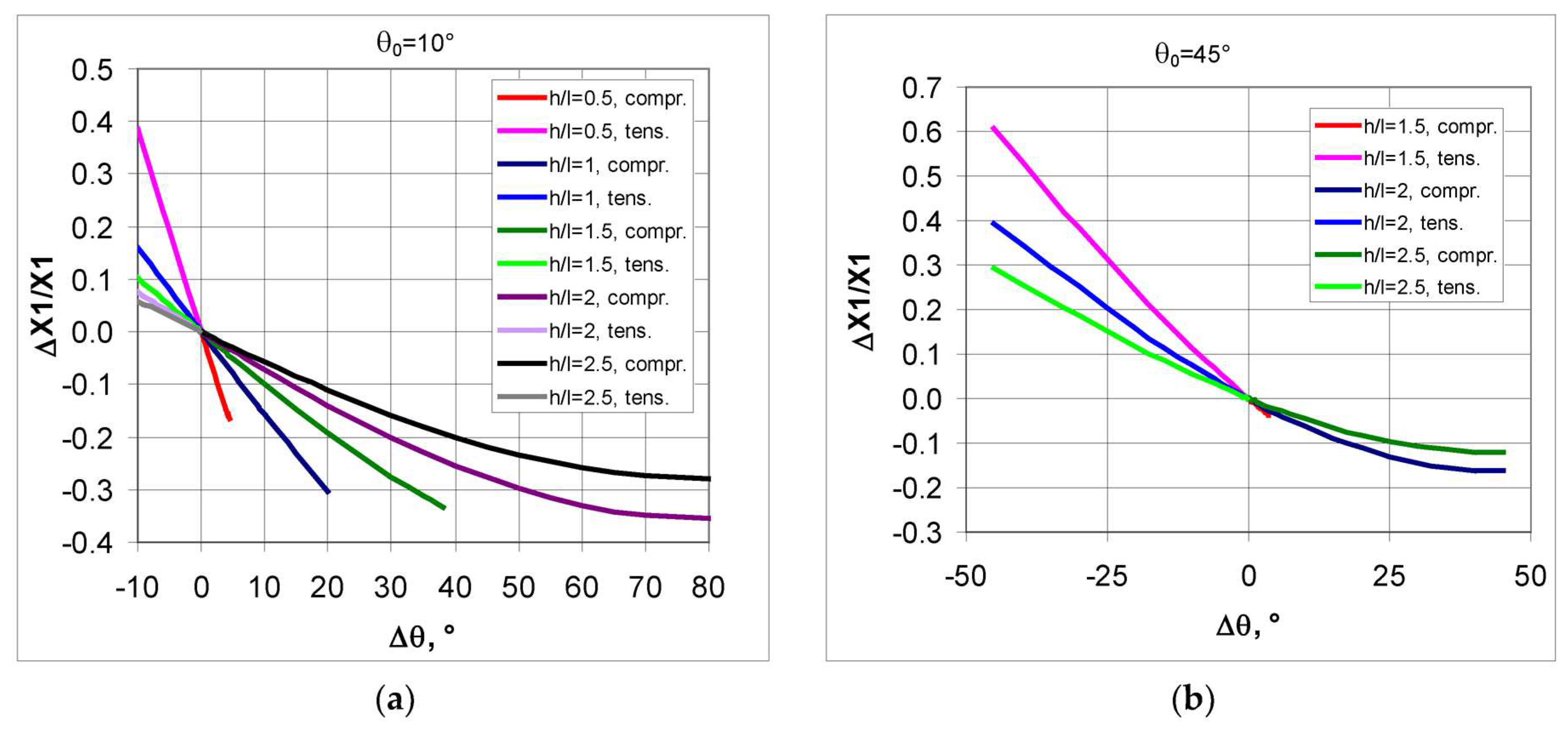
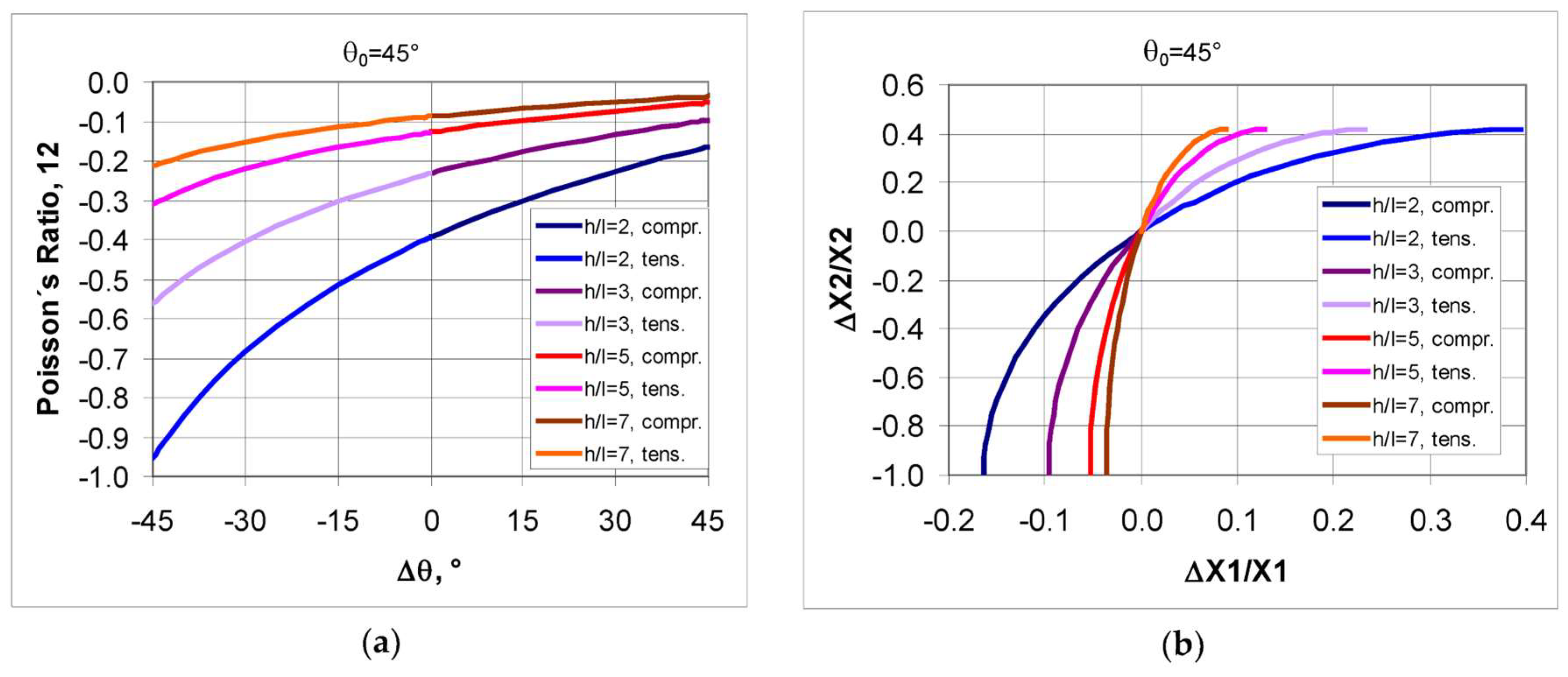
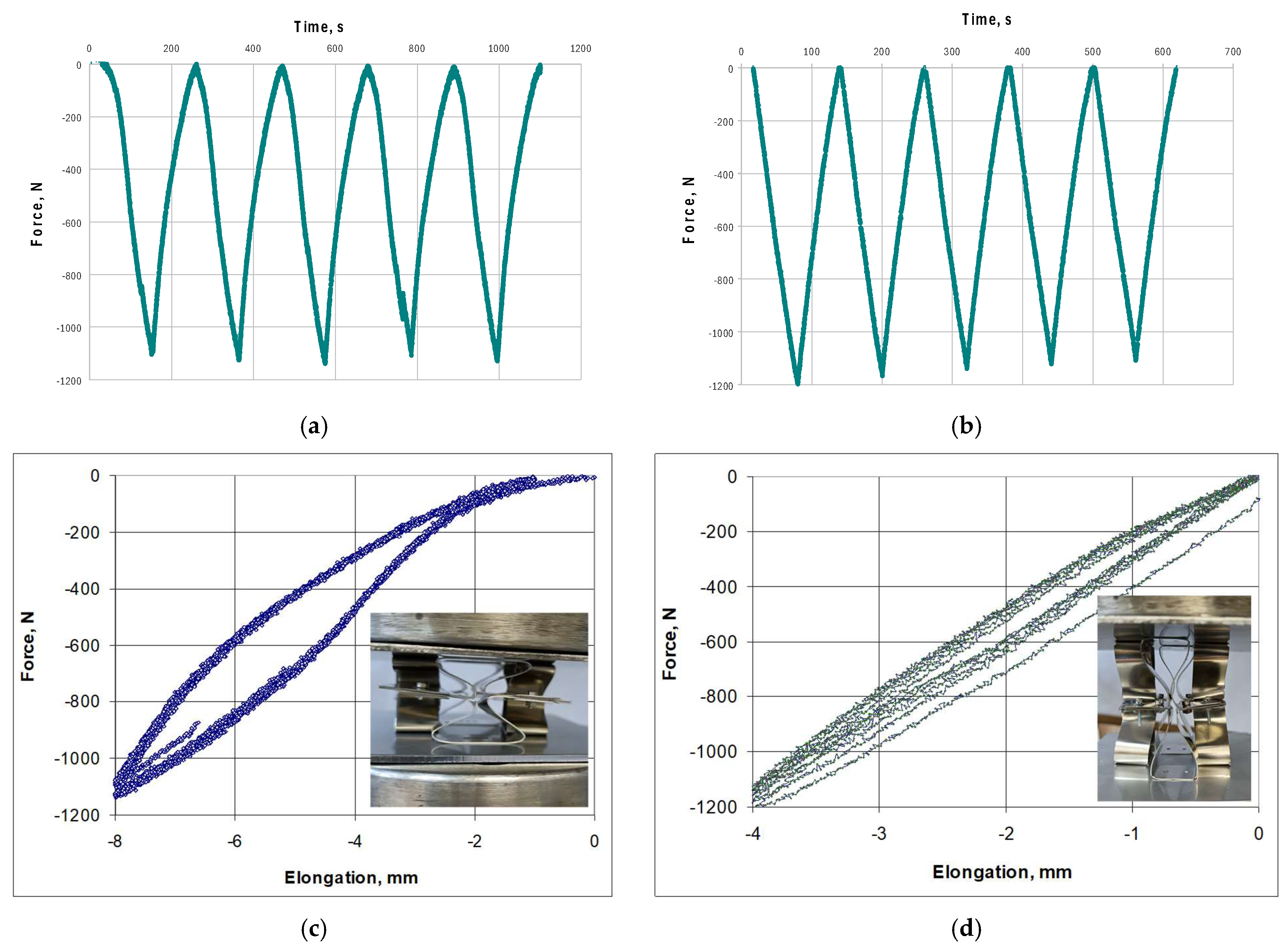
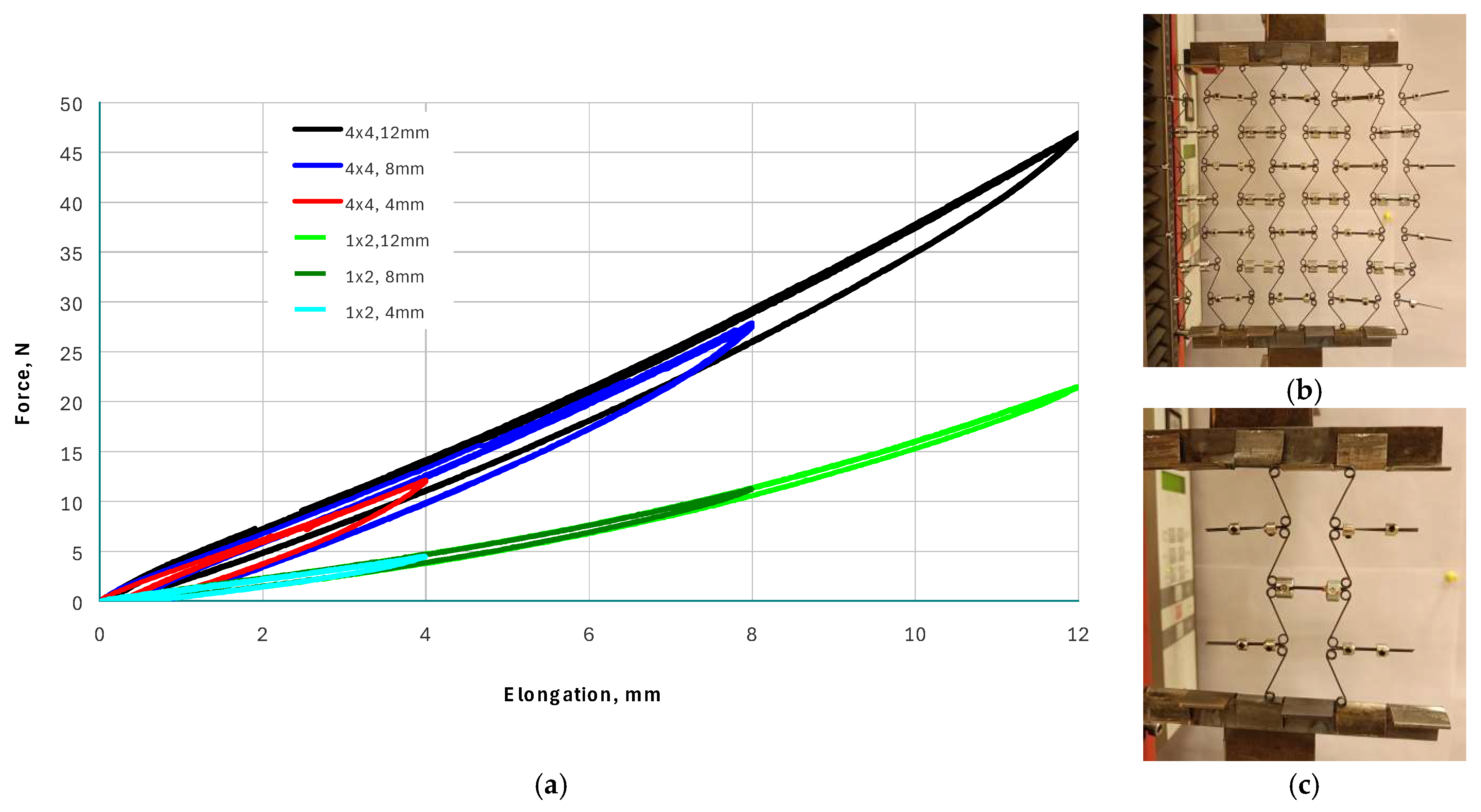
3. Models of Auxetic Structures
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Callister, W.D., Jr. Materials Science and Engineering. An Introduction, 7th ed.; John Wiley and Sons Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Ziolkowski, R.W. Metamaterials: The early years in the USA. EPJ Appl. Metamater. 2014, 1, 5. [Google Scholar] [CrossRef]
- Pendry, J.; Zhou, J.; Sun, J. Metamaterials: From Engineered Materials to Engineering Materials. Engineering 2022, 17, 1–2. [Google Scholar] [CrossRef]
- Boardman, A. Pioneers in metamaterials: John Pendry and Victor Veselago. J. Opt. 2011, 13, 020401. [Google Scholar] [CrossRef]
- Yu, X.; Zhou, J.; Liang, H.; Jiang, Z.; Wu, L. Mechanical metamaterials associated with stiffness, rigidity and compressibility: A brief review. Prog. Mater. Sci. 2018, 94, 114–173. [Google Scholar] [CrossRef]
- Sun, J.; Liu, X.; Zhou, J.; Kudyshev, Z.; Litchinitser, N.M. All-Dielectric Transition Magnetic Metamaterials. Sci. Rep. 2015, 5, 16154. [Google Scholar] [CrossRef]
- Sklan, S.R.; Li, B. Thermal metamaterials: Functions and prospects. Natl. Sci. Rev. 2018, 5, 138–141. [Google Scholar] [CrossRef]
- Available online: http://people.ee.duke.edu/~drsmith/metamaterials/metamaterials_homogenization.htm (accessed on 20 August 2024).
- Smith, D.R.; Pendry, J.B. Homogenization of metamaterials by field averaging. J. Opt. Soc. Am. B 2006, 23, 321. [Google Scholar] [CrossRef]
- Elipe, A.C.; Lantada, A.D. Comparative study of auxetic geometries by means of computer-aided design and Engineering. Smart Mater. Struct. 2012, 21, 105004. [Google Scholar] [CrossRef]
- Grima, J.N.; Evans, K.E. Auxetic behavior from rotating squares. J. Mater. Sci. Lett. 2000, 19, 1563–1565. [Google Scholar] [CrossRef]
- Almgren, R.F. An isotropic three-dimensional structure with Poisson’s ratio = −1. J. Elast. 1985, 15, 427–430. [Google Scholar] [CrossRef]
- Masters, I.G.; Evans, K.E. Models for the elastic deformation of honeycombs. Compos. Struct. 1996, 35, 403–422. [Google Scholar] [CrossRef]
- Gibson, L.; Ashby, M. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Tarlochan, F. Sandwich Structures for Energy Absorption Applications: A Review. Materials 2021, 14, 4731. [Google Scholar] [CrossRef] [PubMed]
- Francisco, M.B.; Pereira, J.L.J.; Oliver, G.A.; da Silva, L.R.R.; Cunha, S.S., Jr.; Gomes, G.F. A review on the energy absorption response and structural applications of auxetic structures. Mech. Adv. Mater. Struct. 2022, 29, 5823–5842. [Google Scholar] [CrossRef]
- Hu, L.L.; Zhou, M.Z.; Deng, H. Dynamic crushing response of auxetic honeycombs under large deformation: Theoretical analysis and numerical simulation. Thin-Walled Struct. 2018, 131, 373–384. [Google Scholar] [CrossRef]
- Han, D.; Ren, X.; Zhang, Y.; Zhang, X.Y.; Zhang, X.G.; Luo, C.; Xie, Y.M. Lightweight auxetic metamaterials: Design and characteristic study. Compos. Struct. 2022, 293, 115706. [Google Scholar] [CrossRef]
- Han, D.; Zhang, Y.; Zhang, X.Y.; Xie, Y.M.; Ren, X. Lightweight auxetic tubular metamaterials: Design and mechanical characteristics. Comp. Struct. 2023, 311, 116849. [Google Scholar] [CrossRef]
- Shirzad, M.; Zolfagharian, A.; Bodaghi, M.; Nam, S.Y. Auxetic metamaterials for bone-implanted medical devices: Recent advances and new perspectives. Eur. J. Mech.-A Solids 2023, 98, 104905. [Google Scholar] [CrossRef]
- Fardan, M.F.; Lenggana, B.W.; Ubaidillah, U.; Choi, S.-B.; Susilo, D.D.; Khan, S.Z. Revolutionizing Prosthetic Design with Auxetic Metamaterials and Structures: A Review of Mechanical Properties and Limitations. Micromachines 2023, 14, 165. [Google Scholar] [CrossRef]
- Yang, C.; Vora, H.D.; Chang, Y. Behavior of auxetic structures under compression and impact forces. Smart Mater. Struct. 2018, 27, 025012. [Google Scholar] [CrossRef]
- Curtis, S.M.; Dengiz, D.; Bumke, L.; Quandt, E. Shape Memory Alloy Thin Film Auxetic Structures. In Proceedings of the International Conference on Shape Memory and Superelastic Technologies, SMST 2022, Carlsbad, CA, USA, 16–20 May 2022; ASM International: San Diego, CA, USA, 2022; pp. 11–13. [Google Scholar]
- Isaac, C.W.; Duddeck, F. Recent progress in 4D printed energy-absorbing metamaterials and structures. Virtual Phys. Prototyp. 2023, 18, e2197436. [Google Scholar] [CrossRef]
- Naboni, R.; Mirante, L. Metamaterial computation and fabrication of auxetic patterns for Architecture. Digit. Manuf. Rapid Prototyp. 2015, 2, 129–136. [Google Scholar] [CrossRef]
- Jiang, W.; Ren, X.; Wang, S.L.; Zhang, X.G.; Zhang, X.Y.; Luo, C.; Xie, Y.M.; Scarpa, F.; Alderson, A.; Evans, K.E. Manufacturing, characteristics and applications of auxetic foams: A state-of-the-art review. Compos. Part B 2022, 235, 109733. [Google Scholar] [CrossRef]
- Li, X.; Peng, W.; Wu, W.; Xiong, J.; Lu, Y. Auxetic mechanical metamaterials: From soft to stiff. Int. J. Extrem. Manuf. 2023, 5, 042003. [Google Scholar] [CrossRef]
- Balan, M.; Mertens, J.; Bahubalendruni, M.R. Auxetic mechanical metamaterials and their futuristic developments: A state-of-art review. Mater. Today 2023, 34, 105285. [Google Scholar] [CrossRef]
- Yin, H.; Xiao, Y.; Wen, G.; Qing, Q.; Deng, Y. Multiobjective optimization for foam-filled multi-cell thin-walled structures under lateral impact. Thin-Walled Struct. 2015, 94, 1–12. [Google Scholar] [CrossRef]
- Necemer, B.; Klemenc, J.; Glodež, S. The computational LCF-analyses of chiral and Re-entrant auxetic structure using the direct cyclic algorithm. Mater. Sci. Eng. A 2020, 789, 139618. [Google Scholar] [CrossRef]
- Ghiasvand, A.; Khanigi, A.F.; Guerrero, J.W.G.; Derazkola, H.A.; Tomków, J.; Janeczek, A.; Wolski, A. Investigating the Effects of Geometrical Parameters of Re-Entrant Cells of Aluminum 7075-T651 Auxetic Structures on Fatigue Life. Coatings 2023, 13, 405. [Google Scholar] [CrossRef]
- Dong, Z.; Li, Y.; Zhao, T.; Wu, W.; Xiao, D.; Liang, J. Experimental and numerical studies on the compressive mechanical properties of the metallic auxetic reentrant honeycomb. Mater. Des. 2019, 182, 108036. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, G.; Wang, Z.; Ruan Alomarah, D.A.; Durandet, Y. Large Deformation of an Auxetic Structure in Tension: Experiments and Finite Element Analysis. Compos. Struct. 2017, 184, 92–101. [Google Scholar] [CrossRef]
- Sangsefidi, A.R.; Dibajian, S.H.; Kadkhodapour, J.; Anaraki, A.P.; Schmauder, S.; Schneider, Y. An Abaqus plugin for evaluation of the Auxetic structure performance. Eng. Comput. 2022, 38 (Suppl. S2), S1681–S1704. [Google Scholar] [CrossRef]
- Xiao, D. Insight into the negative Poisson’s ratio effect of metallic auxetic reentrant honeycomb under dynamic compression. Mater. Sci. Eng. A 2019, 763, 138151. [Google Scholar] [CrossRef]
- Francesconi, L.; Baldi, A.; Dominguez, G.; Taylor, M.L. An Investigation of the Enhanced Fatigue Performance of Low-porosity Auxetic Metamaterials. Exp. Mech. 2020, 60, 6093–6107. [Google Scholar] [CrossRef]
- Amin, F.; Najabat Ali, M.; Ansari, U.; Mir, M.; Minhas, M.A.; Shahid, W. Auxetic Coronary Stent Endoprosthesis: Fabrication and Structural Analysis. J Appl. Biomater. Funct. Mater. 2015, 13, e127–e135. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhou, C.; Shu, Z.; Jia, L.-J. Effect of Two-Dimensional Re-Entrant Honeycomb Configuration on Elastoplastic Performance of Perforated Steel Plate. Appl. Sci. 2020, 10, 3067. [Google Scholar] [CrossRef]
- Nedoushan, R.J. Improvement of energy absorption of expanded metal tubular structures under compressive loads. Thin-Walled Struct. 2020, 157, 107058. [Google Scholar] [CrossRef]
- Arifurrahman, F.; Critchley, R.; Horsfallm, I. Experimental numerical study of auxetic sandwich panels on 160 g of PE4 blast loading. J. Sandw. Struct. Mater. 2021, 23, 3902–3931. [Google Scholar] [CrossRef]
- Box, F.; Johnson, C.G.; Pihler-Puzović, D. Hard auxetic metamaterials. Extrem. Mech. Lett. 2020, 40, 100980. [Google Scholar] [CrossRef]
- Dallago, M.; Raghavendra, S.; Luchin, V.; Zappini, G.; Pasini, D.; Benedetti, M. Geometric assessment of lattice materials built via selective Laser Melting. Mater. Today Proc. 2019, 7, 7353–7361. [Google Scholar] [CrossRef]
- Kranz, J.; Herzog, D.; Emmelmann, C. Design guidelines for laser additive manufacturing of lightweight structures in TiAl6V4. J. Laser Appl. 2015, 27, S14001. [Google Scholar] [CrossRef]
- Bourell, D.; Kruth, J.P.; Leu, M.; Levy, G.; Rosen, D.; Beese, A.M.; Clare, A. Materials for additive manufacturing. CIRP Ann. Manuf. Technol. 2017, 66, 659–681. [Google Scholar] [CrossRef]
- Yánez, A.; Cuadrado, A.; Martel, O.; Afonso, H.; Monopoli, D. Gyroid porous titanium structures: A versatile solution to be used as scaffolds in bone defect reconstruction. Mater. Des. 2018, 140, 21–29. [Google Scholar] [CrossRef]
- Yang, L.; Harrysson, O.; West, H.; Cormier, D. Compressive properties of Ti–6Al–4V auxetic mesh structures made by electron beam melting. Acta Mater. 2012, 60, 3370–3379. [Google Scholar] [CrossRef]
- Brown, T.D.; Dalton, P.D.; Hutmacher, D.W. Melt electrospinning today: An opportune time for an emerging polymer process. Prog. Polym. Sci. 2016, 56, 116–166. [Google Scholar] [CrossRef]
- Hassanin, H.; Abena, A.; Elsayed, M.A.; Essa, K. 4D printing of NiTi auxetic structure with improved ballistic performance. Micromachines 2020, 11, 745. [Google Scholar] [CrossRef] [PubMed]
- Shivdeo, A.; Hardikar, A.; Bhikule, R.; Wagholikar, S.; Borhade, O.; Walame, M.V. Analysis of 2D Auxetic Metamaterial as a Variable Macro and Micro Structural Filter. Int. Res. J. Eng. Technol. 2019, 6, 695–700. [Google Scholar]
- Ghaedizadeh, A.; Shen, J.; Ren, X.; Xie, Y.M.M. Tuning the Performance of Metallic Auxetic Metamaterials by Using Buckling and Plasticity. Materials 2016, 9, 54. [Google Scholar] [CrossRef]
- Dengiz, D.; Goldbeck, H.; Curtis, S.M.; Bumke, L.; Jetter, J.; Quandt, E. Shape Memory Alloy Thin Film Auxetic Structures. Adv. Mater. Technol. 2023, 8, 2201991. [Google Scholar] [CrossRef]
- He, G.; Tan, Q.; Jiang, G.; Li, Q. A novel mechanism for auxetic behavior in entangled materials with a spiral wire structure. Smart Mater. Struct. 2014, 23, 095011. [Google Scholar] [CrossRef]
- Joseph, A.; Mahesh, V.; Harursampath, D. On the application of additive manufacturing methods for auxetic structures: A review. Adv. Manuf. 2021, 9, 342–368. [Google Scholar] [CrossRef]
- Friis, E.A.; Lakes, R.S.; Park, J.B. Negative Poisson’s ratio polymeric and metallic foams. J. Mater. Sci. 1988, 23, 4406–4414. [Google Scholar] [CrossRef]
- Plewa, J.; Płońska, M.; Junak, G. Experimental study of auxetic structures made of reentrant cells (“bow” type). Materials 2024, 17, 3061. [Google Scholar] [CrossRef] [PubMed]
- Smith, C.W.; Grima, J.N.; Evans, K.E. A novel mechanism for generating auxetic behaviour in reticulated foams: Missing rib foam model. Acta Mater. 2000, 48, 4349–4356. [Google Scholar] [CrossRef]
- Levy, O.; Goldfarb, I. Design considerations for negative Poisson ratio structures under large deflection for MEMS applications. Smart Mater. Struct. 2006, 15, 1459–1466. [Google Scholar] [CrossRef]
- Lekesiz, H.; Bhullar, S.K.; Karaca, A.A.; Jun, M.B.G. Mechanical characterization of auxetic stainless steel thin sheets with reentrant Structure. Smart Mater. Struct. 2017, 26, 085022. [Google Scholar] [CrossRef]
- Lvov, V.A.; Senatov, F.S.; Korsunsky, A.M.; Salimon, A.I. Design and Mechanical Properties of 3D-Printed Auxetic Honeycomb Structure. Mater. Today Comm. 2020, 24, 1011173. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plewa, J.; Płońska, M.; Junak, G. Metallic Metamaterials with Auxetic Properties: Re-Entrant Structures. Metals 2024, 14, 1272. https://doi.org/10.3390/met14111272
Plewa J, Płońska M, Junak G. Metallic Metamaterials with Auxetic Properties: Re-Entrant Structures. Metals. 2024; 14(11):1272. https://doi.org/10.3390/met14111272
Chicago/Turabian StylePlewa, Julian, Małgorzata Płońska, and Grzegorz Junak. 2024. "Metallic Metamaterials with Auxetic Properties: Re-Entrant Structures" Metals 14, no. 11: 1272. https://doi.org/10.3390/met14111272
APA StylePlewa, J., Płońska, M., & Junak, G. (2024). Metallic Metamaterials with Auxetic Properties: Re-Entrant Structures. Metals, 14(11), 1272. https://doi.org/10.3390/met14111272







