Simulation of Localized Stress Impact on Solidification Pattern during Plasma Cladding of WC Particles in Nickel-Based Alloys by Phase-Field Method
Abstract
1. Introduction
2. Phase-Field Models
2.1. Phase-Field Model
2.2. Phase Field
2.3. Elastic Strain Energy
2.4. Solving Parameters
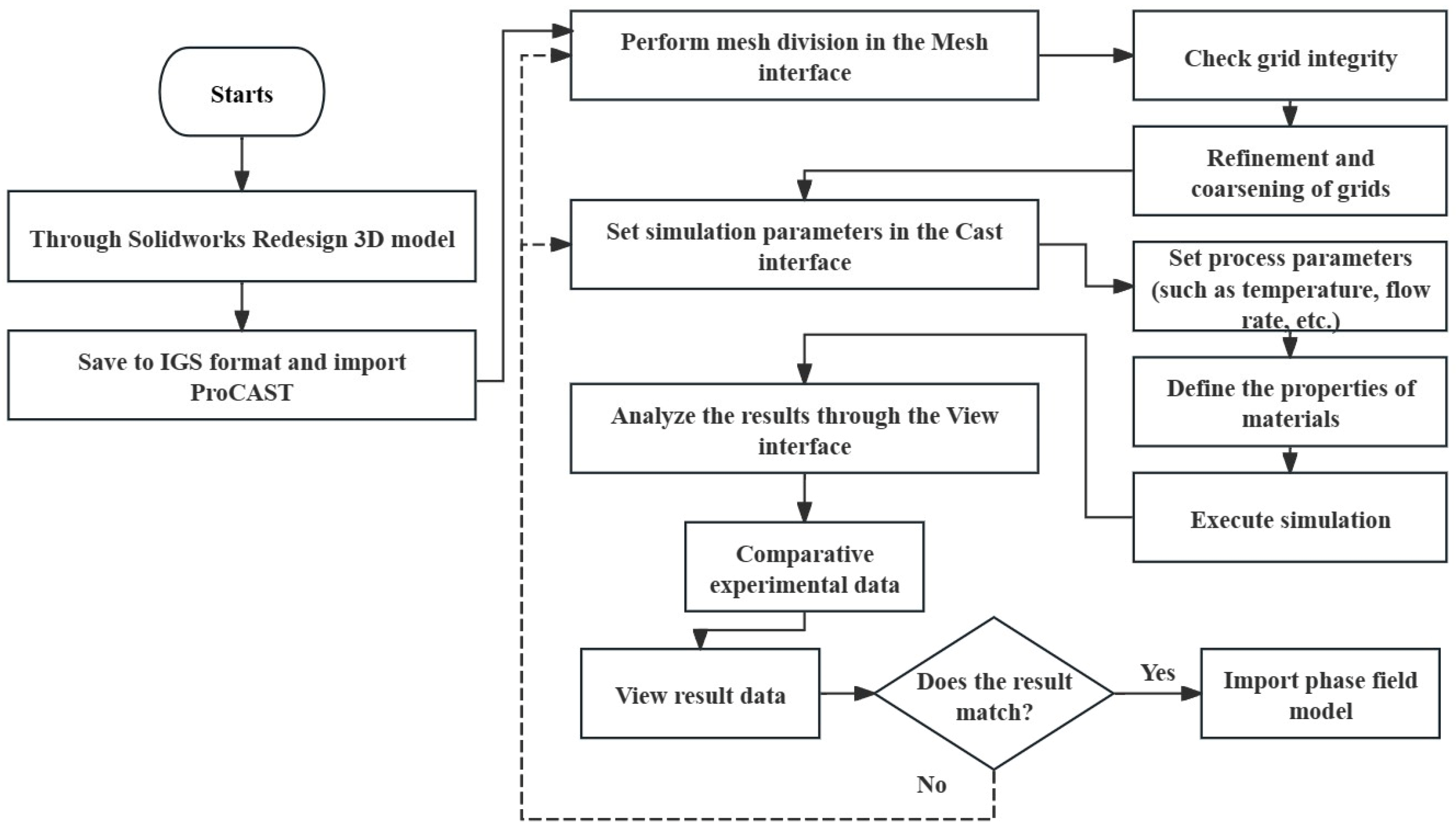
3. Macro-Simulation
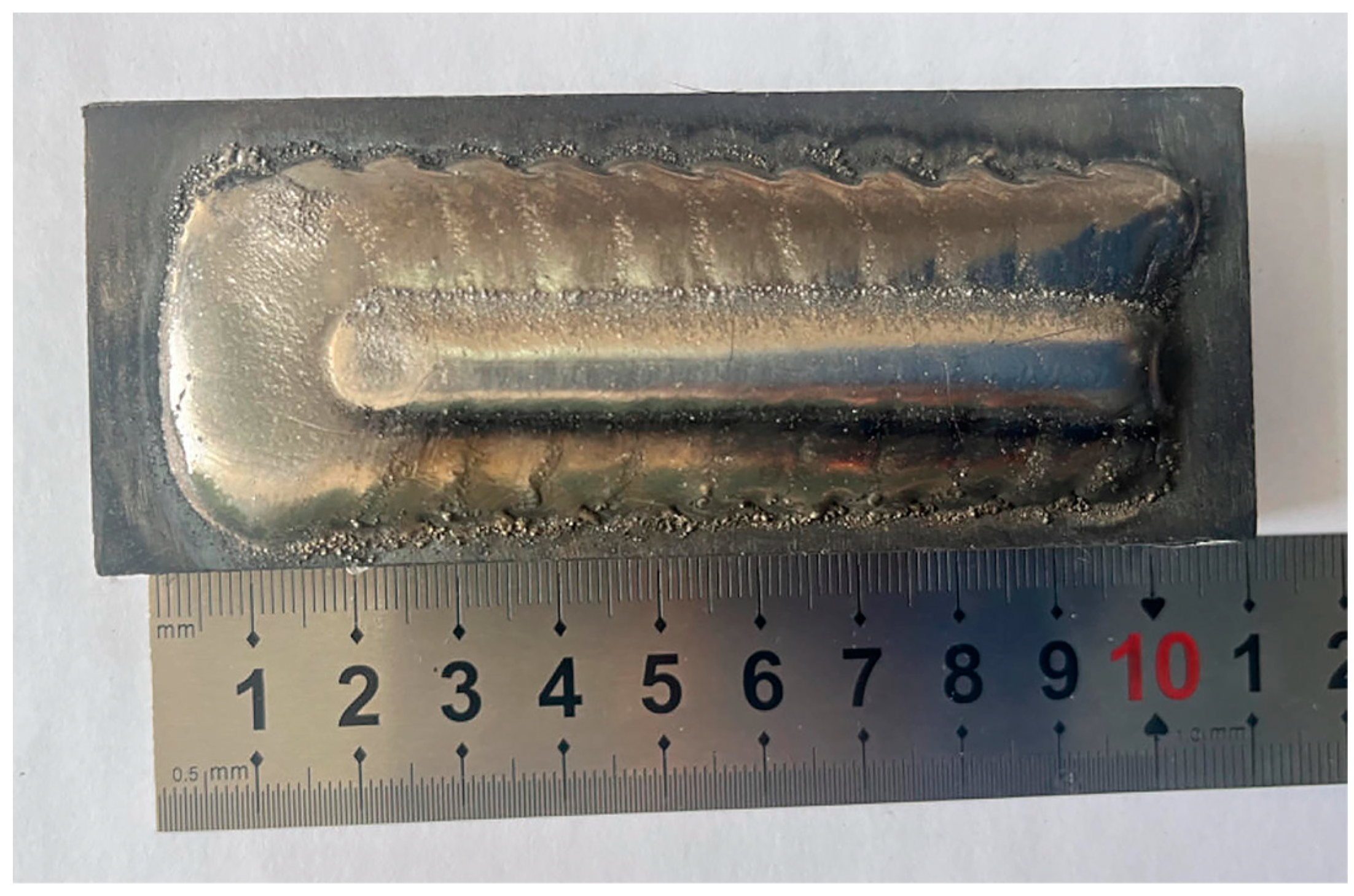
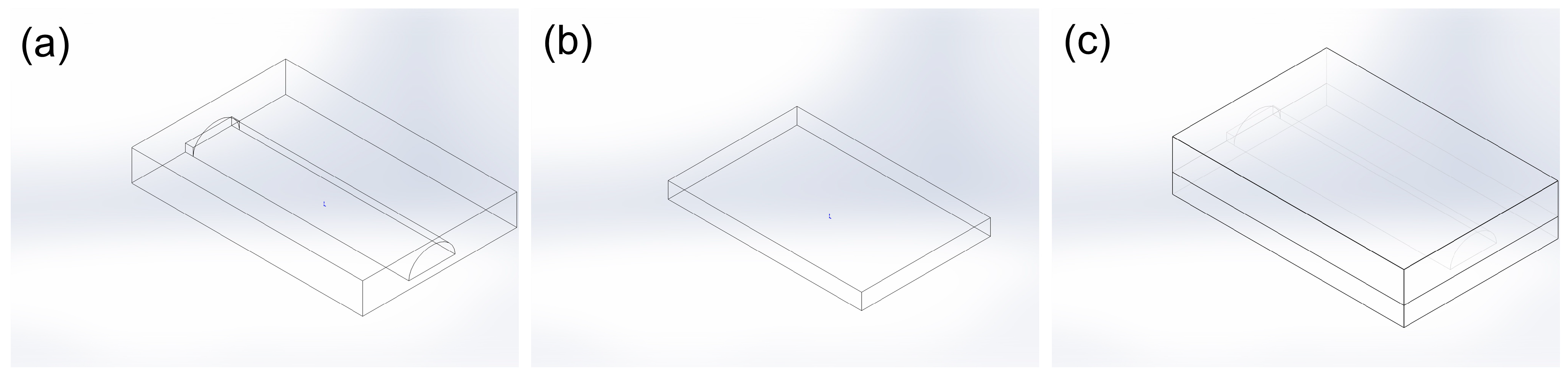
3.1. Model Establishment and Grid Partitioning
3.2. Boundary Conditions
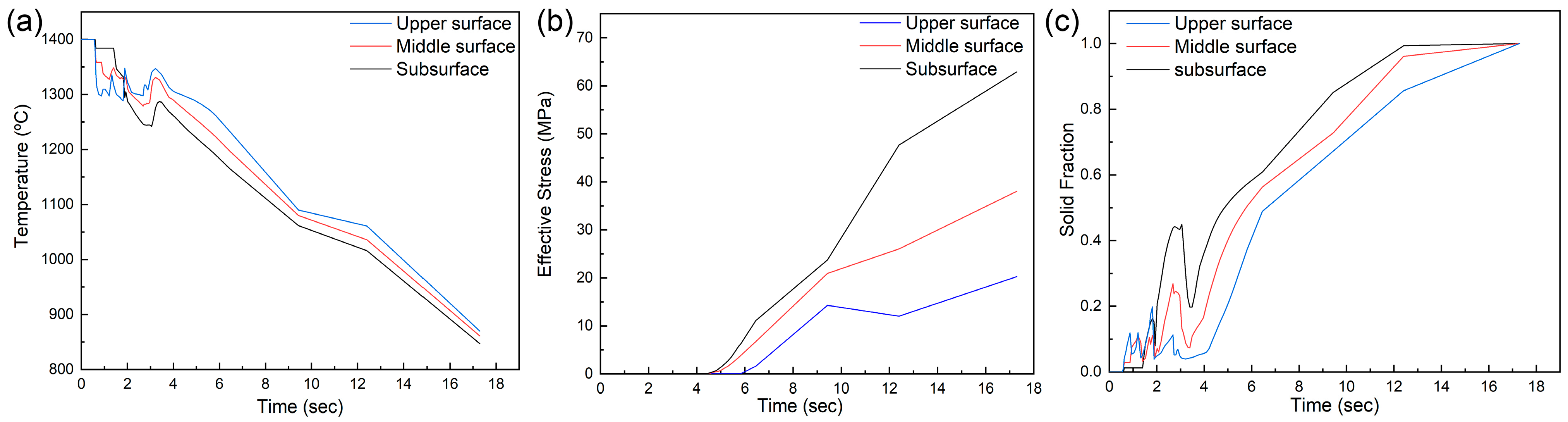
3.3. Analysis of the Process
4. Simulation Results and Discussion
5. Conclusions
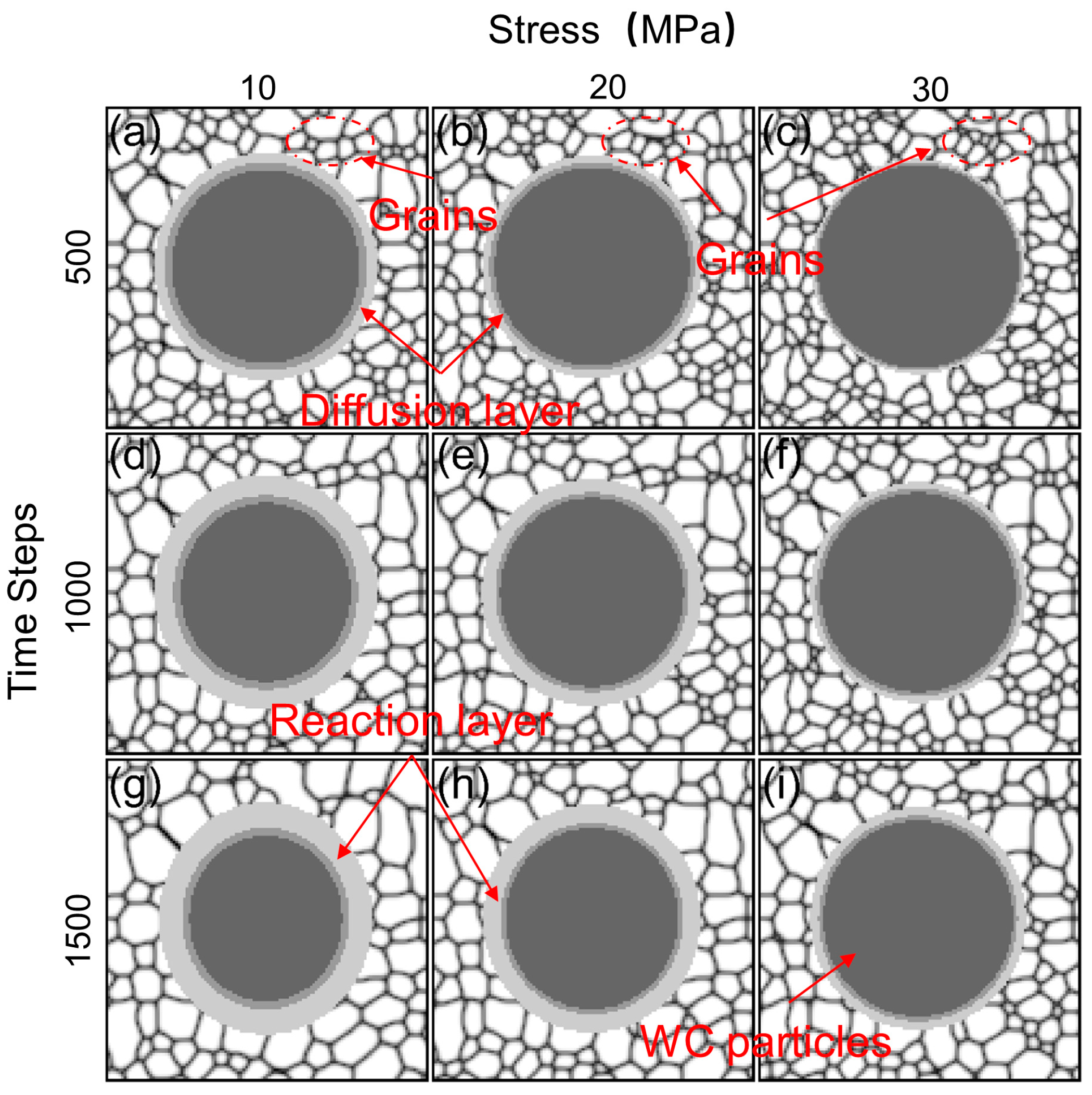
- When the localized stress is high, the mobility of grain boundaries within the system decreases significantly. Consequently, the dissolution and diffusion of WC particles are markedly hindered, leading to smaller surrounding grain sizes and preserving the shape of WC particles. This stability minimizes the formation of WC singularities and reduces stress concentration, thereby contributing to a more stable microstructural configuration of the material.
- At lower levels of localized stress, WC particles undergo pronounced dissolution and diffusion, resulting in an expanded reaction layer with the surrounding nickel-based alloys. Additionally, the Ostwald ripening of grains around WC particles becomes more evident, potentially forming new phases and structures that enhance the overall performance of the material.
- This study demonstrates that optimizing the microstructure during the solidification process can enhance the wear resistance, hardness, and overall performance of coatings. These findings offer a theoretical foundation for advancing material properties through surface modification techniques, which are particularly beneficial for materials exposed to extreme conditions in metallurgical, aerospace, and automotive applications.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fayed, E.M.; Brailovski, V.; Jahazi, M.; Medraj, M. Stability of the Microstructure and Elevated-Temperature Mechanical Properties of Additively Manufactured Inconel 718 Superalloy Subjected to Long-Term in-Service Thermal Cycling. Mater. Sci. Eng. A-Struct. Mater. Prop. Microstruct. Process. 2022, 838, 142790. [Google Scholar] [CrossRef]
- Xu, S.; Cai, Q.; Li, G.; Lu, X.; Zhu, X. Effect of Scanning Speed on Microstructure and Properties of Tic/Ni60 Composite Coatings on Ti6al4v Alloy by Laser Cladding. Opt. Laser Technol. 2022, 154, 108309. [Google Scholar] [CrossRef]
- Kim, G.; Kim, Y.C.; Cho, J.E.; Yim, C.H.; Yun, D.S.; Lee, T.G.; Park, N.K.; Chung, R.H.; Hong, D.G. Microstructural Evolution, Hardness and Wear Resistance of Wc-Co-Ni Composite Coatings Fabricated by Laser Cladding. Materials 2024, 17, 2116. [Google Scholar] [CrossRef] [PubMed]
- Obadele, B.A.; Andrews, A.; Olubambi, P.A.; Mathew, M.T.; Pityana, S. Effect of Zro 2 Addition on the Dry Sliding Wear Behavior of Laser Clad Ti6al4v Alloy. Wear 2015, 328–329, 295–300. [Google Scholar] [CrossRef]
- Shen, X.; Peng, H.; Xue, Y.; Wang, B.; Su, G.; Zhu, J.; Li, A. Microstructure and Properties of Wc/Ni-Based Laser-Clad Coatings with Different Wc Content Values. Materials 2022, 15, 6309. [Google Scholar] [CrossRef]
- Chen, B.J.; Xu, M.K. Preparation and Performance Analysis of Micro-Nano Composite Coatings Reinforced with Wc Particles. Mater. Res. Express 2024, 11, 026508. [Google Scholar] [CrossRef]
- Nomoto, S.; Kusano, M.; Kitano, H.; Watanabe, M. Multi-Phase Field Method for Solidification Microstructure Evolution for a Ni-Based Alloy in Wire Arc Additive Manufacturing. Metals 2022, 12, 1720. [Google Scholar] [CrossRef]
- Li, M.; Yang, J.; Han, B.; Song, L.; Li, P.; Dong, W.; Xue, X. Comparative Investigation on Microstructures and Properties of Wc/Cr3c2 Reinforced Laser Cladding Ni-Based Composite Coatings Subjected to Ultrasonic Impact Treatment. Mater. Today Commun. 2023, 34, 105219. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, J.; Zhang, T.; Li, P.; Zhu, H.; Meng, X. Effects of Wc Particles on the Microstructure of In718/Wc Composite Coatings Fabricated by Laser Cladding: A Two-Dimensional Phase-Field Study. Coatings 2023, 13, 432. [Google Scholar] [CrossRef]
- Teferra, K.; Rowenhorst, D.J. Optimizing the Cellular Automata Finite Element Model for Additive Manufacturing to Simulate Large Microstructures. Acta Mater. 2021, 213, 116930. [Google Scholar] [CrossRef]
- Zinovieva, O.; Zinoviev, A.; Patel, M.N.; Molotnikov, A.; Easton, M.A. Modelling Grain Refinement under Additive Manufacturing Solidification Conditions Using High Performance Cellular Automata. Mater. Des. 2024, 245, 113248. [Google Scholar] [CrossRef]
- Ushmaev, D.; Liao, Z.; Notron, A.; Axinte, D. On the Importance of Interface Stability in Cellular Automata Models: Planar and Dendritic Solidification in Laser Melted Ysz. Mater. Des. 2022, 219, 110823. [Google Scholar] [CrossRef]
- Tourret, D.; Liu, H.; Llorca, J. Phase-Field Modeling of Microstructure Evolution: Recent Applications, Perspectives and Challenges. Prog. Mater. Sci. 2022, 123, 100810. [Google Scholar] [CrossRef]
- Lv, S.J.; Wu, H.H.; Wang, K.Y.; Zhang, C.L.; Zhu, J.M.; Wang, S.Z.; Wu, G.L.; Gao, J.H.; Yang, X.S.; Mao, X.P. Phase Field Simulation of Eutectoid Microstructure During Austenite-Pearlite Phase Transformation. J. Mater. Res. Technol. 2023, 26, 8922–8933. [Google Scholar] [CrossRef]
- Wu, Y.; Xiong, J.L.; Luo, Q.; Chen, J.B.; Zeng, R.T.; Wang, S. Estimation of the Critical Value of the Second-Phase Particles in the Microstructure of Az31 Mg Alloy by Phase-Field Methods. Crystals 2022, 12, 1504. [Google Scholar] [CrossRef]
- Schwen, D.; Schunert, S.; Jokisaari, A. Evolution of Microstructures in Radiation Fields Using a Coupled Binary-Collision Monte Carlo Phase Field Approach. Comput. Mater. Sci. 2021, 192, 110321. [Google Scholar] [CrossRef]
- Zhang, Z.; Ge, P.; Li, J.Y.; Ren, D.X.; Wu, T. Monte Carlo Simulations of Solidification and Solid-State Phase Transformation during Directed Energy Deposition Additive Manufacturing. Prog. Addit. Manuf. 2022, 7, 671–682. [Google Scholar] [CrossRef]
- Zheng, Y.; Liu, J.P.; Liang, Y.F.; Wu, P.P. Monte-Carlo-Assisted Phase Field Simulations of Grain Structure Evolution During the Welding Process. Metals 2023, 13, 623. [Google Scholar] [CrossRef]
- Browne, D.J.; Hunt, J.D. A Fixed Grid Front-Tracking Model of the Growth of a Columnar Front and an Equiaxed Grain during Solidification of an Alloy. Numer. Heat Transf. Part B Fundam. 2004, 45, 395–419. [Google Scholar] [CrossRef]
- Karma, A.; Rappel, W.-J. Quantitative Phase-Field Modeling of Dendritic Growth in Two and Three Dimensions. Phys. Rev. E 1998, 57, 4323–4349. [Google Scholar] [CrossRef]
- Chen, L.-Q. Phase-Field Models for Microstructure Evolution. Annu. Rev. Mater. Res. 2002, 32, 113–140. [Google Scholar] [CrossRef]
- Moelans, N.; Blanpain, B.; Wollants, P. An Introduction to Phase-Field Modeling of Microstructure Evolution. Calphad 2008, 32, 268–294. [Google Scholar] [CrossRef]
- Echebarria, B.; Folch, R.; Karma, A.; Plapp, M. Quantitative Phase-Field Model of Alloy Solidification. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2004, 70 Pt 1, 061604. [Google Scholar] [CrossRef] [PubMed]
- Tegze, G.; Bansel, G.; Tóth, G.I.; Pusztai, T.; Fan, Z.; Gránásy, L. Advanced Operator Splitting-Based Semi-Implicit Spectral Method to Solve the Binary Phase-Field Crystal Equations with Variable Coefficients. J. Comput. Phys. 2009, 228, 1612–1623. [Google Scholar] [CrossRef]
- Wang, Y.B.; Zhang, Y.; Liu, X.T.; Wang, J.X.; Xie, X.Y.; Jiang, J.J.; Liu, J.X.; Liu, H.; Wu, Y.J.; Dong, S.; et al. Simulation of Microstructure Evolution in Mg Alloys by Phase-Field Methods: A Review. Crystals 2022, 12, 1305. [Google Scholar] [CrossRef]
- Munoz, E.J.; Attari, V.; Martinez, M.C.; Dickerson, M.B.; Radovic, M.; Arroyave, R. Phase-Field Model of Silicon Carbide Growth During Isothermal Condition. Comput. Mater. Sci. 2024, 242, 113058. [Google Scholar] [CrossRef]
- Chen, L.-Q.; Fan, D. Computer Simulation Model for Coupled Grain Growth and Ostwald Ripening—Application to Al2O3-ZrO2 Two-Phase Systems. J. Am. Ceram. Soc. 2005, 79, 1163–1168. [Google Scholar] [CrossRef]
- Allen, S.M.; Cahn, J.W. A Microscopic Theory for Antiphase Boundary Motion and Its Application to Antiphase Domain Coarsening. Acta Metall. 1979, 27, 1085–1095. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free Energy of a Nonuniform System. I. Interfacial Free Energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Zheng, S.; Sokoluk, M.; Yao, G.; de Rosa, I.; Li, X. Fe–Ni Invar Alloy Reinforced by Wc Nanoparticles with High Strength and Low Thermal Expansion. SN Appl. Sci. 2019, 1, 172. [Google Scholar] [CrossRef]
- Chen, L.Q.; Shen, J. Applications of Semi-Implicit Fourier-Spectral Method to Phase Field Equations. Comput. Phys. Commun. 1998, 108, 147–158. [Google Scholar] [CrossRef]
- Gránásy, L.; Börzsönyi, T.; Pusztai, T. Crystal Nucleation and Growth in Binary Phase-Field Theory. J. Cryst. Growth 2002, 237–239, 1813–1817. [Google Scholar] [CrossRef]
- Hu, Z.; Wise, S.M.; Wang, C.; Lowengrub, J.S. Stable and Efficient Finite-Difference Nonlinear-Multigrid Schemes for the Phase Field Crystal Equation. J. Comput. Phys. 2009, 228, 5323–5339. [Google Scholar] [CrossRef]
- Eiken, J.; Bottger, B.; Steinbach, I. Multiphase-Field Approach for Multicomponent Alloys with Extrapolation Scheme for Numerical Application. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 2006, 73 Pt 2, 066122. [Google Scholar] [CrossRef] [PubMed]
- Yoon, S.; Jeong, D.; Lee, C.; Kim, H.; Kim, S.; Lee, H.G.; Kim, J. Fourier-Spectral Method for the Phase-Field Equations. Mathematics 2020, 8, 1385. [Google Scholar] [CrossRef]
- Jaatinen, A.; Achim, C.V.; Elder, K.R.; Ala-Nissila, T. Thermodynamics of Bcc Metals in Phase-Field-Crystal Models. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 2009, 80 Pt 1, 031602. [Google Scholar] [CrossRef]
- Tegze, G.; Granasy, L.; Toth, G.I.; Podmaniczky, F.; Jaatinen, A.; Ala-Nissila, T.; Pusztai, T. Diffusion-Controlled Anisotropic Growth of Stable and Metastable Crystal Polymorphs in the Phase-Field Crystal Model. Phys. Rev. Lett. 2009, 103, 035702. [Google Scholar] [CrossRef]
- Wang, Y.U.; Jin, Y.M.; Cuitiño, A.M.; Khachaturyan, A.G. Nanoscale Phase Field Microelasticity Theory of Dislocations: Model and 3d Simulations. Acta Mater. 2001, 49, 1847–1857. [Google Scholar] [CrossRef]
- Choudhury, A.; Nestler, B. Grand-Potential Formulation for Multicomponent Phase Transformations Combined with Thin-Interface Asymptotics of the Double-Obstacle Potential. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 2012, 85 Pt 1, 021602. [Google Scholar] [CrossRef]
- Oono, Y.; Puri, S. Computationally Efficient Modeling of Ordering of Quenched Phases. Phys. Rev. Lett. 1987, 58, 836–839. [Google Scholar] [CrossRef]
- Xia, M.J.; Gu, D.D.; Ma, C.L.; Zhang, H.M.; Dai, D.H.; Chen, H.Y.; Li, C.P.; Zhou, Z.J.; Chen, G.F.; Kelbassa, I. Fragmentation and Refinement Behavior and Underlying Thermodynamic Mechanism of Wc Reinforcement During Selective Laser Melting of Ni-Based Composites. J. Alloys Compd. 2019, 777, 693–702. [Google Scholar] [CrossRef]
- Fan, D.; Chen, L.Q. Computer Simulation of Grain Growth Using a Continuum Field Model. Acta Mater. 1997, 45, 611–622. [Google Scholar] [CrossRef]
- Olyslager, F. Overview of the Singular Behavior of Electromagnetic Fields at Edges and Tips in Bi-Isotropic and Special Bianisotropic Media. Radio Sci. 1995, 30, 1349–1354. [Google Scholar] [CrossRef]
- Valagiannopoulos, C.A. On Smoothening the Singular Field Developed in the Vicinity of Metallic Edges. Int. J. Appl. Electromagn. Mech. 2009, 31, 67–77. [Google Scholar] [CrossRef]




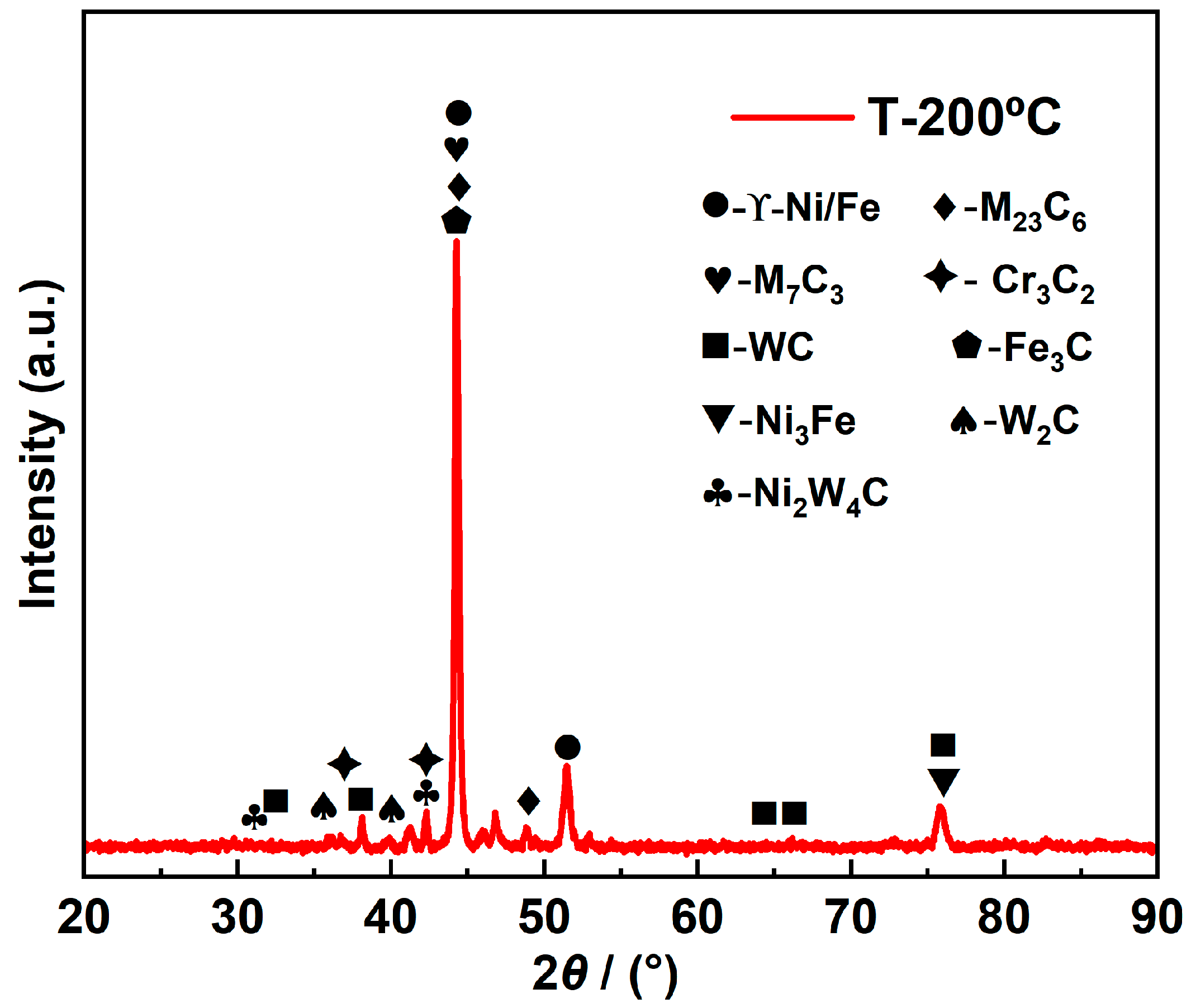

| Symbol | Description | Value | Ref. |
|---|---|---|---|
| Space step | 2.0 | [27] | |
| Time step | 0.1 | ||
| Gradient energy coefficient of phase | 2.5 | ||
| Gradient energy coefficient of phase | 2.0 | ||
| Gradient energy coefficient of concentration | 0.5 | ||
| Benchmark migration rate | 3.0 | ||
| - | 2.0 | ||
| - | 9.88 | ||
| - | 1.52 | ||
| - | 1.23 | ||
| - | 1.0 | ||
| Stress sensitivity coefficient | 0.06 | - | |
| k | Physical constant | 1.025 | |
| Lattice expansion coefficient | 2.6 × 10−6 | [30] | |
| Thermal expansion coefficient | 9.6 × 10−6 | [41] |
| Element | C | Cr | B | Si | Fe | Cu | W | Ni |
|---|---|---|---|---|---|---|---|---|
| Ni40A | 0.07 | 11.09 | 1.23 | 3.46 | 3.01 | 3.66 | - | Bal |
| Ni40A-45 wt.% WC | 1.83 | 0.1 | 1.24 | 1.76 | 1.44 | - | 43.2 | Bal |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, D.; Chen, M.; Zhang, C.; Ai, X.; Xie, Z. Simulation of Localized Stress Impact on Solidification Pattern during Plasma Cladding of WC Particles in Nickel-Based Alloys by Phase-Field Method. Metals 2024, 14, 1022. https://doi.org/10.3390/met14091022
Wei D, Chen M, Zhang C, Ai X, Xie Z. Simulation of Localized Stress Impact on Solidification Pattern during Plasma Cladding of WC Particles in Nickel-Based Alloys by Phase-Field Method. Metals. 2024; 14(9):1022. https://doi.org/10.3390/met14091022
Chicago/Turabian StyleWei, Dongsheng, Ming Chen, Chunlin Zhang, Xingang Ai, and Zhiwen Xie. 2024. "Simulation of Localized Stress Impact on Solidification Pattern during Plasma Cladding of WC Particles in Nickel-Based Alloys by Phase-Field Method" Metals 14, no. 9: 1022. https://doi.org/10.3390/met14091022
APA StyleWei, D., Chen, M., Zhang, C., Ai, X., & Xie, Z. (2024). Simulation of Localized Stress Impact on Solidification Pattern during Plasma Cladding of WC Particles in Nickel-Based Alloys by Phase-Field Method. Metals, 14(9), 1022. https://doi.org/10.3390/met14091022







