Design of New Energy-Absorbing Lattice Cell Configuration by Dynamic Topology Optimization
Abstract
:1. Introduction
2. Topology Optimization of Energy-Absorbing Lattice Cell
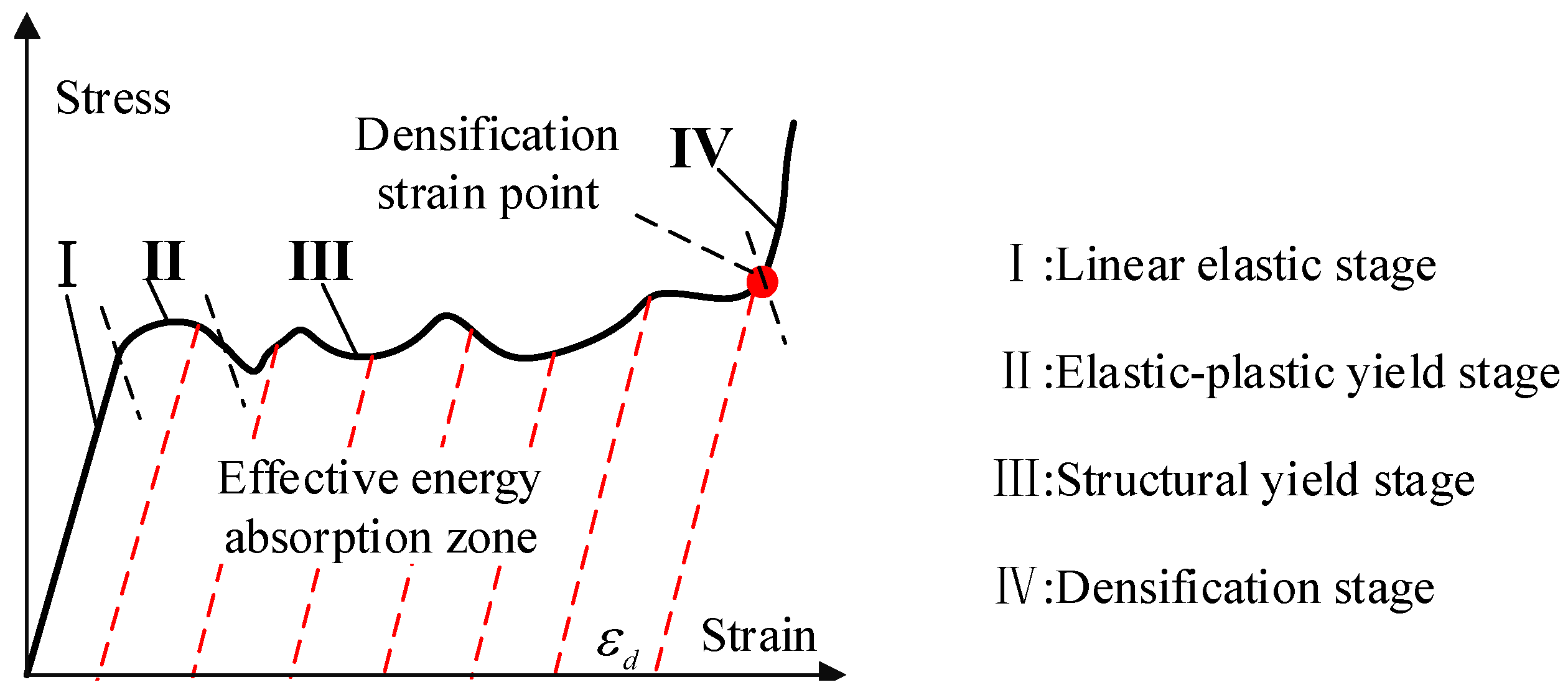
2.1. Definition of Densification Strain
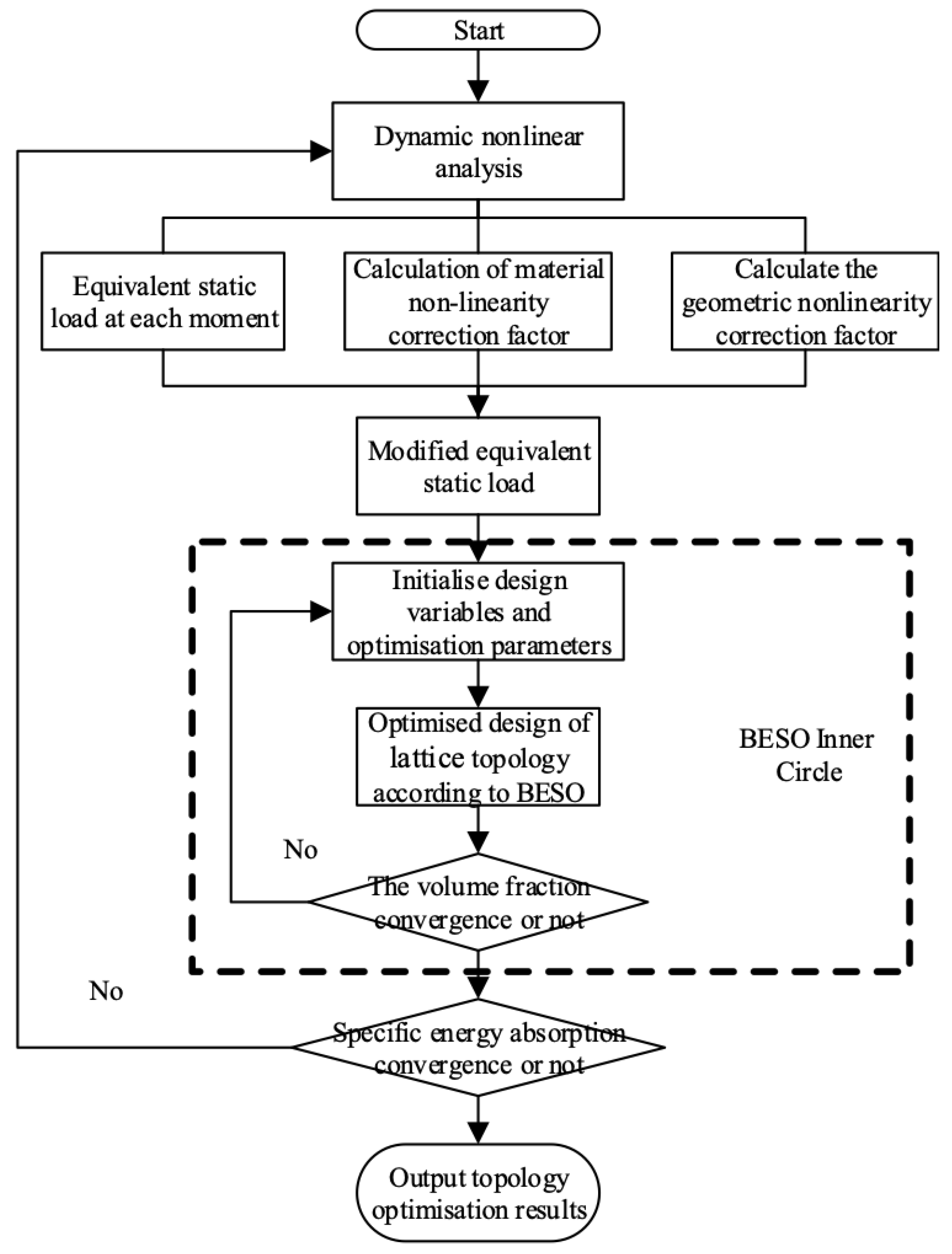
2.2. Algorithm Implementation on BESO
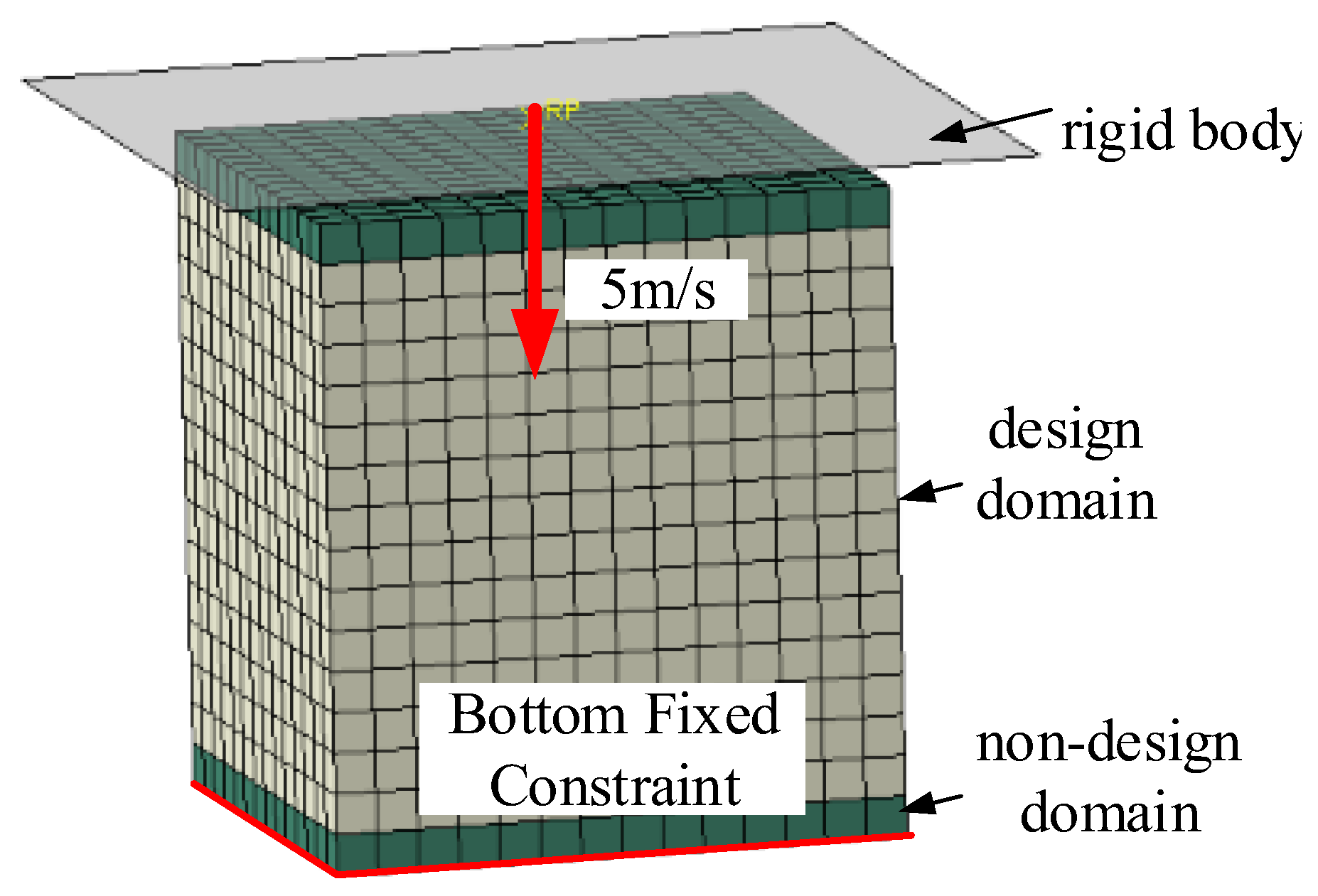
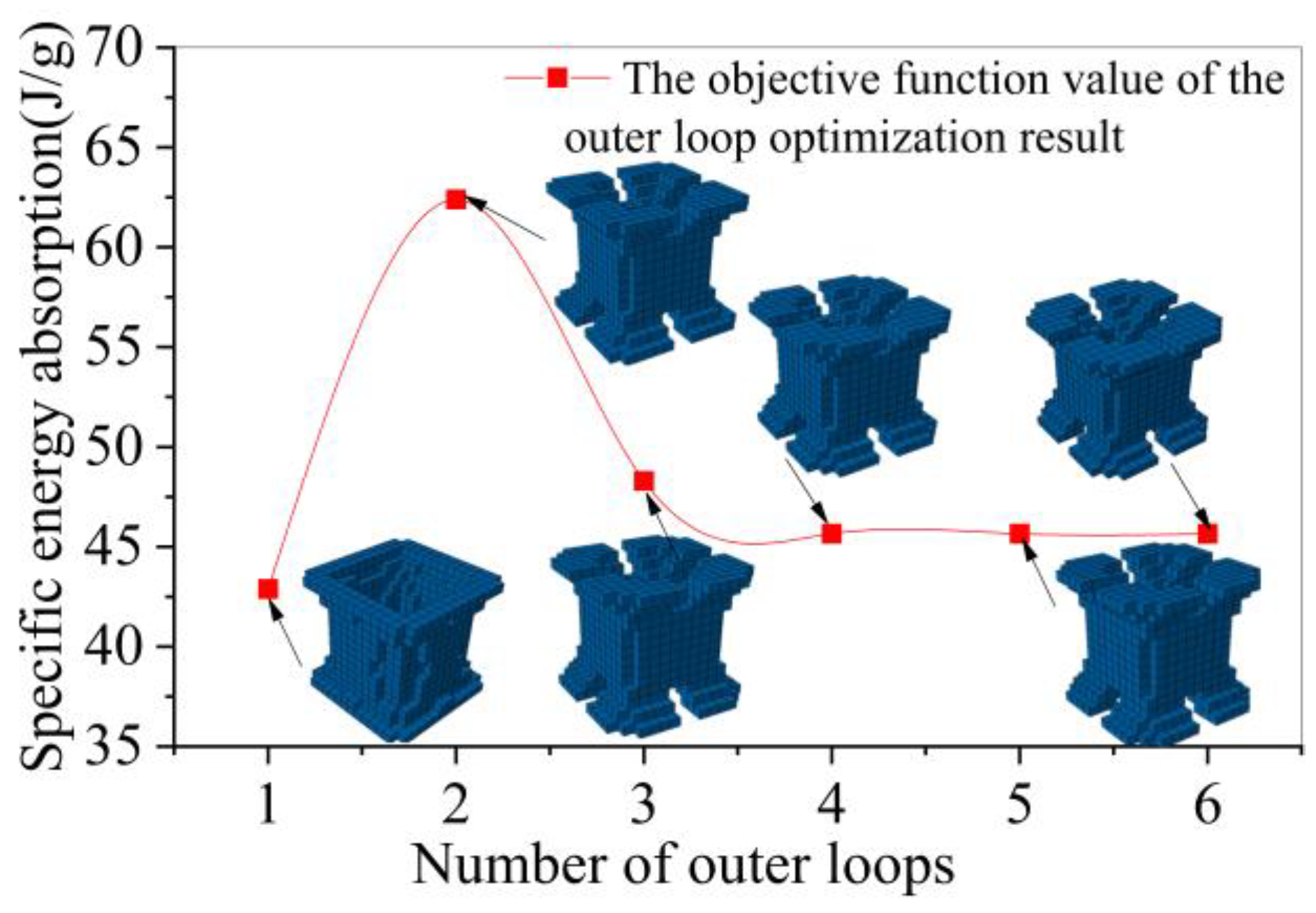
3. Cellular Configuration Optimization of Energy-Absorbing Lattice
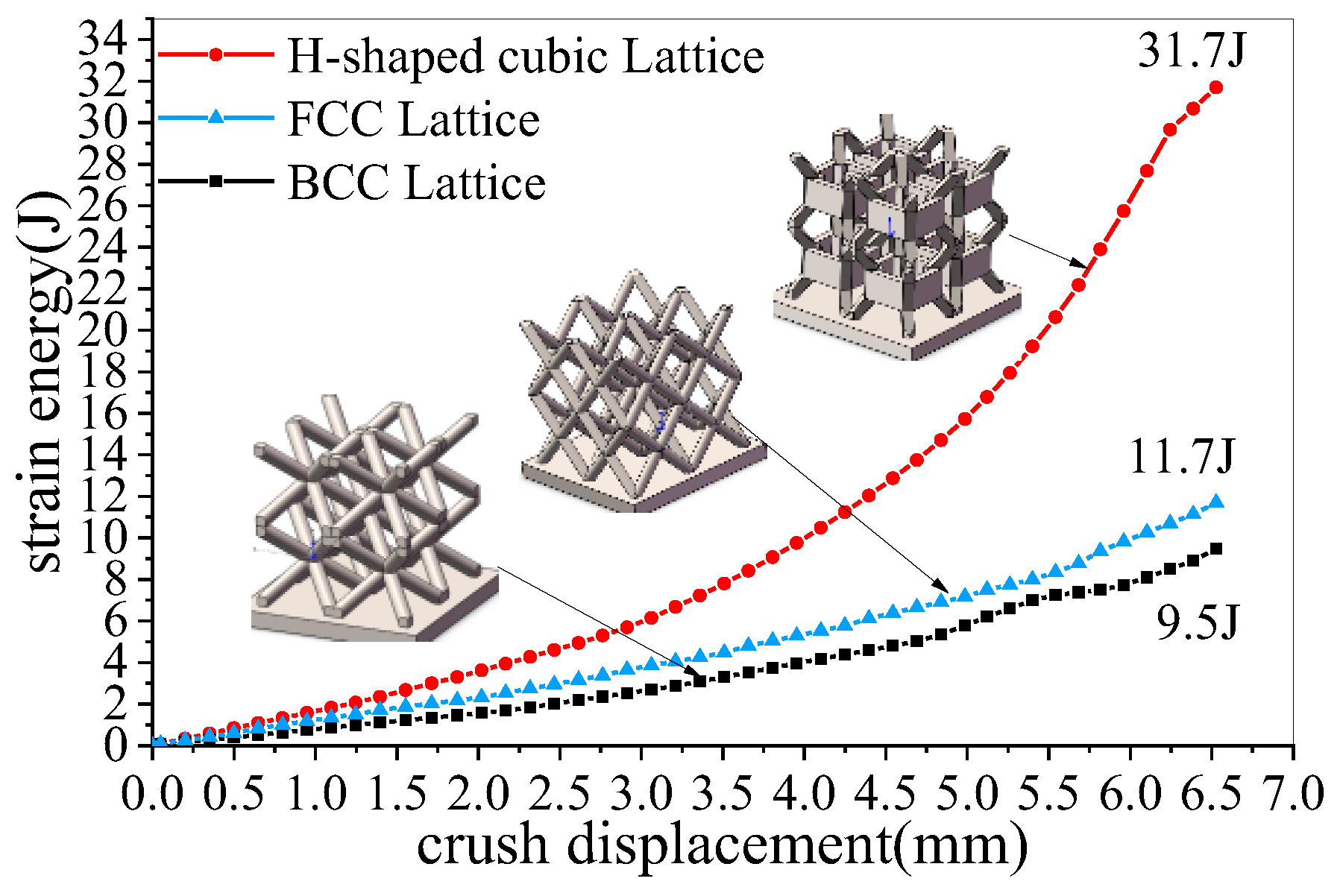
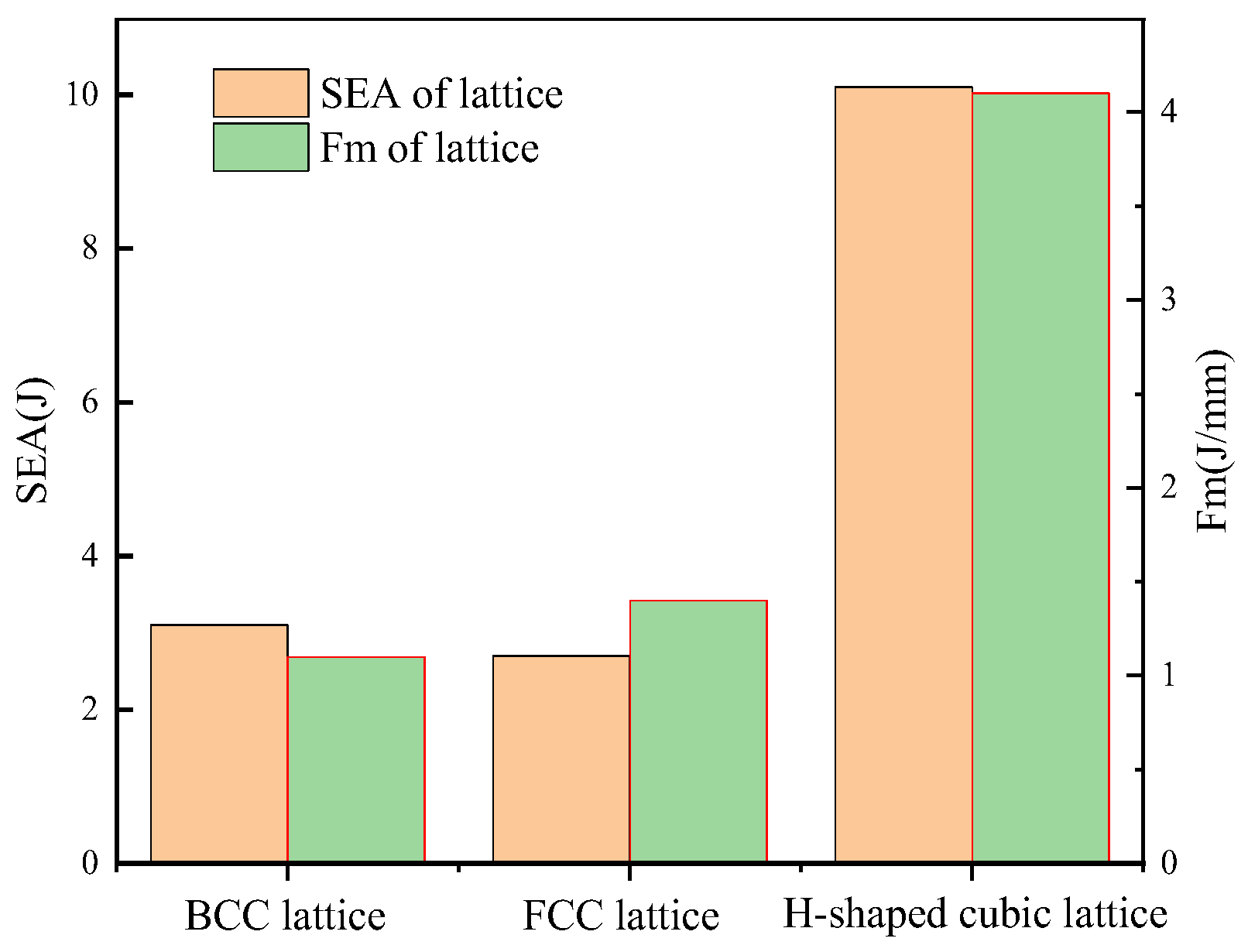
4. Quasistatic Compression Test of Lattice Configuration
5. Conclusions
- (1)
- It was proposed to determine the occurrence of densification in the analysis process by establishing the ratio of the adjacent equivalent plastic moduli for the calculation of the effective energy absorption of the topological structure during the optimization iteration. A dynamic topology optimization program was also developed.
- (2)
- A new energy-absorbing lattice cell configuration consisting of a pillar structure and a middle thin-walled structure was obtained by dynamic topology optimization. Moreover, additive manufacturing of the specimens was realized by selective laser melting. The energy absorption performance of the new energy-absorbing lattice and BCC and FCC lattice configurations is experimentally analyzed and compared. The results show that the absorbed energy of the new energy-absorbing lattice is approximately three times those of BCC and FCC lattice configurations with the same mass and the same collapse displacement at the low impact speed of 5 m/s.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Dong, Z.; Liang, J.; Ge, J. Determination of the strength of a multilayer BCC lattice structure with face sheets. Int. J. Mech. Sci. 2019, 152, 568–575. [Google Scholar] [CrossRef]
- Gorban, V.F.; Firstov, S.A.; Krapivka, M.O. The Influence of Different Factors on Physicomechanical Properties of High Entropy Alloys with fcc Lattice. Mater. Sci. 2024, 59, 145–151. [Google Scholar] [CrossRef]
- Wei, K.; Yang, Q.D.; Ling, B.; Xie, H.; Qu, Z.; Fang, D.N. Mechanical Responses of Titanium 3d Kagome Lattice Structure Manufactured by Selective Laser Melting. Extrem. Mech. Lett. 2018, 23, 41–48. [Google Scholar] [CrossRef]
- Habib, F.; Iovenitti, P.; Masood, S.; Nikzad, M.; Ruan, D. Design and evaluation of 3D printed polymeric cellular materials for dynamic energy absorption. Int. J. Adv. Manuf. Technol. 2019, 103, 2347–2361. [Google Scholar] [CrossRef]
- Maskery, I.; Aboulkhair, N.T.; Aremu, A.O.; Tuck, C.J.; Ashcroft, I.A. Compressive failure modes and energy absorption in additively manufactured double gyroid lattice. Addit. Manuf. 2017, 16, 24–29. [Google Scholar] [CrossRef]
- Xu, P.; Guo, W.N.; Yang, L.Y.; Yang, C.X.; Ruan, D.; Xu, J.; Yao, S. Crashworthiness analysis of the biomimetic lotus root lattice structure. Int. J. Mech. Sci. 2024, 263, 108774. [Google Scholar] [CrossRef]
- Kumar, A.; Verma, S.; Jeng, J.Y. Supportless Lattice Structures for Energy Absorption Fabricated by Fused Deposition Modeling. 3d Print. Addit. Manuf. 2020, 7, 85–96. [Google Scholar] [CrossRef]
- Yu, Z.; Xin, R.; Xu, Z.; Sha, L.; Chen, L.; Zhu, Y.; Liang, P.; Zhang, Z.; Liu, Z.; Cao, Q. Shock-Resistant and Energy-Absorbing Properties of Bionic NiTi Lattice Structure Manufactured by SLM. J. Bionic Eng. 2022, 19, 1684–1698. [Google Scholar] [CrossRef]
- Zhang, W.Z.; Yin, H.F.; Wu, Y.C.; Jin, Q.; Wu, L.; Wen, G.; Liu, J.; Wu, X. A novel auxetic 3D lattice structure for enhancing energy absorption. Compos. Struct. 2023, 326, 117620. [Google Scholar] [CrossRef]
- Zhang, P.; Biligetu; Qi, D.; Xue, R.; Liu, K.; Huang, Z.; Wu, W.; Li, Y. Mechanical design and energy absorption of 3D novel hybrid lattice metamaterials. Sci. China Technol. Sci. 2021, 64, 2220–2228. [Google Scholar] [CrossRef]
- Wang, X.; Qin, R.X.; Chen, B.Z. Mechanical properties and energy absorption capability of a topology-optimized lattice structure manufactured via selective laser melting under axial and offset loading. Proc. Inst. Mech. Eng. Part C-J. Mech. Eng. Sci. 2022, 236, 10221–10236. [Google Scholar] [CrossRef]
- Cheng, F.T.; Zhao, Q.H.; Mao, Z.B.; Wang, F.J. Mechanical Response of Gradient Lattice Structures Based on Topology Optimization. Adv. Eng. Mater. 2024, 26, 8. [Google Scholar] [CrossRef]
- Chen, L.; Chen, T.; Feng, S.; Cui, C.Y.; Cui, X.G.; Lu, J.Z. Self-similar nesting strategy enables lattices achieve dual energy-absorbing plateaus. Int. J. Mech. Sci. 2024, 276, 109445. [Google Scholar] [CrossRef]
- Afrousheh, M.; Marzbanrad, J.; Göhlich, D. Topology Optimization of Energy Absorbers under Crashworthiness Using Modified Hybrid Cellular Automata (MHCA) Algorithm. Struct. Multidiscip. Optim. 2019, 60, 1021–1034. [Google Scholar] [CrossRef]
- Jang, H.H.; Lee, H.A.; Lee, J.Y.; Park, G.J. Dynamic Response Topology Optimization in the Time Domain Using Equivalent Static Loads. AIAA J. 2012, 50, 226–234. [Google Scholar] [CrossRef]
- Lee, H.A.; Park, G.J. Nonlinear Dynamic Response Topology Optimization Using the Equivalent Static Loads Method. Comput. Methods Appl. Mech. Eng. 2015, 283, 956–970. [Google Scholar] [CrossRef]
- Li, Y.X.; He, X.X.; Li, K.L.; Yang, Q.W. Nonlinear Dynamic Topology Optimization Based on Equivalent Static Load Method. Chin. J. Comput. Mech. 2020, 38, 377–383. [Google Scholar]
- Maconachie, T.; Leary, M.; Lozanovski, B.; Zhang, X.; Qian, M.; Faruque, O.; Brandt, M. SLM lattice structures: Properties, performance, applications and challenges. Mater. Des. 2019, 183, 108137. [Google Scholar] [CrossRef]
- Zhao, X. Kagome Lattice Sandwich Structure Design and Compression Energy Absorption Research. Master’s Thesis, Changchun University of Technology, ChangChun, China, 2021. [Google Scholar]
- Zhang, H.R.; Zhou, H.; Zhou, Z.X.; Zeng, H.; Zhang, X.; Yang, J.; Lei, H.; Han, F. Energy Absorption Diagram Characteristic of Metallic Self-Supporting 3D Lattices Fabricated by Additive Manufacturing and Design Method of Energy Absorption Structure. Int. J. Solids Struct. 2021, 226–227, 111082. [Google Scholar] [CrossRef]
- Maskery, I.; Aboulkhair, N.T.; Aremu, A.O.; Tuck, C.J.; Ashcroft, I.A.; Wildman, R.D.; Hague, R.J. A Mechanical Property Evaluation of Graded Density Al-Si10-Mg Lattice Structures Manufactured by Selective Laser Melting. Mater. Sci. Eng. 2016, 670, 264–274. [Google Scholar] [CrossRef]
- Xie, Y.M.; Felicetti, P.; Tang, J.W.; Burry, M.C. Form finding for complex structures using evolutionary structural optimization method. Des. Stud. 2005, 26, 55–72. [Google Scholar] [CrossRef]
- Baroutaji, A.; Sajjia, M.; Olabi, A.G. On the Crashworthiness Performance of Thin-Walled Energy Absorbers: Recent Advances and Future Developments. Thin-Walled Struct. 2017, 118, 137–163. [Google Scholar] [CrossRef]
- Li, Y.X.; Guo, C.C.; Li, K.L.; Yu, T. Filling Lightweight Research on Pyramid Lattice with Small Slenderness Ratio Fabricated by SLM. J. Mech. Eng. 2021, 57, 132–138. [Google Scholar]



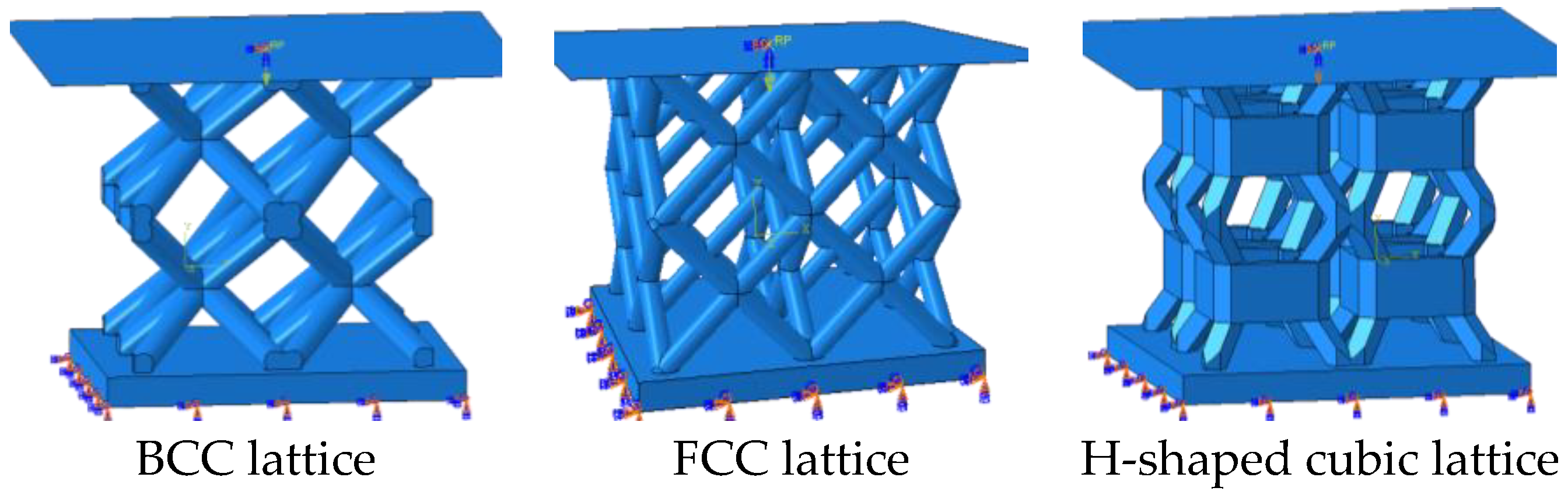


| 0.7 mm | 0.86 | 5 mm | 2 mm | 1.8 mm | 3 mm | 4 mm |
| Displacement | 2 mm | 4 mm | 6.5 mm |
|---|---|---|---|
| BCC Lattice |  |  |  |
| H-shaped cubic Lattice |  |  |  |
| FCC Lattice |  |  |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Li, Q.; He, X.; Li, S.; Wang, Y. Design of New Energy-Absorbing Lattice Cell Configuration by Dynamic Topology Optimization. Metals 2024, 14, 1348. https://doi.org/10.3390/met14121348
Li Y, Li Q, He X, Li S, Wang Y. Design of New Energy-Absorbing Lattice Cell Configuration by Dynamic Topology Optimization. Metals. 2024; 14(12):1348. https://doi.org/10.3390/met14121348
Chicago/Turabian StyleLi, Yongxin, Qinghua Li, Xingxing He, Shenshan Li, and Yongle Wang. 2024. "Design of New Energy-Absorbing Lattice Cell Configuration by Dynamic Topology Optimization" Metals 14, no. 12: 1348. https://doi.org/10.3390/met14121348
APA StyleLi, Y., Li, Q., He, X., Li, S., & Wang, Y. (2024). Design of New Energy-Absorbing Lattice Cell Configuration by Dynamic Topology Optimization. Metals, 14(12), 1348. https://doi.org/10.3390/met14121348








