Optimized Modeling Strategies for the Parametrization of a Two-Parameter Friction Model Through Inverse Modeling of Conical Tube-Upsetting Tests
Abstract
:1. Introduction and State of the Art
2. Simulation Model
3. Inverse Approach Using Upsetting Tests with Constant Tool Velocity
4. Inverse Approach Using Multiple Upsetting Tests with Two Different Tool Velocities
5. Experimental Procedure
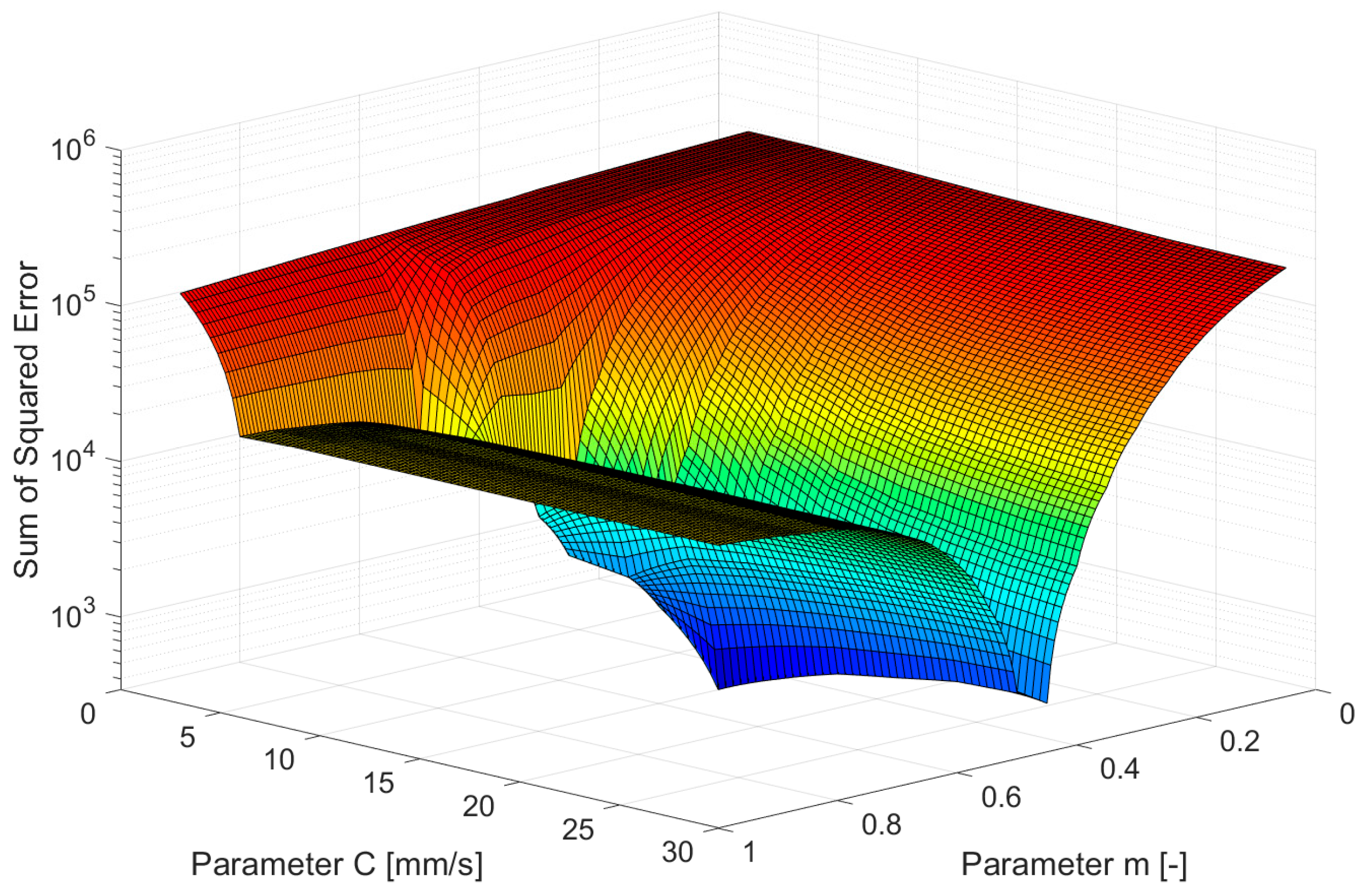
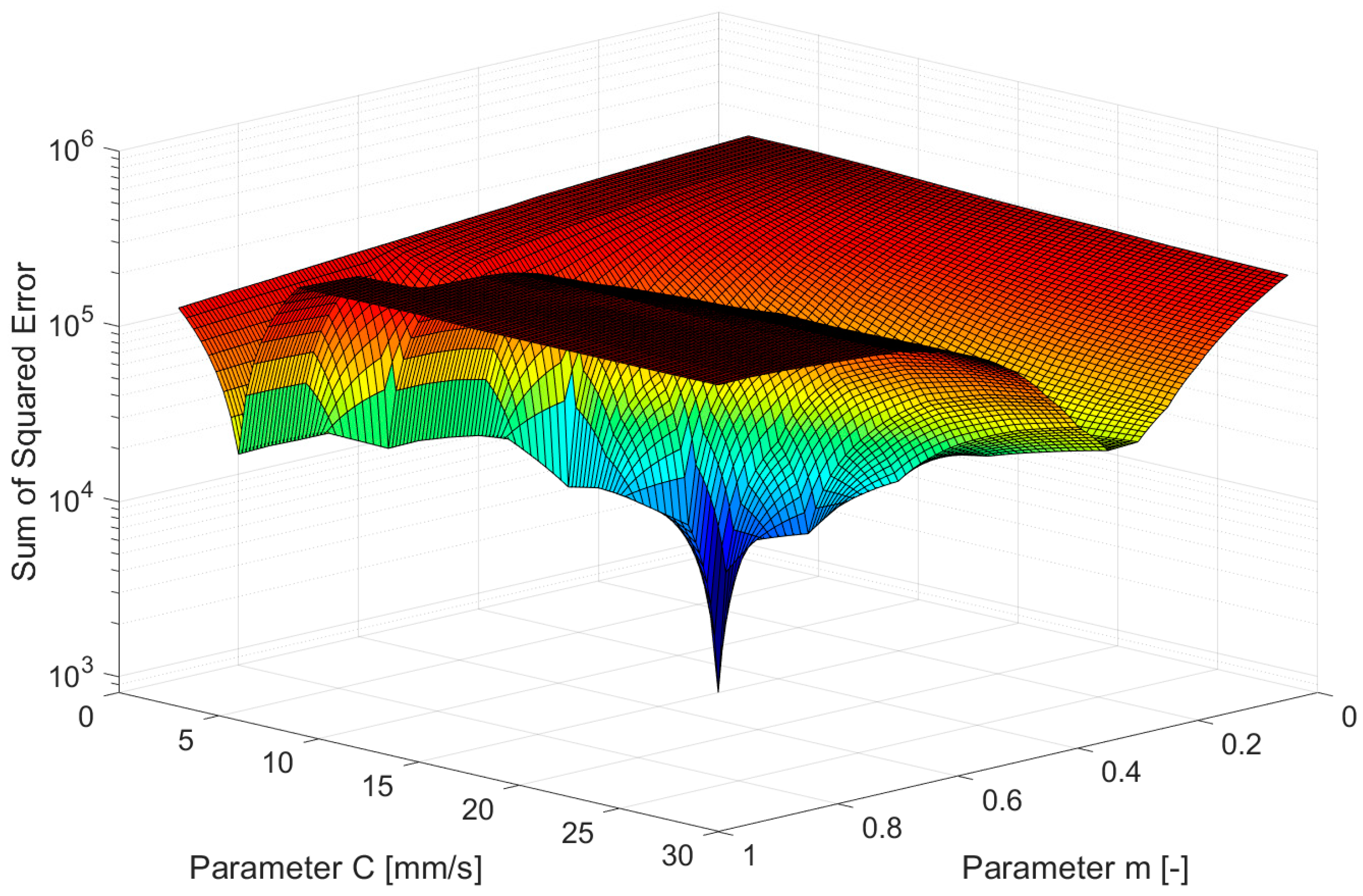
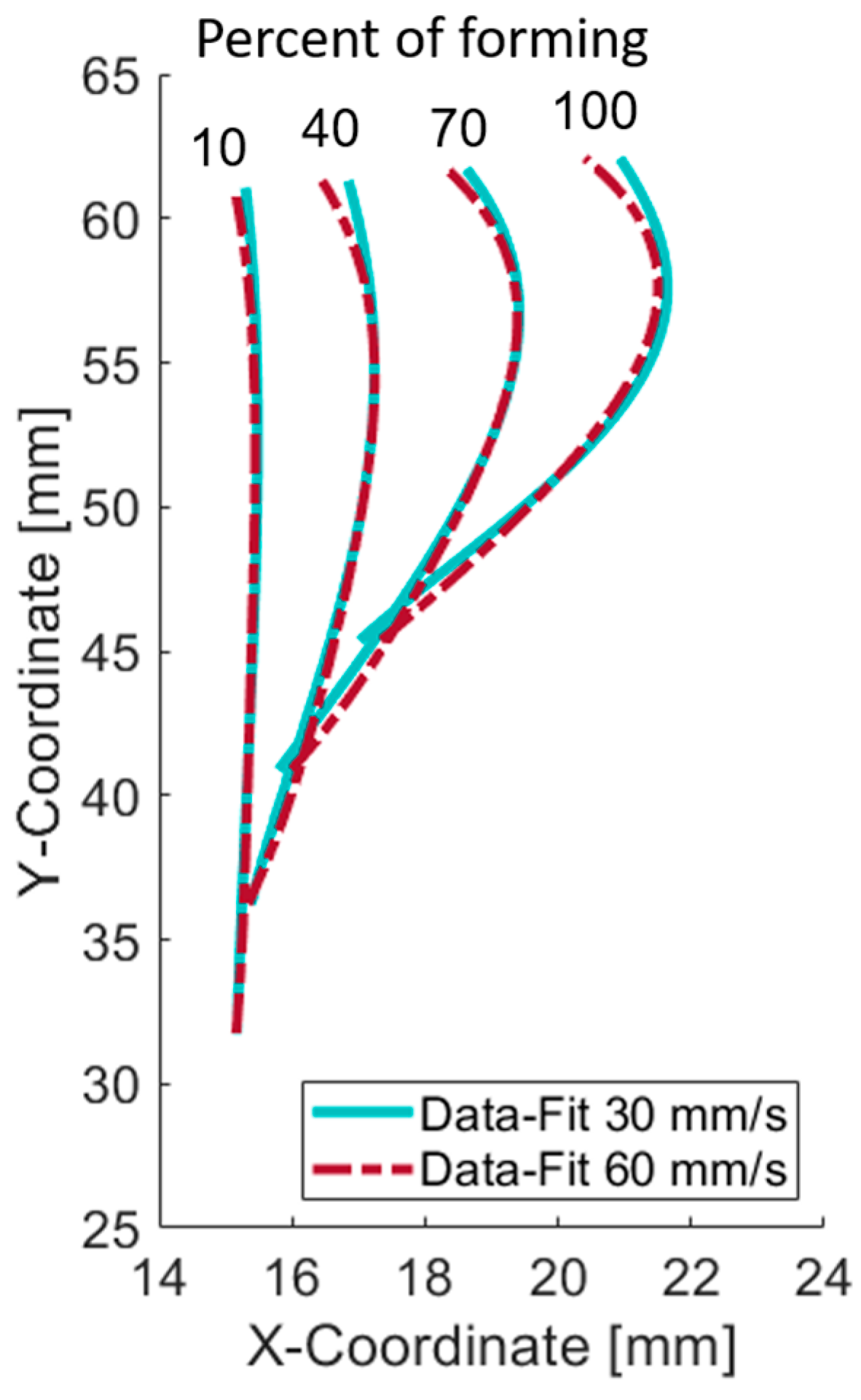
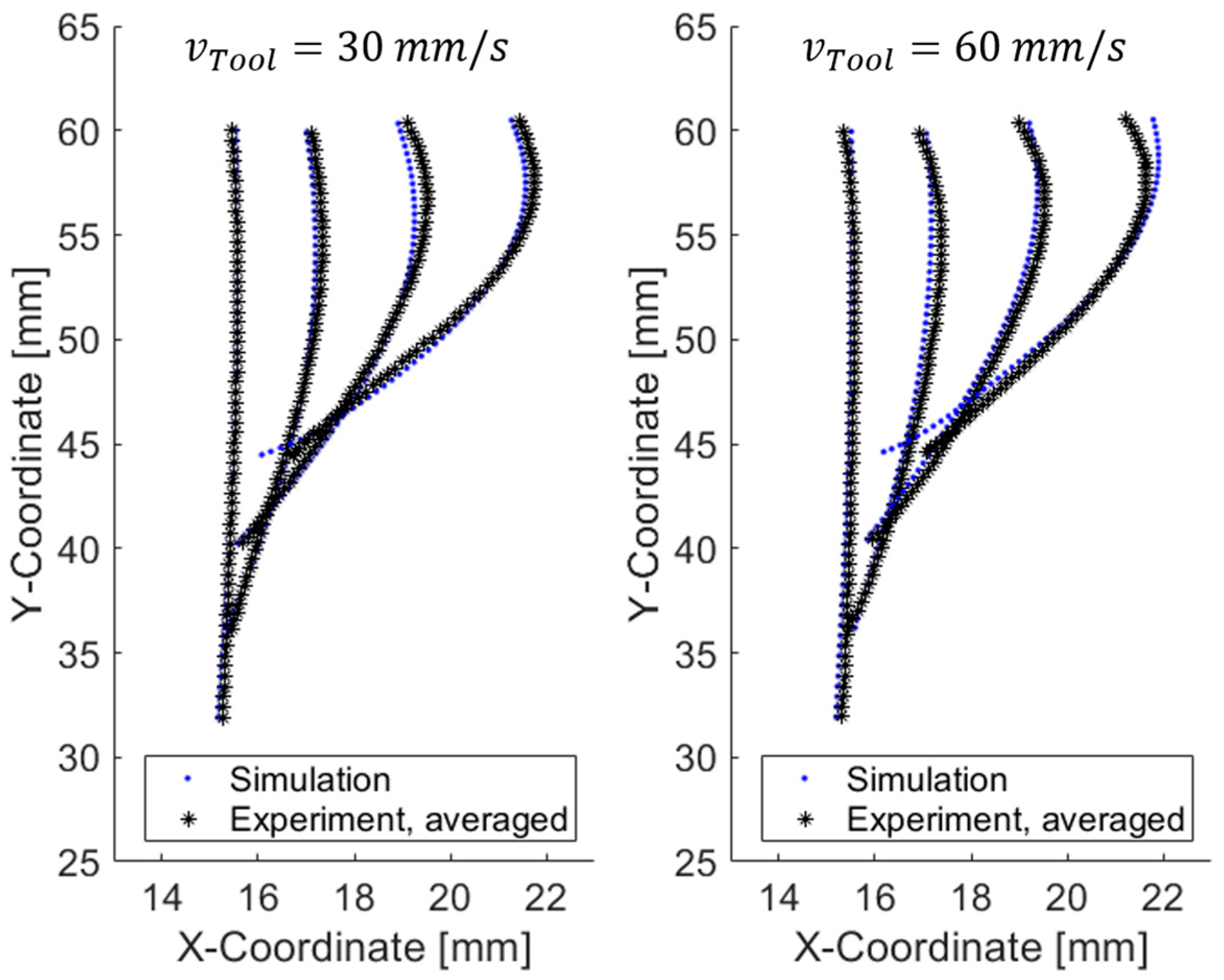
6. Inverse Modeling Using Experimental Data
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bay, N. Friction Stress and Normal Stress in Bulk Metal-Forming Processes. J. Mech. Work. Technol. 1987, 14, 203–223. [Google Scholar] [CrossRef]
- Nielsen, C.V.; Bay, N. Overview of friction modelling in metal forming processes. Procedia Eng. 2017, 207, 2257–2262. [Google Scholar] [CrossRef]
- Orowan, E. The Calculation of Roll Pressure in Hot and Cold Flat Rolling. Proc. Inst. Mech. Eng. 1943, 150, 140–167. [Google Scholar] [CrossRef]
- Bay, N.; Wanheim, T. Real Area of Contact and Friction Stress at High Pressure Sliding Contact. Wear 1976, 38, 201–209. [Google Scholar] [CrossRef]
- Bay, N.; Wanheim, T. Contact Phenomena under Bulk Plastic Deformation Conditions. In Proceedings of the Third International Conference on Technology of Plasticity: Advanced Technology of Plasticity, Kyoto, Japan, 1–6 July 1990; Japan Society for Technology of Plasticity: Tokyo, Japan, 1990; pp. 1677–1691. [Google Scholar]
- Chen, C.C.; Kobayashi, S. Rigid Plastic Finite Element Analysis of Ring Compression. Appl. Numer. Methods Form. Process. 1978, 28, 163–174. [Google Scholar]
- Behrens, B.-A.; Alasti, M.; Bouguecha, A.; Hadifi, T.; Mielke, J.; Schäfer, F. Numerical and experimental investigations on the extension of friction and heat transfer models for an improved simulation of hot forging processes. Int. J. Mater. Form. 2009, 2, 121–124. [Google Scholar] [CrossRef]
- Behren Bouguecha, A.; Mielke, J.; Hirt, G.; Bambach, M.; Al Baouni, M.S.H.; Demant, A. Verbesserte numerische Prozesssimulation mittels eines innovativen Reibgesetzes für die Warmmassivumformung: Improved numerical process simulation by means of an innovative friction law for hot forging. Schmiede-J. März 2010, 20–24. [Google Scholar]
- Behrens, B.-A.; Bouguecha, A.; Hadifi, T.; Mielke, J. Advanced friction modeling for bulk metal forming processes. Prod. Eng. 2011, 5, 621–627. [Google Scholar] [CrossRef]
- Tan, X. Comparisons of friction models in bulk metal forming. Tribol. Int. 2002, 35, 385–393. [Google Scholar] [CrossRef]
- Joun, M.; Moon, H.; Choi, I.; Lee, M.; Jun, B. Effects of Friction Laws on Metal Forming Processes. Tribol. Int. 2009, 42, 311–319. [Google Scholar] [CrossRef]
- Henke, T.; Hirt, G.; Bambach, M. Randwertermittlung für die robuste Auslegung von Schmiedeprozessen. Wt Werkstattstech. Online 2013, 103, 783–788. [Google Scholar] [CrossRef]
- Lenard, J.G. Tribology in Metal Rolling Keynote Presentation Forming Group F. CIRP Ann. 2000, 49, 567–590. [Google Scholar] [CrossRef]
- Dellah, A.; Wild, P.M.; Moore, T.N.; Shalaby, M.; Jeswiet, J. An Embedded Friction Sensor Based on a Strain-Gauged Diaphragm. J. Manuf. Sci. Eng. 2002, 124, 523–527. [Google Scholar] [CrossRef]
- Masters, I.G.; Williams, D.K.; Roy, R. Friction behaviour in strip draw test of pre-stretched high strength automotive aluminium alloys. Int. J. Mach. Tools Manuf. 2013, 73, 17–24. [Google Scholar] [CrossRef]
- Mandic, V.; Stefanovic, M. Friction Studies Utilizing the Ring—Compression Test—Part I. Tribol. Ind. 2003, 25, 33–40. [Google Scholar]
- Mandic, V.; Stefanovic, M. Friction Studies Utilizing the Ring—Compression Test—Part II. Tribol. Ind. 2003, 25, 76–82. [Google Scholar]
- Plančak, M.; Car, Z.; Kršulja, M.; Vilotić, D.; Kačmarčik, I.; Movrin, D. Possibilities To Measure Contact Friction In Bulk Metal Forming. Teh. Vjesn. Tech. Gaz. 2012, 19, 727–734. [Google Scholar]
- Male, A.T.; DePierre, V. The Validity of Mathematical Solutions for Determining Friction From the Ring Compression Test. J. Lubr. Technol. 1970, 92, 389–395. [Google Scholar] [CrossRef]
- Kopp, R.; Al Baouni, M.S.H.; Volles, R. Conical Tube Upsetting Test—A New Method for Accurate Determination of The Friction Coefficient. In Proceedings of the 8th International Conference on Technology of Plasticity, Verona, Italy, 9–13 October 2005. [Google Scholar]
- Kopp, R.; Philipp, F.-D. Physical parameters and boundary conditions for the numerical simulation of hot forming processes. Steel Res. 1992, 63, 392–398. [Google Scholar] [CrossRef]
- Teller, M.; Klubakov, A.; Franzke, M.; Lohmar, J.; Hirt, G. Extended Conical Tube-Upsetting Test to Investigate the Evolution of Friction Conditions. Key Eng. Mater. 2016, 716, 157–164. [Google Scholar] [CrossRef]
- Szeliga, D.; Gawad, J.; Pietrzyk, M. Inverse analysis for identification of rheological and friction models in metal forming. Comput. Methods Appl. Mech. Eng. 2006, 195, 6778–6798. [Google Scholar] [CrossRef]
- Szeliga, D.; Gawąd, J.; Pietrzyk, M. Parameters identification of material models based on the inverse analysis. Int. J. Appl. Math. Comput. Sci. 2004, 14, 549–556. [Google Scholar]
- Cho, H.; Ngalle, G.; Altan, T. Simultaneous Determination of Flow Stress and Interface Friction by Finite Element Based Inverse Analysis Technique. CIRP Ann. 2003, 52, 221–224. [Google Scholar] [CrossRef]
- Henze, M.; Teller, M.; Hirt, G. Parametrization of Bi-Parametric Friction Models Through Inverse Modelling of Conical Tube-Upsetting Tests. AIP Conf. Proc. 2019, 2113, 120002. [Google Scholar]
- Spittel, M.; Spittel, T. Steel symbol/number: 18CrNiMo7–6/1.6587, In Metal Forming Data of Ferrous Alloys—Deformation Behaviour; Martienssen, W., Warlimont, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 984–989. [Google Scholar] [CrossRef]
- Byrd, R.H.; Schnabel, R.B.; Shultz, G.A. Approximate solution of the trust region problem by minimization over two-dimensional subspaces. Math. Program. 1988, 40, 247–263. [Google Scholar] [CrossRef]
- MathWorks. Optimization Toolbox: User’s Guide. Available online: https://de.mathworks.com/help/optim/ug/least-squares-model-fitting-algorithms.html (accessed on 14 November 2024).
- Moré, J.J.; Sorensen, D.C. Computing a Trust Region Step. SIAM J. Sci. Stat. Comput. 1983, 4, 553–572. [Google Scholar] [CrossRef]






| Contact Normal Stress [MPa] | Heat Transfer Coefficient [] |
|---|---|
| 1.6 | 5.000 ± 0 |
| 8 | 7.500 ± 1870 |
| 16 | 14.500 ± 3240 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Henze, M.; Koch, L.; Bailly, D.; Teller, M.; Hirt, G. Optimized Modeling Strategies for the Parametrization of a Two-Parameter Friction Model Through Inverse Modeling of Conical Tube-Upsetting Tests. Metals 2024, 14, 1355. https://doi.org/10.3390/met14121355
Henze M, Koch L, Bailly D, Teller M, Hirt G. Optimized Modeling Strategies for the Parametrization of a Two-Parameter Friction Model Through Inverse Modeling of Conical Tube-Upsetting Tests. Metals. 2024; 14(12):1355. https://doi.org/10.3390/met14121355
Chicago/Turabian StyleHenze, Michel, Lena Koch, David Bailly, Marco Teller, and Gerhard Hirt. 2024. "Optimized Modeling Strategies for the Parametrization of a Two-Parameter Friction Model Through Inverse Modeling of Conical Tube-Upsetting Tests" Metals 14, no. 12: 1355. https://doi.org/10.3390/met14121355
APA StyleHenze, M., Koch, L., Bailly, D., Teller, M., & Hirt, G. (2024). Optimized Modeling Strategies for the Parametrization of a Two-Parameter Friction Model Through Inverse Modeling of Conical Tube-Upsetting Tests. Metals, 14(12), 1355. https://doi.org/10.3390/met14121355






