Numerical Simulation Research on the Temperature Field and Hot Roll Crown Model of Hot Continuous Rolling Mills
Abstract
1. Introduction
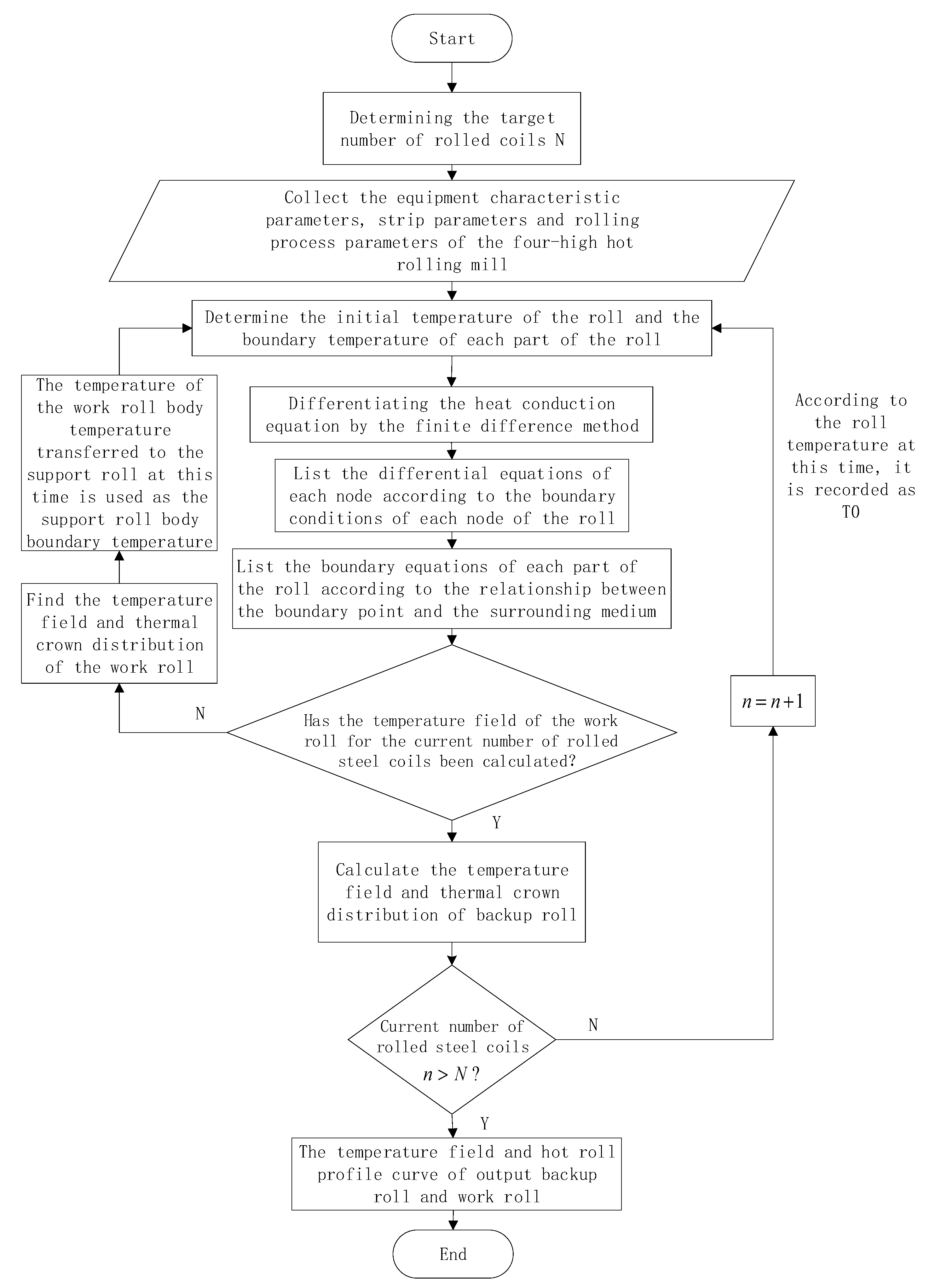
2. Materials and Methods
2.1. Model Parameter Settings
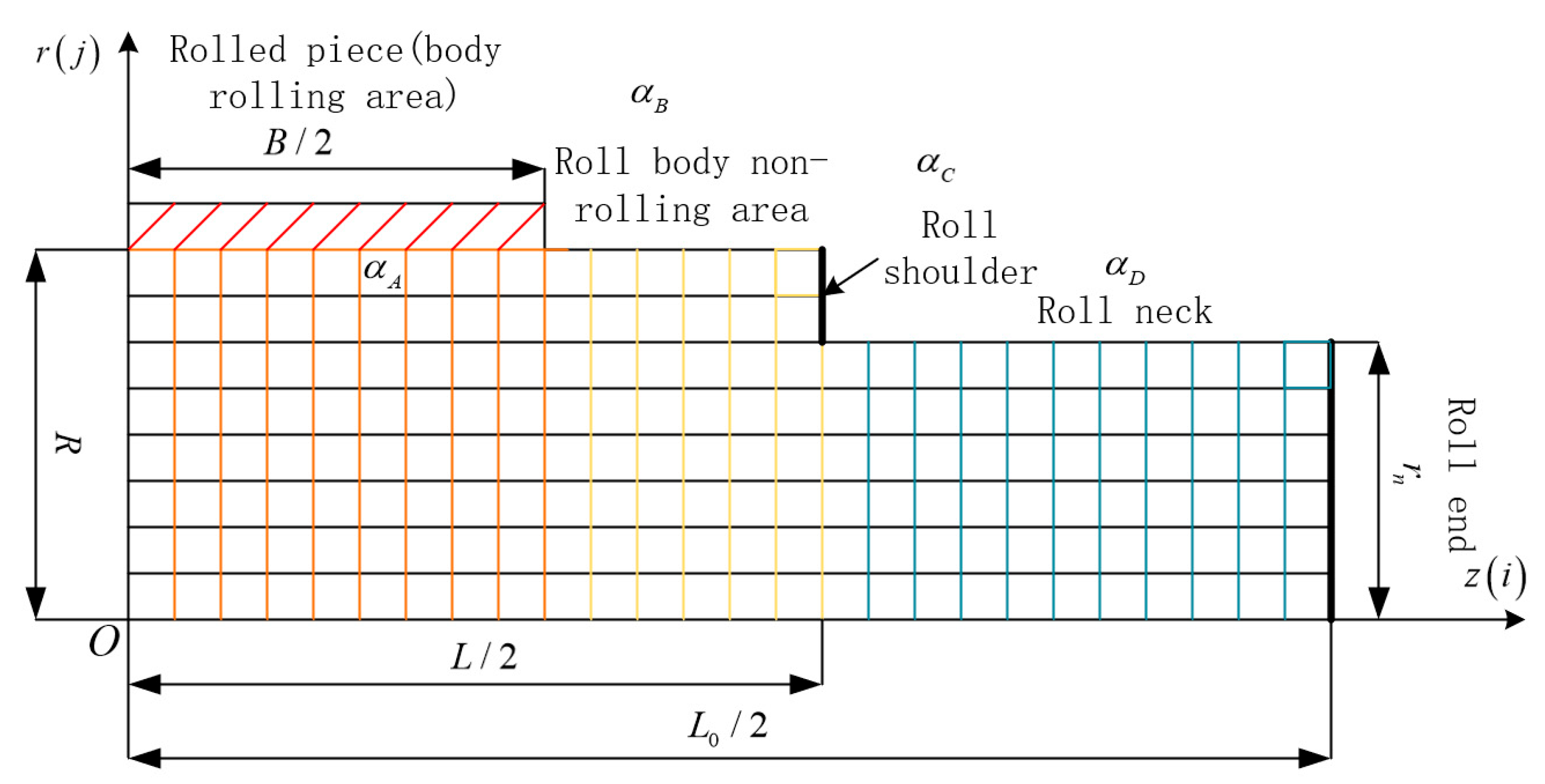
2.2. Establishment of Basic Requirements for Roller Temperature Field
2.3. Calculation and Processing of Boundary Conditions
2.4. Hot Roll Crown Model
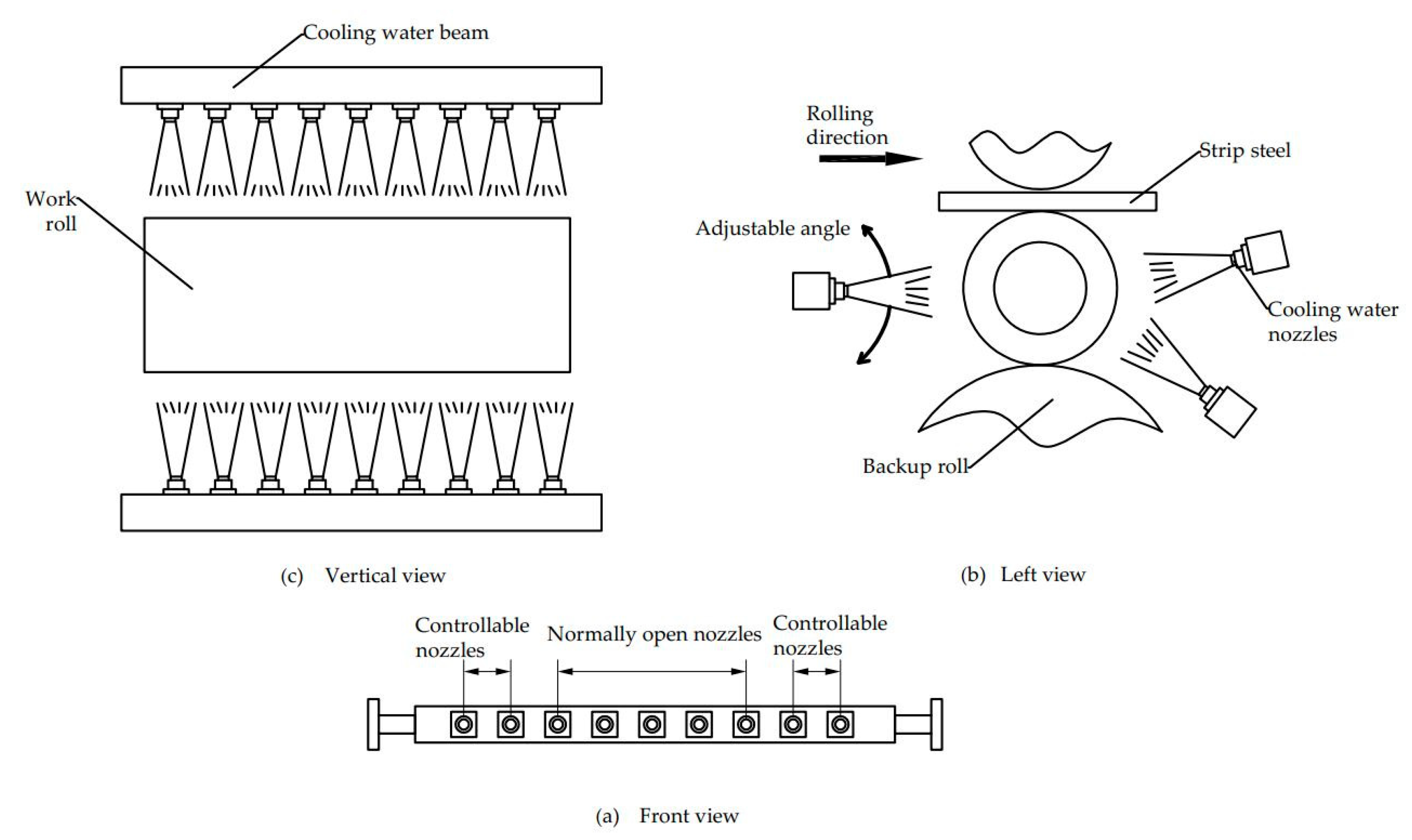
2.5. Cooling Water Section Cooling System
3. Results and Discussion
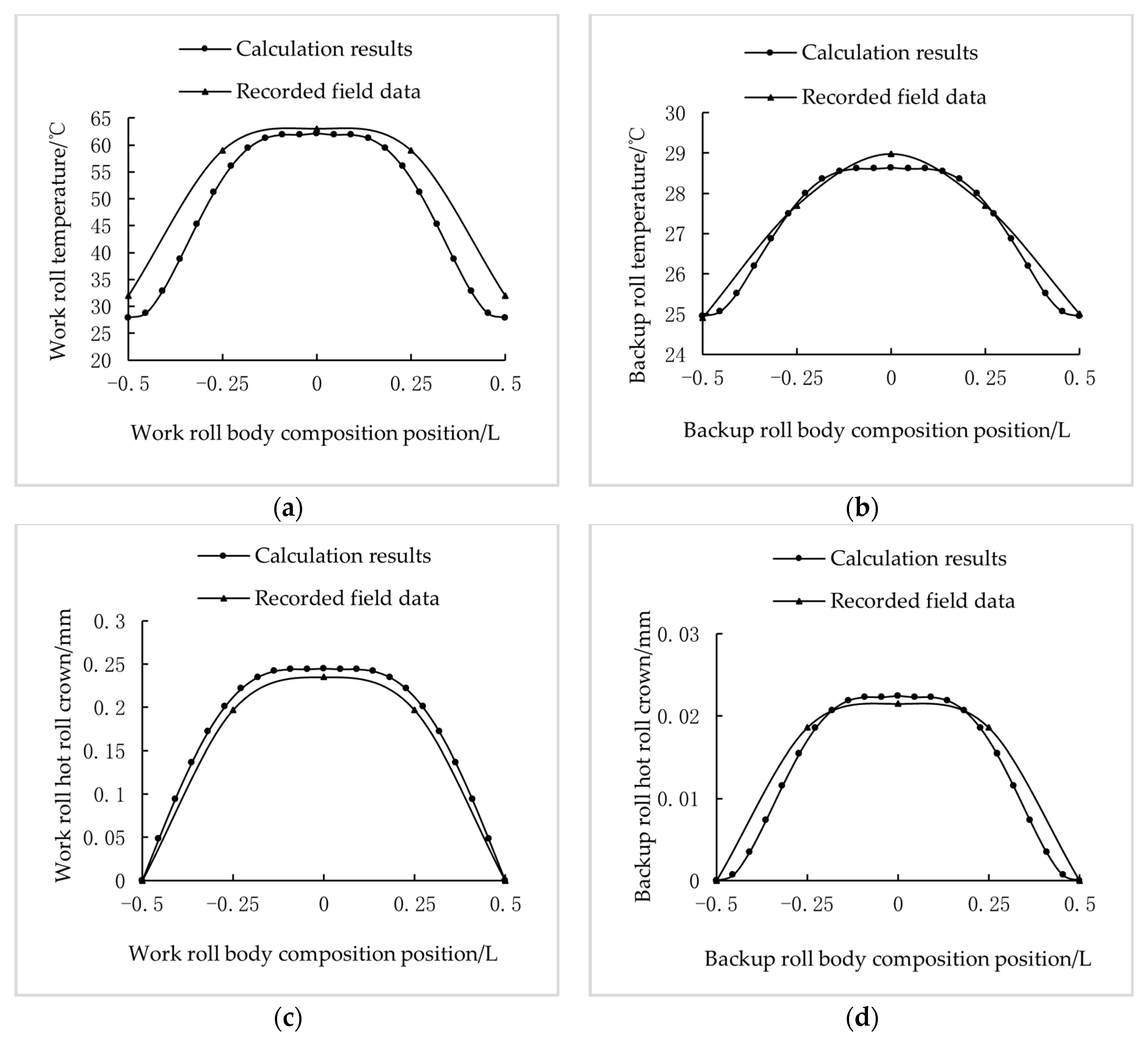
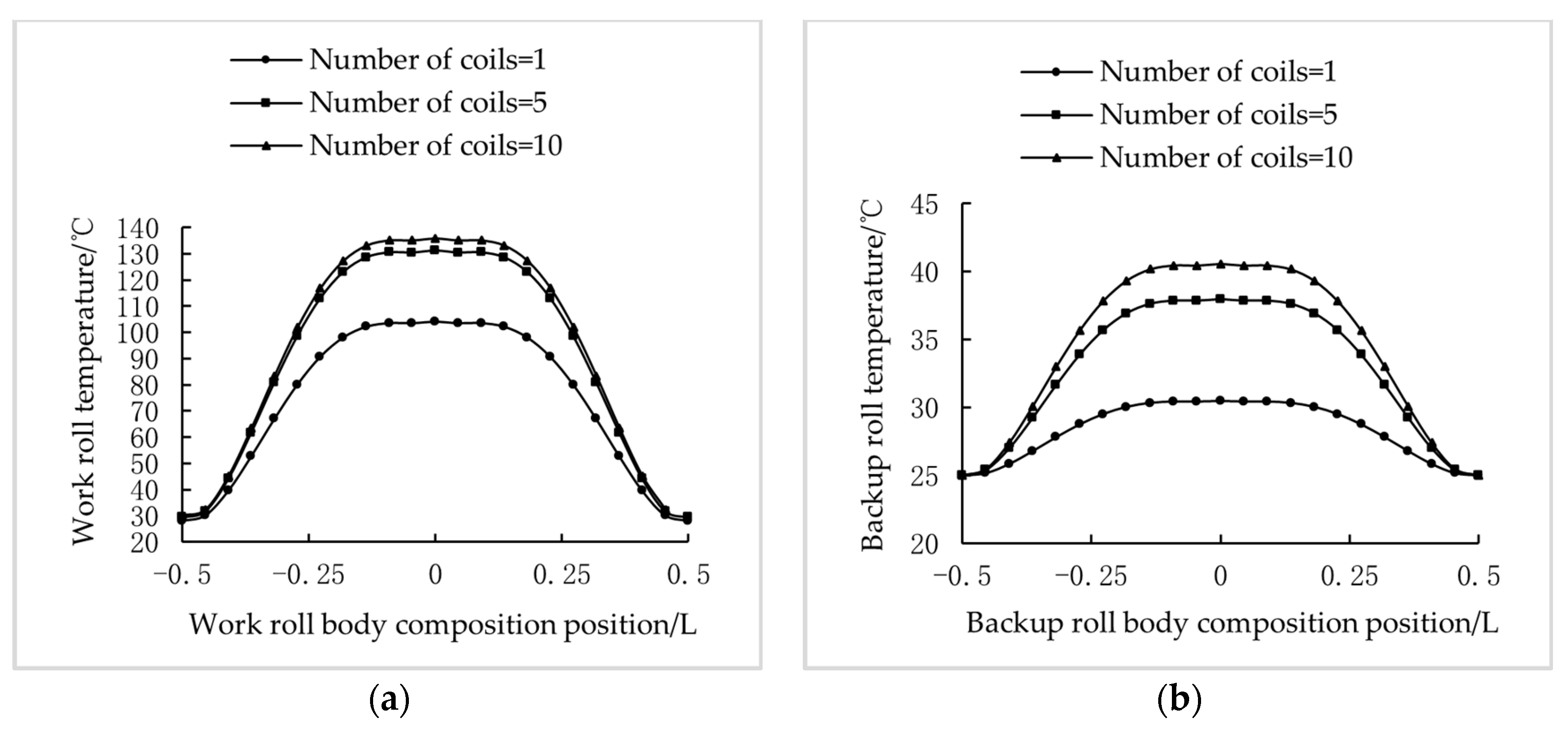
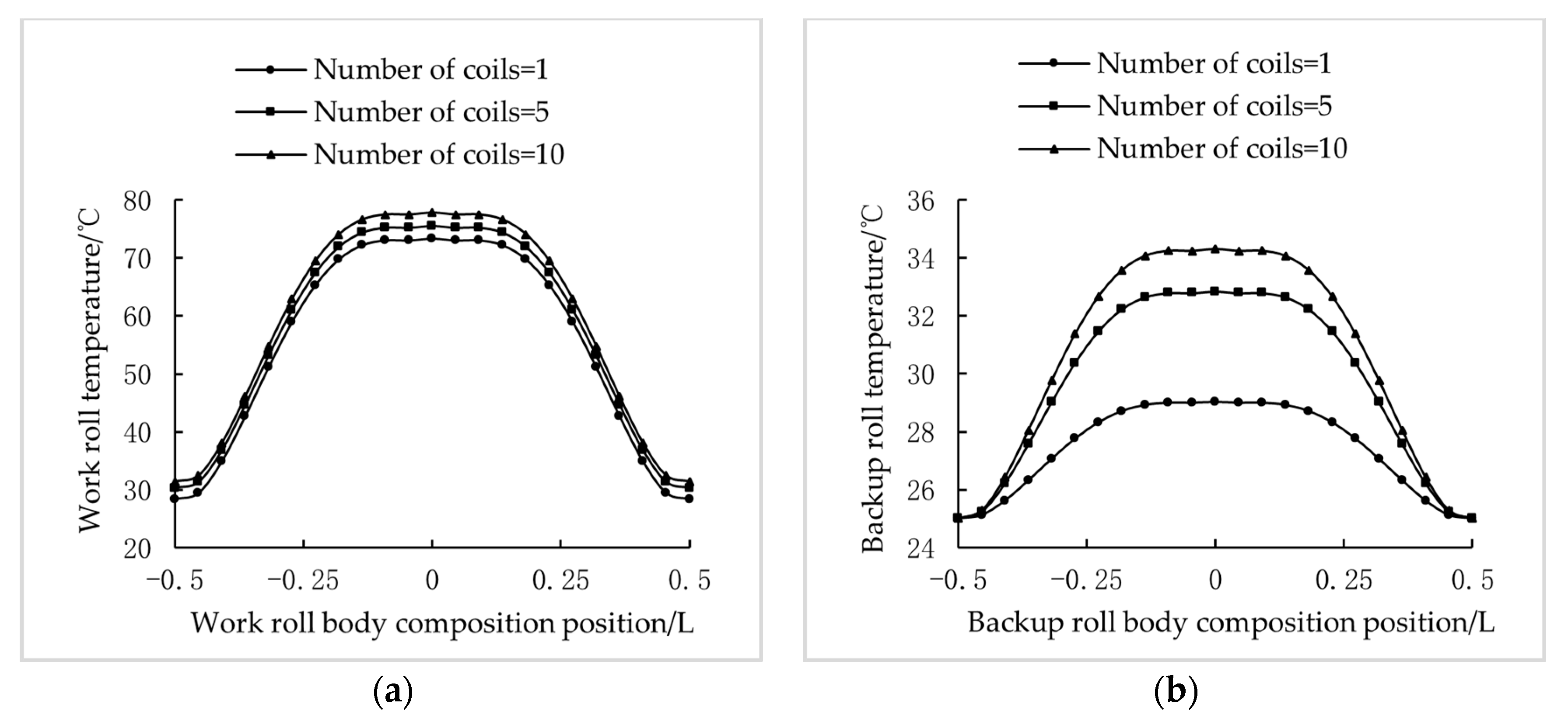
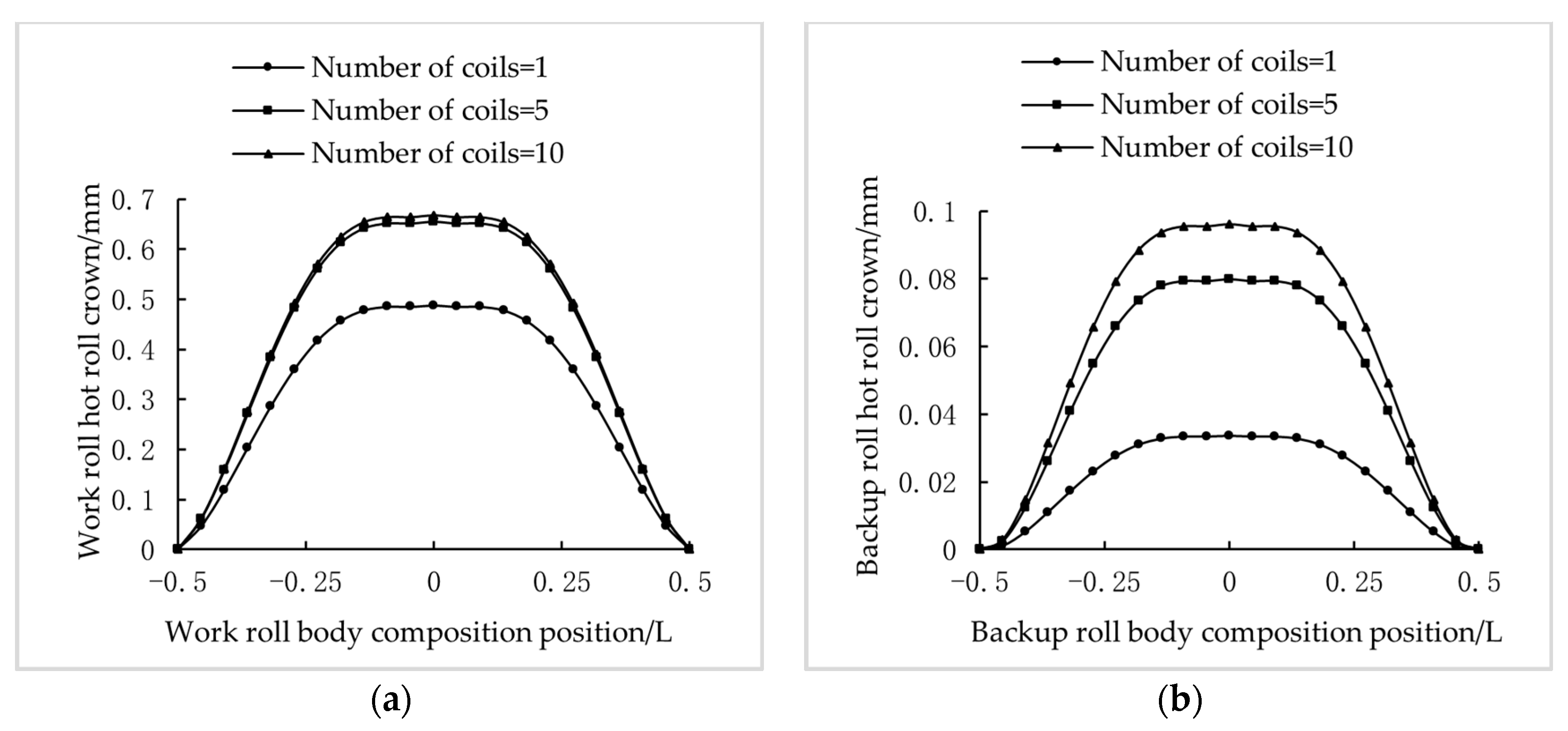
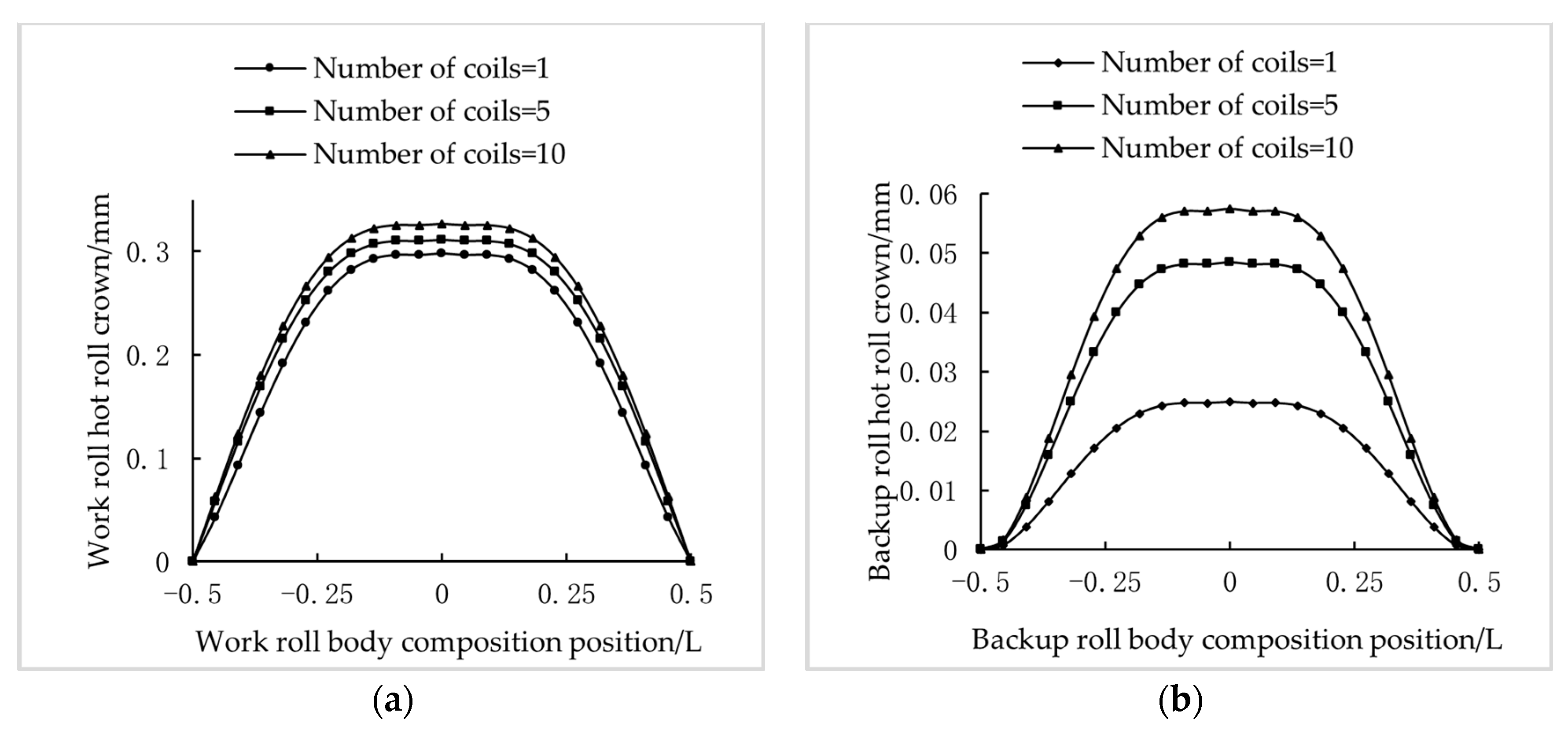
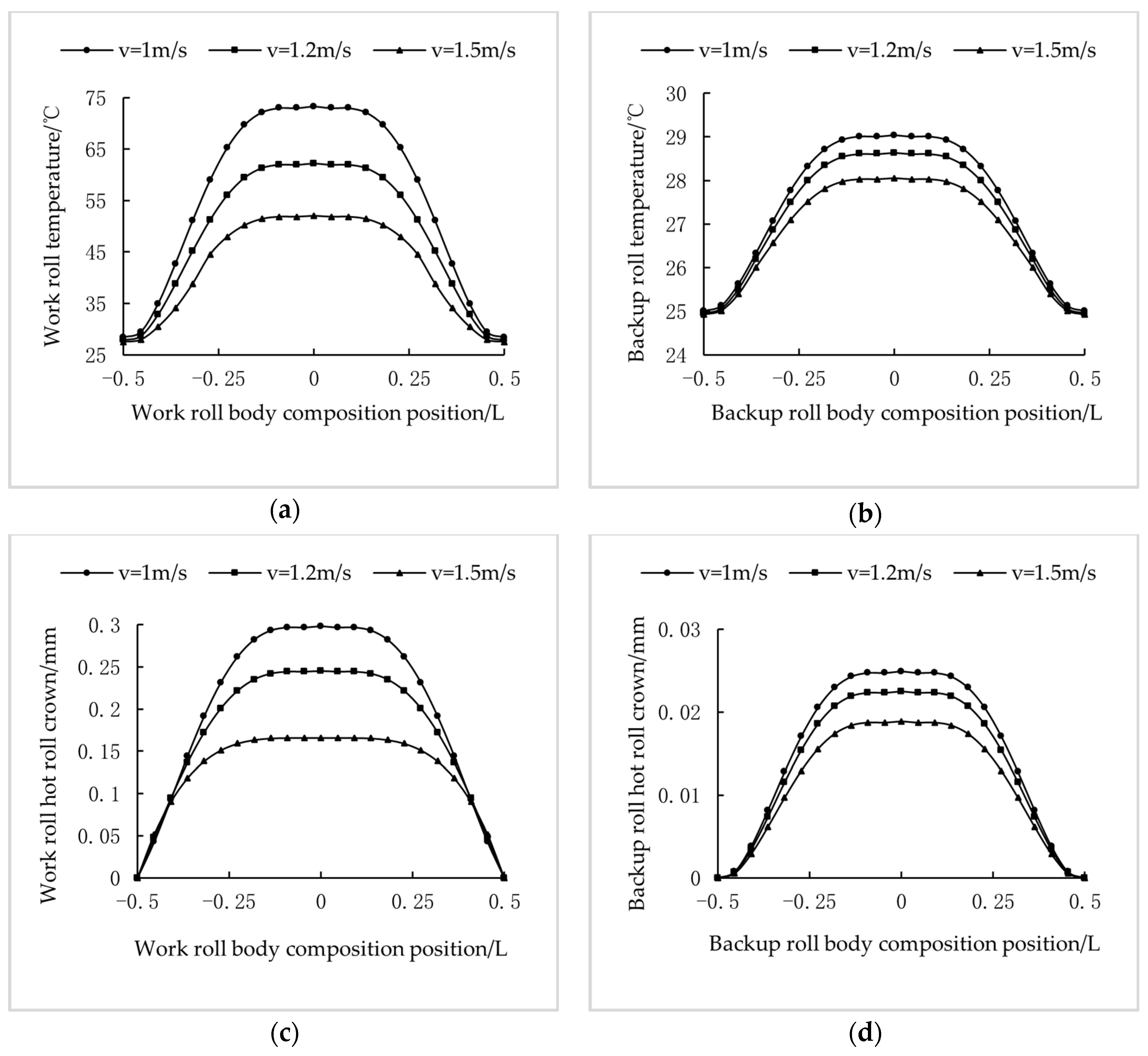
3.1. Numerical Simulation and Practical Application of Temperature Field and Hot Roll Crown
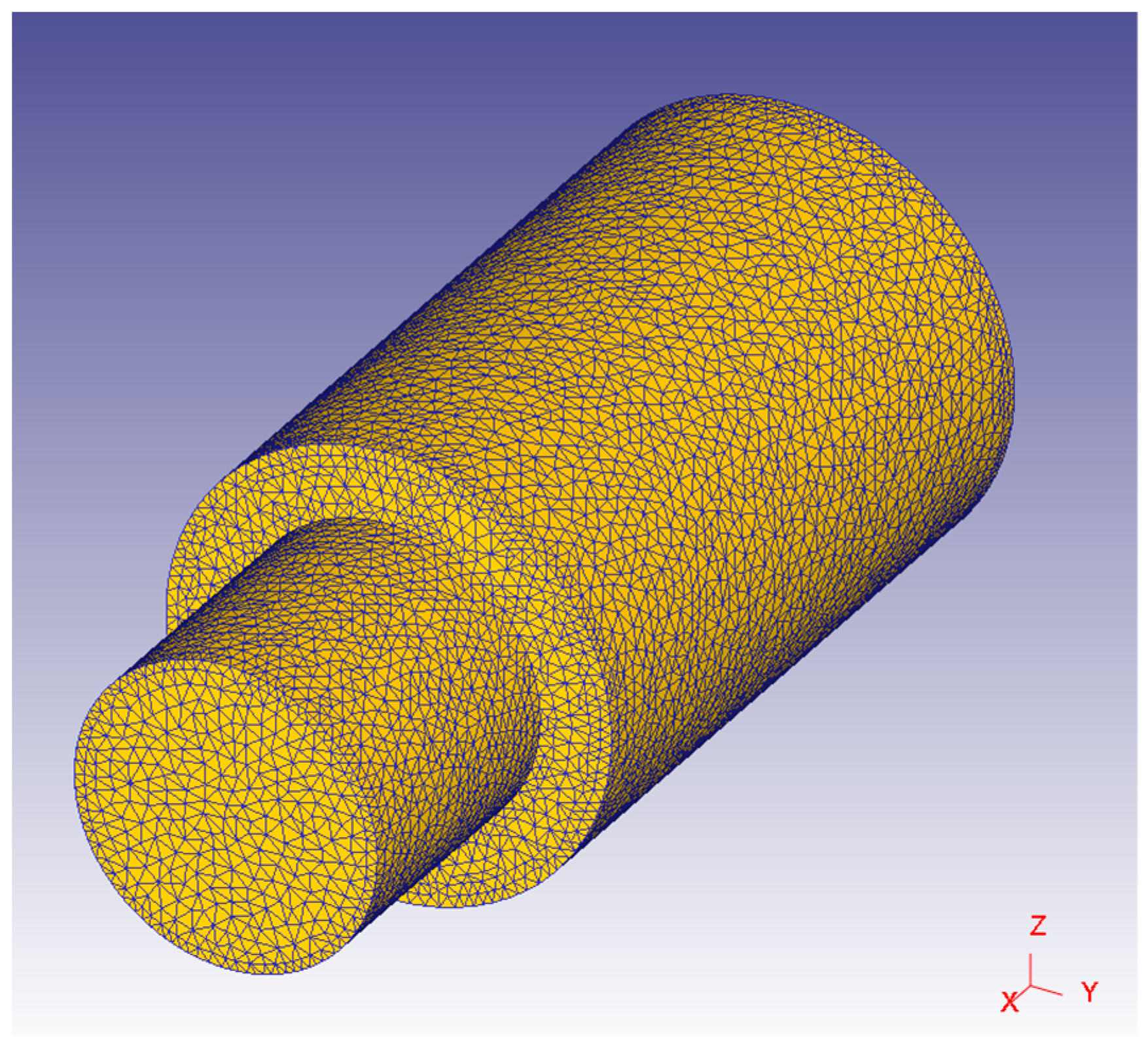
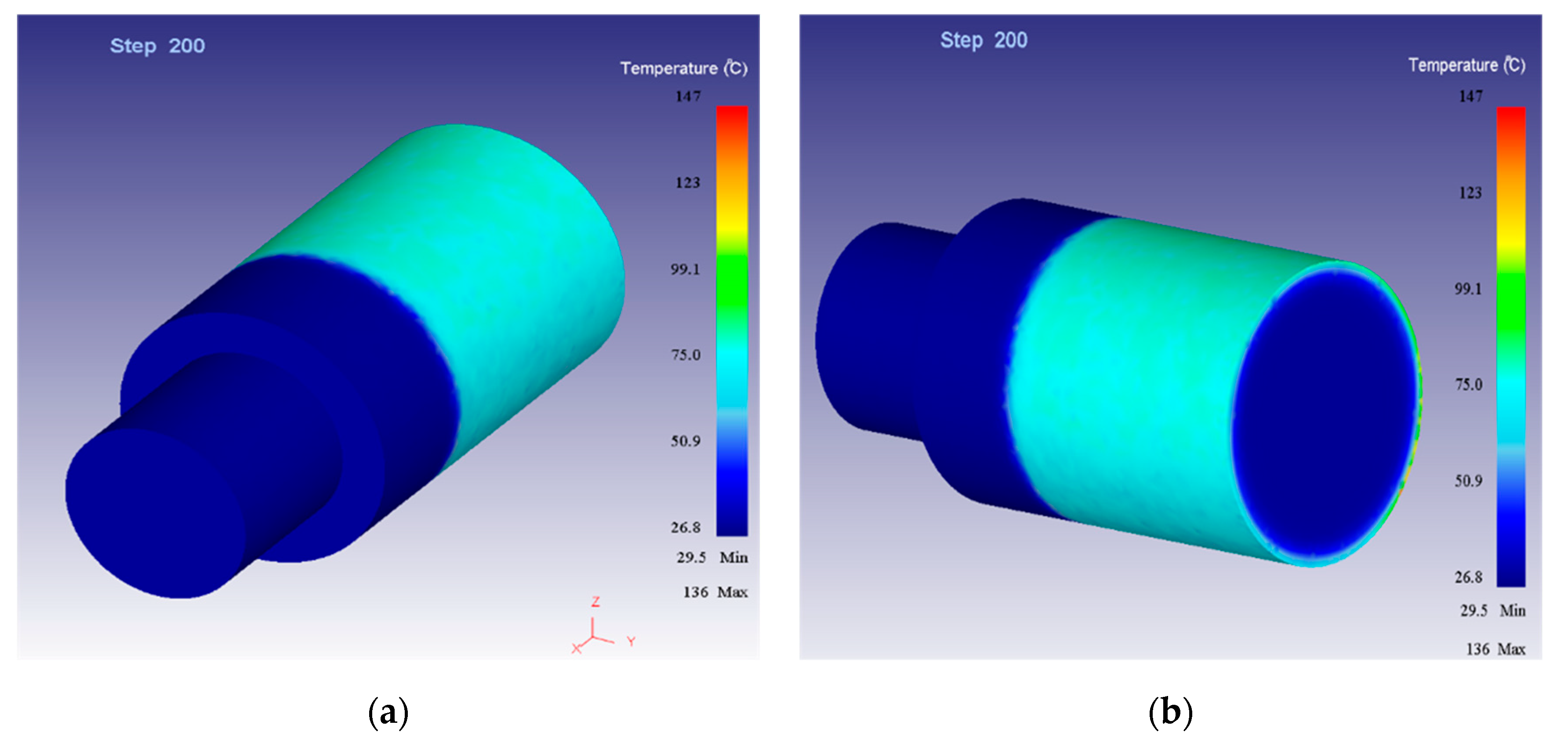
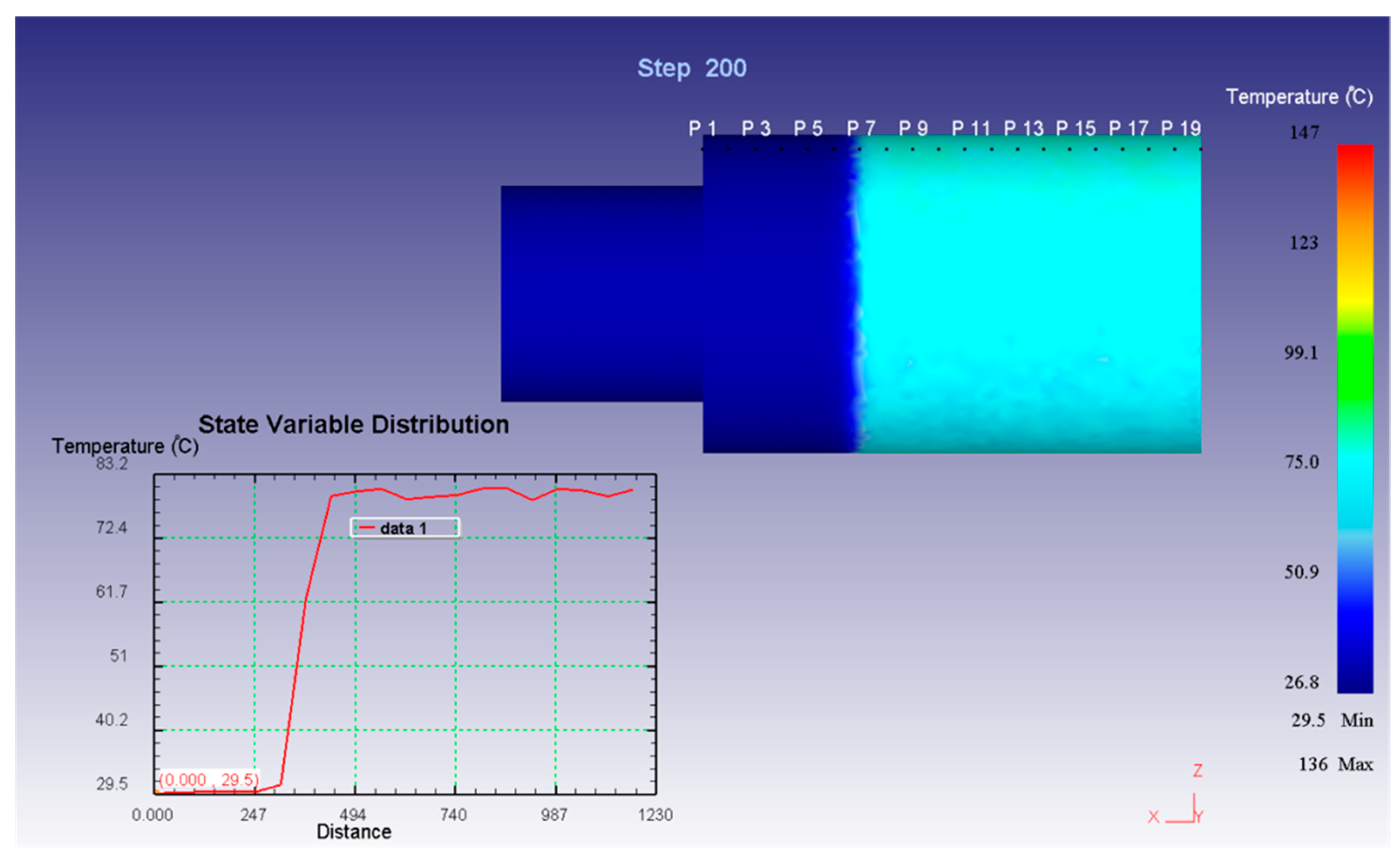
3.2. Finite Element Numerical Simulation Verification
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, X.T.; Zhang, Y.D. Comprehensive optimization technology of rolling temperature for seven stand hot strip mill. Iron Steel 2023, 58, 104–110. [Google Scholar]
- Xu, J.; Guan, B. Tailoring the microstructure and mechanical properties of Cu–Fe alloy by varying the rolling path and rolling temperature. J. Mater. Res. Technol. 2023, 27, 182–193. [Google Scholar] [CrossRef]
- Guo, Z.F.; Xu, J.Z. Temperature Field and Thermal Crown of Work Rolls on 1700Hot Strip mill. J. Northeast. Univ. (Nat. Sci. Ed.) 2008, 4, 517–520. [Google Scholar]
- Qu, F.Q.; Li, X. Thermal crown of cold rolling work roll and its effect on strip shape. China Metall. 2022, 32, 84–93. [Google Scholar]
- Li, B.Q.; Fan, X. Parameter optimization of shape setting model and application of control technology. Iron Steel 2019, 54, 41–47. [Google Scholar]
- Meng, L.M.; Ding, J.G. Prediction of roll wear and thermal expansion based on informer network in hot rolling process and application in the control of crown and thickness. J. Manuf. Process. 2023, 103, 248–260. [Google Scholar] [CrossRef]
- Wei, C.; Song, S.X. Evaluation of elastic-plastic deformation in HSS work roll under coupling of residual stress thermal stress and contact stress during hot rolling. Mater. Today Commun. 2022, 33, 104613. [Google Scholar] [CrossRef]
- Atack, P.A.; Robinson, I.S. Control of thermal camber by spray cooling when hot rolling aluminum. Iron Steel 1996, 23, 69–73. [Google Scholar]
- Serajzadeh, S.; Mucciardi, F. Modeling the work-roll temperature variation at unsteady state condition. Model. Simul. Mater. Sci. Eng. 2003, 11, 179–194. [Google Scholar] [CrossRef]
- Sonboli, A.; Serajzadeh, S. A model for evaluating thermal mechanical stresses within work-rolls in hot-strip rolling. J. Eng. Math. 2012, 72, 73–85. [Google Scholar] [CrossRef]
- Chen, B.G.; Chen, X.L. Prediction of work roll thermal deformarion with finite element method on hot strip mill. Iron Steel 1991, 8, 40–44. [Google Scholar]
- Wang, J.; Cao, Y. Finite element analysis on tehperature field of work roll in hot rolling strip mill. Hot Work. Technol. 2013, 42, 102–104. [Google Scholar]
- Kong, X.W.; Li, R.L. Fem Calculation of Temperature Field and Axial Thermal Crown for Work Roller. J. Iron Steel Res. 2000, 12, 51–54. [Google Scholar]
- Jiang, M.; Li, X.; Wu, J.; Wang, G. A precision on-line model for the prediction of thermal crown in hot rolling processes. Int. J. Heat Mass Transf. 2014, 78, 967–973. [Google Scholar] [CrossRef]
- Chen, S.X.; Li, W.G.; Liu, X.H. Thermal crown model and shifting effect analysis of work roll in hot strip mills. J. Iron Steel Res. Int. 2015, 22, 777–784. [Google Scholar] [CrossRef]
- Li, X.D.; Liu, X.D. Research on the hot ro11 shape and the cooling system of the hot mill. Metall. Equip. 2005, 5, 1–4+56. [Google Scholar]
- Hiremath, P.; Sharma, S. Effect of post carburizing treatments on residual stress distribution in plain carbon and alloy steels—A numerical analysis. J. Mater. Res. Technol. 2020, 9, 8439–8450. [Google Scholar] [CrossRef]
- Kumar, A.; Rath, S.L. Simulation of plate rolling process using finite element method. Mater. Today Proc. 2021, 42, 650–659. [Google Scholar] [CrossRef]
- Chrysanidis, T. Experimental and numerical research on cracking characteristics of medium-reinforced prisms under variable uniaxial degrees of elongation. Eng. Fail. Anal. 2023, 145, 107014. [Google Scholar] [CrossRef]
- Guo, W.T.; He, A.R. Research on work roll thermal coutour model in hot strip mill based on the turning direction two dimensional difference method. Metall. Equip. 2009, 1, 20–23. [Google Scholar]
- Li, Y.W.; Yan, S.L. Deformation behavior of high-chromium cast iron / low-carbon steel laminates based on hot rolling and finite element simulation. Vacuum 2023, 214, 112218. [Google Scholar] [CrossRef]
- Yu, H.; Guo, Z.Y. Study on the thermal profile of work rolls for four high mills. Shanghai Met. 2005, 1, 26–30. [Google Scholar]
- Wang, G.D. Plate Shape Control and Plate Shape Theory; Metallurgical Industry Press: Beijing, China, 1980; pp. 10–86. [Google Scholar]
- Li, J.H.; Lian, J.C. Prediction Model of Temperature Field and Crown of Work Roll for Hot Strip Mill. J. Iron Steel Res. 2003, 6, 25–28. [Google Scholar]
- Sun, Y.K. Model and Control of Hot Strip Rolling; Metallurgical Industry Press: Beijing, China, 2007; pp. 56–106. [Google Scholar]
- Beeston, J.W.; Edwards, W.J. Thermal Camber Analysis in Cold Rolling. Iron Steel Inst. 1973, 5, 320–324. [Google Scholar]
- Onah, O.T.; Ekwueme, B.N. Improved design and comparative evaluation of controlled water jet impingement cooling system for hot-rolled steel plates. Int. J. Thermofluids 2022, 15, 100172. [Google Scholar] [CrossRef]
- Zhang, R.; Li, Z.L. Numerical simulation of multi-array spray cooling for hot rolled seamless steel pipes. Int. J. Heat Mass Transf. 2024, 221, 125017. [Google Scholar] [CrossRef]
- Lu, H.M.; Chen, Y.Y. Mechanical Engineering Material Properties Data Sheet; China Machine Press: Beijing, China, 2007; pp. 441–726. [Google Scholar]
- Li, Z.Z.; Liu, L.X. Research on roll temperature field and hot roll crown of hot continuous rolling mills. Iron Steel 2023, 1, 1–10. [Google Scholar]
- Raja, N.; Kumar, A. Finite element modelling and microstructural correlation of hot forged Al-Zn-Mg-Cu alloy (T6) using DEFORM-3D. Mater. Today Proc. 2023; in press. [Google Scholar] [CrossRef]
| Roll-Specific Heat Capacity/ ( | Roll Density/ ( | Thermal Conductivity/ ( | Thermal Expansion Coefficient/ ( | Poisson Ratio |
|---|---|---|---|---|
| 460 | 7.38 × 10−6 | 0.029 | 12 × 10−6 | 0.287 |
| Rolled Piece Temperature/() | Cooling Water Temperature/() | Bearing Temperature /() | Air Temperature /() |
|---|---|---|---|
| 900 | 60 | 35 | 25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Elmi, S.A.; Liu, L.; Yin, B.; Kuang, S.; Bai, Z. Numerical Simulation Research on the Temperature Field and Hot Roll Crown Model of Hot Continuous Rolling Mills. Metals 2024, 14, 166. https://doi.org/10.3390/met14020166
Li Z, Elmi SA, Liu L, Yin B, Kuang S, Bai Z. Numerical Simulation Research on the Temperature Field and Hot Roll Crown Model of Hot Continuous Rolling Mills. Metals. 2024; 14(2):166. https://doi.org/10.3390/met14020166
Chicago/Turabian StyleLi, Zizheng, Sahal Ahmed Elmi, Luxuan Liu, Baoliang Yin, Shuang Kuang, and Zhenhua Bai. 2024. "Numerical Simulation Research on the Temperature Field and Hot Roll Crown Model of Hot Continuous Rolling Mills" Metals 14, no. 2: 166. https://doi.org/10.3390/met14020166
APA StyleLi, Z., Elmi, S. A., Liu, L., Yin, B., Kuang, S., & Bai, Z. (2024). Numerical Simulation Research on the Temperature Field and Hot Roll Crown Model of Hot Continuous Rolling Mills. Metals, 14(2), 166. https://doi.org/10.3390/met14020166






