First-Principles Investigation on the Adsorption and Diffusion of Oxygen at the B2(110)–O(001) Interface in Ti2AlNb Alloys
Abstract
:1. Introduction
2. Computational Methods and Models
2.1. Computational Details
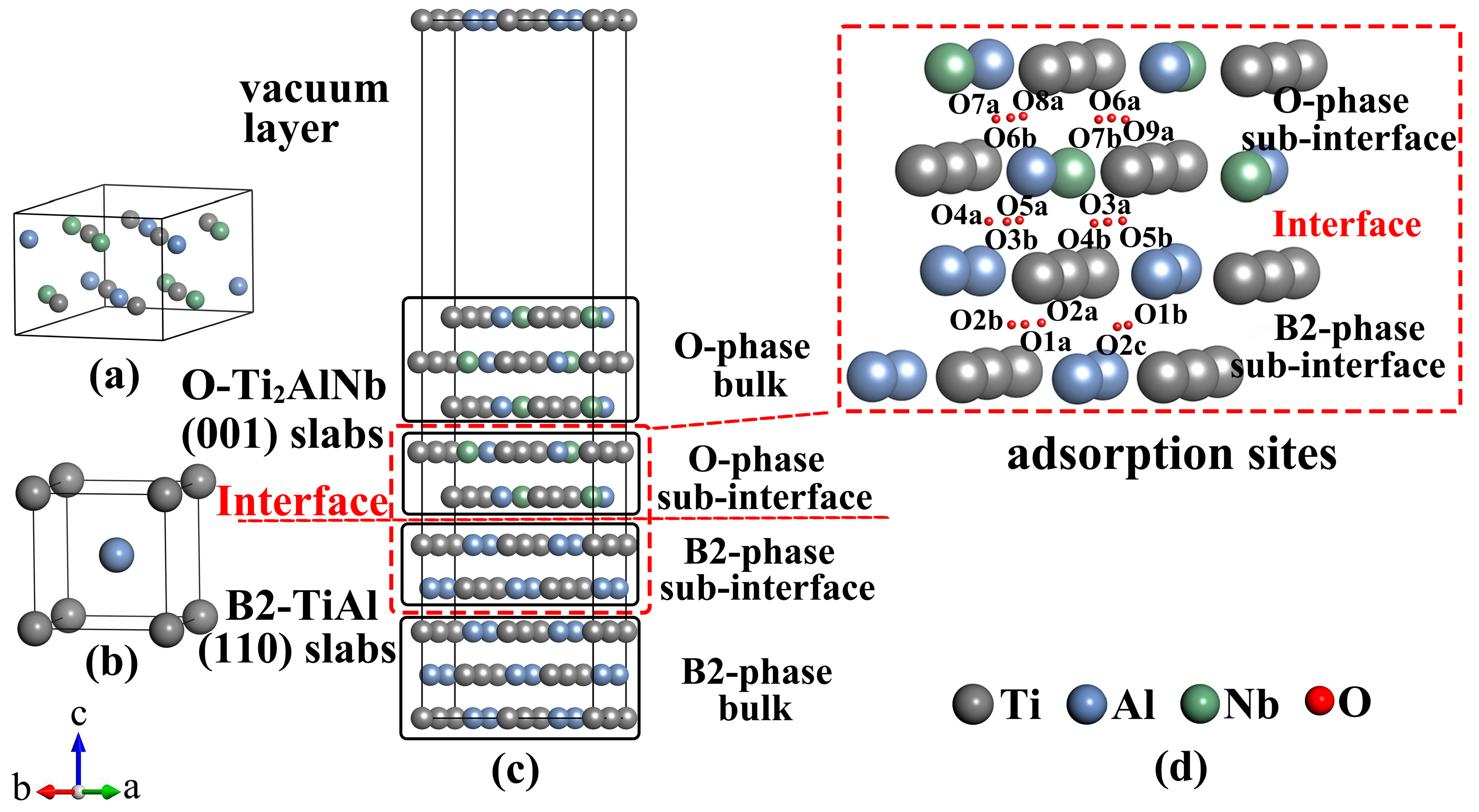
2.2. Structural Models
3. Results and Discussion
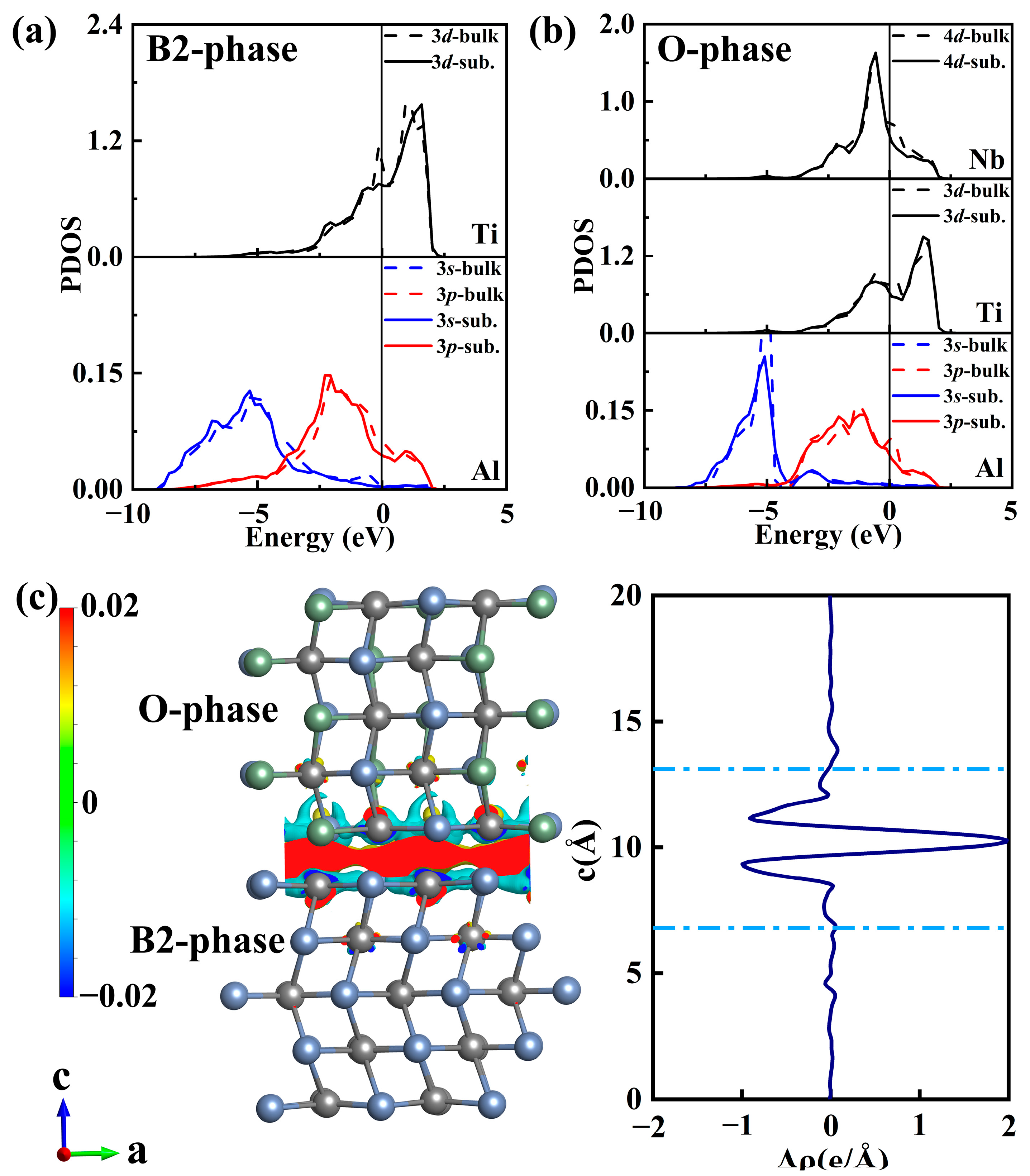
3.1. B2(110)/O(001) Interface
3.2. Oxygen Adsorption at B2(110)–O(001) Interface
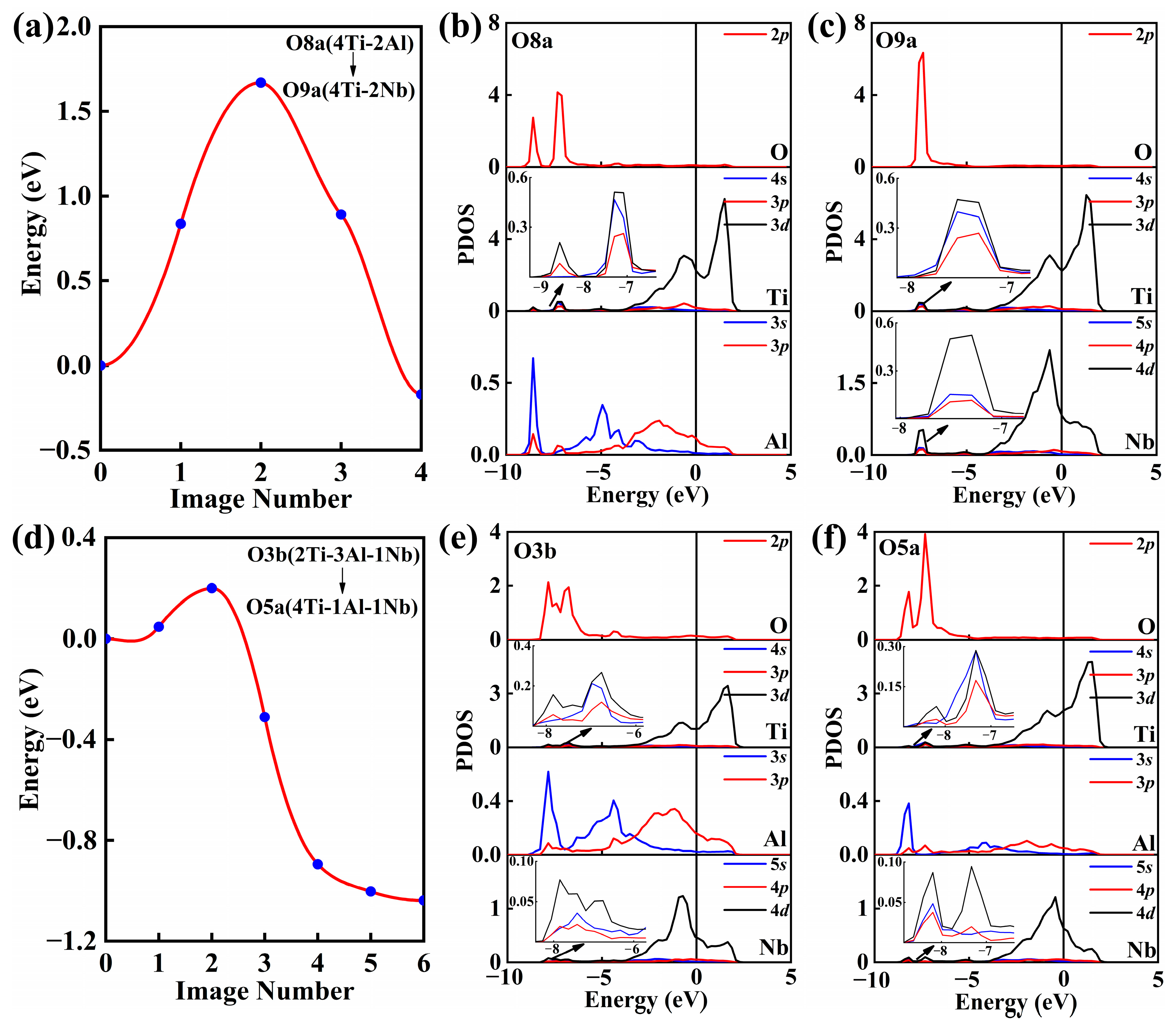
3.3. Oxygen Diffusion at B2(110)–O(001) Interface
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goyal, K.; Sardana, N. Mechanical Properties of the Ti2AlNb Intermetallic: A Review. Trans. Indian Inst. Met. 2021, 74, 1839–1853. [Google Scholar] [CrossRef]
- Goyal, K.; Bera, C.; Sardana, N. Temperature-dependent structural, mechanical, and thermodynamic properties of B2-phase Ti2AlNb for aerospace applications. J. Mater. Sci. 2022, 57, 19553–19570. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Yang, Y.; Lan, X.; Zhang, Z.; Li, H. Study on Creep-Fatigue Mechanical Behavior and Life Prediction of Ti2AlNb-Based Alloy. Materials 2022, 15, 6238. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, D. The intermetallic Ti2AlNb. Prog. Mater. Sci. 1997, 42, 135–158. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Yan, N.; Liang, H.Y.; Liu, Y.C. Phase transformation and microstructure control of Ti2AlNb-based alloys: A review. J. Mater. Sci. Technol. 2021, 80, 203–216. [Google Scholar] [CrossRef]
- Dai, J.; Sun, C.; Wang, A.; Zhang, H.; Li, S.; Zhang, H. High temperature oxidation and hot corrosion behaviors of Ti2AlNb alloy at 923 K and 1023 K. Corros. Sci. 2021, 184, 109336. [Google Scholar] [CrossRef]
- He, Y.S.; Hu, R.; Luo, W.Z.; He, T.; Liu, X.H. Oxidation behavior of a novel multi-element alloyed Ti2AlNb-based alloy in temperature range of 650–850 degrees C. Rare Met. 2018, 37, 838–845. [Google Scholar] [CrossRef]
- Chen, W.; Huang, L.; Liu, Y.Y.; Zhao, Y.F.; Wang, Z.; Xie, Z.W. Oxidative Corrosion Mechanism of Ti2AlNb-Based Alloys during Alternate High Temperature-Salt Spray Exposure. Coatings 2022, 12, 1374. [Google Scholar] [CrossRef]
- Qu, S.J.; Tang, S.Q.; Feng, A.H.; Feng, C.; Shen, J.; Chen, D.L. Microstructural evolution and high-temperature oxidation mechanisms of a titanium aluminide based alloy. Acta Mater. 2018, 148, 300–310. [Google Scholar] [CrossRef]
- Cheng, J.; Li, J.; Rao, Q. Time-resolved in-situ XRD study on oxidation evolution of Ti2AlNb-based alloys. Mater. Today Commun. 2023, 36, 106660. [Google Scholar] [CrossRef]
- Malecka, J. Investigation of the oxidation behavior of orthorhombic Ti2AlNb alloy. J. Mater. Eng. Perform. 2015, 24, 1834–1840. [Google Scholar] [CrossRef]
- Chen, J.; Chen, Q.; Qu, S.J.; Xiang, H.P.; Wang, C.; Gao, J.B.; Feng, A.H.; Chen, D.L. Oxidation mechanisms of an intermetallic alloy at high temperatures. Scr. Mater. 2021, 199, 113852. [Google Scholar] [CrossRef]
- Ralison, A.; Dettenwanger, F.; Schutze, M. Oxidation of orthorhombic Ti2AlNb alloys in the temperature range 550-1000 degrees C in air. Mater. High Temp. 2003, 20, 607–629. [Google Scholar] [CrossRef]
- Xiang, J.M.; Mi, G.B.; Qu, S.J.; Huang, X.; Chen, Z.; Feng, A.H.; Shen, J.; Chen, D.L. Thermodynamic and microstructural study of Ti2AlNb oxides at 800 °C. Sci. Rep. 2018, 8, 12761. [Google Scholar] [CrossRef] [PubMed]
- Cai, Q.; Li, M.C.; Zhang, Y.R.; Liu, Y.C.; Ma, Z.Q.; Li, C.; Li, H.J. Precipitation behavior of Widmanstatten O phase associated with interface in aged Ti2AlNb-based alloys. Mater. Charact. 2018, 145, 413–422. [Google Scholar] [CrossRef]
- Zheng, Y.P.; Zeng, W.D.; Li, D.; Xu, J.W.; Ma, X.; Liang, X.B.; Zhang, J.W. Orthorhombic precipitate variant selection in a Ti2AlNb based alloy. Mater. Des. 2018, 158, 46–61. [Google Scholar] [CrossRef]
- Wang, L.; Shang, J.X.; Wang, F.H.; Chen, Y.; Zhang, Y. Oxygen adsorption on γ-TiAl surfaces and the related surface phase diagrams: A density-functional theory study. Acta Mater. 2013, 61, 1726–1738. [Google Scholar] [CrossRef]
- Wei, L.J.; Guo, J.X.; Dai, X.H.; Guan, L.; Wang, Y.L.; Liu, B.T. First-principles calculations of oxygen adsorption on the Ti3Al (0001) surface. Surf. Interface Anal. 2016, 48, 1337–1340. [Google Scholar] [CrossRef]
- Bakulin, A.V.; Kulkov, S.S.; Kulkova, S.E. Diffusion properties of oxygen in the α2-Ti3Al alloy. Intermetallics 2021, 137, 107281. [Google Scholar] [CrossRef]
- Li, Y.; Dai, J.H.; Song, Y.; Yang, R. Adsorption properties of oxygen atom on the surface of Ti2AlNb by first principles calculations. Comput. Mater. Sci. 2017, 139, 412–418. [Google Scholar] [CrossRef]
- Li, D.H.; Wang, B.B.; Luo, L.S.; Li, X.W.; Xu, Y.J.; Li, B.Q.; Wang, L.; Liu, W.Y.; Han, B.S.; Su, Y.Q.; et al. The interface structure and its impact on the mechanical behavior of TiAl/ Ti2AlNb laminated composites. Mater. Sci. Eng. A-Struct. Mater. Prop. Microstruct. Process. 2021, 827, 142095. [Google Scholar] [CrossRef]
- Zou, C.X.; Li, J.S.; Zhu, L.; Zhang, Y.; Yao, G.; Tang, B.; Wang, J.; Kou, H.C.; Song, H.F.; Wang, W.Y. Electronic structures and properties of TiAl/Ti2AlNb heterogeneous interfaces: A comprehensive first-principles study. Intermetallics 2021, 133, 107173. [Google Scholar] [CrossRef]
- Ishkildin, A.D.; Kistanov, A.A.; Izosimov, A.A.; Korznikova, E.A. The nitriding effect on the stability and mechanical properties of the iron titan phase: First-principles investigation. Phys. Chem. Chem. Phys. 2023, 25, 24060–24068. [Google Scholar] [CrossRef]
- Wei, Y.; Zhou, H.B.; Zhang, Y.; Lu, G.H.; Xu, H. Effects of O in a binary-phase TiAl-Ti3Al alloy: From site occupancy to interfacial energetics. J. Phys. Condens. Matter. 2011, 23, 225504. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Kohn, W.; Sham, L. Self-consistent equations including exchange and correlation effects. Phys. Rev. A 1965, 140, 1133–1138. [Google Scholar] [CrossRef]
- Blochl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Methfessel, M.; Paxton, A.T. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. B 1989, 40, 3616–3621. [Google Scholar] [CrossRef]
- Henkelman, G.; Uberuaga, B.P.; Jonsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. [Google Scholar] [CrossRef]
- Nelson, R.; Ertural, C.; George, J.; Deringer, V.L.; Hautier, G.; Dronskowski, R. LOBSTER: Local orbital projections, atomic charges, and chemical-bonding analysis fromprojector-augmented-wave-baseddensity-functional theory. J. Comput. Chem. 2020, 41, 1931–1940. [Google Scholar] [CrossRef] [PubMed]
- Wang, A.Q.; Liu, P.; Xie, J.P.; Ma, D.Q.; Mao, Z.P. First-principles investigation on the atomic structure, stability and electronic property of O(001)/B2(110) interface in Ti2AlNb alloys. J. Alloys Compd. 2020, 817, 152734. [Google Scholar] [CrossRef]
- Li, Y.; Dai, J.H.; Song, Y. First-principles investigation on stability and oxygen adsorption behavior of a O/B2 interface in Ti2AlNb alloys. J. Alloys Compd. 2020, 818, 152926. [Google Scholar] [CrossRef]
- Liu, P.; Han, X.; Sun, D.; Chen, Z.; Wang, Q. Adhesion, stability and electronic properties of Ti2AlN(0001)/TiAl(111) coherent interface from first-principles calculation. Intermetallics 2018, 96, 49–57. [Google Scholar] [CrossRef]

| Location | Site (Coord.) | E(O-system) (eV) | Eads (eV) |
|---|---|---|---|
| B2-phase sub-interface | O1a (2Ti-4Al) | −548.205 | - |
| O1b (2Ti-4Al) | −548.377 | - | |
| O2a (4Ti-2Al) | −548.090 | −3.460 | |
| O2b (4Ti-2Al) | −548.380 | −3.750 | |
| O2c (4Ti-2Al) | −548.394 | −3.764 | |
| Interface | O3a (2Ti-3Al-1Nb) | −548.698 | - |
| O3b (2Ti-3Al-1Nb) | −547.340 | −2.710 | |
| O4a (4Ti-2Al) | −548.195 | −3.565 | |
| O4b (4Ti-2Al) | −548.596 | −3.966 | |
| O5a (4Ti-1Al-1Nb) | −548.379 | −3.749 | |
| O5b (4Ti-1Al-1Nb) | −548.701 | −4.071 | |
| O-phase sub-interface | O6a (2Ti-2Al-2Nb) | −548.915 | - |
| O6b (2Ti-2Al-2Nb) | −547.820 | −3.190 | |
| O7a (4Ti-1Al-1Nb) | −548.306 | −3.676 | |
| O7b (4Ti-1Al-1Nb) | −548.377 | −3.747 | |
| O8a (4Ti-2Al) | −548.747 | −4.117 | |
| O9a (4Ti-2Nb) | −548.917 | −4.287 |
| Location | Initial (Coord.) | Final (Coord.) | Energy Barrier (eV) |
|---|---|---|---|
| B2-phase sub-int. | O2a (4Ti–2Al) | O2b (4Ti–2Al) | 1.580 |
| O2b (4Ti–2Al) | O2c (4Ti–2Al) | 1.844 | |
| Interface | O3b (2Ti–3Al–1Nb) | O5a (4Ti–1Al–1Nb) | 0.199 |
| O4a (4Ti–2Al) | O4b (4Ti–2Al) | 1.698 | |
| O5a (4Ti–1Al–1Nb) | O5b (4Ti–1Al–1Nb) | 1.518 | |
| O-phase sub-int. | O6b (2Ti–2Al–2Nb) | O7a (4Ti–1Al–1Nb) | 0.568 |
| O7a (4Ti–1Al–1Nb) | O8a (4Ti–2Al) | 1.427 | |
| O8a (4Ti–2Al) | O9a (4Ti–2Nb) | 1.667 | |
| B2-phase sub-int.—Interface | O2c (4Ti–2Al) | O5b (4Ti–1Al–1Nb) | 1.632 |
| O2b (4Ti–2Al) | O4b (4Ti–2Al) | 1.825 | |
| Interface—O-phase sub-int. | O5b (4Ti–1Al–1Nb) | O9a (4Ti–2Nb) | 1.773 |
| O4b (4Ti–2Al) | O9a (4Ti–2Nb) | 1.584 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Xiang, H.; Xu, L.; Feng, A.; Qu, S.; Chen, D. First-Principles Investigation on the Adsorption and Diffusion of Oxygen at the B2(110)–O(001) Interface in Ti2AlNb Alloys. Metals 2024, 14, 316. https://doi.org/10.3390/met14030316
Zhang M, Xiang H, Xu L, Feng A, Qu S, Chen D. First-Principles Investigation on the Adsorption and Diffusion of Oxygen at the B2(110)–O(001) Interface in Ti2AlNb Alloys. Metals. 2024; 14(3):316. https://doi.org/10.3390/met14030316
Chicago/Turabian StyleZhang, Ming, Hongping Xiang, Lin Xu, Aihan Feng, Shoujiang Qu, and Daolun Chen. 2024. "First-Principles Investigation on the Adsorption and Diffusion of Oxygen at the B2(110)–O(001) Interface in Ti2AlNb Alloys" Metals 14, no. 3: 316. https://doi.org/10.3390/met14030316
APA StyleZhang, M., Xiang, H., Xu, L., Feng, A., Qu, S., & Chen, D. (2024). First-Principles Investigation on the Adsorption and Diffusion of Oxygen at the B2(110)–O(001) Interface in Ti2AlNb Alloys. Metals, 14(3), 316. https://doi.org/10.3390/met14030316









