Study on the Process Window in Wire Arc Additive Manufacturing of a High Relative Density Aluminum Alloy
Abstract
:1. Introduction
2. Theory and Methods
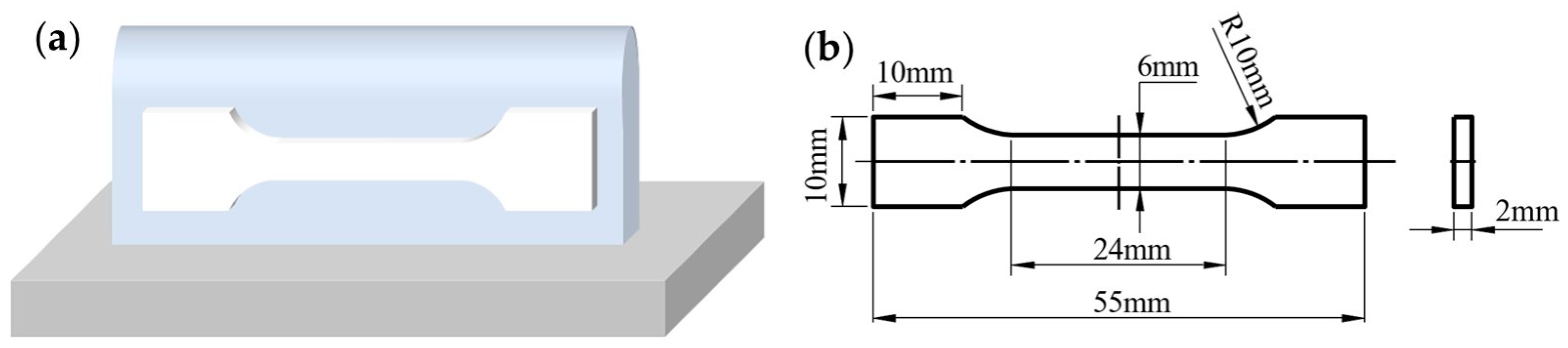
2.1. Experimental Methods
2.2. eXtreme Gradient Boosting Algorithm
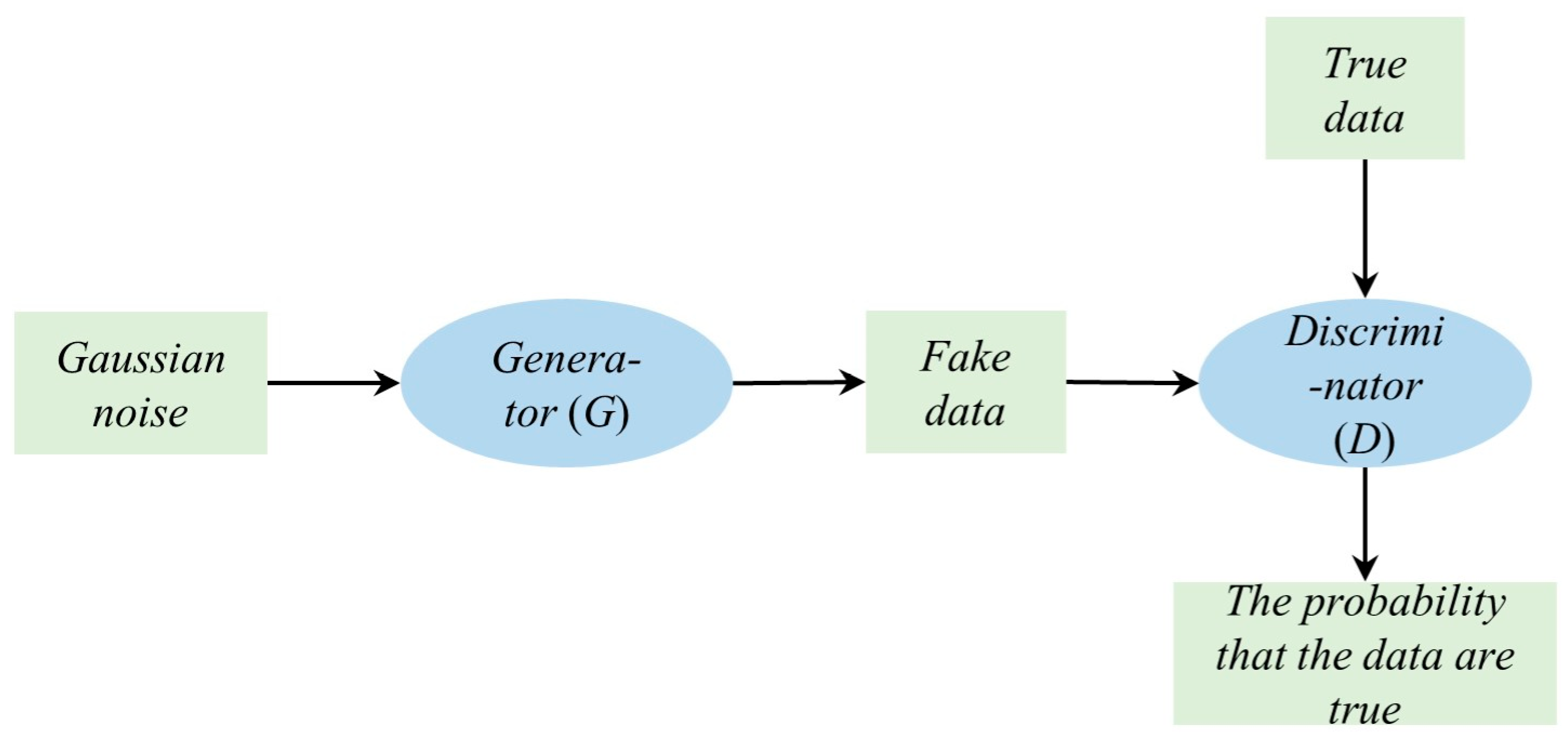
2.3. Wasserstein Generative Adversarial Networks with Gradient Penalty Terms
3. Results and Discussion
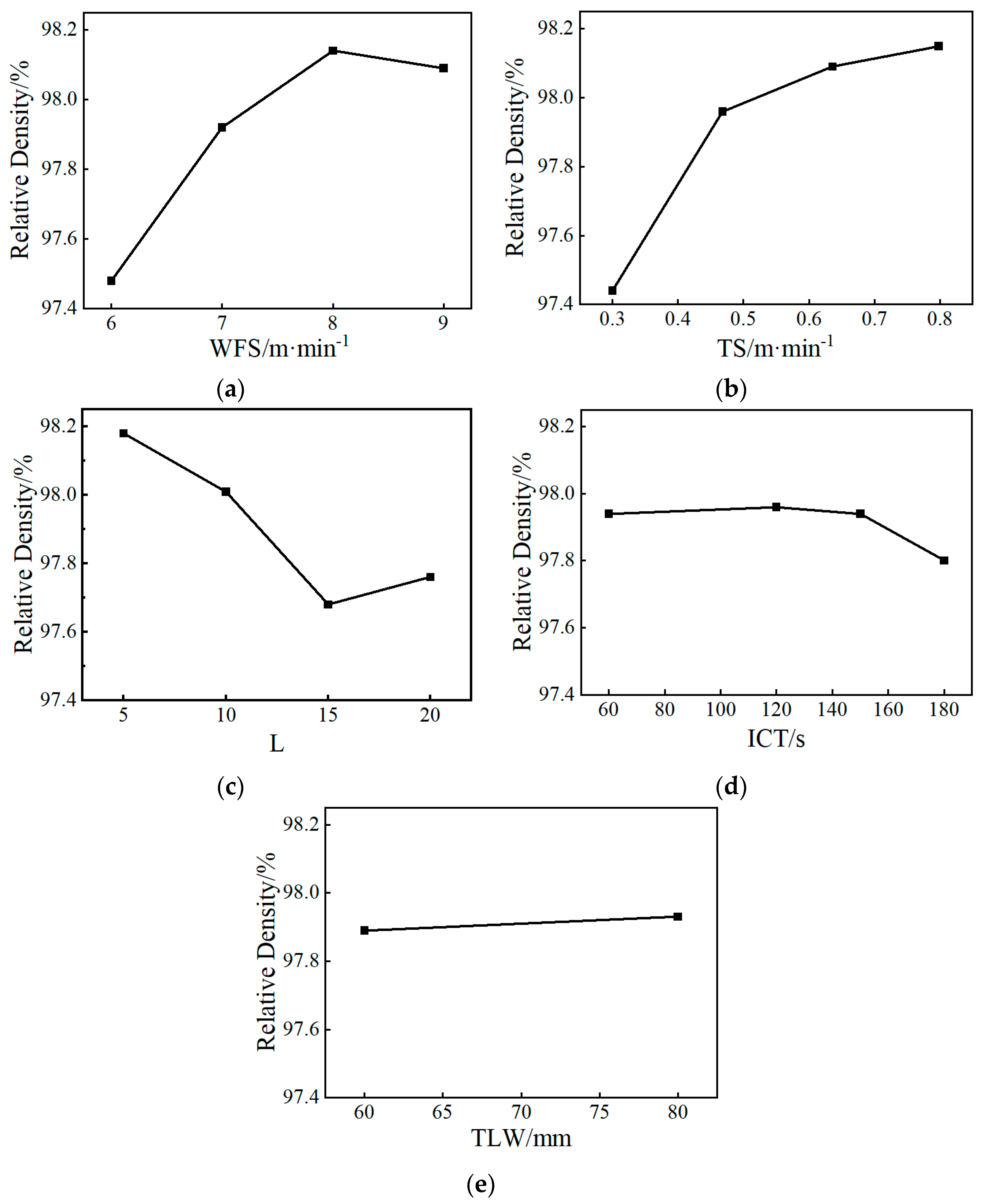
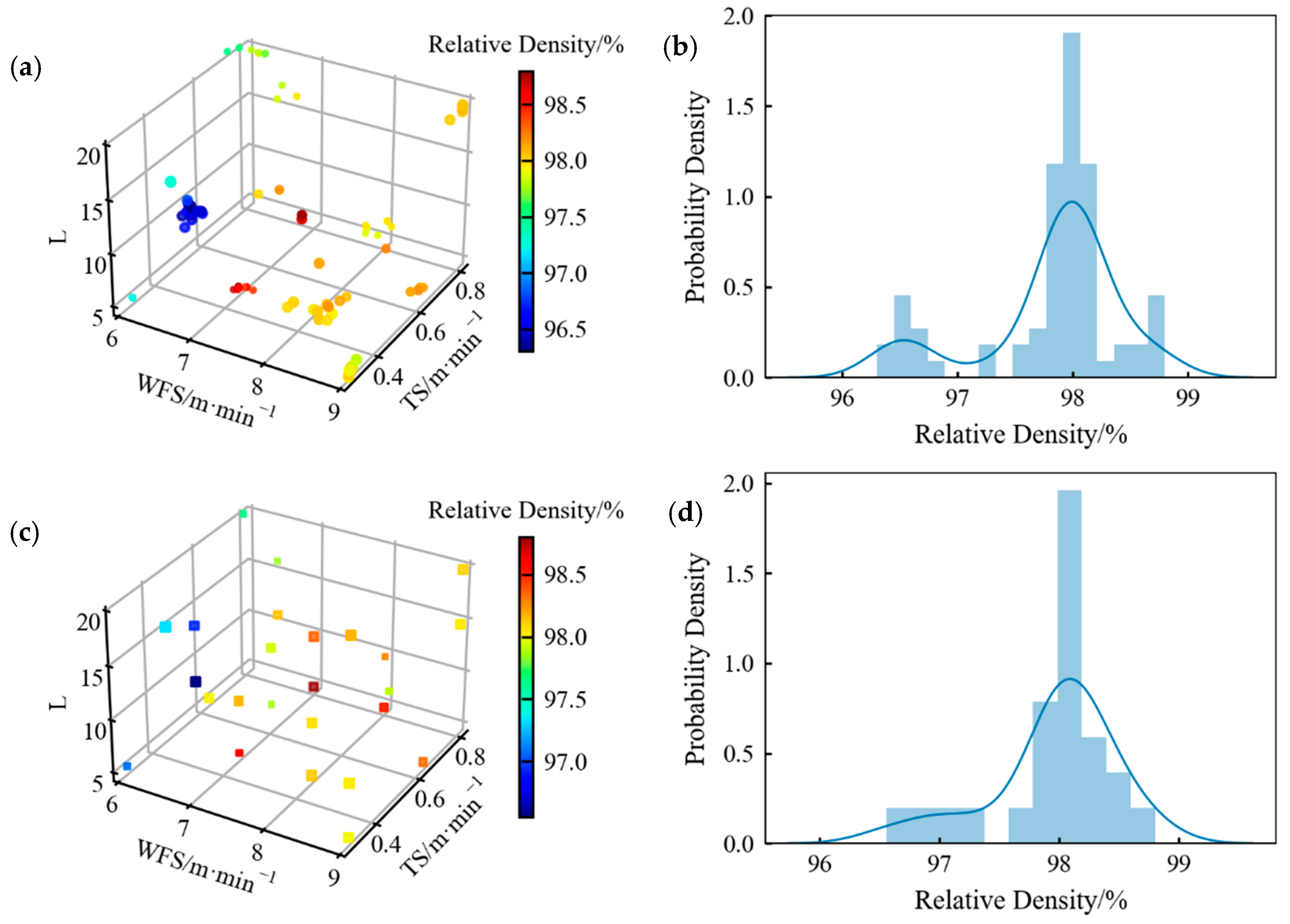
3.1. Effects of Print Parameters on Relative Density
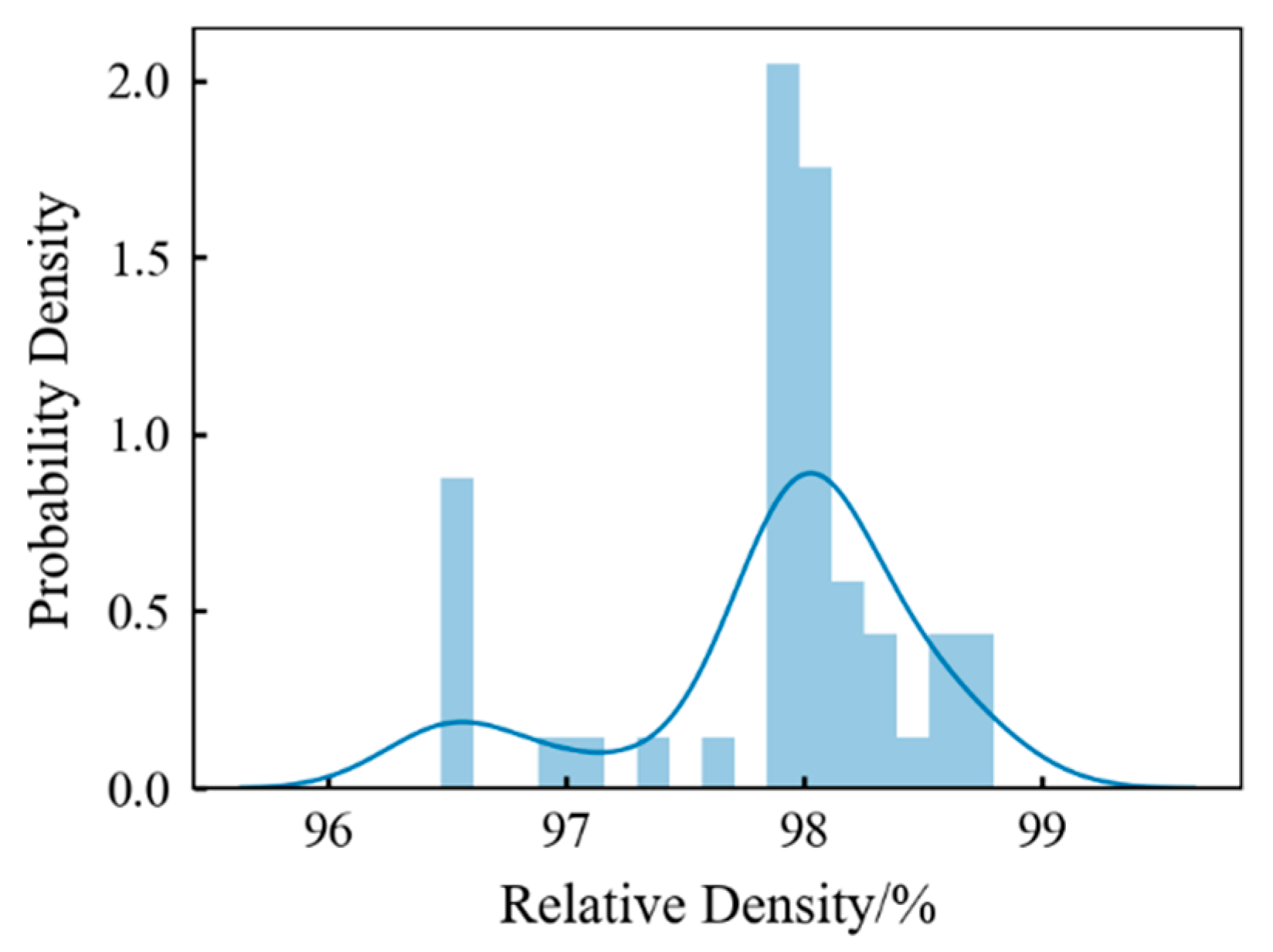
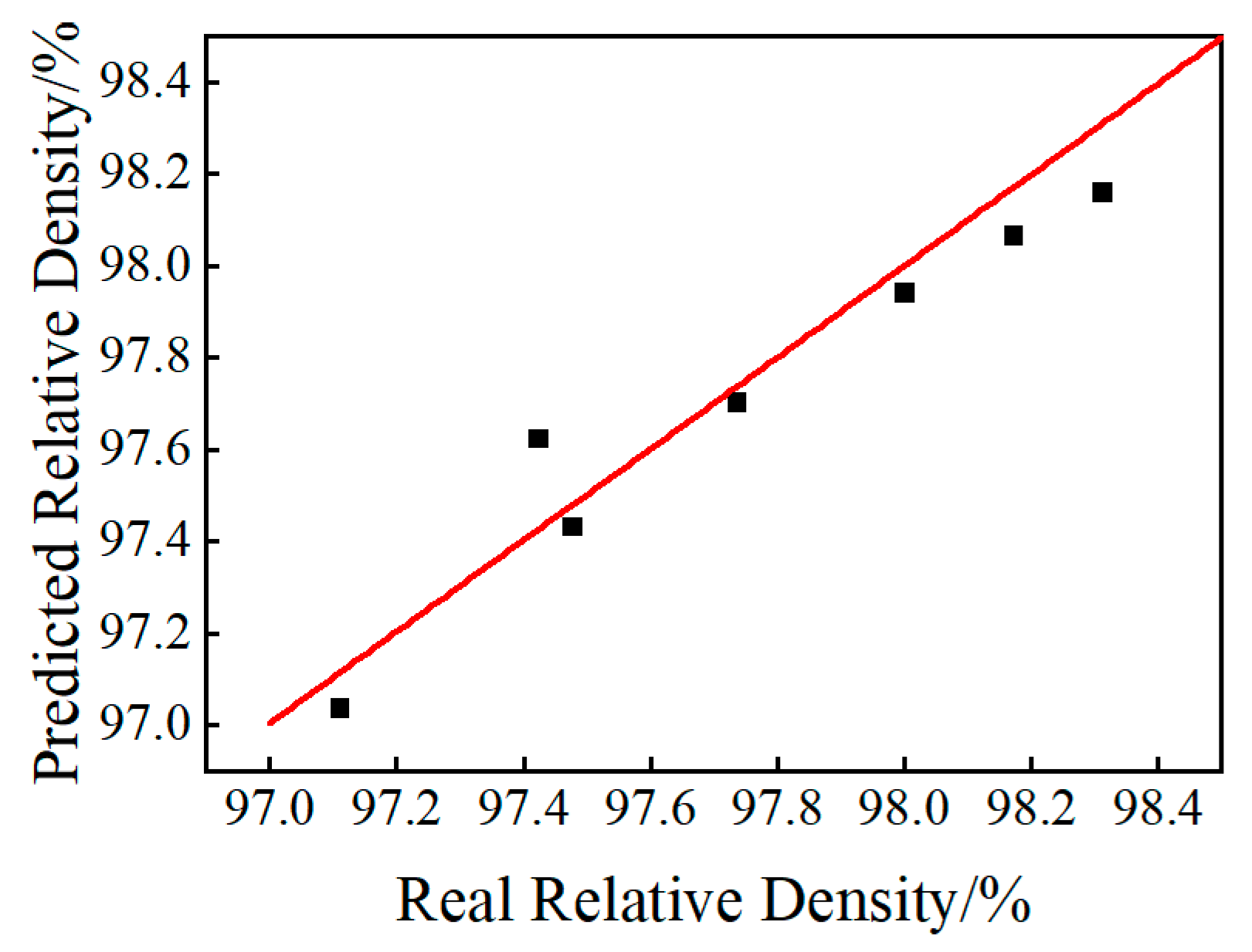
3.2. Modeling of Process Parameter–Relative Density Relationships
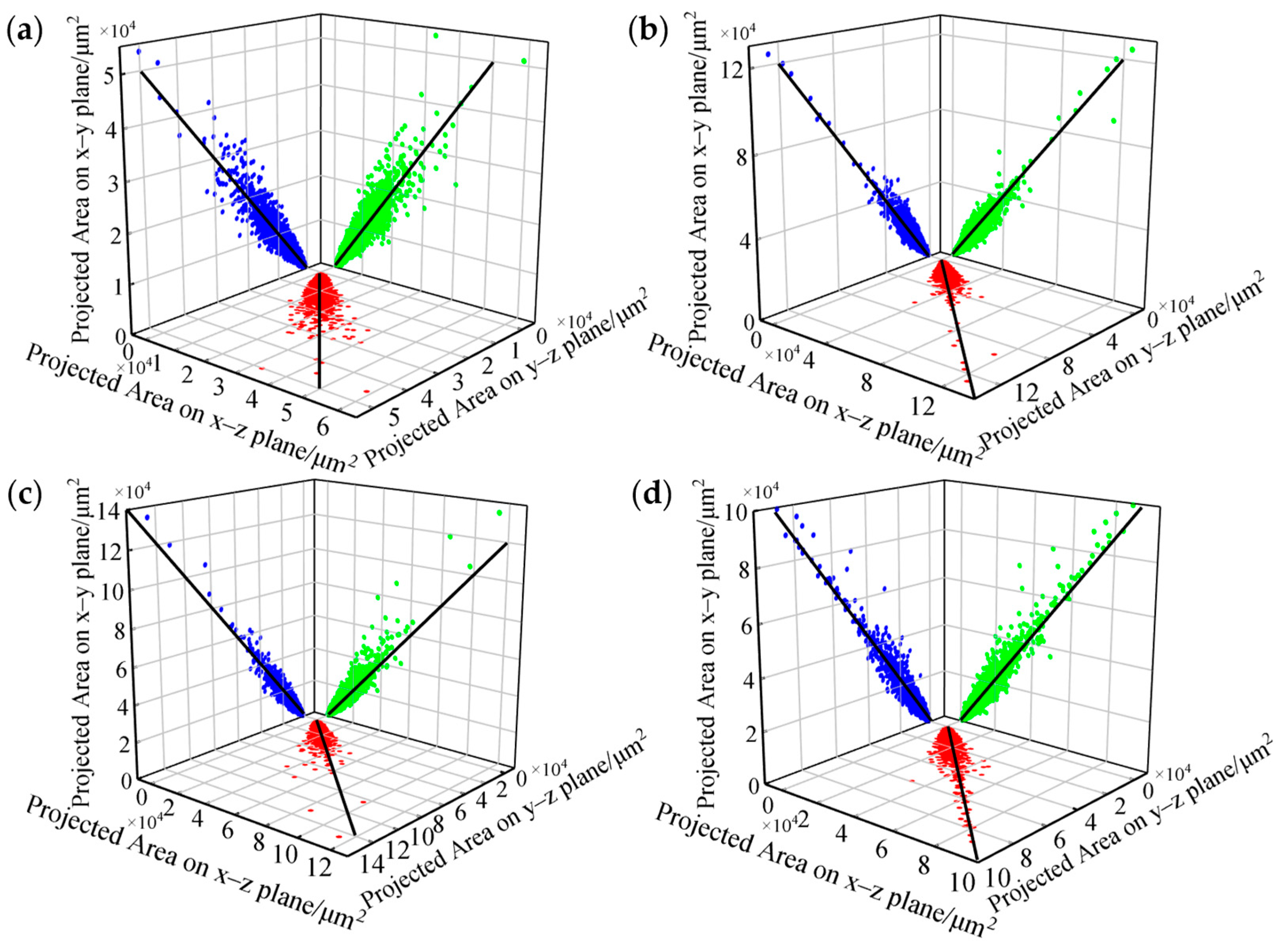
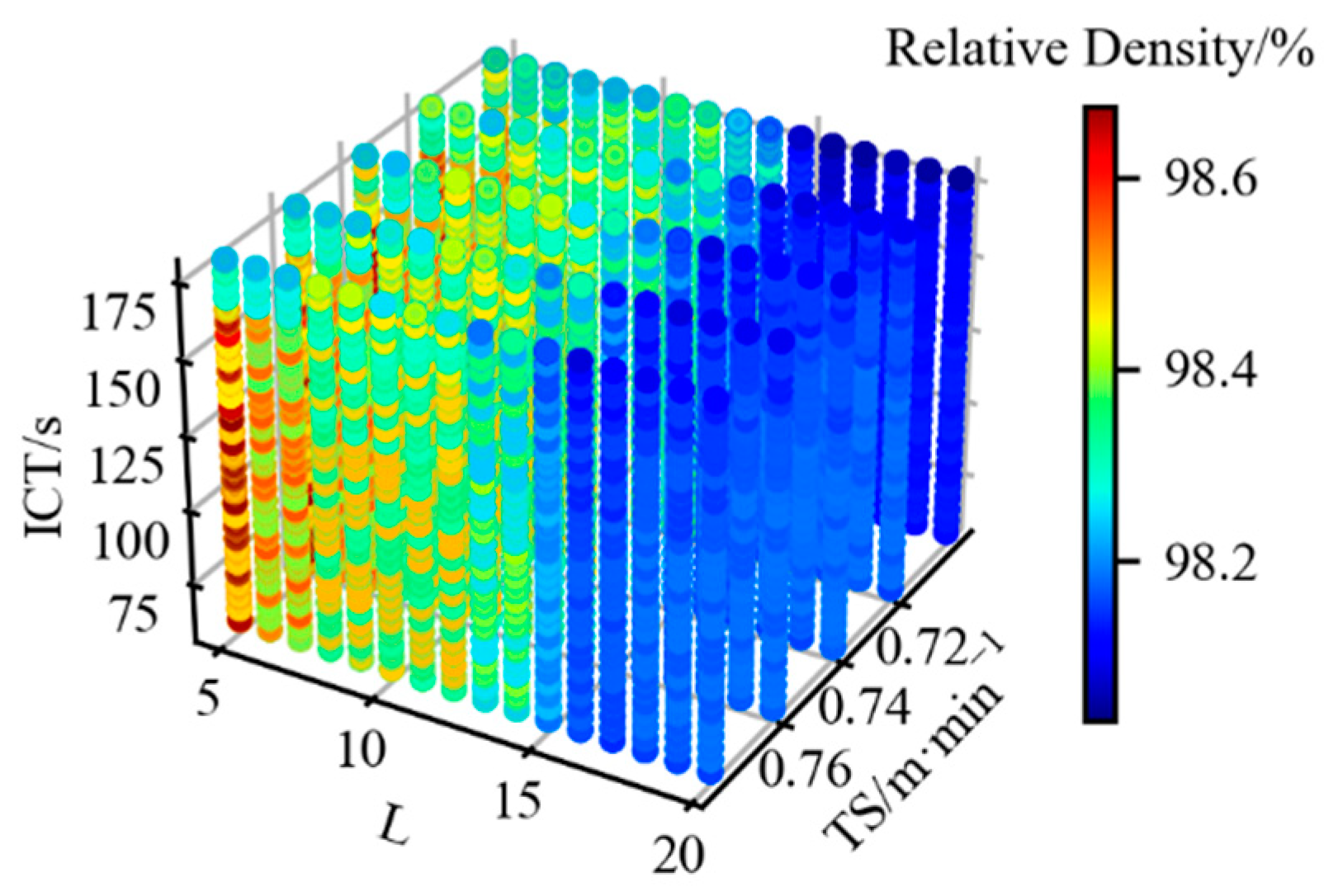
3.3. High Relative Density Process Window Reliability Verification
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kumar Sinha, A.; Pramanik, S.; Yagati, K.P. Research Progress in Arc Based Additive Manufacturing of Aluminium Alloys—A Review. Measurement 2022, 200, 111672. [Google Scholar] [CrossRef]
- Bartsch, H.; Kühne, R.; Citarelli, S.; Schaffrath, S.; Feldmann, M. Fatigue Analysis of Wire Arc Additive Manufactured (3D Printed) Components with Unmilled Surface. Structures 2021, 31, 576–589. [Google Scholar] [CrossRef]
- Vishnukumar, M.; Pramod, R.; Rajesh Kannan, A. Wire Arc Additive Manufacturing for Repairing Aluminium Structures in Marine Applications. Mater. Lett. 2021, 299, 130112. [Google Scholar] [CrossRef]
- Bermingham, M.J.; Nicastro, L.; Kent, D.; Chen, Y.; Dargusch, M.S. Optimising the Mechanical Properties of Ti-6Al-4V Components Produced by Wire + Arc Additive Manufacturing with Post-Process Heat Treatments. J. Alloys Compd. 2018, 753, 247–255. [Google Scholar] [CrossRef]
- Wu, B.; Pan, Z.; Ding, D.; Cuiuri, D.; Li, H.; Xu, J.; Norrish, J. A Review of the Wire Arc Additive Manufacturing of Metals: Properties, Defects and Quality Improvement. J. Manuf. Process. 2018, 35, 127–139. [Google Scholar] [CrossRef]
- Li, Q.; Wu, A.; Li, Y.; Wang, G.; Yan, D.; Liu, J. Influence of Temperature Cycles on the Microstructures and Mechanical Properties of the Partially Melted Zone in the Fusion Welded Joints of 2219 Aluminum Alloy. Mater. Sci. Eng. A 2015, 623, 38–48. [Google Scholar] [CrossRef]
- Zhou, Y.; Lin, X.; Kang, N.; Huang, W.; Wang, J.; Wang, Z. Influence of Travel Speed on Microstructure and Mechanical Properties of Wire + Arc Additively Manufactured 2219 Aluminum Alloy. J. Mater. Sci. Technol. 2020, 37, 143–153. [Google Scholar] [CrossRef]
- Hu, Y.; Deng, X.; Kan, Q.; Wu, S.; Li, Y.; Lei, L.; Wang, L.; Kang, G. Influence of Temperature on Deformation and Damage Mechanisms of Wire + Arc Additively Manufactured 2219 Aluminum Alloy. Eng. Fract. Mech. 2023, 292, 109675. [Google Scholar] [CrossRef]
- Wang, Z.; Lin, X.; Wang, L.; Cao, Y.; Zhou, Y.; Huang, W. Microstructure Evolution and Mechanical Properties of the Wire + Arc Additive Manufacturing Al-Cu Alloy. Addit. Manuf. 2021, 47, 102298. [Google Scholar] [CrossRef]
- Gu, J.; Gao, M.; Yang, S.; Bai, J.; Ding, J.; Fang, X. Pore Formation and Evolution in Wire + Arc Additively Manufactured 2319 Al Alloy. Addit. Manuf. 2019, 30, 100900. [Google Scholar] [CrossRef]
- Li, Q.; Feng, C.; Liu, B.; Zhou, Q.; Hu, W.; Wang, F. Influence of WAAM Process Parameters on Micro Porosities of Additively Manufactured 2219Aluminum Alloy. Aerosp. Mater. Technol. 2022, 52, 129–133. [Google Scholar]
- Ryan, E.M.; Sabin, T.J.; Watts, J.F.; Whiting, M.J. The Influence of Build Parameters and Wire Batch on Porosity of Wire and Arc Additive Manufactured Aluminium Alloy 2319. J. Mater. Process. Technol. 2018, 262, 577–584. [Google Scholar] [CrossRef]
- Hauser, T.; Reisch, R.T.; Breese, P.P.; Lutz, B.S.; Pantano, M.; Nalam, Y.; Bela, K.; Kamps, T.; Volpp, J.; Kaplan, A.F.H. Porosity in Wire Arc Additive Manufacturing of Aluminium Alloys. Addit. Manuf. 2021, 41, 101993. [Google Scholar] [CrossRef]
- Derekar, K.; Lawrence, J.; Melton, G.; Addison, A.; Zhang, X.; Xu, L. Influence of Interpass Temperature on Wire Arc Additive Manufacturing (WAAM) of Aluminium Alloy Components. MATEC Web Conf. 2019, 269, 05001. [Google Scholar] [CrossRef]
- Le, V.T.; Mai, D.S.; Doan, T.K.; Paris, H. Wire and Arc Additive Manufacturing of 308L Stainless Steel Components: Optimization of Processing Parameters and Material Properties. Eng. Sci. Technol. Int. J. 2021, 24, 1015–1026. [Google Scholar] [CrossRef]
- Naveen Srinivas, M.; Vimal, K.E.K.; Manikandan, N.; Sritharanandh, G. Parametric Optimization and Multiple Regression Modelling for Fabrication of Aluminium Alloy Thin Plate Using Wire Arc Additive Manufacturing. Int. J. Interact. Des. Manuf. IJIDeM 2022, 1–11. [Google Scholar] [CrossRef]
- Ni, M.; Zhou, Y.; Hu, Z.; Qin, X.; Xiong, X.; Ji, F. Forming Optimization for WAAM with Weaving Deposition on Curved Surfaces. Int. J. Mech. Sci. 2023, 252, 108366. [Google Scholar] [CrossRef]
- Ouyang, J.; Li, M.; Lian, Y.; Peng, S.; Liu, C. A Fast Prediction Model for Liquid Metal Transfer Modes during the Wire Arc Additive Manufacturing Process. Materials 2023, 16, 2911. [Google Scholar] [CrossRef]
- Singh Sivam Sundarlingam Paramasivam, S.; Damodar Sawant, L.; Natarajan, H.; Sumanth, U.; Pratap Singh, K. Numerical Simulation Process Parameter Optimization in Metal Additive Manufacturing for Getting Better Quality of Products. Mater. Today Proc. 2022, 66, 850–857. [Google Scholar] [CrossRef]
- Xiao, X.; Waddell, C.; Hamilton, C.; Xiao, H. Quality Prediction and Control in Wire Arc Additive Manufacturing via Novel Machine Learning Framework. Micromachines 2022, 13, 137. [Google Scholar] [CrossRef]
- Dharmawan, A.G.; Xiong, Y.; Foong, S.; Song Soh, G. A Model-Based Reinforcement Learning and Correction Framework for Process Control of Robotic Wire Arc Additive Manufacturing. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 4030–4036. [Google Scholar] [CrossRef]
- Ling, Y.; Ni, J.; Antonissen, J.; Ben Hamouda, H.; Vande Voorde, J.; Abdel Wahab, M. Numerical Prediction of Microstructure and Hardness for Low Carbon Steel Wire Arc Additive Manufacturing Components. Simul. Model. Pract. Theory 2023, 122, 102664. [Google Scholar] [CrossRef]
- Tapia, G.; Elwany, A.H.; Sang, H. Prediction of Porosity in Metal-Based Additive Manufacturing Using Spatial Gaussian Process Models. Addit. Manuf. 2016, 12, 282–290. [Google Scholar] [CrossRef]
- Liu, Q.; Wu, H.; Paul, M.J.; He, P.; Peng, Z.; Gludovatz, B.; Kruzic, J.J.; Wang, C.H.; Li, X. Machine-Learning Assisted Laser Powder Bed Fusion Process Optimization for AlSi10Mg: New Microstructure Description Indices and Fracture Mechanisms. Acta Mater. 2020, 201, 316–328. [Google Scholar] [CrossRef]
- GB/T 3850-2015; Impermeable Sintered Metal Materials and Hardmetals—Determination of Density. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China; Standardization Administration of the People’s Republic of China: Beijing, China, 2015.
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Pan, B. Application of XGBoost Algorithm in Hourly PM2.5 Concentration Prediction. IOP Conf. Ser. Earth Environ. Sci. 2018, 113, 012127. [Google Scholar] [CrossRef]
- Ding, P. Modeling Method for Complex Industrial Process Based on GANs Data Augmentation. Master’s Thesis, China University of Mining and Technology, Xuzhou, China, 2021. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CMFD&dbname=CMFD202201&filename=1021774558.nh&v= (accessed on 18 February 2023).
- Fu, W.; Zhang, D.; Fu, Y.; Li, J.; Xie, Y. Arrears Prediction for Electricity Customer through Wgan-Gp. In Proceedings of the 2017 IEEE 2nd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chengdu, China, 15–17 December 2017; IEEE: Chengdu, China, 2017; pp. 1667–1670. [Google Scholar] [CrossRef]
- Cong, B.; Ouyang, R.; Qi, B.; Ding, J. Influence of Cold Metal Transfer Process and Its Heat Input on Weld Bead Geometry and Porosity of Aluminum-Copper Alloy Welds. Rare Met. Mater. Eng. 2016, 45, 606–611. [Google Scholar] [CrossRef]
- Sanaei, N.; Fatemi, A.; Phan, N. Defect Characteristics and Analysis of Their Variability in Metal L-PBF Additive Manufacturing. Mater. Des. 2019, 182, 108091. [Google Scholar] [CrossRef]
- Wu, S.; Hu, Y.; Yang, B.; Zhang, H.; Guo, G.; Kang, G. Review on Defect Characterization and Structural Integrity Assessment Method of Additively Manufactured Materials. J. Mech. Eng. 2021, 57, 3–34. [Google Scholar]
- Jiang, G.; Liu, Y.; Li, Y.; Su, Y.; Guo, J. A model for calculating solubility of hydrogen in molten aluminum alloys. Acta Metall. Sin. 2008, 44, 129–133. [Google Scholar]
- Hsu, W.-C.; Shen, T.-E.; Liang, Y.-C.; Yeh, J.-W.; Tsai, C.-W. In Situ Analysis of the Portevin-Le Chatelier Effect from Low to High-Entropy Alloy in Equal HfNbTaTiZr System. Acta Mater. 2023, 253, 118981. [Google Scholar] [CrossRef]
- Nie, X.; Zhang, H.; Zhu, H.; Hu, Z.; Qi, Y.; Zeng, X. On the Role of Zr Content into Portevin-Le Chatelier (PLC) Effect of Selective Laser Melted High Strength Al-Cu-Mg-Mn Alloy. Mater. Lett. 2019, 248, 5–7. [Google Scholar] [CrossRef]
- Uijl, N.J.D.; Carless, L.J. Advanced Metal-Forming Technologies for Automotive Applications. In Advanced Materials in Automotive Engineering; Woodhead Publishing: Sawston, UK, 2012; pp. 28–56. [Google Scholar] [CrossRef]
- Fang, X.; Zhang, L.; Li, H.; Li, C.; Huang, K.; Lu, B. Microstructure Evolution and Mechanical Behavior of 2219 Aluminum Alloys Additively Fabricated by the Cold Metal Transfer Process. Materials 2018, 11, 812. [Google Scholar] [CrossRef] [PubMed]
- Fang, Y.; Wang, L.; Sun, L.; Lyu, F.; Zhang, J.; Zhan, X. Influence of Heat Flow on the Grain Morphology and Porosity of Wire Arc Additive Manufactured 2319 Aluminum Alloy. Met. Mater. Int. 2023, 1–13. [Google Scholar] [CrossRef]




| Si | Fe | Cu | Mn | Mg | Zn | Ti | V | Zr | Al |
|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 0.3 | 5.8–6.8 | 0.20–0.40 | 0.02 | 0.10 | 0.1–0.2 | 0.05–0.15 | 0.1–0.25 | other |
| Parameters | Level | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| WFS/m·min−1 | 6 | 7 | 8 | 9 |
| TS/m·min−1 | 0.300 | 0.468 | 0.636 | 0.798 |
| L | 5 | 10 | 15 | 20 |
| ICT/s | 60 | 120 | 150 | 180 |
| TLW/mm | 60 | 80 | / | / |
| Network Layer | Number of Kernel | Kernel Size | Output Size | Activation Function | D/G |
|---|---|---|---|---|---|
| Fully connected layer | / | / | (None, 6) | relu | G |
| Reshape layer | / | / | (None, 6, 1) | / | |
| 1D convolutional layer | 32 | 3 | (None, 6, 32) | relu | |
| 1D convolutional layer | 32 | 3 | (None, 6, 32) | relu | |
| 1D convolutional layer | 1 | 3 | (None, 6, 1) | tanh | |
| Input layer | / | / | (None, 6, 1) | / | D |
| 1D convolutional layer | 32 | 3 | (None, 6, 32) | leakyrelu | |
| 1D convolutional layer | 32 | 3 | (None, 6, 32) | leakyrelu | |
| 1D convolutional layer | 32 | 3 | (None, 6, 32) | leakyrelu | |
| Flatten layer | / | / | (None, 192) | / | |
| Fully connected layer | / | / | (None, 64) | / | |
| Dropout layer | / | / | (None, 64) | / | |
| Fully connected layer | / | / | (None, 1) | / |
| Sample | WFS/m·min−1 | TS/m·min−1 | L | ICT/s | TLW/mm | Relative Density/% |
|---|---|---|---|---|---|---|
| 1 | 6 | 0.300 | 5 | 60 | 60 | 97.06 |
| 2 | 6 | 0.636 | 5 | 150 | 80 | 98.02 |
| 3 | 7 | 0.468 | 5 | 60 | 60 | 98.59 |
| 4 | 7 | 0.798 | 5 | 150 | 80 | 98.80 |
| 5 | 8 | 0.468 | 5 | 180 | 80 | 98.13 |
| 6 | 8 | 0.798 | 5 | 120 | 60 | 98.49 |
| 7 | 9 | 0.300 | 5 | 180 | 80 | 98.01 |
| 8 | 9 | 0.636 | 5 | 120 | 60 | 98.35 |
| 9 | 6 | 0.300 | 10 | 120 | 80 | 97.11 |
| 10 | 6 | 0.636 | 10 | 180 | 60 | 97.74 |
| 11 | 7 | 0.468 | 10 | 120 | 80 | 98.17 |
| 12 | 7 | 0.798 | 10 | 180 | 60 | 98.38 |
| 13 | 8 | 0.468 | 10 | 150 | 60 | 98.07 |
| 14 | 8 | 0.798 | 10 | 60 | 80 | 98.30 |
| 15 | 9 | 0.300 | 10 | 150 | 60 | 98.03 |
| 16 | 9 | 0.636 | 10 | 60 | 80 | 98.31 |
| 17 | 6 | 0.468 | 15 | 180 | 60 | 97.32 |
| 18 | 6 | 0.798 | 15 | 120 | 80 | 97.42 |
| 19 | 7 | 0.300 | 15 | 180 | 60 | 96.56 |
| 20 | 7 | 0.636 | 15 | 120 | 80 | 98.14 |
| 21 | 8 | 0.300 | 15 | 60 | 80 | 97.86 |
| 22 | 8 | 0.636 | 15 | 150 | 60 | 98.17 |
| 23 | 9 | 0.468 | 15 | 60 | 80 | 97.90 |
| 24 | 9 | 0.798 | 15 | 150 | 60 | 98.04 |
| 25 | 6 | 0.468 | 20 | 150 | 80 | 97.48 |
| 26 | 6 | 0.798 | 20 | 60 | 60 | 97.65 |
| 27 | 7 | 0.300 | 20 | 150 | 80 | 96.90 |
| 28 | 7 | 0.636 | 20 | 60 | 60 | 97.85 |
| 29 | 8 | 0.300 | 20 | 120 | 60 | 97.95 |
| 30 | 8 | 0.636 | 20 | 180 | 80 | 98.17 |
| 31 | 9 | 0.468 | 20 | 120 | 60 | 98.00 |
| 32 | 9 | 0.798 | 20 | 180 | 80 | 98.10 |
| Factors | WFS/m·min−1 | TS/m·min−1 | L | ICT/s | TLW/mm |
|---|---|---|---|---|---|
| K1j | 779.806 | 779.483 | 785.452 | 783.517 | 1566.258 |
| K2j | 783.374 | 783.642 | 784.103 | 783.640 | 1566.812 |
| K3j | 785.151 | 784.755 | 781.414 | 783.511 | / |
| K4j | 784.741 | 785.191 | 782.102 | 782.403 | / |
| k1j | 97.476 | 97.435 | 98.181 | 97.940 | 97.891 |
| k2j | 97.922 | 97.955 | 98.013 | 97.955 | 97.926 |
| k3j | 98.144 | 98.094 | 97.677 | 97.938 | / |
| k4j | 98.093 | 98.149 | 97.763 | 97.800 | / |
| Original range (R) | 0.668 | 0.714 | 0.504 | 0.155 | 0.035 |
| Range after conversion (R′) | 0.85 | 0.91 | 0.64 | 0.20 | 0.03 |
| Data Enhancement | Similarity Ordering | MAE | R2 |
|---|---|---|---|
| No | No | 0.138 | 0.816 |
| Yes | No | 0.113 | 0.870 |
| Yes | Yes | 0.096 | 0.924 |
| Process Parameters | Lower Limit | Upper Limit |
|---|---|---|
| WFS/m·min−1 | 7.1 | 8.0 |
| TS/m·min−1 | 0.720 | 0.798 |
| ICT/s | 60 | 156 |
| Specimen | WFS /m·min−1 | TS /m·min−1 | ICT/s | Relative Density/% | UTS/MPa | YS/MPa | εef/% |
|---|---|---|---|---|---|---|---|
| S1 | 7.1 | 0.720 | 90 | 98.77 | 267.76 | 123.22 | 8.47 |
| S2 | 7.5 | 0.759 | 90 | 98.49 | 251.24 | 129.52 | 7.18 |
| S3 | 8.0 | 0.798 | 90 | 98.63 | 279.96 | 132.77 | 11.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Li, Z.; Wang, Y.; Guo, W.; Lu, B. Study on the Process Window in Wire Arc Additive Manufacturing of a High Relative Density Aluminum Alloy. Metals 2024, 14, 330. https://doi.org/10.3390/met14030330
Wu Y, Li Z, Wang Y, Guo W, Lu B. Study on the Process Window in Wire Arc Additive Manufacturing of a High Relative Density Aluminum Alloy. Metals. 2024; 14(3):330. https://doi.org/10.3390/met14030330
Chicago/Turabian StyleWu, Yajun, Zhanxin Li, Yuzhong Wang, Wenhua Guo, and Bingheng Lu. 2024. "Study on the Process Window in Wire Arc Additive Manufacturing of a High Relative Density Aluminum Alloy" Metals 14, no. 3: 330. https://doi.org/10.3390/met14030330
APA StyleWu, Y., Li, Z., Wang, Y., Guo, W., & Lu, B. (2024). Study on the Process Window in Wire Arc Additive Manufacturing of a High Relative Density Aluminum Alloy. Metals, 14(3), 330. https://doi.org/10.3390/met14030330





