Steel Sheet Deformation in Clinch-Riveting Joining Process
Abstract
:1. Introduction
2. Experimental Measurements
2.1. Sheet Material
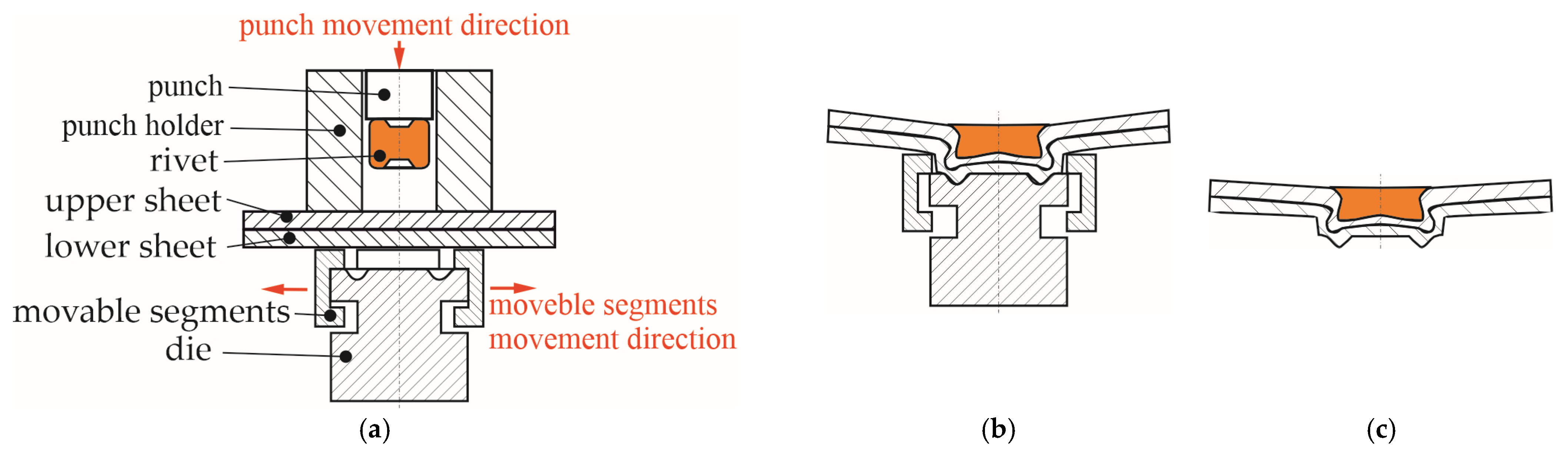
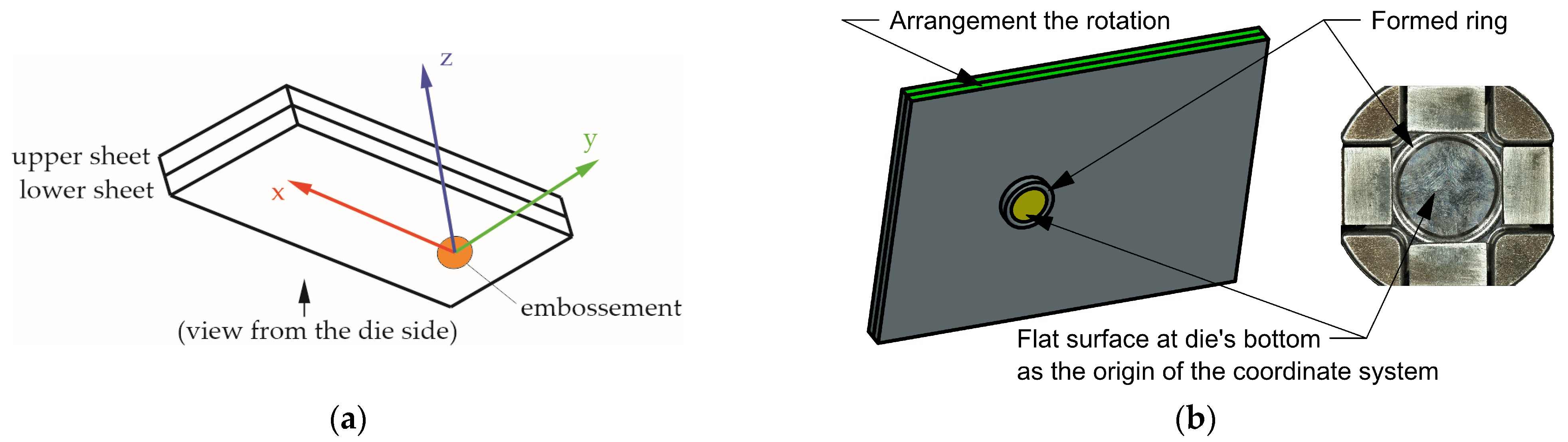
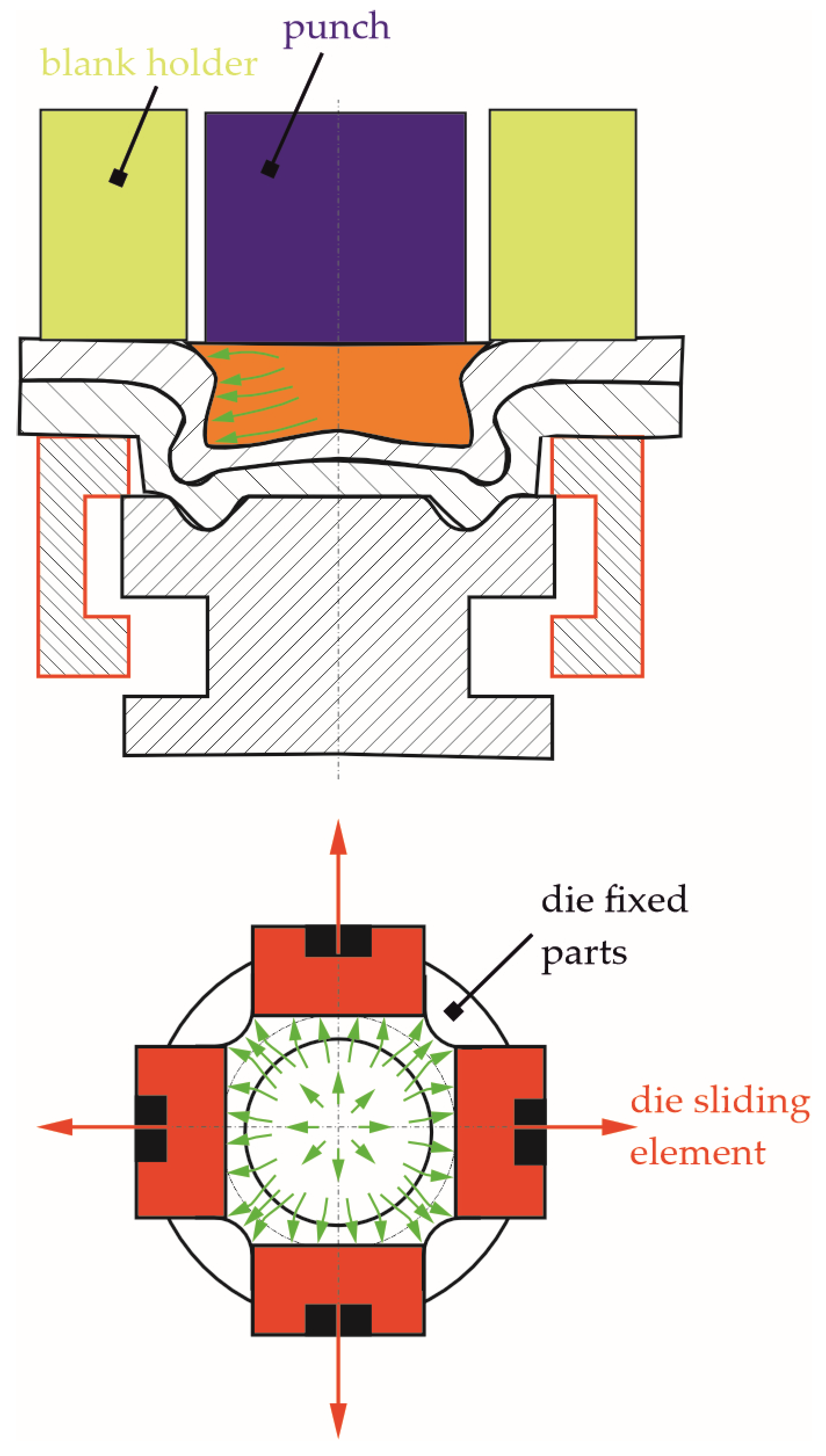
2.2. Clinch-Riveting Joining Process
- -
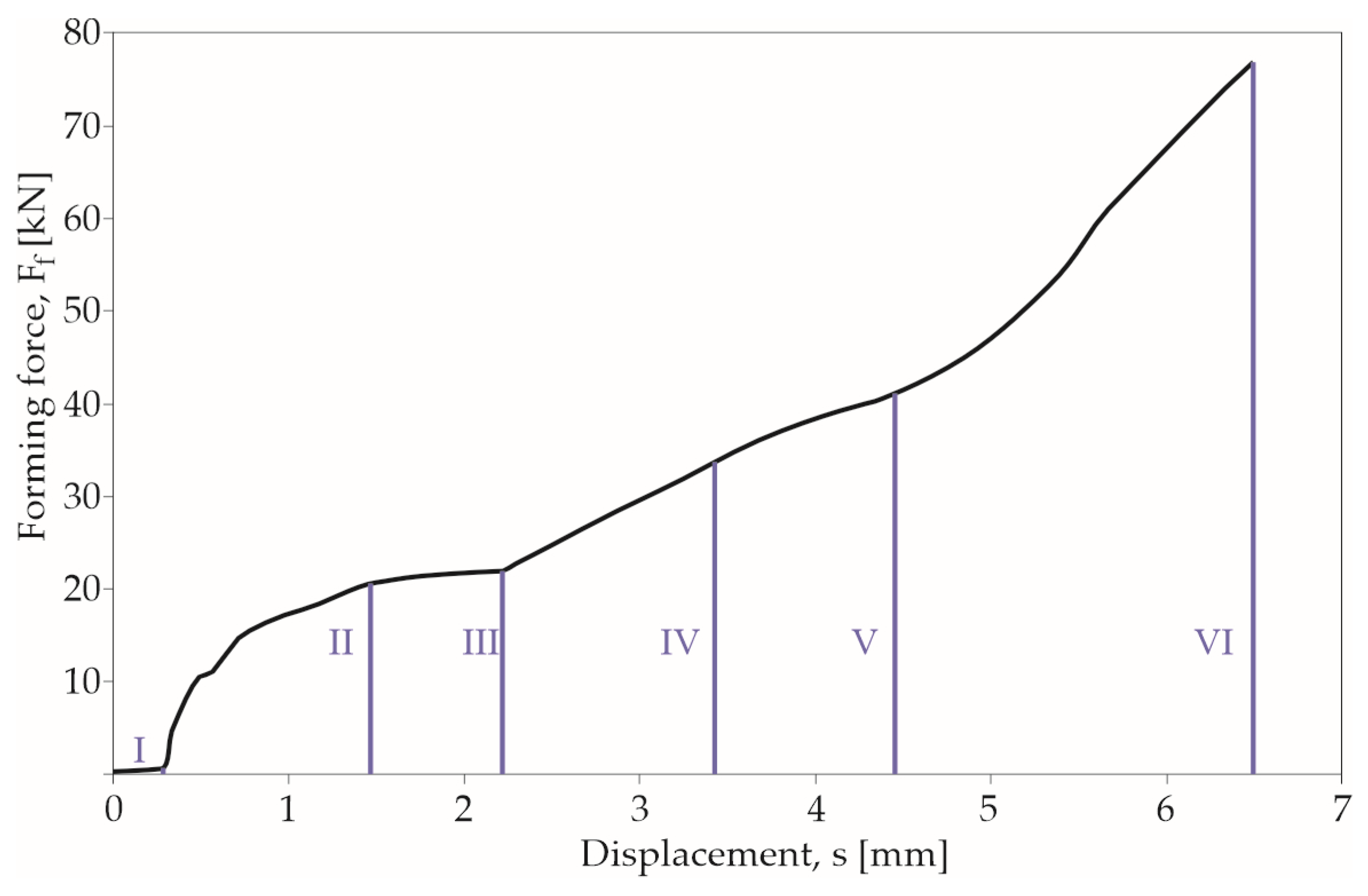
- Phase I—special rivet feeder with an automatic rivet insertion mechanism positions the rivet by the movement of the holder springs (at two levels);
- -
- Phase II—rivet contacts the upper sheet;
- -
- Phase III—rivet is pressed with sheets into the die groove;
- -
- Phase IV—the lower surface of the lower sheet touches the bottom surface of the die;
- -
- Phase V—the rivet material fills the free space formed after the movement of the sheet material in the die cavity and space formed after displacement of the die’s movable segments;
- -
- Phase VI—the rivet material flows intensively in its lower part in the transverse direction—the joint interlock is formed;
- -
- Phase VII—the punch system moves to basic point.
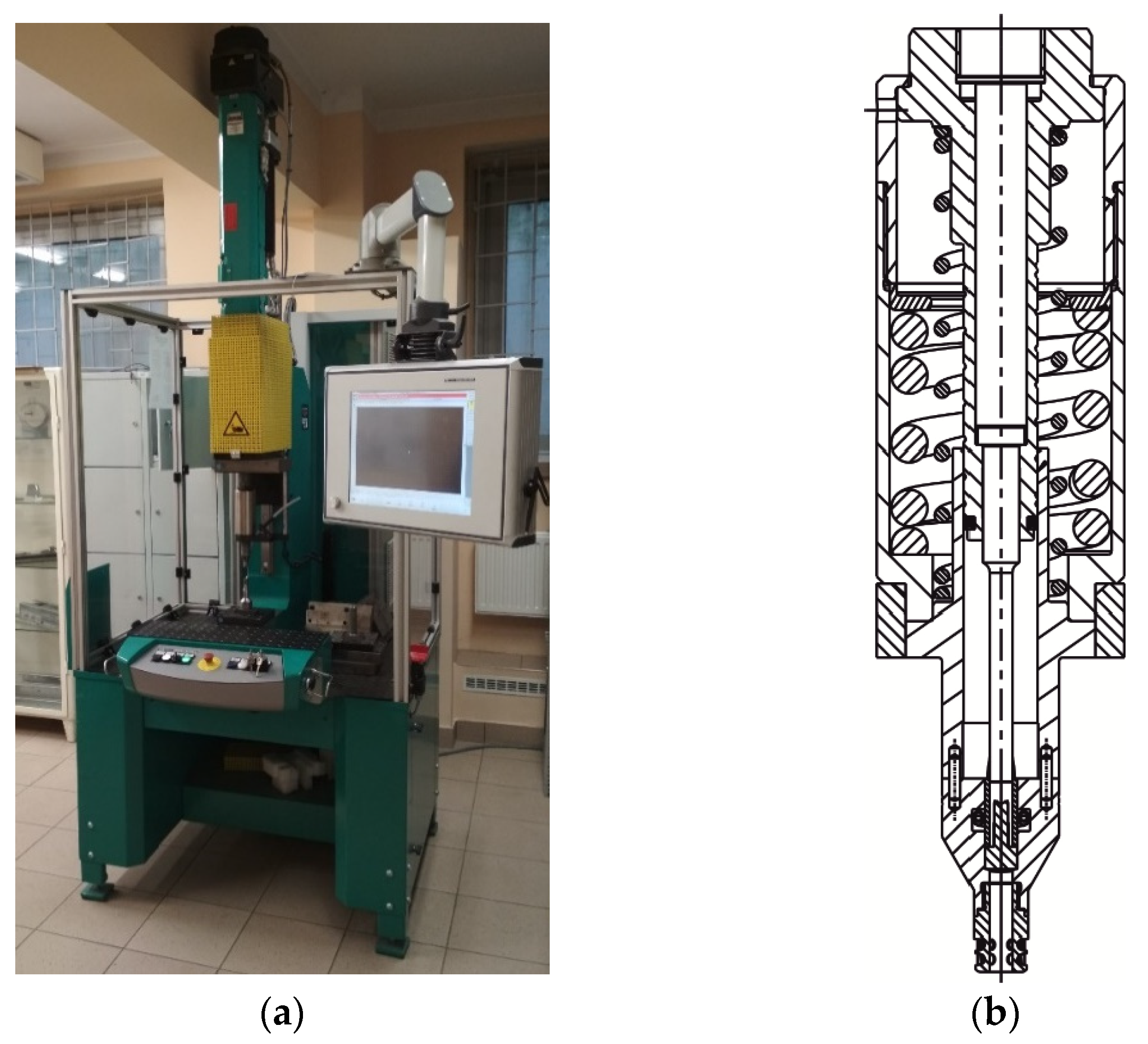
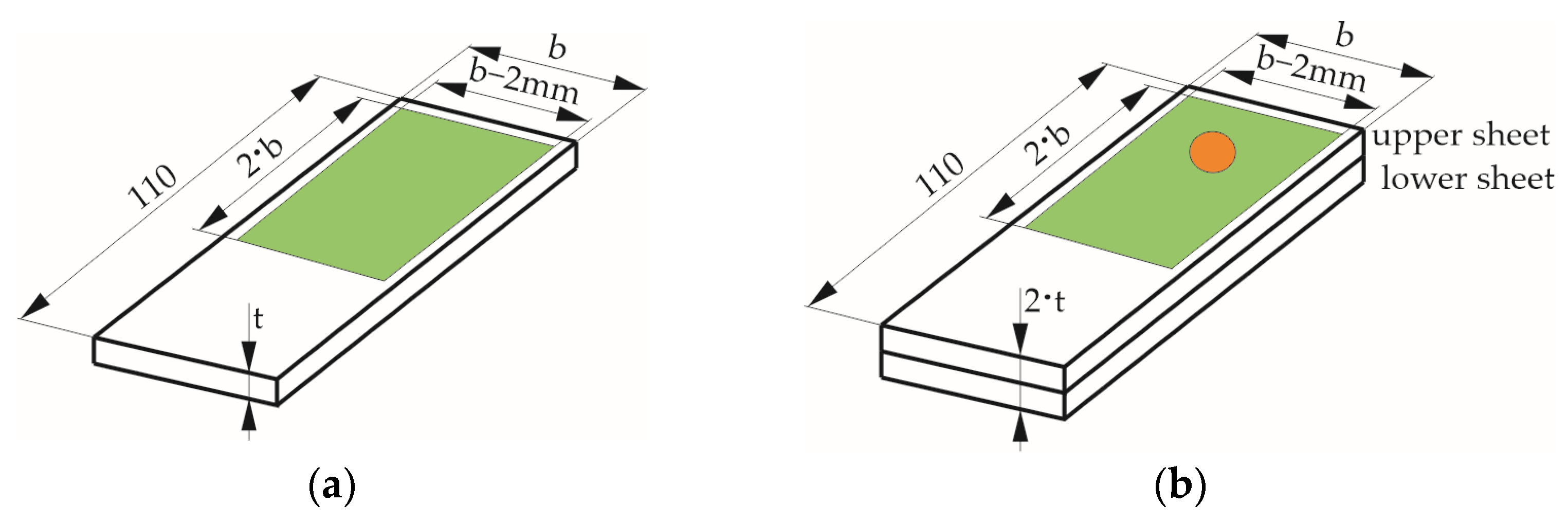
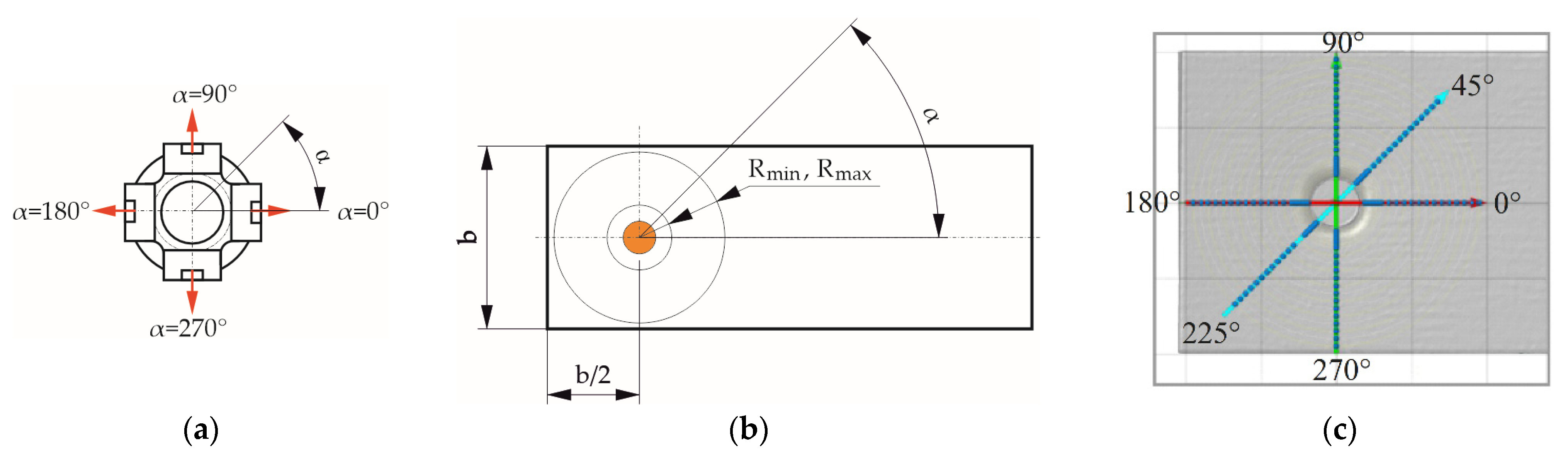
2.3. Sheet Deformation Measurements
3. Results and Discussion
3.1. Forming Process of the Clinch-Rivet Joint
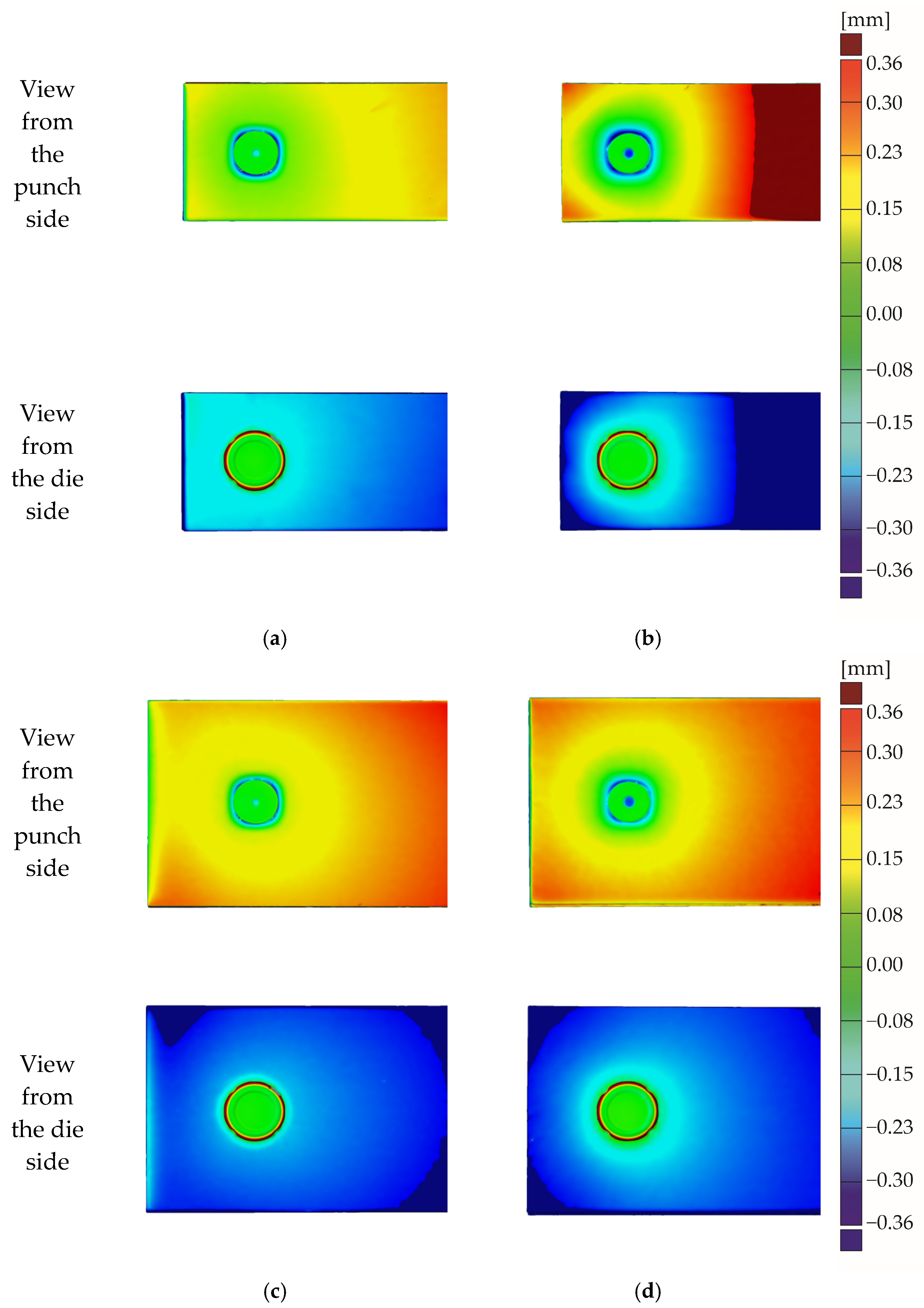
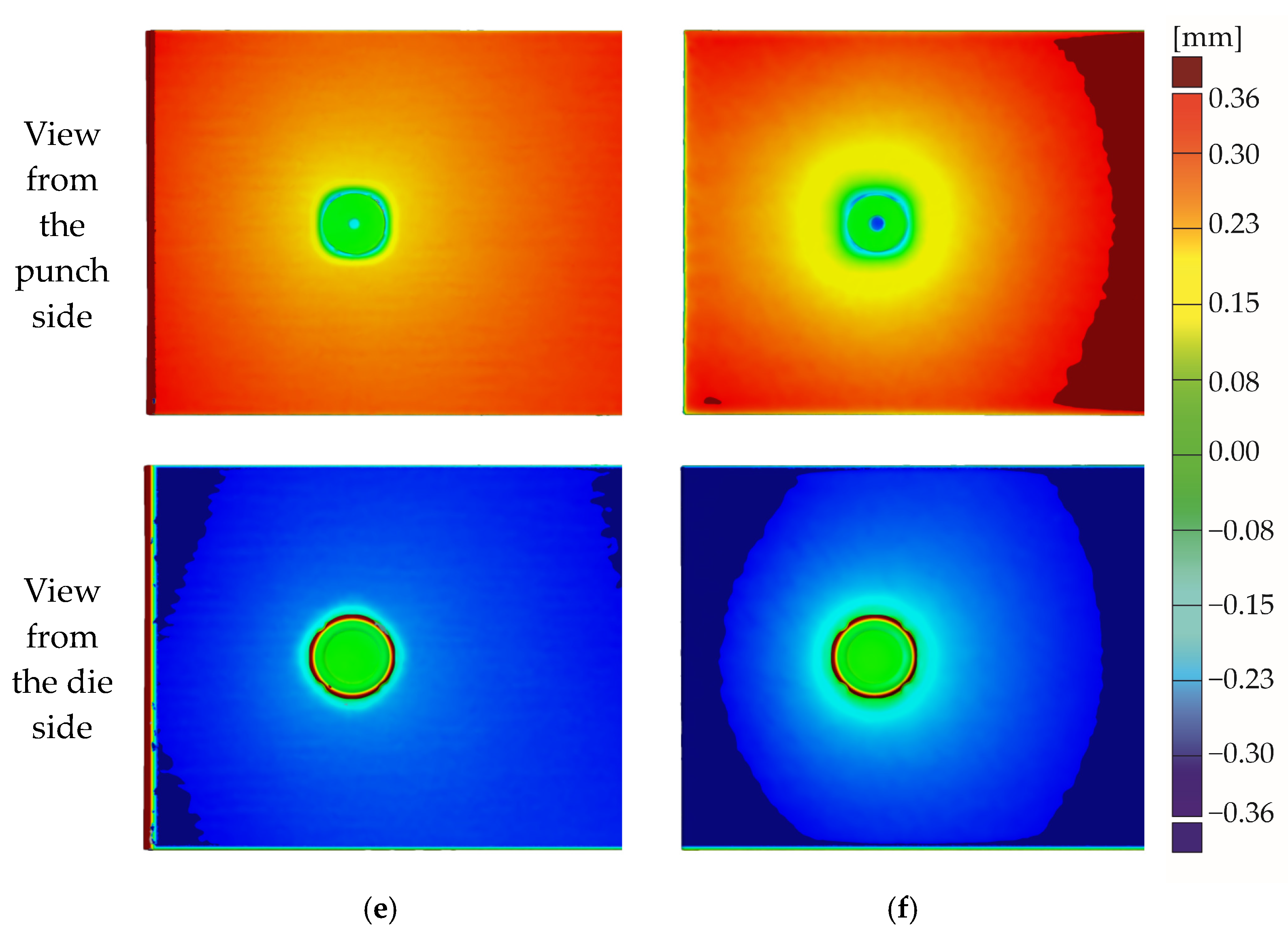
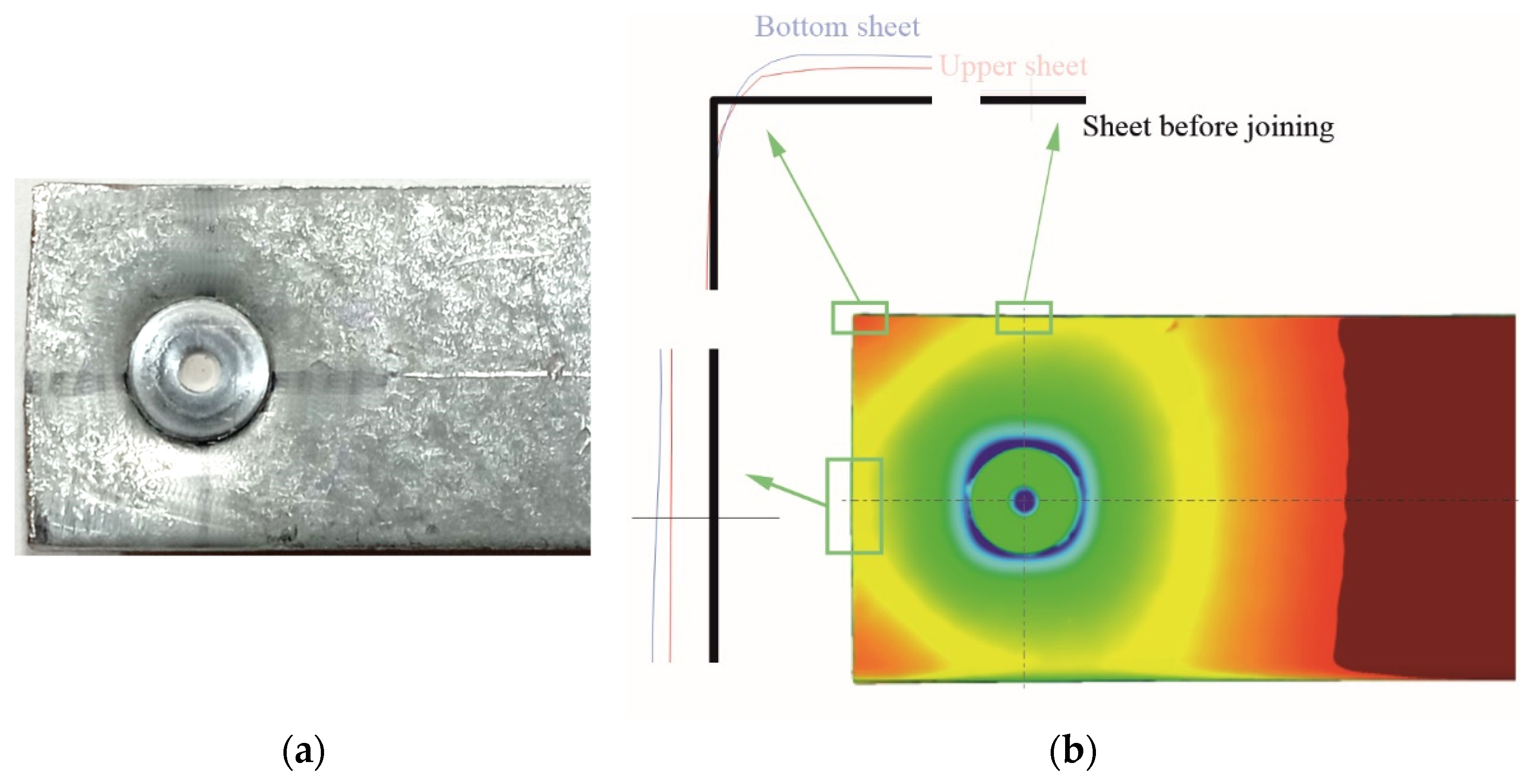
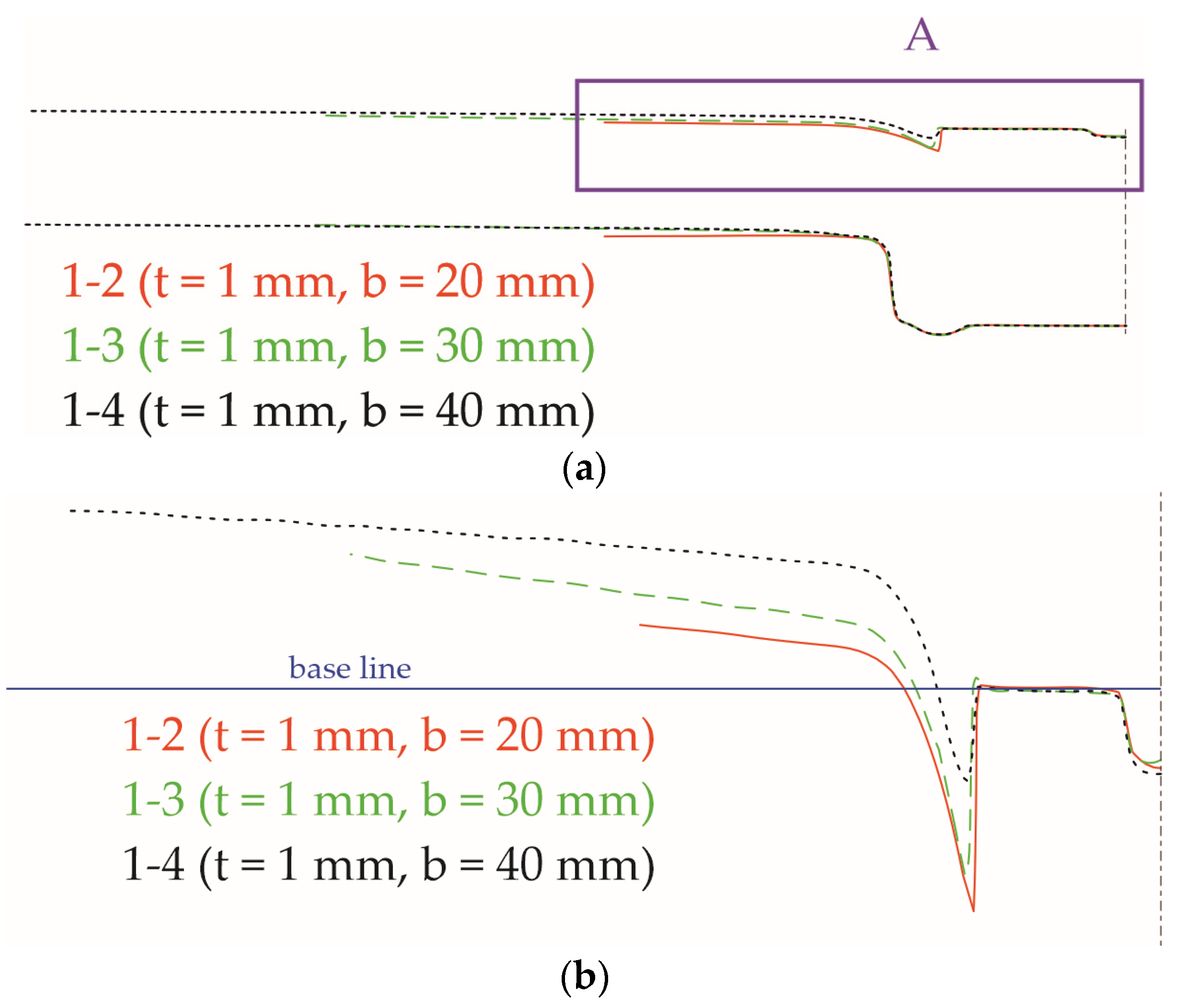
3.2. Sheet Deformation Measurement before Joining Process
3.3. Sheet Deformation Measurement after Joining Process
4. Conclusions
- The energy consumption of the forming force and the forming process can be reduced by reducing the distance between the joint axis and the edge of the sheet. The forming force was reduced by 2.95% for sheets with a thickness of 1 mm and by 2.65% for sheets with a thickness of 1.5 mm when the distance between the joint axis and the edge of the sheet was reduced from 20 mm to 10 mm.
- The deformation of a sheet depends on the angle between the movable segments and the edge of the sheet. For angles α = 0° and α = 180°, there were no differences in sheet deformation despite the fact that for 180°, there was less material at the sheet edge than for 0°.
- The differences in the sheet deformation for angles α = 45° and α = 225° are caused by the lower stiffness of the sheet from the closer edge (α = 225°).
- For a small distance between the joint axis and the edge of the sheet, the bulk can be obtained. For a sheet width of 20 mm and thicknesses of 1 mm and 1.5 mm, the material of the sheet was pushed more intensively in the radial directions for all angles except 0°—the sheet material along 0° blocked sheet deformation in that direction.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Leite, W.O.; Campos Rubio, J.C.; Mata, F.; Hanafi, I.; Carrasco, A. Dimensional and Geometrical Errors in Vacuum Thermoforming Products: An Approach to Modeling and Optimization by Multiple Response Optimization. Meas. Sci. Rev. 2018, 3, 113–122. [Google Scholar] [CrossRef]
- Valíček, J.; Harničárová, M.; Kušnerová, M.; Zavadil, J.; Grznárik, R. Method of Maintaining the Required Values of Surface Roughness and Prediction of Technological Conditions for Cold Sheet Rolling. Meas. Sci. Rev. 2014, 3, 144–151. [Google Scholar] [CrossRef]
- Hultman, H.; Cedergren, S.; Wärmefjord, K.; Söderberg, R. Predicting Geometrical Variation in Fabricated Assemblies Using a Digital Twin Approach Including a Novel Non-Nominal Welding Simulation. Aerospace 2022, 9, 512. [Google Scholar] [CrossRef]
- Meschut, G.; Janzen, V.; Olfermann, T. Innovative and Highly Productive Joining Technologies for Multi-Material Lightweight Car Body Structures. J. Mater. Eng. Perform. 2014, 23, 1515–1523. [Google Scholar] [CrossRef]
- Eckert, A.; Israel, M.; Neugebauer, R.; Rössinger, M.; Wahl, M.; Schulz, F. Local–global approach using experimental and/or simulated data to predict distortion caused by mechanical joining technologies. Prod. Eng. Res. Devel. 2013, 7, 339–349. [Google Scholar] [CrossRef]
- Varis, J.P.; Lepisto, J. A simple testing-based procedure and simulation of the clinching process using finite element analysis for establishing clinching parameters. Thin Wall. Struct. 2003, 41, 691–709. [Google Scholar] [CrossRef]
- Zheng, B.; Yu, H.; Lai, X. Assembly deformation prediction of riveted panels by using equivalent mechanical model of riveting process. Int. J. Adv. Manuf. Technol. 2017, 92, 1955–1966. [Google Scholar] [CrossRef]
- He, X.; Wang, Y.; Lu, Y.; Zeng, K.; Gu, F.; Ball, A. Self-piercing riveting of similar and dissimilar titanium sheet materials. Int. J. Adv. Manuf. Technol. 2015, 80, 2105–2115. [Google Scholar] [CrossRef]
- Xing, B.; He, X.; Zeng, K.; Wang, Y. Mechanical properties of self-piercing riveted joints in aluminum alloy 5052. Int. J. Adv. Manuf. Technol. 2014, 75, 351–361. [Google Scholar] [CrossRef]
- Zhang, X.; He, X.; Gu, F.; Ball, A. Self-piercing riveting of aluminium–lithium alloy sheet materials. J. Mater. Process. Technol. 2019, 268, 192–200. [Google Scholar] [CrossRef]
- Zhao, L.; He, X.; Xing, B.; Zhang, X.; Cheng, Q.; Gu, F.; Ball, A. Fretting behavior of self-piercing riveted joints in titanium sheet materials. J. Mater. Process. Technol. 2017, 249, 246–254. [Google Scholar] [CrossRef]
- Mucha, J.; Kaščák, L.; Spišák, E. Joining the car-body sheets using clinching process with various thickness and mechanical property arrangements. Arch. Civ. Mech. Eng. 2011, 1, 135–148. [Google Scholar] [CrossRef]
- Lee, C.-J.; Shen, G.; Kim, B.-M.; Lambiase, F.; Ko, D.-C. Analysis of failure-mode dependent joint strength in hole clinching from the aspects of geometrical interlocking parameters. Metals 2018, 8, 1020. [Google Scholar] [CrossRef]
- Zhang, Y.; He, X.; Wang, Y.; Lu, Y.; Gu, F.; Ball, A. Study on failure mechanism of mechanical clinching in aluminium sheet materials. Int. J. Adv. Manuf. Technol. 2018, 96, 3057–3068. [Google Scholar] [CrossRef]
- Abe, Y.; Kato, T.; Mori, K.-I.; Nishino, S. Mechanical clinching of ultra-high strength steel sheets and strength of joints. J. Mater. Process. Technol. 2014, 10, 2112–2118. [Google Scholar] [CrossRef]
- Ge, Y.; Xia, Y. Mechanical characterization of a steel-aluminum clinched joint under impact loading. Thin. Wall. Struct. 2020, 151, 106759. [Google Scholar] [CrossRef]
- Chen, C.; Zhao, S.; Cui, M.; Han, X.; Fan, S. Mechanical properties of the two-steps clinched joint with a clinch-rivet. J. Mater. Process. Technol. 2016, 237, 361–370. [Google Scholar] [CrossRef]
- Grimm, T.; Drossel, W.-G. Process development for self-pierce riveting with solid formable rivet of boron steel in multi-material design. Procedia Manuf. 2019, 29, 271–279. [Google Scholar] [CrossRef]
- Neugebauer, R.; Rössinger, M.; Wahl, M.; Schulz, F.; Eckert, A.; Schützle, W. Predicting Dimensional Accuracy of Mechanically Joined Car Body Assemblies. Key Eng. Mater. 2011, 473, 973–980. [Google Scholar] [CrossRef]
- Neugebauer, R.; Jesche, F.; Kraus, C.; Hensel, S. Mechanical joining with self piercing solid-rivets at elevated tool velocities. AIP Conf. Proc. 2011, 1353, 1278–1283. [Google Scholar]
- Mucha, J. The effect of material properties and joining process parameters on behavior of self-pierce riveting joints made with the solid rivet. Mater. Des. 2013, 52, 932–946. [Google Scholar] [CrossRef]
- Mucha, J. The failure mechanics analysis of the solid self-piercing riveting joints. Eng. Fail. Anal. 2015, 47, 77–88. [Google Scholar] [CrossRef]
- Neugebauer, R.; Jesche, F.; Israel, M. Enlargement of the application range of solid punch riveting by two-piece dies. Int. J. Mater. Form. 2010, 3, 999–1002. [Google Scholar] [CrossRef]
- Mucha, J.; Kaščák, Ľ.; Witkowski, W. Research on the influence of the AW 5754 aluminum alloy state condition and sheet arrangements with AW 6082 aluminum alloy on the forming process and strength of the clinch-rivet joints. Materials 2021, 14, 2980. [Google Scholar] [CrossRef]
- Mucha, J.; Boda, Ł.; Witkowski, W. Geometrical parameters and strength of clinching joint formed with the use of an additional rivet. Arch. Civ. Mech. Eng. 2023, 23, 114. [Google Scholar] [CrossRef]
- Ren, X.; Chen, C.; Ran, X.; Gao, X.; Gao, Y. Investigation on lightweight performance of tubular rivet-reinforced joints for joining AA5052 sheets. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 333. [Google Scholar] [CrossRef]
- Chen, C.; Wu, J.; Li, H. Optimization design of cylindrical rivet in flat bottom riveting. Thin. Wall. Struct. 2021, 168, 108292. [Google Scholar] [CrossRef]
- Mucha, J.; Boda, Ł.; Witkowski, W.; Poręba, M. Mixed-mode loading tests for determining the mechanical properties of clinched joints with an additional rivet used in the assembly of thin-walled structures. Thin Wall. Struct. 2023, 190, 110965. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, X.; Wen, C.; Yin, Y. Effect of blank holder force on joining quality of the flat clinch-rivet process. Int. J. Adv. Manuf. Technol. 2022, 121, 6315–6323. [Google Scholar] [CrossRef]
- Abe, Y.; Maeda, T.; Yoshioka, D.; Mori, K.-I. Mechanical clinching and self-pierce riveting of thin three sheets of 5000 series aluminium alloy and 980 MPa grade cold rolled ultra-high strength steel. Materials 2020, 13, 4741. [Google Scholar] [CrossRef]
- Mori, K.; Abe, Y.; Kato, T.; Sakai, S. Self-pierce riveting of three aluminium alloy and mild steel sheets. AIP Conf. Proc. 2010, 1252, 673–680. [Google Scholar]
- Abe, Y.; Kato, T.; Mori, K. Self-pierce riveting of three high strength steel and aluminium alloy sheets. Int. J. Mater. Form. 2008, 1, 1271–1274. [Google Scholar] [CrossRef]
- Kaščák, Ľ.; Spišák, E.; Majerníková, J. Joining three car body steel sheets by clinching method. Open Eng. 2016, 6, 566–573. [Google Scholar] [CrossRef]
- Kaščák, L.; Spišák, E.; Kubik, R.; Mucha, J. FEM analysis of clinching tool load in a joint of dual-phase steels. Strength Mater. 2016, 48, 533–539. [Google Scholar] [CrossRef]
- Karim, M.A.; Murugan, S.P.; Bae, K.; Baek, J.; Ji, C.; Noh, W.; Lee, H.J.; Jang, W.; Kim, D.B.; Park, Y.D. Effect of top sheet materials on joint performance of self-piercing riveting. J. Weld. Join. 2022, 6, 512–524. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, G.; Zheng, X.; Li, J.; Li, X.; Zhu, W.; Yanagimoto, J. A self-piercing riveting method for joining of continuous carbon fiber reinforced composite and aluminum alloy sheets. Compos. Struct. 2021, 259, 113219. [Google Scholar] [CrossRef]
- Sankaranarayanan, R.; Hynes, N.; Nikolova, M.P.; Królczyk, J.B. Self-pierce riveting: Development and assessment for joining polymer—Metal hybrid structures in lightweight automotive applications. Polymers 2023, 15, 4053. [Google Scholar] [CrossRef]
- Jäckel, M.; Grimm, T.; Niegsch, R.; Drossel, W.-G. Overview of current challenges in self-pierce riveting of lightweight materials. Proceedings 2018, 2, 384. [Google Scholar]
- Gröger, B.; Troschitz, J.; Vorderbrüggen, J.; Vogel, C.; Kupfer, R.; Meschut, G.; Gude, M. Clinching of thermoplastic composites and metals—A comparison of three novel joining technologies. Materials 2021, 9, 2286. [Google Scholar] [CrossRef] [PubMed]
- Galińska, A.; Galiński, C. Mechanical Joining of Fibre Reinforced Polymer Composites to Metals—A Review. Part II: Riveting, Clinching, Non-adhesive form-locked joints, pin and loop joining. Polymers 2020, 8, 1681. [Google Scholar] [CrossRef] [PubMed]
- Lambiase, F.; Scipioni, S.I.; Lee, C.-J.; Ko, D.-C.; Liu, F. A state-of-the-Art review on advanced joining processes for metal-Composite and metal-Polymer hybrid structures. Materials 2021, 8, 1890. [Google Scholar] [CrossRef]
- Lambiase, F. Mechanical behaviour of polymer–metal hybrid joints produced by clinching using different tools. Mater. Des. 2015, 87, 606–618. [Google Scholar] [CrossRef]
- Lambiase, F.; Durante, M. Mechanical behavior of punched holes produced on thin glass fiber reinforced plastic laminates. Compos. Struct. 2017, 173, 25–34. [Google Scholar] [CrossRef]
- Meschut, G.; Gude, M.; Augenthaler, F.; Geske, V. Evaluation of damage to carbon-fibre composites induced by self-pierce riveting. Procedia CIRP 2014, 18, 186–191. [Google Scholar] [CrossRef]
- Lambiase, F.; Paoletti, A. Friction-assisted clinching of aluminum and CFRP sheets. J. Manuf. Process. 2018, 31, 812–822. [Google Scholar] [CrossRef]
- Vorderbrüggen, J.; Köhler, D.; Grüber, B.; Troschitz, J.; Gude, M.; Meschut, G. Development of a rivet geometry for solid self-piercing riveting of thermally loaded CFRP-metal joints in automotive construction. Compos. Struct. 2022, 291, 115583. [Google Scholar] [CrossRef]
- Wiesenmayer, S.; Graser, M.; Merklein, M. Influence of the properties of the joining partners on the load-bearing capacity of shear-clinched joints. J. Mater. Process. Technol. 2020, 283, 116696. [Google Scholar] [CrossRef]
- Wiesenmayer, S.; Merklein, M. Potential of shear-clinching technology for joining of three sheets. J. Adv. Join. Process. 2021, 3, 100043. [Google Scholar] [CrossRef]
- Latorre, N.; Casellas, D.; Costa, J. A mechanical interlocking joint between sheet metal and carbon fibre reinforced polymers through punching. IOP Conf. Ser. Mater. Sci. Eng. 2023, 1284, 012001. [Google Scholar] [CrossRef]
- Lin, P.-C.; Fang, J.-C.; Lin, J.-W.; Tran, X.V.; Ching, Y.-C. Preheated (Heat-Assisted) Clinching Process for Al/CFRP Cross-Tension Specimens. Materials 2020, 13, 4170. [Google Scholar] [CrossRef] [PubMed]
- Witkowski, W.; Kurc, K. Shape deformation of the clinching joints upper sheet. Mechanik 2018, 91, 253–255. [Google Scholar] [CrossRef]
- Ren, X.; Chen, C.; Gao, X.; Qin, D.; Ouyang, Y. The effect of clinching process on mechanical properties of the single strap butt joint. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 134. [Google Scholar] [CrossRef]
- Tozaki, Y.; Uematsu, Y.; Tokaji, K. Effect of tool geometry on microstructure and static strength in friction stir spot welded aluminium alloys. Int. J. Mach. Tools Manuf. 2007, 47, 2230–2236. [Google Scholar] [CrossRef]
- Cai, W.; Lesperance, R.M.; Marin, S.P.; Meyer, W.W.; Oetjens, T.J. Digital Panel Assembly for Automotive Body-in-White. In Proceedings of the ASME 2002 International Mechanical Engineering Congress and Exposition, New Orleans, LA, USA, 17–22 November 2002; ASME: New York, NY, USA, 2008; pp. 453–466. [Google Scholar] [CrossRef]
- Cai, W.; Wang, P.C.; Yang, W. Assembly dimensional prediction for self-piercing riveted aluminum panels. Int. J. Mach. Tools Manuf. 2005, 45, 695–704. [Google Scholar] [CrossRef]
- Pinger, T.; Rückriem, E.M. Investigation on the corrosion and mechanical behavior of thin film batch galvanized thick plate components in clinch joints. Int. J. Adv. Manuf. Technol. 2016, 86, 29–36. [Google Scholar] [CrossRef]
- Mhawesh, Z.T.; Kara, İ.H.; Zeyvel, M. Corrosion resistance of interstitial free steel and Mg alloys sheets joined by mechanical clinching. J. Mater. Eng. Perform. 2023, 32, 2793–2800. [Google Scholar] [CrossRef]
- EN 10327:2004; Continuously Hot-Dip Coated Strip and Sheet of Low Carbon Steels for Cold Forming. Technical Delivery Conditions. CEN: Brussels, Belgium, 2004.
- ISO 6507-1:2018; Metallic Materials—Vickers Hardness Test—Part 1: Test Method. Technical Committee ISO/TC 164, Mechanical Testing of Metals, Subcommittee SC 3, Hardness Testing. ISO: Geneva, Switzerland, 2018.
- VDI/VDE 2634-3:2008-12; Optical 3D-Measuring Systems—Multiple View Systems Based on Area Scanning. Beuth Verlag GmbH: Berlin, Germany, 2008.
- Boda, Ł.; Mucha, J.; Witkowski, W. Performance Tests of HX340 Microalloyed Steel Sheets Joined Using Clinch-Rivet Technology. Materials 2024, 17, 596. [Google Scholar] [CrossRef]












| Material Designation | Surface Finish + Z [g/m2] | Young’s Modulus E [GPa] | Poisson’s Ratio ν [–] | Yield Strength Rp0.2 [MPa] | Tensile Strength Rm [MPa] | Elongation after Fracture A80 [%] |
|---|---|---|---|---|---|---|
| DX51D+Z275 | zinc layer quality 275 | 188 | 0.3 | 330 | 438 | 29 |
| Mn | Si | Ti | C | P | S | Fe |
|---|---|---|---|---|---|---|
| 1.2 | 0.5 | 0.3 | 0.18 | 0.12 | 0.045 | rest |
| Sheet Width b [mm] | Sheet Thickness t [mm] | Rmin [mm] | Rmax [mm] |
|---|---|---|---|
| 20 | 1 | 3.75 | 9 |
| 30 | 1 | 3.75 | 14 |
| 40 | 1 | 3.75 | 19 |
| 20 | 1.5 | 3.75 | 9 |
| 30 | 1.5 | 3.75 | 14 |
| 40 | 1.5 | 3.75 | 19 |
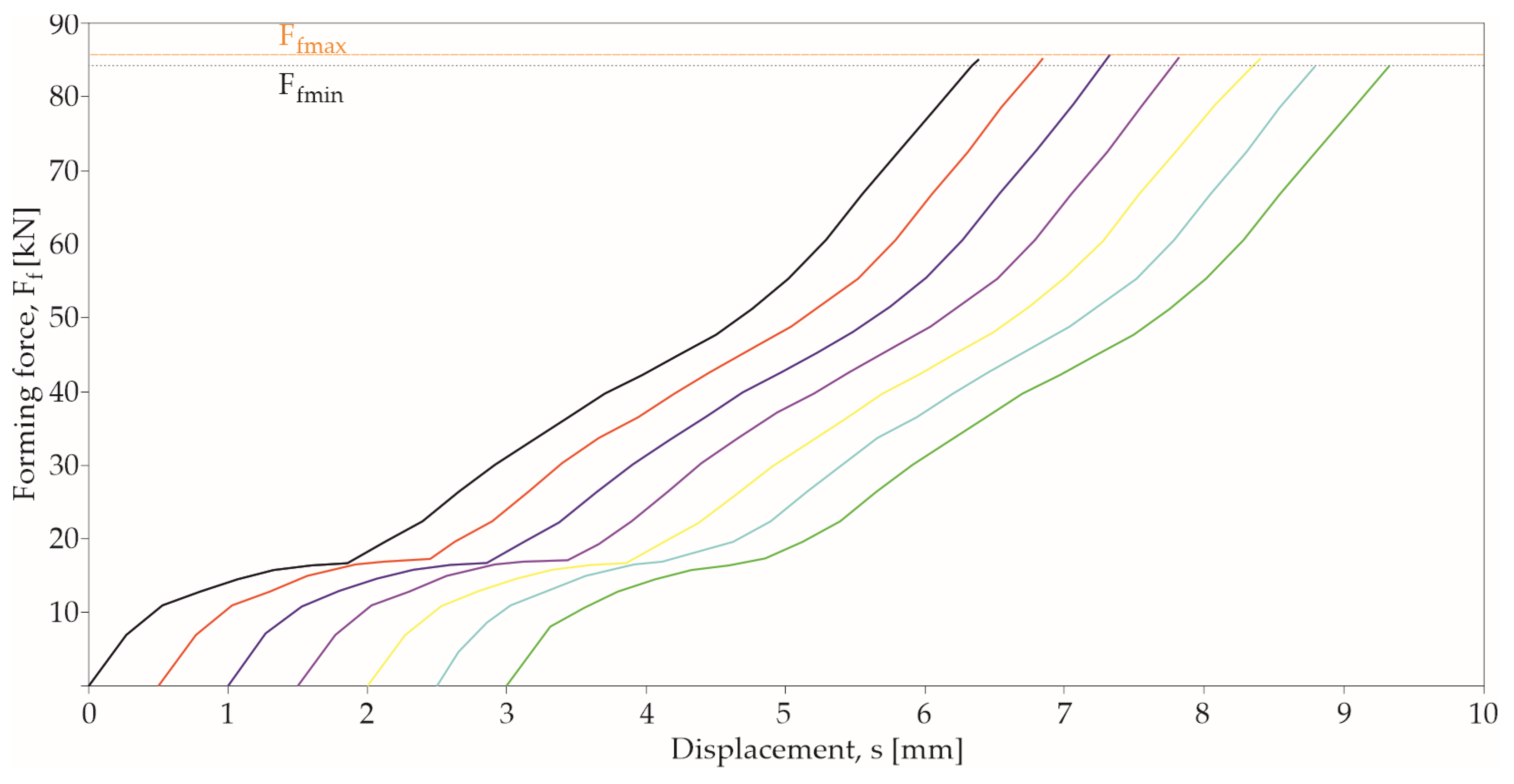
| Sample Nomenclature | Sheet Width b [mm] | Sheet Thickness t [mm] | Forming Force Ff [kN] | Standard Deviation s [kN] | Coefficient of Variation cv [%] | Forming Energy Ef [J] |
|---|---|---|---|---|---|---|
| 1-2 | 20 | 1 | 85.18 | 0.398 | 0.467 | 232 |
| 1-3 | 30 | 1 | 87.35 | 0.397 | 0.454 | 236 |
| 1-4 | 40 | 1 | 87.77 | 0.426 | 0.485 | 237 |
| 2-2 | 20 | 1.5 | 72.32 | 0.398 | 0.550 | 210 |
| 2-3 | 30 | 1.5 | 74.57 | 0.356 | 0.477 | 218 |
| 2-4 | 40 | 1.5 | 74.29 | 0.416 | 0.560 | 213 |
| Measured Parameter | Values |
|---|---|
| Sheet thickness t [mm] | 1 |
| Manufacturer sheet thickness tolerance [mm] | ±0.07 |
| Measured sheet thickness [mm] | 0.98 |
| Sheet width b [mm] | 20, 30, 40 |
| Sheet width tolerance [mm] | ±0.1 |
| Measured sheet width [mm] | 20.07, 30.05, 40.03 |
| Sheet thickness t [mm] | 1.5 |
| Manufacturer sheet thickness tolerance [mm] | ±0.11 mm |
| Measured sheet thickness [mm] | 1.45 |
| Sheet width b [mm] | 20, 30, 40 |
| Sheet width tolerance [mm] | ±0.1 |
| Measured sheet width [mm] | 20.05, 30.06, 40.03 |
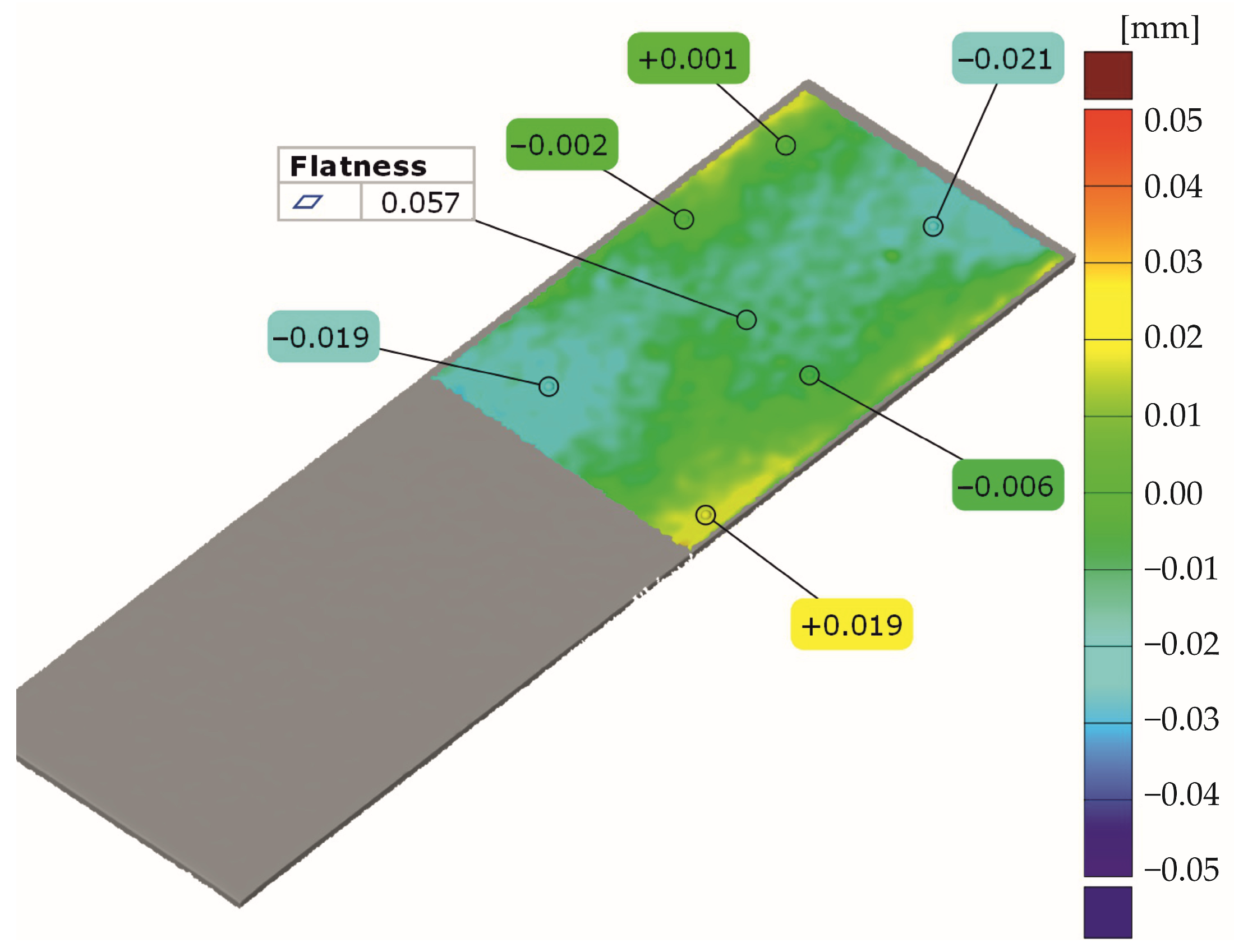
| Adjustment Result | Sheet Dimensions b × t [mm × mm] | ||||||
|---|---|---|---|---|---|---|---|
| 20 × 1 | 30 × 1 | 40 × 1 | 20 × 1.5 | 30 × 1.5 | 40 × 1.5 | ||
| Fitting plane (axis Z = 0.0 mm) | Minimum mm | −0.031 | −0.004 | −0.005 | −0.0036 | −0.0045 | −0.0049 |
| Maximum mm | 0.0045 | 0.0068 | 0.0073 | 0.0041 | 0.0058 | 0.0046 | |
| Sigma mm | 0.002 | 0.0029 | 0.0036 | 0.0022 | 0.0029 | 0.0028 | |
| Residual mm | 0.0017 | 0.0024 | 0.0031 | 0.0019 | 0.0024 | 0.0025 | |
| Number of nodes for base creation | 608 | 691 | 904 | 521 | 568 | 631 | |
| Fitting torus (axes X = 0.0. Y = 0.0 mm) | Minimum mm | −0.0187 | −0.0219 | −0.0142 | −0.0196 | −0.0297 | −0.0187 |
| Maximum mm | 0.0197 | 0.0216 | 0.0103 | 0.0128 | 0.0148 | 0.0139 | |
| Sigma mm | 0.0069 | 0.074 | 0.0049 | 0.0062 | 0.0086 | 0.0068 | |
| Residual mm | 0.0054 | 0.0057 | 0.0039 | 0.0049 | 0.0065 | 0.0053 | |
| Sample Nomenclature | 1-2 | 1-3 | 1-4 | 2-2 | 2-3 | 2-4 |
| Sheet thickness t [mm] | 1 | 1 | 1 | 1.5 | 1.5 | 1.5 |
| Sheet width b [mm] | 20 | 30 | 40 | 20 | 30 | 40 |
| Lower sheet dimension for angle 90° and 270° | 0.29 | 0.04 | 0.02 | 0.03 | 0.01 | 0.01 |
| Upper sheet dimension for angle 90° and 270° | 0.14 | 0.03 | 0.01 | 0.01 | 0.02 | 0.01 |
| Lower sheet dimension for angle 180° | 0.11 | 0.03 | 0.03 | 0.02 | 0.01 | 0.01 |
| Upper sheet dimension for angle 180° | 0.09 | 0.02 | 0.03 | 0.02 | 0.01 | 0.01 |
| Average sheet width before joining [mm] | 20.07 | 30.05 | 40.03 | 20.05 | 30.06 | 40.03 |
| Sheet thickness t [mm] | 1 | 1 | 1 | 1 | 1 | 1 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 |
| Measurement angle α [°] | 0° | 45° | 90° | 180° | 225° | 270° | 0° | 45° | 90° | 180° | 225° | 270° |
| Values of the point deviations | ||||||||||||
| Measurement radius R [mm] | ||||||||||||
| 3.75 | 0.08 | −0.03 | 0.03 | 0.06 | −0.05 | 0.07 | 0.02 | -0.07 | -0.02 | 0.01 | -0.06 | 0.02 |
| 4.00 | 0.14 | 0.05 | 0.10 | 0.13 | 0.05 | 0.14 | 0.05 | -0.01 | 0.02 | 0.05 | -0.01 | 0.05 |
| 4.25 | 0.17 | 0.11 | 0.14 | 0.17 | 0.11 | 0.18 | 0.08 | 0.02 | 0.05 | 0.07 | 0.03 | 0.08 |
| 4.50 | 0.19 | 0.15 | 0.17 | 0.19 | 0.15 | 0.2 | 0.10 | 0.05 | 0.07 | 0.09 | 0.05 | 0.10 |
| 4.75 | 0.20 | 0.17 | 0.19 | 0.20 | 0.18 | 0.21 | 0.11 | 0.08 | 0.09 | 0.10 | 0.07 | 0.11 |
| 5.00 | 0.21 | 0.19 | 0.20 | 0.20 | 0.20 | 0.22 | 0.13 | 0.09 | 0.10 | 0.11 | 0.09 | 0.13 |
| 5.25 | 0.21 | 0.19 | 0.20 | 0.21 | 0.21 | 0.22 | 0.13 | 0.11 | 0.11 | 0.12 | 0.1 | 0.14 |
| 5.50 | 0.21 | 0.20 | 0.20 | 0.21 | 0.21 | 0.22 | 0.14 | 0.12 | 0.12 | 0.13 | 0.12 | 0.14 |
| 5.75 | 0.21 | 0.20 | 0.20 | 0.21 | 0.22 | 0.22 | 0.15 | 0.13 | 0.13 | 0.13 | 0.13 | 0.15 |
| 6.00 | 0.21 | 0.20 | 0.20 | 0.22 | 0.22 | 0.22 | 0.15 | 0.14 | 0.14 | 0.14 | 0.13 | 0.15 |
| 7.00 | 0.22 | 0.21 | 0.21 | 0.22 | 0.22 | 0.23 | 0.17 | 0.16 | 0.16 | 0.16 | 0.16 | 0.17 |
| 8.00 | 0.23 | 0.22 | 0.22 | 0.23 | 0.24 | 0.24 | 0.19 | 0.18 | 0.18 | 0.18 | 0.18 | 0.19 |
| 9.00 | 0.24 | 0.23 | 0.23 | 0.24 | 0.24 | 0.24 | 0.21 | 0.20 | 0.19 | 0.20 | 0.20 | 0.20 |
| 10.00 | 0.24 | 0.23 | 0.24 | 0.25 | 0.25 | 0.25 | 0.22 | 0.22 | 0.21 | 0.21 | 0.22 | 0.22 |
| 11.00 | 0.25 | 0.24 | 0.24 | 0.26 | 0.26 | 0.26 | 0.23 | 0.22 | 0.22 | 0.22 | 0.23 | 0.23 |
| 12.00 | 0.25 | 0.24 | 0.25 | 0.27 | 0.27 | 0.26 | 0.24 | 0.24 | 0.24 | 0.23 | 0.24 | 0.24 |
| 13.00 | 0.26 | 0.25 | 0.25 | 0.27 | 0.27 | 0.27 | 0.26 | 0.25 | 0.25 | 0.24 | 0.26 | 0.25 |
| 14.00 | 0.27 | 0.26 | 0.26 | 0.28 | 0.28 | 0.27 | 0.27 | 0.26 | 0.26 | 0.25 | 0.26 | 0.26 |
| 15.00 | 0.27 | 0.26 | 0.26 | 0.29 | 0.29 | 0.27 | 0.28 | 0.27 | 0.27 | 0.26 | 0.27 | 0.27 |
| 16.00 | 0.27 | 0.27 | 0.27 | 0.3 | 0.29 | 0.28 | 0.29 | 0.28 | 0.28 | 0.27 | 0.29 | 0.28 |
| 17.00 | 0.28 | 0.27 | 0.27 | 0.3 | 0.3 | 0.28 | 0.3 | 0.29 | 0.29 | 0.28 | 0.29 | 0.29 |
| 18.00 | 0.29 | 0.28 | 0.27 | 0.31 | 0.3 | 0.29 | 0.31 | 0.3 | 0.3 | 0.28 | 0.3 | 0.3 |
| 19.00 | 0.29 | 0.28 | 0.28 | 0.32 | 0.31 | 0.29 | 0.32 | 0.31 | 0.31 | 0.26 | 0.31 | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Witkowski, W.; Mucha, J.; Boda, Ł. Steel Sheet Deformation in Clinch-Riveting Joining Process. Metals 2024, 14, 367. https://doi.org/10.3390/met14030367
Witkowski W, Mucha J, Boda Ł. Steel Sheet Deformation in Clinch-Riveting Joining Process. Metals. 2024; 14(3):367. https://doi.org/10.3390/met14030367
Chicago/Turabian StyleWitkowski, Waldemar, Jacek Mucha, and Łukasz Boda. 2024. "Steel Sheet Deformation in Clinch-Riveting Joining Process" Metals 14, no. 3: 367. https://doi.org/10.3390/met14030367
APA StyleWitkowski, W., Mucha, J., & Boda, Ł. (2024). Steel Sheet Deformation in Clinch-Riveting Joining Process. Metals, 14(3), 367. https://doi.org/10.3390/met14030367







