First Principles Study of the Effects of Si, P, and S on the ∑5 (210)[001] Grain Boundary of γ-Fe
Abstract
:1. Introduction
2. Methodology
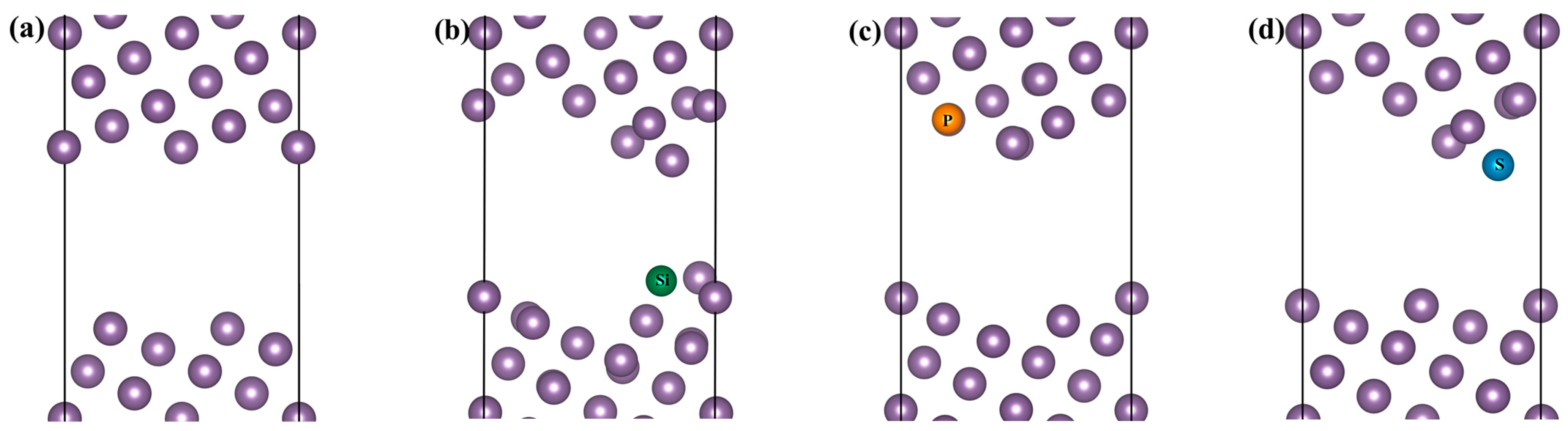
2.1. Computational Model
2.2. Computational Details
3. Results and Discussion
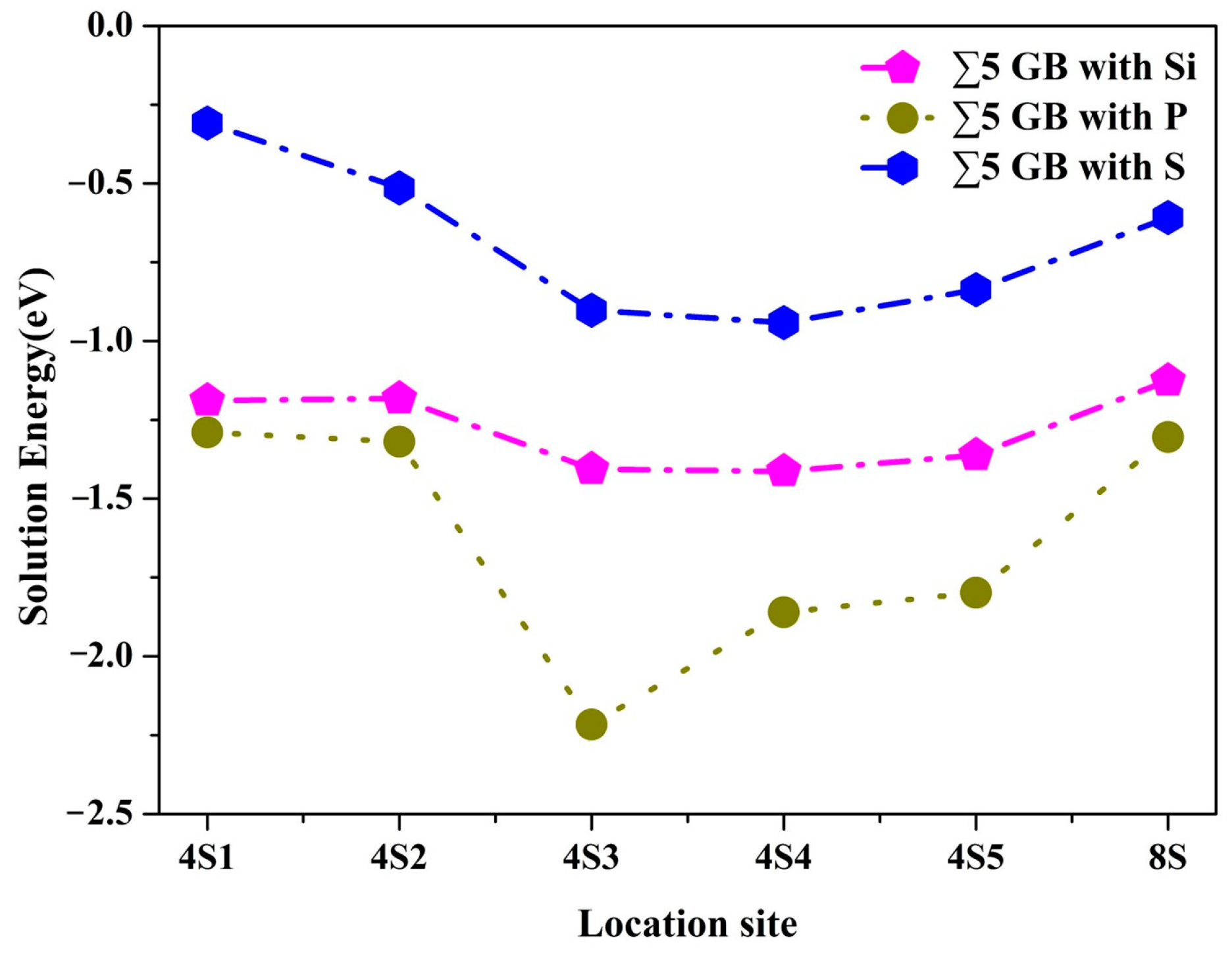
3.1. Site Preference
3.2. Segregation Behavior
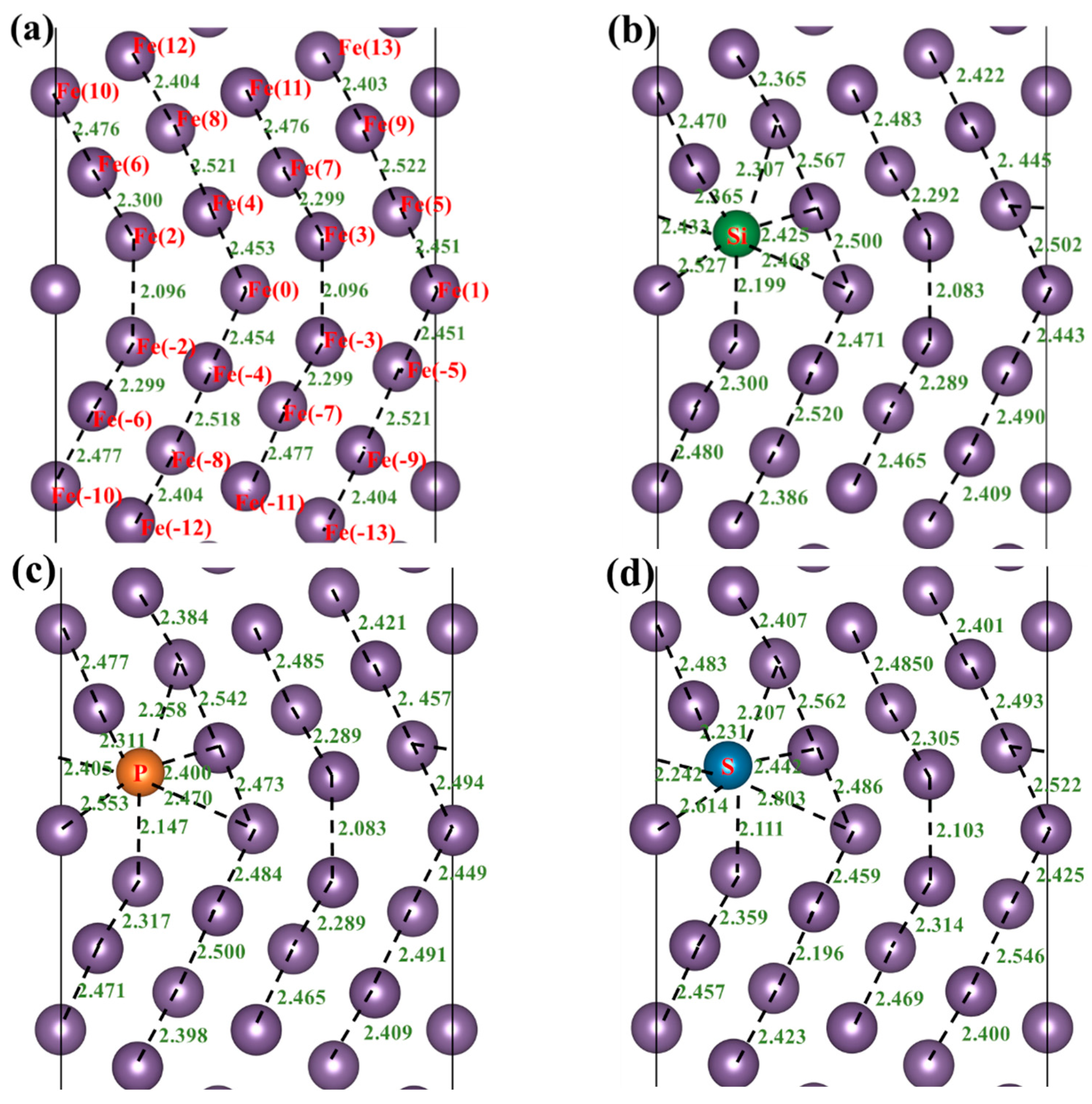
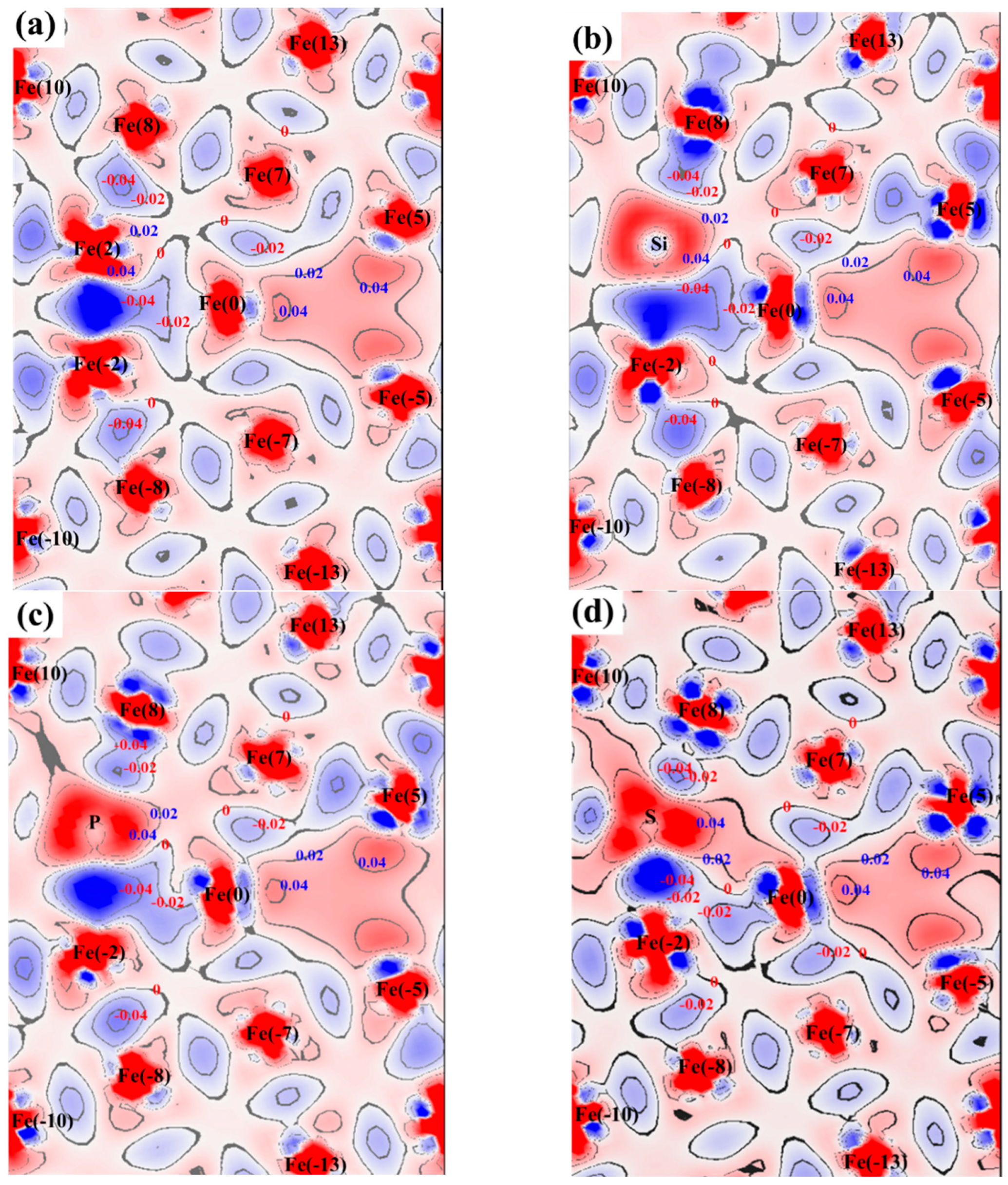
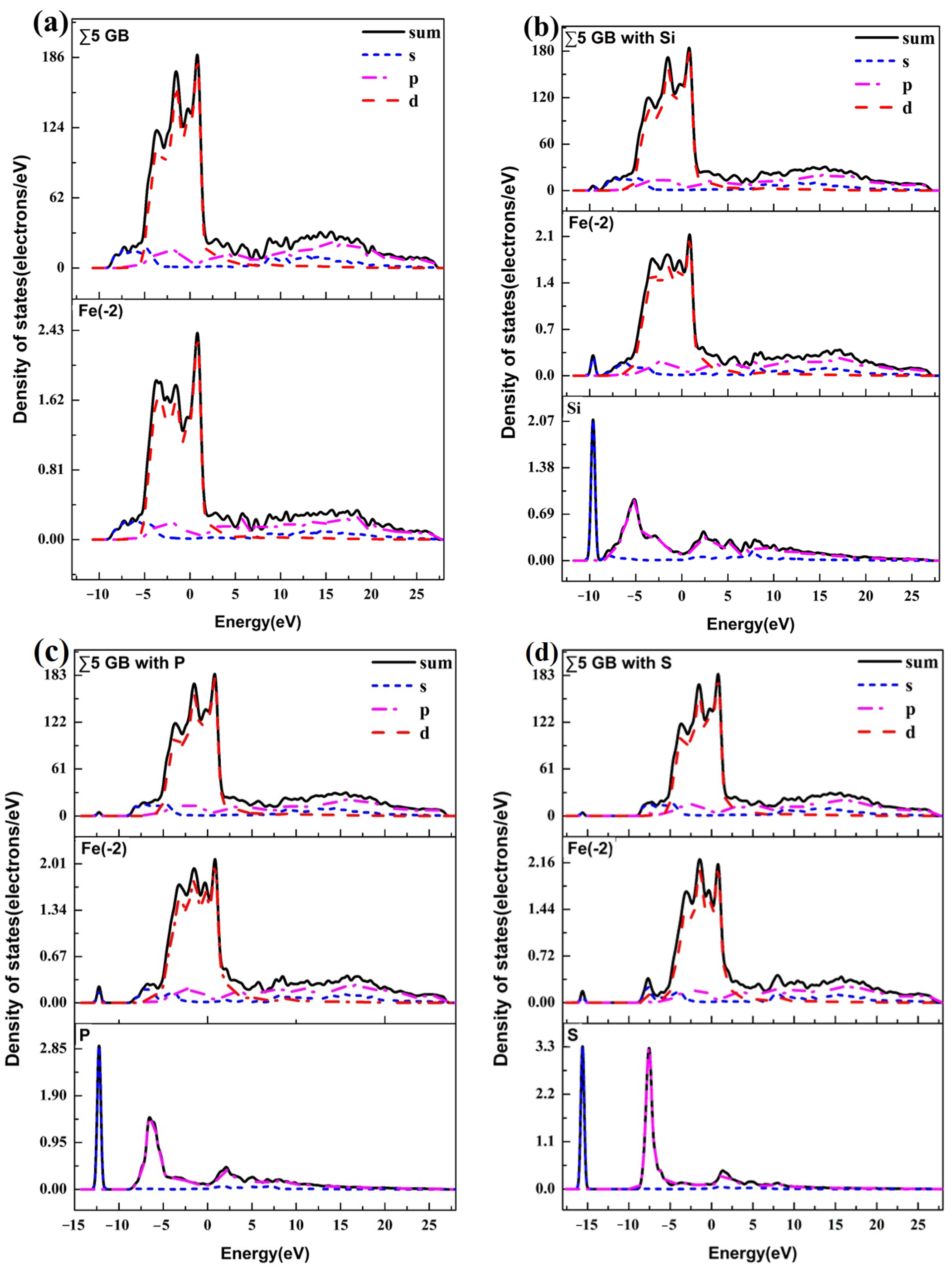
3.3. Atomic Configuration and Electron Distribution
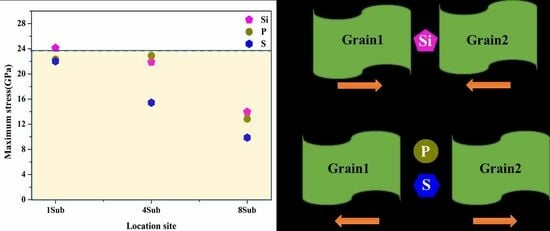
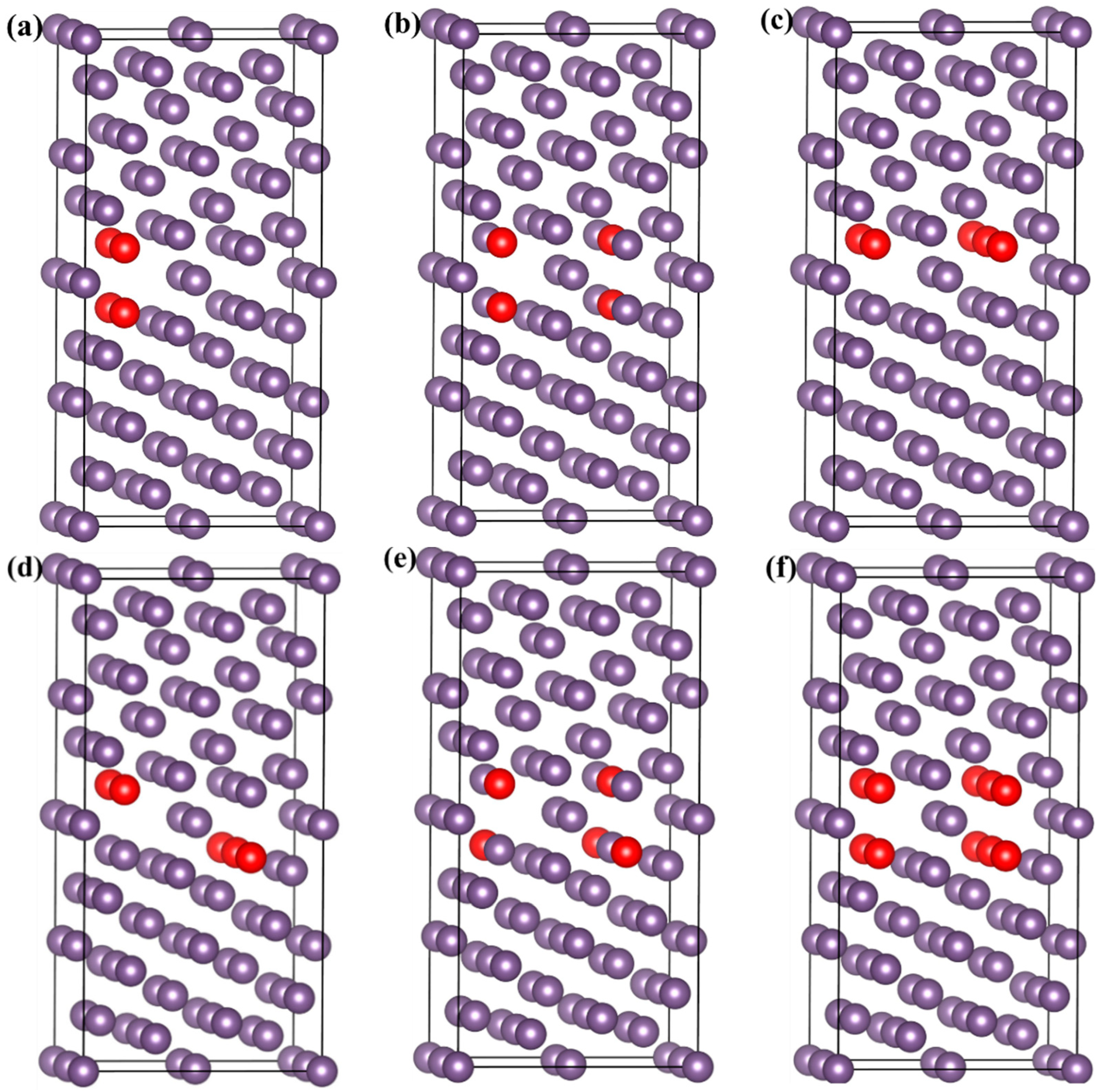
3.4. Strengthening Energies and Tensile Tests
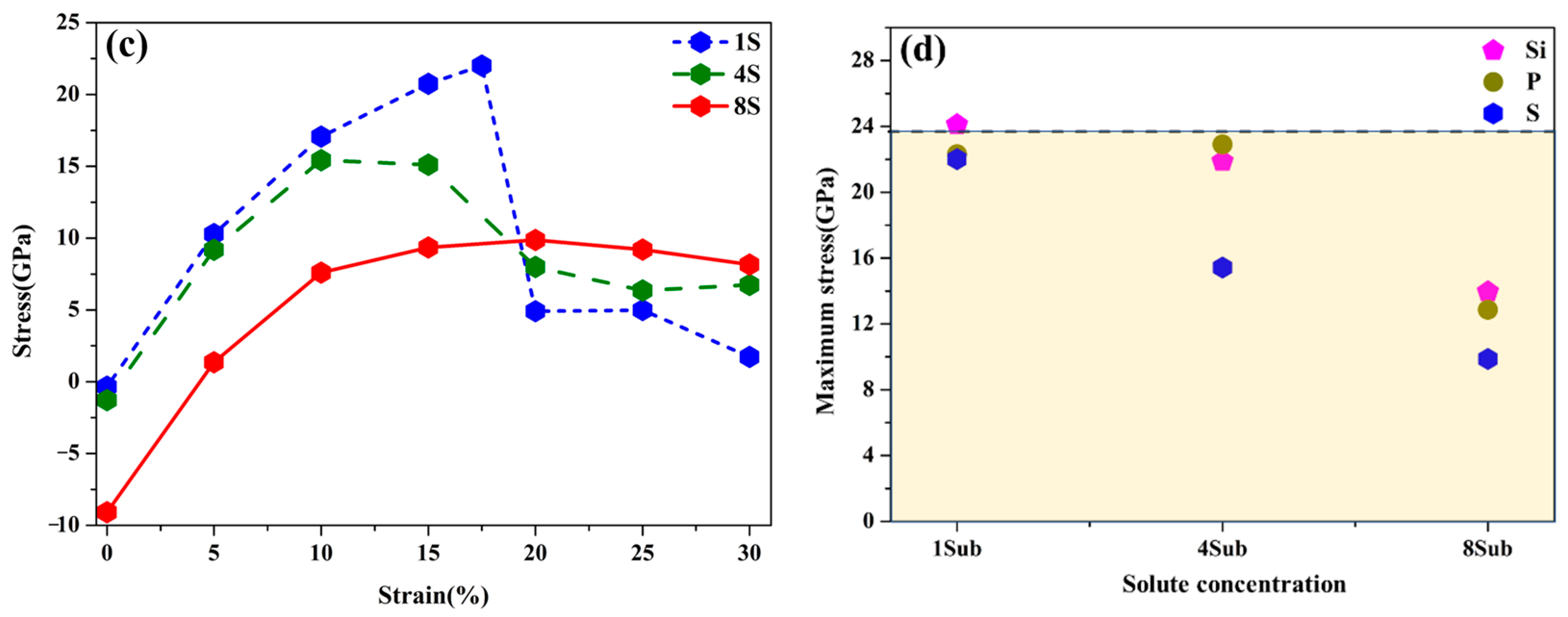
3.5. Effects of Si, P, and S Concentrations on the GB
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tokita, S.; Kokawa, H.; Sato, Y.S.; Fujii, H.T. In situ EBSD observation of grain boundary character distribution evolution during thermomechanical process used for grain boundary engineering of 304 austenitic stainless steel. Mater. Charact. 2017, 131, 31–38. [Google Scholar] [CrossRef]
- Sabzi, H.E.; Hernandez-Nava, E.; Li, X.-H.; Fu, H.; San-Martín, D.; Rivera-Díaz-del-Castillo, P.E.J. Strengthening control in laser powder bed fusion of austenitic stainless steels via grain boundary engineering. Mater. Design 2021, 212, 110246. [Google Scholar] [CrossRef]
- Shimada, M.; Kokawa, H.; Wang, Z.J.; Sato, Y.S.; Karibe, I. Optimization of grain boundary character distribution for intergranular corrosion resistant 304 stainless steel by twin-induced grain boundary engineering. Acta Mater. 2002, 50, 2331–2341. [Google Scholar] [CrossRef]
- Shang, B.; Lei, L.; Wang, X.; He, P.; Yuan, X.; Dai, W.; Li, J.; Jiang, Y.; Sun, Y. Effects of grain boundary characteristics changing with cold rolling deformation on intergranular corrosion resistance of 443 ultra-pure ferritic stainless steel. Corros. Commun. 2022, 8, 27–39. [Google Scholar] [CrossRef]
- Zhuo, Z.; Xia, S.; Bai, Q.; Zhou, B. The effect of grain boundary character distribution on the mechanical properties at different strain rates of a 316L stainless steel. J. Mater. Sci. 2017, 53, 2844–2858. [Google Scholar] [CrossRef]
- Liu, T.; Hui, J.; Zhang, B.; He, X.; Liu, M.; Qiu, J.; Liu, W. Corrosion mechanism of lead-bismuth eutectic at grain boundary in ferritic steels and the effect of alloying elements: A first-principles study. J. Nucl. Mater. 2022, 569, 153915. [Google Scholar] [CrossRef]
- Peng, H.R.; Huo, W.T.; Zhang, W.; Tang, Y.; Zhang, S.; Huang, L.K.; Hou, H.Y.; Ding, Z.G.; Liu, F. Correlation between stabilizing and strengthening effects due to grain boundary segregation in iron-based alloys: Theoretical models and first-principles calculations. Acta Mater. 2023, 251, 118899. [Google Scholar] [CrossRef]
- Hu, Y.-J.; Wang, Y.; Wang, W.Y.; Darling, K.A.; Kecskes, L.J.; Liu, Z.-K. Solute effects on the Σ3 111[11-0] tilt grain boundary in BCC Fe: Grain boundary segregation, stability, and embrittlement. Comp. Mater. Sci. 2020, 171, 109271. [Google Scholar] [CrossRef]
- Niu, M.C.; Chen, C.J.; Li, W.; Yang, K.; Luan, J.H.; Wang, W.; Jiao, Z.B. Atomic-scale understanding of solute interaction effects on grain boundary segregation, precipitation, and fracture of ultrahigh-strength maraging steels. Acta Mater. 2023, 253, 118972. [Google Scholar] [CrossRef]
- Ito, K.; Tanaka, Y.; Tsutsui, K.; Omura, T. Effect of Mo addition on hydrogen segregation at α-Fe grain boundaries: A first-principles investigation of the mechanism by which Mo addition improves hydrogen embrittlement resistance in high-strength steels. Comp. Mater. Sci. 2023, 218, 111951. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, Y.; Ren, J.; Dong, N.; Zhang, C.; Ma, J.; Jiang, Z.; Li, H.; Han, P. Effect of Mo and Cr on S-induced intergranular fracture in γ-Fe. Metals 2022, 12, 1606. [Google Scholar] [CrossRef]
- Ito, K.; Tanaka, Y.; Mitsunobu, T.; Kohtake, T.; Tsutsui, K.; Sawada, H. First-principles computational tensile test of γ-Fe grain boundaries considering the effect of magnetism: Electronic origin of grain boundary embrittlement due to Zn segregation. Phys. Rev. Mater. 2022, 6, 053604. [Google Scholar] [CrossRef]
- Peng, W.; Peng, H.; Wu, G.; Zhang, J. Effect of zinc-doping on tensile strength of Σ5 bcc Fe symmetric tilt grain boundary. Comp. Mater. Sci. 2020, 171, 109204. [Google Scholar] [CrossRef]
- Wang, J.; Yang, X.; Qian, R.; Rong, X.; Xie, Z.; Shang, C. First-Principles Study of B segregation at austenite grain boundary and its effect on the hardenability of low-alloy steels. Metals 2022, 12, 2006. [Google Scholar] [CrossRef]
- Ito, K.; Sawada, H. First-principles analysis of the grain boundary segregation of transition metal alloying elements in γ-Fe. Comp. Mater. Sci. 2022, 210, 111050. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, C.; Xu, W. Effect of solutes on the performance of Zn-coating and Zn-inducing transgranular cracking in steel based on DFT calculations. J. Mater. Res. Technol. 2022, 21, 1519–1527. [Google Scholar] [CrossRef]
- Ding, C.; Peng, W.; Ma, Z.; Zhao, Y.; Teng, H.; Wu, G. Effect of Ni doping on the embrittlement of liquid Zinc at Σ5 Fe austenite grain boundary. Metals 2021, 12, 27. [Google Scholar] [CrossRef]
- Yue, Y.; Zhang, X.; Xu, D.; Qin, J.; Zhang, X.; Liu, R. Segregation behaviors of nonmetallic impurities on grain boundary of austenitic steel. Mater. Chem. Phys. 2023, 296, 127227. [Google Scholar] [CrossRef]
- Wang, R.; Cheng, L.; Yin, C.; Lou, W.; Wu, K. The effects of hydrogen and vacancy on the tensile deformation behavior of Σ3 symmetric tilt grain boundaries in pure Fe. Int. J. Hydrogen Energy 2023, 48, 30930–30948. [Google Scholar] [CrossRef]
- Li, Y.; Lin, J.; Li, J.; Ogata, S.; Geng, W. Friedel oscillations induce hydrogen accumulation near the Σ3 (111) twin boundaries in γ-Fe. Steel. Res. Int. 2022, 93, 2200324. [Google Scholar] [CrossRef]
- He, Y.; Su, Y.; Yu, H.; Chen, C. First-principles study of hydrogen trapping and diffusion at grain boundaries in γ-Fe. Int. J. Hydrogen Energy 2021, 46, 7589–7600. [Google Scholar] [CrossRef]
- Du, Y.A.; Ismer, L.; Rogal, J.; Hickel, T.; Neugebauer, J.; Drautz, R. First-principles study on the interaction of H interstitials with grain boundaries in α- and γ-Fe. Phys. Rev. B 2011, 84, 144121. [Google Scholar] [CrossRef]
- Ahmadian, A.; Scheiber, D.; Zhou, X.; Gault, B.; Liebscher, C.H.; Romaner, L.; Dehm, G. Aluminum depletion induced by co-segregation of carbon and boron in a bcc-iron grain boundary. Nat. Commun. 2021, 12, 6008. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Ding, J.; Zhang, P.; Mei, X.; Huang, S.; Zhao, J. The effect of Cr on He segregation and diffusion at Σ3(112) grain boundary in α-Fe. Nucl. Instrum. Meth. B 2019, 456, 7–11. [Google Scholar] [CrossRef]
- He, Y.; Zhao, X.; Yu, H.; Chen, C. Effect of S on H-induced grain-boundary embrittlement in γ-Fe by first-principles calculations. Int. J. Hydrogen Energy 2021, 46, 28346–28357. [Google Scholar] [CrossRef]
- Wang, J.; Enomoto, M.; Shang, C. First-principles study on the P-induced embrittlement and de-embrittling effect of B and C in ferritic steels. Acta Mater. 2021, 219, 117260. [Google Scholar] [CrossRef]
- Verkhovykh, A.V.; Mirzoev, A.A.; Dyuryagina, N.S. Ab Initio Modeling of Interactions of P, H, C, S with Grain Boundaries in α-Iron. Bull. South. Ural. Stat. 2021, 13, 57–68. [Google Scholar] [CrossRef]
- Ito, K.; Sawada, H.; Tanaka, S.; Ogata, S.; Kohyama, M. Electronic origin of grain boundary segregation of Al, Si, P, and S in bcc-Fe: Combined analysis of ab initio local energy and crystal orbital Hamilton population. Model. Simul. Mater. Sci. Eng. 2020, 29, 015001. [Google Scholar] [CrossRef]
- Yuasa, M.; Mabuchi, M. Grain Boundary Embrittlement of Fe Induced by P Segregation: First-Principles Tensile Tests. Adv. Mater. 2011, 409, 455–460. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Krist.—Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892–7895. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef] [PubMed]
- Ropo, M.; Kokko, K.; Vitos, L. Assessing the Perdew-Burke-Ernzerhof exchange-correlation density functional revised for metallic bulk and surface systems. Phys. Rev. B 2008, 77, 195445. [Google Scholar] [CrossRef]
- Scheiber, D.; Pippan, R.; Puschnig, P.; Ruban, A.; Romaner, L. Ab-initio search for cohesion-enhancing solute elements at grain boundaries in molybdenum and tungsten. Int. J. Refract. Met. Hard Mater. 2016, 60, 75–81. [Google Scholar] [CrossRef]
- Rice, J.R.; Wang, J.-S. Embrittlement of interfaces by solute segregation. Mat. Sci. Eng. A 1989, 107, 23–40. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, S.L. Thermodynamic and kinetic modeling of grain boundary equilibrium segregation of P in α-Fe. Calphad 2017, 57, 134–141. [Google Scholar] [CrossRef]

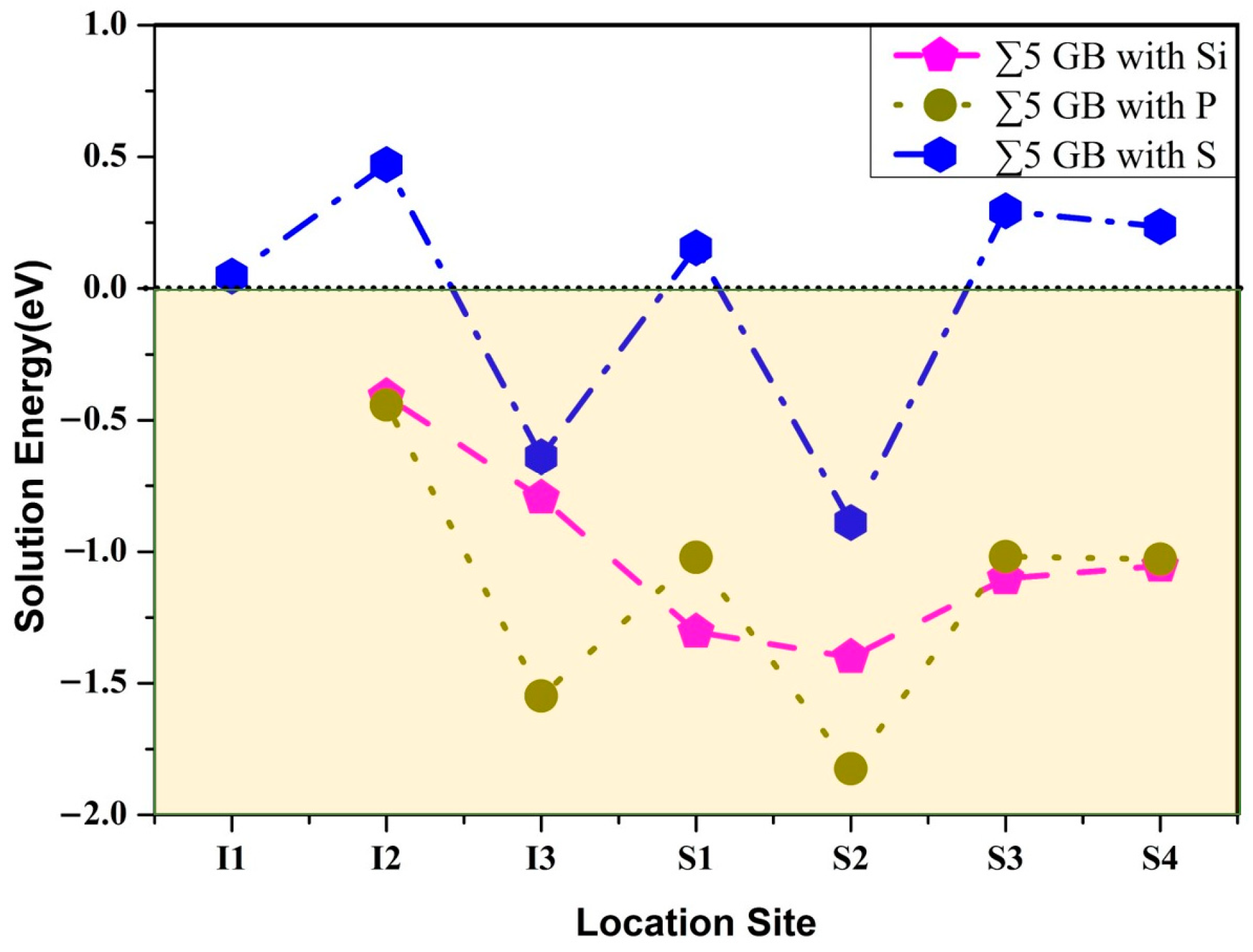





| Element | Site | Eseg/eV | ||
|---|---|---|---|---|
| Si | S2 | −0.14 | −0.66 | 0.52 |
| P | S2 | −0.80 | −0.76 | −0.04 |
| S | S2 | −1.43 | −1.04 | −0.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Cao, W.; Huang, M.; Zhang, F. First Principles Study of the Effects of Si, P, and S on the ∑5 (210)[001] Grain Boundary of γ-Fe. Metals 2024, 14, 471. https://doi.org/10.3390/met14040471
Xu Y, Cao W, Huang M, Zhang F. First Principles Study of the Effects of Si, P, and S on the ∑5 (210)[001] Grain Boundary of γ-Fe. Metals. 2024; 14(4):471. https://doi.org/10.3390/met14040471
Chicago/Turabian StyleXu, Ying, Weigang Cao, Mengzhe Huang, and Fucheng Zhang. 2024. "First Principles Study of the Effects of Si, P, and S on the ∑5 (210)[001] Grain Boundary of γ-Fe" Metals 14, no. 4: 471. https://doi.org/10.3390/met14040471
APA StyleXu, Y., Cao, W., Huang, M., & Zhang, F. (2024). First Principles Study of the Effects of Si, P, and S on the ∑5 (210)[001] Grain Boundary of γ-Fe. Metals, 14(4), 471. https://doi.org/10.3390/met14040471