Microstructural Evolution and Mechanical Behavior of Pure Aluminum Ultra-Thin Strip under Roller Vibration

Abstract

As the demand for lithium-ion batteries increases, higher quality requirements are being placed on pure aluminum ultra-thin strips, one of the main materials used in lithium-ion battery current collectors. Roller vibration during the rolling process of pure aluminum ultra-thin strips is unavoidable and significantly affects the quality of the strips. This paper uses 1A99 pure aluminum ultra-thin strips as raw materials and employs a controlled vibration method during the rolling process to obtain products under two conditions: stable rolling and vibrational rolling. The surface and cross-section of the aluminum strips were characterized using scanning electron microscopy (SEM), and the microstructure of the surface and cross-section was studied using electron backscatter diffraction (EBSD) technology. The results show that, during stable rolling, the surface quality of the aluminum strip is good without defects. Under vibration, obvious vibration marks appear on the surface of the aluminum strip, showing characteristics of peaks and troughs. With the increase in strain at the trough position, there is a transition from low-angle grain boundaries to high-angle grain boundaries, and the grain size is uneven at the peak and trough positions, with noticeable grain refinement at the troughs. At the same time, under the influence of vibration, the aluminum strip induces a different texture morphology from conventional rolling. Due to the different plastic strains at the peak and trough positions, a texture alternation phenomenon occurs at these positions. The tensile test results indicate that aluminum strips exhibit poor mechanical properties under roller vibration, with the reduction in mechanical performance primarily attributed to the uneven microstructure distribution caused by roller vibration.

1. Introduction

Lithium-ion batteries play a crucial role in portable electronic devices and electric vehicles [1,2]. Their high energy efficiency may also improve the quality of energy collected from wind, solar, geothermal, and other renewable sources, thereby contributing to a wider adoption of lithium-ion batteries and establishing a sustainable energy economy [3,4]. Additionally, lithium-ion batteries have enormous global potential in terms of energy sustainability and a significant reduction in carbon emissions [5,6]. The pure aluminum ultra-thin strip is a key material in lithium-ion batteries [7], and also the main material in the current collector of lithium-ion batteries [8,9]. Due to its high electrical conductivity, high stability, strong adhesion, low cost, and flexible and thin characteristics, pure aluminum ultra-thin strips are often used as anode materials [10,11]. In order to ensure the safe and stable operation of lithium-ion batteries, different from the general pure aluminum ultra-thin strip, higher strength, fewer defects, and lower surface roughness are required for the pure aluminum ultra-thin strip used in lithium batteries [12,13]. Currently, there are mainly two methods for preparing pure aluminum ultra-thin strips: the electrolytic method and rolling method. Among them, the rolling method involves material deformation during the rolling process, leading to changes in its microstructure, which, in turn, meets the performance requirements of pure aluminum ultra-thin strips for lithium-ion batteries. Therefore, rolled pure aluminum ultra-thin strips with a better material performance are more commonly used in lithium-ion batteries.

The preparation of aluminum-based materials with smooth surfaces and dense interiors has become a research hotspot. Hee Tae Jeong et al. [14] and Colin Bonatti et al. [15] studied the influence of grain size on the properties of aluminum foils. Refining the grain size of aluminum foils improves their mechanical properties. Leilei Yang et al. [16] studied the grain boundary density of aluminum foils and found that a high grain boundary density can improve their structural stability. Nadja Berndt et al. [17] and Soroosh Naghdy et al. [18] studied the microstructure and texture changes of pure aluminum under extrusion and torsion, respectively. Harishchandra Lanjewar et al. [19] studied the microstructure and mechanical properties of plastically deformed pure aluminum and found that severe plastic deformation changes the grain orientation and affects the mechanical properties. Byakov et al. [20] studied the relationship between the acoustic signal characteristics and damage during the tensile loading process of aluminum plates. Through signal processing, structural defects can be identified and their remaining service life can be predicted.

Since the thickness of ultra-thin strip materials is usually only tens of micrometers or even a few micrometers, the ratio of the surface grain volume to total deformation zone volume increases, highlighting the surface effects of the material [21]. Kenmochi et al. [22] studied four types of micro-defects: micro-pits on the strip surface, oil pits formed during cold rolling, grooves formed by intergranular corrosion during pickling, and scratches caused by the roughness of the roll surface. Previous studies believed that the surface morphology characteristics of metal strip materials mainly transferred from the working rolls during the cold-rolling process. Zengqiang Zhang et al. [23] studied the effect of the roll surface morphology on the surface characteristics, structure, and mechanical properties of stainless steel ultra-thin strip materials. The microstructure characteristics of the strip steel after rolling are significantly affected by the roll surface morphology. This finding indicates that surface morphology characteristics may significantly affect the microstructure and properties of ultra-thin strip materials.

In actual production, the rolling of pure aluminum ultra-thin strips often has the characteristics of multiple specifications and small batches, which will lead to frequent changes in the process parameters, making it easier for the rolling mill to experience vibration phenomena. The vibration of the rolling mill has a significant impact on the surface morphology of the ultra-thin strip, and the resulting vibration marks seriously affect the quality of the strip [24]. Therefore, studying the influence of vibration on their microstructure is crucial. Guided by the Stone formula for minimum achievable thickness [25], the preparation of thinner sheet strips is mainly achieved by reducing the diameter of the working rolls. To support thinner working rolls, multi-roll rolling systems are needed. Thus, various multi-roll rolling mills, represented by twenty-roll Sendzimir mills, have emerged. The Sendzimir mill is the core equipment of thin-strip cold-rolling mills and can produce various high-precision sheet strips. However, current twenty-roll Sendzimir mills still have certain vibration issues. Rolling parameters such as the rolling tension and rolling force [26,27], rolling lubrication, and roll gap conditions [28,29] may all be causes of vibration. Zhong et al. [30] and Kim et al. [31] studied vibration marks but have not yet discovered the vibration characteristics and mechanisms of these marks. Wu Shengli et al. [32] established a dynamic model of the Sendzimir twenty-roll mill, analyzed its vibration characteristics, and revealed the relationship between the vibration characteristics and vibration marks.

In summary, there is a lack of targeted research on the evolution of the microstructure and mechanical properties of pure aluminum ultra-thin strips under roller vibration. The uneven plastic deformation caused by roller vibration on the surface of pure aluminum ultra-thin strips leads to the uneven distribution of grain size, grain boundary misorientation angle, and texture, thereby affecting its mechanical properties. Therefore, the impact of roller vibration on the microevolution and mechanical properties of pure aluminum ultra-thin strips cannot be ignored. In this study, aluminum strips affected by roller vibration were prepared using a vibration test bench. The surface and cross-section of the pure aluminum ultra-thin strips were characterized using SEM, and the microstructure of the surface and cross-section was analyzed using EBSD. The mechanical properties were studied through tensile tests. The study explored the impact of roller vibration on the microstructure and mechanical properties of pure aluminum ultra-thin strips. This research will provide a theoretical basis for the future exploration of the microstructure and mechanical property evolution of rolled products under the non-steady-state operation of rolling mills, and provide a basis for optimizing the process parameters to improve product quality and production efficiency.

2. Experimental Procedures

2.1. Materials and Methods

The material used in this study is pure aluminum 1A99, sourced from Wenghou Metal Materials Company in Shushan District, Hefei, China, and its chemical composition is listed in

Table 1. Chemical compositions of the as-received Al strips (wt.%).

Materials	Al	Si	Fe	Cu	C
1A99	99.9	0.003	0.003	0.003	0.001

. The aluminum strips were cut along the rolling direction into dimensions of 100 mm × 20 mm × 0.1 mm and 100 mm × 20 mm × 0.08 mm.

The experiment described in this paper was conducted on a vibration test bench, as illustrated in Figure 1, which consists of a signal generator, a power amplifier, an exciter, and a vibration platform. By adjusting the signal from the signal generator to simulate the vibration conditions of the rolling mill, the generated analog signal was input into the power amplifier. The power amplifier transmitted the analog signal to the exciter, which drove the exciter to operate according to the set conditions. The exciter transferred the excitation force to the working rolls of the vibration test bench, causing the working rolls to operate under the vibration excitation. The working rolls are composed of a set of twenty rolls with a diameter of 16 mm each, forming the working rolls of a twenty-roll mill.

Through on-site testing, the vibration frequency of the rolling mill was determined to be 135 Hz. Therefore, in the vibration test setup, a signal generator was used to simulate a sine wave signal with a frequency of 135 Hz, which excited the working rolls to operate under vibration conditions with an amplitude of 0.01 mm and an excitation force of 150 N. The experimental samples are pure aluminum ultra-thin strips, and rolling experiments were conducted under the excitation of the working rolls in a vibrating state. The schematic diagram of the rolling process is shown in Figure 2a. After rolling under vibration excitation, the experimental samples showed surface vibration marks and uneven thickness in the cross-section. Three sets of samples were prepared for the experiment, with each set undergoing three repeated tests. Samples within the same set exhibited similar surface characteristics. Therefore, one sample from each set was selected for microstructural characterization, which are as follows:

Sample A (Figure 2b): thickness of 0.08 mm, rolling speed of 6 m/min, without setting the vibration frequency;

Sample B (Figure 2c): thickness of 0.08 mm, rolling speed of 6 m/min, vibration frequency of 135 Hz, and the amplitude of 0.01 mm;

Sample C (Figure 2d): thickness of 0.1 mm, rolling speed of 6 m/min, vibration frequency of 135 Hz, and the amplitude of 0.01 mm.

2.2. Microstructural Characterization

Samples for microstructure observation were taken from samples A, B, and C, and their surfaces and cross-sections were characterized using SEM. Sample A, without vibration, had a smooth and flat surface (Figure 3a) and a uniform cross-section width (Figure 3b). Under vibration rolling, Sample B showed alternating light and dark patterns on the surface (Figure 3c) and thickness variations in the cross-section (Figure 3d), exhibiting clear peak and trough features, and the thickness at the peak is 0.08 mm, while the thickness at the trough is 0.07 mm. Similarly, Sample C, also subjected to vibration rolling, exhibited alternating light and dark patterns on the surface (Figure 3e) and thickness variations in the cross-section (Figure 3f), showing distinct peak and trough features, and the thickness at the peak is 0.1 mm, while the thickness at the trough is 0.09 mm. The microstructure of samples A, B, and C was characterized using EBSD. EBSD samples were ground with sandpaper, followed by polishing with 9 μm, 3 μm, and 1 μm diamond polishing agents, and then polished with OPS for 10 min. EBSD characterization was performed at 20 kV voltage with a scanning step of 0.3 μm, and EBSD data analysis was conducted using “Aztec crystal 2.1” software.

2.3. Tensile Test

In order to better explore the impact of surface vibration marks on material properties, a group of 0.1 mm smooth-rolled aluminum strips was added in the experiment as the contrast group for Sample C. The Shimadzu AGS-X universal testing machine (Kyoto, Japan) was used to conduct a series of room-temperature tensile tests on Samples A, B, and C, as well as the contrast group of Sample C. The tensile tests were conducted in accordance with GB/T 16865-2013 “Test pieces and method for tensile test for wrought aluminium and magnesium alloys products” [33]. We cut and stretch samples along the rolling direction (RD) from samples A, B, and C and the control group of Sample C. The gauge length of the tensile test samples was 140 mm, the width was 15 mm, and the thicknesses were 0.1 mm and 0.08 mm, respectively. The tensile test speed was 1 mm/min.

3. Results and Discussion

3.1. Microstructure

Figure 4 shows the inverse pole figure (IPF) of the surface and cross-section of the pure aluminum ultra-thin strips. As shown in Figure 4a, the surface of Sample A is free from cracks, holes, and other defects, indicating a good surface quality. Continuous roller vibrations induce additional compressive strain on the aluminum strip, altering its stress state significantly. Apart from the deformation during rolling, there exists a much larger compressed deformation zone compared to conventional rolling, leading to a significant alteration in the original crystal structure of the aluminum strip. The uneven strain generated on the surface of the aluminum strip by the rolling rolls (with the maximum strain at troughs and minimum strain at peaks) changes the stress state between grains, promoting uneven plastic deformation in the strip and resulting in noticeable peaks and troughs. This phenomenon significantly degrades the surface quality of the aluminum strip, making it unsuitable for practical applications. Additionally, the surface deformation involves both compressive and additional shear deformations, leading to more slip system motions and types.

Figure 4a,b display the surface and cross-section of Sample A, showing a significant presence of subgrain boundaries and the average grain size of the surface is 43.7 μm, and the average grain size of the cross-section is 49.54 μm. Due to the impact of the rolling rolls, the angles of these subgrain boundaries increase, leading to the formation of these fine grains at trough positions. Figure 4c,d show the surface and cross-section of Sample B. From the surface view (Figure 4c), distinct trough features are observed; the average grain size of Sample B at position II is 35 μm, while, at position I, it is 35.4 μm. Additionally, the average grain size of Sample B at position IV is 4 μm, while, at position III, it is 10.1 μm, indicating that the grain size at trough positions is smaller than at peak positions. Therefore, the deformation strain at trough positions is stronger than that at peak positions.

For Sample C, as shown in Figure 4e,f, distinct trough features are also observed. From the surface view (Figure 4e), the trend of the grain size variation in Sample C is similar to that in Sample B. The grain size of Sample C at position II (19.9 μm) is smaller than at position I (21.5 μm). From the cross-section view (Figure 4f), the average grain size at position IV (2.4 μm) is smaller than the average grain size at position III (5.5 μm), and, compared to the middle section of the aluminum strip, the intense strain near the edges leads to grain refinement. The grain size at the edges of the aluminum strip (3.8 μm) is smaller than in the middle section (10.6 μm), indicating that severe plastic deformation benefits grain refinement.

Intense plastic deformation can effectively refine the grains of aluminum strips, thereby affecting their mechanical properties [34]. However, the grain refinement caused by roller vibrations is not uniform, and differences in grain size in different regions may lead to a localized stress concentration in the material, thereby affecting its strength and toughness. Uneven grain refinement may also result in differences in the electrical and thermal conductivity in the material [35,36]. Non-uniform plastic deformation can cause the rearrangement and deformation of the molecular structure of the material, leading to an uneven stress distribution within the material and the generation of residual stresses. These residual stresses have an impact on the performance and stability of the material. Therefore, it is necessary to control these residual stresses in the production of pure aluminum ultra-thin strips.

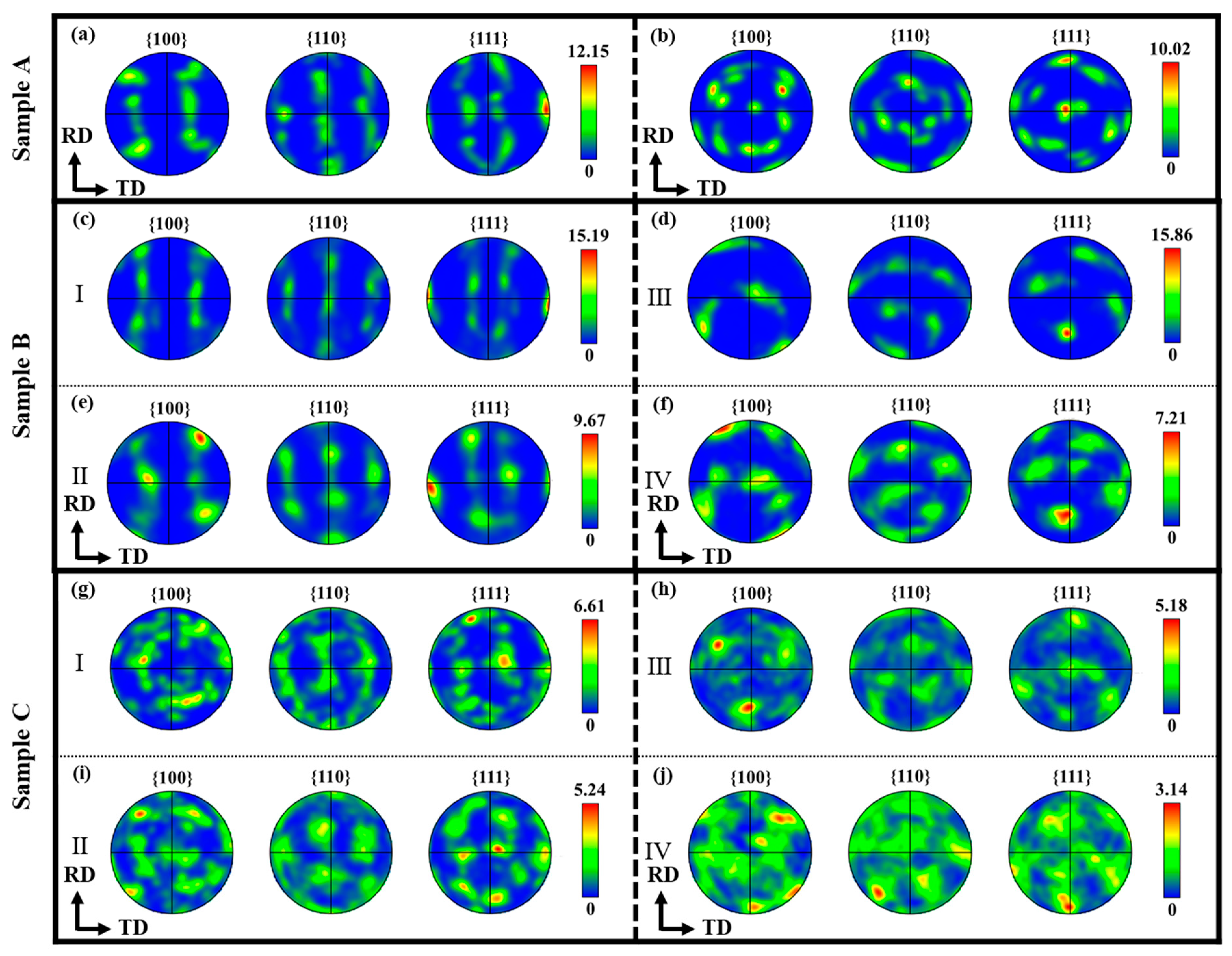
3.2. Texture

Figure 5a,b show the pole figures (PFs) of the surface and cross-section of Sample A, where the {110}<112> and {111}<112> textures are observed, common in cold-rolled materials. In this state, there is no texture change, indicating that the grain orientation has not been influenced by external deformation in the initial state of the material. However, after being affected by vibration during rolling, Sample B shows significant texture changes at positions I and II. At position I (Figure 5c), due to minimal plastic deformation, the texture is similar to the initial state, with the {110}<112> texture and a maximum texture intensity of 15.19. In contrast, at position II (Figure 5e), the {111}<110> texture appears with a maximum texture intensity of 9.67. The pole figures of the cross-sections (Figure 5d,f) also show different textures at positions III and IV. The trough position experiences a greater vibration impact, leading to more significant plastic deformation and a change in grain orientation at the trough position.

For Sample C, at positions III and IV (Figure 5h,j), the {111}<112> texture is observed at position III with a peak intensity of 5.18, while the {100}<110> texture appears at position IV with a maximum texture intensity of 3.14. The texture formed at these two positions are very different, and both textures are typical deformation textures of face-centered cubic (FCC) metals [37]. The texture intensity of aluminum decreases from peak to trough after deformation. In traditional rolling processes, aluminum tends to form typical FCC rolling textures, while roller vibrations influence the grain orientation during the rolling process, resulting in variations in the texture with peak and trough positions.

Grain orientation has a significant impact on the mechanical properties of metals [38]. Aluminum easily forms typical FCC rolling and recrystallization textures, which primarily affect the performance of sheets in terms of strength, ductility, and related anisotropy [39,40]. When pure aluminum undergoes cold-rolling deformation, grain orientation begins to occur mainly due to the deformation along the rolling direction (RD) and transverse direction (TD) during the rolling process. Cold rolling induces grain deformation, causing grains to gradually align in the rolling direction, forming a certain orientation. However, under the influence of vibration, aluminum strips induce special texture forms different from conventional rolling. Due to the different plastic strains at the peak and trough positions, the textures at these two positions also differ. Therefore, aluminum strips experience uneven plastic deformation due to vibration, leading to differences in peak and trough textures, thereby affecting their ductility and mechanical properties.

3.3. Misorientation Angle

Figure 6 illustrates the distribution of grain boundary misorientation angles at the peak and trough positions in the pure aluminum ultra-thin strip. For Sample B, at position III (Figure 6b), the percentage of low-angle grain boundaries (LAGBs, 2–15°) is 75.83%, and the percentage of high-angle grain boundaries (HAGBs, >15°) is 24.17%, with an average misorientation angle of 10.82°. At position IV (Figure 6d), the percentage of LAGBs decreases to 64.84%, while that of HAGBs increases to 35.16%, and the average misorientation angle increases to 15.40°. For position I (Figure 6a), the percentage of LAGBs is 82.42%, HAGBs are 17.58%, and the average misorientation angle is 9.17°. At position II (Figure 6c), the percentage of LAGBs decreases to 80.82%, HAGBs increase to 19.18%, and the average misorientation angle increases to 10.24°. This indicates that significant plastic deformation leads to an increase in dislocation density during the rolling process. Due to the substantial deformation strain, more slip systems can be activated at the trough position, resulting in higher stored deformation energy at the trough position. This phenomenon can promote recrystallization and grain refinement in aluminum.

For Sample C, at position I (Figure 6e), the percentage of low-angle grain boundaries (LAGBs) is 87.39%, while that of high-angle grain boundaries (HAGBs) is 12.61%, with an average misorientation angle of 7.49° at the peak position. However, at position II (Figure 6g), the percentage of LAGBs decreases to 84.30%, while that of HAGBs increases to 15.70%, and the average misorientation angle increases to 8.43°. For position III (Figure 6f), the percentage of LAGBs is 36.47%, while that of HAGBs is 63.53%. However, at position IV (Figure 6h), the percentage of LAGBs decreases to 35.85%, while that of HAGBs increases to 64.15%. With the increase in deformation strain, there is a significant increase in the deformation of HAGBs from the peak to the trough. The decrease in LAGBs and increase in HAGBs are due to the increased deformation [41]. The average misorientation angle at the peak position is 25.23°, and, at the trough position, it is is 25.97°. Both values are greater than 15°. Therefore, HAGBs dominate at both the peak and trough positions.

Mechanical processes such as rolling, drawing, and extrusion can induce deformation in metals, leading to grain refinement. This is because the deformation during processing introduces a high density of dislocations, which promotes grain boundary migration and impedes grain growth. Due to the higher strain at the trough positions providing more energy, more subgrains are formed during severe deformation, further promoting the transition from low-angle grain boundaries (LAGBs) to high-angle grain boundaries (HAGBs). Therefore, the percentage of HAGBs in the troughs is higher than that at the peaks in both thicknesses of aluminum strips, resulting in uneven grain sizes between the peaks and troughs.

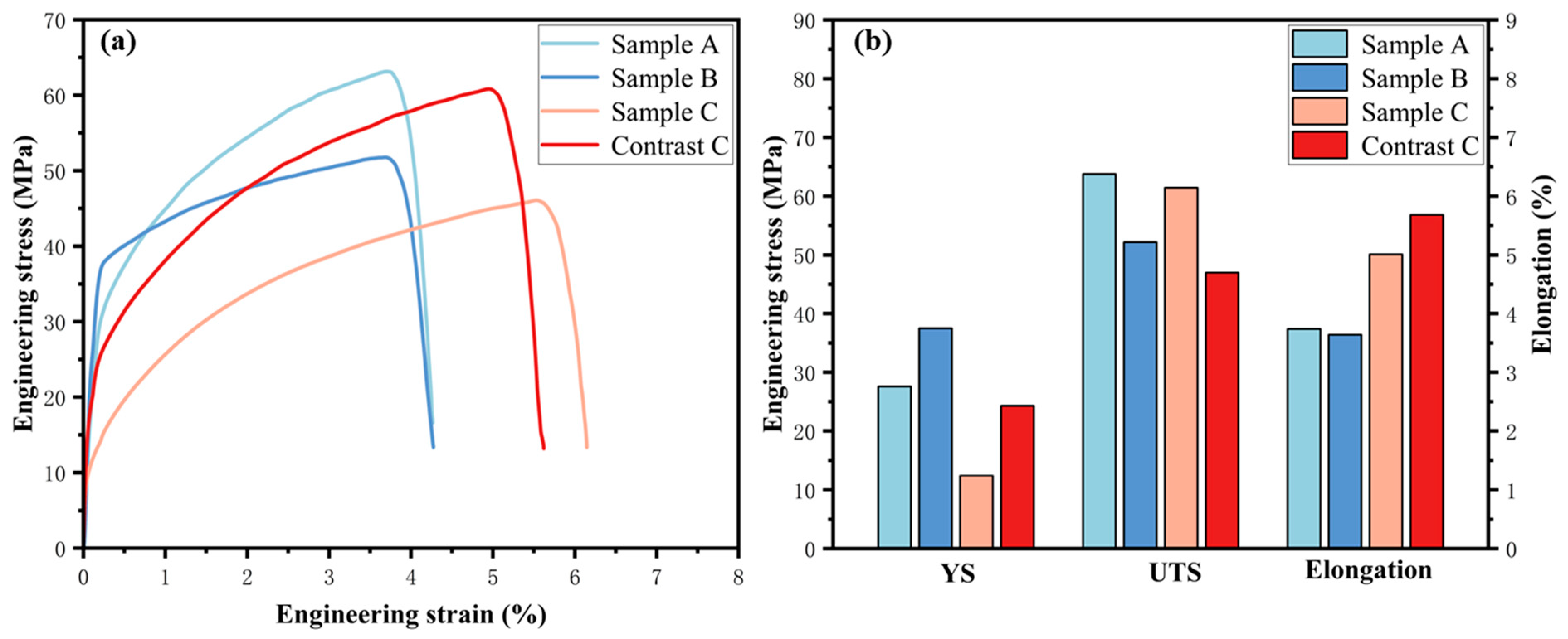
3.4. Mechanical Properties

Figure 7a shows the engineering stress–strain curves. Figure 7b shows the yield strength, ultimate tensile strength, and elongation of each strip. As shown in Figure 7b, Sample A exhibits a tensile strength of 63.76 MPa and an elongation of 3.74%. Sample B has a tensile strength of 52.19 MPa and an elongation of 3.64%. The tensile strength of Sample B, which was subjected to vibration rolling, is lower, while its elongation is similar. This indicates that roller vibration affects the mechanical properties of the aluminum strip, reducing its tensile strength. For Contrast C, which was not subjected to vibration rolling, the tensile strength is 61.42 MPa, and the elongation is 5.01%. Its tensile strength is close to that of Sample A, but its elongation is 1.27% higher, indicating that as the thickness decreases, the elongation of the aluminum strip decreases. The vibration-rolled Sample C exhibits the highest tensile strength of 46.98 MPa, which is also lower than the tensile strength of the non-vibration rolled Contrast C. However, its elongation is 5.68%, which is 0.67% higher than that of Contrast C. This suggests that roller vibration induces uneven plastic deformation in the aluminum strip, affecting its tensile strength and elongation. This is because the roller vibration causes grain refinement at the trough positions of the aluminum strip, and grain refinement increases elongation. However, the grain refinement caused by roller vibration is not uniform, leading to a decrease in the tensile strength of the aluminum strip.

4. Conclusions

In this study, vibration rolling experiments were conducted on pure aluminum ultra-thin strips, and the microstructure and mechanical properties of the experimental samples were studied using EBSD technology and tensile tests. The evolution of the microstructure and the changes in the mechanical properties of pure aluminum ultra-thin strips under roller vibration were revealed, providing experimental support for exploring the microstructure evolution mechanism of pure aluminum ultra-thin strips under different processes. At the same time, it provides a theoretical basis for optimizing the process parameters to improve product quality and production efficiency. The main conclusions are as follows:

(1)

Roller vibration leads to local grain refinement in pure aluminum ultra-thin strips, with uneven grain sizes at the peaks and troughs. The average grain size of Sample B at position IV is 4 μm, while, at position III, it is 10.1 μm, indicating significant grain refinement at the trough position. From the peak position to the trough position, LAGBs transition to HAGBs, and the average misorientation angle at the trough position is higher compared to the peak position. The average misorientation angle of Sample B at position III is 10.82°, increasing to 15.40° at position IV, as the impact generated by roller vibration leads to a greater plastic deformation at the trough position, resulting in an increase in the grain boundary misorientation angle.

(2)

At the troughs of pure aluminum ultra-thin strips, a texture different from conventional rolling is induced. In Sample B, at position I, a {110}<112> texture appears, while, at position II, a {111}<110> texture emerges. In Sample C, the {111}<112> texture at position III transitions to a {100}<110> texture at position IV, exhibiting alternating textures at the peaks and troughs. This is primarily due to the uneven impact on the surface of the strip caused by roller vibration, leading to uneven plastic deformation and changes in grain orientation, resulting in the texture differences between peaks and troughs. This alternating texture phenomenon will affect the ductility and mechanical properties of pure aluminum ultra-thin strips.

(3)

The mechanical properties of pure aluminum ultra-thin strips are affected by roller vibration, resulting in increased elongation but decreased tensile strength. This is because roller vibration causes grain refinement at the trough positions of the aluminum strip, which increases its elongation. However, due to the uneven grain refinement, the tensile strength of the aluminum strip is reduced.