Local Buckling of Locally Sharp-Notched C2700 Brass Circular Tubes Subjected to Cyclic Bending
Abstract
:1. Introduction
2. Experiments
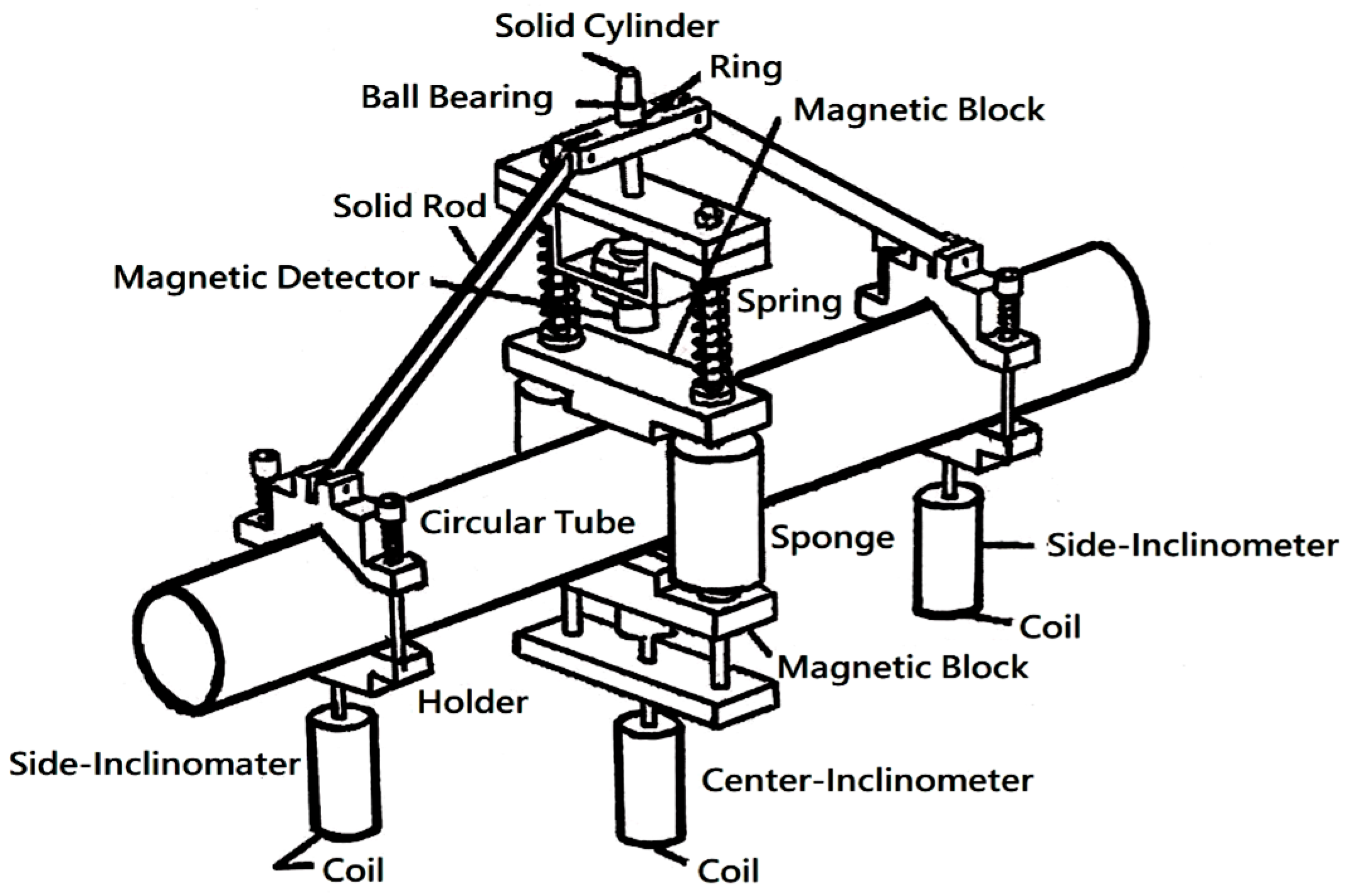
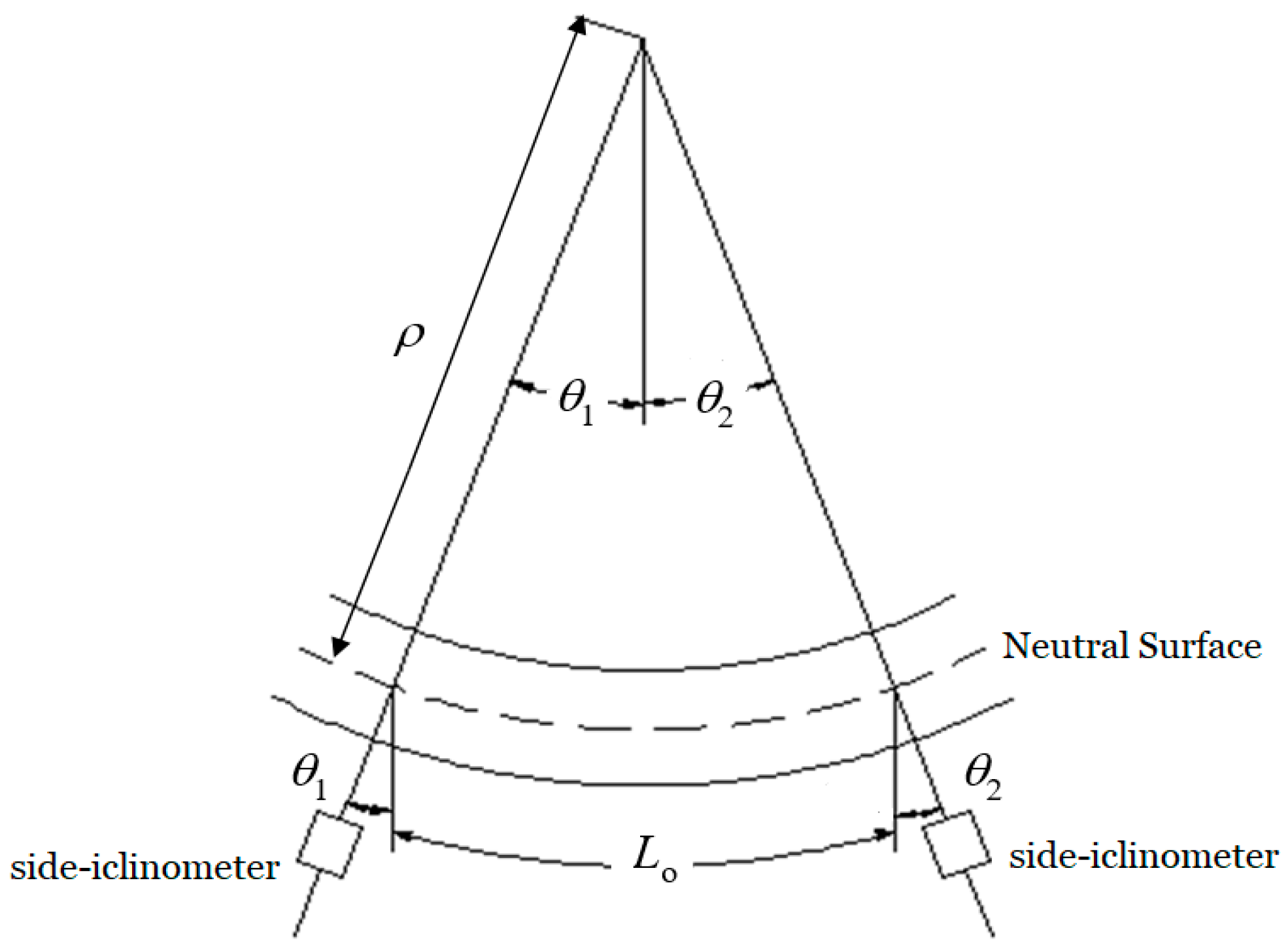
2.1. Experimental Devices
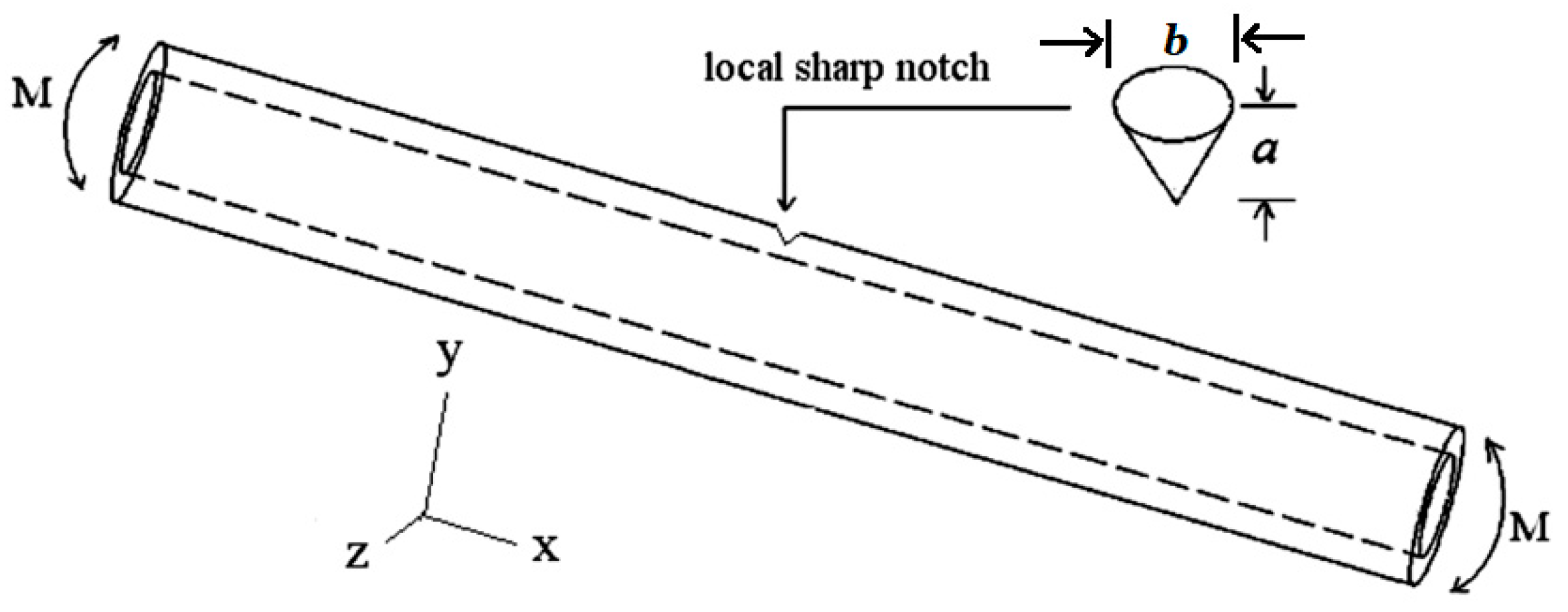
2.2. Material and Specimens
2.3. Test Procedures
3. Experimental Results and Discussion
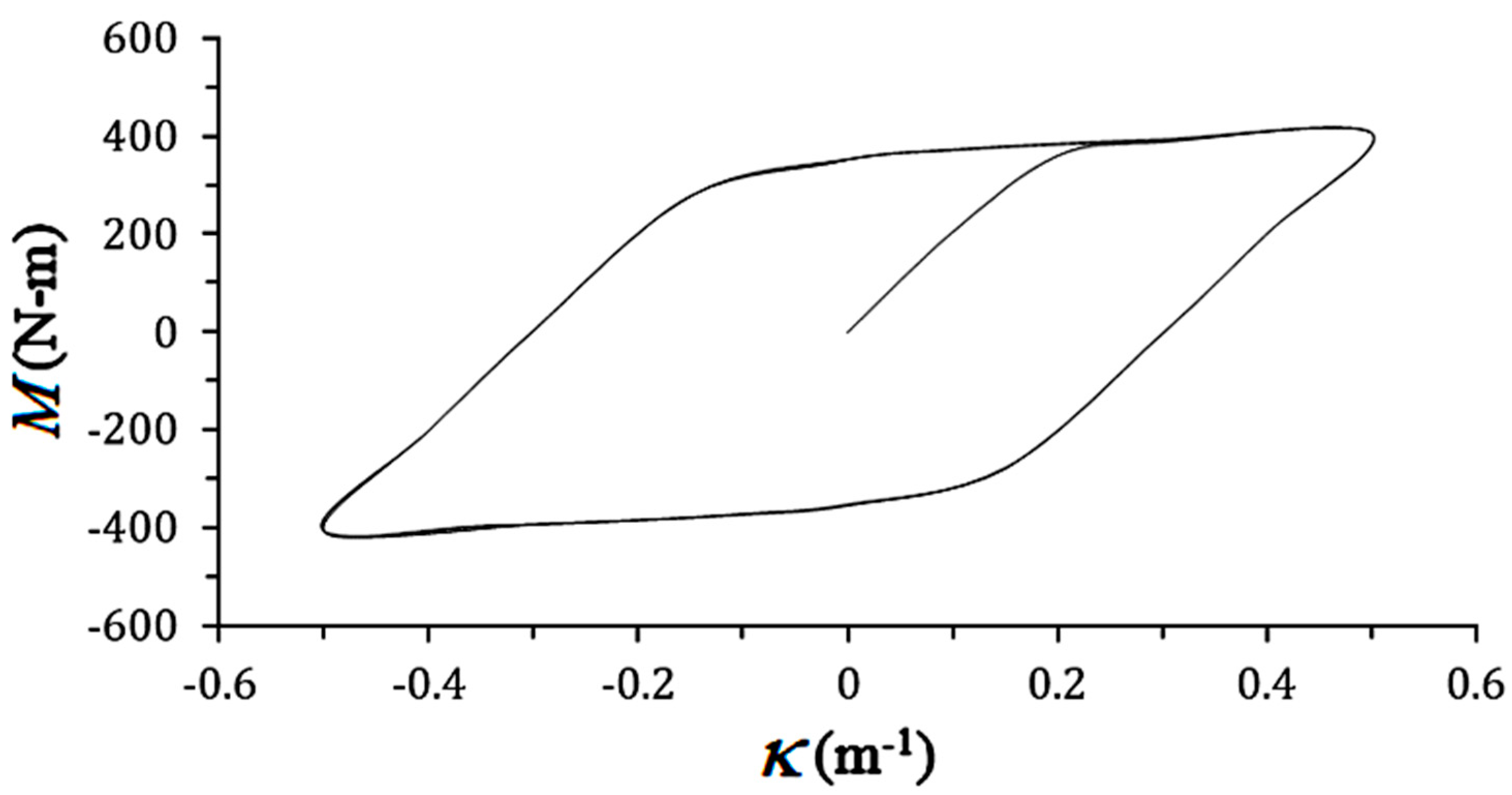
3.1. M-κ Relationships
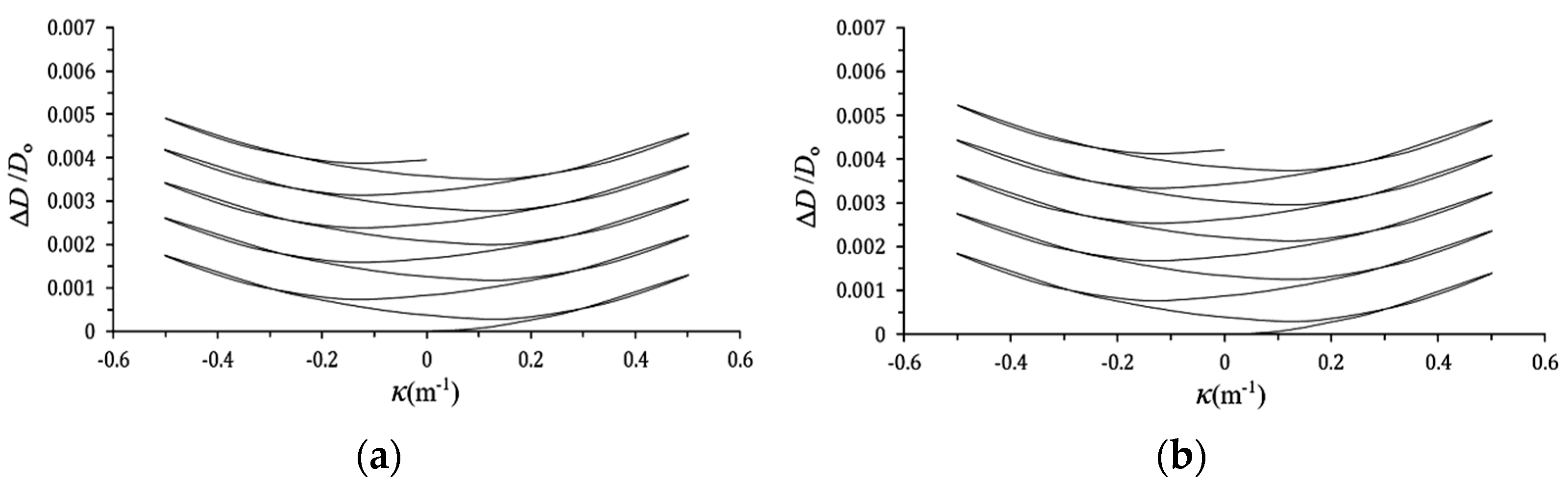
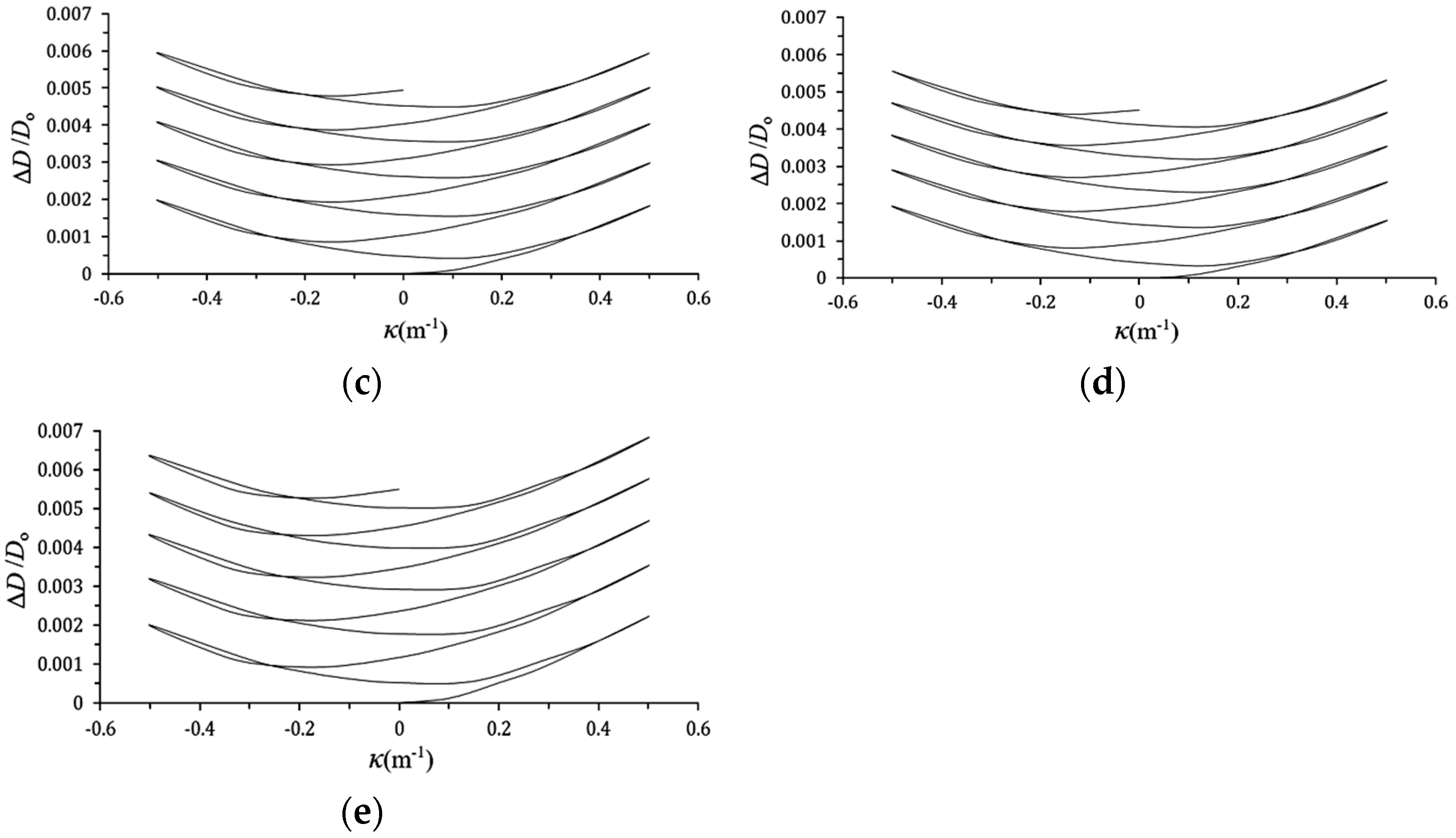
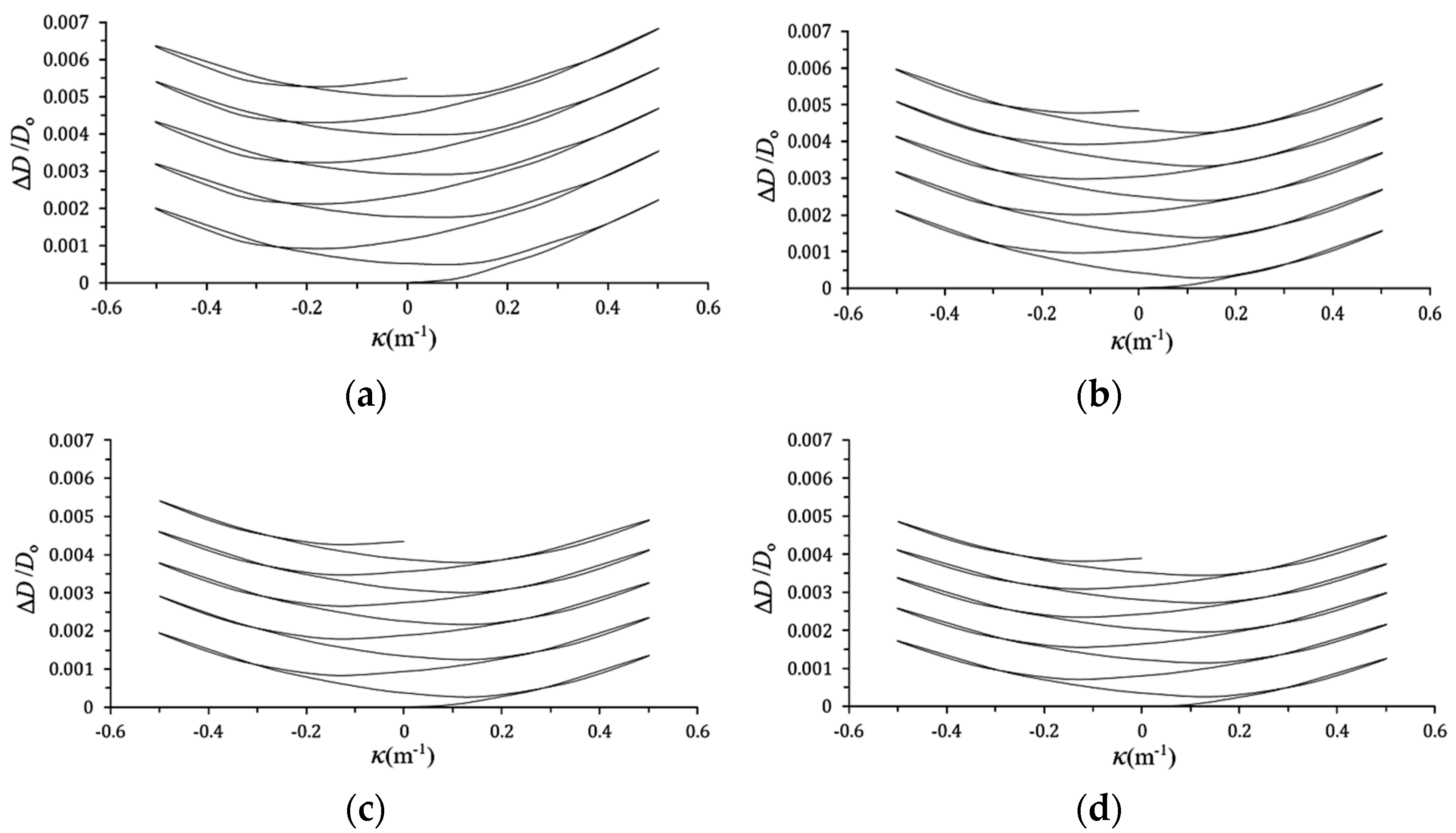
3.2. D/Do-κ Relationships
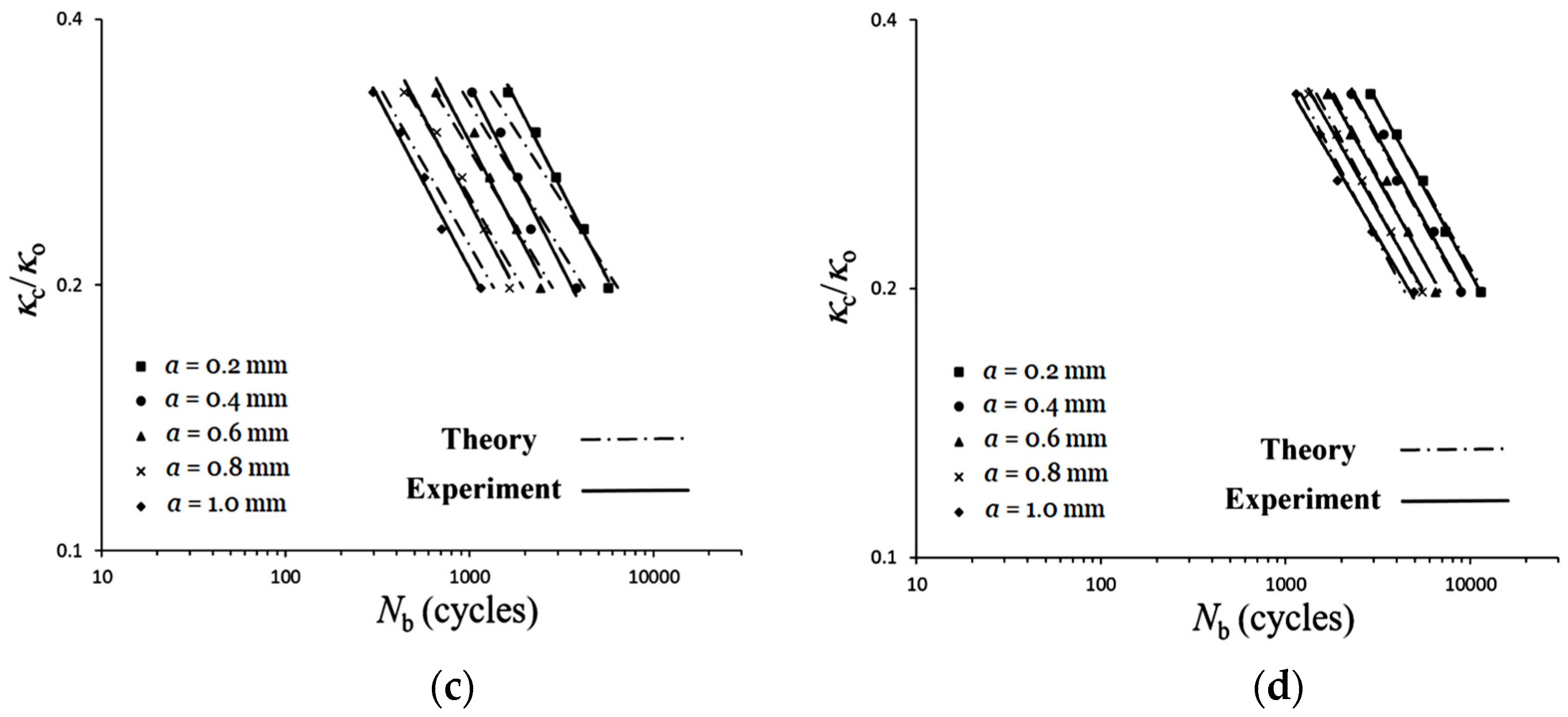
3.3. Controlled Curvature (κc/κo)-Nb Relationships
4. Conclusions
- (1)
- When local buckling has not yet occurred, it is observed from the experimental M-κ relationships that as κ increases, M also increases. Under cyclic bending loads, the M-κ relationship exhibits a stable loop until eventual local buckling failure. Additionally, results indicate that for different values of ϕ and a, the M-κ relationships show similar loops. This phenomenon is consistent with the experimental results reported by Lee et al. [29].
- (2)
- When local buckling has not yet occurred, it is observed from the experimental ΔD/Do-κ relationships that higher κ leads to increased ΔD/Do. Larger a or smaller ϕ values correspond to increased ΔD/Do. This phenomenon is consistent with the experimental results of Lee et al. [29]. In addition, under cyclic bending loads, the ΔD/Do-κ relationships exhibit a ratcheting, symmetrical, and growing trend. A less consistent observation with the experimental results of Lee et al. [29] is that when a is small, the ΔD/Do-κ relationships are symmetrical, but when a is large, the ΔD/Do-κ relationships are asymmetrical.
- (3)
- The experimental κc/κo-Nb relationships reveal that, when ϕ and a are fixed, larger κc/κo leads to fewer Nb. Fixing ϕ and κc/κo, larger a results in fewer Nb. Conversely, when fixing a and κc/κo, larger ϕ leads to more Nb. When ϕ is fixed, the relationships of κc/κo-Nb for five different a on double logarithmic coordinates exhibit nearly straight lines. This phenomenon is consistent with the experimental results of Lee et al. [29]. However, for a certain ϕ, they show almost-parallel lines, while we found non-parallel lines.
- (4)
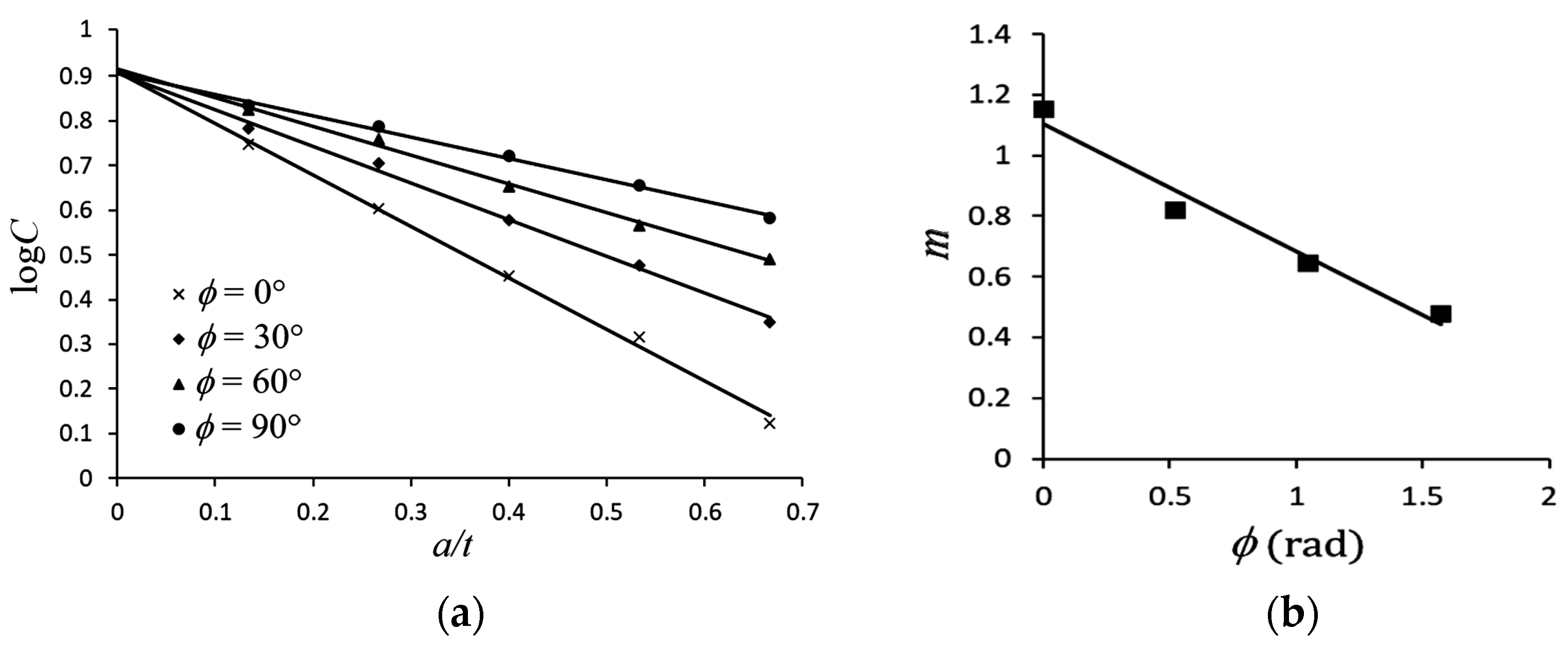
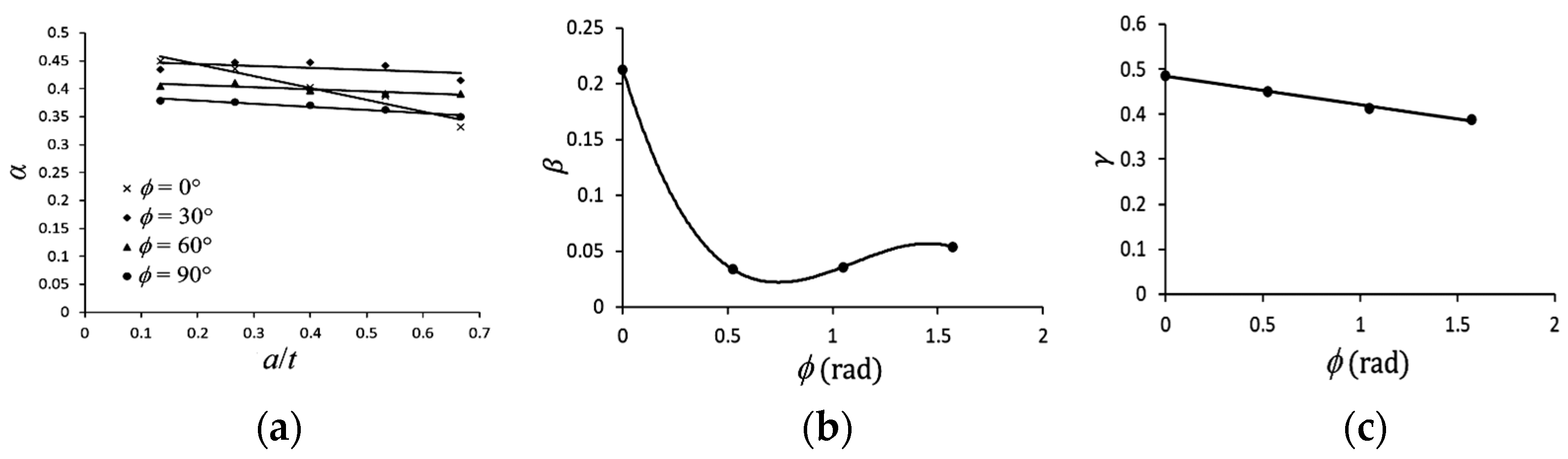
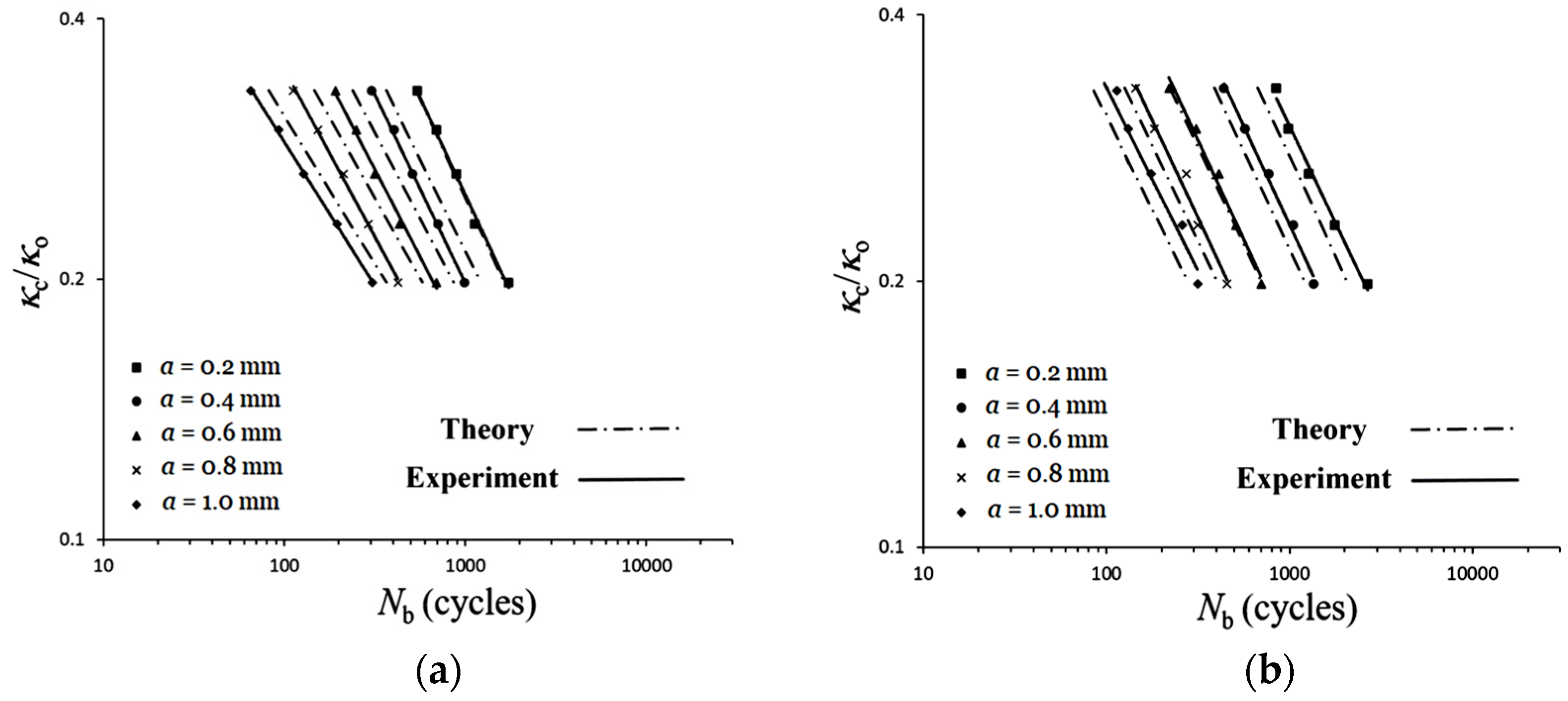
- This study adopts the formula (Equation (3)) proposed by Kyriakides and Shaw [1] to describe the κc/κo-Nb relationships. The formulation of the material parameter C in Equation (4) proposed by Lee et al. [29] was used in this study. However, the material parameter m (Equation (5)) was proposed based on the experimental data. Additionally, a new equation for the material parameter α is proposed (Equation (8)), where material parameters β and γ are derived from Equations (9) and (10), respectively. Note that Equations (5), (9) and (10) are restricted to use between 0° and 90°. Finally, the theoretical Equations (Equations (3)–(5) and (7)–(10)) are employed to describe the κc/κo-Nb relationships for LSN C2700 brass circular tubes under cyclic bending with varying ϕ values: 0°, 30°, 60°, 90°, and different a (dashed lines in Figure 14a–d), and the results of experimental and theoretical analyses are reasonably consistent.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kyriakides, S.; Shaw, P.K. Inelastic buckling of tubes under cyclic bending. J. Press. Vessel Technol. 1987, 109, 169–178. [Google Scholar] [CrossRef]
- Corona, E.; Kyriakides, S. An experimental investigation of the degradation and buckling of circular tubes under cyclic bending and external pressure. Thin-Walled Struct. 1991, 12, 229–263. [Google Scholar] [CrossRef]
- Corona, E.; Kyriakides, S. Asymmetric collapse modes of pipes under combined bending and pressure. Int. J. Solids Struct. 2000, 24, 505–535. [Google Scholar] [CrossRef]
- Corona, E.; Lee, L.H.; Kyriakides, S. Yield anisotropic effects on buckling of circular tubes under bending. Int. J. Solids Struct. 2006, 43, 7099–7118. [Google Scholar] [CrossRef]
- Limam, A.; Lee, L.H.; Corana, E. Inelastic wrinkling and collapse of tubes under combined bending and internal pressure. Int. J. Mech. Sci. 2010, 52, 37–47. [Google Scholar] [CrossRef]
- Limam, A.; Lee, L.H.; Corona, E.; Kyriakides, S. On the collapse of dented tubes under combined bending and internal pressure. Int. J. Solids Struct. 2012, 55, 1–12. [Google Scholar] [CrossRef]
- Bechle, N.J.; Kyriakides, S. Localization of NiTi tubes under bending. Int. J. Solids Struct. 2014, 51, 967–980. [Google Scholar] [CrossRef]
- Jiang, D.; Kyriakides, S.; Bechle, N.J.; Landis, C.M. Bending of pseudoelastic NiTi tubes. Int. J. Solids Struct. 2017, 124, 192–214. [Google Scholar] [CrossRef]
- Kazinakis, K.; Kyriakides, S.; Jiang, D.; Bechle, N.J.; Landis, C.M. Buckling and collapse of pseudoelastic NiTi tubes under bending. Int. J. Solids Struct. 2021, 221, 2–17. [Google Scholar] [CrossRef]
- Yuan, W.; Mirmiran, A. Buckling analysis of concrete-filled FRP tubes. Int. J. Struct. Stab. Dyn. 2001, 1, 367–383. [Google Scholar] [CrossRef]
- Elchalakani, M.; Zhao, X.L.; Grzebieta, R.H. Plastic mechanism analysis of circular tubes under pure bending. Int. J. Mech. Sci. 2002, 44, 1117–1143. [Google Scholar] [CrossRef]
- Elchalakani, M.; Zhao, X.L.; Grzebieta, R.H. Variable amplitude cyclic pure bending tests to determine fully ductile section slenderness limits for cold-formed CHS. Eng. Struct. 2006, 28, 1223–1235. [Google Scholar] [CrossRef]
- Zhi, X.D.; Fan, F.; Shen, S.Z. Failure mechanism of single-layer cylindrical reticulated shells under earthquake motion. Int. J. Struct. Stab. Dyn. 2012, 12, 233–249. [Google Scholar] [CrossRef]
- Yazdani, H.; Nayebi, A. Continuum damage mechanics analysis of thin-walled tube under cyclic bending and internal constant pressure. Int. J. Appl. Mech. 2013, 5, 1350038. [Google Scholar] [CrossRef]
- Guo, L.; Yang, S.; Jiao, H. Behavior of thin-walled circular hollow section tubes subjected to bending. Thin-Walled Struct. 2013, 73, 281–289. [Google Scholar] [CrossRef]
- Elchalakani, M.; Karrech, A.; Hassanein, M.F.; Yang, B. Plastic and yield slenderness limits for circular concrete filled tubes subjected to static pure bending. Thin-Walled Struct. 2016, 109, 50–64. [Google Scholar] [CrossRef]
- Shamass, R.; Alfano, G.; Guarracino, F. On elastoplastic buckling analysis of cylinders under nonproportional loading by differential quadrature method. Int. J. Struct. Stab. Dyn. 2017, 17, 1750072. [Google Scholar] [CrossRef]
- Chegeni, B.; Jayasuriya, S.; Das, S. Effect of corrosion on thin-walled pipes under combined internal pressure and bending. Thin-Walled Struct. 2019, 143, 106218. [Google Scholar] [CrossRef]
- Jin, S.; Cheng, P.; Saneian, M.; Yong, B. Mechanical behavior of thin tubes under combined axial compression and bending. Thin-Walled Struct. 2021, 159, 107255. [Google Scholar] [CrossRef]
- Silveira1, T.; Pinto, V.T.; Neufeld, J.P.S.; Pavlovic, A.; Rocha, L.A.O.; Santos, E.D.; Isoldi, L.A. Applicability evidence of constructal design in structural engineering: Case study of biaxial elasto-plastic buckling of square steel plates with elliptical cutout. J. Appl. Comp. Mech. 2021, 7, 922–934. [Google Scholar]
- Montes, D.; Janer, M.; Caminati, R.; Plantà, X. Experimental study on the bending of a polyamide tube using high-power ultrasound. J. Adv. Man. Sys. 2021, 20, 191–204. [Google Scholar] [CrossRef]
- Shi, J.; Zhong, S.; Nie, X.; Shi, J.; Zheng, J. Study on steel wire reinforced thermoplastic pipes under combined internal pressure and bending moment at various temperatures. Thin-Walled Struct. 2022, 169, 108381. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, Y.; Wang, F.; Feng, B. Experimental and analytical study of hollow section concrete-filled GFRP tubes in bending. Thin-Walled Struct. 2022, 177, 109297. [Google Scholar] [CrossRef]
- Lavayen-Farfan, D.; Butenegro-Garcia, J.A.; Boada, M.J.L.; Martinez-Casanova, M.A.; Rodriguez-Hernandez, J.A. Theoretical and experimental study of the bending collapse of partially reinforced CFRP–Steel square tubes. Thin-Walled Struct. 2022, 177, 109457. [Google Scholar] [CrossRef]
- He, Z.R.; Li, G.J.; Yang, J.C.; Guo, X.Z.; Duan, X.Y.; Guo, W.; Liu, X.; Deng, Y.Y.; Cheng, C. Insight into the deformation transition effect in free bending of tubes. Mater. Lett. 2023, 348, 134673. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.R.; Li, H.; Lv, L.Y. Behaviour of square concrete-filled steel tubes reinforced with internal latticed steel angles under bending. Structures 2023, 48, 1436–1454. [Google Scholar] [CrossRef]
- Wu, Z.; Li, J.; Shi, L.; Chen, X. Effect of stacking configuration on the mechanical property and damage behavior of braided composite tube under three-point bending. Thin-Walled Struct. 2023, 187, 110762. [Google Scholar] [CrossRef]
- Duda, S.; Smolnicki, M.; Stabla, P.; Zielonka, P.; Osiecki, T.; Gao, C.; Lesiuk, G. Experimental characterization and modeling of cylindrical CFRP structures under quasi-static multiaxial loading conditions. Thin-Walled Struct. 2024, 195, 111364. [Google Scholar] [CrossRef]
- Lee, K.L.; Chang, K.H.; Pan, W.F. Effects of notch depth and direction on stability of local sharp-notched circular tubes subjected to cyclic bending. Int. J. Struct. Stab. Dyn. 2018, 18, 1850099. [Google Scholar] [CrossRef]
- Pan, W.F.; Wang, T.R.; Hsu, C.M. A curvature-ovalization measurement apparatus for circular tubes under cyclic bending. Exp. Mech. 1998, 38, 99–102. [Google Scholar] [CrossRef]



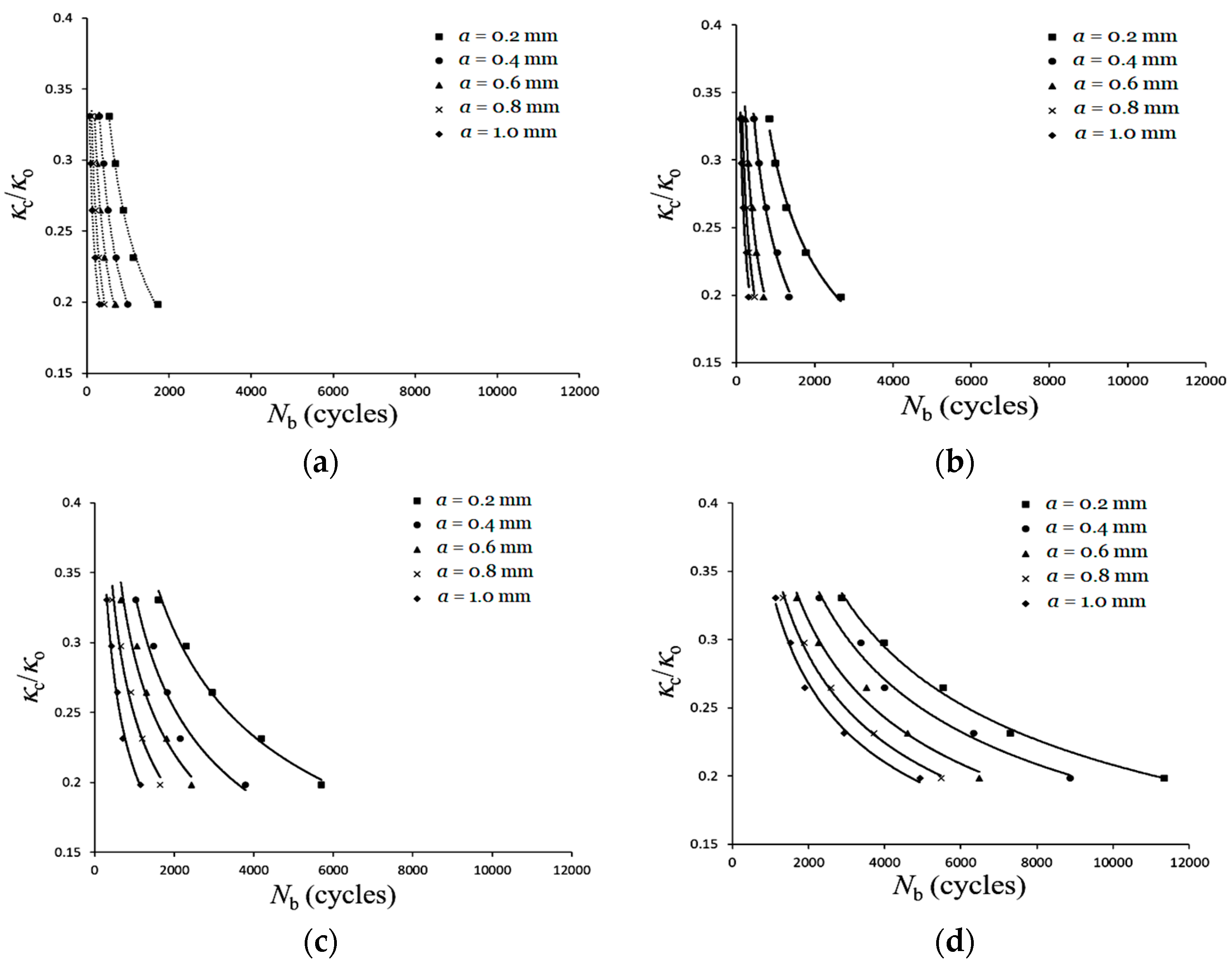
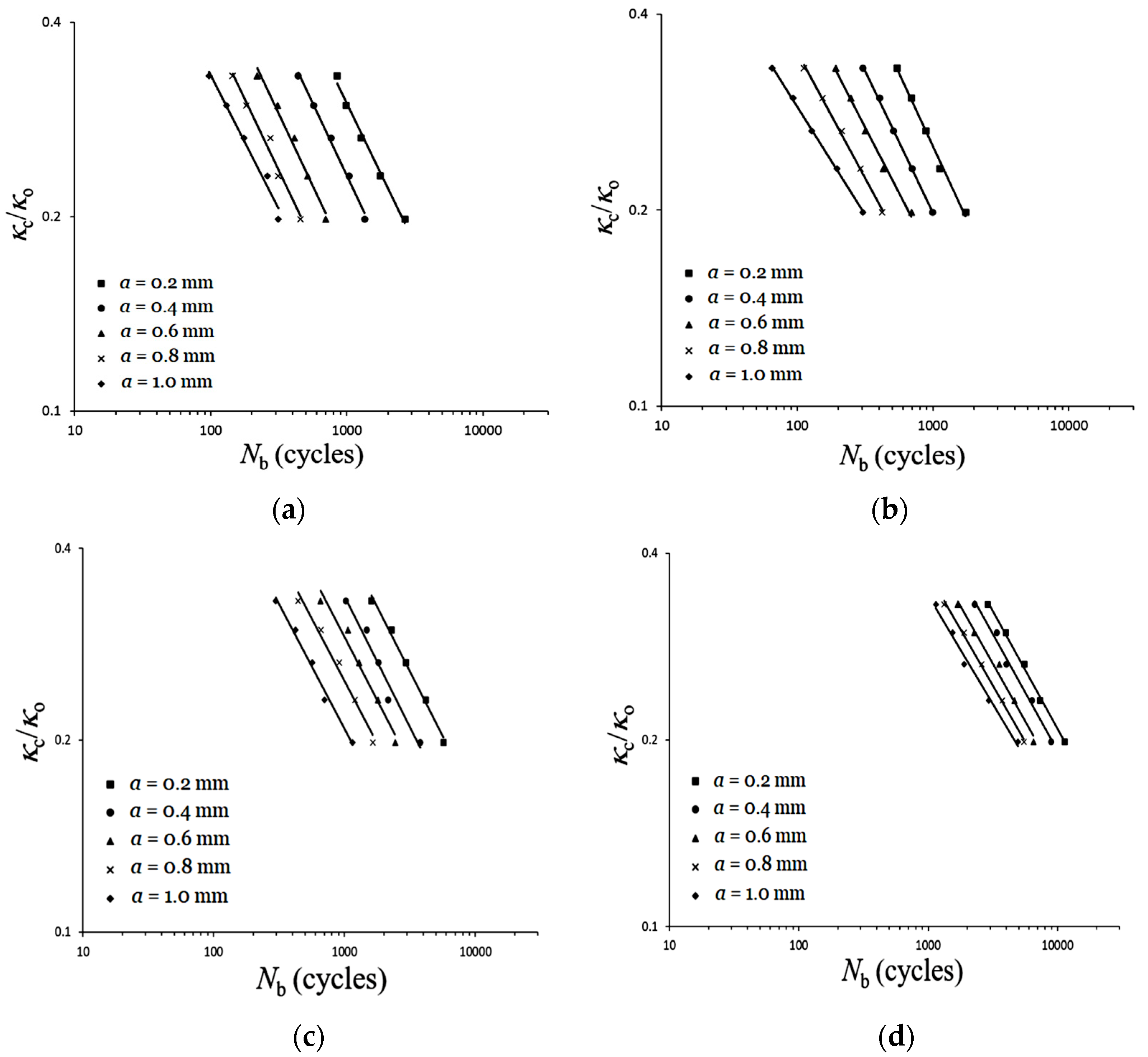
| (a) ϕ = 0° | |||||
| κc/κo | a = 0.2 mm | a = 0.4 mm | a = 0.6 mm | a = 0.8 mm | a = 1.0 mm |
| 0.33 | 542 | 303 | 192 | 112 | 65 |
| 0.29 | 694 | 403 | 249 | 154 | 93 |
| 0.26 | 890 | 511 | 316 | 212 | 128 |
| 0.23 | 1125 | 703 | 432 | 292 | 196 |
| 0.20 | 1734 | 988 | 694 | 423 | 305 |
| (b) ϕ = 30° | |||||
| κc/κo | a = 0.2 mm | a = 0.4 mm | a = 0.6 mm | a = 0.8 mm | a = 1.0 mm |
| 0.33 | 847 | 439 | 219 | 145 | 97 |
| 0.29 | 986 | 571 | 309 | 182 | 131 |
| 0.26 | 1270 | 765 | 413 | 273 | 175 |
| 0.23 | 1765 | 1042 | 512 | 314 | 260 |
| 0.20 | 2664 | 1347 | 698 | 456 | 314 |
| (c) ϕ = 60° | |||||
| κc/κo | a = 0.2 mm | a = 0.4 mm | a = 0.6 mm | a = 0.8 mm | a = 1.0 mm |
| 0.33 | 1605 | 1028 | 657 | 442 | 298 |
| 0.29 | 2293 | 1476 | 1059 | 661 | 422 |
| 0.26 | 2958 | 1821 | 1293 | 913 | 567 |
| 0.23 | 4191 | 2155 | 1803 | 1201 | 704 |
| 0.20 | 5705 | 3792 | 2430 | 1644 | 1155 |
| (d) ϕ = 90° | |||||
| κc/κo | a = 0.2 mm | a = 0.4 mm | a = 0.6 mm | a = 0.8 mm | a = 1.0 mm |
| 0.33 | 2876 | 2277 | 1687 | 1325 | 1141 |
| 0.29 | 3977 | 3374 | 2257 | 1888 | 1534 |
| 0.26 | 5528 | 4002 | 3532 | 2587 | 1898 |
| 0.23 | 7297 | 6339 | 4611 | 3722 | 2936 |
| 0.20 | 11,338 | 8867 | 6487 | 5481 | 4930 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.-A.; Pan, W.-F. Local Buckling of Locally Sharp-Notched C2700 Brass Circular Tubes Subjected to Cyclic Bending. Metals 2024, 14, 656. https://doi.org/10.3390/met14060656
Chen Y-A, Pan W-F. Local Buckling of Locally Sharp-Notched C2700 Brass Circular Tubes Subjected to Cyclic Bending. Metals. 2024; 14(6):656. https://doi.org/10.3390/met14060656
Chicago/Turabian StyleChen, Yu-An, and Wen-Fung Pan. 2024. "Local Buckling of Locally Sharp-Notched C2700 Brass Circular Tubes Subjected to Cyclic Bending" Metals 14, no. 6: 656. https://doi.org/10.3390/met14060656





