A Model for the Temperature Distribution in a Rolled Joint in a CANDU Reactor Exploiting the Decomposition of the β-Zr Phase
Abstract
:1. Introduction
2. Experimental
3. Theory
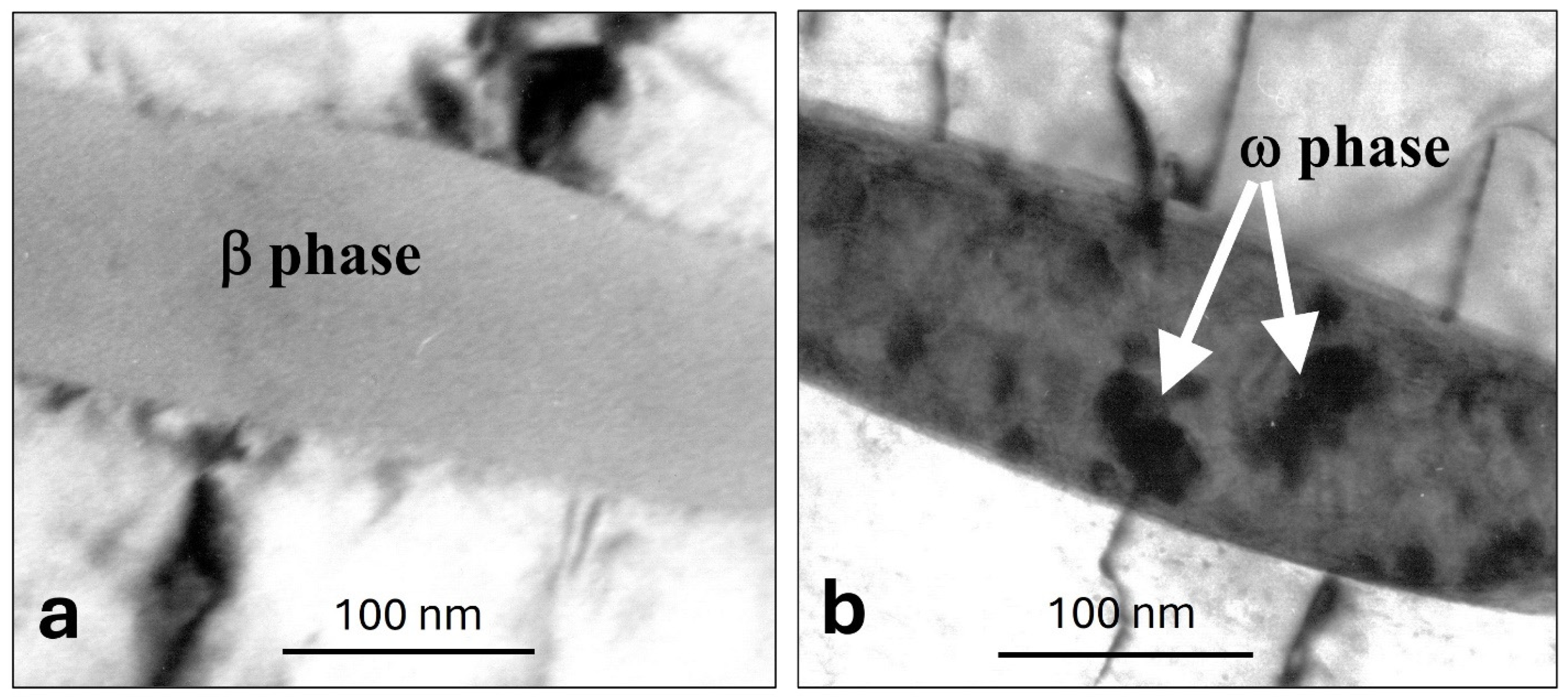
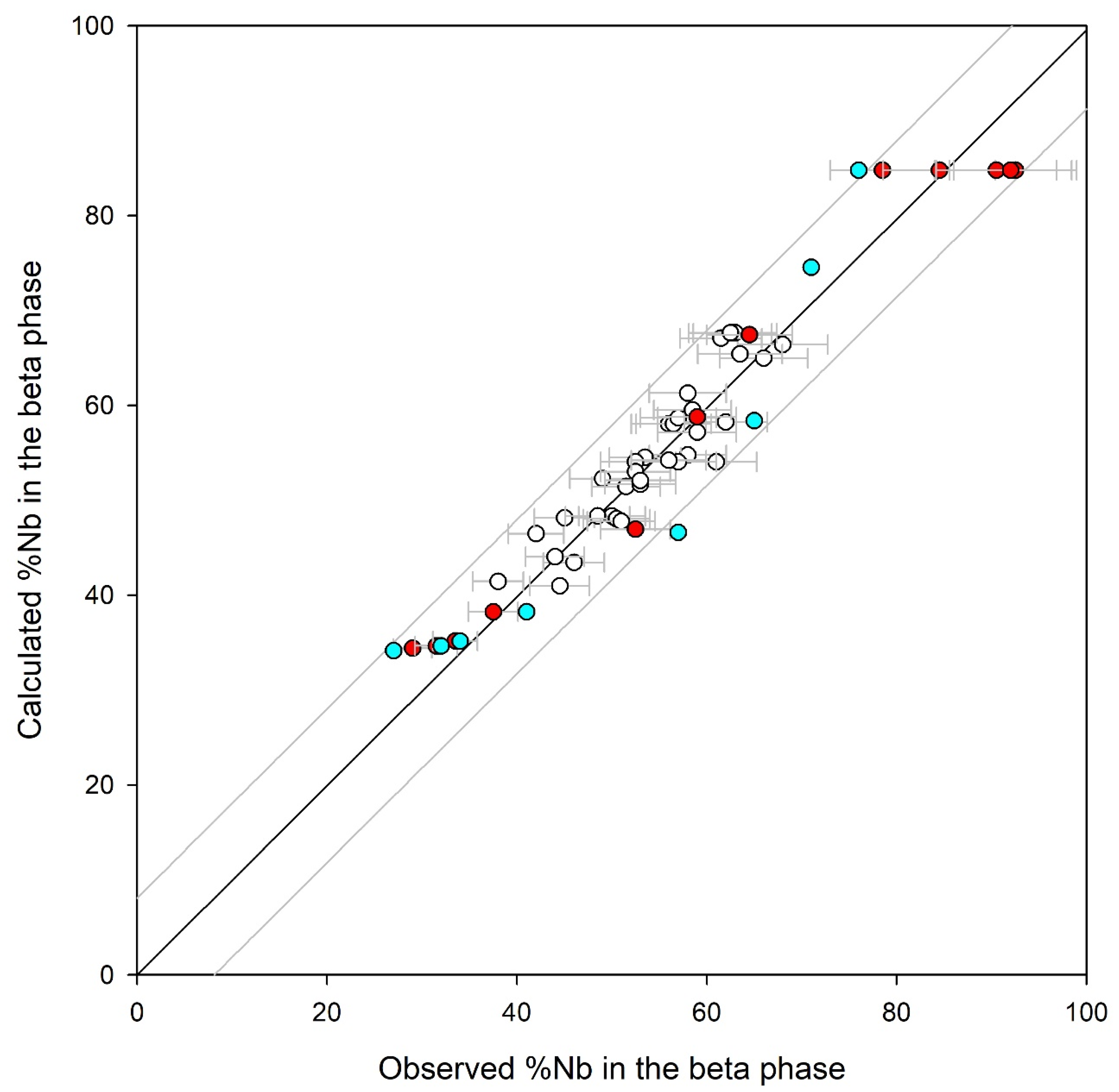
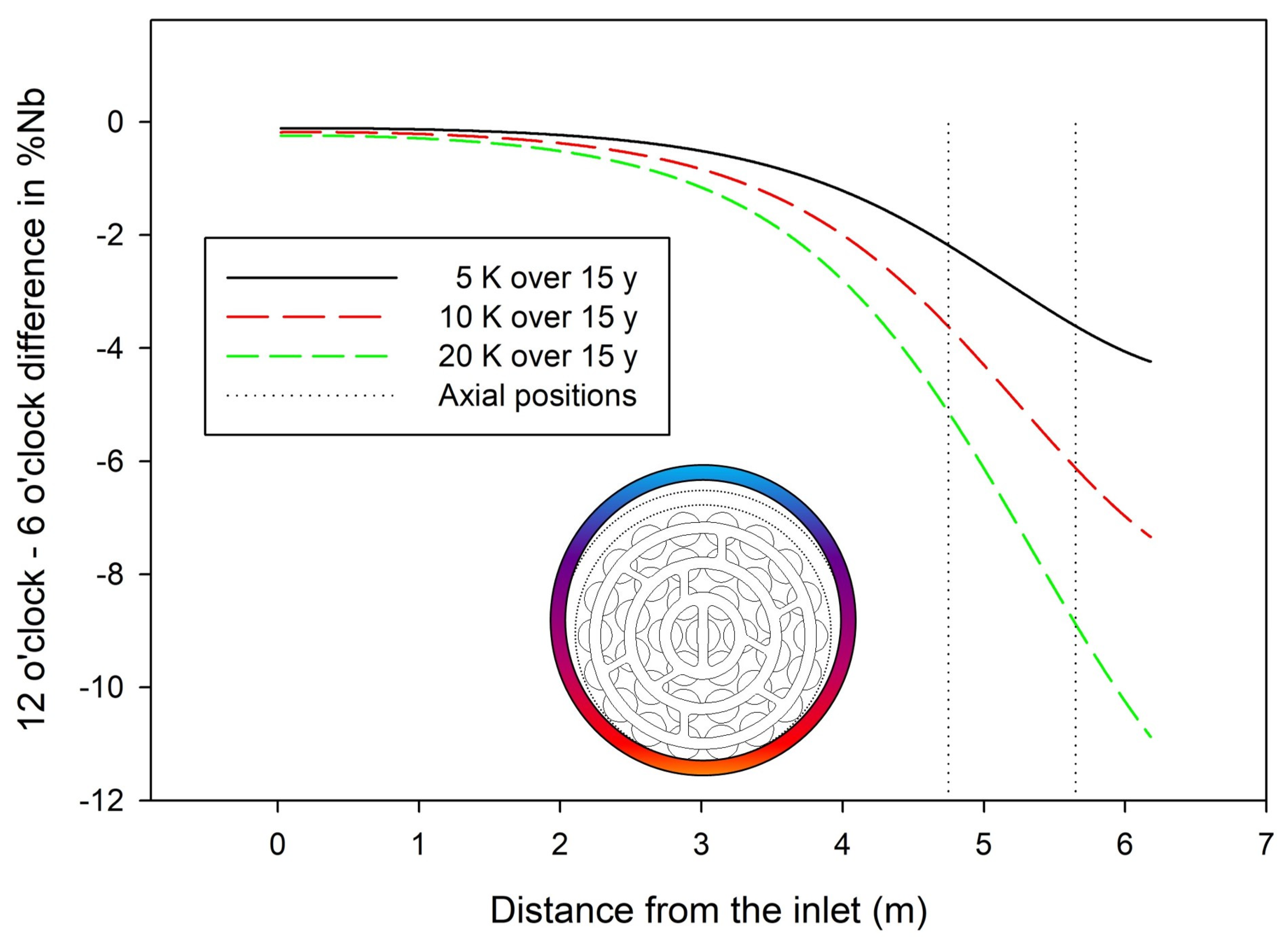
4. Results
5. Discussion

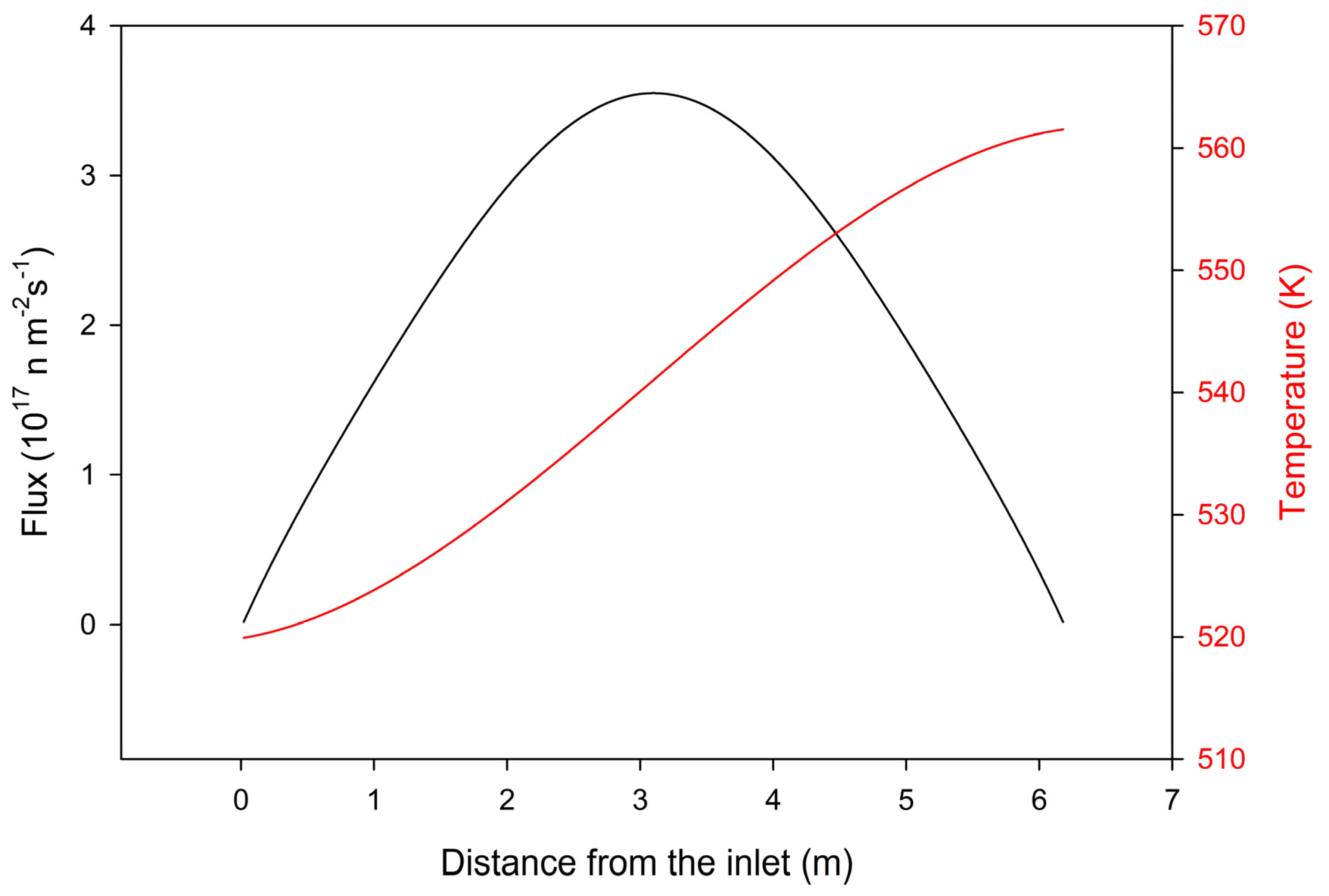
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Canadian Nuclear Safety Commission, 19–20 July 2021, CMD 21-M37. 3 September 2021 Commission Meeting. Available online: https://www.cnsc-ccsn.gc.ca/eng/the-commission/meetings/cmd/ (accessed on 10 June 2024).
- 20210726-Designated-Officer-Order-to-Bruce-Power.pdf (Nuclearsafety.gc.ca), Canadian Nuclear Safety Commission, 26 July 2021. Available online: https://www.cnsc-ccsn.gc.ca/eng/acts-and-regulations/regulatory-action/bruce-power/ (accessed on 10 June 2024).
- Canadian Nuclear Safety Commission, 24 March 2022, Event Initial Report CMD 22-M16. 24 March 2022 Commission Meeting. Available online: https://www.cnsc-ccsn.gc.ca/eng/the-commission/meetings/cmd/ (accessed on 10 June 2024).
- Cheadle, B.A. The development of Zr-2.5Nb pressure tubes for CANDU reactors. J. ASTM Int. 2010, 7, 67–87. [Google Scholar] [CrossRef]
- Winton, J.; Murgatroyd, R.A. The effect of variations in composition and heat treatment on the properties of Z-Nb alloys. Electrochem. Technol. 1966, 4, 358–365. [Google Scholar]
- Cheadle, B.A.; Aldridge, S.A. The transformation and age hardening behaviour of Zr-19 WT% Nb. J. Nucl. Mater. 1973, 47, 255–258. [Google Scholar] [CrossRef]
- Dey, G.K.; Singh, R.N.; Tewari, R.; Srivastava, D.; Banerjee, S.A. Metastability of the β-phase in Zr-rich Zr-Nb alloys. J. Nucl. Mater. 1995, 224, 146–157. [Google Scholar] [CrossRef]
- Griffiths, M.; Winegar, J.E.; Buyers, A. The transformation behaviour of the beta phase in Zr-2.5wt%Nb pressure tubes. J. Nucl. Mater. 2008, 383, 28–33. [Google Scholar] [CrossRef]
- Griffiths, M.; Chow, P.C.K.; Coleman, C.E.; Holt, R.A.; Sagat, S.; Urbanic, V.F. Evolution of microstructure in zirconium alloy core components of nuclear reactors during service. ASTM STP 1993, 1175, 1077–1110. [Google Scholar]
- Griffiths, M.; Mecke, J.F.; Winegar, J.E. Evolution of microstructure in zirconium alloys during irradiation. In Zirconium in the Nuclear Industry: Eleventh International Symposium; ASTM International: West Conshohocken, PA, USA, 1997. [Google Scholar]
- Khatamian, D. Effect of β-Zr decomposition on the solubility limits for H in Zr-2.5Nb. J. Alloys Compd. 2003, 356, 22–26. [Google Scholar] [CrossRef]
- Olander, D.R. Fundamental Aspects of Nuclear Reactor Fuel Elements; TID-26711-P1; National Technical Information Service, U.S. Department of Commerce: Springfield, MA, USA, 1976. [Google Scholar]
- Wollenberger, H. Phase transformations under irradiation. J. Nucl. Mater. 1994, 216, 63–77. [Google Scholar] [CrossRef]
- Lundin, C.E.; Cox, R.H. The determination of the equilibrium phase diagram, zirconium-niobium. In Proceedings of the SAEC Symposium on Zirconium Alloy Development, Pleasanton, CA, USA, 12–14 November 1962; GEAP-4089. Volume 1, pp. 9.1–9.35. [Google Scholar]
- Boltaks, B.I. Diffusion in Semiconductors; Academic Press: New York, NY, USA, 1963. [Google Scholar]
- Abriata, J.P.; Bolcich, J.C. The Nb-Zr (Niobium-Zirconium) System. Bull. Alloy Phase Diagr. 1982, 3, 34–44. [Google Scholar] [CrossRef]
- Sikka, S.K.; Vohra, Y.K.; Chidambaram, R. Omega phase in materials. Prog. Mater. Sci. 1982, 27, 245–310. [Google Scholar] [CrossRef]
- Hood, G.M.; Zou, H.; Schultz, R.J.; Matsuura, N.; Roy, J.A.; Jackman, J.A. Self- and Hf Diffusion in α-Zr and in Dilute, Fe-Free, Zr(Ti) and Zr(Nb) Alloys. Defect Diffus. Forum 1997, 143–147, 49–54. [Google Scholar]
- Hood, G.M.; Zou, H.; Schultz, R.J.; Matsuura, N. Nb Diffusion in Single-Crystal α-Zr. Defect Diffus. Forum 1997, 143–147, 55–60. [Google Scholar] [CrossRef]
- Douglass, D.L. The Metallurgy of Zirconium. Int. At. Energy Rev. 1971, 53, 53084330. [Google Scholar]
- Woo, C.H. Neutron-Induced Displacement Damage Analysis (with Particular Reference to Zirconium). AECL-6189. 1978. Available online: https://inis.iaea.org/collection/NCLCollectionStore/_Public/10/490/10490755.pdf (accessed on 10 June 2024).
- Jenkins, J.D. Rice: A Program to Calculate Primary Recoil Atom Spectra from ENDF/B Data; Technical Report ORNL-TM-2707; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1970. [Google Scholar]
- Naundorf, V. On the origin of freely migrating defects in ion and neutron irradiated metals. J. Nucl. Mater. 1991, 182, 254–257. [Google Scholar] [CrossRef]
- Rehn, L.E.; Birtcher, R.C. Experimental studies of free defect generation during irradiation—Implications for reactor environments. J. Nucl. Mater. 1993, 205, 31–39. [Google Scholar] [CrossRef]
- Lemaignan, C. Irradiation damage, The Metallurgy of Zirconium. Vol. 2. Chap. 6. IAEA. 2023. Available online: https://www-pub.iaea.org/MTCD/Publications/PDF/AdditionalVolumes/PUB1943/Vol2/Pub1943-Vol2-Web.pdf (accessed on 10 June 2024).
- Adamson, R.B.; Coleman, C.E.; Griffiths, M. Irradiation creep and growth of zirconium alloys: A critical review. J. Nucl. Mater. 2019, 521, 167–244. [Google Scholar] [CrossRef]
- Coleman, C.E.; Gilbert, R.W.; Carpenter, G.J.C.; Weatherly, G.C. Precipitation in Zr-2.5Nb during neutron irradiation. Phase stability during irradiation. AIME 1981, 587–599. [Google Scholar]
- Urbanic, V.F.; Griffiths, M. Microstructural aspects of corrosion and hydrogen ingress in Zr-2.5Nb. ASTM STP 1998, 1354, 641–656. [Google Scholar]
- Bickel, G.A.; Griffiths, M.; Chaput, H.; Buyers, A.; Coleman, C.E. Modelling Irradiation Damage in Zr-2.5Nb and its Effect on Delayed Hydride Cracking Growth Rate. ASTM-STP 2015, 1543, 800–829. [Google Scholar]
- McRae, G.A.; Coleman, C.E. Deuterium concentration profiles at the rolled joints of CANDU fuel channels. J. Nucl. Mater. 2023, 573, 154128. [Google Scholar] [CrossRef]
- McRae, G.A.; Coleman, C.E. Heat of transport for hydrogen and hydrides in Zircaloy. J. Nucl. Sci. Technol. 2024, accepted. [Google Scholar] [CrossRef]
- Greening, F. CNSC Staff Update on Elevated Hydrogen Equivalent Concentration Discovery Events in the Pressure Tubes of Reactors in Extended Operation, Addendum 2. Canadian Nuclear Safety Commission. CMD 22-M37.4. 1–3 November 2022 Commission Meeting. Available online: https://www.cnsc-ccsn.gc.ca/eng/the-commission/meetings/cmd/ (accessed on 10 June 2024).
- McRae, G.A. A Model for Hydrogen Terminal Solid Solubility during Hydride Dissolution in Neutron-Irradiated Zr-2.5Nb Pressure Tubes. Available on Request by Email from CANDU Owners Group cog@candu.org COG-04-1032 2006.
- Muehlenkamp, G.T.; Schwope, A.D. Effect of Hydrogen on the Mechanical Properties of Zirconium and Its Tin Alloys; Report, No. BMI-845; US Atomic Energy Commission: Washington, DC, USA, 1953. [Google Scholar]
- Perryman, E.C.W. Pickering pressure tube cracking experience. Nucl. Energy 1978, 17, 95–105. [Google Scholar]
- McRae, G.A.; Coleman, C.E. Thermodynamics and Kinetics of Delayed Hydride Cracking in Zirconium Alloys: A review. J. Nucl. Mater. 2024, 155006. [Google Scholar] [CrossRef]
| Inlet Distance (m) | Fluence (×1025 n/m2) | Time (years) | Temperature (K) | Nβ (%) (110) | Nβ (%) (200) | Nβ (%) Average | Obs-Calc |
|---|---|---|---|---|---|---|---|
| 0.10 | 0.10 | 9.55 | 521 | 51 | 65 | 58.0 | 3.2 |
| 0.50 | 0.35 | 1.46 | 521 | 57 | 65 | 61.0 | 7.0 |
| 0.13 | 0.20 | 6.23 | 522 | 42 | 65 | 53.5 | −1.0 |
| 0.80 | 4.60 | 10.40 | 522 | 41 | 43 | 42.0 | −4.4 |
| 0.60 | 3.56 | 11.93 | 522 | 45 | 45 | 45.0 | −3.1 |
| 0.20 | 0.50 | 14.10 | 523 | 54 | 60 | 57.0 | 3.0 |
| 0.50 | 3.48 | 14.10 | 523 | 50 | 50 | 50.0 | 1.7 |
| 0.50 | 3.48 | 14.10 | 523 | 50 | 47 | 48.5 | 0.2 |
| 0.20 | 0.50 | 14.10 | 523 | 50 | 55 | 52.5 | −1.5 |
| 3.10 | 1.30 | 1.67 | 542 | 51 | 47 | 49.0 | −3.2 |
| 3.20 | 0.94 | 1.46 | 543 | 50 | 55 | 52.5 | −0.5 |
| 3.06 | 10.78 | 14.10 | 543 | 47 | 42 | 44.5 | 3.6 |
| 0.52 | 2.11 | 5.92 | 543 | 51 | 52 | 51.5 | 0.1 |
| 3.00 | 10.37 | 13.39 | 544 | 39 | 37 | 38.0 | −3.4 |
| 3.45 | 8.20 | 10.40 | 545 | 47 | 45 | 46.0 | 2.6 |
| 3.30 | 7.94 | 6.26 | 552 | 47 | 41 | 44.0 | 0.0 |
| 5.30 | 3.21 | 12.77 | 554 | 57 | 55 | 56.0 | 1.8 |
| 4.90 | 7.41 | 10.40 | 557 | 54 | 47 | 50.5 | 2.5 |
| 4.84 | 8.76 | 13.39 | 557 | 54 | 48 | 51.0 | 3.2 |
| 4.84 | 2.84 | 3.84 | 558 | 54 | 52 | 53.0 | 1.3 |
| 5.88 | 2.20 | 13.39 | 561 | 59 | 57 | 58.0 | −3.3 |
| 6.10 | 0.60 | 13.39 | 561 | 63 | 69 | 66.0 | 1.0 |
| 5.80 | 4.58 | 14.10 | 562 | 57 | 55 | 56.0 | −2.0 |
| 5.80 | 4.58 | 14.10 | 562 | 57 | 56 | 56.5 | −1.5 |
| 5.80 | 3.36 | 11.93 | 562 | 57 | 57 | 57.0 | −1.7 |
| 6.20 | 0.20 | 12.77 | 562 | 60 | 76 | 68.0 | 1.6 |
| 6.10 | 0.50 | 14.10 | 563 | 63 | 63 | 63.0 | −4.6 |
| 6.20 | 0.15 | 10.40 | 563 | 56 | 71 | 63.5 | −1.9 |
| 5.50 | 2.88 | 8.14 | 563 | 60 | 58 | 59.0 | 1.9 |
| 3.95 | 3.24 | 3.56 | 563 | 55 | 51 | 53.0 | 0.9 |
| 6.13 | 0.50 | 13.39 | 563 | 60 | 63 | 61.5 | −5.5 |
| 6.10 | 0.50 | 14.10 | 563 | 63 | 62 | 62.5 | −5.1 |
| 6.21 | 0.02 | 3.00 | 563 | 57 | 67 | 62.0 | 3.8 |
| 5.80 | 2.73 | 9.55 | 564 | 60 | 57 | 58.5 | −1.0 |
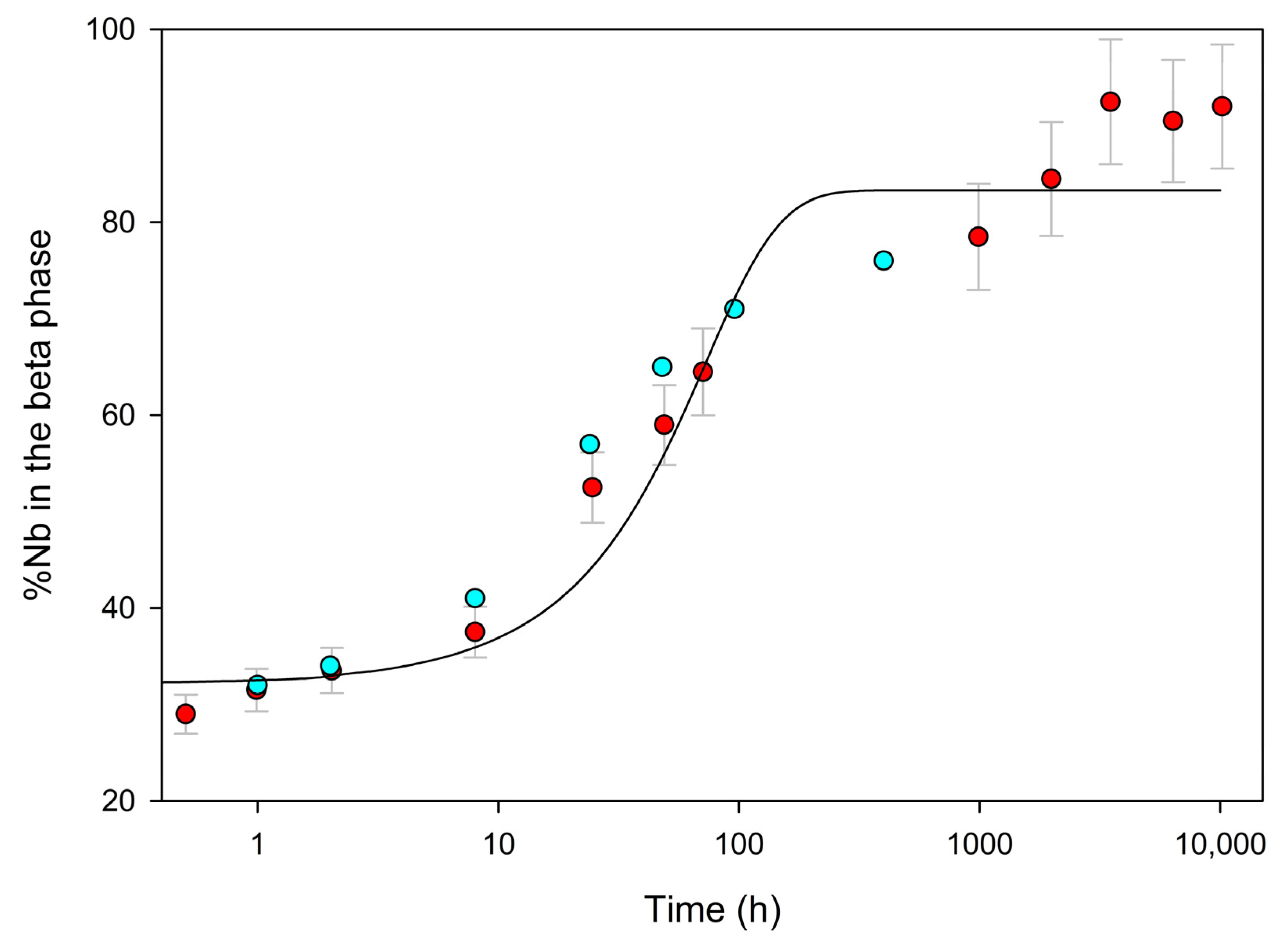
| Time (h) | Temperature (K) | Nβ (%) (110) | Nβ (%) (200) | Nβ (%) Average | Obs-Calc |
|---|---|---|---|---|---|
| 0.5 | 673 | 24 | 34 | 29 | −5.4 |
| 1 | 673 | 26 | 37 | 31.5 | −3.1 |
| 2 | 673 | 28 | 39 | 33.5 | −1.7 |
| 8 | 673 | 32 | 43 | 37.5 | −0.7 |
| 24 | 673 | 44 | 61 | 52.5 | 5.6 |
| 49 | 673 | 54 | 64 | 59 | 0.2 |
| 71 | 673 | 60 | 69 | 64.5 | −2.9 |
| 989 | 673 | 77 | 80 | 78.5 | −6.3 |
| 1986 | 673 | 83 | 86 | 84.5 | −0.3 |
| 3500 | 673 | 87 | 98 | 92.5 | 7.7 |
| 6373 | 673 | 87 | 94 | 90.5 | 5.7 |
| 10,181 | 673 | 90 | 94 | 92 | 7.2 |
| Time (h) | Temperature (K) | Nβ (%) | Obs-Calc |
|---|---|---|---|
| 0 | 673 | 27 | −7.1 |
| 1 | 673 | 32 | −2.6 |
| 2 | 673 | 34 | −1.1 |
| 8 | 673 | 41 | 2.8 |
| 24 | 673 | 57 | 10.4 |
| 48 | 673 | 65 | 6.6 |
| 96 | 673 | 71 | −3.5 |
| 400 | 673 | 76 | −8.8 |
| σ | 24.5 (±4) barns |
| iNβ (no flux) | 0.34 ± 0.01 |
| iNβ (irradiated) | 0.55 ± 0.01 |
| eqNβ (523−573)K | 0.85± 0.02 |
| E | 2.43 (±0.01) eV/atom |
| A | fixed at 1013s−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
McRae, G.A.; Griffiths, M.; Coleman, C.E. A Model for the Temperature Distribution in a Rolled Joint in a CANDU Reactor Exploiting the Decomposition of the β-Zr Phase. Metals 2024, 14, 692. https://doi.org/10.3390/met14060692
McRae GA, Griffiths M, Coleman CE. A Model for the Temperature Distribution in a Rolled Joint in a CANDU Reactor Exploiting the Decomposition of the β-Zr Phase. Metals. 2024; 14(6):692. https://doi.org/10.3390/met14060692
Chicago/Turabian StyleMcRae, Glenn A., Malcolm Griffiths, and Christopher E. Coleman. 2024. "A Model for the Temperature Distribution in a Rolled Joint in a CANDU Reactor Exploiting the Decomposition of the β-Zr Phase" Metals 14, no. 6: 692. https://doi.org/10.3390/met14060692
APA StyleMcRae, G. A., Griffiths, M., & Coleman, C. E. (2024). A Model for the Temperature Distribution in a Rolled Joint in a CANDU Reactor Exploiting the Decomposition of the β-Zr Phase. Metals, 14(6), 692. https://doi.org/10.3390/met14060692





