Slip Statistics for a Bulk Metallic Glass Treated by Cryogenic Thermal Cycling Reflect Its Optimized Plasticity
Abstract
:1. Introduction
2. Materials and Methods
3. Results
4. Discussion
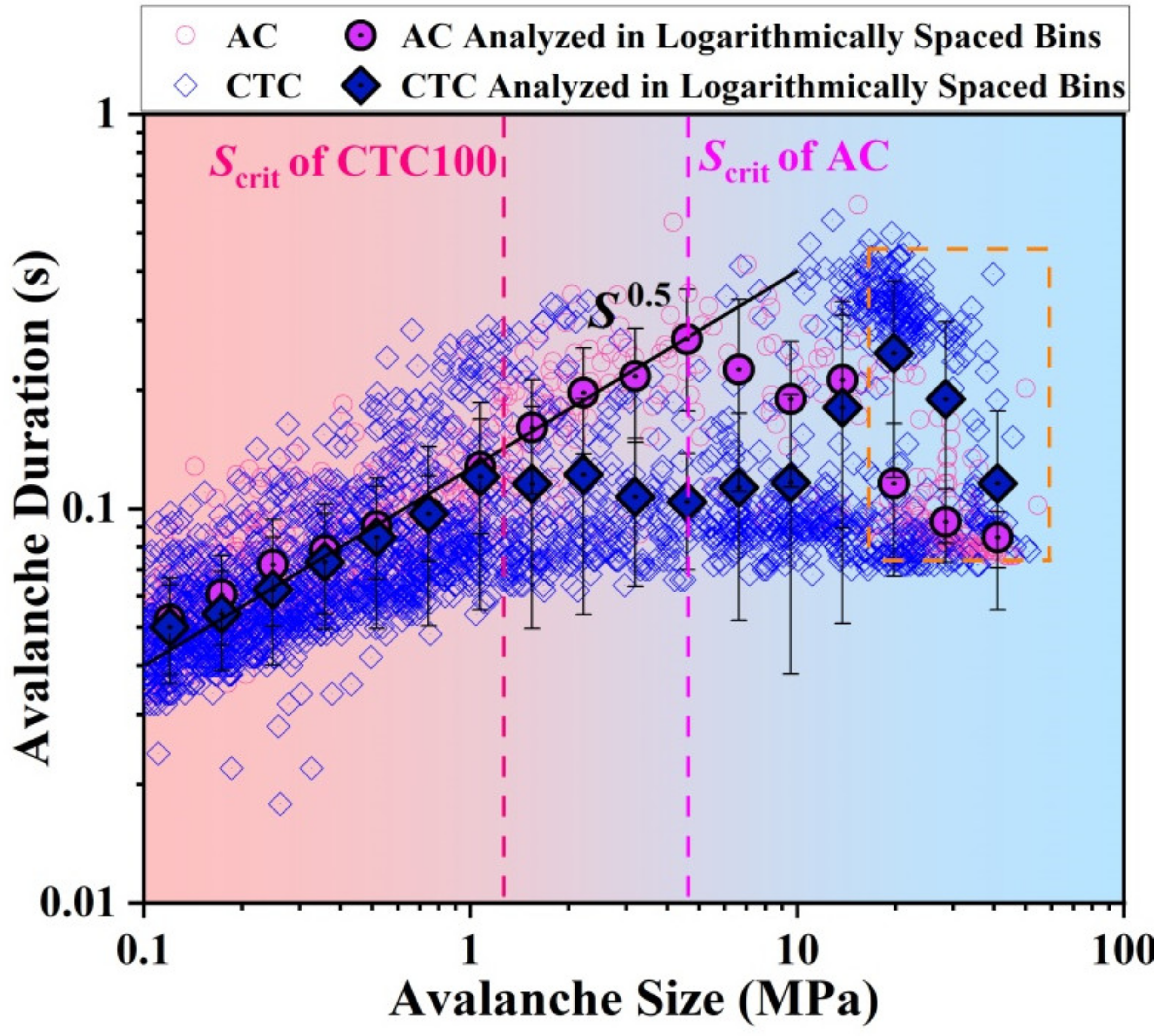
4.1. Slip Avalanches Statistics Depending on Thermal Rejuvenation
4.2. Slip Avalanches Decoding Shear Banding
4.3. Slip Avalanches Tuned by Applied Stress for the CTC100 BMG
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, W.H.; Dong, C.; Shek, C.H. Bulk metallic glasses. Mater. Sci. Eng. R Rep. 2004, 44, 45–89. [Google Scholar] [CrossRef]
- Ge, J.C.; Gu, Y.; Yao, Z.Z.; Liu, S.N.; Ying, H.Q.; Lu, C.Y.; Wu, Z.D.; Ren, Y.; Suzuki, J.; Xie, Z.H.; et al. Evolution of medium-range order and its correlation with magnetic nanodomains in Fe-Dy-B-Nb bulk metallic glasses. J. Mater. Sci. Technol. 2024, 176, 224–235. [Google Scholar] [CrossRef]
- Bordeenithikasem, P.; Carpenter, K.C.; Hofmann, D.C.; White, V.E.; Yee, K.Y.; Rizzardi, Q.; Maa, R. Miniaturized bulk metallic glass gripping structures for robotic mobility platforms. Acta Astronaut. 2024, 219, 399–407. [Google Scholar] [CrossRef]
- Gao, K.; Zhu, X.G.; Chen, L.; Li, W.H.; Xu, X.; Pan, B.T.; Li, W.R.; Zhou, W.H.; Li, L.; Huang, W.; et al. Recent development in the application of bulk metallic glasses. J. Mater. Sci. Technol. 2022, 11, 115–121. [Google Scholar] [CrossRef]
- Gu, Y.C.; Cappola, J.; Wang, J.; Li, L. A Hall-Petch-like relationship linking nanoscale heterogeneity to yield stress of heterogeneous metallic glasses. Int. J. Plast. 2023, 170, 103759. [Google Scholar] [CrossRef]
- Thurnheer, P.; Maaß, R.; Laws, K.J.; Pogatscher, S.; Löffler, J.F. Dynamic properties of major shear bands in Zr–Cu–Al bulk metallic glasses. Acta Mater. 2015, 96, 428–436. [Google Scholar] [CrossRef]
- Li, J.J.; Fan, J.F.; Wang, Z.; Wu, Y.C.; Dahmen, K.A.; Qiao, J.W. Temperature rises during strain-rate dependent avalanches in bulk metallic glasses. Intermetallics 2020, 116, 106637. [Google Scholar] [CrossRef]
- Spaepen, F. A microscopic mechanism for steady state inhomogeneous flow in metallic glasses. Acta Metall. 1977, 25, 407–415. [Google Scholar] [CrossRef]
- Li, L.; Homer, E.R.; Schuh, C.A. Shear transformation zone dynamics model for metallic glasses incorporating free volume as a state variable. Acta Mater. 2013, 61, 3347–3359. [Google Scholar] [CrossRef]
- Antonaglia, J.; Wright, W.J.; Gu, X.; Byer, R.R.; Hufnagel, T.C.; LeBlanc, M.; Uhl, J.T.; Dahmen, K.A. Bulk metallic glasses deform via slip avalanches. Phys. Rev. Lett. 2014, 112, 155501. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, W.H. Flow units as dynamic defects in metallic glassy materials. Natl. Sci. Rev. 2019, 6, 304–323. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.B.; Xu, M.Q.; Yang, G.J.; Wu, B.Q.; Lu, W.Q.; Gharbi, A.; Sun, Q.J.; Yi, J.J. Cryogenic thermal cycling effects on serration behavior in wide glass transition temperature Zr-based bulk metallic glasses. J. Non. Cryst. Solids 2024, 627, 122838. [Google Scholar] [CrossRef]
- Zhou, H.B.; Shen, L.Q.; Sun, B.A.; Wang, W.H. Research progress on the shear band of metallic glasses. J. Alloys Compd. 2023, 995, 170164. [Google Scholar] [CrossRef]
- Mo, Y.H.; Tang, X.C.; Meng, L.Y.; Qiao, J.W.; Yao, X.H. Spatial–Temporal evolution of shear banding in bulk metallic glasses. Mater. Sci. Eng. A 2021, 800, 140286. [Google Scholar] [CrossRef]
- Ding, G.; Li, C.; Zaccone, A.; Wang, W.H.; Lei, H.C.; Jiang, F.; Ling, Z.; Jiang, M.Q. Ultrafast extreme rejuvenation of metallic glasses by shock compression. Sci. Adv. 2019, 5, eaaw6249. [Google Scholar] [CrossRef]
- Ma, E. Tuning order in disorder. Nat. Mater. 2015, 14, 547–552. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.P.; Lin, Y.; Duan, F.H.; Chen, Q.; Wang, H.T.; Li, N.; Wen, J.L.; Pan, J.; Liu, L. Unexpected creep behavior in a rejuvenated metallic glass. J. Mater. Sci. Technol. 2023, 163, 140–149. [Google Scholar] [CrossRef]
- Amigo, N. Cryogenic thermal cycling rejuvenation in metallic glasses: Structural and mechanical assessment. J. Non. Cryst. Solids 2022, 596, 121850. [Google Scholar] [CrossRef]
- Ketov, S.V.; Sun, Y.H.; Nachum, S.; Lu, Z.; Checchi, A.; Beraldin, A.R.; Bai, H.Y.; Wang, W.H.; Louzguine-Luzgin, D.V.; Carpenter, M.A.; et al. Rejuvenation of metallic glasses by non-affine thermal strain. Nature 2015, 524, 200–203. [Google Scholar] [CrossRef]
- Luo, Y.S.; Wang, Z.; Qiao, J.W. Flow serrations of rejuvenation behavior through cryogenic thermal cycling for Zr-based bulk metallic glass. Philos. Mag. 2021, 101, 2261–2272. [Google Scholar] [CrossRef]
- Das, A.; Dufresne, E.M.; Maaß, R. Structural dynamics and rejuvenation during cryogenic cycling in a Zr-based metallic glass. Acta Mater. 2020, 196, 723–732. [Google Scholar] [CrossRef]
- Song, W.L.; Meng, X.H.; Wu, Y.; Cao, D.; Wang, H.; Liu, X.J.; Wang, X.Z.; Lu, Z.P. Improving plasticity of the Zr46Cu46Al8 bulk metallic glass via thermal rejuvenation. Sci. Bull. 2018, 63, 840–844. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.Z.; Huang, P.; Fan, X.L.; Wang, F. Heterogeneity dependent cryogenic thermal cycling behavior of metallic glasses: A potential energy landscape perspective. Intermetallics 2023, 159, 107935. [Google Scholar] [CrossRef]
- Guo, W.; Yu, S.; Ding, J.; Liu, S.L.; Zhao, M. Tailoring rejuvenation behavior of Zr-based metallic glass upon deep cryogenic cycling treatment. Trans. Nonferrous Met. Soc. China 2024, 34, 582–591. [Google Scholar] [CrossRef]
- Ketov, S.V.; Trifonov, A.S.; Ivanov, Y.P.; Churyumov, A.Y.; Lubenchenko, A.V.; Batrakov, A.A.; Jiang, J.; Louzguine-Luzgin, D.V.; Eckert, J.; Orava, J.; et al. On cryothermal cycling as a method for inducing structural changes in metallic glasses. NPG Asia Mater. 2018, 10, 137. [Google Scholar] [CrossRef]
- Zhu, Q.Y.; Jin, X.; Yang, H.J.; Jia, L.; Qiao, J.W. Effect of deep cryogenic cycling treatment on shear transformation zone volume and size of Zr-based metallic glass. J. Mater. Res. 2021, 36, 2047–2055. [Google Scholar] [CrossRef]
- Meng, Y.H.; Zhang, S.Y.; Zhou, W.H.; Yao, J.H.; Liu, S.N.; Li, Y. Rejuvenation by enthalpy relaxation in metallic glasses. Acta Mater. 2022, 241, 118376. [Google Scholar] [CrossRef]
- Gao, T.; Yang, C.; Ding, G.; Dai, L.H.; Jiang, M.Q. Structural rejuvenation of a well-aged metallic glass. Fundam. Res. 2023, 14, 57. [Google Scholar] [CrossRef]
- Das, A.; Ott, C.; Pechimuthu, D.; Moosavi, R.; Stoica, M.; Derlet, P.M.; Maa, R. Shear-band cavitation determines the shape of the stress-strain curve of metallic glasses. Phys. Rev. Lett. 2023, 7, 023602. [Google Scholar] [CrossRef]
- Wang, Z.; Li, J.J.; Zhang, W.; Qiao, J.W.; Wang, B.C. The self-organized critical behavior in Pd-based bulk metallic glass. Metals 2015, 5, 1188–1196. [Google Scholar] [CrossRef]
- Antonaglia, J.; Xie, X.; Schwarz, G.; Wraith, M.; Qiao, J.; Zhang, Y.; Liaw, P.K.; Uhl, J.T.; Dahmen, K.A. Tuned critical avalanche scaling in bulk metallic glasses. Sci. Rep. 2014, 4, 4382. [Google Scholar] [CrossRef]
- Du, Y.; Zhou, Q.; Jia, Q.; Shi, Y.; Wang, H.; Wang, J. Imparities of shear avalanches dynamic evolution in a metallic glass. Mater. Res. Lett. 2020, 8, 357–363. [Google Scholar] [CrossRef]
- Sun, B.A.; Yu, H.B.; Jiao, W.; Bai, H.Y.; Zhao, D.Q.; Wang, W.H. Plasticity of ductile metallic glasses: A self-organized critical state. Phys. Rev. Lett. 2010, 105, 035501. [Google Scholar] [CrossRef]
- Wright, W.J.; Liu, Y.; Gu, X.; Van Ness, K.D.; Robare, S.L.; Liu, X.; Antonaglia, J.; LeBlanc, M.; Uhl, J.T.; Hufnagel, T.C.; et al. Experimental evidence for both progressive and simultaneous shear during quasistatic compression of a bulk metallic glass. J. Appl. Phys. 2016, 119, 084908. [Google Scholar] [CrossRef]
- Maaß, R. Beyond Serrated Flow in Bulk Metallic Glasses: What Comes Next? Metall. Mater. Trans. A 2020, 51, 5597–5605. [Google Scholar] [CrossRef]
- Long, A.A.; Wright, W.J.; Gu, X.J.; Thackray, A.; Nakib, M.; Uhl, J.T.; Dahmen, K.A. Experimental evidence that shear bands in metallic glasses nucleate like cracks. Sci. Rep. 2022, 12, 8499. [Google Scholar] [CrossRef] [PubMed]
- Qu, R.T.; Liu, Z.Q.; Wang, G.; Zhang, Z.F. Progressive shear band propagation in metallic glasses under compression. Acta Mater. 2015, 91, 19–33. [Google Scholar] [CrossRef]
- Li, J.J.; Qiao, J.W.; Wu, Y.C. Seismic-like size dynamics of slip avalanches in bulk metallic glasses. J. Alloys Compd. 2020, 819, 152941. [Google Scholar] [CrossRef]
- McFaul, L.W.; Wright, W.J.; Gu, X.; Uhl, J.T.; Dahmen, K.A. Aftershocks in slowly compressed bulk metallic glasses: Experiments and theory. Phys. Rev. E 2018, 97, 063005. [Google Scholar] [CrossRef]
- Long, A.A.; Denisov, D.V.; Schall, P.; Hufnagel, T.C.; Gu, X.; Wright, W.J.; Dahmen, K.A. From critical behavior to catastrophic runaways: Comparing sheared granular materials with bulk metallic glasses. Granul. Matter 2019, 21, 99. [Google Scholar] [CrossRef]
- Salje, E.K.; Saxena, A.; Planes, A. (Eds.) Avalanches in Functional Materials and Geophysics; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Dahmen, K.A.; Ben-Zion, Y.; Uhl, J.T. Micromechanical model for deformation in solids with universal predictions for stress-strain curves and slip avalanches. Phys. Rev. Lett. 2009, 102, 175501. [Google Scholar] [CrossRef] [PubMed]
- Maaß, R.; Wraith, M.; Uhl, J.T.; Greer, J.R.; Dahmen, K.A. Slip statistics of dislocation avalanches under different loading modes. Phys. Rev. E 2015, 91, 042403. [Google Scholar] [CrossRef] [PubMed]
- Cao, P.H.; Dahmen, K.A.; Kushima, A.; Wright, W.J.; Park, H.S.; Short, M.P.; Yip, S. Nanomechanics of slip avalanches in amorphous plasticity. J. Mech. Phys. Solids 2018, 114, 158–171. [Google Scholar] [CrossRef]
- Derlet, P.M.; Maaß, R. Thermally-activated stress relaxation in a model amorphous solid and the formation of a system-spanning shear event. Acta Mater. 2018, 143, 205–213. [Google Scholar] [CrossRef]
- Zhao, P.; Li, J.; Hwang, J.; Wang, Y. Influence of nanoscale structural heterogeneity on shear banding in metallic glasses. Acta Mater. 2017, 134, 104–115. [Google Scholar] [CrossRef]
- Liu, C.; Ikeda, Y.; Maaß, R. Strain-dependent shear-band structure in a Zr-based bulk metallic glass. Scr. Mater. 2021, 190, 75–79. [Google Scholar] [CrossRef]
- Şopu, D.; Scudino, S.; Bian, X.L.; Gammer, C. Atomic-scale origin of shear band multiplication in heterogeneous metallic glasses. J. Eckert Scr. Mater. 2020, 178, 57–61. [Google Scholar] [CrossRef]
- Pan, D.; Inoue, A.; Sakurai, T.; Chen, M.W. Experimental characterization of shear transformation zones for plastic flow of bulk metallic glasses, Proc. Natl. Acad. Sci. USA 2008, 105, 14769–14772. [Google Scholar] [CrossRef]
- Qu, R.T.; Wu, S.J.; Wang, S.G.; Wang, X.D.; Zhang, Z.F. Shear banding stability and fracture of metallic glass: Effect of external confinement, J. Mech. Phys. Solids 2020, 138, 103922. [Google Scholar] [CrossRef]
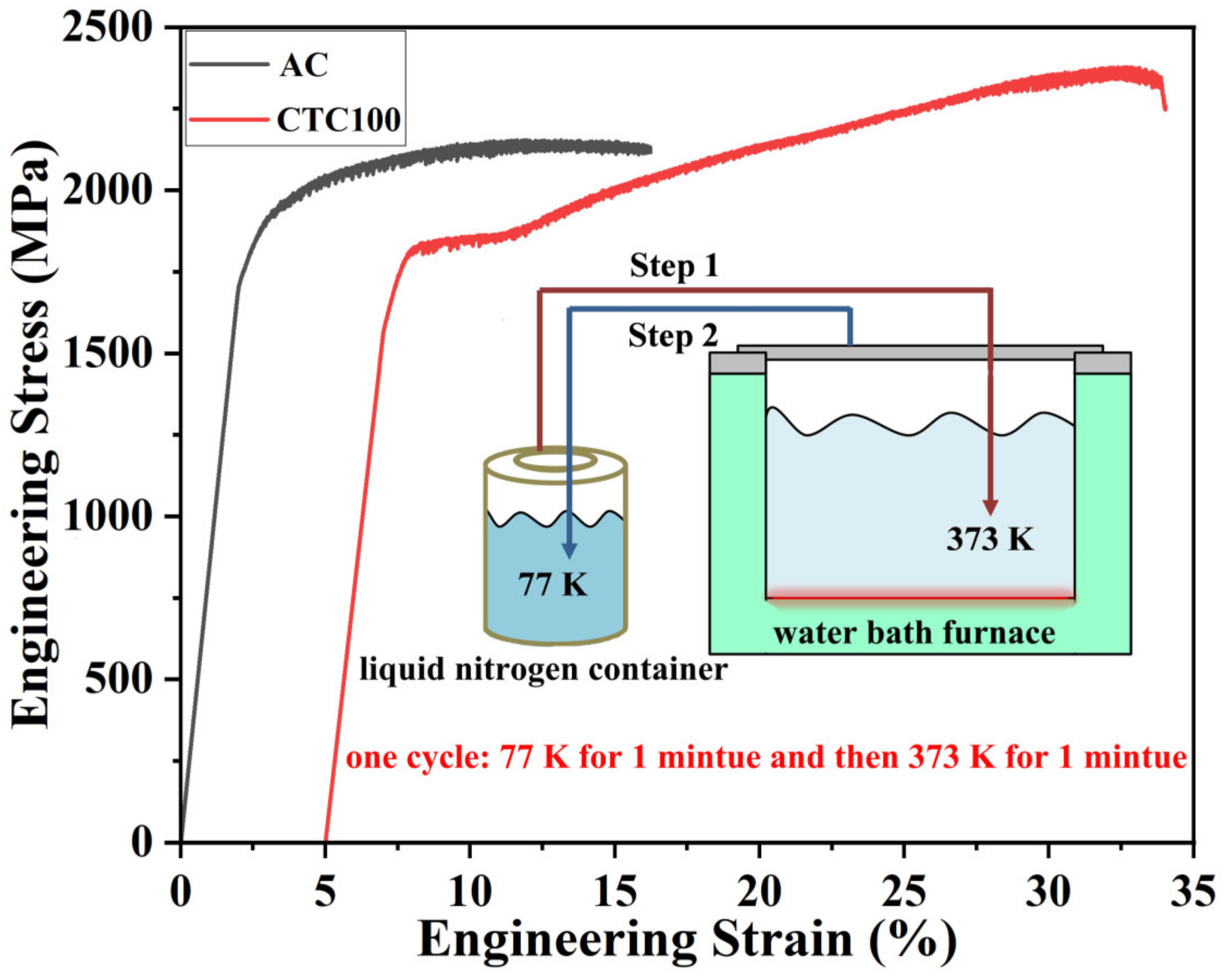

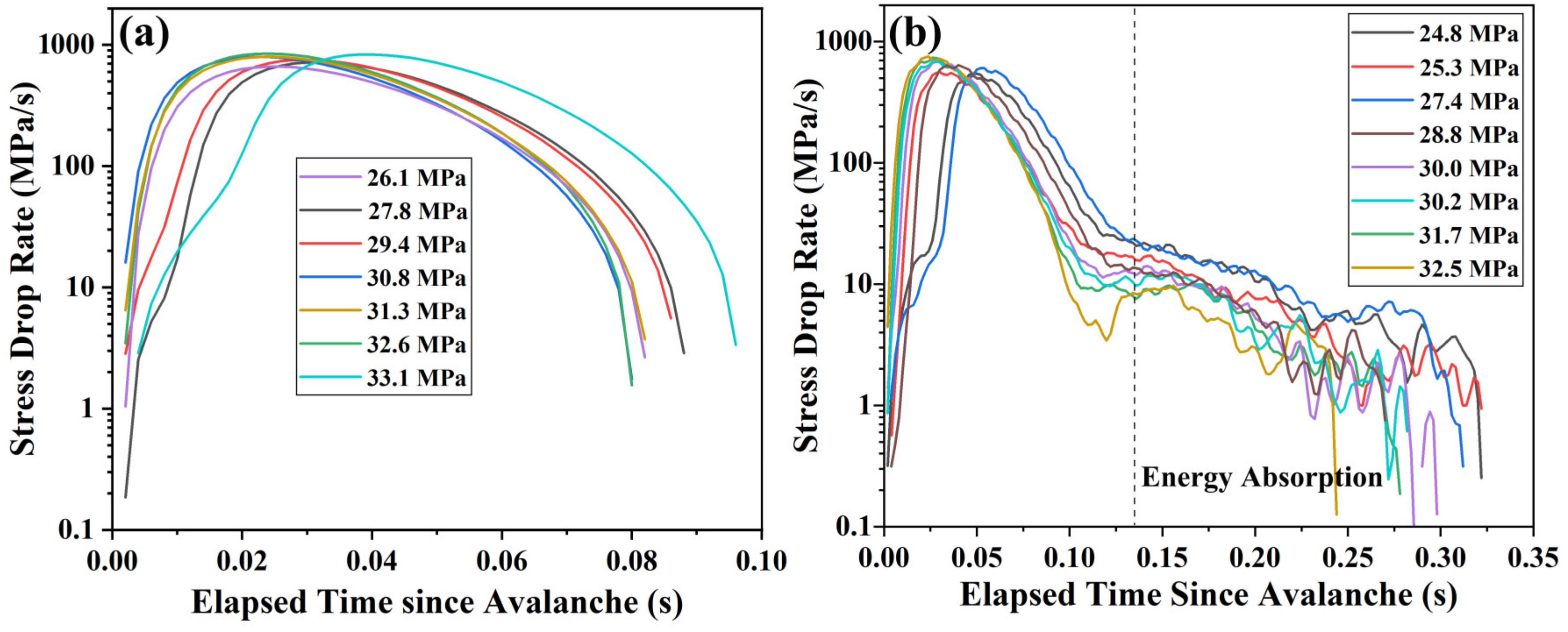
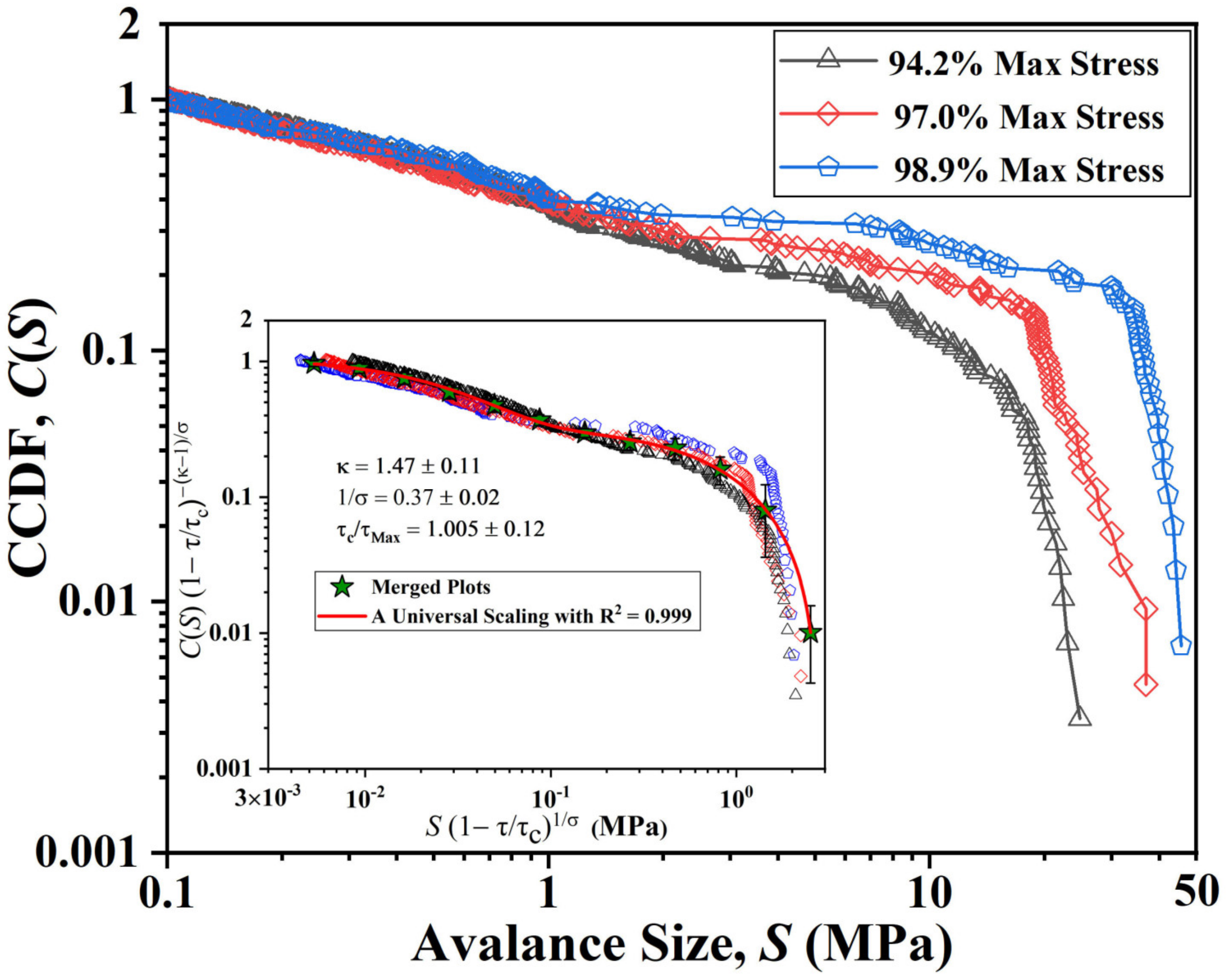
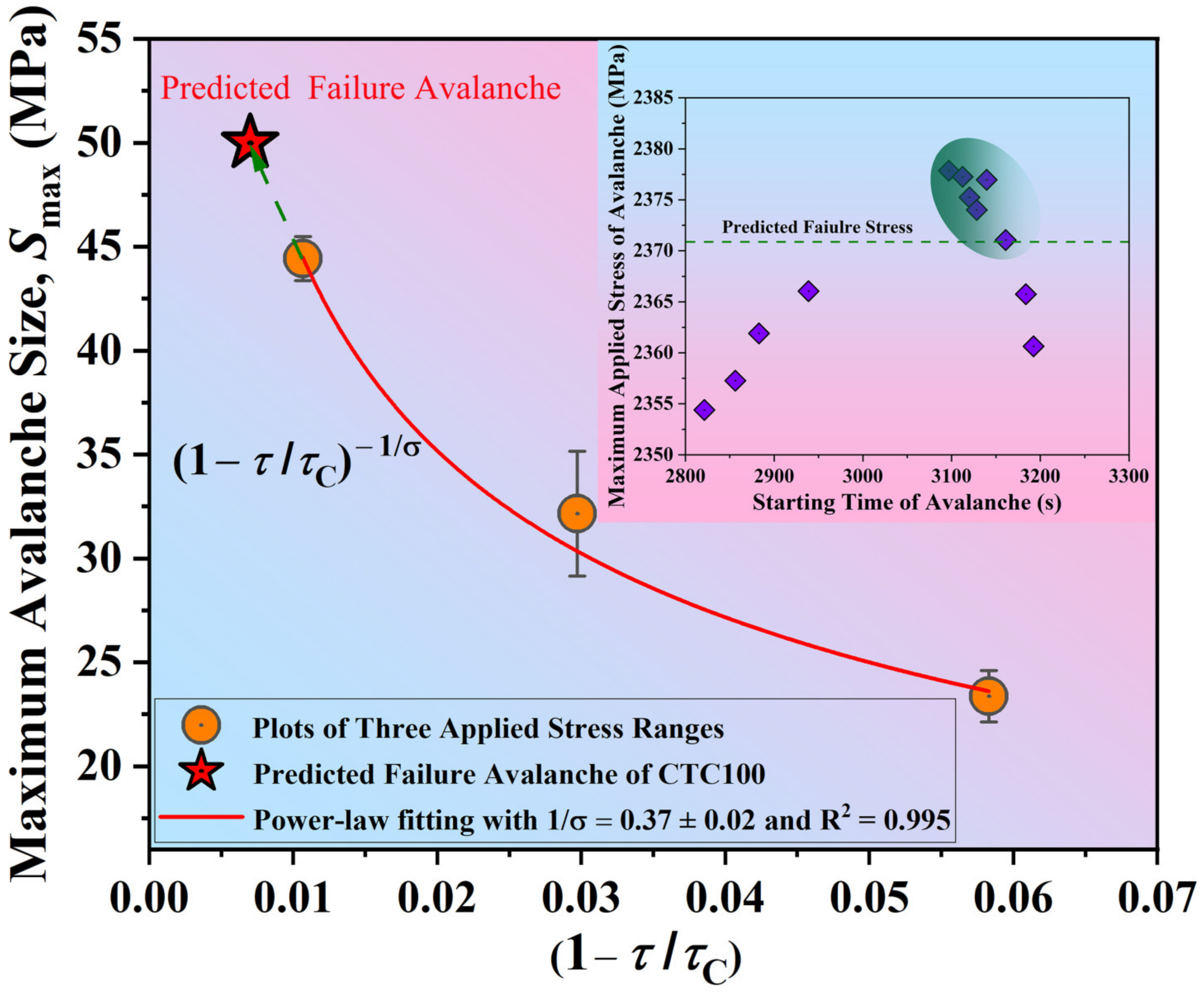
| BMG | (%) | (s) | (MPa) | (MPa/s) | (MPa) | (%) | ||
|---|---|---|---|---|---|---|---|---|
| AC | 14 | 1.96 | 54.3 | 1155 | 4.6 | 70 | 492 | 703 |
| CTC100 | 26 | 1.38 | 51.3 | 1000 | 1.5 | 64 | 1205 | 1885 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Liu, Y.; Zhao, W.; Zhang, H.; Zhang, Y.; Lu, H.; Wang, Z.; Liu, Y. Slip Statistics for a Bulk Metallic Glass Treated by Cryogenic Thermal Cycling Reflect Its Optimized Plasticity. Metals 2024, 14, 731. https://doi.org/10.3390/met14060731
Li J, Liu Y, Zhao W, Zhang H, Zhang Y, Lu H, Wang Z, Liu Y. Slip Statistics for a Bulk Metallic Glass Treated by Cryogenic Thermal Cycling Reflect Its Optimized Plasticity. Metals. 2024; 14(6):731. https://doi.org/10.3390/met14060731
Chicago/Turabian StyleLi, Jiaojiao, Yao Liu, Wei Zhao, Huiyun Zhang, Yajun Zhang, Huihu Lu, Zhong Wang, and Yong Liu. 2024. "Slip Statistics for a Bulk Metallic Glass Treated by Cryogenic Thermal Cycling Reflect Its Optimized Plasticity" Metals 14, no. 6: 731. https://doi.org/10.3390/met14060731
APA StyleLi, J., Liu, Y., Zhao, W., Zhang, H., Zhang, Y., Lu, H., Wang, Z., & Liu, Y. (2024). Slip Statistics for a Bulk Metallic Glass Treated by Cryogenic Thermal Cycling Reflect Its Optimized Plasticity. Metals, 14(6), 731. https://doi.org/10.3390/met14060731








