On the Efficiency of Air-Cooled Metal Foam Heat Exchangers
Abstract
:1. Introduction
2. Methodology
2.1. Samples
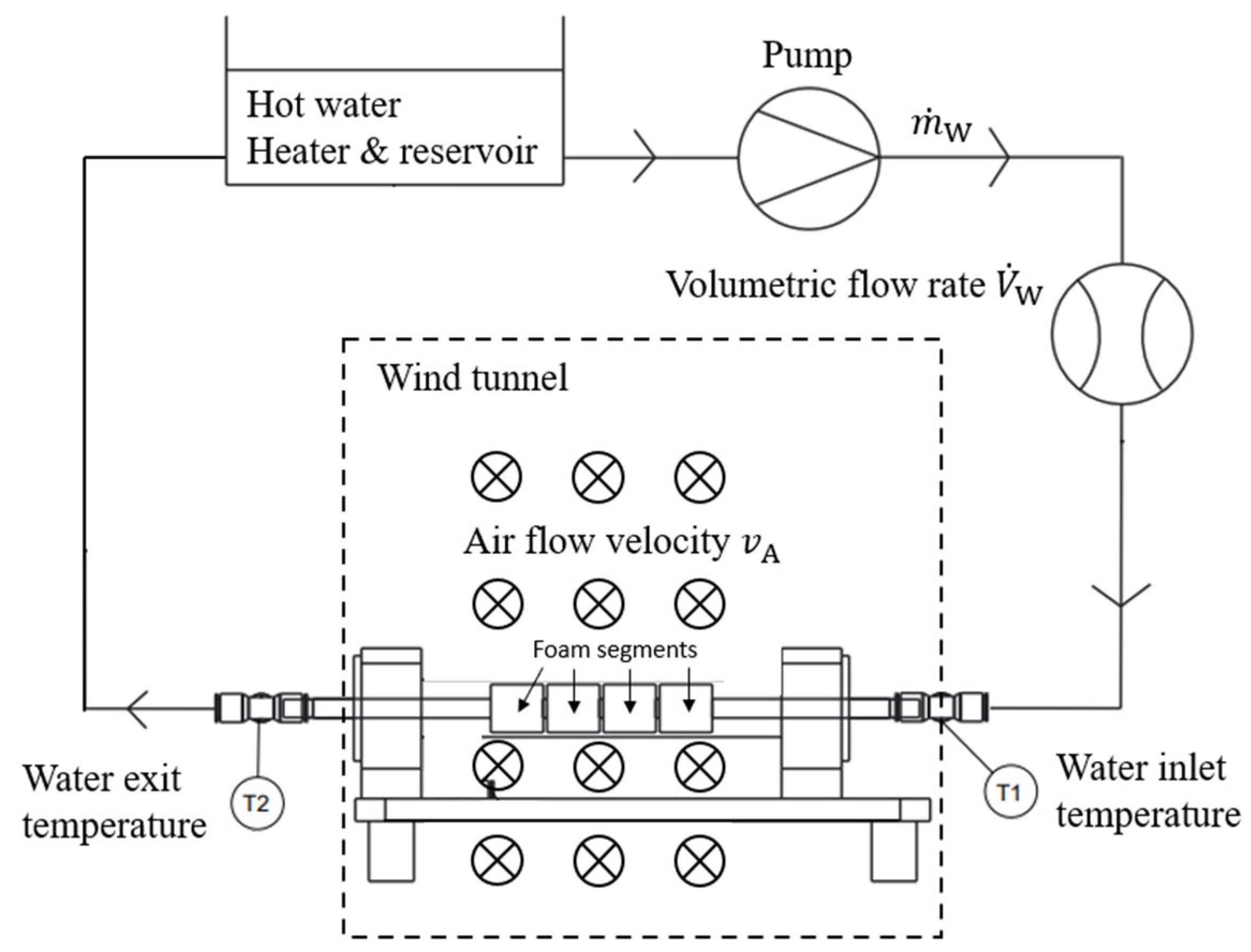
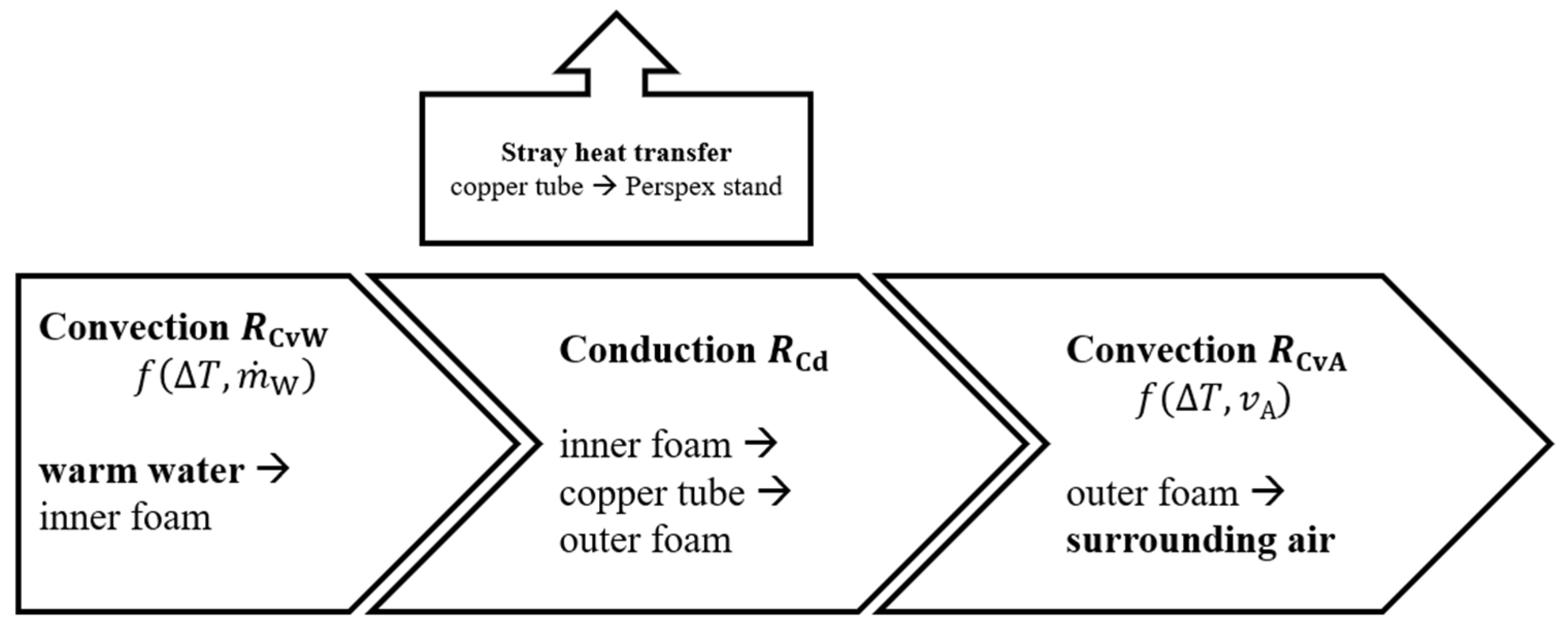
2.2. Heat-Transfer Apparatus
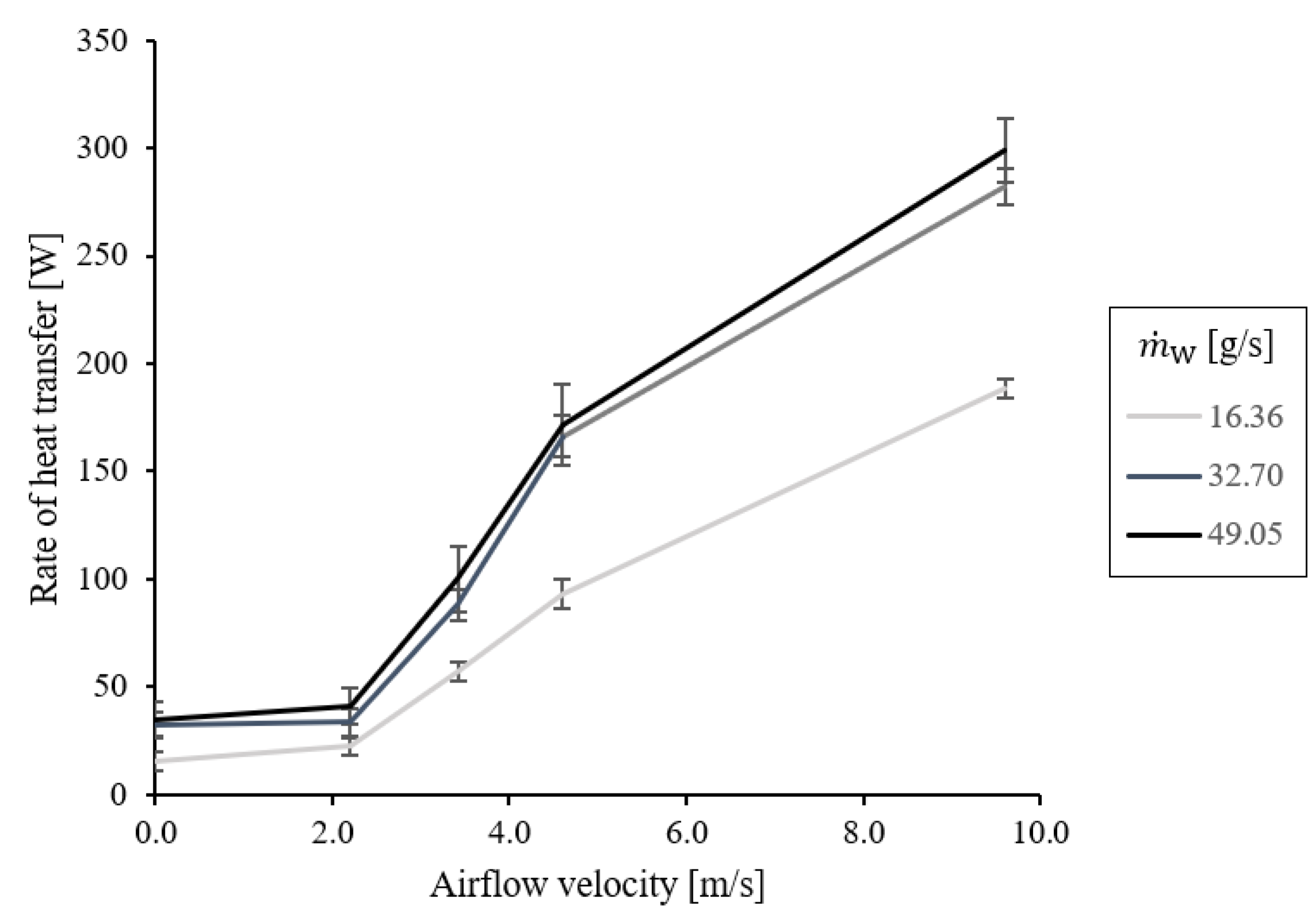
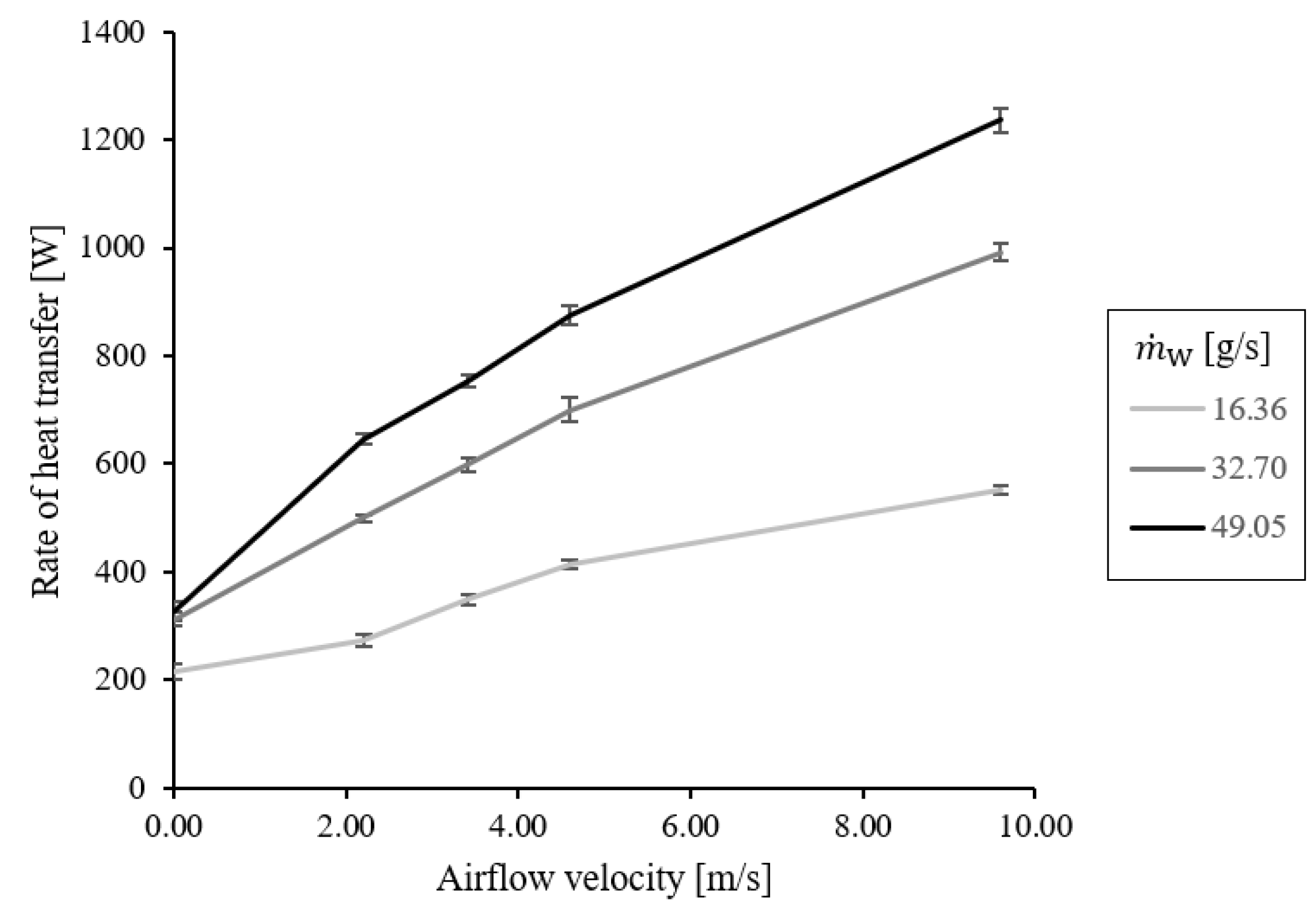
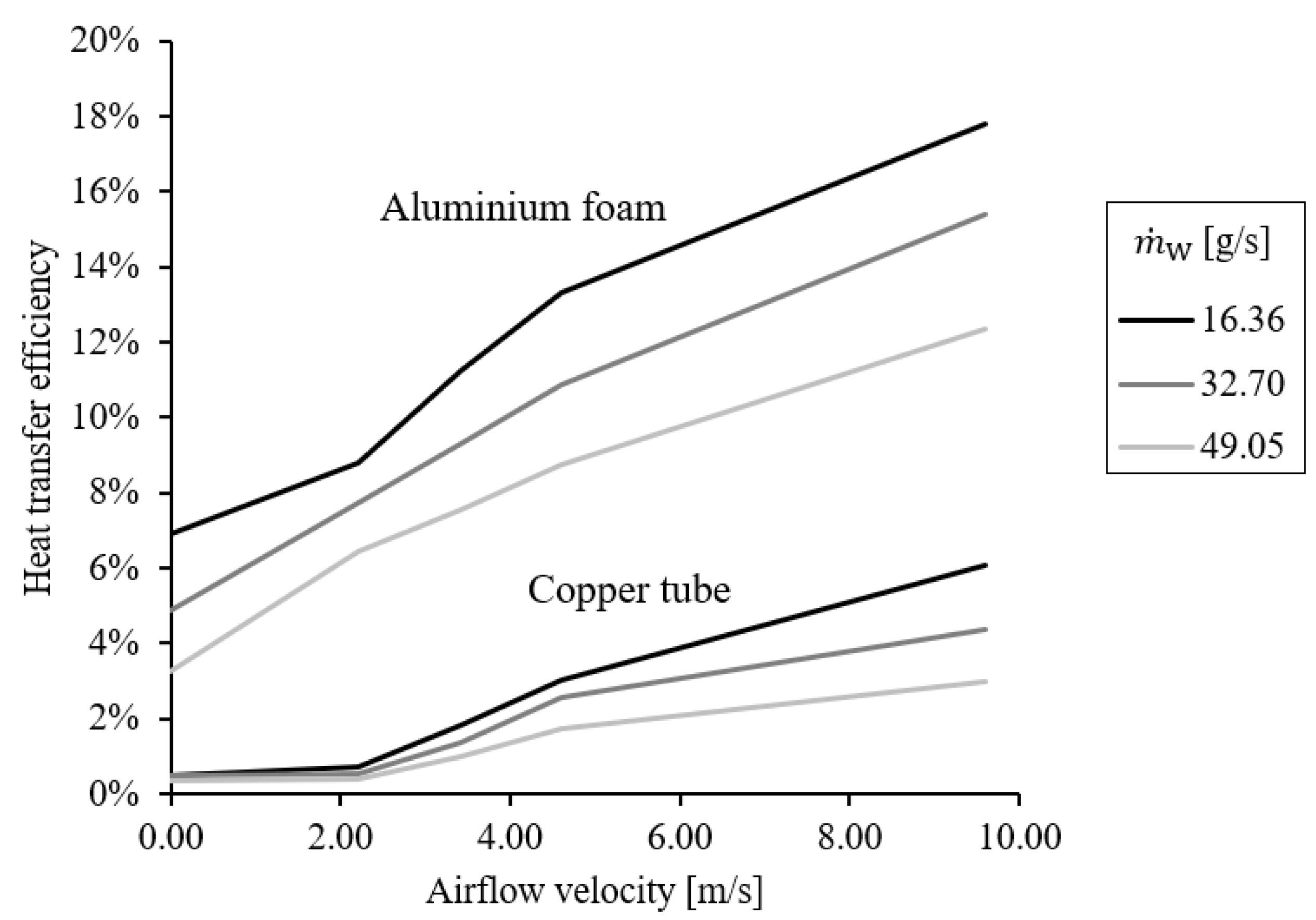
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lu, W.; Zhao, C.Y.; Tassou, S.A. Thermal analysis on metal-foam filled heat exchangers. Part I: Metal-foam filled pipes. Int. J. Heat Mass Transf. 2006, 49, 2751–2761. [Google Scholar] [CrossRef]
- Chandora, N.; Mani, A.; Advaith, S. Investigation of heat transfer and pressure drop characteristics in metal-foam filled channels in a plate heat exchanger: A comparative experimental study. Appl. Therm. Eng. 2024, 241, 122368. [Google Scholar] [CrossRef]
- Feng, S.; Kuang, J.; Wen, T.; Lu, T.; Ichimiya, K. An experimental and numerical study of finned metal foam heat sinks under impinging air jet cooling. Int. J. Heat Mass Transf. 2014, 77, 1063–1074. [Google Scholar] [CrossRef]
- Morkos, B.; Dochibhatla, S.V.S.; Summers, J.D. Effects of Metal Foam Porosity, Pore Size, and Ligament Geometry on Fluid Flow. J. Thermal Sci. Eng. Appl. 2018, 10, 041007. [Google Scholar] [CrossRef]
- Chumpia, A.; Hooman, K. Performance evaluation of single tubular aluminium foam heat exchangers. Appl. Therm. Eng. 2014, 66, 266–273. [Google Scholar] [CrossRef]
- T’joen, C.; De Jaeger, P.; Huisseune, H.; Van Herzeele, S.; Vorst, N.; De Paepe, M. Thermo-hydraulic study of a single row heat exchanger consisting of metal foam covered round tubes. Int. J. Heat Mass Transf. 2010, 53, 3262–3274. [Google Scholar] [CrossRef]
- Ambrosio, G.; Bianco, N.; Chiu, W.K.; Iasiello, M.; Naso, V.; Oliviero, M. The effect of open-cell metal foams strut shape on convection heat transfer and pressure drop. Appl. Therm. Eng. 2016, 103, 333–343. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Zhao, Y. Experimental study on heat transfer enhancement of gas tube partially filled with metal foam. Exp. Therm. Fluid Sci. 2018, 97, 408–416. [Google Scholar] [CrossRef]
- Fiedler, T.; Moore, R.; Movahedi, N. Manufacturing and Characterization of Tube-Filled ZA27 Metal Foam Heat Exchangers. Metals 2021, 11, 1277. [Google Scholar] [CrossRef]
- Fiedler, T.; Movahedi, N. Compact Aluminium Foam Heat Exchangers. Metals 2023, 13, 1440. [Google Scholar] [CrossRef]
- Li, Y.; Niu, Z.; Gao, X.; Guo, J.; Yang, X.; He, Y.-L. Effect of filling height of metal foam on improving energy storage for a thermal storage tank. Appl. Therm. Eng. 2023, 229, 120584. [Google Scholar] [CrossRef]
- Lv, C.; Li, W.; Du, J.; Liang, J.; Yang, H.; Zhu, Y.; Ma, B. Experimental investigation of permeability and Darcy-Forchheimer flow transition in metal foam with high pore density. Exp. Therm. Fluid Sci. 2024, 154, 111149. [Google Scholar] [CrossRef]
- Zhang, Z.; Yan, G.; Sun, M.; Li, S.; Zhang, X.; Song, Y.; Liu, Y. Forced convective heat transfer performance of foam-like structures—Comparison of the Weaire-Phelan and the Kelvin structures with real metal foam. Int. J. Heat Mass Transf. 2024, 227, 125558. [Google Scholar] [CrossRef]
- Konduru, R.N.; Farges, O.; Schick, V.; Hairy, P.; Gaillard, Y.; Parent, G. Experimental and numerical investigation of porous heat exchangers with Kelvin cell structured foam at high temperatures: Coupled conduction-convection and radiation heat transfer. Int. J. Heat Mass Transf. 2024, 224, 125253. [Google Scholar] [CrossRef]


| Sample Characteristics | Average | #1 | #2 | #3 | #4 |
|---|---|---|---|---|---|
| Volume [mL] | 29.3 | 27.8 | 29.7 | 30.8 | 28.9 |
| Surface area/volume [μm2/μm3] | |||||
| 0.00166 | 0.00175 | 0.00154 | 0.00160 | 0.00175 |
| 0.00391 | 0.00397 | 0.00370 | 0.00381 | 0.00416 |
| Surface area enhancement [%] (relative to cylindrical pipe) | |||||
| 1257 | 1285 | 1204 | 1214 | 1326 |
| 1955 | 1985 | 1849 | 1906 | 2080 |
| Porosity, [vol.%] | |||||
| 80.0 | 80.8 | 79.6 | 78.9 | 80.6 |
| 65.9 | 62.9 | 68.7 | 65.0 | 66.9 |
| Average pore size [μm] | |||||
| 1924 | 1757 | 2028 | 2031 | 1879 |
| 2084 | 1874 | 2386 | 1996 | 2079 |
| Values Retrieved from [10] | This Study | |||
|---|---|---|---|---|
| [g/s] | Mass Flow Rate of the Outer Water Stream [g/s] | [m/s] | ||
| 16.4 | 32.7 | 49.0 | 9.6 | |
| 16.4 | 1064 | 1287 | 1403 | 188 |
| 32.7 | 1297 | 1656 | 1760 | 282 |
| 49.0 | 1471 | 1727 | 1789 | 299 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fiedler, T.; Movahedi, N.; Stanger, R. On the Efficiency of Air-Cooled Metal Foam Heat Exchangers. Metals 2024, 14, 750. https://doi.org/10.3390/met14070750
Fiedler T, Movahedi N, Stanger R. On the Efficiency of Air-Cooled Metal Foam Heat Exchangers. Metals. 2024; 14(7):750. https://doi.org/10.3390/met14070750
Chicago/Turabian StyleFiedler, Thomas, Nima Movahedi, and Rohan Stanger. 2024. "On the Efficiency of Air-Cooled Metal Foam Heat Exchangers" Metals 14, no. 7: 750. https://doi.org/10.3390/met14070750
APA StyleFiedler, T., Movahedi, N., & Stanger, R. (2024). On the Efficiency of Air-Cooled Metal Foam Heat Exchangers. Metals, 14(7), 750. https://doi.org/10.3390/met14070750









