Next Article in Journal
On the Efficiency of Air-Cooled Metal Foam Heat Exchangers
Previous Article in Journal
Phase Transformations after Heat Treating an As-Cast Fe-30Mn-8.8Al-0.3Si-0.15C Steel
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Metals
Volume 14
Issue 7
10.3390/met14070749
metals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Temperature-Dependent Mechanical Behaviors and Deformation Mechanisms in a Si-Added Medium-Entropy Superalloy with L12 Precipitation

by
Tuanwei Zhang
1,2,
Tianxiang Bai
1,2,
Renlong Xiong
3,*,
Shunhui Luo
1,2,
Hui Chang
1,2,
Shiyu Du
1,2,
Jinyao Ma
1,4,
Zhiming Jiao
1,2,
Shengguo Ma
1,2,
Jianjun Wang
1,2 and
Zhihua Wang
1,2
1
Institute of Applied Mechanics, College of Mechanical and Vehicle Engineering, Taiyuan University of Technology, Taiyuan 030024, China
2
Shanxi Key Laboratory of Material Strength and Structural Impact, Taiyuan University of Technology, Taiyuan 030024, China
3
Hubei Provincial Key Laboratory of Chemical Equipment Intensification and Intrinsic Safety, School of Mechanical and Electrical Engineering, Wuhan Institute of Technology, Wuhan 430205, China
4
Instrumental Analysis Center, Taiyuan University of Technology, Taiyuan 030024, China
*
Author to whom correspondence should be addressed.
Metals 2024, 14(7), 749; https://doi.org/10.3390/met14070749
Submission received: 11 May 2024 / Revised: 19 June 2024 / Accepted: 21 June 2024 / Published: 25 June 2024
Browse Figures
Versions Notes

Abstract

:
A novel Ni-Co-Cr-based medium-entropy superalloy with a high Si content (7.5 at%) strengthened by an L12 phase was developed. The pure L12 phase, characterized by an average size of 50 nm and a volume fraction of 46%, was precipitated within the FCC matrix. This alloy exhibits excellent mechanical properties over a wide range of temperatures from 77 K to 1073 K. A yield strength of 1005 MPa, an ultimate tensile strength of 1620 MPa, and a tensile elongation of 36% were achieved at 77 K, with a maximum value of 4.8 GPa at the second stage of the work-hardening rate. The alloy maintains a basically consistent yield strength of approximately 800 MPa from 298 K to 973 K, showcasing significant strain-hardening capabilities, with values of 2.5 GPa, 3.7 GPa, and 4.8 GPa at 873 K, 298 K, and 77 K, respectively. Microscopic analysis revealed that at room and cryogenic temperatures, multilayer stacking faults (SFs), SF bands, and SF networks, rather than twins, effectively stored a large number of dislocations and impeded dislocation movement, thereby enhancing the work-hardening ability of the alloy. Furthermore, at 773 K, the primary deformation mechanism involved high-density dislocation walls (HDDWs) consisting of dislocation tangles and SF lines. As the temperature rose to 973 K, the work-hardening process was influenced by the APB shearing mechanism (in the form of dislocation pairs), SF lines, and microtwins generated through atomic rearrangement. This study not only provides valuable insights for the development of new oxidation-resistant superalloys but also enhances our understanding of high-temperature deformation mechanisms.

1. Introduction

With the growing need for load-bearing structures to operate in wide temperature ranges in aerospace and other industries, the limitations of traditional nickel-based and cobalt-based superalloys have become apparent. This has prompted researchers to explore materials capable of withstanding higher temperatures and exhibiting superior performance across a broad temperature spectrum [1,2]. Due to the design concept of multiple principal elements and the presence of high entropy and sluggish diffusion effects, medium-/high-entropy alloys (M/HEAs) offer a new approach to designing alloys for high-temperature applications [3]. The M/HEAs reported so far have shown outstanding overall properties, including excellent high-temperature strength, oxidation resistance, and performance at low temperatures [4,5], making them a promising candidate for the generation of new materials for high-temperature components in the aerospace industry.
Current research on high-temperature M/HEAs primarily centers on two alloy systems. One system involves incorporating refractory elements such as W, Mo, Nb, Ta, and Hf as the main components, resulting in a higher anti-softening temperature and strength [5,6]. Nevertheless, these alloys often exhibit tensile brittleness due to their inherent body-centered cubic (BCC) structure. Research efforts primarily focus on the high-temperature compression properties of BCC M/HEAs [5]. While some newly developed BCC M/HEAs have shown improved tensile plasticity by substituting refractory elements with lower-melting-point elements like Ti, Zr, and Nb, this often results in decreased strength and/or a lower thermal softening temperature [7,8]. Another avenue of research in high-temperature M/HEAs involves the development of a novel type of multi-principal-element L12 phase-strengthened medium-/high-entropy (M/HE) superalloys [9,10,11,12], inspired by L12 phase-strengthened Ni-based and Co-based alloys. Various M/HE superalloy systems have been explored, such as (NiCoFe)86Al7Ti7 MEA [9] and (NiCoCrFe)94Al4Ti2 HEA [10]. For instance, the multi-principal-element L12 phase (the stoichiometric is (Ni43.3Co23.7Fe8)3(Ti14.4Al8.6Fe2))-reinforced (NiCoFe)86Al7Ti7 MEA possesses a yield strength of 1.1 GPa, tensile strength of 1.5 GPa, and tensile elongation of 50% at room temperature. In addition, other M/HEAs doped with Al and Ti demonstrate exceptional mechanical properties at room temperature, attributed not only to inherent mechanical properties of the M/HEA matrix but also to the presence of multi-principal and high-density L12 precipitates [11,12]. Notably, M/HEAs are prone to precipitating high-density coherent precipitates through intentional precipitation design [9,12,13,14].
Current research on L12 phase-strengthened M/HEAs primarily examines their tensile properties at room temperature [5,10,12,14]. However, there is limited information available on their mechanical properties across a wide range of temperatures, particularly at elevated temperatures. He et al. studied the high-temperature plastic flow behavior of (NiCoCrFe)94Al4Ti2 HEA and observed that the presence of a brittle Heusler phase, alongside the L12 phase, in the alloy promotes crack formation at the interface between the brittle phase and the matrix under high temperatures [15]. Similarly, L12 phase-strengthened (Ni2Co2FeCr)92Al4Nb4 HEA exhibits impressive mechanical properties at room temperature but is susceptible to brittle fracture at high temperatures due to the presence of the D019 phase [16]. Furthermore, newly developed L12 phase-strengthened HE-superalloys demonstrate very low plasticity under high-temperature tension, which is attributed to the accumulation of massive carbides at the grain boundaries (GBs) [17]. Therefore, leveraging the unique characteristics of multi-principal-element matrices and multi-principal-element L12 phases in M/HEAs could lead to the development of a novel high-performance superalloy that avoids brittle phases, thereby expanding its application potential from room temperature and cryogenic environments to high-temperature settings.
In the present study, NiCoCrSi0.3 MEA, developed by our group to overcome the strength-ductility trade-off [18], was selected as the base alloy. The Cr content was decreased to prevent a brittle phase, while the Si content was increased to effectively lower the stacking fault energy (SFE) of the matrix and enhance the high-temperature oxidation resistance. Meanwhile, Al and Ti were supplemented, and the content of Ni was increased for the precipitation of a large amount of a Ni3(Al, Ti)-type L12 phase. Thus, we developed a Ni2CoCr0.5Si0.3Al0.1Ti0.1 ME superalloy [19] with a pure “FCC + L12” phase structure. The initial microstructure, mechanical properties, and deformation mechanisms of the “FCC + L12” phase ME superalloy were studied in a wide range of temperatures. The research also examined the influence of the L12 phase on the high-temperature mechanical behaviors of the alloy.

2. Materials and Experimental Methods

2.1. Alloy Preparation

Alloys with a nominal composition of Ni2CoCr0.5Si0.3Al0.1Ti0.1 (in molar ratio) were prepared by arc melting using high-purity (>99.99 wt.%) metals in an argon atmosphere. The alloy ingots were re-melted five to eight times, accompanied by magnetic stirring to ensure chemical homogeneity before being cast into a water-cooled copper mold with dimensions of 5 mm × 20 mm × 100 mm. The as-cast plates were homogenized at 1100 °C for 2 h, cold-rolled to a 60% reduction ratio in thickness, annealed at 1000 °C for 10 min, and aged at 700 °C for 4 h. This alloy is referred to as AT0.1-A700 ME superalloy. Water quenching was used for all quenching processes. The chemical composition of the alloy is listed in Table 1.

2.2. Tensile Testing

Quasi-static tensile samples were prepared by cutting them into dog-bone shapes using electrical discharge machining (EDM), resulting in a gauge geometry of 20 mm (length) × 5 mm (width) × 1.8 mm (thickness). Prior to the tensile test, all surfaces and sides of the samples were polished with 2000-grit SiC paper. For cryogenic tensile experiments, the stretching fixture was immersed in liquid nitrogen, and the sample was soaked for 30 min to ensure it reached the desired temperature. Throughout the experiment, the sample remained immersed in liquid nitrogen to maintain a constant temperature. High-temperature experiments were carried out at 773 K, 873 K, 973 K, and 1073 K. The furnace temperature was first raised to the specified level; then, the sample was held at that temperature for 10 min before being stretched until it broke and subsequently air-cooled. Tensile strain rates were maintained at 1 × 10−3/s, with each loading condition repeated three times.

2.3. Microstructural Characterization

X-ray diffraction (XRD) measurements were conducted using a Rigaku Ultima IV X-ray diffractometer in conjunction with Cu Kα radiation optimized at 40 kV and 40 mA with an increment of 0.01° and a scanning rate of 4°/min over the range of 10–100°. The microstructure was analyzed using a field emission scanning electron microscope (SEM, JEOL JSM-7100F, Tokyo, Japan) equipped with backscattered electron (BSE) and electron backscatter diffraction (EBSD) systems. The EBSD tests had scanning step sizes ranging from 0.1 to 0.5 μm. Differentiation between recrystallized, deformed, and substructured grains was based on the following misorientation criteria: grains with significant deformation (average misorientation > 7.5° in HKL Channel5 software, 5.12.74.0) were classified as deformed, those with moderate misorientation (average misorientation between 1° and 7.5°) were considered substructured, and grains with minimal misorientation (<1°) were identified as recrystallized. Transmission electron microscopy (TEM) observations were carried out using a JEOL JEM-F200 microscope at an acceleration voltage of 200 kV, along with energy-dispersive X-ray spectroscopy (EDS). Sample preparation methods for the microstructural characterization were referenced from a previous study [19].

3. Results and Discussion

3.1. Initial Microstructure

The initial microstructure of the AT0.1-A700 ME superalloy is shown in Figure 1. The alloy consists of equiaxed grains with precipitates present within the grains and at the GBs (Figure 1a,b). Specifically, the TEM dark-field (DF) image (Figure 1c) shows that spherical precipitates are evenly dispersed throughout the grain interior, whereas tapered-rod precipitates are located near the GBs. Both forms of precipitation are L12 phase, as indicated by XRD peaks (Figure 1d). An L12 phase with different morphology in the intragrain and GB has been observed in other (Al, Ti)-added M/HEAs [15,20,21]. This difference in morphology may be attributed to the distinct driving forces of precipitation at GBs compared to within grains. Our results also indicate that L12 precipitation near the GBs seems to have a greater driving force, causing faster growth towards the grain interior (Figure 1b). It is important to highlight that the current alloy does not contain other brittle intermetallic compounds commonly found in (Al, Ti)-added M/HEAs, such as Heusler phase [15,21], sigma phase [22], and D019 phase [16], which can deteriorate the high-temperature properties of alloys. The EBSD inverse pole figure (IPF) indicates that the alloy has a complete recrystallized microstructure with randomly oriented grains and annealing twins (ATs), with an average grain size of 28 μm, which was calculated from measurements of the length of the grain in multiple directions using ImageJ software (ImageJ 1.53t) (Figure 1f). The size and volume fraction of the L12 phase were measured by ImageJ software to be 50 nm and 46%, respectively (Figure 1g). The stacking fault energy (SFE) of the Ni2CoCr0.5Si0.3 matrix alloy was calculated to be 32.4 mJ/m2 by thermodynamic calculation method (see Note S1 in the Supplementary Information). It is noted that the actual SFE of the matrix may be lower as a result of the consumption of Ni and Al in the form of Ni3(Al, Ti).

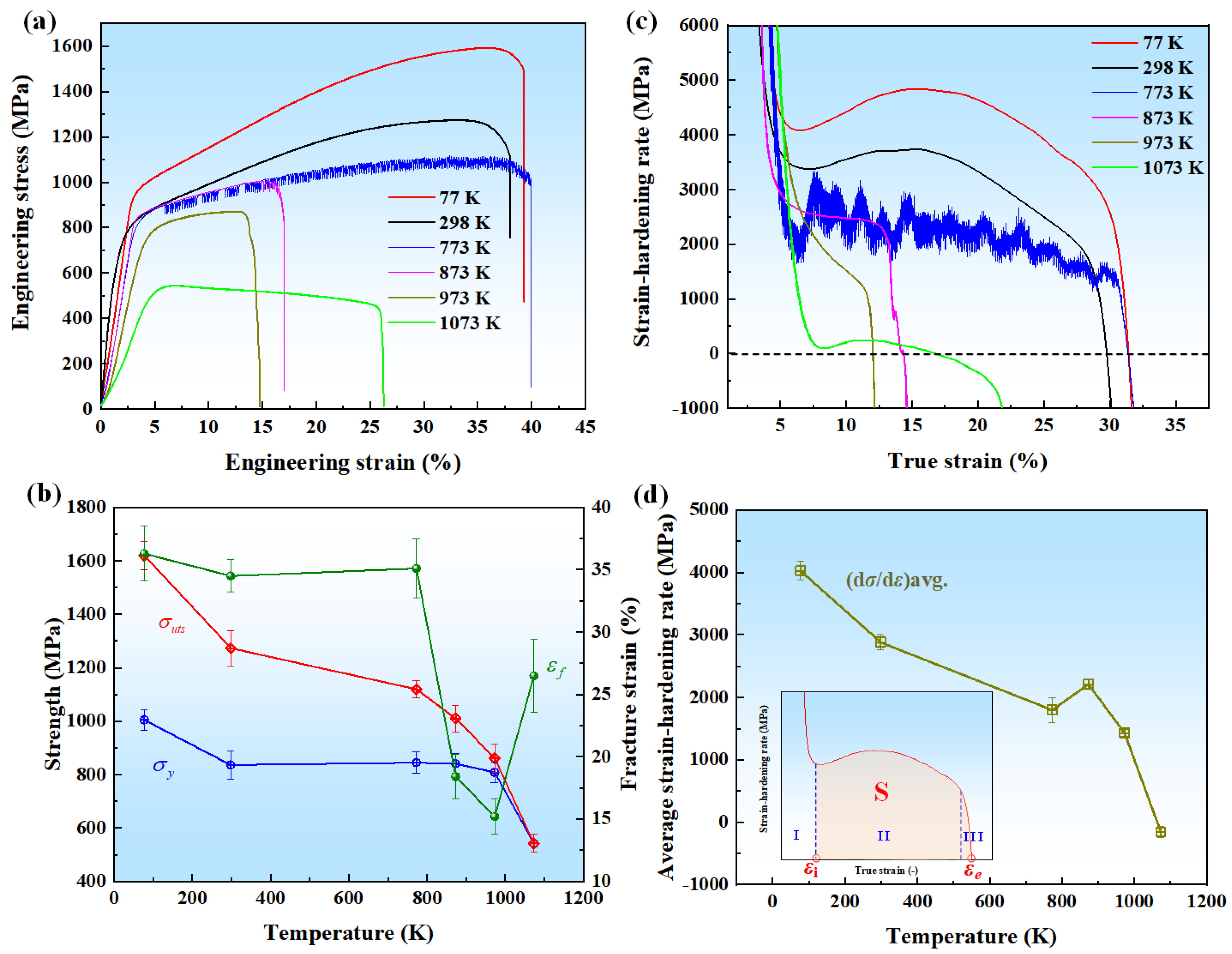
3.2. Mechanical Properties

Figure 2 shows the tensile mechanical properties of the AT0.1-A700 ME superalloy over a wide temperature range from 77 K to 1073 K. The detailed mechanical properties are summarized in Table 2. Figure 2a shows the engineering stress–strain curves at various temperatures. The variations in the yield strength (σy), ultimate tensile strength (σuts), and fracture strain (εf) are plotted in Figure 2b. At room temperature, the alloy demonstrates high σy and σuts of 836 MPa and 1274 MPa, respectively, with an εf of 34%. Upon reducing the temperature to 77 K, the alloy exhibits a further increase in both σy and σuts, reaching 1005 MPa and 1620 MPa, respectively, while the εf slightly increases to 36%. These findings align with the typical characteristics of FCC-structured M/HEAs [23]. It should be noted that the σy of the of AT0.1-A700 ME superalloy remains relatively stable when deformed within the temperature range of 298 K to 873 K but experiences a slight decrease to 808 MPa at 973 K. Specifically, a σuts of 1120 MPa and an εf of 35.1% can be maintained at 773 K, while the high σy value is similar to that at 298 K. However, as the temperature increases to 873 K and 973 K, the elongation of the alloy is almost halved to 18.4% and 15.2%, respectively. Notably, the alloy shows strain-hardening behavior over the temperature range of 77 K to 973 K, as shown in Figure 2c. In particular, the alloy shows a strong strain-hardening capacity during the second stage (Stage II), with a rate exceeding 2 GPa from 77 K to 873 K. The peak strain-hardening rate during Stage II is 3.7 GPa at 298 K and 4.8 GPa at 77 K.
In order to quantitatively assess the strain-hardening capacity at different temperatures, the average strain-hardening during Stage II and Stage III is calculated as follows: (dσ/dε)avg. = S/(εi − εe), where S is the area under Stage II and Stage III of the strain-hardening curve, and εi and εe are the initial strain of Stage II and end strain of Stage III, respectively. The average strain-hardening rates at various temperatures are presented in Figure 2d and Table 2. At 298 K, the average strain-hardening rate of the alloy is 2.88 GPa. Comparatively, at 77 K, the strain-hardening rate significantly improves to an average of about 4 GPa, with the highest value reaching 4.8 GPa, surpassing that of single-phase FCC M/HEAs [23]. This indicates that the strain-hardening behavior of the alloy is significantly affected not only by the SFE of the FCC matrix but also by the distribution and characteristics of the precipitates. At 773 K and 873 K, the alloy exhibits a stable strain-hardening rate during Stage II, averaging 1.8 GPa and 2.2 GPa, respectively, indicating a good resistance to temperature-related softening. The ordered L12 phase, a common strengthening phase in superalloys, plays a crucial role in maintaining high strength at elevated temperatures and can even lead to abnormal high-temperature strengthening effect based on the size, morphology, and crystal orientation of the L12 phase [24]. Despite a rapid decrease in strain-hardening rate at 973 K during Stage II, it remains above 1 GPa, averaging 1.4 GPa. However, at 1073 K, although the alloy retains a σy of 542 MPa and an εf of 26.5%, a strain-softening phenomenon occurs in the late deformation stage, resulting in a poor average work-hardening rate of −155 MPa.
In addition, as shown in Figure 2b, the σy decreases slowly with the increase in temperature, especially from 298 K to 973 K, with the critical softening temperature observed between 973 K and 1073 K. This critical temperature is closely linked to the melting point and grain size of the matrix [25,26], as well as the softening temperature of the second phase [24]. In general, the higher the melting point, the larger the grain size (the limit case is a single crystal) and the higher the softening temperature in alloys, as well as the higher the critical softening temperature of the second phase, leading to delayed inflection points in the strength–temperature curve [24,25,26,27]. Ordered L12 alloys exhibit anomalous yield behavior with temperature, where the flow stress typically rises until reaching a critical point, beyond which further temperature increases result in a rapid decline in strength [24]. This is also the main reason why the L12 phase is commonly used as a high-temperature strengthening phase in superalloys. The critical softening temperature for L12 alloy is usually around 1073 K, which is related to the composition, crystal orientation, and grain size of the L12 ordered alloys [24]. In this study, the L12 phase is the sole strengthening phase in the AT0.1-A700 ME superalloy, characterized by a complex multi-principal-element composition rather than a simple Ni3Al or Ni3Ti structure [9]. In addition, the orientation and size of the L12 phase, along with the properties of the matrix, collectively impact the temperature and extent of softening in the current precipitation-strengthened alloy. Furthermore, the σuts of the alloy decreases significantly with the increase in temperature, attributed to the recovery of dislocation and different dominant mechanisms during deformation. The elongation of the alloy also initially stabilizes, then decreases and finally increases with increasing temperature. This is related to the strain-hardening and deformation mechanism of the alloy, as discussed below.
A serrated flow phenomenon is observed during the majority of the deformation stage at 773 K (from 7% strain to fracture strain of 40%) and in the late deformation stage at 873 K (from 15% to 17%). The phenomenon is attributed to dynamic strain aging (DSA) caused by the interaction between dislocations and solute atoms at specific strain rates [27]. In the current ME superalloy, the non-equal atomic ratio and short-range order [28] make solid solution distinguish between solute and solvent, especially in local regions. Within an appropriate temperature range, the diffusion rate of solute atoms matches the sliding rate of dislocations [27]. Solute atoms can temporarily spread to moving dislocations, gradually accumulating and hindering dislocation movement. This leads to a rise in macroscopic stress. With the increase in applied load, when the stress on the dislocation reaches a critical point, the dislocation overcomes the solute resistance and resumes sliding, resulting in a stress drop [27].

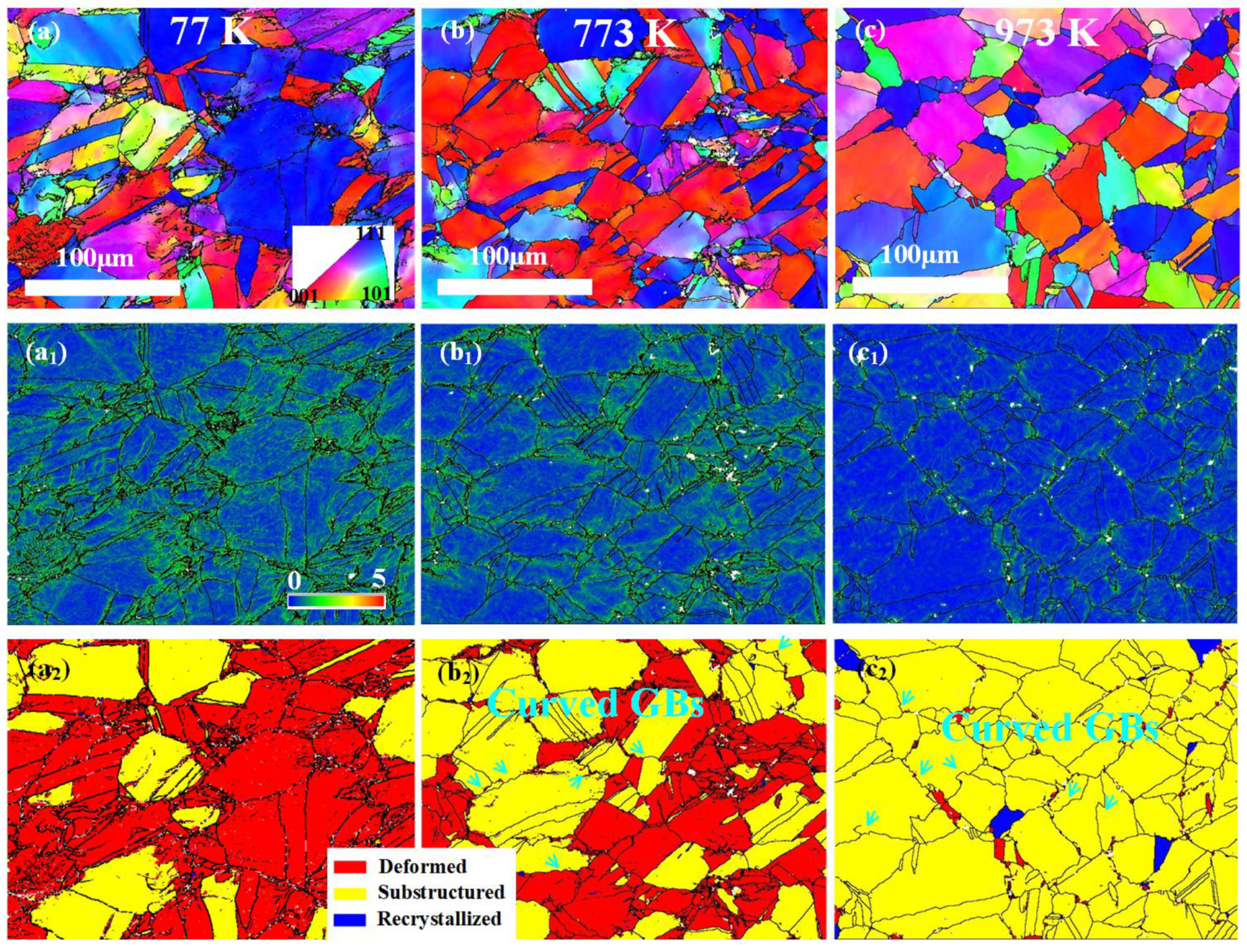
3.3. EBSD Analysis at a Wide Range of Temperatures

Figure 3 shows the EBSD images of the AT0.1-A700 ME superalloy after tensile fracture in the temperature range of 77 K to 973 K. Figure 3a shows the IPF image of the alloy deformed at 77 K. It can be observed that the orientation inside some grains has undergone serious changes, and obvious tensile deformation characteristics can be found at the GBs. Figure 3a1,a2 depict the Kernel Average Misorientation (KAM) map and recrystallized fraction map, respectively, corresponding to Figure 3a. Notably, KAM values at GBs are significantly larger than those within grains, indicating that deformation of the alloy is mainly concentrated at the GBs. The recrystallized fraction map highlights regions of recrystallized, substructured, and deformed microstructure grains through blue, yellow, and red colors, respectively. The majority of grains exhibit severe deformation and are classified as deformed microstructures at 77 K. As the temperature increases to 773 K and 973 K, the extent of grain deformation decreases. The IPF and KAM diagrams reveal that elongated grains exhibit orientations mainly in blue with [111] and red with [001], with a shift from [111] to [110] predominantly occurring at 773 K, a common occurrence in significant plastic deformation of single-phase FCC metals [29]. The KAM in Figure 3b1 is concentrated mainly at the GBs but is significantly smaller than the values and distribution range inside the sample after deformation at 77 K. The higher KAM value at 77 K indicates a higher dislocation density compared to high-temperature tensile deformation [30], resulting in a higher strain-hardening value at 77 K. The recrystallized fraction image in Figure 3b2 indicates that the grains with the deformed structure are relatively fewer compared to those at 77 K. As the loading temperature is increased to 973 K, the grain orientation of AT0.1-A700 ME superalloy slightly changes (Figure 3c), with a low KAM value (Figure 3c1), indicating minimal deformation and low dislocation density at 973 K. It is important to note that dynamic recrystallization (DRX) occurs during deformation at 973 K, as indicated by blue grains in Figure 3c2. As shown in Figure 3a1–c1, the KAM values near the GBs are markedly higher than those within the grain, suggesting substantial obstruction of dislocation movement by the GBs and L12 phase along the GBs at all loading temperatures. Unlike the widespread distribution of KAM values near the GBs at 77 K and 773 K, the KAM value is mainly confined to the GB region and does not extend into the grain at 973 K but still exhibits high tensile plasticity (15%). This indicates that GB slip and dislocation activity at the GBs play a vital role in deformation coordination at 973 K. The presence of abundant large-size, coherent L12 phases at the GBs provides excellent sliding pools, which are not offered by other brittle compound phases.
Curved GBs are observed in grains deformed at 773 K and 973 K, as indicated in Figure 3b2,c2. The quantity and curvature of these curved GBs increase significantly with higher deformation temperatures, suggesting local migration and growth of GBs to help alleviate the stress concentration. This phenomenon is further supported by the corresponding KAM images (Figure 3b1,c1). Curved GBs basically occur in the segments with low KAM values at grain boundaries at 773 K and 973 K, where geometrically necessary dislocation (GND) density is low. The formation of curved GBs under high-temperature loading is attributed to atomic diffusion at the GBs, a precursor to DRX. However, not all DRX processes involve GB bending and bulging [31]. In single-phase metals, DRX often occurs preferentially at triple junctions of GBs, making the bending and bulging of GBs less effective in reducing stress concentrations. Moreover, DRX at triple junctions does not offer as many dislocation pinning sites as curved GBs, which can act as a strengthening factor at high temperatures [31]. Curved (serrated) GBs in superalloys, including the current MEA, not only provide an additional source of dislocation pinning for high-temperature strengthening [32] but also help alleviate the stress concentration at the GBs by allowing for local migration and growth. This, in turn, improves the high-temperature plasticity of the alloys. The dual positive effect of curved or jagged GBs on high-temperature strength and plasticity is a key consideration in the design of materials for high-temperature applications. Alloys with high-density coherent nanoprecipitation are more susceptible to GB bending at high temperatures [33] due to slight differences in the crystal lattice between the matrix and precipitation at the GBs. This is supported by the faster growth rate of the L12 phase at GBs compared to within the grains, indicating lower diffusion resistance at the GB. Consequently, rapid atomic diffusion leads to the L12 phase at the GBs taking on a tapered-rod shape [15,21] rather than a square or round shape within the grain, as shown in Figure 1b. With the increase in deformed temperature, the DRX softening effect of the alloy outweighs the strain-hardening effect, leading to a strain-softening phenomenon occurring at 1073 K.

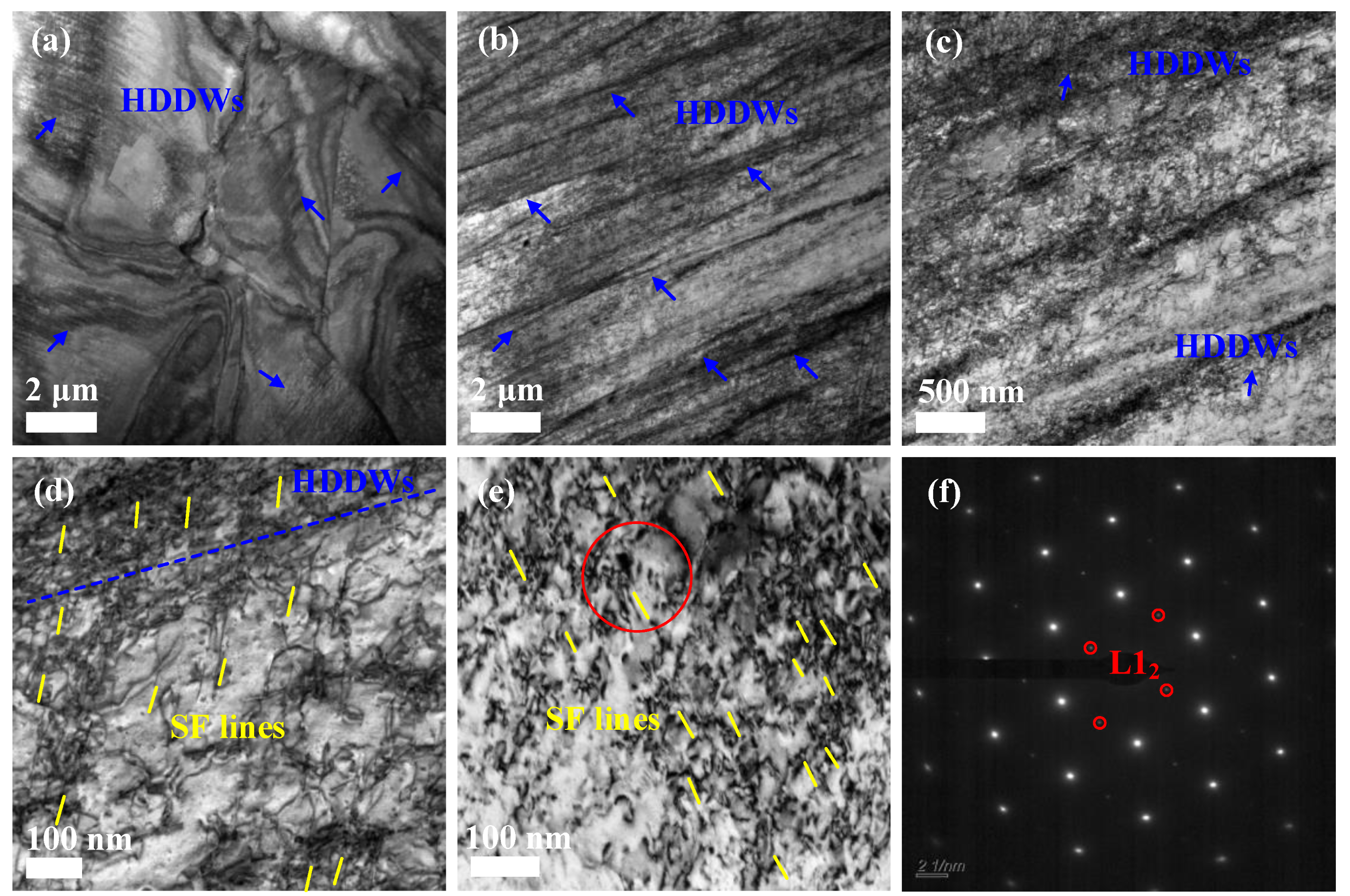
3.4. Low-Temperature Deformation Mechanisms at 298 K and 77 K

The microstructures of AT0.1-A700 ME superalloy were analyzed through TEM after tensile deformation at 298 K, as shown in Figure 4. The predominant observed deformation mechanism was the shearing of the stacking fault (SF) in both the matrix and precipitated phase, accompanied by a high number of dislocation movements. The TEM-EDS images (attached to the right in Figure 4a) clearly differentiate between the matrix and precipitated phase, with rich Ni, Al, and Ti content indicating L12 phase precipitation. During deformation, SFs near the precipitation boundary cut through it (yellow arrow in Figure 4a), causing elongation and deformation of the precipitates into elliptical shapes. A large number of SF networks and L-C locks formed by multiple SFs shear, as shown in Figure 4b,c. This observation confirms that the primary deformation mechanism of the alloy, characterized by a high density of the L12 phase, is mainly driven by SF-mediated dislocation activities [20]. SFs, particularly SF networks and L-C locks, have been demonstrated to significantly enhance the work-hardening ability of alloys due to their significant dynamic pinning effect on dislocations [20,34]. This enhancement can be attributed to two main factors, namely the low SFE of the matrix and the limited spacing between precipitation phases preventing further development into twins. In the current MEA, the addition of Si can significantly reduce the SFE [18], together with the substantial 46% fraction of the L12 phase, which contributes to the deformation mechanism associated with SFs.
Figure 5 shows the deformation microstructure of AT0.1-A700 ME superalloy after tensile fracture at 77 K. Abundant SF networks formed by high-density intersecting SF bands can be observed in most grains (Figure 5a), with SF bands typically measuring 10–30 nm in thickness (Figure 5b). Enlarged views of SF bands in Figure 5c illustrate their composition of a matrix sandwiched in multiple SFs on both sides, contrasting with the shorter and narrower SF networks at room temperature. The formation of SF bands at 77 K is attributed to increased deformation, continuous accumulation, and expansion of SFs. These SF networks, made up of SF bands, have a more significant effect on dislocation pinning and storage, leading to enhanced strain-hardening effects (refer to Figure 5b for dislocation entanglement between SF networks) [35]. Additionally, a few deformation twins (DTs) are present in the alloy deformed at 77 K, as shown in Figure 5d,e. These DTs, along with the SF network, contribute significantly to dislocation pinning and storage, as evident in Figure 5d, with abundant dislocation entanglement between twin forests. Examination of the twin boundary in Figure 5f reveals numerous short SFs surrounding it. Overall, cryogenic deformation results in more abundant SF band networks and DTs, as well as high-density dislocation entanglements, serving as the primary deformation mechanisms. The interface resistance between the L12 phase and matrix typically hinders the expansion of SFs into bands or the formation of twins [16,20,36]. However, at 77 K, higher stress and lower SFE reduce the resistance, allowing for the formation of long, thick SF bands and twins. This, in turn, enhances the strain-hardening effect of dislocations and improves the flow stress.

3.5. Intermediate-Temperature Deformation Mechanisms at 773 K and 973 K

As shown in Figure 6, the formation and interaction of high-density dislocation walls (HDDWs) are present in most deformed grains (see Figure 6a) following tensile deformation at 773 K, serving as the main deformation characteristics. These HDDWs, formed by the accumulation of slip bands, exhibit a complex microstructure, with the dislocation walls intersecting in multiple directions, as shown in Figure 6b. Detailed examination of the HDDWs shows dense dislocation entanglement within the walls (see Figure 6c). Additionally, short and thin fault lines are observed within the HDDWs and other regions lacking dislocation walls (see Figure 6e), causing shear in the L12 precipitates. The presence of these fault lines is confirmed by the diffraction spots in Figure 6f. This research highlights that while room-temperature and cryogenic deformation show abundant stacking fault (SF) activities, including twin activities, deformation at 773 K is primarily governed by a small amount of SF activities and a significant presence of HDDWs. This shift in deformation mechanism is attributed to the increase in SFE and the decrease in flow stress at elevated temperatures.
Raising the temperature to 973 K results in the AT0.1-A700 ME superalloy maintaining high yield strength and strain hardening but experiencing a significant reduction in plasticity. As shown in Figure 7a, abundant dislocation lines and entanglements, predominantly in the form of dislocation pairs (see Figure 7b), are indicative of a shear mechanism related to the anti-phase boundary (APB) [24]. This phenomenon, common in L12-strengthened superalloys during small strain stages [37,38], helps sustain the alloy’s strength across a wide temperature range [39]. The dislocation pairs observed in the DF image in Figure 7c originate from two slip planes (the bright dislocation pair (1) and dark dislocation pair (2)). It should be noted that a small amount of SF lines and microtwins occurs in some grains after tensile deformation at 973 K. The dislocation density within microtwins and at the twinning interfaces remains relatively low, characteristic of the microtwinning mechanism prevalent in L12 phase-strengthened superalloys under low strain rates and low-stress conditions within the intermediate temperature range (673–1073 K) [40]. Multiple theories exist regarding the formation mechanism of microtwinning in superalloys [40]. However, it has been established that the decomposition of a/2 <110> dislocation into two a/6 <112> partial dislocations at the interface between the matrix and L12 phase is a prerequisite. The formation of the twin embryo is linked to the transformation of complex stacking faults (CSFs) into superlattice extrinsic stacking faults (SESFs) through an atomic rearrangement mechanism [40]. This differs from the traditional mechanism of DT formation; a detailed discussion on the mechanism of microtwinning formation can be found in reference [40]. Nevertheless, it is evident that the presence of microtwins can impede dislocation movement and enhance the performance of superalloys [41,42]. Therefore, it is of great significance to introduce microtwins in superalloys during high-temperature deformation [43].

3.6. Temperature-Dependent Correlation between Tensile Properties and Mechanisms

The mechanical properties of alloys at a wide range of temperatures, including yield strength, ultimate tensile strength, strain hardening, and plasticity, are influenced by multiple factors. In recrystallized single-phase polycrystalline metals, yield strength is linked to temperature-dependent lattice friction, solution strengthening, and GB strengthening. At lower temperatures, like those of liquid nitrogen or liquid helium, the crystal lattice contracts, increasing interatomic binding force and enhancing resistance to dislocation slip activation. This results in a significant rise in yield strength explained by the Peierls–Nabarro stress [44]. Solid solution strengthening occurs when atoms with different properties enter the lattice, impacting lattice friction, so that it can generally be folded into the lattice friction of the solid solution [45]. While GB strengthening is often seen as temperature-independent at low temperatures, its temperature sensitivity becomes more significant at higher temperatures, particularly in fine- and nano-grained metals [46]. This sensitivity deviates from the traditional Hall–Petch relationship. For example, in nanocrystals, the presence of numerous grain boundary defects leads to their movement or migration during deformation at temperatures above medium levels, diminishing the effectiveness of the GB strengthening effect [46]. In precipitation-strengthened alloys, the strengthening effect due to temperature is influenced by the temperature of the precipitation phase and the interface between the second phase and the matrix. The temperature-dependent yield strength in current alloys is affected by lattice friction, solid solution strengthening, GB strengthening, and L12 phase strengthening. However, the complex nature of the temperature-dependent L12 phase strengthening effect lacks a comprehensive physical model to explain the temperature-dependent stress anomaly throughout the entire process [24]. Therefore, it is typically approached phenomenologically or empirically [47,48].
In terms of strain hardening ((dσ/dε)avg.), plasticity (εf), and ultimate tensile strength (σuts), the influence of temperature on the alloy mainly focuses on the deformation mechanism. This mechanism is related to the dislocation activity of the matrix affected by precipitation, as well as the dislocation activity and growth of the precipitation phase itself at different temperatures. The impact of temperature on strain hardening and plasticity can be discussed through EBSD and TEM analysis, indirectly affecting the σuts. Figure 8 illustrates the effect of temperature on the tensile properties and deformation mechanisms in the current alloy. In an FCC matrix, the influence of temperature on the deformation mechanism can mainly be attributed to the SFE [49]. The high Si content (7.5 at.%) in the current alloy, which is mostly dissolved into the matrix, results in a low SFE of the matrix (less than 32.4 mJ/m2), potentially leading to twinning and SFs [35]. However, the presence of numerous L12 phases causes the matrix spacing between the precipitation phases to become very narrow. This makes it challenging for the SFs to develop into twins with flat interfaces, resulting in the formation of multilayer SFs, SF bands, and SF networks at room and cryogenic temperatures. These SFs and SF networks can effectively store a large number of dislocations (see dislocation entanglement in Figure 5b) and hinder dislocation movement, thereby enhancing the strain-hardening ability of the alloy. The formation and thickening of SF networks during deformation contribute to the maintenance of higher levels of strain hardening over a wider strain range. This phenomenon is responsible for the alloy’s significant work hardening, plasticity, and ultimate tensile strength at both room and cryogenic temperatures. With the further increase in temperature, there is a decrease in SF activities, with a corresponding increase in dislocation activity due to the increase in SFE. At 773 K, the presence of numerous dislocation entanglements and walls effectively impedes dislocation movement, resulting in increased strain hardening and plasticity. However, at 973 K, dislocation activity shifts towards dislocation multiplication rather than large-scale entanglement, primarily involving the APB shearing mechanism characteristic of L12 phase-strengthened alloys [24]. The alloy’s strength is maintained within the temperature range in which dislocation pair shearing appears [24,39], indicating that the high-temperature strengthening effect of the precipitated phase outweighs the softening effect of the matrix within this range. SF lines and microtwins, along with other factors, contribute significantly to high levels of strain hardening at 973 K. However, the limited dislocation multiplication at this temperature prevents the maintenance of high levels of strain hardening, leading to premature fracture at the grain boundary and a decrease in plasticity and ultimate tensile strength. A sudden drop in ductility at elevated temperatures is commonly observed in Ni-based superalloys, known as the “ductility dip”. This phenomenon is believed to be caused by decreases in both intragranular and grain boundary strength at high temperatures, with grain boundary strength declining more rapidly due to increased grain boundary activity. Consequently, grain boundary cleavage or sliding becomes the primary deformation mechanism, resulting in intergranular fracture [50]. Conversely, at 1073 K, the lower dislocation proliferation and interaction do not result in increased strain hardening. Instead, grain boundary slip and dynamic recrystallization allow for a certain level of strain softening until fracture occurs. It is important to highlight that the presence of curved or serrated grain boundaries at this temperature can help alleviate the stress concentration and enhance the plasticity of the alloy.

4. Conclusions

An “FCC + L12” phase structure was obtained in a novel Ni2CoCr0.5Si0.3Al0.1Ti0.1 medium-entropy (ME) superalloy. The mechanical properties and deformation mechanisms of the ME superalloy were studied over a wide range of temperatures from 77 K to 1073 K, with a focus on the impact of the L12 phase on the alloy’s high-temperature mechanical behavior. The main conclusions are summarized as follows:
  • The alloy consists of equiaxed grains with precipitates present inside the grains and at the grain boundaries (GBs). More specifically, spherical precipitates are evenly dispersed within the grains, while tapered-rod precipitates are situated close to the GBs.
  • A nearly constant yield strength of approximately 800 MPa is achieved within the temperature range of 298 K to 973 K. The alloy exhibits notable strain-hardening capabilities, with strengths of 2.5 GPa, 3.7 GPa, and 4.8 GPa observed at temperatures of 873 K, 298 K, and 77 K, respectively.
  • High Si content (7.5 at.%) is primarily dissolved into the matrix, resulting in a decrease in the stacking fault energy (SFE) within the matrix. Stacking faults (SFs) evolve into multilayer SFs, SF bands, and SF networks rather than twins. Those SF-related microstructures can effectively store a significant amount of dislocations and impede dislocation movement, thereby enhancing the work-hardening capability of the alloy at both room and cryogenic temperatures.
  • At 773 K, significant quantities of dislocation entanglements and dislocation walls form, effectively impeding dislocation movement and storing dislocations, leading to increased work hardening and plasticity. As the temperature rises to 973 K, the typical APB shearing mechanism (in the form of dislocation pairs), SF lines, and microtwins (resulting from atomic rearrangement) also contribute significantly to the high levels of work hardening observed at 973 K.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/met14070749/s1, Note S1: Thermodynamic calculations of stacking fault energy; Table S1: Thermodynamic parameters for calculating the stacking fault energy of Ni2CoCr0.5Si0.3 MEA (T = 298 K). References [51,52,53,54,55,56,57,58,59,60] are cited in the Supplementary Materials.

Author Contributions

Conceptualization, T.Z.; methodology, T.Z., T.B. and S.L.; formal analysis, T.Z. and R.X.; investigation, T.Z., Z.W. and R.X.; data curation, T.B., S.L. and H.C.; writing—original draft preparation, T.Z. and S.L.; writing—review and editing, R.X., H.C., T.B., J.M., S.D., Z.J., J.W. and Z.W.; visualization, S.D., Z.J., S.M., J.M. and J.W.; supervision, Z.W. and R.X.; funding acquisition, T.Z., Z.W., R.X., J.W. and J.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (Grant Nos. 12102291, 12225207, 12072220, 51801139, 12172245, and 52204349) and the Science and Technology Innovation Teams of Shanxi Province (Grant No. 202204051002006).

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors upon request.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Praveen, S.; Kim, H.S. High-Entropy Alloys: Potential Candidates for High-Temperature Applications—An Overview. Adv. Eng. Mater. 2018, 20, 1700645. [Google Scholar] [CrossRef]
  2. Chen, Y.-T.; Chang, Y.-J.; Murakami, H.; Gorsse, S.; Yeh, A.-C. Designing High Entropy Superalloys for Elevated Temperature Application. Scripta Mater. 2020, 187, 177–182. [Google Scholar] [CrossRef]
  3. Li, W.D.; Xie, D.; Li, D.Y.; Zhang, Y.; Gao, Y.F.; Liaw, P.K. Mechanical behavior of high-entropy alloys. Prog. Mater. Sci. 2021, 118, 100777. [Google Scholar] [CrossRef]
  4. Miracle, D.B.; Senkov, O.N. A critical review of high entropy alloys and related concepts. Acta Mater. 2017, 122, 448–511. [Google Scholar] [CrossRef]
  5. George, E.P.; Curtin, W.A.; Tasan, C.C. High entropy alloys: A focused review of mechanical properties and deformation mechanisms. Acta Mater. 2020, 188, 435–474. [Google Scholar] [CrossRef]
  6. Feng, R.; Feng, B.J.; Gao, M.C.; Zhang, C.; Neuefeind, J.C.; Poplawsky, J.D.; Ren, Y.; An, K.; Widom, M.; Liaw, P.K. Superior High-Temperature Strength in a Supersaturated Refractory High-Entropy Alloy. Adv. Mater. 2021, 33, 2102401. [Google Scholar] [CrossRef]
  7. Huang, H.L.; Wu, Y.; He, J.Y.; Wang, H.; Liu, X.J.; An, K.; Wu, W.; Lu, Z.P. Phase-Transformation Ductilization of Brittle High-Entropy Alloys via Metastability Engineering. Adv. Mater. 2017, 29, 1701678.1–1701678.7. [Google Scholar] [CrossRef]
  8. Wang, S.B.; Shu, D.; Shi, P.Y.; Zhang, X.B.; Mao, B.; Wang, D.H.; Liaw, P.K.; Sun, B.D. TiZrHfNb refractory high-entropy alloys with twinning-induced plasticity. J. Mater. Sci. Technol. 2024, 187, 72–85. [Google Scholar] [CrossRef]
  9. Yang, T.; Zhao, Y.L.; Tong, Y.; Jiao, Z.B.; Wei, J.; Cai, J.X.; Han, X.D.; Chen, D.; Hu, A.; Kai, J.J.; et al. Multicomponent intermetallic nanoparticles and superb mechanical behaviors of complex alloys. Science 2018, 362, 933–937. [Google Scholar] [CrossRef]
  10. He, J.Y.; Wang, H.; Huang, H.L.; Xu, X.D.; Chen, M.W.; Wu, Y.; Liu, X.J.; Nieh, T.G.; An, K.; Lu, Z.P. A precipitation-hardened high-entropy alloy with outstanding tensile properties. Acta Mater. 2016, 102, 187–196. [Google Scholar] [CrossRef]
  11. Zhao, Y.Y.; Chen, H.W.; Lu, Z.P.; Nieh, T.G. Thermal stability and coarsening of coherent particles in a precipitation-hardened (NiCoFeCr)94Ti2Al4 high-entropy alloy. Acta Mater. 2018, 147, 184–194. [Google Scholar] [CrossRef]
  12. Liang, Y.J.; Wang, L.J.; Wen, Y.R.; Cheng, B.Y.; Wu, Q.L.; Cao, T.Q.; Xiao, Q.; Xue, Y.F.; Sha, G.; Wang, Y.D.; et al. High-Content Ductile Coherent Nanoprecipitates Achieve Ultrastrong High-Entropy Alloys. Nat. Commun. 2018, 9, 4063. [Google Scholar] [CrossRef] [PubMed]
  13. Zhang, C.; Yu, Q.; Tang, Y.T.; Xu, M.J.; Wang, H.R.; Zhu, C.Y.; Ell, J.; Zhao, S.T.; MacDonald, B.E.; Cao, P.H.; et al. Strong and Ductile Fenicoal-Based High-Entropy Alloys for Cryogenic to Elevated Temperature Multifunctional Applications. Acta Mater. 2023, 242, 118449. [Google Scholar] [CrossRef]
  14. Du, X.H.; Li, W.P.; Chang, H.T.; Yang, T.; Duan, G.S.; Wu, B.L.; Huang, J.C.; Chen, F.R.; Liu, C.T.; Chuang, W.S.; et al. Dual heterogeneous structures lead to ultrahigh strength and uniform ductility in a Co-Cr-Ni medium-entropy alloy. Nat. Commun. 2020, 11, 2390. [Google Scholar] [CrossRef] [PubMed]
  15. He, J.Y.; Wang, H.; Wu, Y.; Liu, X.J.; Nieh, T.G.; Lu, Z.P. High-temperature plastic flow of a precipitation-hardened FeCoNiCr high entropy alloy. Mater. Sci. Eng. A 2017, 686, 34–40. [Google Scholar] [CrossRef]
  16. Zhao, Y.L.; Yang, T.; Li, Y.R.; Fan, L.; Han, B.; Jiao, Z.B.; Chen, D.; Liu, C.T.; Kai, J.J. Superior high-temperature properties and deformation-induced planar faults in a novel L12-strengthened high-entropy alloy. Acta Mater. 2020, 188, 517–527. [Google Scholar] [CrossRef]
  17. Gao, L.; Wu, Y.D.; An, N.; Chen, J.Y.; Liu, X.L.; Bai, R.; Hui, X.D. Nanoscale L12 phase precipitation induced superb ambient and high temperature mechanical properties in Ni–Co–Cr–Al system high-entropy superalloys. Mater. Sci. Eng. A 2024, 898, 145995. [Google Scholar] [CrossRef]
  18. Chang, H.; Zhang, T.W.; Ma, S.G.; Zhao, D.; Xiong, R.L.; Wang, T.; Li, Z.Q.; Wang, Z.H. Novel Si-added CrCoNi medium entropy alloys achieving the breakthrough of strength-ductility trade-off. Mater. Des. 2021, 197, 109202. [Google Scholar] [CrossRef]
  19. Luo, S.H.; Zhang, T.W.; Chang, H.; Du, S.Y.; Jiao, Z.M.; Xiong, R.L.; Kim, H.S.; Wang, Z.H. Ultra-high work hardening mediated by three-level precipitation in a Ni2CoCr0.5Si0.3Al0.2Ti0.2 medium entropy alloy. J. Mater. Res. Technol. 2023, 25, 3093–3103. [Google Scholar] [CrossRef]
  20. Zhao, Y.L.; Yang, T.; Tong, Y.; Wang, J.; Luan, J.H.; Jiao, Z.B.; Chen, D.; Yang, Y.; Hu, A.; Liu, C.T.; et al. Heterogeneous precipitation behavior and stacking-fault-mediated deformation in a CoCrNi-based medium-entropy alloy. Acta Mater. 2017, 138, 72–82. [Google Scholar] [CrossRef]
  21. Yang, T.; Zhao, Y.L.; Fan, L.; Wei, J.; Luan, J.H.; Liu, W.H.; Wang, C.; Jiao, Z.B.; Kai, J.J.; Liu, C.T. Control of nanoscale precipitation and elimination of intermediate-temperature embrittlement in multicomponent high-entropy alloys. Acta Mater. 2020, 189, 47–59. [Google Scholar] [CrossRef]
  22. Du, S.Y.; Zhang, T.W.; Jiao, Z.M.; Zhao, D.; Wang, J.J.; Xiong, R.L.; Kim, H.S.; Wang, Z.H. Strength-ductility synergy and grain refinement mechanisms in a Co-Cr-Ni medium-entropy alloy with novel analogous harmonic structure. Scr. Mater. 2023, 235, 115635. [Google Scholar] [CrossRef]
  23. Li, Z.Z.; Zhao, S.T.; Ritchie, R.O.; Meyers, M.A. Mechanical properties of high-entropy alloys with emphasis on face-centered cubic alloys. Prog. Mater. Sci. 2019, 102, 296–345. [Google Scholar] [CrossRef]
  24. Vitek, V.; Pope, D.P.; Bassani, J.L. Anomalous Yield Behaviour of Compounds with L12 Structure. In L12 Ordered Alloys; Nabarro, F.R.N., Duesbery, M.S., Eds.; Elsevier Science B.V.: Amsterdam, The Netherlands, 1996; pp. 137–185. [Google Scholar]
  25. Senkov, O.N.; Miracle, D.B.; Chaput, K.J.; Couzinie, J.P. Development and exploration of refractory high entropy alloys—A review. J. Mater. Res. 2018, 33, 3092–3128. [Google Scholar] [CrossRef]
  26. Otto, F.; Dlouhý, A.; Somsen, C.; Bei, H.; Eggeler, G.; George, E.P. The influences of temperature and microstructure on the tensile properties of a CoCrFeMnNi high-entropy alloy. Acta Mater. 2013, 61, 5743–5755. [Google Scholar] [CrossRef]
  27. Brechtl, J.; Chen, S.Y.; Xie, X.; Ren, Y.; Qiao, J.W.; Liaw, P.K.; Zinkle, S.J. Towards a greater understanding of serrated flows in an Al-containing high-entropy-based alloy. Int. J. Plast. 2019, 115, 71–92. [Google Scholar] [CrossRef]
  28. Zhang, R.P.; Zhao, S.T.; Ding, J.; Chong, Y.; Jia, T.; Ophus, C.; Asta, M.; Ritchie, R.O.; Minor, A.M. Short-range order and its impact on the CrCoNi medium-entropy alloy. Nature 2020, 581, 283–287. [Google Scholar] [CrossRef]
  29. Zhang, T.W.; Ma, S.G.; Zhao, D.; Wu, Y.C.; Zhang, Y.; Wang, Z.H.; Qiao, J.W. Simultaneous enhancement of strength and ductility in a NiCoCrFe high-entropy alloy upon dynamic tension: Micromechanism and constitutive modeling. Int. J. Plast. 2020, 124, 226–246. [Google Scholar] [CrossRef]
  30. Zhi, H.H.; Zhang, C.; Antonov, S.; Yu, H.Y.; Guo, T.; Su, Y.J. Investigations of dislocation-type evolution and strain hardening during mechanical twinning in Fe-22Mn-0.6C twinning-induced plasticity steel. Acta Mater. 2020, 195, 371–382. [Google Scholar] [CrossRef]
  31. Sakai, T.; Belyakov, A.; Kaibyshev, R.; Miura, H.; Jonas, J.J. Dynamic and post-dynamic recrystallization under hot, cold and severe plastic deformation conditions. Prog. Mater. Sci. 2014, 60, 130–207. [Google Scholar] [CrossRef]
  32. Tang, Y.T.; Karamched, P.; Liu, J.; Haley, J.C.; Reed, R.C.; Wilkinson, A.J. Grain boundary serration in nickel alloy inconel 600: Quantification and mechanisms. Acta Mater. 2019, 181, 352–366. [Google Scholar] [CrossRef]
  33. Wu, S.W.; Yang, T.; Cao, B.X.; Luan, J.H.; Jia, Y.F.; Xu, L.; Mu, Y.K.; Zhang, T.L.; Kong, H.J.; Tong, X.; et al. Multicomponent Ni-rich high-entropy alloy toughened with irregular-shaped precipitates and serrated grain boundaries. Scr. Mater. 2021, 204, 114066. [Google Scholar] [CrossRef]
  34. Zhang, L.; Hu, Z.H.; Zhang, L.; Wang, H.; Li, J.B.; Li, Z.; Yu, J.X.; Wu, B.L. Enhancing the strength-ductility trade-off in a NiCoCr-based medium-entropy alloy with the synergetic effect of ultra fine precipitates, stacking faults, dislocation locks and twins. Scr. Mater. 2022, 211, 114497. [Google Scholar] [CrossRef]
  35. Zhang, Z.; Mao, M.M.; Wang, J.; Gludovatz, B.; Zhang, Z.; Mao, S.X.; George, E.P.; Yu, Q.; Ritchie, R.O. Nanoscale origins of the damage tolerance of the high-entropy alloy CrMnFeCoNi. Nat. Commun. 2015, 6, 10143. [Google Scholar] [CrossRef]
  36. Song, W.; Wang, X.G.; Li, J.G.; Meng, J.; Yang, Y.H.; Liu, J.L.; Liu, J.D.; Zhou, Y.Z.; Sun, X.F. Effect of Ru on tensile behavior and deformation mechanism of a nickel-based single crystal superalloy. Mater. Sci. Eng. A 2021, 802, 140430. [Google Scholar] [CrossRef]
  37. Hou, K.L.; Wang, M.; Zhao, P.; Ou, M.Q.; Li, H.Z.; Ma, Y.C.; Liu, K. Temperature-dependent yield strength and deformation mechanism of a casting Ni-based superalloy containing low volume-fraction gamma’ phase. J. Alloys Compd. 2022, 905, 164–187. [Google Scholar] [CrossRef]
  38. Bai, J.M.; Zhang, H.P.; Liu, J.T.; Zhang, M.D.; Liu, C.S.; Zhang, Y.W. Temperature dependence of tensile deformation mechanisms in a powder metallurgy Ni–Co–Cr based superalloy with Ta addition. Mater. Sci. Eng. A 2022, 856, 143965. [Google Scholar] [CrossRef]
  39. Ding, Q.Q.; Bei, H.B.; Yao, X.; Zhao, X.B.; Wei, X.; Wang, J.; Zhang, Z. Temperature effects on deformation substructures and mechanisms of a Ni-based single crystal superalloy. Appl. Mater. Today 2021, 23, 101061. [Google Scholar] [CrossRef]
  40. Kovarik, L.; Unocic, R.R.; Li, J.; Sarosi, P.; Shen, C.; Wang, Y.; Mills, M.J. Microtwinning and other shearing mechanisms at intermediate temperatures in Ni-based superalloys. Prog. Mater. Sci. 2009, 54, 839–873. [Google Scholar] [CrossRef]
  41. Tian, C.G.; Han, G.M.; Cui, C.Y.; Sun, X.F. Effects of stacking fault energy on the creep behaviors of Ni-base superalloy. Mater. Des. 2014, 64, 316–323. [Google Scholar] [CrossRef]
  42. Yu, S.X.; Wang, Q.; Deng, X.T.; Wang, Z.D. Collaboratively enhancing the strength and ductility of GH3600 Nickel-Based Ultra-Thin strips via the Pre-Precipitation process. Mater. Des. 2023, 234, 112322. [Google Scholar] [CrossRef]
  43. Qi, D.Q.; Fu, B.D.; Du, K.; Yao, T.T.; Cui, C.Y.; Zhang, J.X.; Ye, H.Q. Temperature effects on the transition from Lomer-Cottrell locks to deformation twinning in a Ni-Co-based superalloy. Scr. Mater. 2016, 125, 24–28. [Google Scholar] [CrossRef]
  44. Xu, G.S.; Zhang, C.L. Analysis of dislocation nucleation from a crystal surface based on the Peierls–Nabarro dislocation model. J. Mech. Phys. Solids 2003, 51, 1371–1394. [Google Scholar] [CrossRef]
  45. Wu, Z.; Bei, H.; Pharr, G.M.; George, E.P. Temperature dependence of the mechanical properties of equiatomic solid solution alloys with face-centered cubic crystal structures. Acta Mater. 2014, 81, 428–441. [Google Scholar] [CrossRef]
  46. Figueiredo, R.B.; Langdon, T.G. Deformation mechanisms in ultrafine-grained metals with an emphasis on the Hall–Petch relationship and strain rate sensitivity. J. Mater. Res. Technol. 2021, 14, 137–159. [Google Scholar] [CrossRef]
  47. Li, W.G.; Ma, J.Z.; Kou, H.B.; Shao, J.X.; Zhang, X.Y.; Deng, Y.; Tao, Y.; Fang, D.N. Modeling the effect of temperature on the yield strength of precipitation strengthening Ni-base superalloys. Int. J. Plast. 2019, 116, 143–158. [Google Scholar] [CrossRef]
  48. Yuan, K.B.; Guo, W.G.; Li, D.W.; Li, P.H.; Zhang, Y.; Wang, P.C. Influence of heat treatments on plastic flow of laser deposited Inconel 718: Testing and microstructural based constitutive modeling. Int. J. Plast. 2021, 136, 102865. [Google Scholar] [CrossRef]
  49. Liebig, J.P.; Krauß, S.; Göken, M.; Merle, B. Influence of stacking fault energy and dislocation character on slip transfer at coherent twin boundaries studied by micropillar compression. Acta Mater. 2018, 154, 261–272. [Google Scholar] [CrossRef]
  50. Sang, L.J.; Lu, J.X.; Wang, J.; Ullah, R.; Sun, X.C.; Zhang, Y.F.; Zhang, Z. In-Situ Sem Study of Temperature-Dependent Tensile Behavior of Inconel 718 Superalloy. J. Mater. Sci. 2021, 56, 16097–16112. [Google Scholar] [CrossRef]
  51. Olson, G.B.; Cohen, M. A general mechanism of martensitic nucleation: Part I. General concepts and the FCC HCP transformation. Metall. Trans. A 1976, 7, 1897–1904. [Google Scholar]
  52. Achmad, T.L.; Fu, W.; Chen, H.; Zhang, C.; Yang, Z.-G. Computational thermodynamic and first-principles calculation of stacking fault energy on ternary Co-based alloys. Comput. Mater. Sci. 2018, 143, 112–117. [Google Scholar] [CrossRef]
  53. Tian, X.; Zhang, Y. Effect of Si content on the stacking fault energy in γ-Fe–Mn–Si–C alloys: Part II. Thermodynamic estimation. Mater. Sci. Eng. A 2009, 516, 78–83. [Google Scholar] [CrossRef]
  54. Xiong, R.; Peng, H.; Si, H.; Zhang, W.; Wen, Y. Thermodynamic calculation of stacking fault energy of the Fe–Mn–Si–C high manganese steels. Mater. Sci. Eng. A 2014, 598, 376–386. [Google Scholar] [CrossRef]
  55. Lee, S.-M.; Lee, S.-J.; Lee, S.; Nam, J.-H.; Lee, Y.-K. Tensile properties and deformation mode of Si-added Fe-18Mn-0.6C steels. Acta Mater. 2018, 144, 738–747. [Google Scholar] [CrossRef]
  56. Lee, Y.-K.; Choi, C. Driving force for γ→ε martensitic transformation and stacking fault energy of γ in Fe-Mn binary system. Metall. Mater. Trans. A 2000, 31, 355–360. [Google Scholar] [CrossRef]
  57. Xiong, R.; Liu, Y.; Si, H.; Peng, H.; Wang, S.; Sun, B.; Chen, H.; Kim, H.S.; Wen, Y. Effects of Si on the Microstructure and Work Hardening Behavior of Fe–17Mn–1.1C–xSi High Manganese Steels. Met. Mater. Int. 2020, 27, 3891–3904. [Google Scholar] [CrossRef]
  58. Dinsdale, A.T. SGTE data for pure elements. Calphad 1991, 15, 317–425. [Google Scholar] [CrossRef]
  59. Yang, S.; Jiang, M.; Li, H.; Liu, Y.; Wang, L. Assessment of Co-Cr-Ni ternary system by CALPHAD technique. Rare Met. 2012, 31, 75–80. [Google Scholar] [CrossRef]
  60. Oikawa, K.; Qin, G.-W.; Ikeshoji, T.; Kainuma, R.; Ishida, K. Direct evidence of magnetically induced phase separation in the fcc phase and thermodynamic calculations of phase equilibria of the Co–Cr system. Acta Mater. 2002, 50, 2223–2232. [Google Scholar] [CrossRef]
Metals 14 00749 g001
Figure 1. The initial microstructures of AT0.1-A700 ME superalloy: (a,b) SEM-BSE and (c) TEM dark-field (DF) images of matrix and L12 precipitation, respectively; (d) XRD pattern, (e) EBSD inverse pole figure (IPF) image, and (f,g) the size distribution of FCC matrix and L12 phase, respectively.
Figure 1. The initial microstructures of AT0.1-A700 ME superalloy: (a,b) SEM-BSE and (c) TEM dark-field (DF) images of matrix and L12 precipitation, respectively; (d) XRD pattern, (e) EBSD inverse pole figure (IPF) image, and (f,g) the size distribution of FCC matrix and L12 phase, respectively.
Metals 14 00749 g001
Metals 14 00749 g002
Figure 2. Mechanical properties of AT0.1-A700 ME superalloy over a wide temperature range from 77 K to 1073 K: (a) engineering stress–strain curves and (b) variations in yield strength (σy), ultimate tensile strength (σuts), and fracture strain (εf) with temperature; (c) strain-hardening rates versus true strain curves; (d) average strain-hardening values as a function of deformation temperature (the inset shows the calculation method of the average hardening rate).
Figure 2. Mechanical properties of AT0.1-A700 ME superalloy over a wide temperature range from 77 K to 1073 K: (a) engineering stress–strain curves and (b) variations in yield strength (σy), ultimate tensile strength (σuts), and fracture strain (εf) with temperature; (c) strain-hardening rates versus true strain curves; (d) average strain-hardening values as a function of deformation temperature (the inset shows the calculation method of the average hardening rate).
Metals 14 00749 g002
Metals 14 00749 g003
Figure 3. EBSD image of AT0.1-A700 ME superalloy after tensile fracture at 77–973 K: (a–c) IPFs deformed at 77, 773, and 973 K, respectively; (a1–c1) and (a2–c2) are the corresponding KAM and recrystallized fraction images, respectively, for 77, 773, and 973 K.
Figure 3. EBSD image of AT0.1-A700 ME superalloy after tensile fracture at 77–973 K: (a–c) IPFs deformed at 77, 773, and 973 K, respectively; (a1–c1) and (a2–c2) are the corresponding KAM and recrystallized fraction images, respectively, for 77, 773, and 973 K.
Metals 14 00749 g003
Metals 14 00749 g004
Figure 4. TEM deformation microstructures of AT0.1-A700 ME superalloy after tensile fracture at 298 K: (a) bright-field (BF) image of SFs and the corresponding TEM-EDS maps in (a); (b) micromorphology and (c) high-magnification image of SF networks and L-C locks.
Figure 4. TEM deformation microstructures of AT0.1-A700 ME superalloy after tensile fracture at 298 K: (a) bright-field (BF) image of SFs and the corresponding TEM-EDS maps in (a); (b) micromorphology and (c) high-magnification image of SF networks and L-C locks.
Metals 14 00749 g004
Metals 14 00749 g005
Figure 5. TEM deformation microstructures of AT0.1-A700 ME superalloy after tensile fracture at 77 K: (a–c) BF images of SF band networks at different magnifications and (d–f) images showing the DT and tangled dislocations at different magnifications; (d,e) morphology and BF images located in different regions, respectively; (f) enlarged image of the red circle in (e).
Figure 5. TEM deformation microstructures of AT0.1-A700 ME superalloy after tensile fracture at 77 K: (a–c) BF images of SF band networks at different magnifications and (d–f) images showing the DT and tangled dislocations at different magnifications; (d,e) morphology and BF images located in different regions, respectively; (f) enlarged image of the red circle in (e).
Metals 14 00749 g005
Metals 14 00749 g006
Figure 6. TEM deformation microstructures of AT0.1-A700 ME superalloy after tensile fracture at 773 K: (a–c) BF images of HDDWs at different magnifications; (d) BF image of SF lines within HDDWs and (e) morphology of SF line shearing in the L12 phase; (f) diffraction spot of the red circle in (e), indicating the L12 phase.
Figure 6. TEM deformation microstructures of AT0.1-A700 ME superalloy after tensile fracture at 773 K: (a–c) BF images of HDDWs at different magnifications; (d) BF image of SF lines within HDDWs and (e) morphology of SF line shearing in the L12 phase; (f) diffraction spot of the red circle in (e), indicating the L12 phase.
Metals 14 00749 g006
Metals 14 00749 g007
Figure 7. TEM deformation microstructures of AT0.1-A700 ME superalloy after tensile fracture at 973 K: (a) BF image of dislocation lines and dislocation entanglements; (b) BF and (c) DF images of dislocation pairs, indicating of two sets of dislocation pairs from different slip surfaces; (d) BF image of SF and dislocation lines; (e) morphology of microtwins and (f) an enlarged version of the same image.
Figure 7. TEM deformation microstructures of AT0.1-A700 ME superalloy after tensile fracture at 973 K: (a) BF image of dislocation lines and dislocation entanglements; (b) BF and (c) DF images of dislocation pairs, indicating of two sets of dislocation pairs from different slip surfaces; (d) BF image of SF and dislocation lines; (e) morphology of microtwins and (f) an enlarged version of the same image.
Metals 14 00749 g007
Metals 14 00749 g008
Figure 8. Schematic of the effect of temperature on the tensile properties and deformation mechanisms.
Figure 8. Schematic of the effect of temperature on the tensile properties and deformation mechanisms.
Metals 14 00749 g008
Table 1. Chemical composition of AT0.1-700 ME superalloy (at%).
Table 1. Chemical composition of AT0.1-700 ME superalloy (at%).
ElementsNiCoCrSiAlTi
Nominal composition502512.57.52.52.5
Actual composition47.7725.3112.298.703.112.83
Table 2. The tensile properties of AT0.1-A700 ME superalloy at different temperatures.
Table 2. The tensile properties of AT0.1-A700 ME superalloy at different temperatures.
Temp. (K)Tensile Properties
σy (MPa)σuts (MPa)εf (%)(dσ/dε)avg. (MPa)
771005 ± 381620 ± 5336.3 ± 2.24025 ± 153
298836 ± 521274 ± 6634.5 ± 1.32884 ± 120
773835 ± 401120 ± 3235.1 ± 2.41800 ± 200
873841 ± 371010 ± 4918.4 ± 1.82212 ± 85
973808 ± 38862 ± 5315.2 ± 1.41430 ± 53
1073542 ± 34542 ± 3426.5 ± 2.9−155 ± 95
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Zhang, T.; Bai, T.; Xiong, R.; Luo, S.; Chang, H.; Du, S.; Ma, J.; Jiao, Z.; Ma, S.; Wang, J.; et al. Temperature-Dependent Mechanical Behaviors and Deformation Mechanisms in a Si-Added Medium-Entropy Superalloy with L12 Precipitation. Metals 2024, 14, 749. https://doi.org/10.3390/met14070749

AMA Style

Zhang T, Bai T, Xiong R, Luo S, Chang H, Du S, Ma J, Jiao Z, Ma S, Wang J, et al. Temperature-Dependent Mechanical Behaviors and Deformation Mechanisms in a Si-Added Medium-Entropy Superalloy with L12 Precipitation. Metals. 2024; 14(7):749. https://doi.org/10.3390/met14070749

Chicago/Turabian Style

Zhang, Tuanwei, Tianxiang Bai, Renlong Xiong, Shunhui Luo, Hui Chang, Shiyu Du, Jinyao Ma, Zhiming Jiao, Shengguo Ma, Jianjun Wang, and et al. 2024. "Temperature-Dependent Mechanical Behaviors and Deformation Mechanisms in a Si-Added Medium-Entropy Superalloy with L12 Precipitation" Metals 14, no. 7: 749. https://doi.org/10.3390/met14070749

APA Style

Zhang, T., Bai, T., Xiong, R., Luo, S., Chang, H., Du, S., Ma, J., Jiao, Z., Ma, S., Wang, J., & Wang, Z. (2024). Temperature-Dependent Mechanical Behaviors and Deformation Mechanisms in a Si-Added Medium-Entropy Superalloy with L12 Precipitation. Metals, 14(7), 749. https://doi.org/10.3390/met14070749

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop