Experimental Characterization and Phase-Field Damage Modeling of Ductile Fracture in AISI 316L
Abstract
1. Introduction
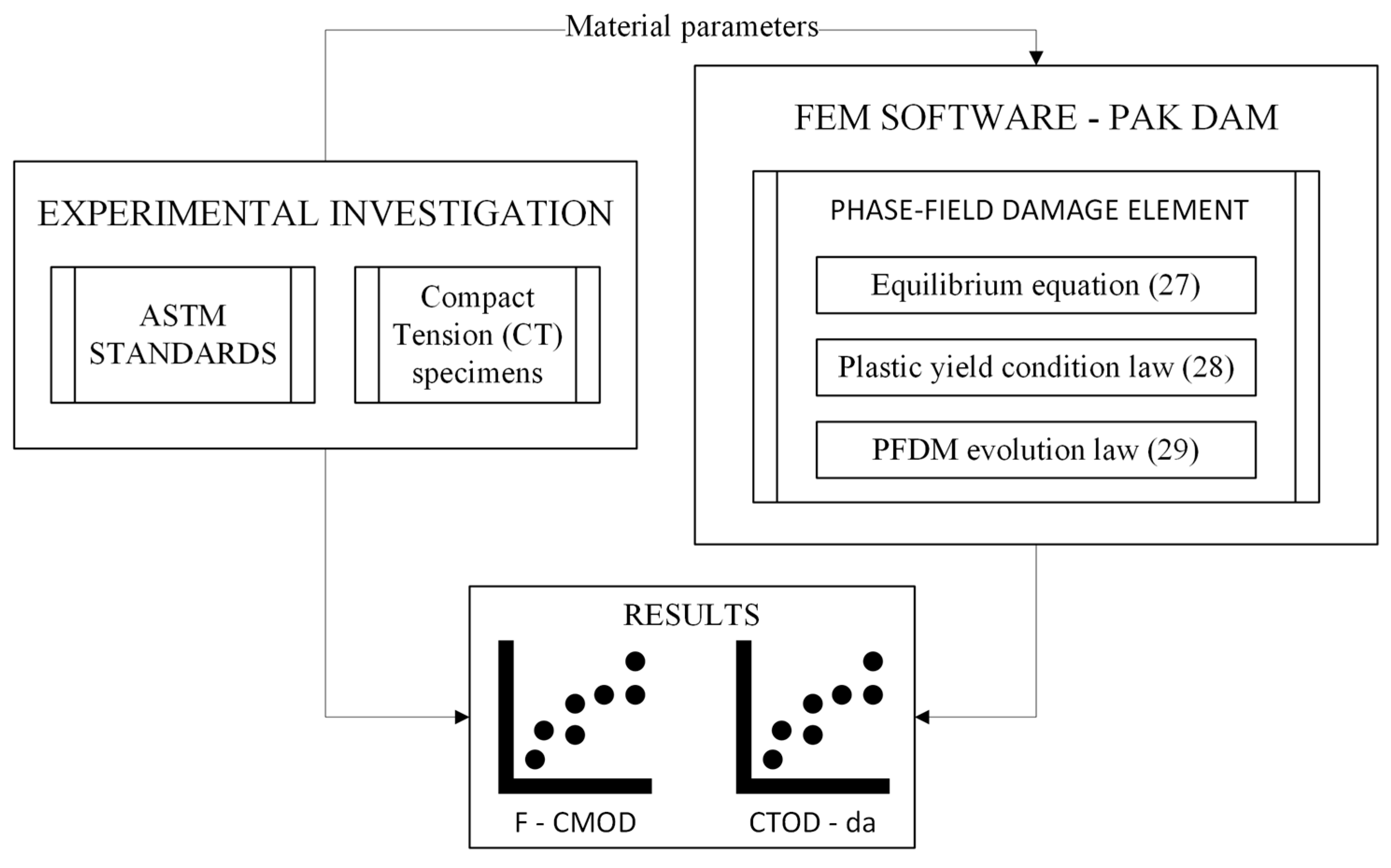
2. Improved Phase-Field Damage Model for Ductile Behavior of Materials
2.1. Energy State Potential in a Damaged Solid
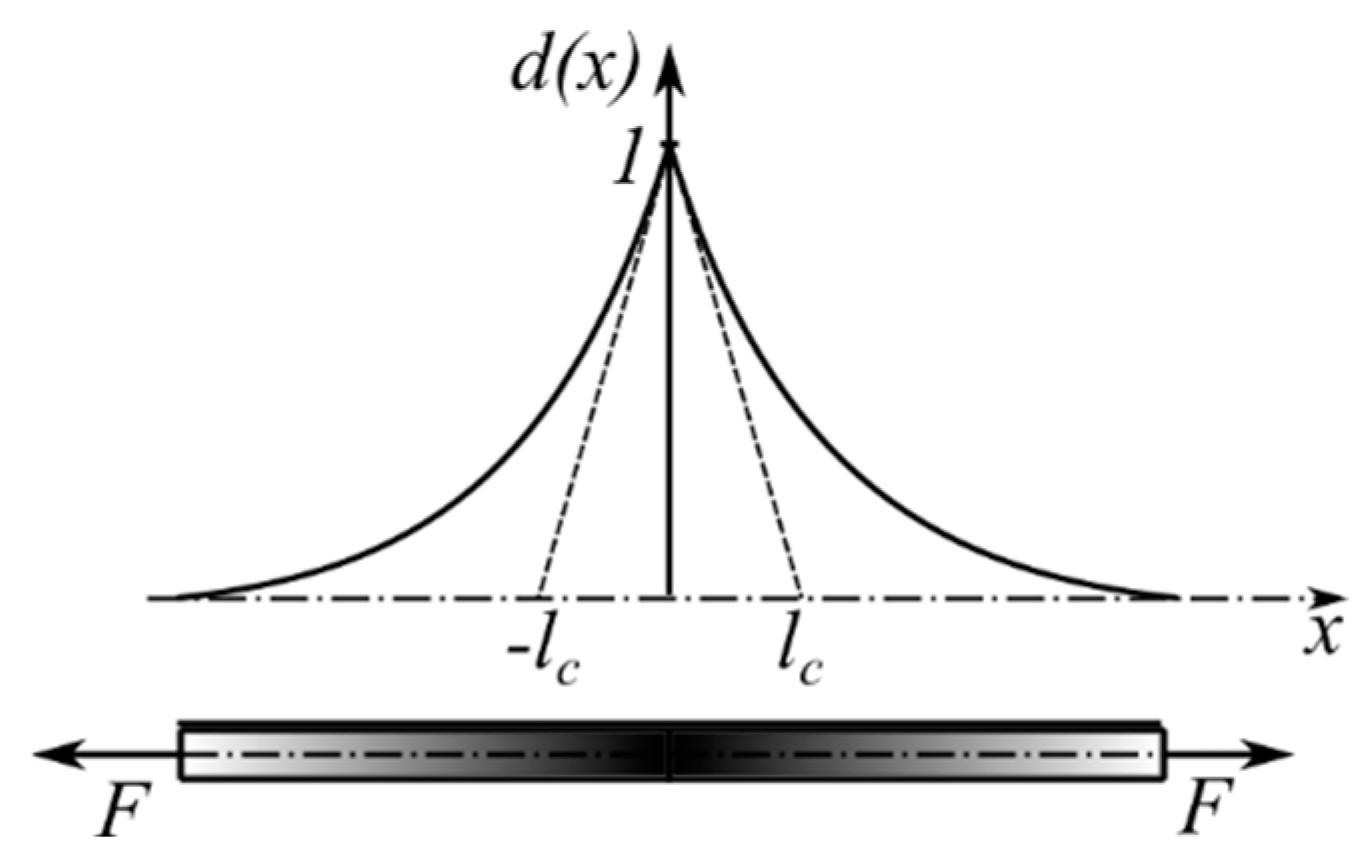
2.2. A Critical Total Strain vs. Threshold Value of Fracture Energy
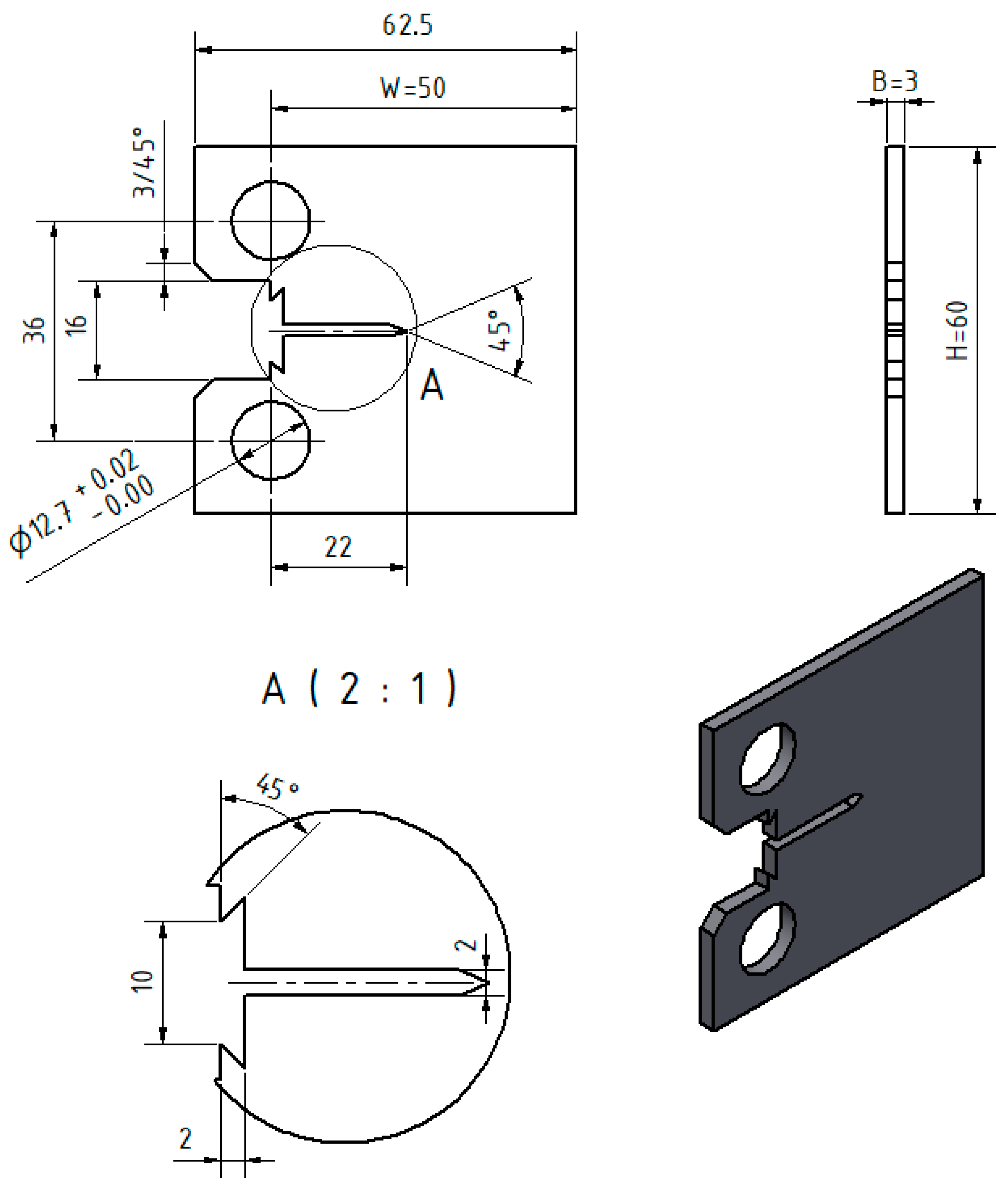
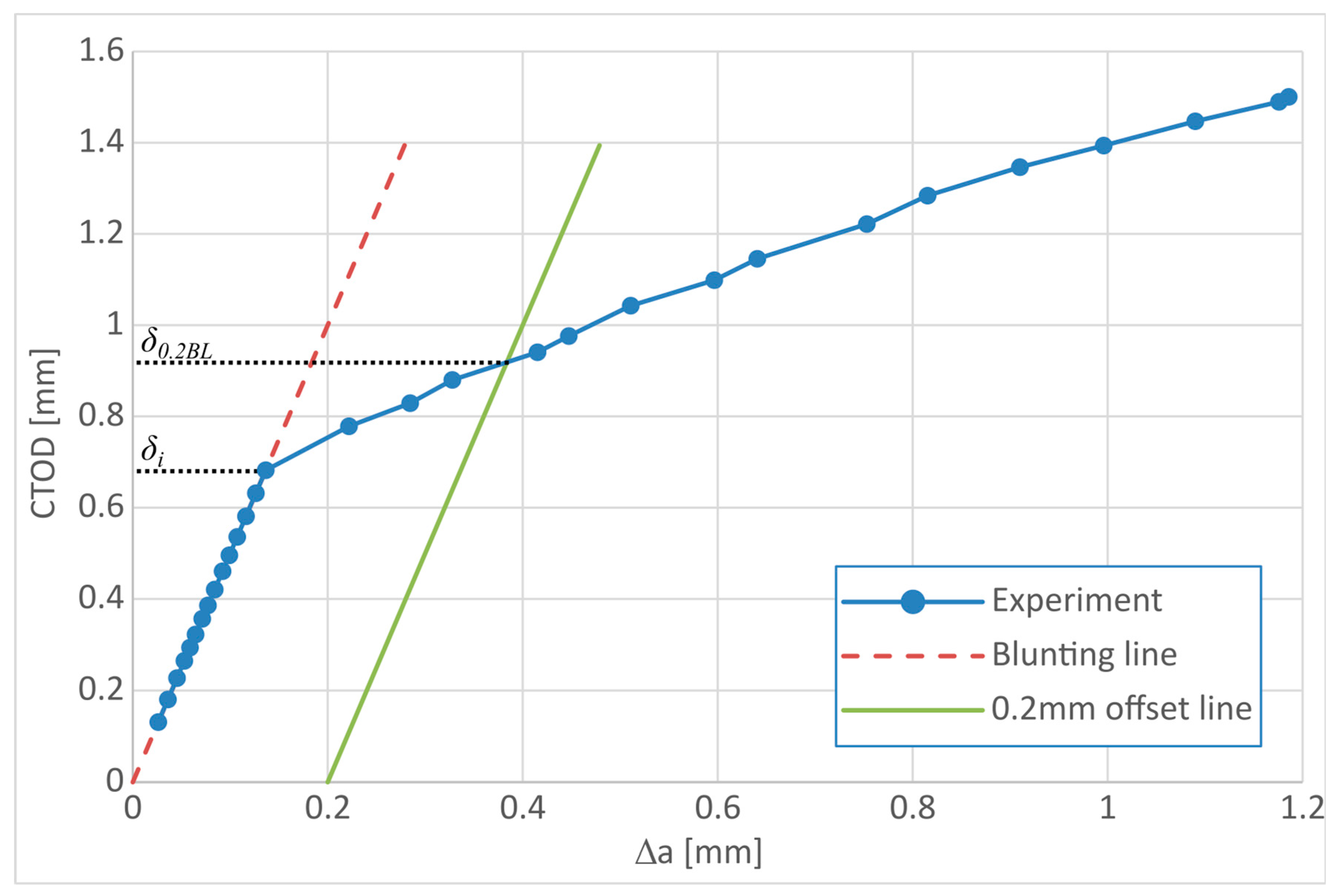
2.3. Experimental Investigation of Metallic CT Specimens
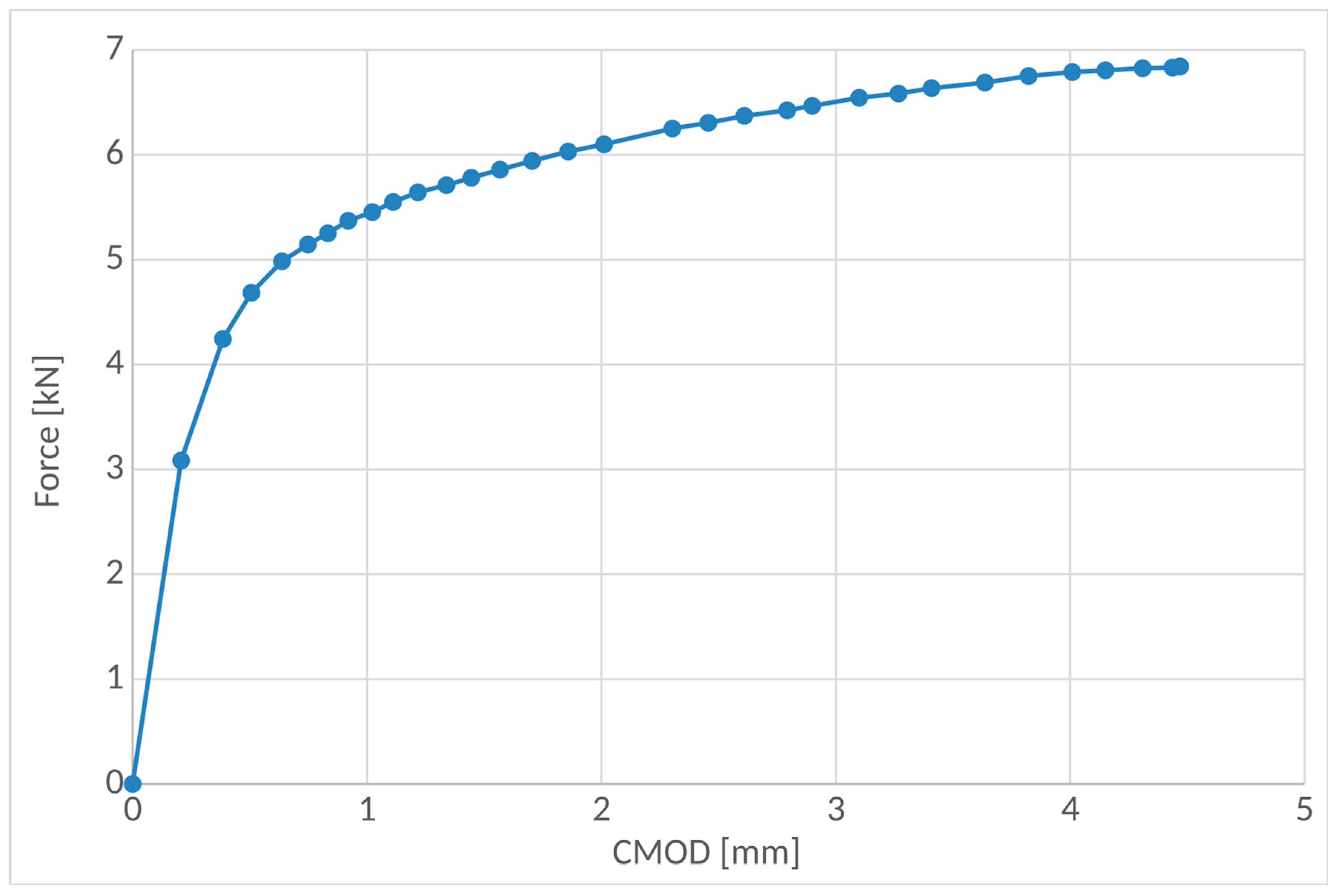
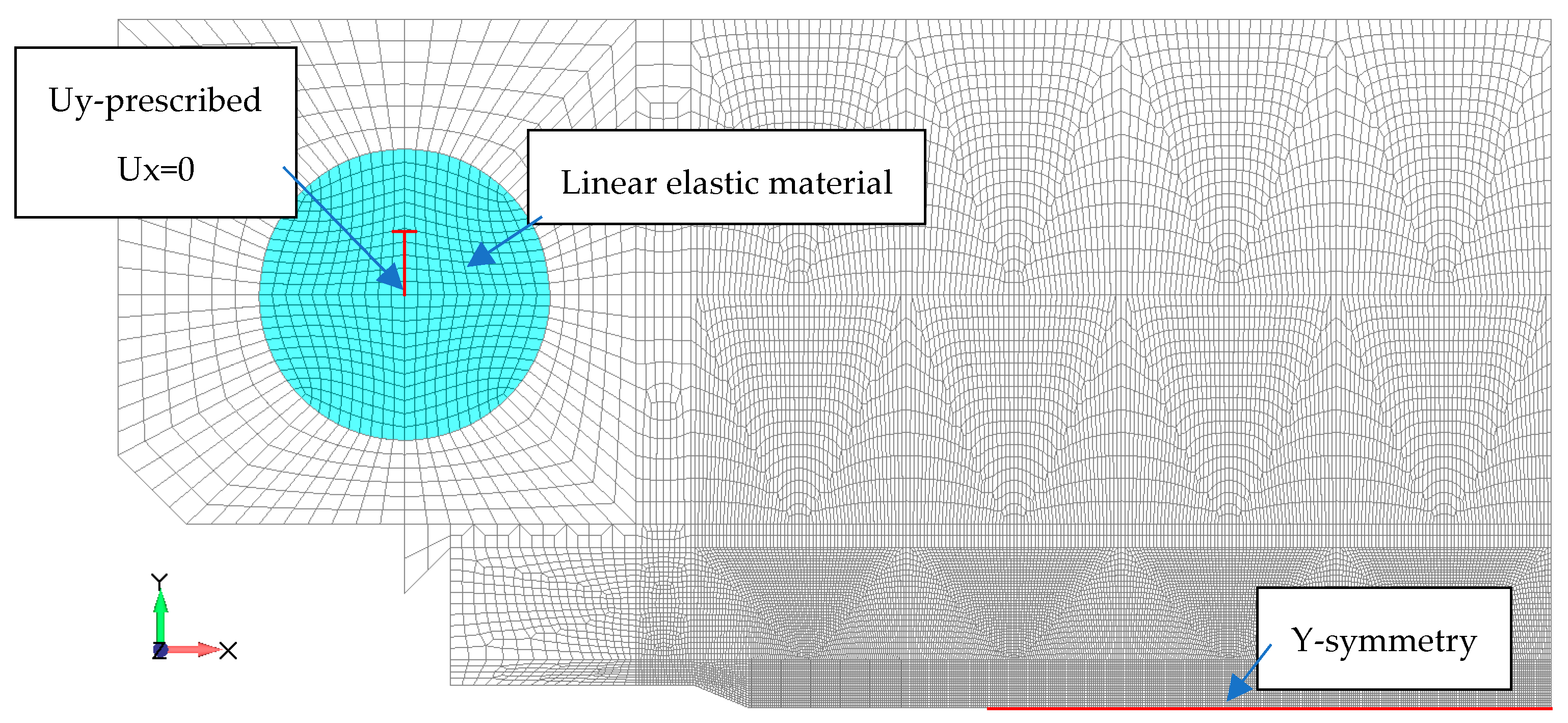
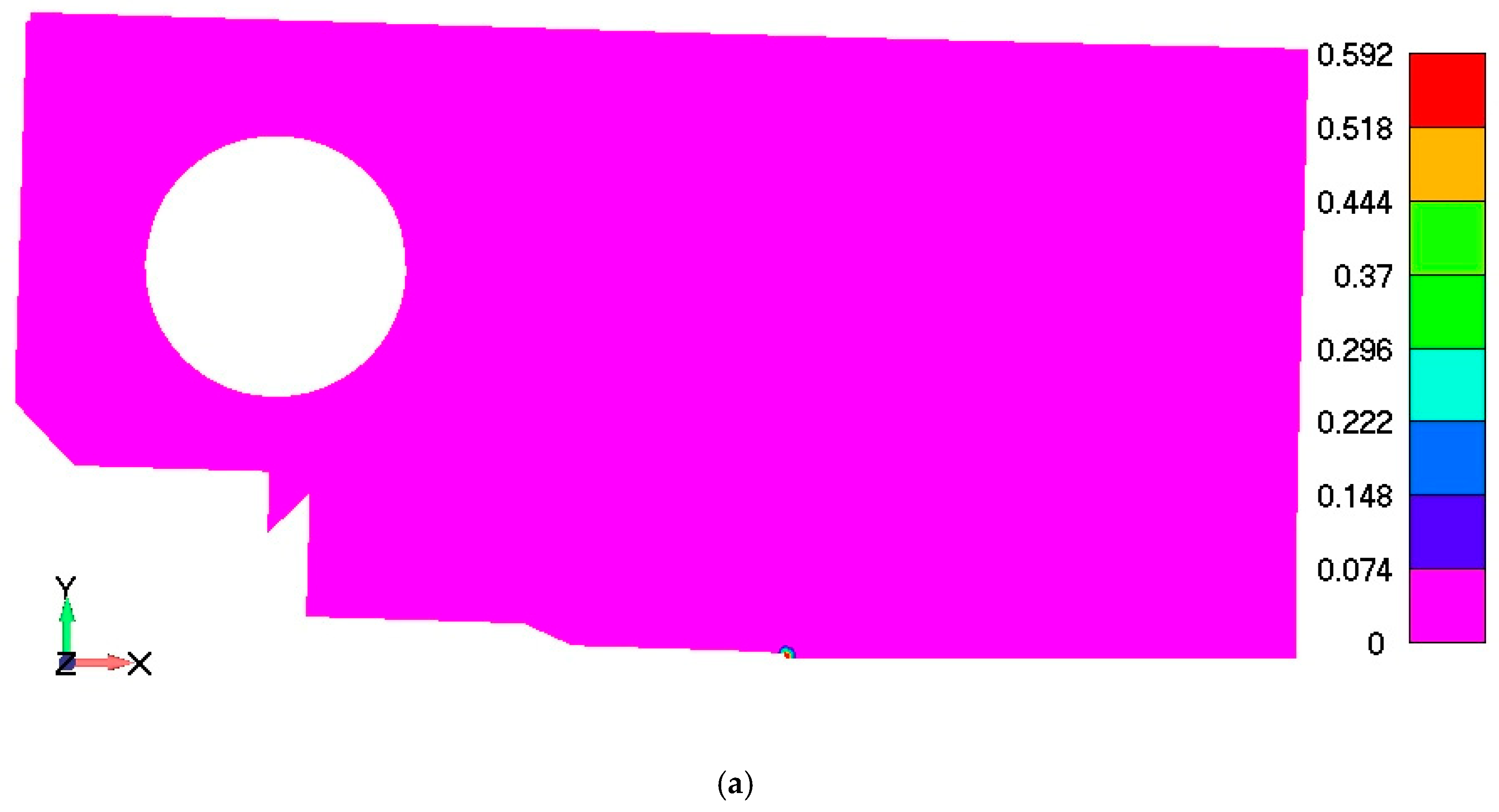
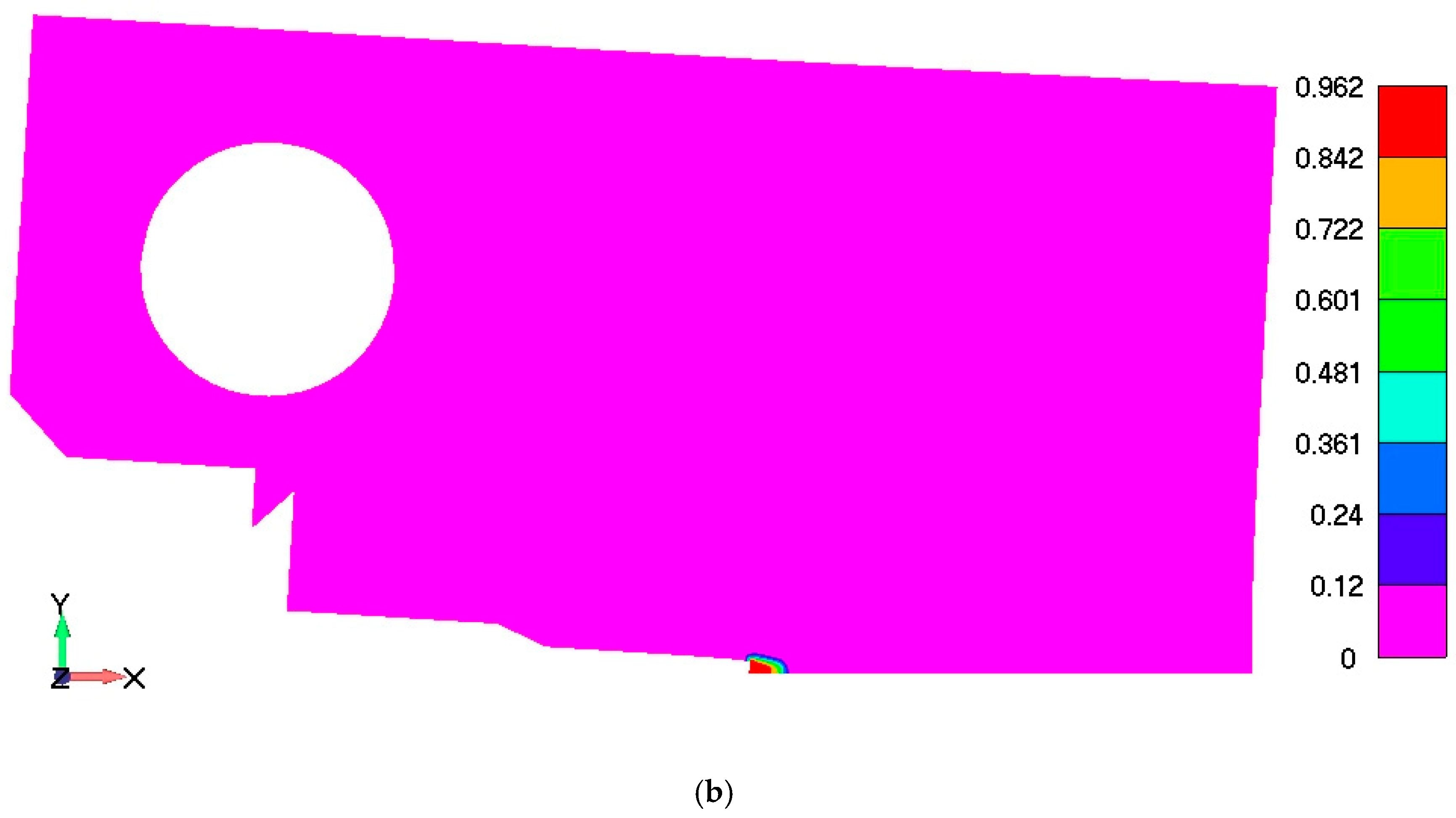
3. PFDM Simulation of Ductile Fracture
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhu, X.-K.; Joyce, J.A. Review of fracture toughness (G, K, J, CTOD, CTOA) testing and standardization. Eng. Fract. Mech. 2012, 85, 1–46. [Google Scholar] [CrossRef]
- Garcia-Gonzalez, A.; Aguilera, J.A.; Cerezo, P.M.; Castro-Egler, C.; Lopez-Crespo, P. A Literature Review of Incorporating Crack Tip Plasticity into Fatigue Crack Growth Models. Materials 2023, 16, 7603. [Google Scholar] [CrossRef] [PubMed]
- Ajmal, M.; Lopez-Crespo, C.; Cruces, A.S.; Lopez-Crespo, P. New Plastic Crack-Tip Opening Displacement Tool Based on Digital Image Correlation for Estimating the Fatigue-Crack-Growth Law on 316L Stainless Steel. Materials 2023, 16, 4589. [Google Scholar] [CrossRef] [PubMed]
- Khor, W.L. Crack Tip Opening Displacement (CTOD) in Single Edge Notched Bend (SEN(B)). Ph.D. Thesis, Brunel University, London, UK, 2018. [Google Scholar]
- BS 7448-1:1991; Fracture Mechanics Toughness Tests—Part 1: Method for Determination of KIc, Critical CTOD and Critical J Values of Metallic Materials. BSI: London, UK, 2007.
- ISO 12135-2016; Metallic Materials—Unified Method of Test for the Determination of Quasistatic Fracture Toughness. ISO: Geneva, Switzerland, 2016.
- ASTM E1820 Standard; Standard Test Method for Measurement of Fracture Toughness. American Society for Testing and Materials: Philadelphia, PA, USA, 2019.
- WES 1108:2016; Standard test method for Crack-Tip Opening Displacement (CTOD) fracture toughness measurement. The Japan Welding Engineering Society: Tokyo, Japan, 1995.
- Griffith, A.A., VI. The phenomena of rupture and flow in solids. Philos. Trans. R. Soc. Lond. A 1921, 221, 163–198. [Google Scholar] [CrossRef]
- Seleš, K.; Tomić, Z.; Tonković, Z.; Gubeljak, N. Validation of the Phase-Field Model for Brittle Fracture. Procedia Struct. Integr. 2022, 42, 1721–1727. [Google Scholar] [CrossRef]
- Seleš, K.; Aldakheel, F.; Tonković, Z.; Sorić, J.; Wriggers, P. A general phase-field model for fatigue failure in brittle and ductile solids. Comput. Mech. 2021, 67, 1431–1452. [Google Scholar] [CrossRef]
- Khandelwal, N.; Ramachandra Murthy, A. Ductile fracture simulation using phase field method with various damage models based on different degradation and geometric crack functions. Mater. Today Commun. 2023, 35, 105627. [Google Scholar] [CrossRef]
- Yin, B.; Kaliske, M. A ductile phase-field model based on degrading the fracture toughness: Theory and implementation at small strain. Comput. Methods Appl. Mech. Eng. 2020, 366, 113068. [Google Scholar] [CrossRef]
- Eldahshan, H.; Bouchard, P.-O.; Alves, J.; Perchat, E.; Muñoz, D.P. Phase field modeling of ductile fracture at large plastic strains using adaptive isotropic remeshing. Comput. Mech. 2021, 67, 763–783. [Google Scholar] [CrossRef]
- Ambati, M.; Gerasimov, T.; De Lorenzis, L. Phase-field modeling of ductile fracture. Comput. Mech. 2015, 55, 1017–1040. [Google Scholar] [CrossRef]
- Ambati, M.; Kruse, R.; De Lorenzis, L. A phase-field model for ductile fracture at finite strains and its experimental verification. Comput. Mech. 2016, 57, 149–167. [Google Scholar] [CrossRef]
- Miehe, C.; Hofacker, M.; Schänzel, L.-M.; Aldakheel, F. Phase field modeling of fracture in multi-physics problems. Part II. Coupled brittle-to-ductile failure criteria and crack propagation in thermo-elastic–plastic solids. Comput. Methods Appl. Mech. Eng. 2015, 294, 486–522. [Google Scholar] [CrossRef]
- Huang, C.; Gao, X. Development of a phase field method for modeling brittle and ductile fracture. Comput. Mater. Sci. 2019, 169, 109089. [Google Scholar] [CrossRef]
- Lesičar, T.; Polančec, T.; Tonković, Z. Convergence Check Phase-Field Scheme for Modelling of Brittle and Ductile Fractures. Appl. Sci. 2023, 13, 7776. [Google Scholar] [CrossRef]
- Liu, S.; Han, F.; Deng, X.; Lin, Y. Thermomechanical Peridynamic Modeling for Ductile Fracture. Materials 2023, 16, 4074. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.-J.; Su, M.-N.; Wang, Y.-H.; Zhu, R.-H. Experimental and numerical investigations of crack growth of hot-rolled steel Q420C using cohesive zone model. Theor. Appl. Fract. Mech. 2023, 127, 104036. [Google Scholar] [CrossRef]
- Živković, M.; Dunić, V.; Rakić, D.; Grujović, N.; Slavković, R.; Kojić, M. PAK-DAM Software for Damage and Fracture Simulation; Faculty of Engineering, University of Kragujevac: Kragujevac, Serbia, 2024. [Google Scholar]
- Miehe, C. A multi-field incremental variational framework for gradient-extended standard dissipative solids. J. Mech. Phys. Solids 2011, 59, 898–923. [Google Scholar] [CrossRef]
- Francfort, G.; Marigo, J.-J. Revisiting brittle fracture as an energy minimization problem. J. Mech. Phys. Solids 1998, 46, 1319–1342. [Google Scholar] [CrossRef]
- Bourdin, B.; Francfort, G.A.; Marigo, J.-J. Numerical experiments in revisited brittle fracture. J. Mech. Phys. Solids 2000, 48, 797–826. [Google Scholar] [CrossRef]
- Živković, J.; Dunić, V.; Milovanović, V.; Pavlović, A.; Živković, M. A Modified Phase-Field Damage Model for Metal Plasticity at Finite Strains: Numerical Development and Experimental Validation. Metals 2021, 11, 47. [Google Scholar] [CrossRef]
- Miehe, C.; Welschinger, F.; Hofacker, M. Thermodynamically consistent phase-field models of fracture: Variational principles and multi-field FE implementations. Int. J. Numer. Methods Eng. 2010, 83, 1273–1311. [Google Scholar] [CrossRef]
- Dunić, V.; Živković, J.; Milovanović, V.; Pavlović, A.; Radovanović, A.; Živković, M. Two-Intervals Hardening Function in a Phase-Field Damage Model for the Simulation of Aluminum Alloy Ductile Behavior. Metals 2021, 11, 1685. [Google Scholar] [CrossRef]
- Ambati, M.; Gerasimov, T.; De Lorenzis, L. A review on phase-field models of brittle fracture and a new fast hybrid formulation. Comput. Mech. 2015, 55, 383–405. [Google Scholar] [CrossRef]
- Kojić, M.; Bathe, K.J. Inelastic Analysis of Solids and Structures; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Das, A.; Chakraborti, P.C.; Tarafder, S.; Bhadeshia, H.K.D.H. Analysis of deformation induced martensitic transformation in stainless steels. Mater. Sci. Technol. 2011, 27, 366–370. [Google Scholar] [CrossRef]
- Solomon, N.; Solomon, I. Deformation induced martensite in AISI 316 stainless steel. Rev. Metal. 2010, 46, 121–128. [Google Scholar] [CrossRef]
- Jagarinec, D.; Kirbiš, P.; Predan, J.; Vuherer, T.; Gubeljak, N. Analysis of deformation induced martensite in AISI 316L stainless steel. Mater. Test. 2016, 58, 547–552. [Google Scholar] [CrossRef]
- ASTM E8/E8M Standard; Standard Test Methods for Tension Testing of Metallic Materials. American Society for Testing and Materials: Philadelphia, PA, USA, 2015.
- Haneef, T.; Lahiri, B.B.; Bagavathiappan, S.; Mukhopadhyay, C.K.; Philip, J.; Rao, B.P.C.; Jayakumar, T. Study of the tensile behavior of AISI type 316 stainless steel using acoustic emission and infrared thermography techniques. J. Mater. Res. Technol. 2015, 4, 241–253. [Google Scholar] [CrossRef]
- ASTM E1290 Standard; Standard Test Method for Crack-Tip Opening Displacement (CTOD) Fracture Toughness Measurement. American Society for Testing and Materials: Philadelphia, PA, USA, 2017.
- Kudari, S.K.; Kodancha, K. On the relationship between J-integral and CTOD for CT and SENB specimens. Frat. Integrita. Strut. 2013, 2, 3–10. [Google Scholar] [CrossRef]

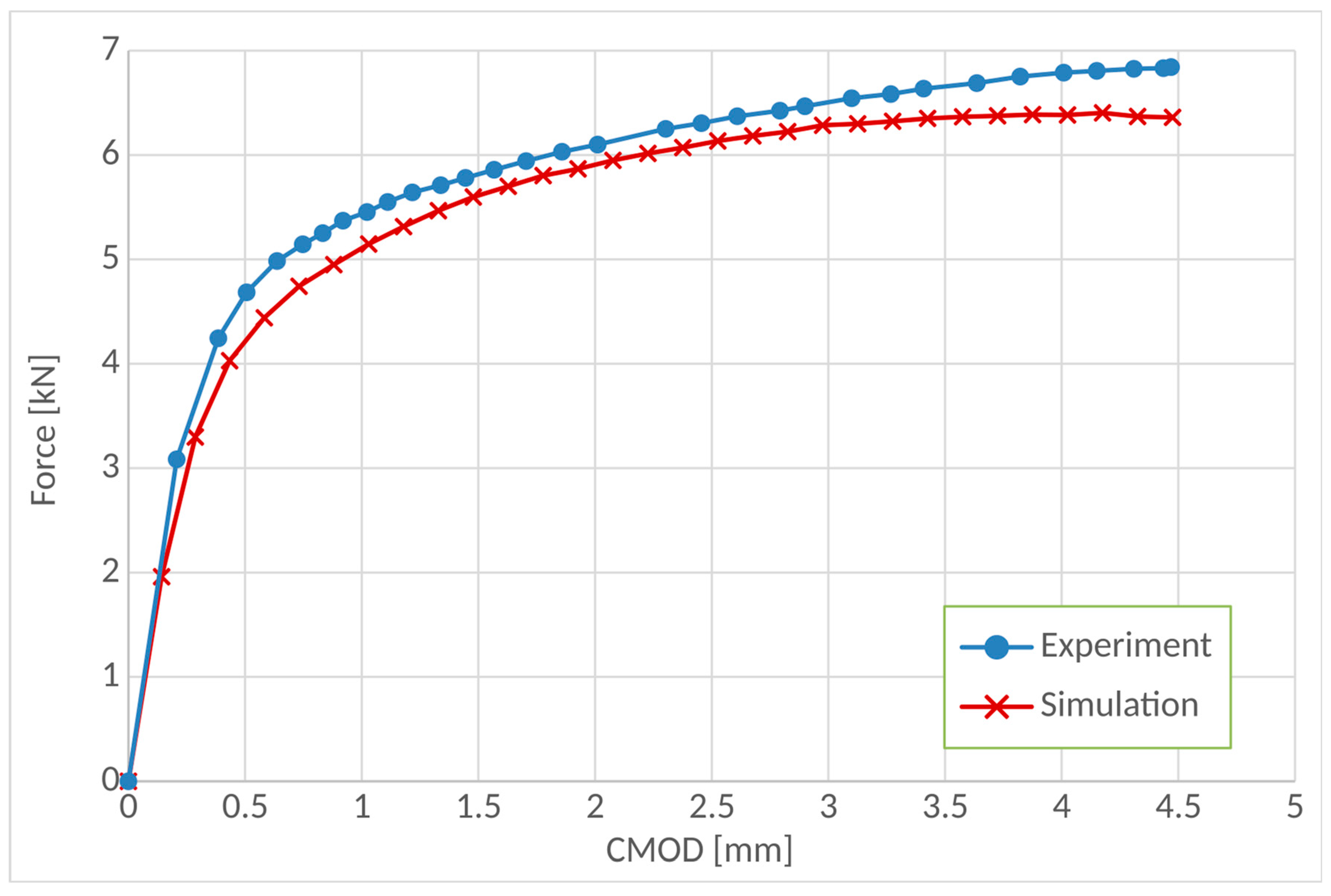
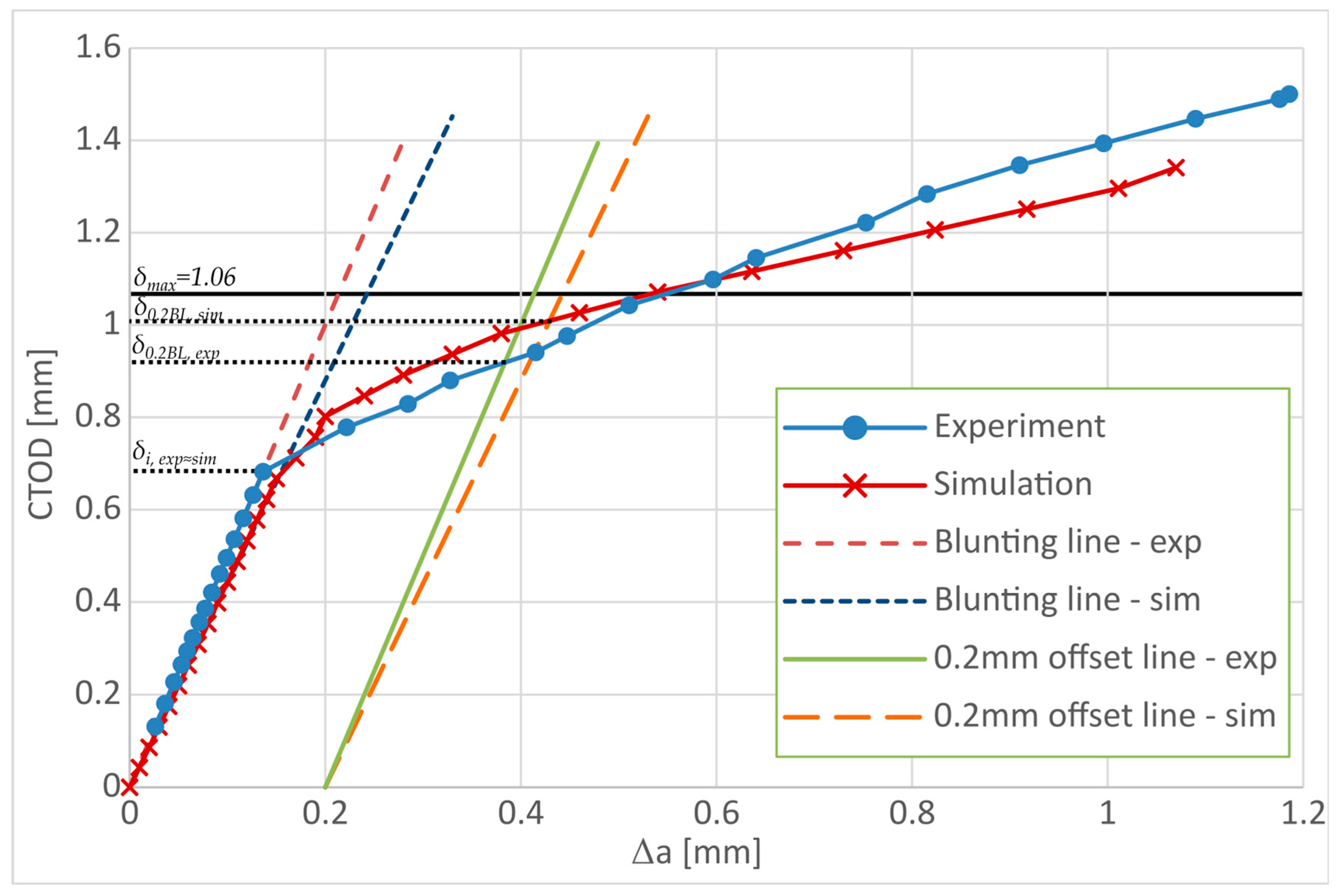

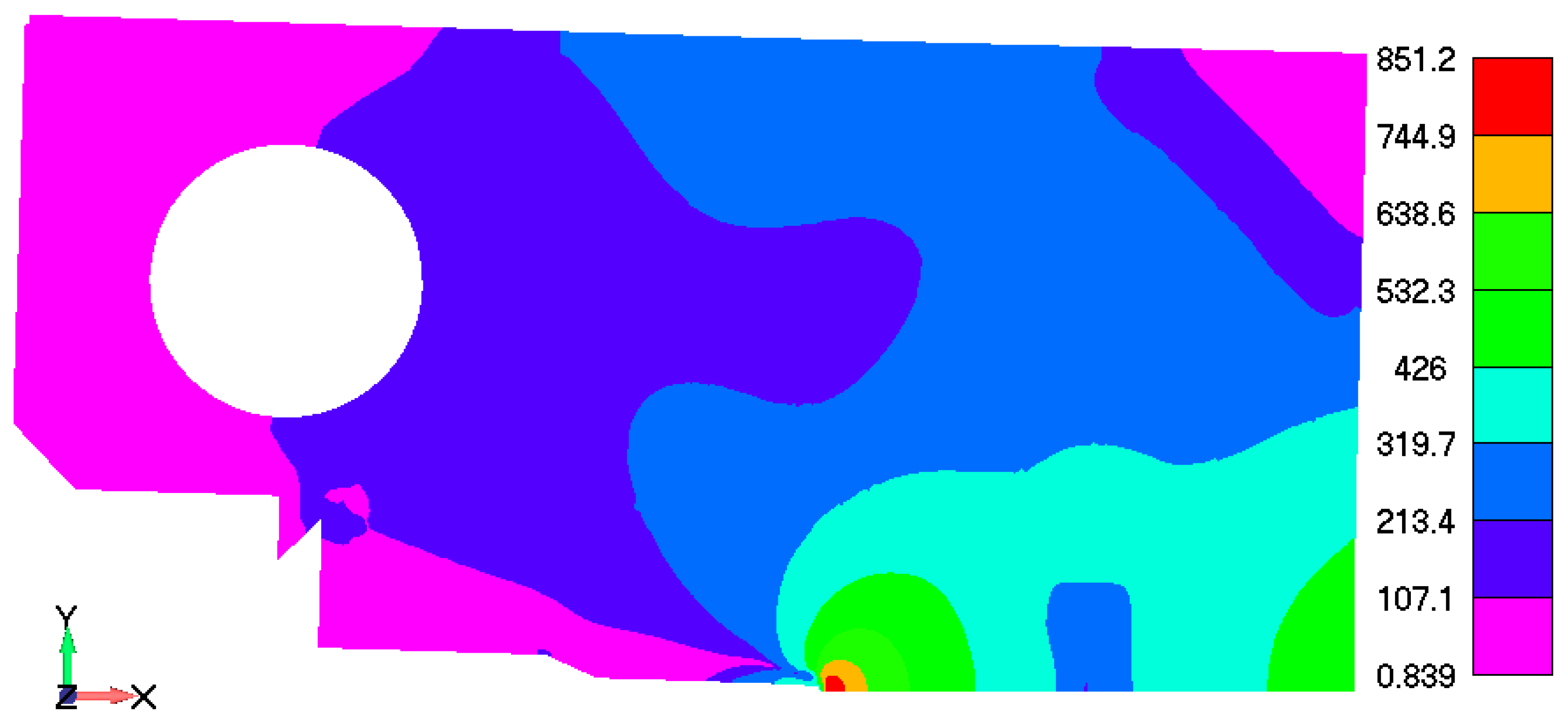

| Material Parameter | Average Value |
|---|---|
| 188,000 | |
| 0.33 | |
| 280 | |
| 575 | |
| Rotation factor according to standard ASTM E-1820 | 0.44 |
| Material Parameter | Value |
|---|---|
| 25.35 | |
| 26.40 | |
| 1.05 |
| Material Parameter | Value |
|---|---|
| 1200 | |
| 0.1 | |
| 1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dunić, V.; Gubeljak, N.; Živković, M.; Milovanović, V.; Jagarinec, D.; Djordjevic, N. Experimental Characterization and Phase-Field Damage Modeling of Ductile Fracture in AISI 316L. Metals 2024, 14, 787. https://doi.org/10.3390/met14070787
Dunić V, Gubeljak N, Živković M, Milovanović V, Jagarinec D, Djordjevic N. Experimental Characterization and Phase-Field Damage Modeling of Ductile Fracture in AISI 316L. Metals. 2024; 14(7):787. https://doi.org/10.3390/met14070787
Chicago/Turabian StyleDunić, Vladimir, Nenad Gubeljak, Miroslav Živković, Vladimir Milovanović, Darko Jagarinec, and Nenad Djordjevic. 2024. "Experimental Characterization and Phase-Field Damage Modeling of Ductile Fracture in AISI 316L" Metals 14, no. 7: 787. https://doi.org/10.3390/met14070787
APA StyleDunić, V., Gubeljak, N., Živković, M., Milovanović, V., Jagarinec, D., & Djordjevic, N. (2024). Experimental Characterization and Phase-Field Damage Modeling of Ductile Fracture in AISI 316L. Metals, 14(7), 787. https://doi.org/10.3390/met14070787










