Estimation of Mechanical Properties of Aluminum Alloy Based on Indentation Curve and Projection Area of Contact Zone
Abstract
:1. Introduction
2. Materials and Methods
2.1. Projection Methodology
2.2. Experiment Process
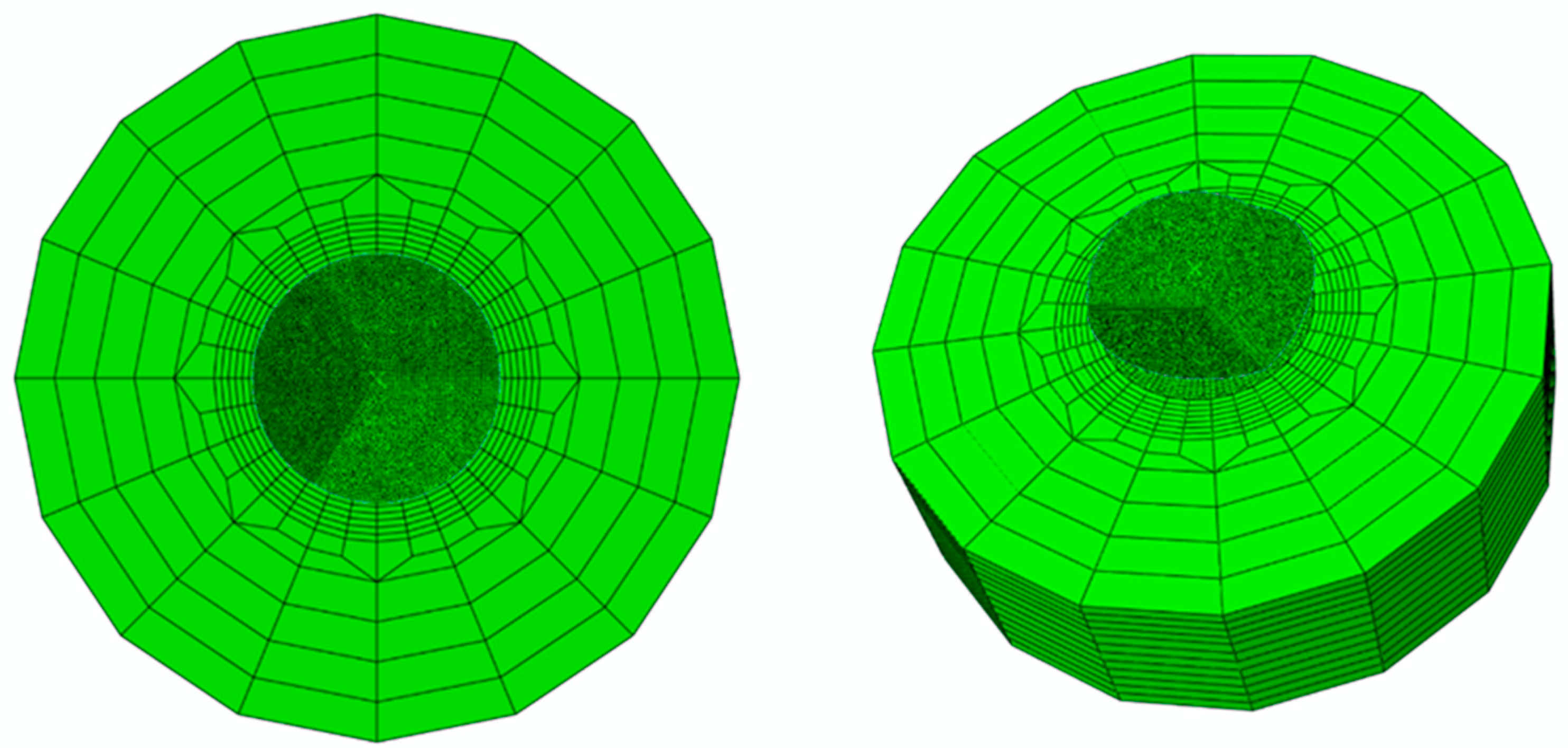
2.3. Finite Element Simulation
3. Results and Discussion
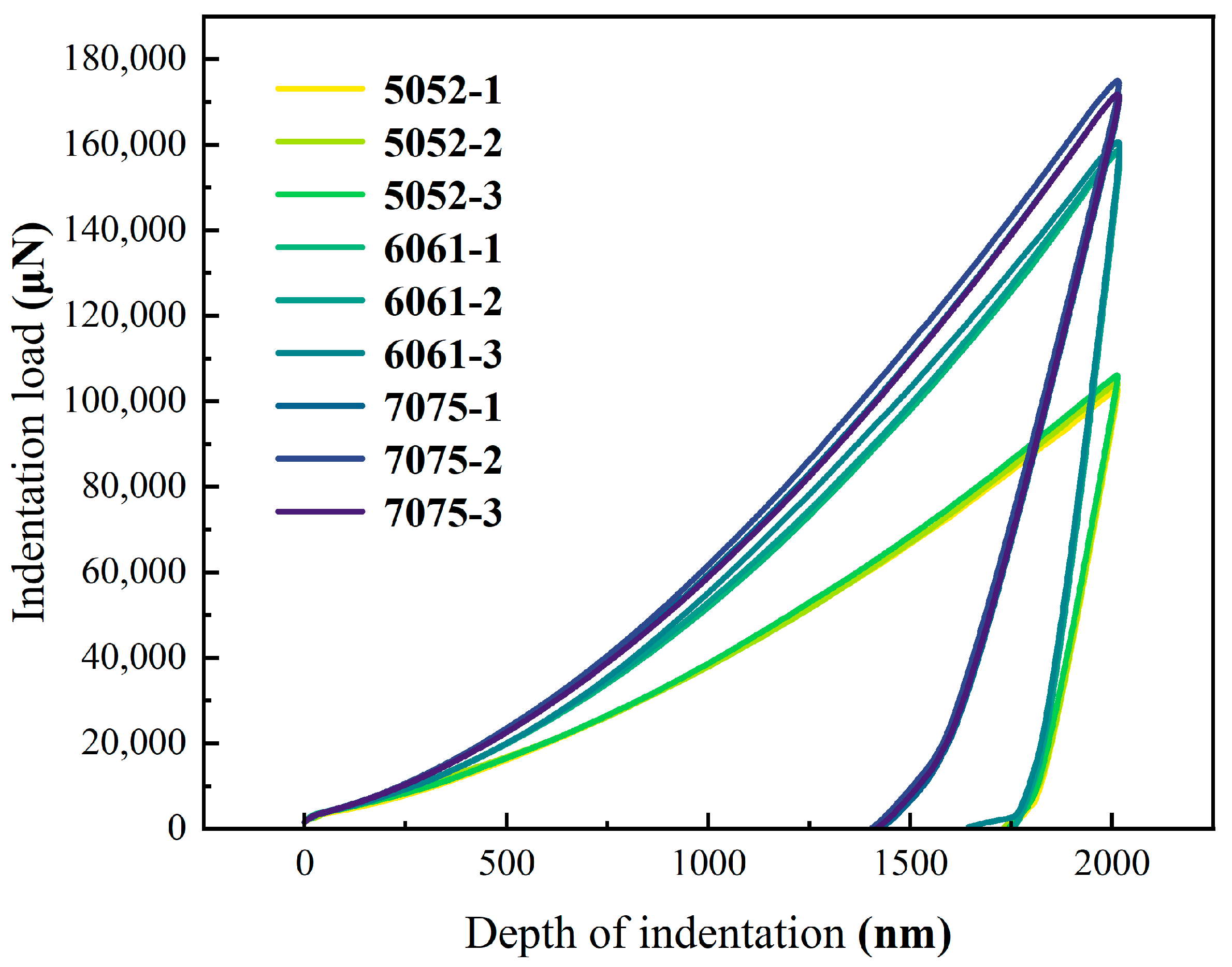
3.1. Indentation Mechanical Response
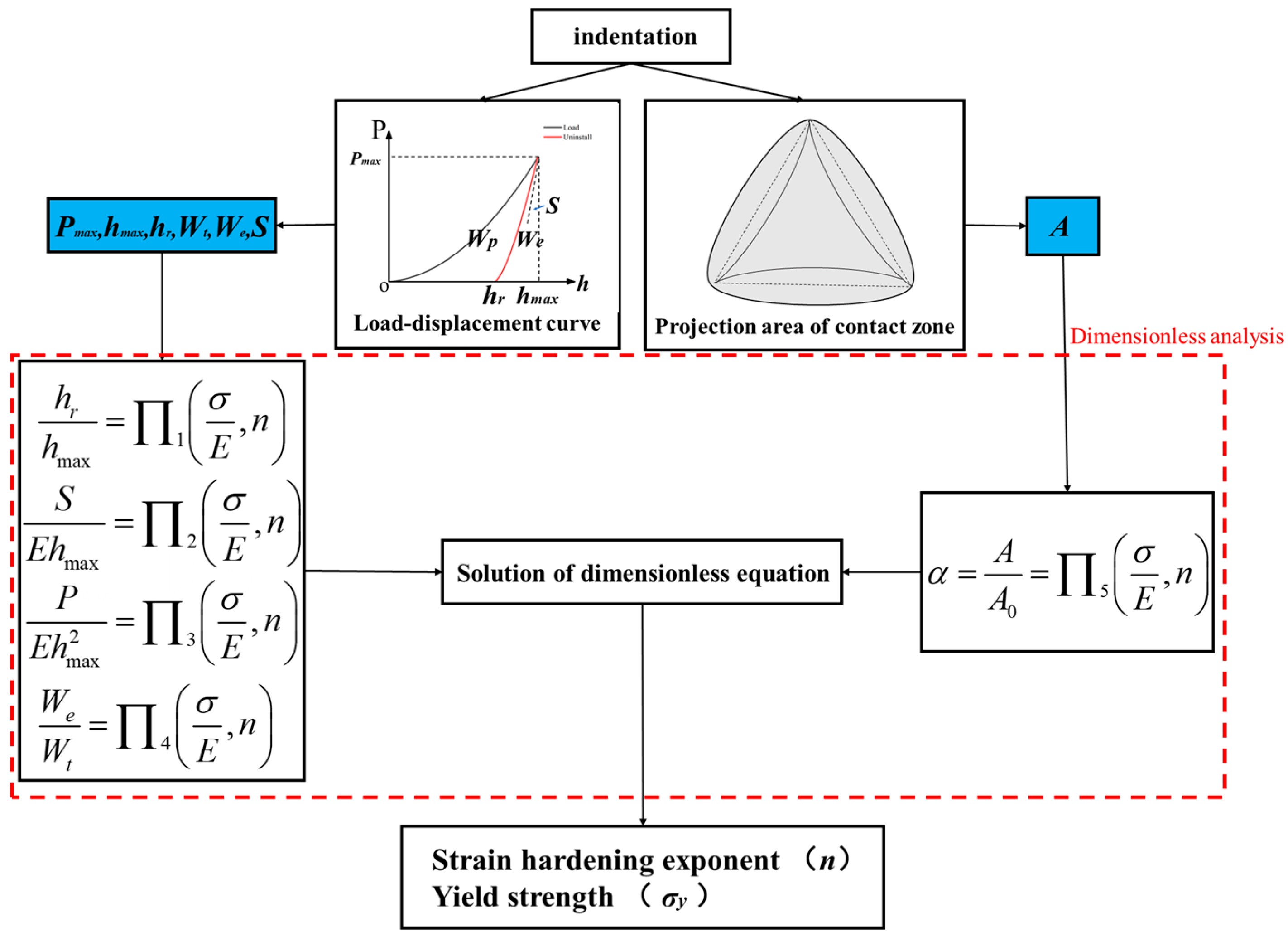
3.2. Extraction of Parameters from P-h Curves for Dimensionless Analysis
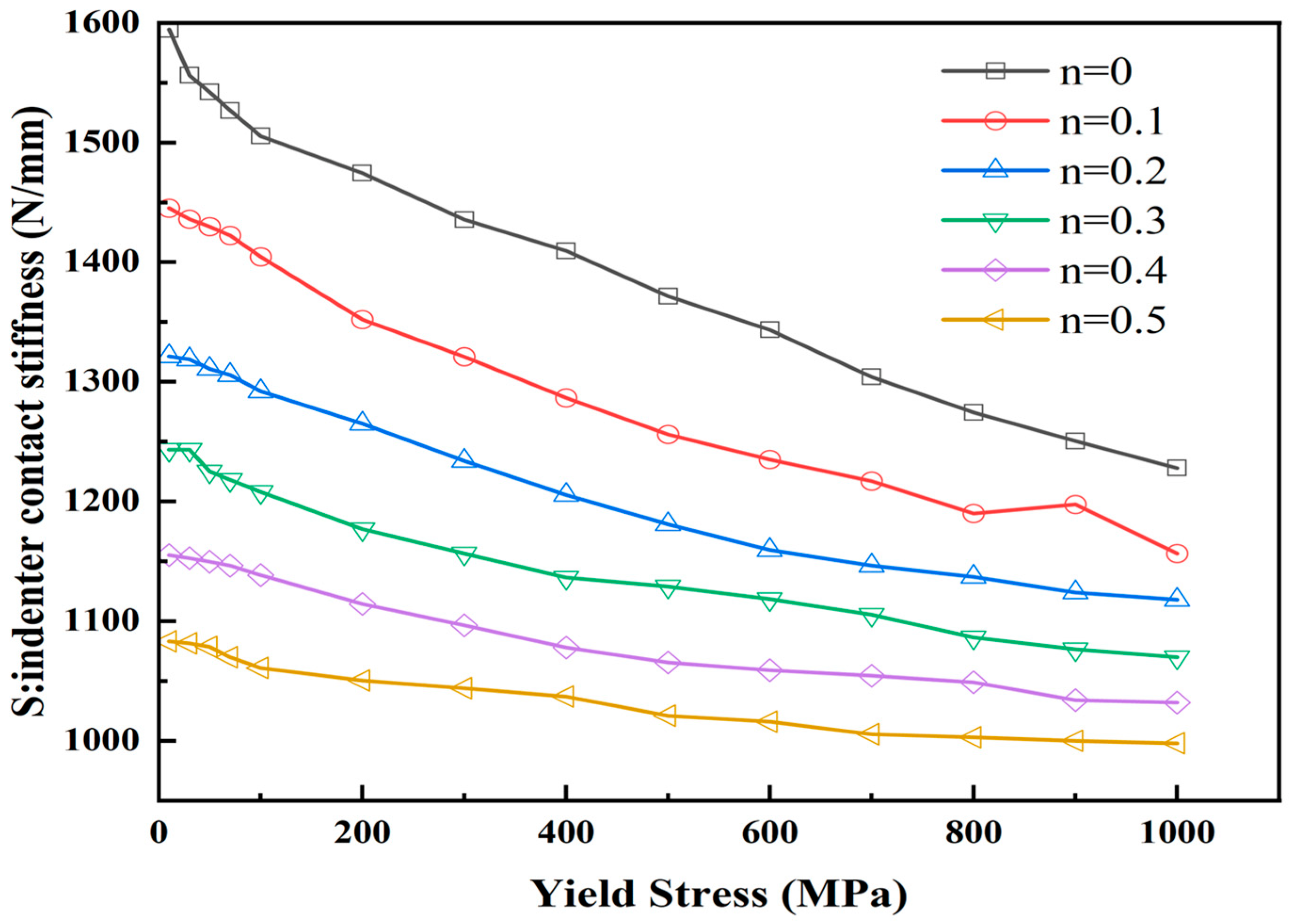
3.2.1. Parameters Obtained from the Load-Displacement Curve
3.2.2. Dimensionless Analysis
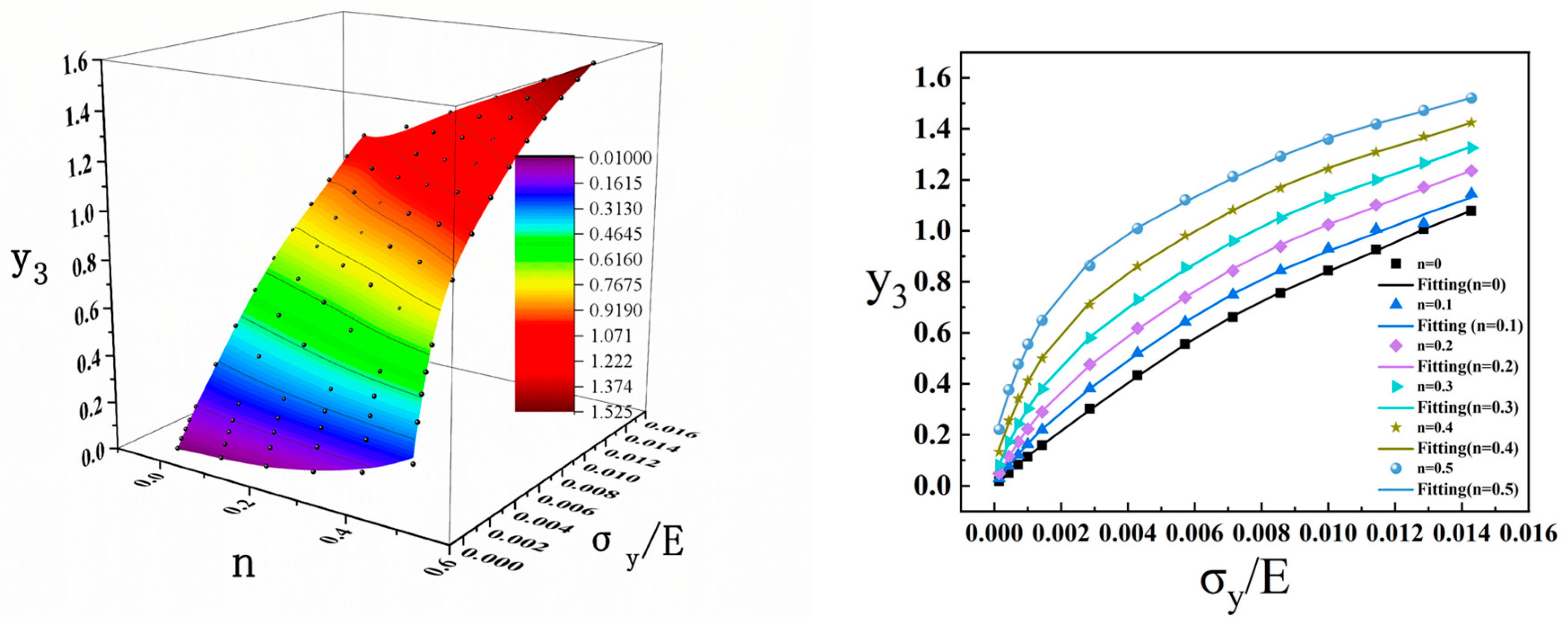
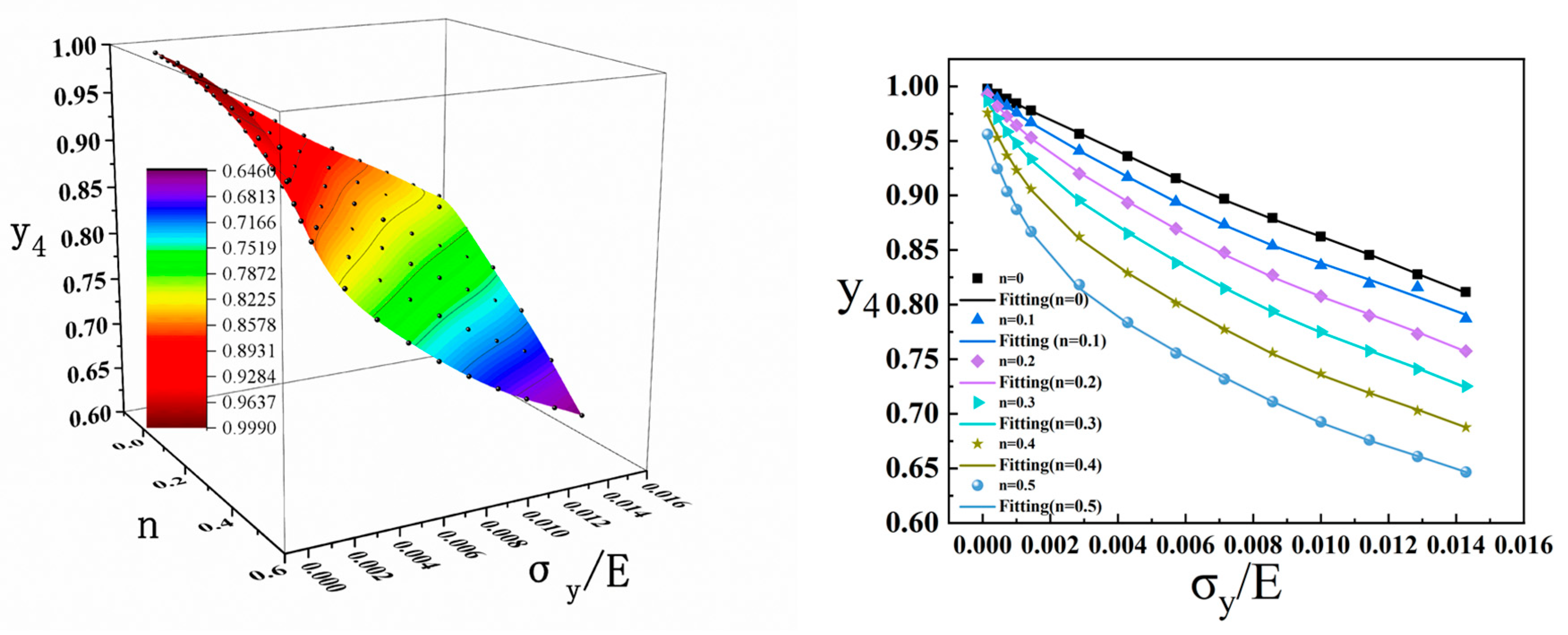
3.3. Extraction of Parameters from Projection area of contact zone for Dimensionless Analysis
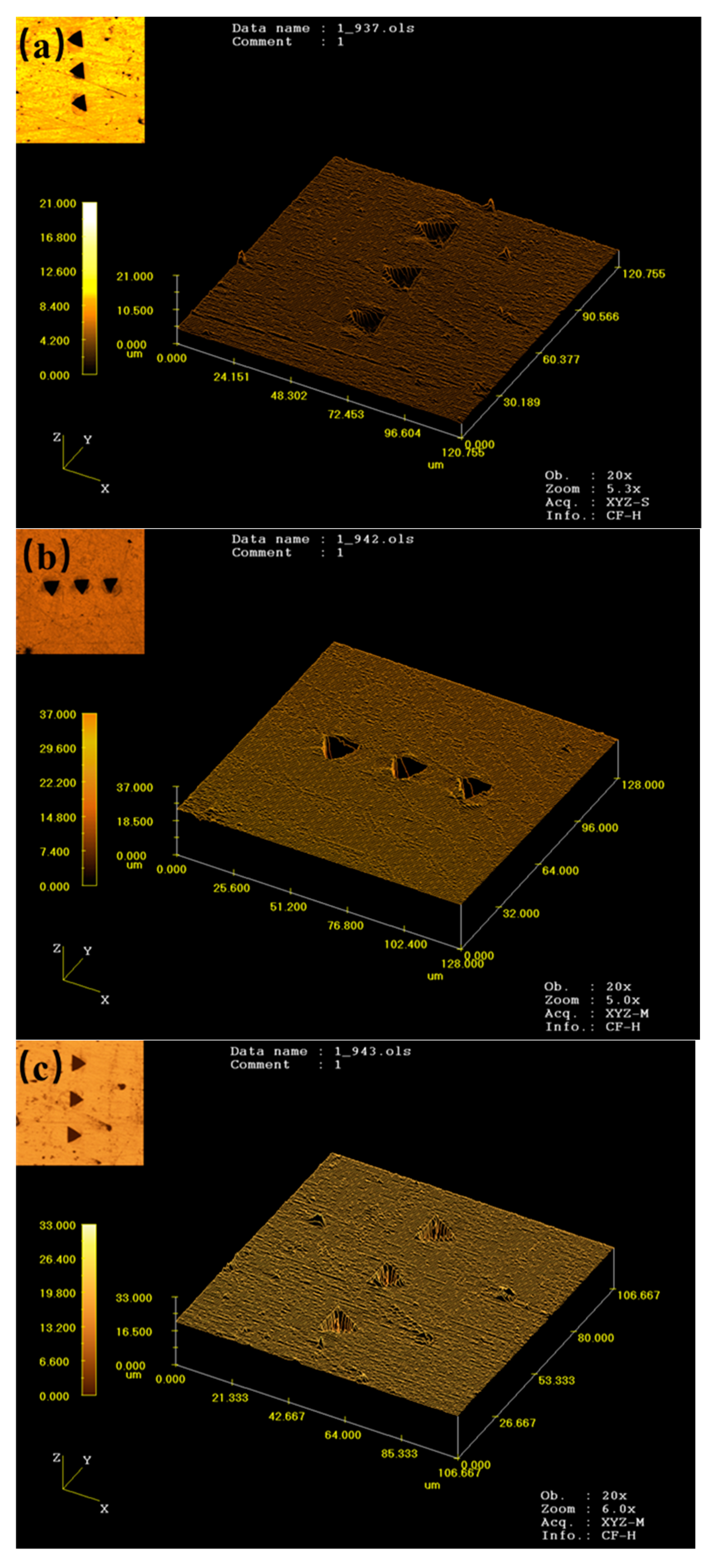
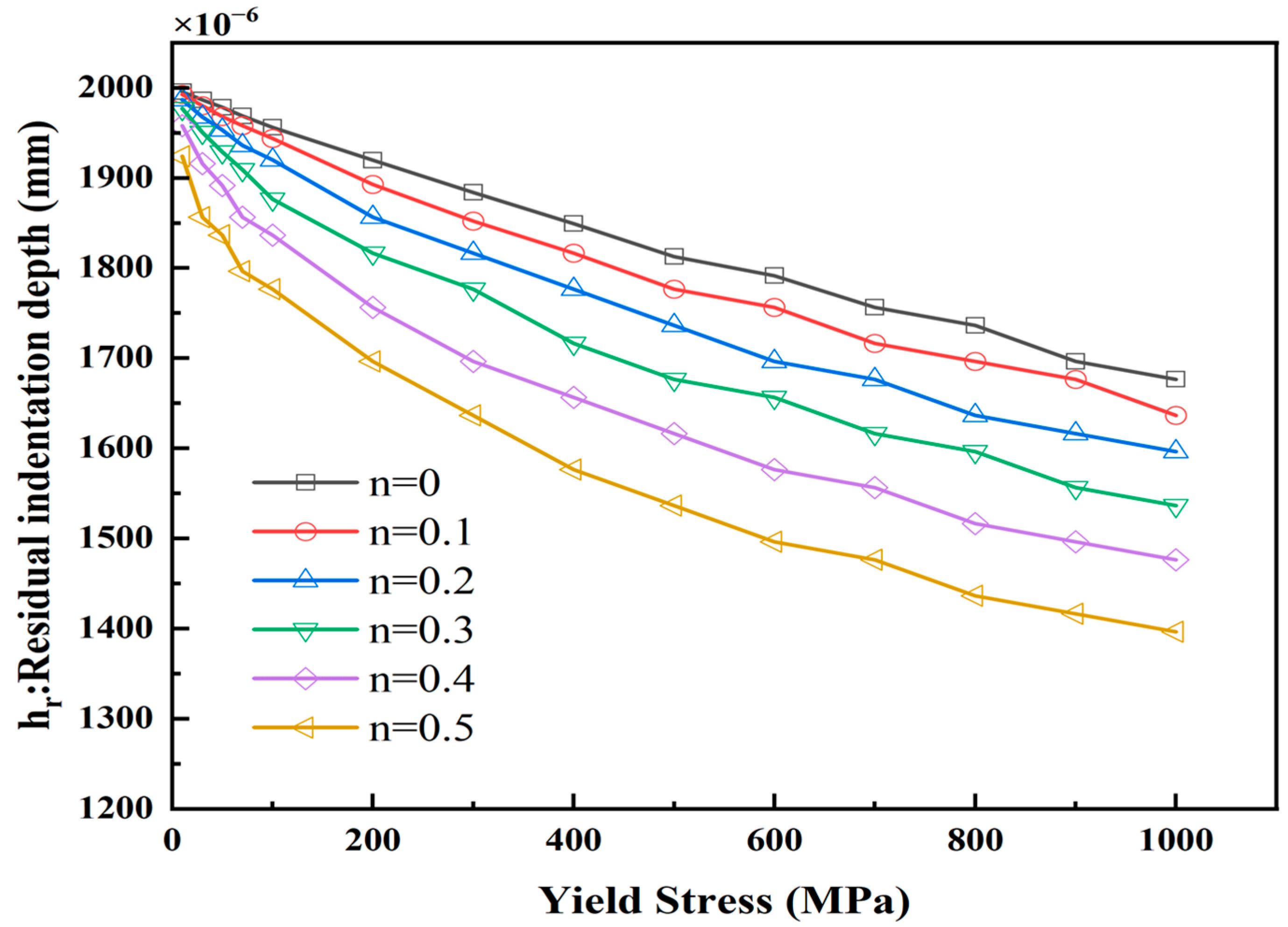
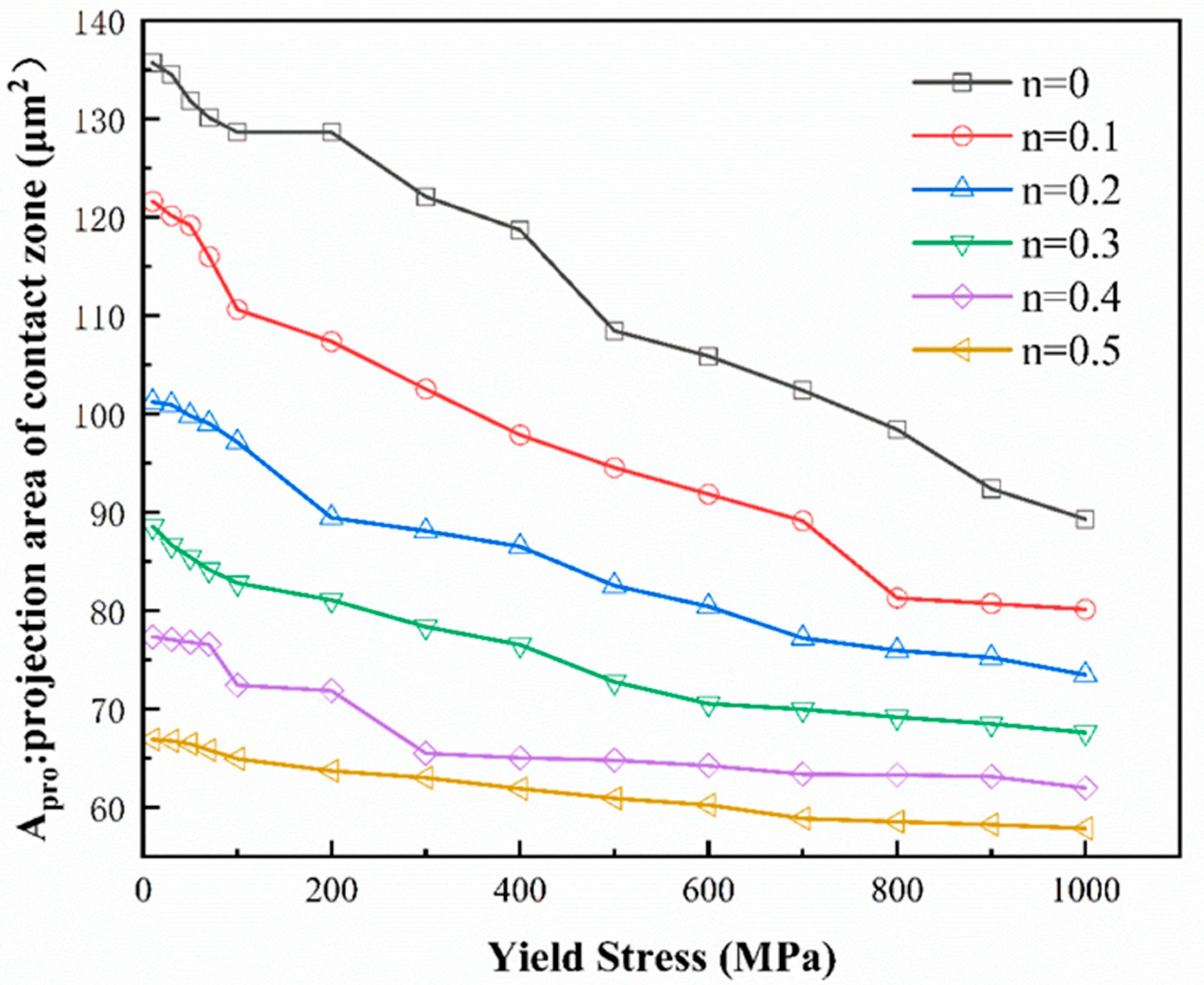
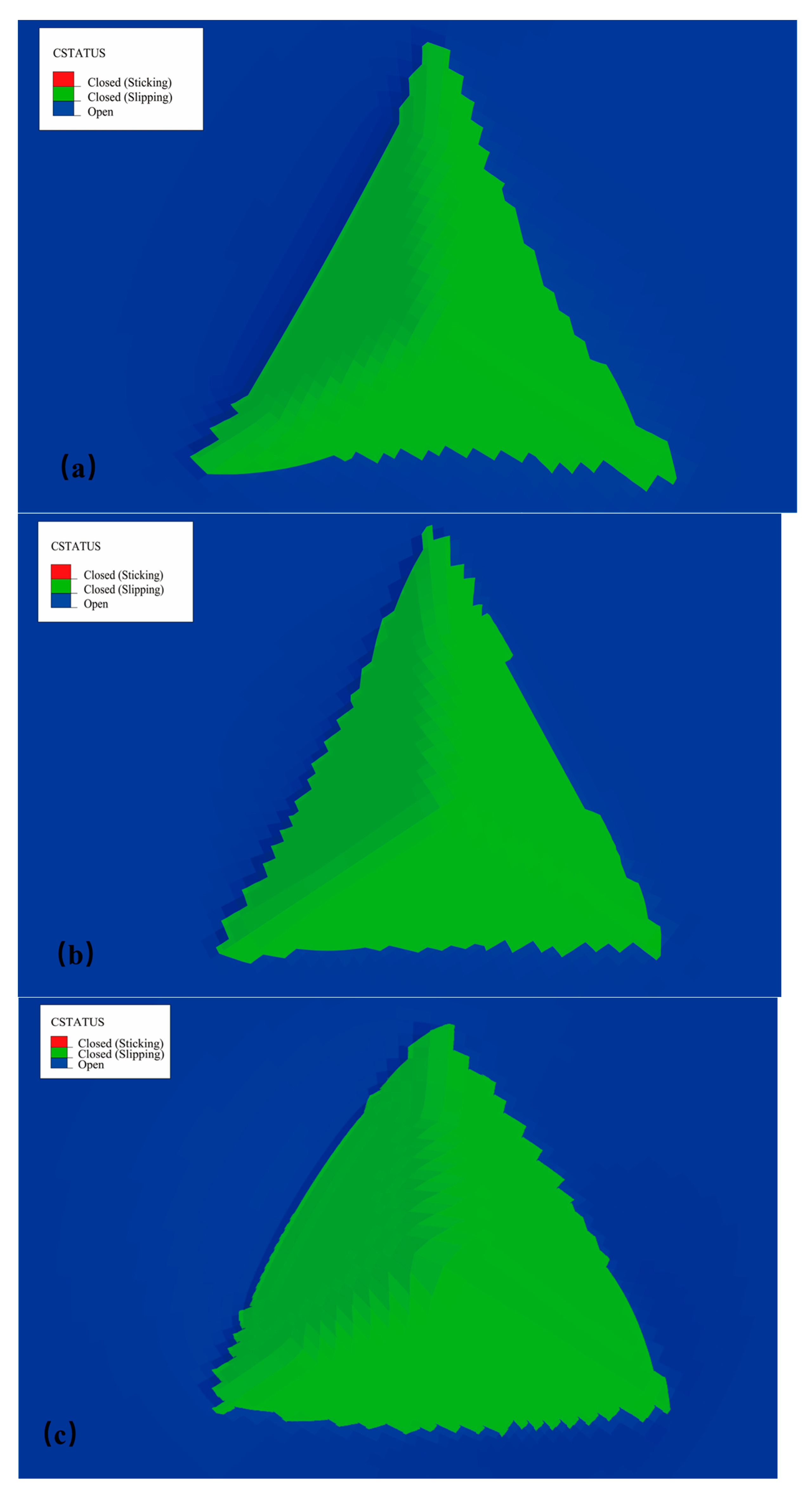
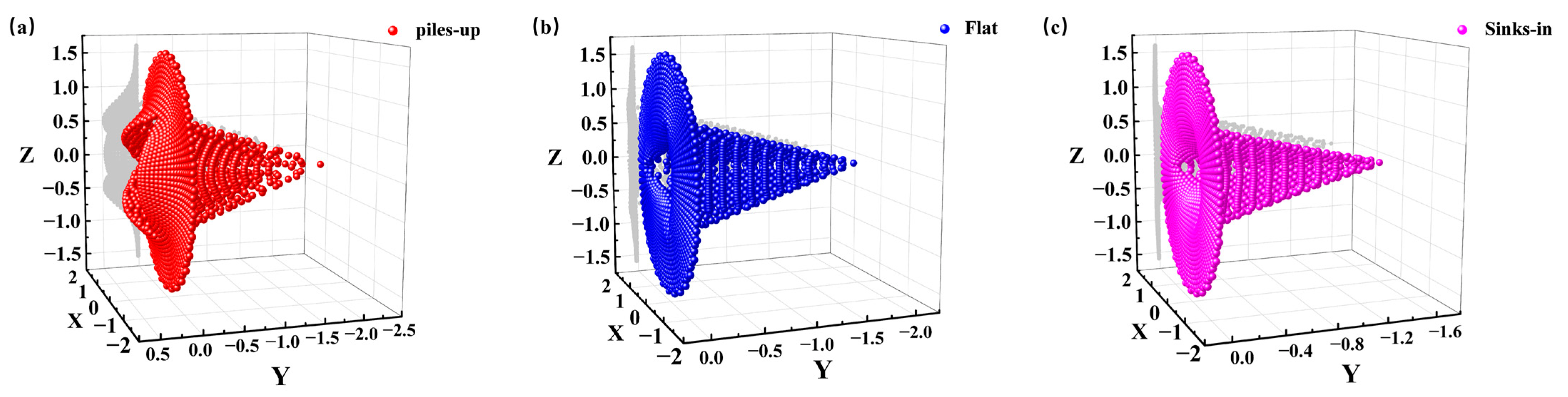
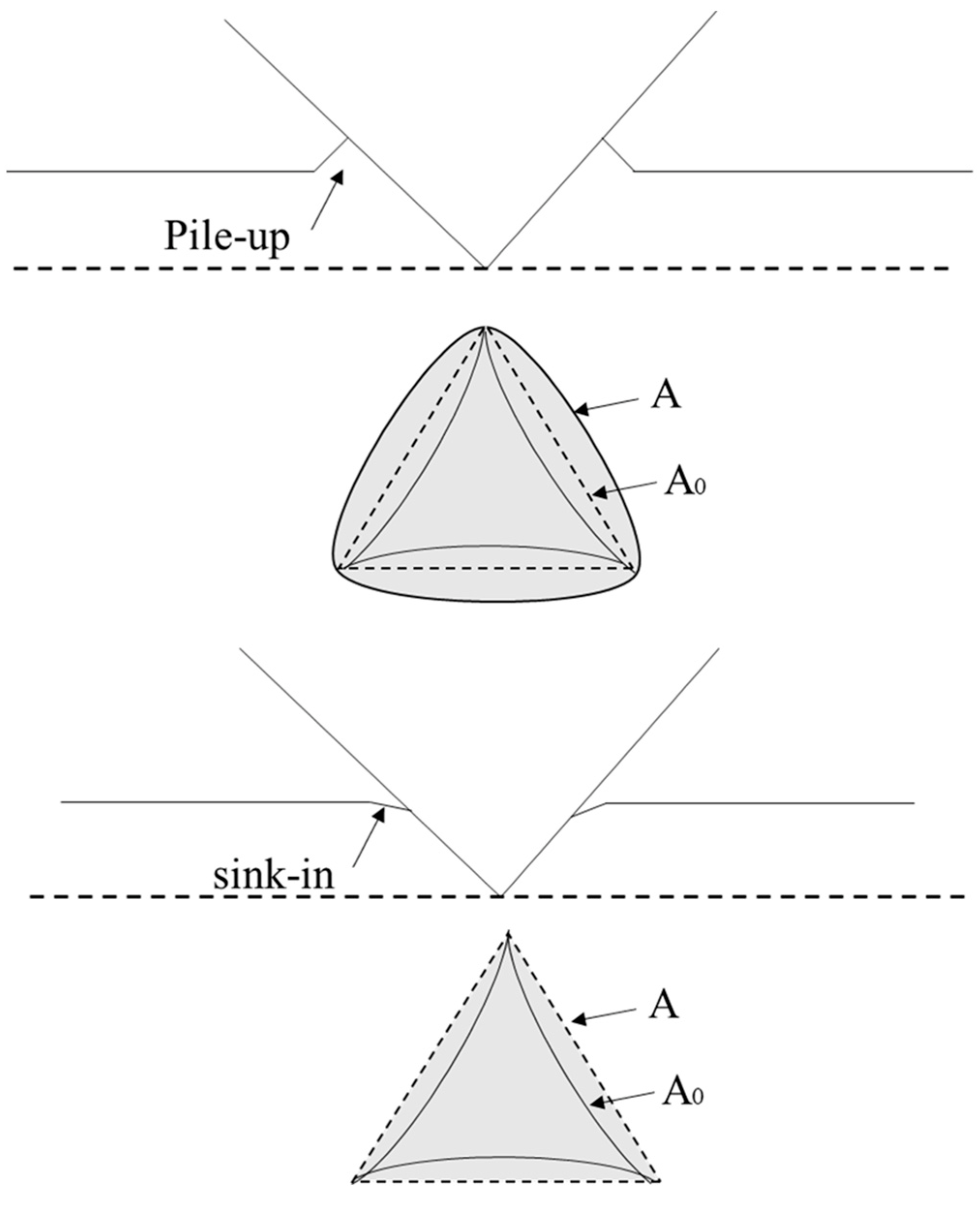
3.3.1. Projection Area of Contact Zone
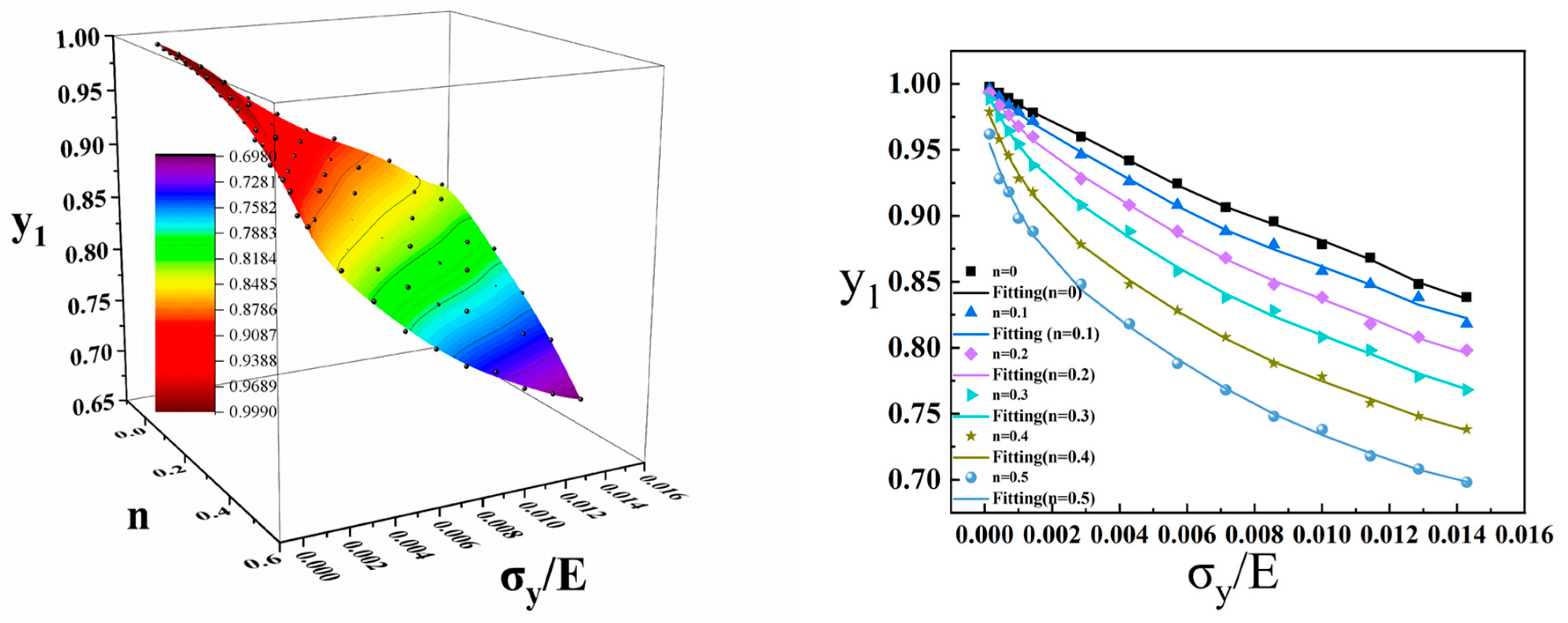
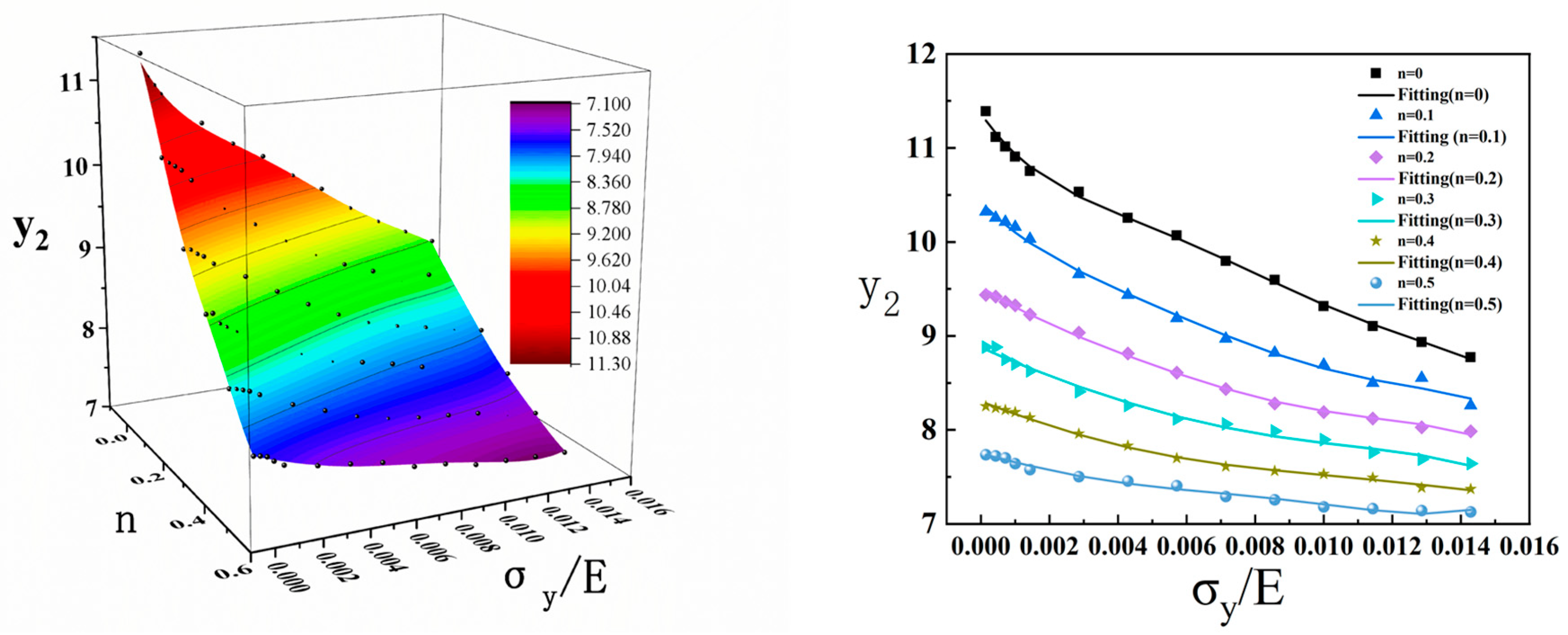
3.3.2. Dimensionless Analysis
3.4. Dimensionless Equation Solution
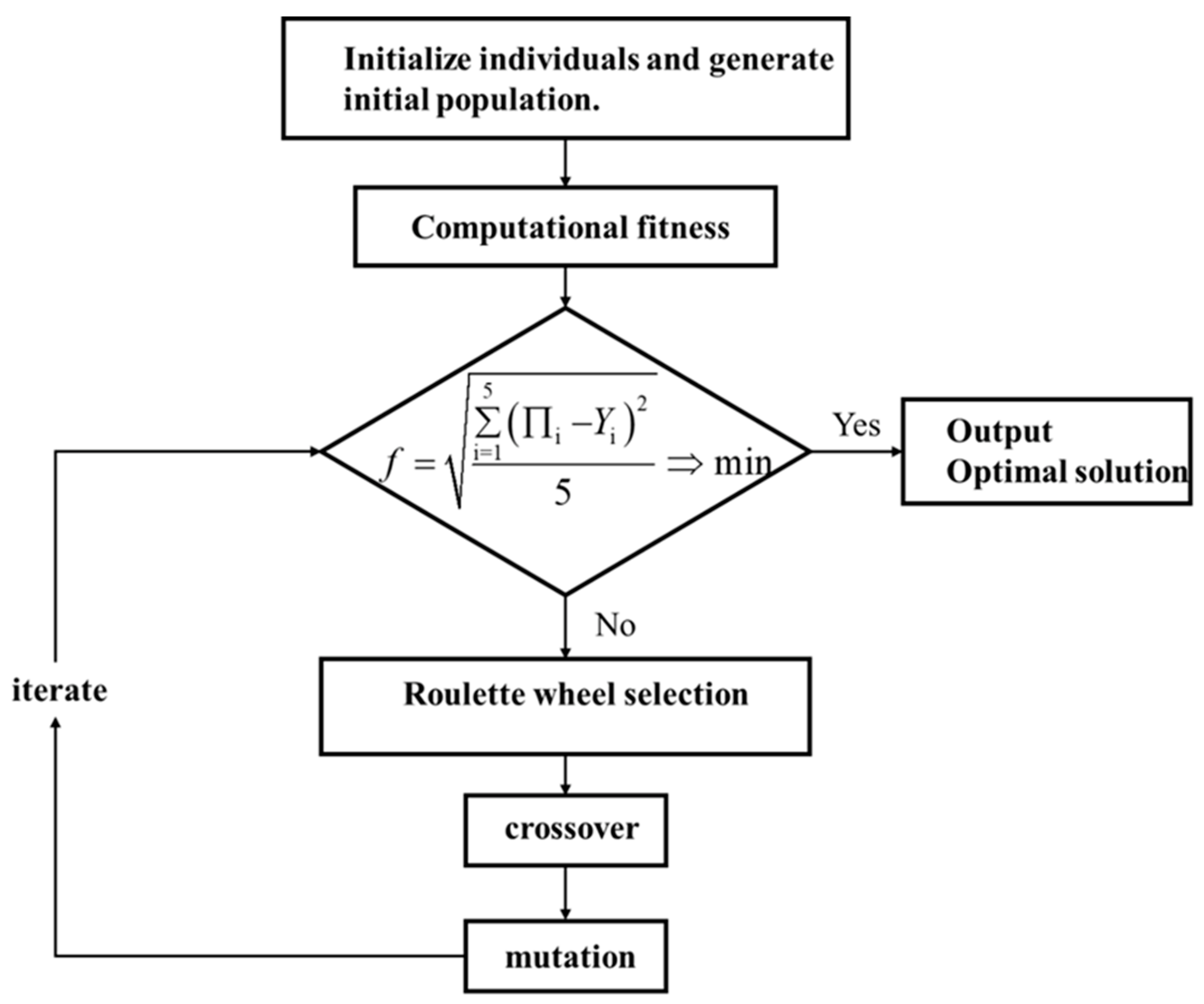
3.5. Optimization Algorithms
3.6. Mysterious Materials
4. Conclusions
- (1)
- The proposed method effectively extracts plasticity-related parameters from the P-h curve and the projection area of the contact zone, allowing for the accurate characterization of the material’s plastic behavior.
- (2)
- The variations in the indentation parameters concerning the yield stress and hardening index were investigated. The maximum load, total work, and elastic work increase with the increase in σy and n, while the residual indentation depth, contact stiffness, and projection area of the contact zone decrease with the increase in σy and n.
- (3)
- The residual imprint after unloading the indenter is influenced by the material itself, with lower values of n and σy resulting in a more pronounced pile-up, whereas higher values of n and σy lead to sink-in.
- (4)
- Random materials within the specified range also yielded satisfactory results using the implemented program.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tabor, D. The Hardness of Metals. In Monographs on the Physics and Chemistry of Materials; Clarendon Press: Oxford, UK; Oxford University Press: London, UK, 1951. [Google Scholar]
- Johnson, K.L. Correlation of indentation experiments. J. Mech. Phys. Solids 1970, 18, 115–126. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, C. Inconsistent nanoindentation test hardness using different Berkovich indenters. J. Mater. Res. Technol. 2023, 25, 6198–6208. [Google Scholar] [CrossRef]
- Niu, J.; Miao, B.; Guo, J.; Ding, Z.; He, Y.; Chi, Z.; Wang, F.; Ma, X. Leveraging Deep Neural Networks for Estimating Vickers Hardness from Nanoindentation Hardness. Materials 2024, 17, 148. [Google Scholar] [CrossRef]
- Chen, S.; Yuan, J.; Wang, S.; Mei, L.; Yan, J.; Li, L.; Zhang, Q.; Zhu, Z.; Lv, J.; Xue, Y.; et al. Towards a reliable nanohardness-dose correlation of ion-irradiated materials from nanoindentation tests: A case study in proton-irradiated vanadium. Int. J. Plast. 2023, 171, 103804. [Google Scholar] [CrossRef]
- Phani, P.S.; Hackett, B.; Walker, C.; Oliver, W.; Pharr, G. On the measurement of hardness at high strain rates by nanoindentation impact testing. J. Mech. Phys. Solids 2023, 170, 105105. [Google Scholar] [CrossRef]
- Sedlatschek, T.; Krämer, M.; Gibson, J.S.-L.; Korte-Kerzel, S.; Bezold, A.; Broeckmann, C. Mechanical properties of heterogeneous, porous LiFePO4 cathodes obtained using statistical nanoindentation and micromechanical simulations. J. Power Sources 2022, 539, 231565. [Google Scholar] [CrossRef]
- Zhang, H.; Stewart, M.; De Luca, F.; Smet, P.F.; Sousanis, A.; Poelman, D.; Rungger, I.; Gee, M. Young’s modulus of thin SmS films measured by nanoindentation and laser acoustic wave. Surf. Coat. Technol. 2021, 421, 127428. [Google Scholar] [CrossRef]
- Taniguchi, T. Exploration of elastic moduli of molecular crystals via database screening by pretrained neural network potential. CrystEngComm 2024, 26, 631–638. [Google Scholar] [CrossRef]
- Yang, Y.; Peng, R.; Li, J.; Chen, X.; Zhang, H.; Zhao, J.; He, Y.; Liu, Z. Elastic-plastic properties of ceramic matrix composites characterization by nanoindentation testing coupled with computer modeling. Ceram. Int. 2024, 50, 18540–18548. [Google Scholar] [CrossRef]
- Peng, G.; Liu, Y.; Xu, F.; Jiang, H.; Jiang, W.; Zhang, T. On determination of elastic modulus and indentation hardness by instrumented spherical indentation: Influence of surface roughness and correction method. Mater. Res. Express 2023, 10, 086503. [Google Scholar] [CrossRef]
- Ying, P.; Xia, Y. Elastic modulus identification of particles in particulate composite through nanoindentation. Int. J. Mech. Sci. 2023, 260, 108660. [Google Scholar] [CrossRef]
- Lee, J.; Marimuthu, K.P.; Han, G.; Lee, H. A dual indentation method for evaluating intrinsic material properties of metals under residual stress. J. Mater. Res. Technol. 2024, 30, 4181–4191. [Google Scholar] [CrossRef]
- Kong, D.; Yang, B.; Hu, P. Binary Newton Calculation Method of Residual Stress Based on the Indentation Energy Difference Theory. Metals 2022, 12, 1439. [Google Scholar] [CrossRef]
- Han, G.; Lee, B.; Lee, S.; Jeong, C.; Lee, H. Evaluation of plastic properties and equi-biaxial residual stress via indentation and ANN. Mater. Des. 2024, 239, 112745. [Google Scholar] [CrossRef]
- Liu, X.; Cai, L.; Chen, H. Residual stress indentation model based on material equivalence. Chin. J. Aeronaut. 2022, 35, 304–313. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Q.; Lu, C.; Xue, T.; Hu, B.; Zhang, C. Microscopic residual stress evolution at the SiC/Al interface during nanoindentation via molecular dynamics simulation. Surf. Interfaces 2022, 33, 102210. [Google Scholar] [CrossRef]
- Darnbrough, E.; Aspinall, J.; Pasta, M.; Armstrong, D.E. Elastic and plastic mechanical properties of lithium measured by nanoindentation. Mater. Des. 2023, 233, 112200. [Google Scholar] [CrossRef]
- Jiao, Q.; Chen, Y.; Kim, J.-H.; Han, C.-F.; Chang, C.-H.; Vlassak, J.J. A machine learning perspective on the inverse indentation problem: Uniqueness, surrogate modeling, and learning elasto-plastic properties from pile-up. J. Mech. Phys. Solids 2024, 185, 105557. [Google Scholar] [CrossRef]
- Jeong, K.; Lee, K.; Kwon, D.; Lee, M.-G.; Han, H.N. Parameter determination of anisotropic yield function using neural network-based indentation plastometry. Int. J. Mech. Sci. 2024, 263, 108776. [Google Scholar] [CrossRef]
- Gallardo-Basile, F.-J.; Roters, F.; Jentner, R.M.; Best, J.P.; Kirchlechner, C.; Srivastava, K.; Scholl, S.; Diehl, M. Application of a nanoindentation-based approach for parameter identification to a crystal plasticity model for bcc metals. Mater. Sci. Eng. A 2023, 881, 145373. [Google Scholar] [CrossRef]
- Yin, B.; Xue, X.; Zhang, M.; Deng, T.; Li, J.; Tang, B. Parameter identification and pileup behavior of TiAl alloy through nanoindentation and crystal plasticity simulation. J. Alloy. Compd. 2023, 948, 169743. [Google Scholar] [CrossRef]
- Campbell, J.E.; Thompson, R.P.; Dean, J.; Clyne, T.W. Experimental and computational issues for automated extraction of plasticity parameters from spherical indentation. Mech. Mater. 2018, 124, 118–131. [Google Scholar] [CrossRef]
- Hosseinzadeh, A.; Mahmoudi, A. Determination of mechanical properties using sharp macro-indentation method and genetic algorithm. Mech. Mater. 2017, 114, 57–68. [Google Scholar] [CrossRef]
- Najjar, I.; Sadoun, A.; Alsoruji, G.S.; Elaziz, M.A.; Wagih, A. Predicting the mechanical properties of Cu–Al2O3 nanocomposites using machine learning and finite element simulation of indentation experiments. Ceram. Int. 2021, 48, 7748–7758. [Google Scholar] [CrossRef]
- Long, X.; Ding, X.; Li, J.; Dong, R.; Su, Y.; Chang, C. Indentation Reverse Algorithm of Mechanical Response for Elastoplastic Coatings Based on LSTM Deep Learning. Materials 2023, 16, 2617. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, G.; Liu, T.; Wang, W. Determination of Elastoplastic Properties of 2024 Aluminum Alloy Using Deep Learning and Instrumented Nanoindentation Experiment. Acta Mech. Solida Sin. 2023, 36, 327–339. [Google Scholar] [CrossRef]
- Ghanbari, S.S.; Mahmoudi, A. An improvement in data interpretation to estimate residual stresses and mechanical properties using instrumented indentation: A comparison between machine learning and Kriging model. Eng. Appl. Artif. Intell. 2022, 114, 105186. [Google Scholar] [CrossRef]
- Huang, L.Y.; Guan, K.S.; Xu, T.; Zhang, J.M.; Wang, Q.Q. Investigation of the mechanical properties of steel using instrumented indentation test with simulated annealing particle swarm optimization. Theor. Appl. Fract. Mech. 2019, 102, 116–121. [Google Scholar] [CrossRef]
- Noii, N.; Aghayan, I. Characterization of elastic-plastic coated material properties by indentation techniques using optimisation algorithms and finite element analysis. Int. J. Mech. Sci. 2019, 152, 465–480. [Google Scholar] [CrossRef]
- Kang, J.J.; Becker, A.A.; Wen, W.; Sun, W. Extracting elastic-plastic properties from experimental loading-unloading indentation curves using different optimization techniques. Int. J. Mech. Sci. 2018, 144, 102–109. [Google Scholar] [CrossRef]
- Wang, M.Z.; Wu, J.J.; Hui, Y.; Zhang, Z.K.; Zhan, X.F.; Guo, R.C. Identification of elastic-plastic properties of metal materials by using the residual imprint of spherical indentation. Mater. Sci. Eng. A 2017, 679, 143–154. [Google Scholar] [CrossRef]
- Fernandez-Zelaia, P.; Joseph, V.R.; Kalidindi, S.R.; Melkote, S.N. Estimating mechanical properties from spherical indentation using Bayesian approaches. Mater. Des. 2018, 147, 92–105. [Google Scholar] [CrossRef]
- Su, J.; He, Y.; Li, Y. An improved analytic model for extracting plastic mechanical property of matrix in hot-extruded in-situ TiB2/2024 composite based on Berkovich indentation experimental results. Mater. Sci. Eng. A 2023, 881, 145285. [Google Scholar] [CrossRef]
- Wang, M.; Wang, W. An Inverse Method for Measuring Elastoplastic Properties of Metallic Materials Using Bayesian Model and Residual Imprint from Spherical Indentation. Materials 2021, 14, 7105. [Google Scholar] [CrossRef]
- Clyne, T.W.; Campbell, J.E.; Burley, M.; Dean, J. Profilometry-Based Inverse Finite Element Method Indentation Plastometry. Adv. Eng. Mater. 2021, 23, 202100437. [Google Scholar] [CrossRef]
- Hwang, Y.; Marimuthu, K.P.; Kim, N.; Lee, C.; Lee, H. Extracting plastic properties from in-plane displacement data of spherical indentation imprint. Int. J. Mech. Sci. 2021, 197, 106291. [Google Scholar] [CrossRef]
- Goto, K.; Watanabe, I.; Ohmura, T. Inverse estimation approach for elastoplastic properties using the load-displacement curve and pile-up topography of a single Berkovich indentation. Mater. Des. 2020, 194, 108925. [Google Scholar] [CrossRef]
- Iracheta, O.; Bennett, C.J.; Sun, W. A holistic inverse approach based on a multi-objective function optimisation model to recover elastic-plastic properties of materials from the depth-sensing indentation test. J. Mech. Phys. Solids 2019, 128, 1–20. [Google Scholar] [CrossRef]
- Chen, X.; Ogasawara, N.; Zhao, M.; Chiba, N. On the uniqueness of measuring elastoplastic properties from in-dentation: The indistinguishable mystical materials. J. Mech. Phys. Solids 2007, 55, 1618–1660. [Google Scholar] [CrossRef]
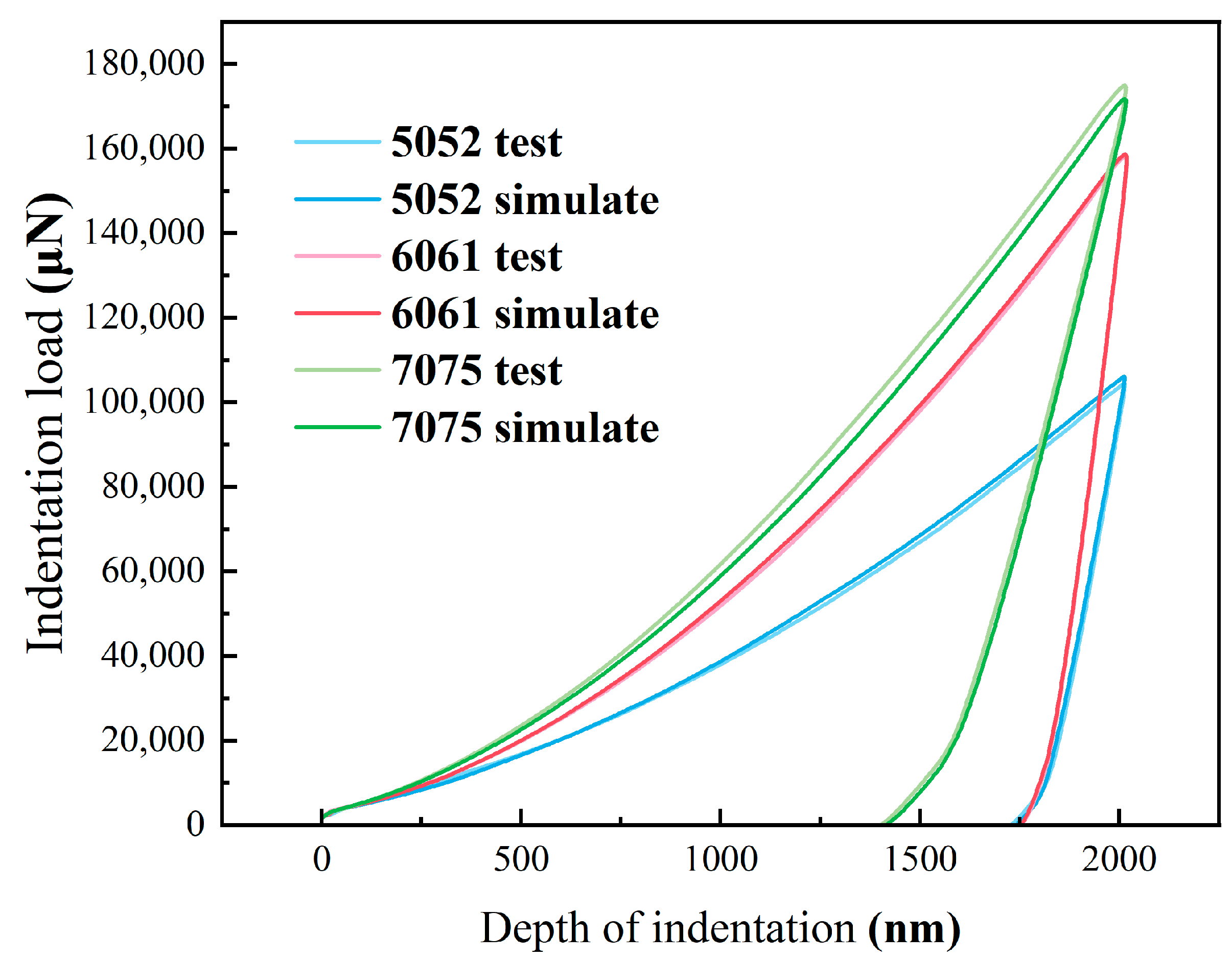
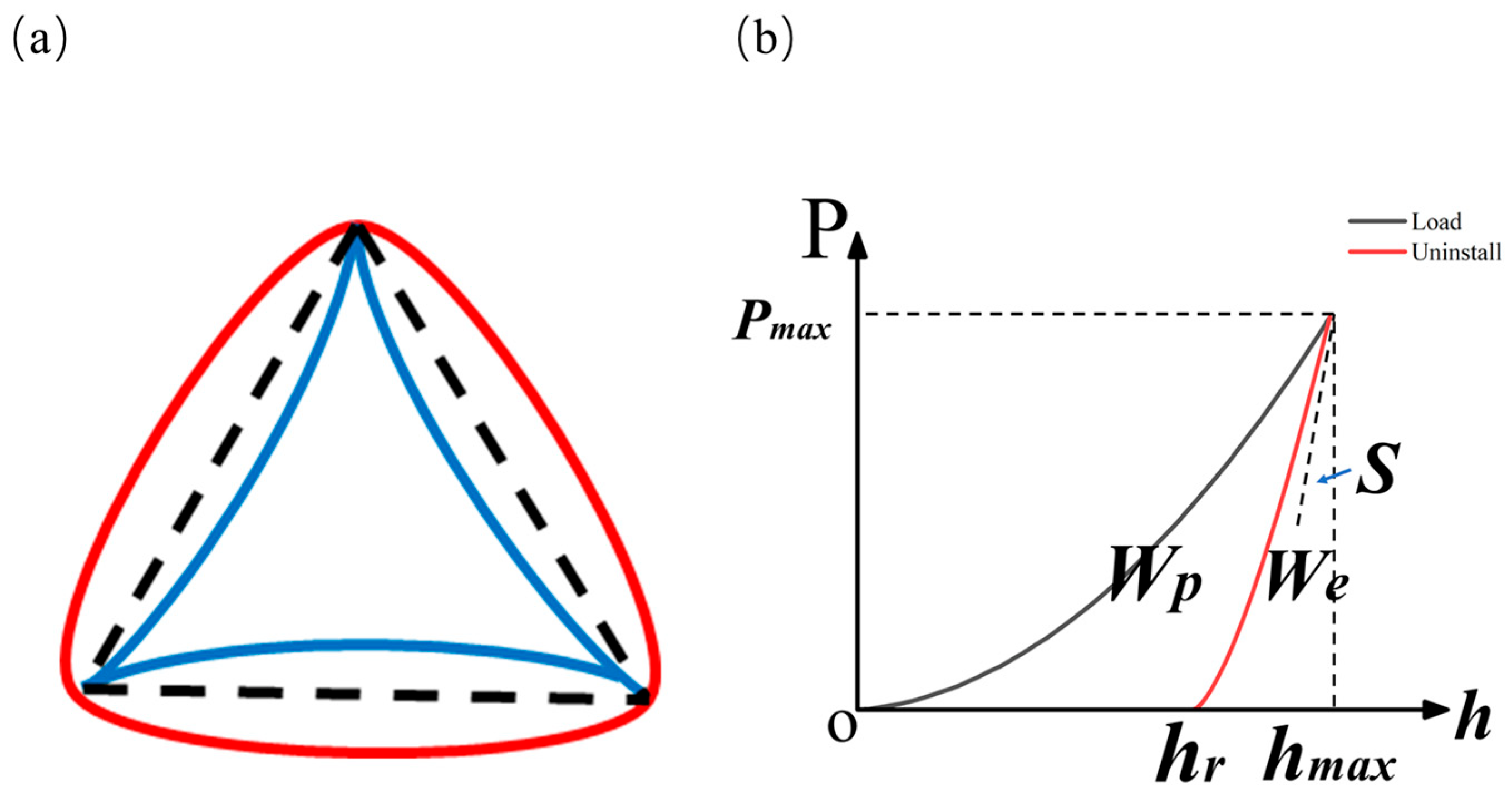
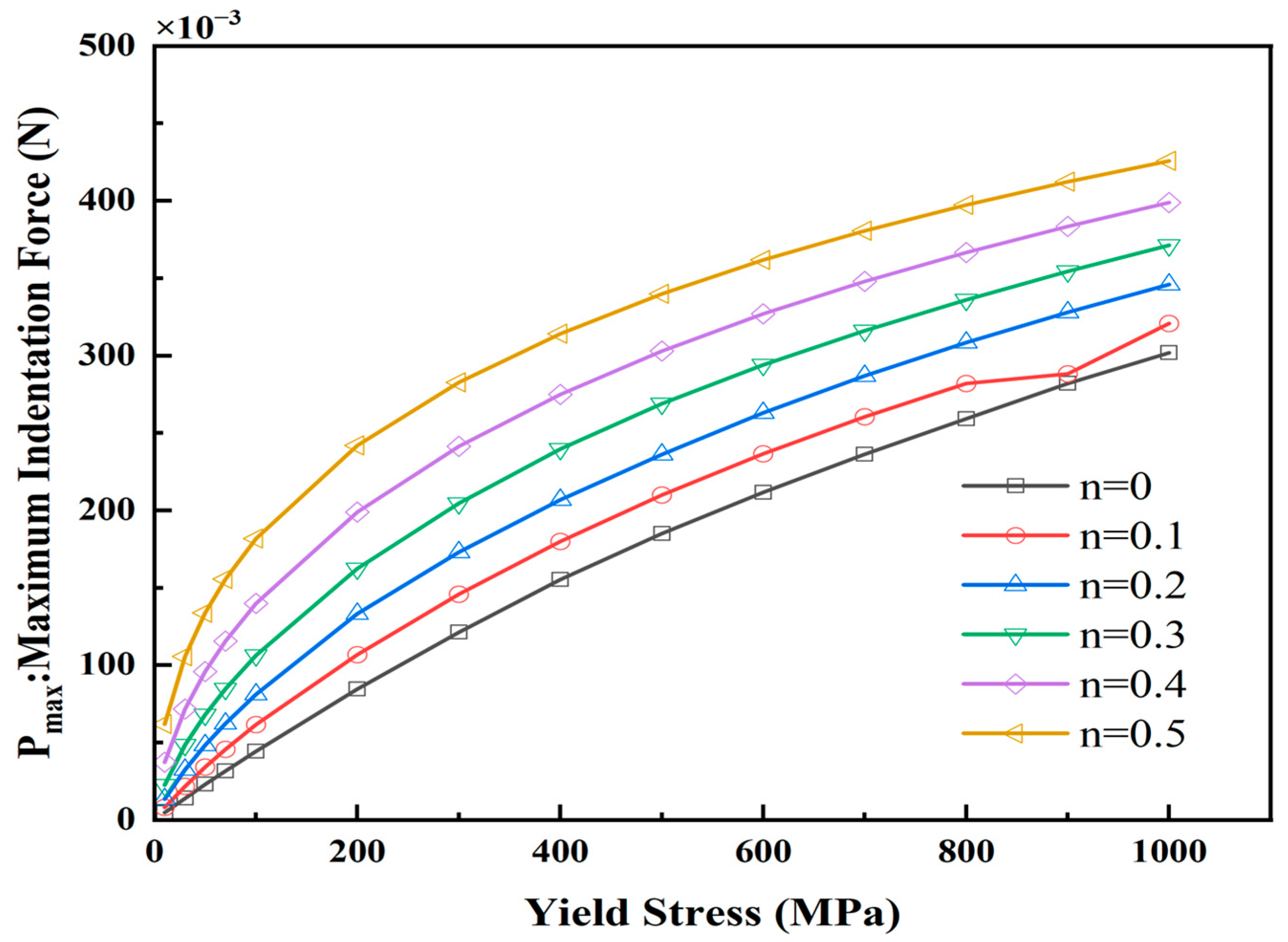

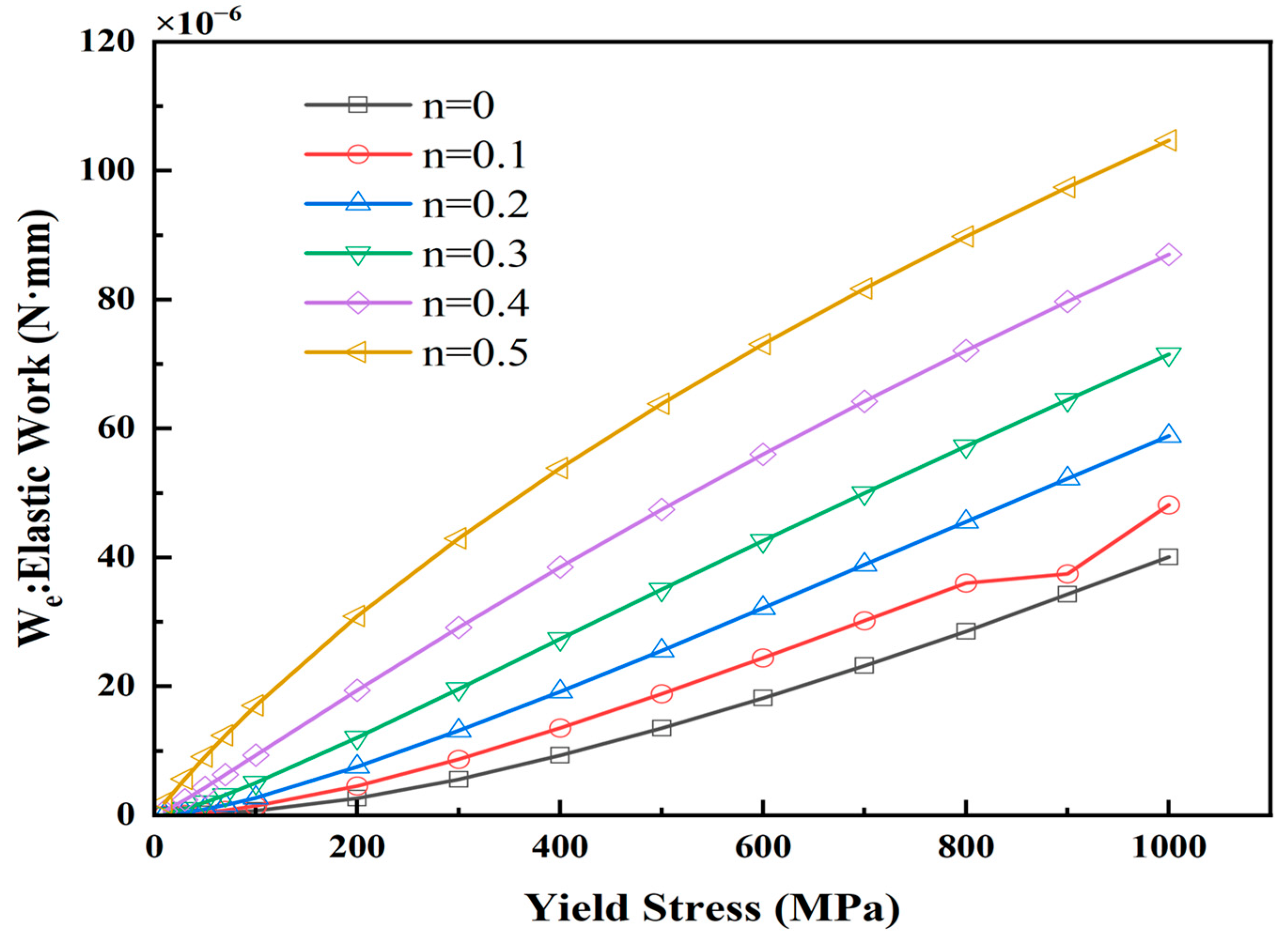


| Element | Mg | Si | Fe | Cu | Zn | Ti | Mn | Cr | Al |
|---|---|---|---|---|---|---|---|---|---|
| 7075 | 2.52 | 0.09 | 0.21 | 1.4 | 5.4 | 0.02 | 0.04 | 0.2 | Bal. |
| 6061 | 1.03 | 0.62 | 0.18 | 0.24 | 0.16 | 0.03 | 0.07 | 0.04 | Bal. |
| 5052 | 2.4 | 0.05 | 0.26 | 0.06 | 0.08 | 0.01 | 0.06 | 0.16 | Bal. |
| Material | E (MPa) | σy (MPa) | n |
|---|---|---|---|
| 7075 | 68,440 | 480.22 | 0.09 |
| 6061 | 67,661 | 263.47 | 0.08 |
| 5052 | 66,844 | 132.59 | 0.18 |
| Material | Test n | Predict n | Error | Test σy | Predict σy | Error |
|---|---|---|---|---|---|---|
| 7075 | 0.09 | 0.093 | 3.33% | 480.22 MPa | 500.23 MPa | 4.17% |
| 6061 | 0.08 | 0.084 | 5% | 263.47 MPa | 270.35 MPa | 2.61% |
| 5052 | 0.18 | 0.17 | 5.56% | 132.59 MPa | 136.78 MPa | 3.16% |
| Material | Test n | Predict n | Error | Test σy | Predict σy | Error |
|---|---|---|---|---|---|---|
| 1 | 0.1 | 0.097 | 3% | 500 MPa | 488.85 MPa | 2.23% |
| 2 | 0.5 | 0.49 | 2% | 100 MPa | 103.95 MPa | 3.95% |
| Material | Test n | Predict n | Error | Test σy | Predict σy | Error |
|---|---|---|---|---|---|---|
| 1 | 0.06 | 0.062 | 3.3% | 120 MPa | 128.84 MPa | 7.37% |
| 2 | 0.12 | 0.125 | 4.16% | 240 MPa | 261.19 MPa | 8.83% |
| 3 | 0.26 | 0.24 | 7.69% | 360 MPa | 343.43 MPa | 4.6% |
| 4 | 0.34 | 0.32 | 5.88% | 480 MPa | 457.57 MPa | 4.57% |
| 5 | 0.48 | 0.47 | 2.08% | 600 MPa | 648.69 MPa | 8.11% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, Y.; Liu, C. Estimation of Mechanical Properties of Aluminum Alloy Based on Indentation Curve and Projection Area of Contact Zone. Metals 2024, 14, 576. https://doi.org/10.3390/met14050576
Bai Y, Liu C. Estimation of Mechanical Properties of Aluminum Alloy Based on Indentation Curve and Projection Area of Contact Zone. Metals. 2024; 14(5):576. https://doi.org/10.3390/met14050576
Chicago/Turabian StyleBai, Yunfeng, and Chunguo Liu. 2024. "Estimation of Mechanical Properties of Aluminum Alloy Based on Indentation Curve and Projection Area of Contact Zone" Metals 14, no. 5: 576. https://doi.org/10.3390/met14050576
APA StyleBai, Y., & Liu, C. (2024). Estimation of Mechanical Properties of Aluminum Alloy Based on Indentation Curve and Projection Area of Contact Zone. Metals, 14(5), 576. https://doi.org/10.3390/met14050576









