A First-Principles Study of the Structural, Elastic, and Mechanical Characteristics of Mg2Ni Subjected to Pressure Conditions
Abstract
1. Introduction
2. Calculation Details
2.1. First-Principles Calculations
2.2. Calculation of Elastic Constants
3. Results and Discussion
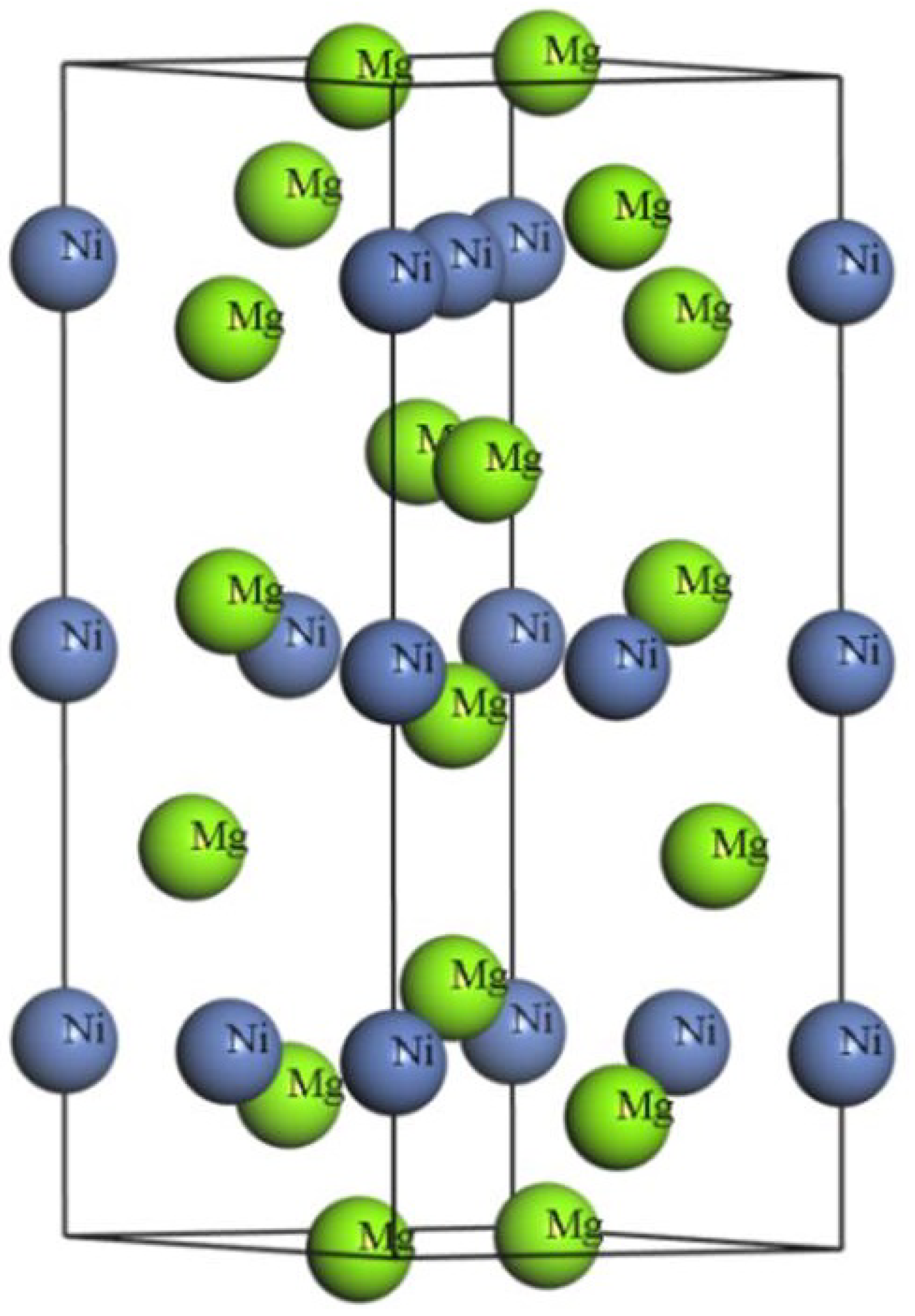
3.1. High-Pressure Structural Properties
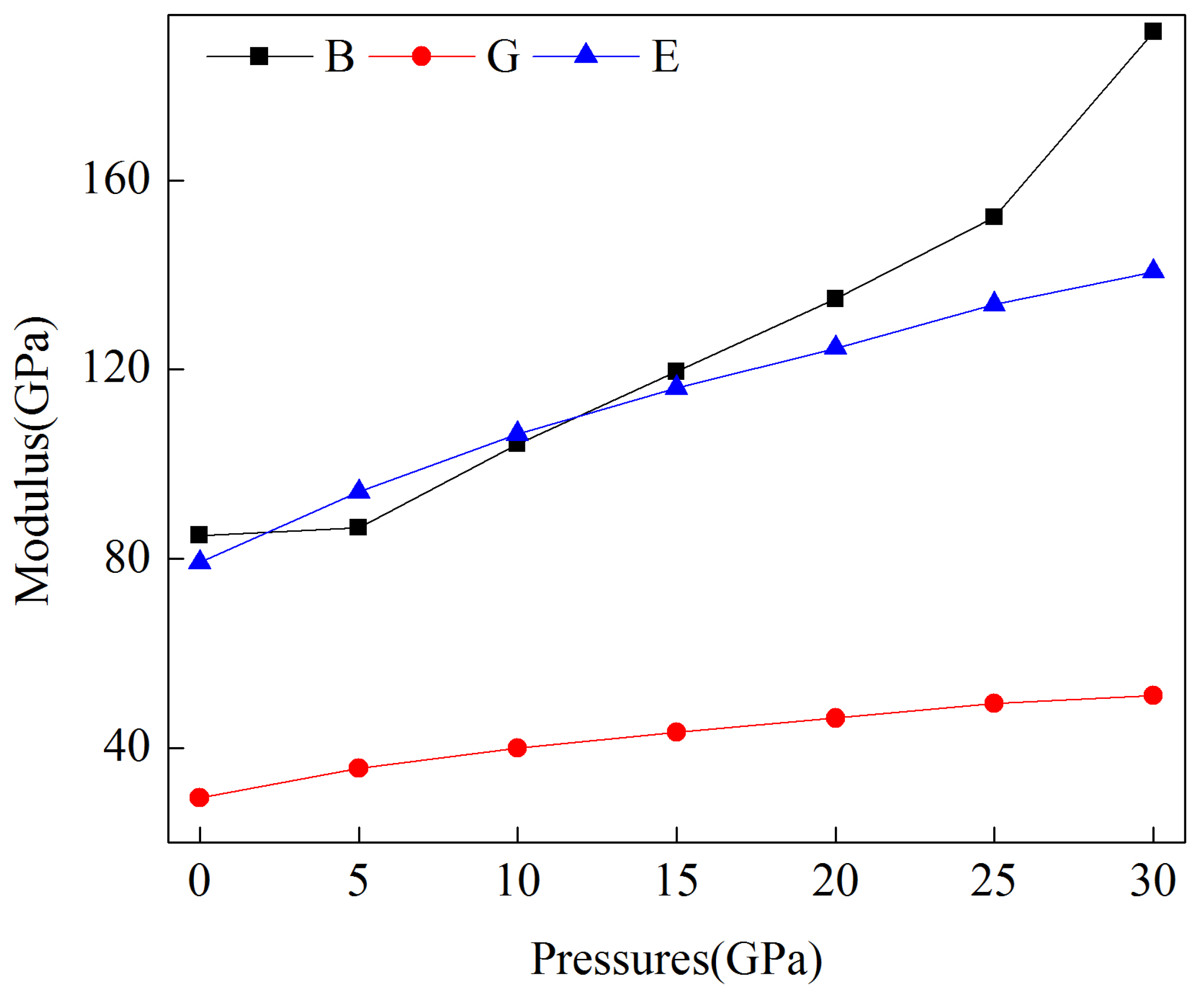
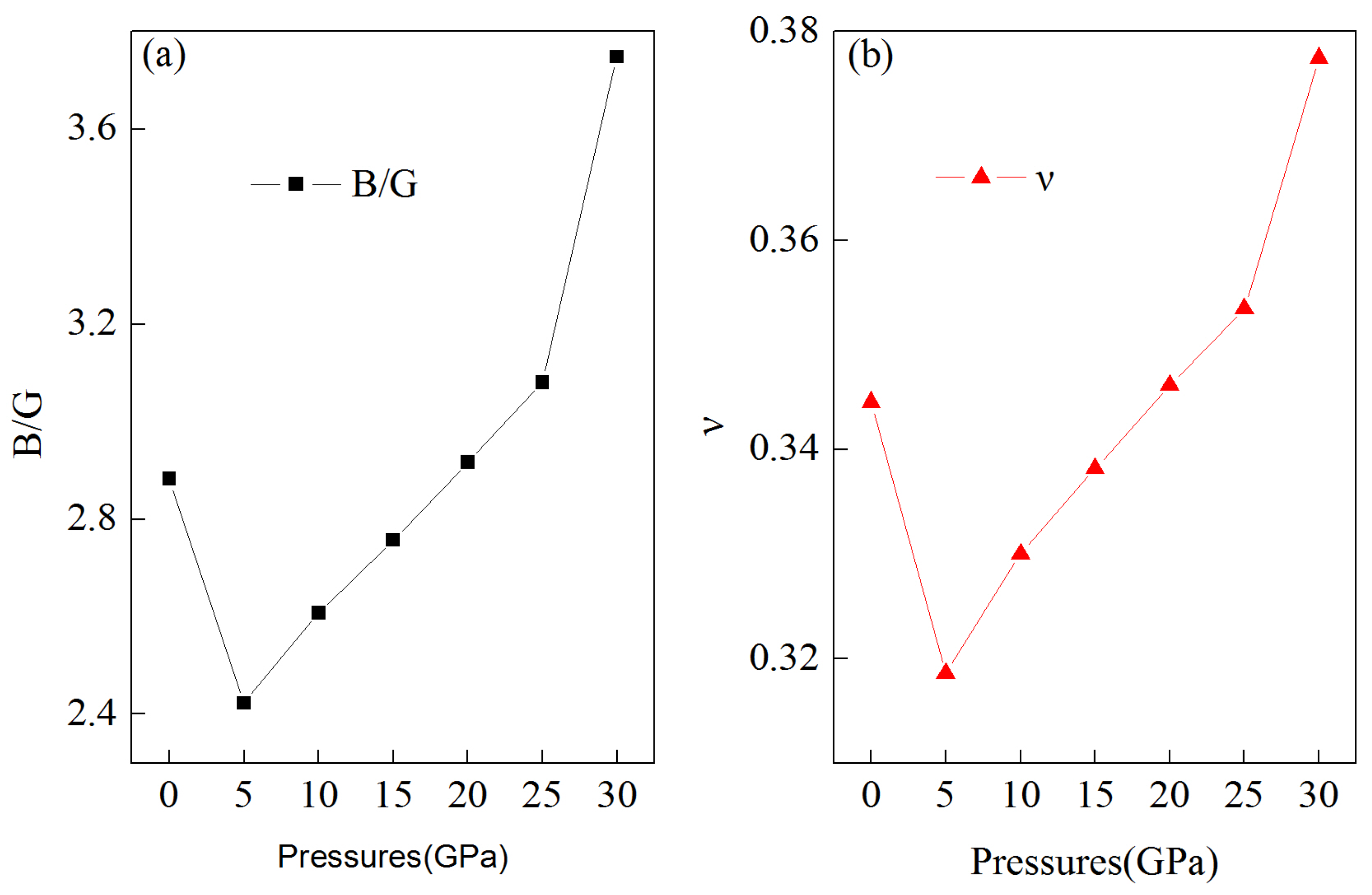
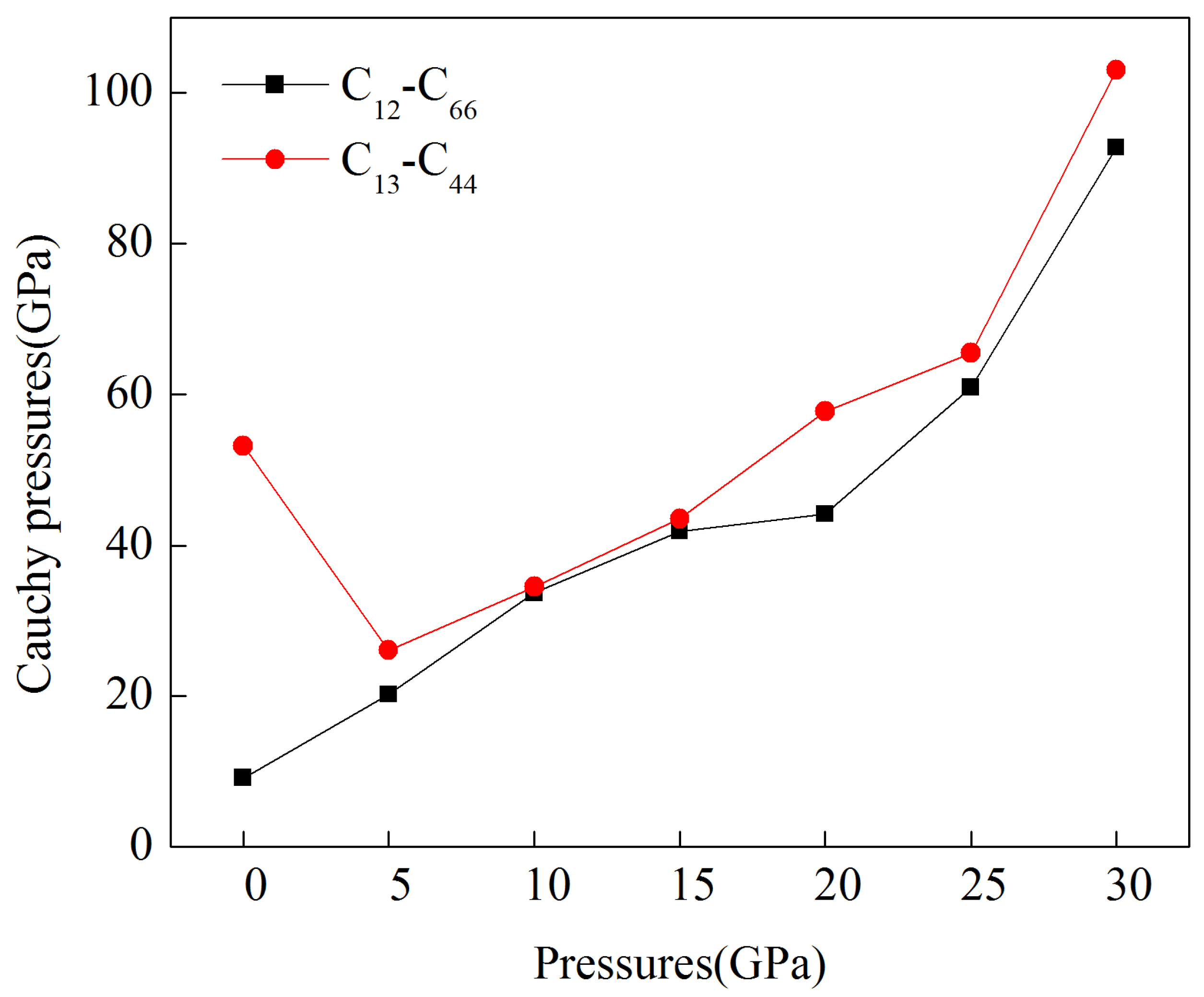
3.2. Mechanical Properties under Pressure
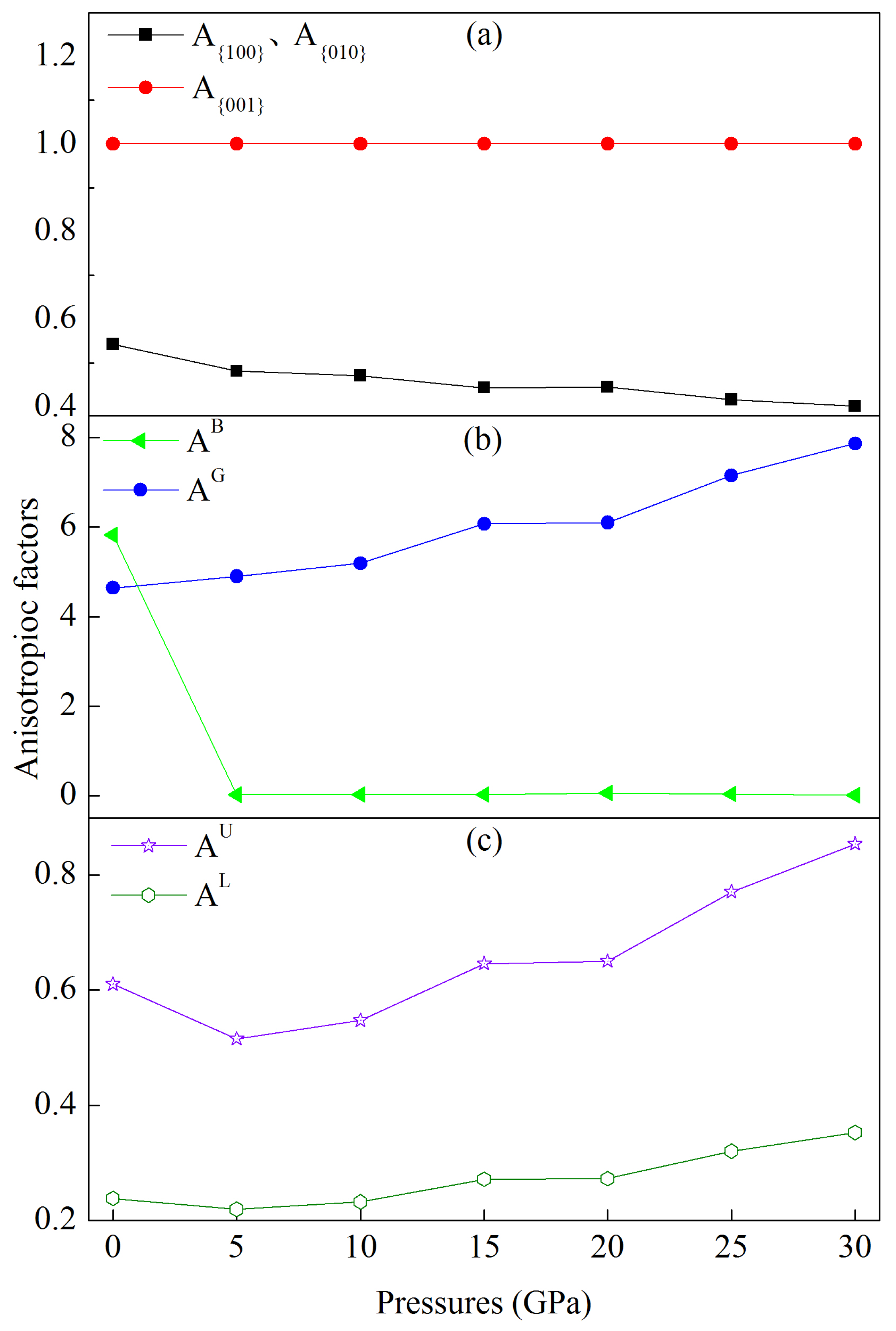
3.3. Elastic Anisotropy under Pressure
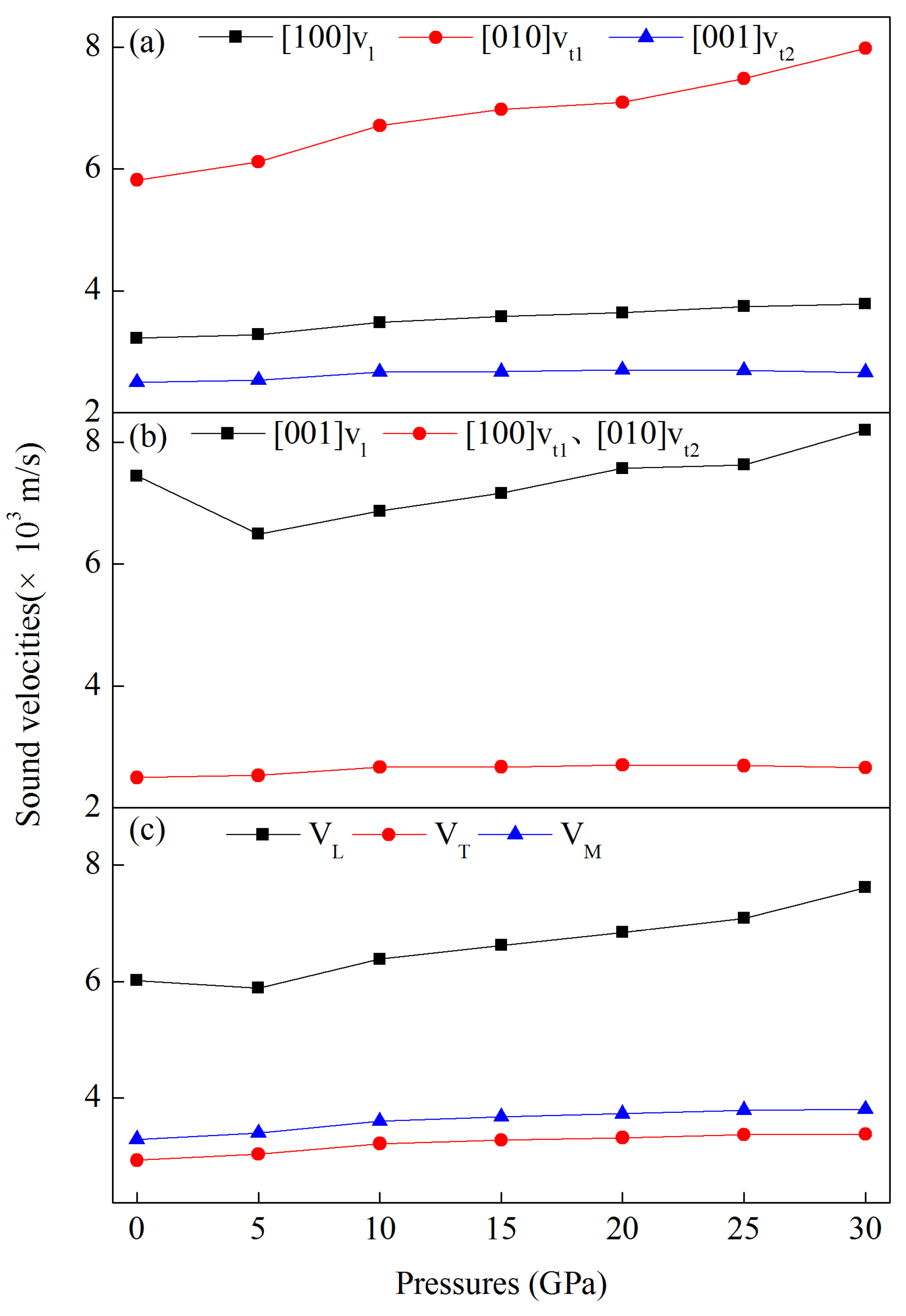
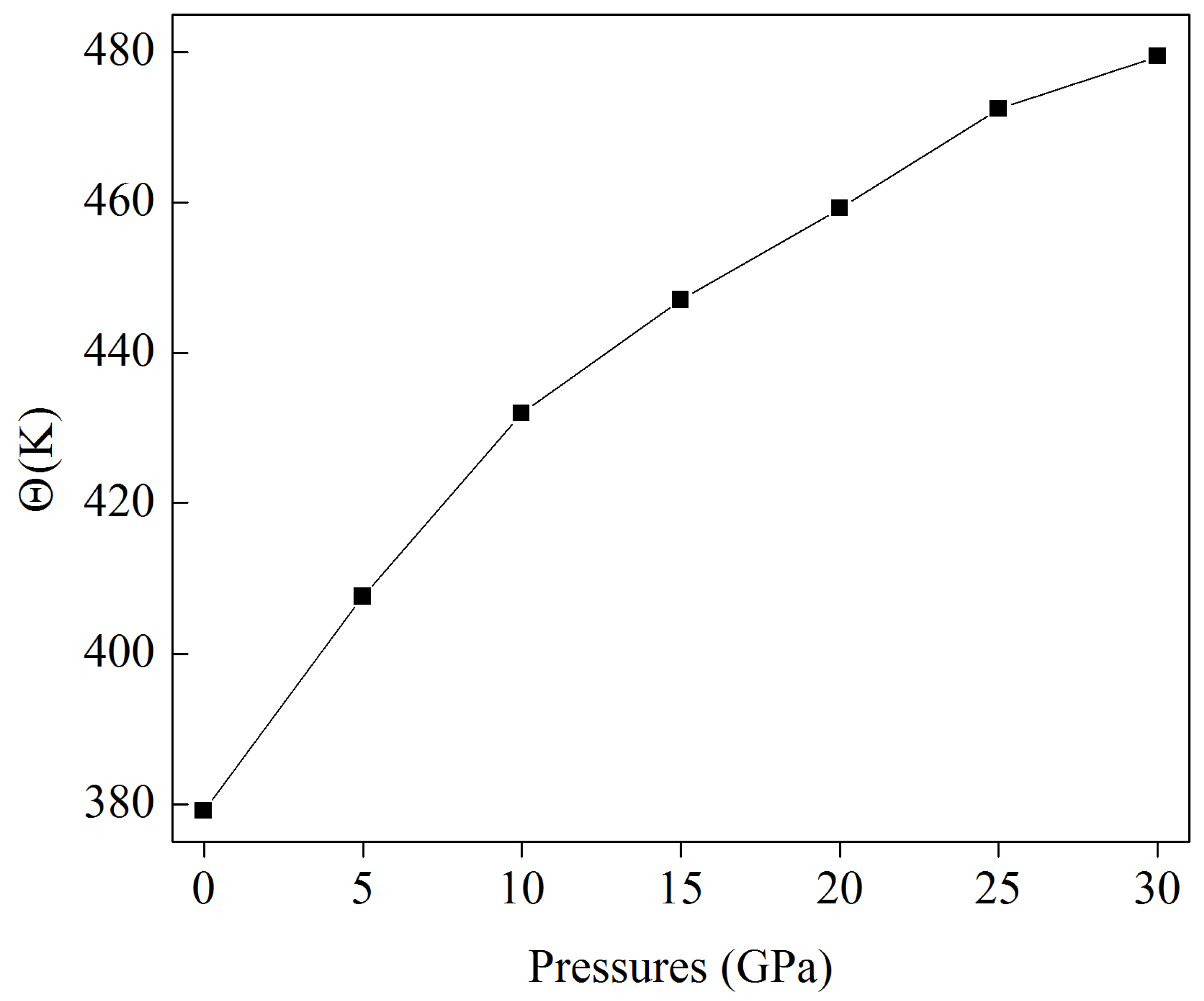
3.4. Speed of Sound at Pressure and Related Properties
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Schlapbach, L.; Züttel, A. Hydrogen-storage materials for mobile applications. Nature 2001, 414, 353–358. [Google Scholar] [CrossRef] [PubMed]
- Reilly, J.J., Jr.; Wiswall, R.H., Jr. Reaction of hydrogen with alloys of magnesium and nickel and the formation of Mg2NiH4. Inorg. Chem. 1968, 7, 2254–2256. [Google Scholar] [CrossRef]
- Xu, Y.; Deng, Y.; Liu, W.; Zhao, X.; Xu, J.; Yuan, Z. Research progress of hydrogen energy and metal hydrogen storage materials. Sustain. Energy Technol. Assess. 2023, 55, 102974. [Google Scholar] [CrossRef]
- Song, W.; Dong, H.; Zhang, G.; Liu, J.; Yang, G.; Liu, Y.; Li, Y.; Li, J.; Shen, J.; Chen, Y.; et al. Enhanced hydrogen absorption kinetics by introducing fine eutectic and long-period stacking ordered structure in ternary eutectic Mg–Ni–Y alloy. J. Alloys Compd. 2020, 820, 153187. [Google Scholar] [CrossRef]
- Hou, X.; Hu, R.; Zhang, T.; Kou, H.; Li, J. Hydrogenation thermodynamics of melt-spun magnesium rich Mg–Ni nanocrystalline alloys with the addition of multiwalled carbon nanotubes and TiF3. J. Power Sources 2016, 306, 437–447. [Google Scholar] [CrossRef]
- Yao, J.; Wu, Z.; Wang, H.; Yang, F.; Ren, J.; Zhang, Z. Application-oriented hydrolysis reaction system of solid-state hydrogen storage materials for high energy density target: A review. J. Energy Chem. 2022, 74, 218–238. [Google Scholar] [CrossRef]
- Ren, L.; Li, Y.; Zhang, N.; Li, Z.; Lin, X.; Zhu, W.; Lu, C.; Ding, W.; Zou, J. Nanostructuring of Mg-based hydrogen storage materials: Recent advances for promoting key applications. Nano-Micro Lett. 2023, 15, 93. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Tong, L.; Yin, S.; Liu, Y.; Wang, L.; Qiu, Y.; Ding, Y. Status and challenges of applications and industry chain technologies of hydrogen in the context of carbon neutrality. J. Clean. Prod. 2022, 376, 134347. [Google Scholar] [CrossRef]
- Skryabina, N.; Aptukov, V.; de Rango, P.; Fruchart, D. Effect of temperature on fast forging process of Mg-Ni samples for fast formation of Mg2Ni for hydrogen storage. Int. J. Hydrogen Energy 2020, 45, 3008–3015. [Google Scholar] [CrossRef]
- Guo, F.; Zhang, T.; Shi, L.; Song, L. Precipitation of nanocrystalline LaH3 and Mg2Ni and its effect on de-/hydrogenation thermodynamics of Mg-rich alloys. Int. J. Hydrogen Energy 2020, 45, 32221–32233. [Google Scholar] [CrossRef]
- Gao, S.; Zhang, S.; Li, Y.; Hu, R.; Heng, Z.; Shi, X.; Jin, P.; Shui, J. The rare earth doped Mg2Ni (010) surface enhances hydrogen storage. Appl. Surf. Sci. 2023, 614, 156243. [Google Scholar] [CrossRef]
- Agnarelli, L.; Prots, Y.; Burkhardt, U.; Schmidt, M.; Kozelj, P.; Leithe-Jasper, A.; Grin, Y. Mg3Pt2: Anionic chains in a Eu3Ga2-type structure. Inorg. Chem. 2021, 60, 13681–13690. [Google Scholar] [CrossRef] [PubMed]
- Boom, R.; de Boer, F. Enthalpy of formation of binary solid and liquid Mg alloys—Comparison of Miedema-model calculations with data reported in literature. Calphad 2020, 68, 101647. [Google Scholar] [CrossRef]
- Matheus, F.H.; Zepon, G.; Oliveira, V.B.; Leiva, D.R. Highly reactive hydrogen storage Mg2Ni alloy prepared by mechanochemistry and H-cycling. Int. J. Hydrogen Energy 2024, 51, 320–328. [Google Scholar] [CrossRef]
- Chen, J.; Sakai, T.; Kitamura, N.; Tanaka, H.; Kiyobayashi, T.; Takeshita, H.; Kuriyama, N. High pressure experiments on the Mg2Ni and Mg2NiH4–H systems. J. Alloys Compd. 2002, 330, 162–165. [Google Scholar] [CrossRef]
- Xiao, C.; Tu, Z.; Liao, L.; Liu, Z.; Wen, Y.; Zeng, X. Investigating the β-Mg17Al12 Alloy under Pressure Using First-Principles Methods: Structure, Elastic Properties, and Mechanical Properties. Crystals 2022, 12, 1741. [Google Scholar] [CrossRef]
- Wen, Y.; Zeng, X.; Ye, Y.; Gou, Q.; Liu, B.; Lai, Z.; Jiang, D.; Sun, X.; Wu, M. Theoretical Study on the Structural, Elastic, Electronic and Thermodynamic Properties of Long-Period Superstructures h-and r-Al2Ti under High Pressure. Materials 2022, 15, 4236. [Google Scholar] [CrossRef]
- Zeng, X.; Liao, L.; Wang, M.; Wang, H. Rare-earth metal-N6 centers in porous carbon for electrocatalytic CO2 reduction. Phys. Chem. Chem. Phys. 2023, 25, 20381–20394. [Google Scholar] [CrossRef] [PubMed]
- Wen, Y.; Zeng, X.; Xiao, Y.; Ruan, W.; Xiong, K.; Lai, Z. Density Functional Study of Electrocatalytic Carbon Dioxide Reduction in Fourth-Period Transition Metal–Tetrahydroxyquinone Organic Framework. Molecules 2024, 29, 2320. [Google Scholar] [CrossRef]
- Wen, Y.; Jiang, D.; Lai, Z.; Zeng, X.; Liu, B.; Xiao, Y.; Ruan, W.; Xiong, K. Exploring the CO2 Electrocatalysis Potential of 2D Metal–Organic Transition Metal–Hexahydroxytriquinoline Frameworks: A DFT Investigation. Molecules 2024, 29, 2896. [Google Scholar] [CrossRef]
- Zeng, X.; Tu, Z.; Yuan, Y.; Liao, L.; Xiao, C.; Wen, Y.; Xiong, K. Two-Dimensional Transition Metal-Hexaaminobenzene Monolayer Single-Atom Catalyst for Electrocatalytic Carbon Dioxide Reduction. Nanomaterials 2022, 12, 4005. [Google Scholar] [CrossRef] [PubMed]
- Zeng, X.; Liao, L.; Wang, M.; Wang, H. Density functional theory calculation of two-dimensional transition metal–hexaiminotriphenylene (TM-HITP) electrocatalytic CO2 reduction. Catal. Sci. Technol. 2023, 13, 5351–5364. [Google Scholar] [CrossRef]
- Zeng, X.; Liao, L.; Yu, Q.; Wang, M.; Wang, H. Theoretical Prediction of Electrocatalytic Reduction of CO2 Using a 2D Catalyst Composed of 3D Transition Metal and Hexaamine Dipyrazino Quinoxaline. Chem. Eur. J. 2023, 29, e202302232. [Google Scholar] [CrossRef] [PubMed]
- Zeng, X.; Xiao, C.; Liao, L.; Tu, Z.; Lai, Z.; Xiong, K.; Wen, Y. Two-Dimensional (2D) TM-Tetrahydroxyquinone Metal–Organic Framework for Selective CO2 Electrocatalysis: A DFT Investigation. Nanomaterials 2022, 12, 4049. [Google Scholar] [CrossRef] [PubMed]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Milman, V.; Winkler, B.; White, J.; Pickard, C.; Payne, M.; Akhmatskaya, E.; Nobes, R. Electronic structure, properties, and phase stability of inorganic crystals: A pseudopotential plane-wave study. Int. J. Quantum Chem. 2000, 77, 895–910. [Google Scholar] [CrossRef]
- Segall, M.; Lindan, P.J.; Probert, M.a.; Pickard, C.J.; Hasnip, P.J.; Clark, S.; Payne, M. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Physics: Condens. Matter 2002, 14, 2717. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Für Krist.-Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Mull, T.; Baumeister, B.; Menges, M.; Freund, H.J.; Weide, D.; Fischer, C.; Andresen, P. Bimodal velocity distributions after ultraviolet-laser-induced desorption of NO from oxide surfaces. Experiments and results of model calculations. J. Chem. Phys. 1992, 96, 7108–7116. [Google Scholar] [CrossRef]
- Hamann, D. Optimized norm-conserving Vanderbilt pseudopotentials. Phys. Rev. B 2013, 88, 085117. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Yvon, K.; Schefer, J.; Stucki, F. Structural studies of the hydrogen storage material Mg2NiH4. 1. Cubic high-temperature structure. Inorg. Chem. 1981, 20, 2776–2778. [Google Scholar] [CrossRef]
- Shao, H.; Li, X. Effect of nanostructure and partial substitution on gas absorption and electrochemical properties in Mg2Ni-based alloys. J. Alloys Compd. 2016, 667, 191–197. [Google Scholar] [CrossRef]
- Le Page, Y.; Saxe, P. Symmetry-general least-squares extraction of elastic data for strained materials from ab initio calculations of stress. Phys. Rev. B 2002, 65, 104104. [Google Scholar] [CrossRef]
- Wu, X.; Vanderbilt, D.; Hamann, D. Systematic treatment of displacements, strains, and electric fields in density-functional perturbation theory. Phys. Rev. B 2005, 72, 035105. [Google Scholar] [CrossRef]
- Liu, C.H.; Ouyang, C.Y.; Ji, Y.H. First principles investigation of electronic structuresand stabilities of Mg2Ni and its complex hydrides. Acta Phys. Sin. 2011, 60, 553–558. [Google Scholar]
- Zeng, X.; Peng, R.; Yu, Y.; Hu, Z.; Wen, Y.; Song, L. Pressure effect on elastic constants and related properties of Ti3Al intermetallic compound: A first-principles study. Materials 2018, 11, 2015. [Google Scholar] [CrossRef]
- Sin’Ko, G.; Smirnov, N. Ab initio calculations of elastic constants and thermodynamic properties of bcc, fcc, and hcp Al crystals under pressure. J. Phys. Condens. Matter 2002, 14, 6989. [Google Scholar]
- Cheng, H.C.; Yu, C.F.; Chen, W.H. First-principles density functional calculation of mechanical, thermodynamic and electronic properties of CuIn and Cu2In crystals. J. Alloys Compd. 2013, 546, 286–295. [Google Scholar] [CrossRef]
- Voigt, W. Lehrbuch der Kristallphysik (Textbook of Crystal Physics); BG Teubner: Leipzig/Berlin, Germany, 1928. [Google Scholar]
- Reuss, A. Calculation of the flow limits of mixed crystals on the basis of the plasticity of monocrystals. Z. Angew. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Pugh, S. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Ed. Dub. Philos. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Frantsevich, I.N.; Voronov, F.F.; Bokuta, S.A. Elastic Constants and Elastic Moduli of Metals and Insulators Handbook; Frantsevich, I.N., Ed.; Naukova Dumka: Kiev, Ukraine, 1983; pp. 60–180. [Google Scholar]
- Pettifor, D. Theoretical predictions of structure and related properties of intermetallics. Mater. Sci. Technol. 1992, 8, 345–349. [Google Scholar] [CrossRef]
- Chen, X.Q.; Niu, H.; Li, D.; Li, Y. Modeling hardness of polycrystalline materials and bulk metallic glasses. Intermetallics 2011, 19, 1275–1281. [Google Scholar] [CrossRef]
- Mao, P.; Yu, B.; Liu, Z.; Wang, F.; Ju, Y. First-principles investigation on mechanical, electronic, and thermodynamic properties of Mg2Sr under high pressure. J. Appl. Phys. 2015, 117, 115903. [Google Scholar] [CrossRef]
- Chung, D.; Buessem, W. The elastic anisotropy of crystals. J. Appl. Phys. 1967, 38, 2010–2012. [Google Scholar] [CrossRef]
- Ranganathan, S.I.; Ostoja-Starzewski, M. Universal elastic anisotropy index. Phys. Rev. Lett. 2008, 101, 055504. [Google Scholar] [CrossRef] [PubMed]
- Kube, C.M. Elastic anisotropy of crystals. AIP Adv. 2016, 6, 095209. [Google Scholar] [CrossRef]
- Brugger, K. Determination of third-order elastic coefficients in crystals. J. Appl. Phys. 1965, 36, 768–773. [Google Scholar] [CrossRef]
- Duan, Y.; Sun, Y.; Peng, M.; Zhou, S. Anisotropic elastic properties of the Ca–Pb compounds. J. Alloys Compd. 2014, 595, 14–21. [Google Scholar] [CrossRef]
- Sun, L.; Gao, Y.; Xiao, B.; Li, Y.; Wang, G. Anisotropic elastic and thermal properties of titanium borides by first-principles calculations. J. Alloys Compd. 2013, 579, 457–467. [Google Scholar] [CrossRef]
- Screiber, E.; Anderson, O.; Soga, N. Elastic Constants and Their Measurements; McGrawHill: New York, NY, USA, 1973. [Google Scholar]
- Anderson, O.L. A simplified method for calculating the Debye temperature from elastic constants. J. Phys. Chem. Solids 1963, 24, 909–917. [Google Scholar] [CrossRef]


| Pressure | ||||||
|---|---|---|---|---|---|---|
| 0 | 115.857 | 44.723 | 74.463 | 190.004 | 21.289 | 35.567 |
| 5 | 144.622 | 61.676 | 50.827 | 162.876 | 24.762 | 41.473 |
| 10 | 174.032 | 80.436 | 61.925 | 182.278 | 27.401 | 46.798 |
| 15 | 196.713 | 93.473 | 72.256 | 207.105 | 28.764 | 51.620 |
| 20 | 210.861 | 99.683 | 88.357 | 240.581 | 30.569 | 55.589 |
| 25 | 243.136 | 121.670 | 96.967 | 252.583 | 31.446 | 60.733 |
| 30 | 284.700 | 156.732 | 134.682 | 300.764 | 31.681 | 63.984 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, C.; Liu, L.; Liu, S.; Lai, Z.; Liu, Y.; Zeng, X.; Liao, L. A First-Principles Study of the Structural, Elastic, and Mechanical Characteristics of Mg2Ni Subjected to Pressure Conditions. Metals 2024, 14, 789. https://doi.org/10.3390/met14070789
Xiao C, Liu L, Liu S, Lai Z, Liu Y, Zeng X, Liao L. A First-Principles Study of the Structural, Elastic, and Mechanical Characteristics of Mg2Ni Subjected to Pressure Conditions. Metals. 2024; 14(7):789. https://doi.org/10.3390/met14070789
Chicago/Turabian StyleXiao, Chuncai, Lei Liu, Shihuan Liu, Zhangli Lai, Yuxin Liu, Xianshi Zeng, and Luliang Liao. 2024. "A First-Principles Study of the Structural, Elastic, and Mechanical Characteristics of Mg2Ni Subjected to Pressure Conditions" Metals 14, no. 7: 789. https://doi.org/10.3390/met14070789
APA StyleXiao, C., Liu, L., Liu, S., Lai, Z., Liu, Y., Zeng, X., & Liao, L. (2024). A First-Principles Study of the Structural, Elastic, and Mechanical Characteristics of Mg2Ni Subjected to Pressure Conditions. Metals, 14(7), 789. https://doi.org/10.3390/met14070789






