Ductile-to-Brittle Transition of Steel Due to Dynamic Loading
Abstract
:1. Introduction
- Absence of methodological framework to identify the ductile-to-brittle transition prior to real-scale testing.
- Lack of know-how regarding the material-related physical variables triggering the dynamic brittleness.
- Lack of an experimentally controlled and validated apparatus able to identify the transition point between plastic and brittle behavior.
- Total loss of predictiveness of numerical methods once the plastic-to-brittle transition emerges in a real-scale event.
- Inability of plastic strain-rate material models to capture the brittle behavior, as they incorporate a progressive increase in strength in accordance with the increase in the strain rate, generally validating intermediate strain rates and pointing to a continuous variation in plastic flow without any sudden major reductions in material deformability.
2. Material and Experiments
3. Ductile to Brittle Transition Induced by Extreme Dynamic Events
4. Strain Rate-Dependent Plasticity and Experimental, Classic, and Innovative Approaches
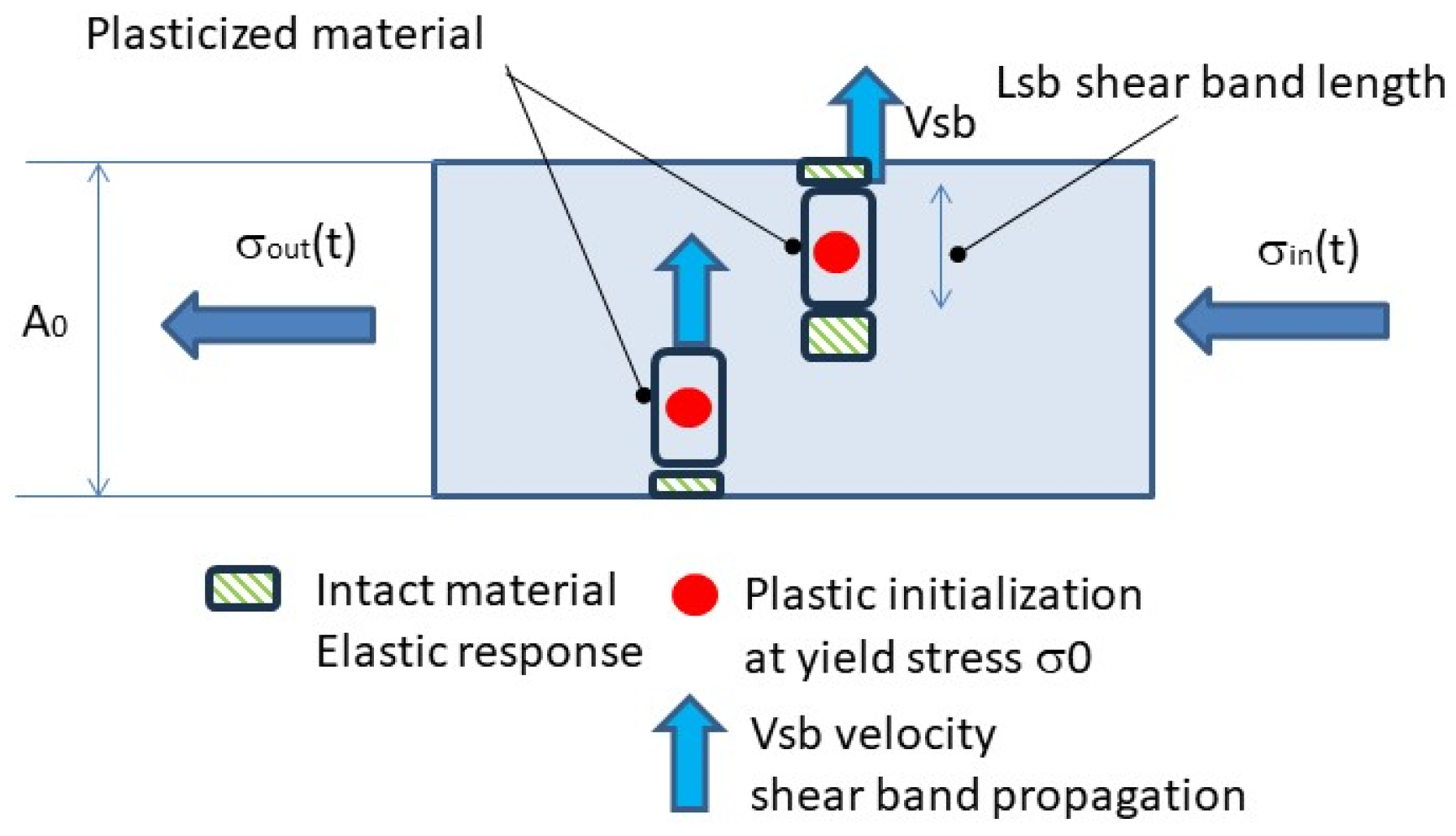
5. DAMP-PLAST Model: The Plastic Propagation through Material Microstructure
6. The Brittle Behavior as a Physical Limit for the Material Due to Shear-Band-to-Loading-Wave Velocities
Ductile–Brittle Transition: The Critical Kinetic Energy Content
7. Identification of DAMP-PLAST Material Parameters
7.1. DAMP-PLAST Material Model Identification
- (a)
- Via static tests, the yield stress and static plastic response are found;
- (b)
- Via SHB tests, the strain rate-dependent plasticity is identified;
- (c)
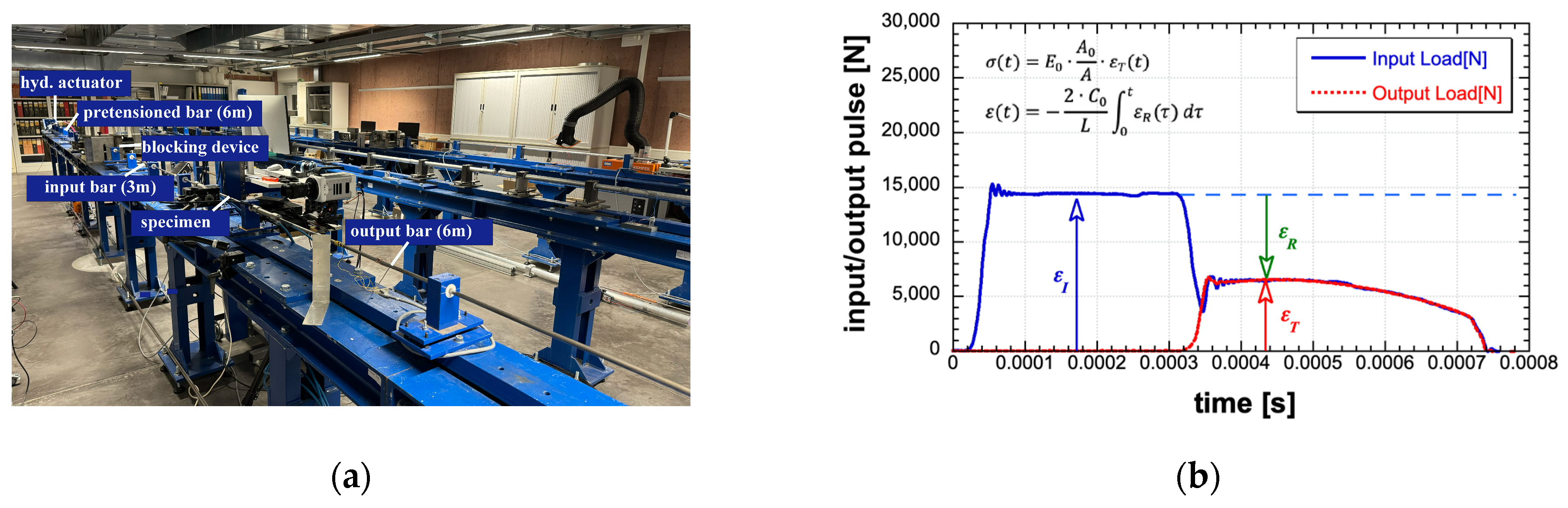
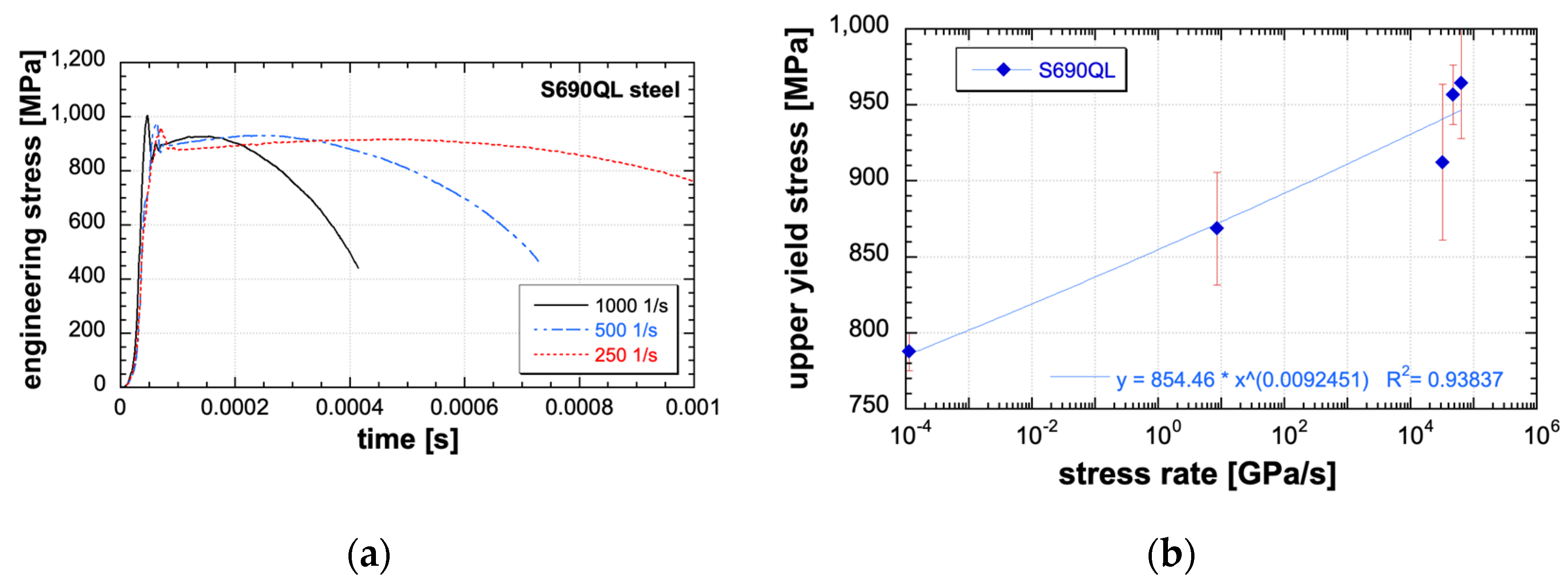
- Via the use of SHB tests, high loading rates are obtained, and upper yield appears on the output signal (see Figure 2a). By the amplitude of the upper yield and knowing the loading rate, the identification starts. The experimental response of SHB tests can be used as a starting point for applying the test numerical reconstruction and tuning the numerical model up so that the virtual and real experimental signals are identical. The fitting is made by modifying the shear band propagation speed and the characteristic propagation length while the initial yield point has already been obtained by the static test. This method is fully engineer-oriented, as it uses repeatable experiments that are fully focused on a specific loading rate;
- (d)
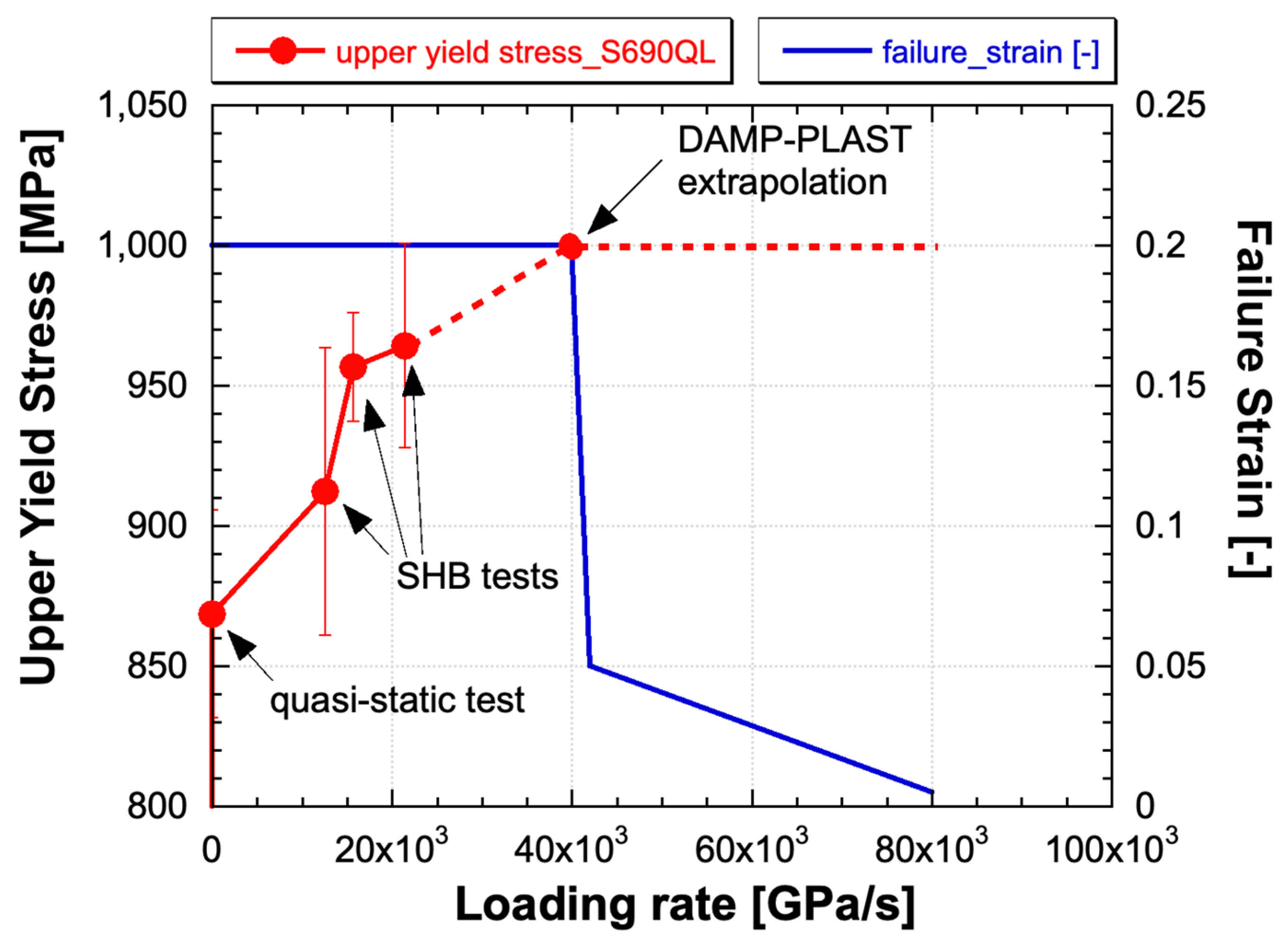
- Finally, the critical brittle loading rate is found via the analytic relation (18).
7.2. DAMP-PLAST Material Response Triggered by the Yielding Propagation Time Driving the Failure-Mode Changes
- (1)
- Quasi-static response: As the loading rate is very small, the yield occurs at the static value. The yield acts instantaneously compared to the physical time by which the loads rise over the structure.
- (2)
- Intermediate strain and loading rates are characterized by a loading rate smaller than the critical loading rate but big enough to create a significant stress increase while the shear band completes its path. In this case, the material acts in accordance with the strain rate-dependent plasticity models, resulting in an increase in the plastic flow within the loading rate. Additionally, in the elastic-to-plastic transition, the upper yield can appear or not, with variable intensity dependent on the possible combination between the shear band propagation, the loading rate, and the yield increase due to the classical strain rate-dependent plasticity.
- (3)
- Extreme loading rates, characterized by a loading rate higher than the critical loading rate, brittle behavior, fracture localization, and overall deformation reduction, are found.
8. Application of DAMP-PLAST Model: Structural Mesh Size vs. Mesh Sensitivity
- (i)
- Considering the real-scale event, the mesh size that the engineer can apply is generally macroscopic due to the structure size and computational effectiveness. To avoid large systematic errors, the material properties should be tuned to the mesh size used in the real-scale application [39].
- (ii)
- Having as the actual goal the SHB test reconstruction dedicated to the real test simulation, the application requires the tuning of the material properties on the finest mesh size, in accordance with the true stress–strain in the necking region during the plastic flow but applying the tuning of the SHB signal using the structural mesh size used to compute the final real-scale blast event.
- (iii)
- With the goal of identifying the yield propagation speed as a principal parameter linked to the brittle transition prediction in the DAMP-PLAST material model, it is important to note how the upper yield occurs when the specimen is not yet subject to large deformation; hence, the geometrical non-linearities do not apply. During the early loading of the specimen subject to uniform stress through the cross-section, the element formulation proposed in the DAMP-PLAST model has very limited sensitivity in regard to mesh size, as intrinsically the element formulation incorporates at the value of the shear band length and speed.
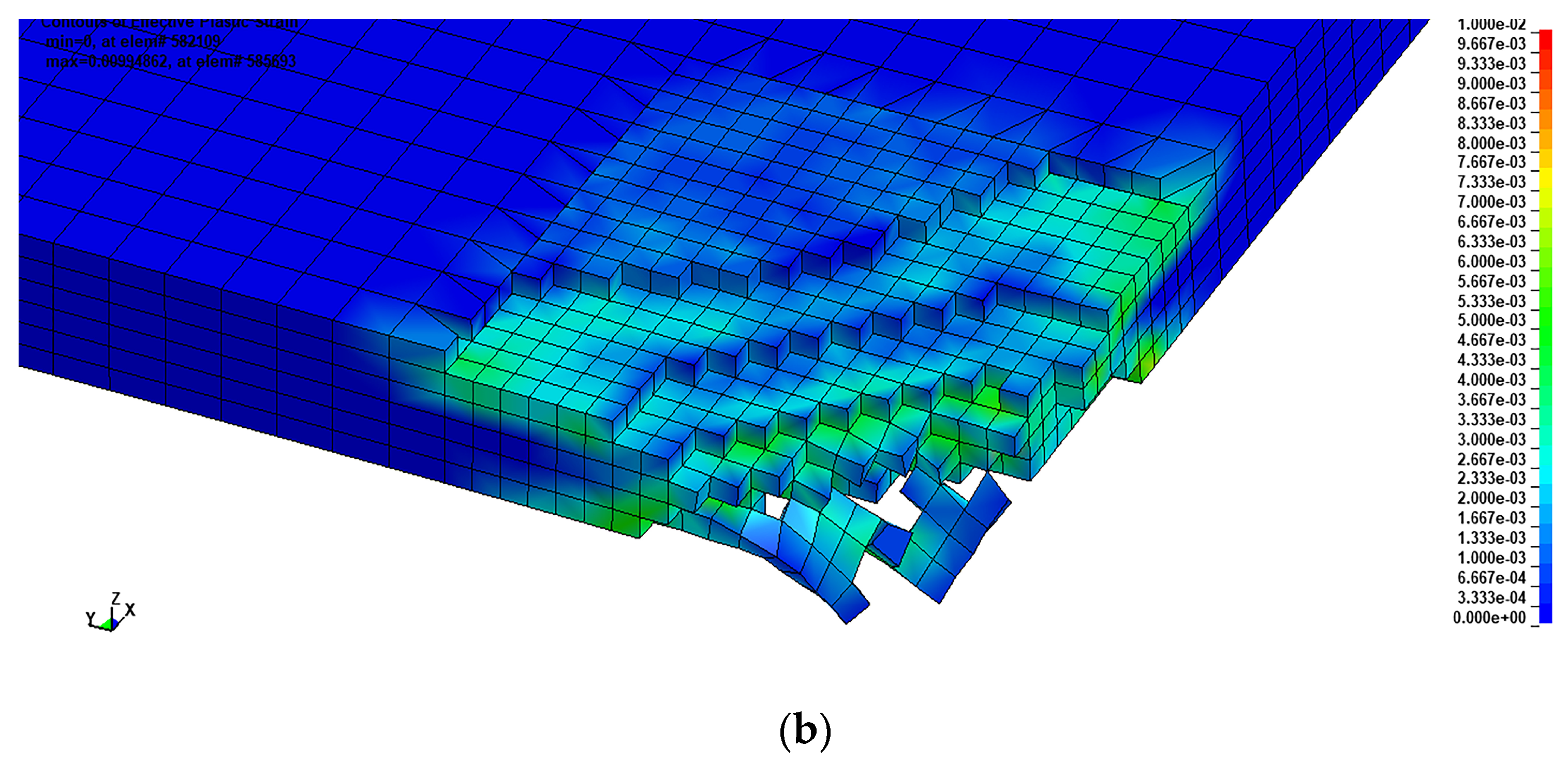
9. Model Assessment of Critical Blast Charge over Thick Metal Slab
Results
10. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Koyama, M.; Shimomura, Y.; Chiba, A.; Akiyama, E.; Tsuzaki, K. Room-temperature blue brittleness of Fe-Mn-C austenitic steels. Scr. Mater. 2017, 141, 20–23. [Google Scholar] [CrossRef]
- Darnbrough, J.; Roebuck, B.; Flewitt, P. The influence of temperature and grain boundary volume on the resistivity of nanocrystalline nickel. J. Appl. Phys. 2015, 118, 184302. [Google Scholar] [CrossRef]
- Albertini, C.; Cadoni, E.; Solomos, G. Advances in the Hopkinson bar testing of irradiated/non-irradiated nuclear materials and large specimens. Phil. Trans. Royal Soc. A 2015, 372, 20130197. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Zhang, B. Material embrittlement in high strain-rate loading. Int. J. Extrem. Manuf. 2019, 1, 022003. [Google Scholar] [CrossRef]
- Dowding, I.; Schuh, C.A. Metals strengthen with increasing temperature at extreme strain rates. Nature 2024, 630, 91–95. [Google Scholar] [CrossRef] [PubMed]
- Majzoobi, G.H.; Mahmoudi, A.H.; Moradi, S. Ductile to brittle failure transition of HSLA-100 Steel at high strain rates and subzero temperatures. Eng. Fract. Mech. 2016, 158, 179–193. [Google Scholar] [CrossRef]
- Gauder, P.; Seidenfuß, M. Experimental and numerical investigations of tensile specimens containing multiple flaws in the ductile-to-brittle transition region. Eng. Fract. Mech. 2021, 248, 107714. [Google Scholar] [CrossRef]
- Klepaczko, J.R. Plastic shearing at high and very high strain rates. J. Phys. IV 1994, 4, C8–C35. [Google Scholar] [CrossRef]
- Su, G.; Su, Q.; Sheng, J.; Wang, B.; Zhang, H.; Du, J.; Zhang, P.; Shen, X.; Liu, Z. Modelling of ductile fracture in pure iron considering the ductile–brittle transition at very high strain rate. Eng. Fract. Mech. 2023, 281, 109145. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, Y.; Sun, Z.; Hu, H.; Huang, F. On shear failure behaviors of an armor steel over a large range of strain rates. Int. J. Imp. Eng. 2018, 118, 24–38. [Google Scholar] [CrossRef]
- Li, Y.; Pallaspuro, S.; Ren, X.; He, J.; Kömi, J.; Zhang, Z. A multi-barrier model assisted CAFE method for predicting ductile-to-brittle transition with application to a low-carbon ultrahigh-strength steel. Mech. Mat. 2021, 153, 103669. [Google Scholar] [CrossRef]
- Needleman, A.; Tvergaard, V. Numerical modeling of the ductile-brittle transition. Int. J. Fract. 2000, 101, 73–97. [Google Scholar] [CrossRef]
- Orowan, E. Problems of plastic gliding. Proc. Phys. Soc. 1940, 52, 8–22. [Google Scholar] [CrossRef]
- Campbell, J.D. Dynamic plasticity: Macroscopic and microscopic aspects. Mat. Sci. Eng. 1973, 12, 3–21. [Google Scholar] [CrossRef]
- Campbell, J.D.; Ferguson, W.G. The temperature and strain-rate dependence of the shear strength of mild steel. Philos. Mag. 1970, 21, 63–82. [Google Scholar] [CrossRef]
- Harding, J. Effect of High strain rate on the room temperature strength and ductility of five alloy steels. J. Iron Steel Inst. 1972, 210, 425–432. [Google Scholar]
- Cadoni, E.; Forni, D. Strain-rate effects on S690QL high strength steel under tensile loading. J. Constr. Steel Res. 2020, 175, 106348. [Google Scholar] [CrossRef]
- Cadoni, E.; Briccola, D.; Dotta, M.; Forni, D. Combined effect of elevated temperature and high strain rates on S690QL high strength steel. J. Constr. Steel Res. 2022, 199, 107519. [Google Scholar] [CrossRef]
- Escobedo, J.P.; Brown, E.N.; Trujillo, C.P.; Cerreta, E.K.; Gray, G.T.I. The effect of shock-wave profile on dynamic brittle failure. J. Appl. Phys. 2013, 113, 103506. [Google Scholar] [CrossRef]
- Scheibert, J.; Guerra, C.; Cйlariй, F.; Dalmas, D.; Bonamy, D. Brittle-Quasibrittle Transition in Dynamic Fracture: An Energetic Signature. Phys. Rev. Lett. 2010, 104, 045501. [Google Scholar] [CrossRef]
- Ravi-Chandar, K. Dynamic Fracture; Elsevier Science: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Torre do Vale Arriaga e Cunha, M. Stability Analysis of Metals Capturing Brittle and Ductile Fracture through a Phase Field Method and Shear Band. Ph.D. Thesis, Columbia University, New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Knott, J. Brittle fracture in structural steels: Perspectives at different size-scales. Phil. Trans. Royal Soc. A 2015, 373, 20140126. [Google Scholar] [CrossRef] [PubMed]
- Qin, K.; Yang, L.M.; Hu, S. Interpretation of Strain Rate Effect of Metals. In Dynamic Behavior of Materials; Song, B., Casem, D., Kimberley, J., Eds.; Springer International Publisher: New York, NY, USA, 2014; Volume 1, pp. 21–27. [Google Scholar]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Johnson, G.; Holmquist, T.M.; Meyer, M.A. (Eds.) Chapter A Computational Constitutive Model for Brittle Materials Subjected to Large Strains, High Strain Rates, and High Pressures. In Shock Wave and High-Strain-Rate Phenomena in Materials; CRC Press: Boca Raton, FL, USA, 1992; pp. 1075–1081. [Google Scholar]
- Selyutina, N.; Petrov, Y. Comparative Analysis of Dynamic Plasticity Models. Rev. Adv. Mat. Sci. 2018, 57, 199–211. [Google Scholar] [CrossRef]
- Zerilli, F.J.; Armstrong, R.W. Dislocation mechanics based constitutive equation incorporating dynamic recovery and applied to thermomechanical shear instability. AIP Conf. Proc. 1998, 429, 215–218. [Google Scholar]
- Cowper, G.; Symonds, P. Strain-Hardening and Strain-Rate Effects in the Impact Loading of Cantilever Beams; Division of Applied Mathematics, Brown University: Brown, RI, USA, 1957. [Google Scholar]
- Riganti, G.; Cadoni, E. Multiple Pseudo-Plastic Appearance of the Dynamic Fracture in Quasi-Brittle Materials. Materials 2020, 13, 4976. [Google Scholar] [CrossRef] [PubMed]
- Riganti, G.; Cadoni, E. Numerical simulation of the high strain-rate behavior of quenched and self-tempered reinforcing steel in tension. Mat. Des. 2014, 57, 156–167. [Google Scholar] [CrossRef]
- Kolsky, H. An Investigation of the Mechanical Properties of Materials at very High Rates of Loading. Proc. Phys. Soc. Sect. B 1949, 62, 676. [Google Scholar] [CrossRef]
- Albertini, C.; Montagnani, M. Testing techniques based on the SHPB. Inst. Phys. Conf. Ser. 1974, 21, 22–32. [Google Scholar]
- Bigoni, D.; Dal Corso, F.; Dal Corso, F. The unrestrainable growth of a shear band in a prestressed material. Proc. R. Soc. Lond. A 2008, 464, 2365–2390. [Google Scholar] [CrossRef]
- Xue, Q.; Meyers, M.; Nesterenko, V. Self organization of shear bands in stainless steel. Mat. Sci. Eng. A 2004, 384, 35–46. [Google Scholar] [CrossRef]
- Liu, C.; Roddatis, V.; Kenesei, P.; Maaßs, R. Shear-band thickness and shear-band cavities in a Zr-based metallic glass. Acta Mat. 2017, 140, 206–216. [Google Scholar] [CrossRef]
- Johnston, W.G.; Gilman, J.J. Dislocation Velocities, Dislocation Densities, and Plastic Flow in Lithium Fluoride Crystals. J. Appl. Phys. 1959, 30, 129–144. [Google Scholar] [CrossRef]
- LsDyna. LsDyna Keyword and Theory Manual. Available online: www.dynasupport.com/manuals (accessed on 1 March 2024).
- Yudhifa, C.; Satriawan, G.; Harwijayanti, W.; Ridwan, R.; Prabowo, A.R.; Fajri, A.; Cho, J.H.; Do, Q.T. Nonlinear analysis of an idealized I-beam member: An investigation of mesh size on the structural behaviors using FE approach. Proc. Struct. Int. 2023, 48, 50–57. [Google Scholar]



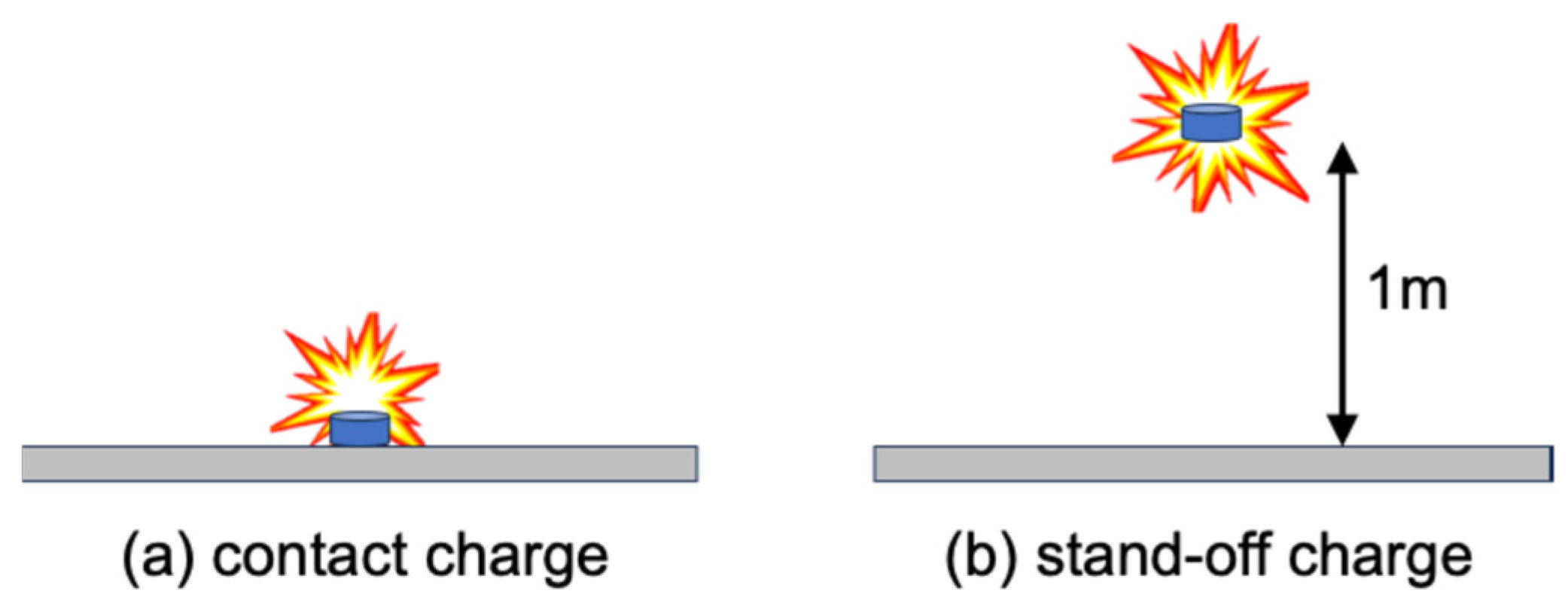
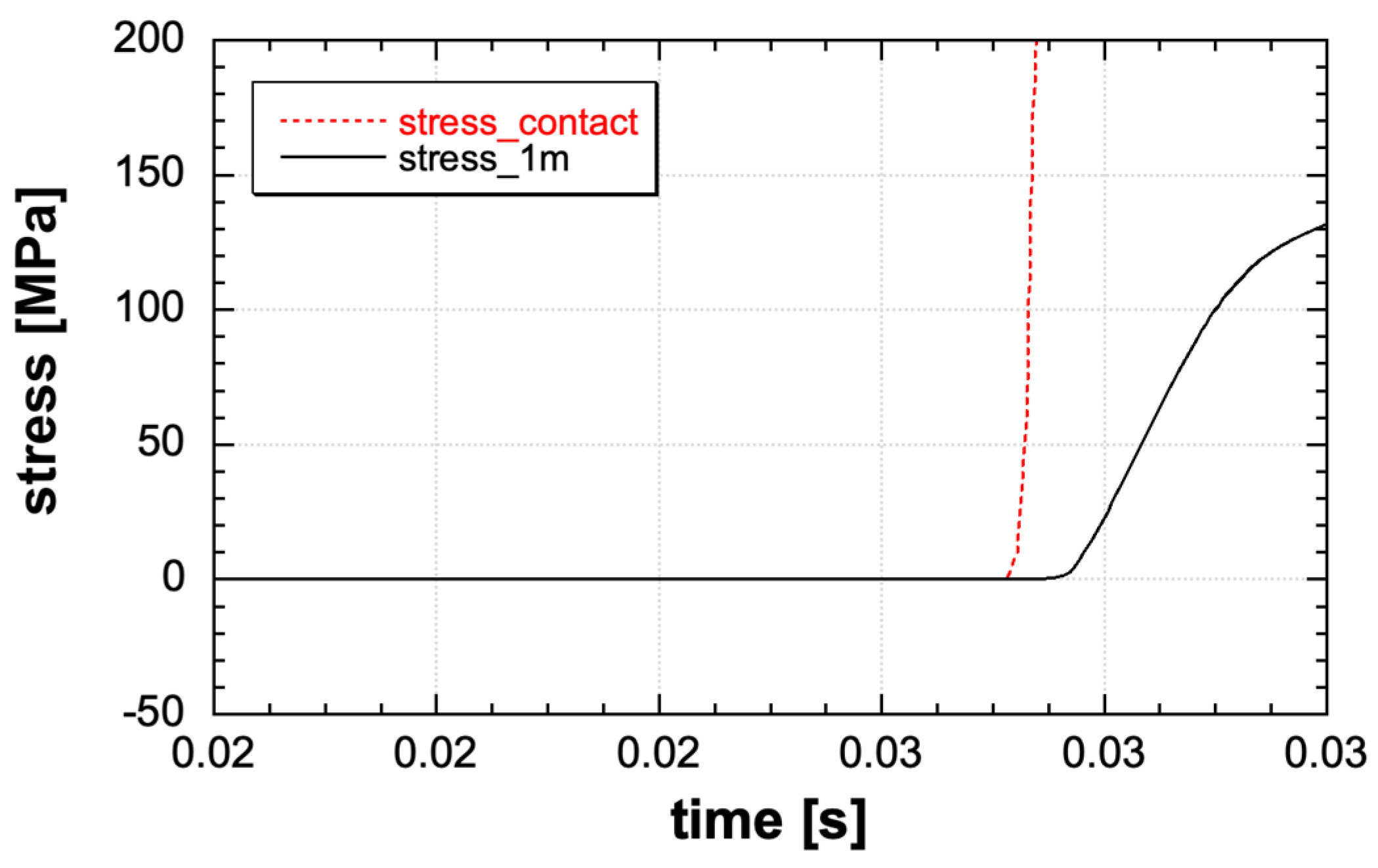
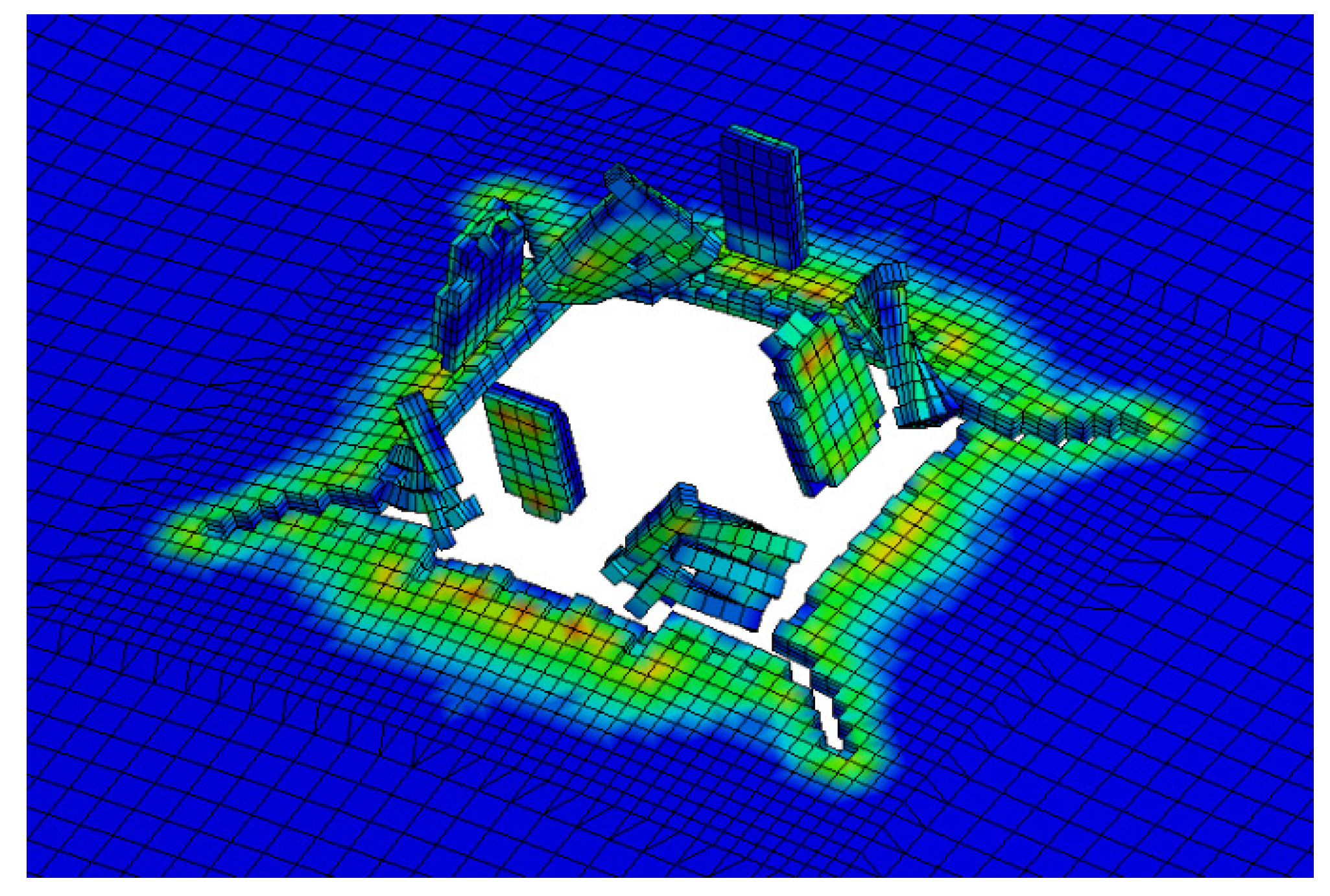
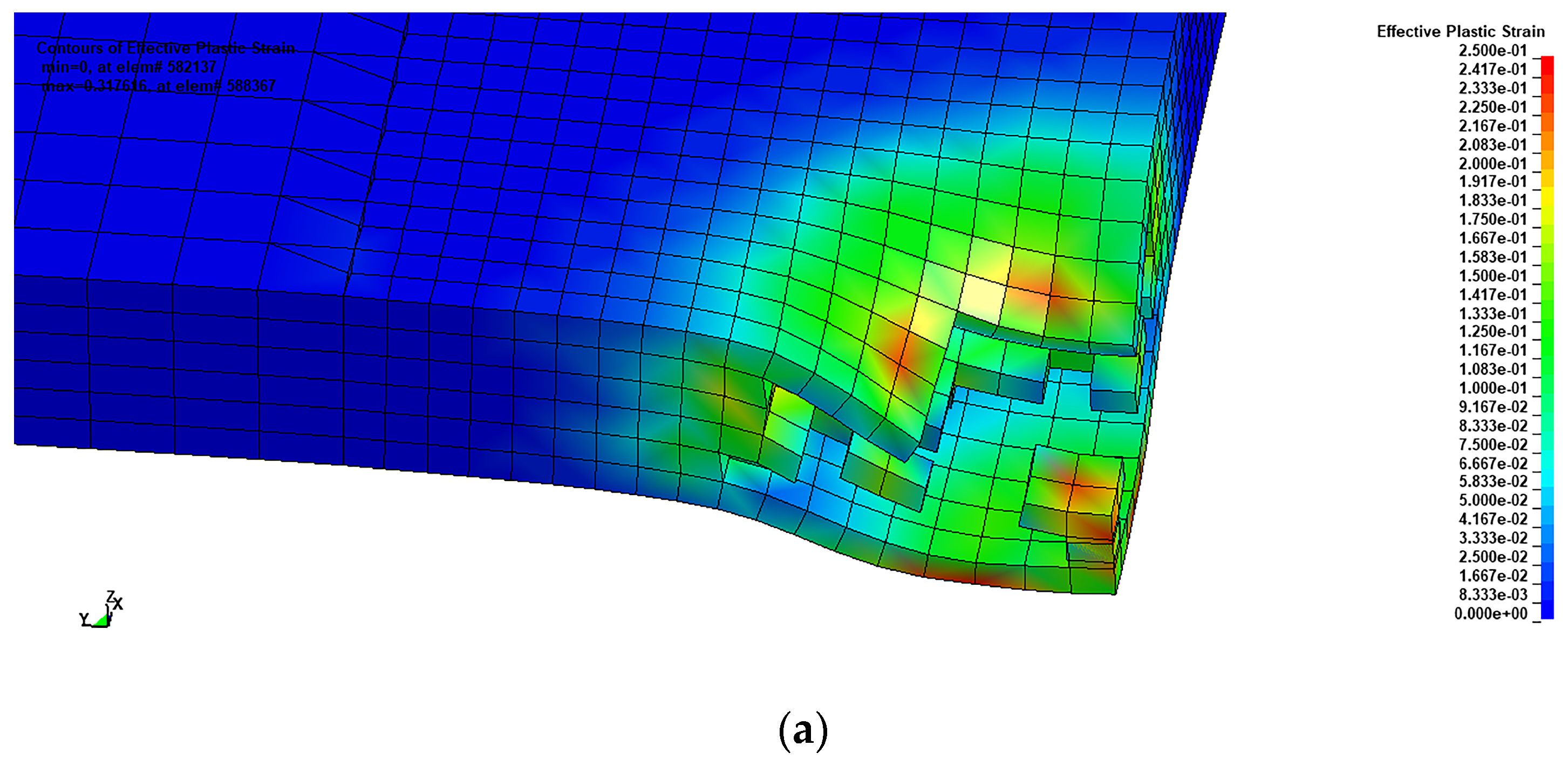

| Test Case | Material Model | Result | Failure by |
|---|---|---|---|
| Contact charge | MatPlast | Plastic failure | Deformation |
| Contact charge | DAMP-PLAST | Brittle failure | Fracture and debris |
| 1 m stand-off | MatPlast | Plastic failure | Deformation |
| 1 m stand-off | DAMP-PLAST | Plastic failure | Deformation |
| Test Case | Material Model | Result | Failure by |
|---|---|---|---|
| Contact charge | MatPlast | Plastic failure | Deformation |
| Contact charge | DAMP-PLAST | Brittle failure | Fracture and debris |
| 1 m stand-off | MatPlast | Plastic failure | Deformation |
| 1 m stand-off | DAMP-PLAST | Brittle failure | Fracture and debris |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riganti, G.; Cadoni, E. Ductile-to-Brittle Transition of Steel Due to Dynamic Loading. Metals 2024, 14, 807. https://doi.org/10.3390/met14070807
Riganti G, Cadoni E. Ductile-to-Brittle Transition of Steel Due to Dynamic Loading. Metals. 2024; 14(7):807. https://doi.org/10.3390/met14070807
Chicago/Turabian StyleRiganti, Gianmario, and Ezio Cadoni. 2024. "Ductile-to-Brittle Transition of Steel Due to Dynamic Loading" Metals 14, no. 7: 807. https://doi.org/10.3390/met14070807
APA StyleRiganti, G., & Cadoni, E. (2024). Ductile-to-Brittle Transition of Steel Due to Dynamic Loading. Metals, 14(7), 807. https://doi.org/10.3390/met14070807







