Research on Multiscale Numerical Simulation Method for SLM Melting Process
Abstract
:1. Introduction
2. SLM Single-Layer Numerical Modelling and Validation
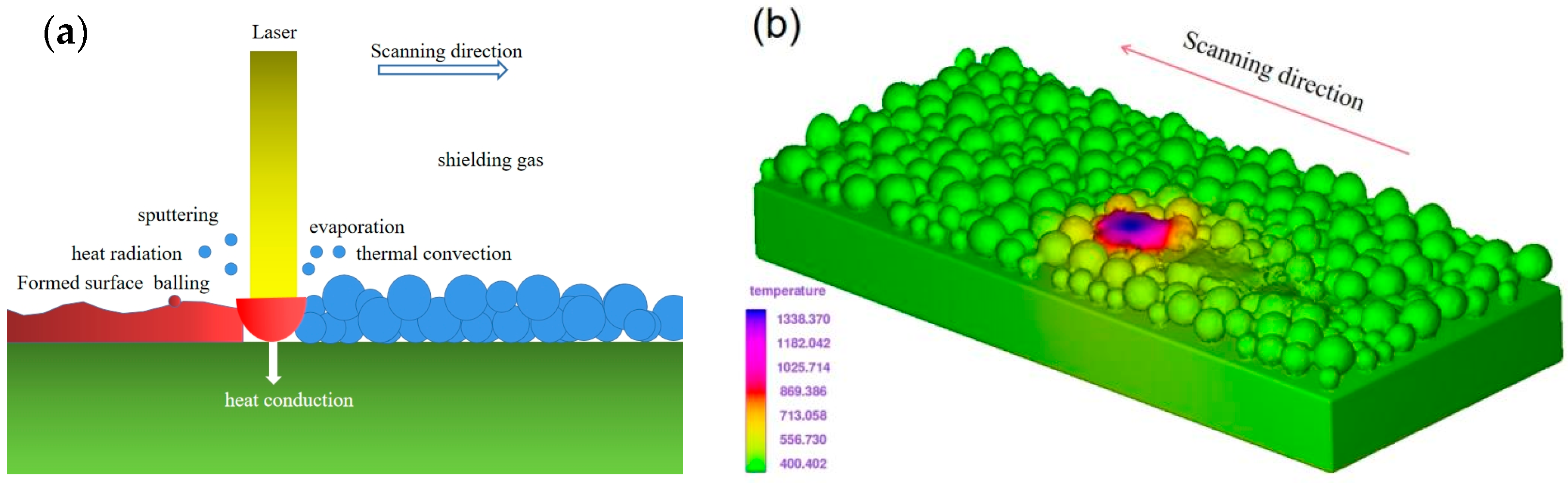
2.1. Physical Models and Control Equations
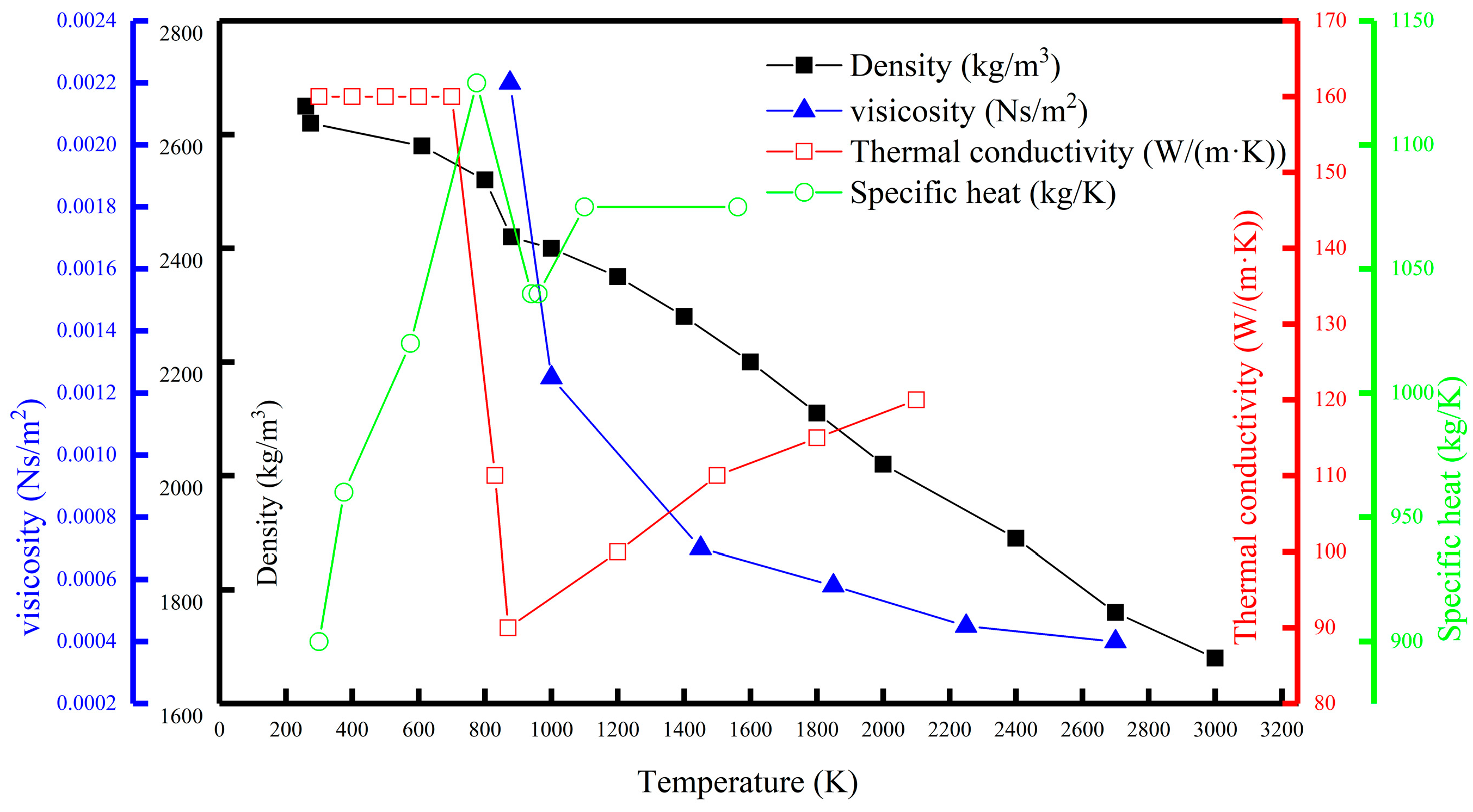
2.2. Material Parameter Setting
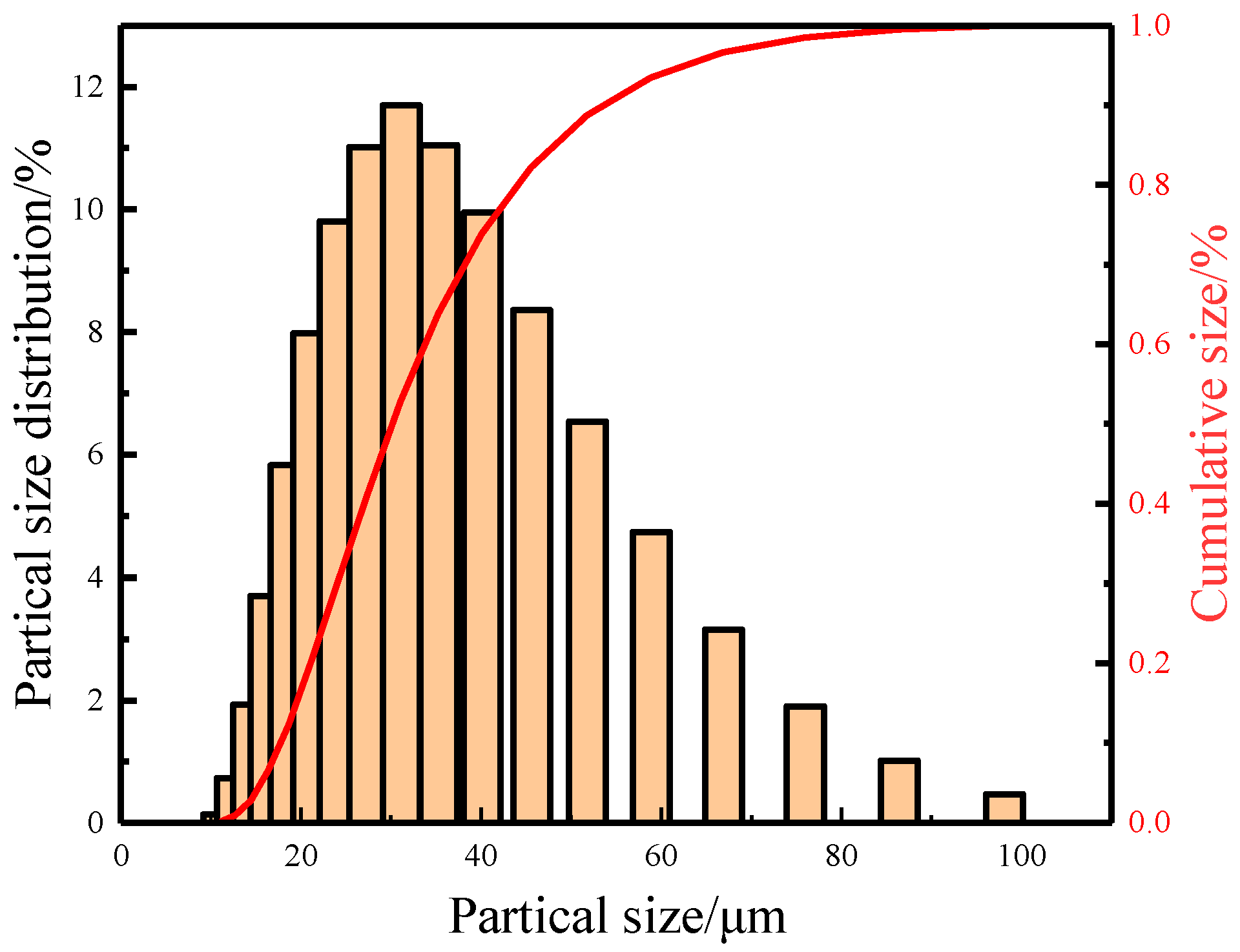
2.3. Experimental Materials and Forming Equipment
2.4. Model Validation
3. Numerical Modelling of SLM Multiscale Melt Channel Formation
3.1. Metal Material Property Setting
3.2. Melt Pool Mobility Equivalent
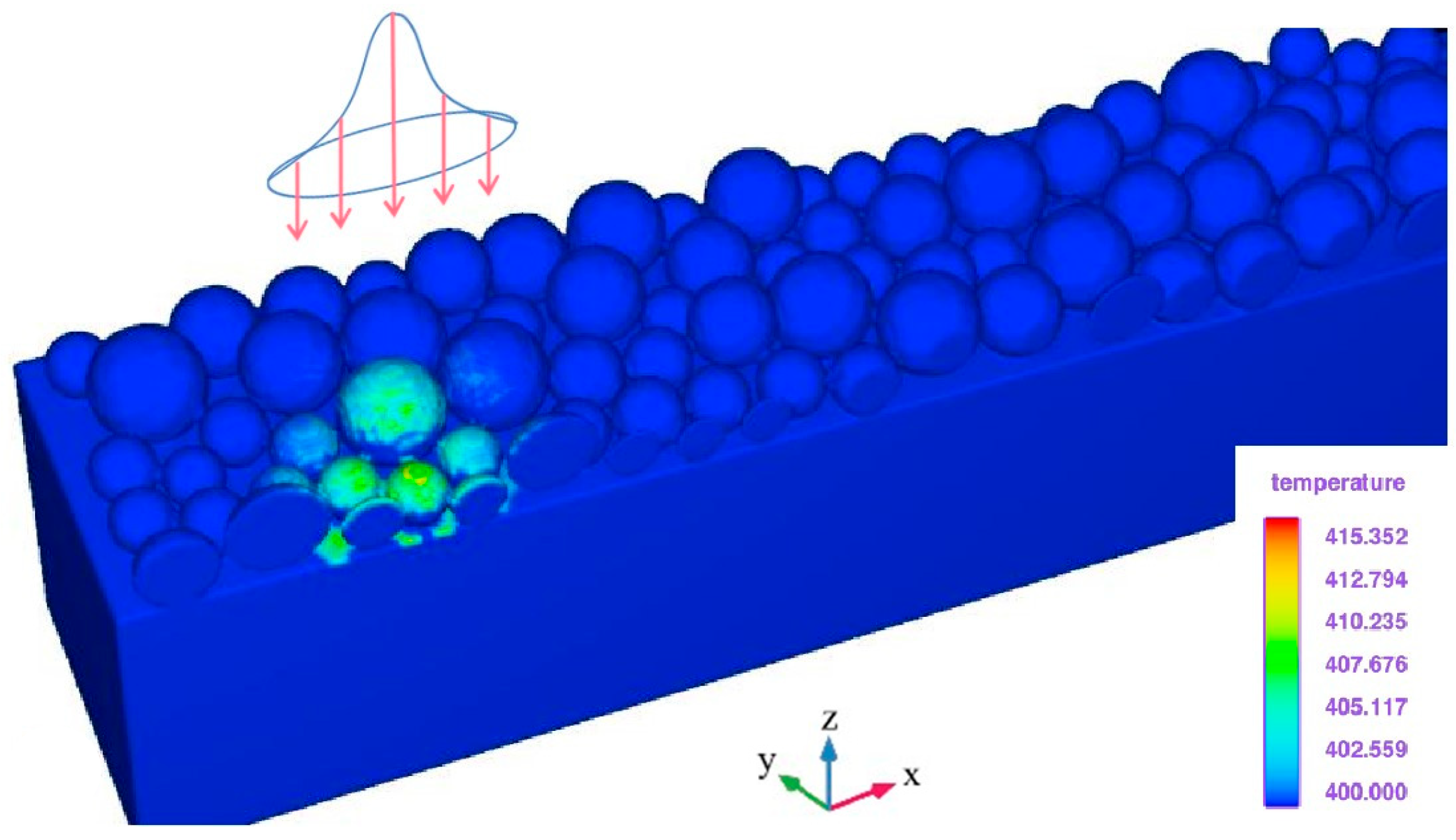
3.3. Pore Modelling in Sedimentary Regions
3.4. Establishment of SLM Multilayer Melt-Channel-Forming Process
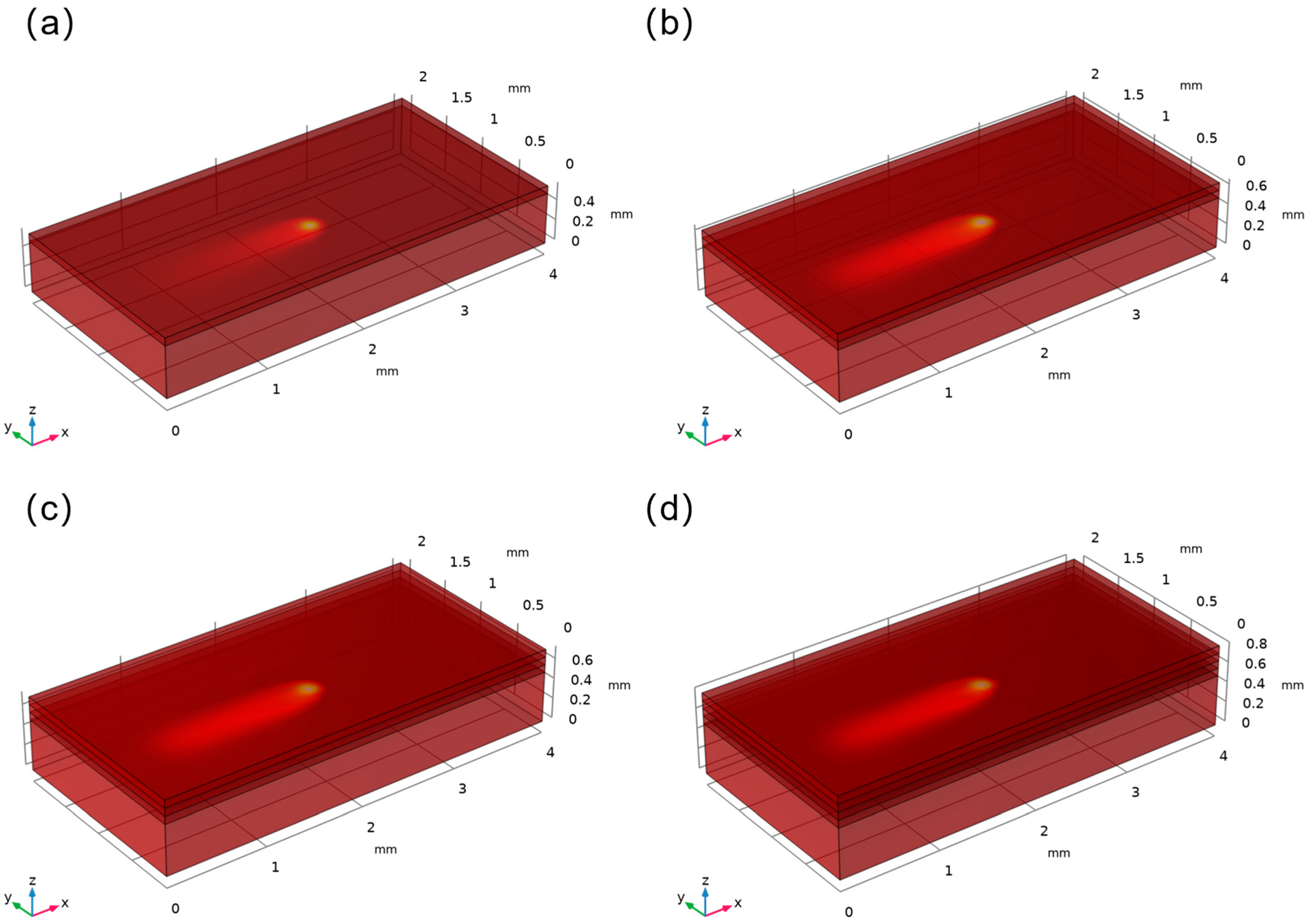
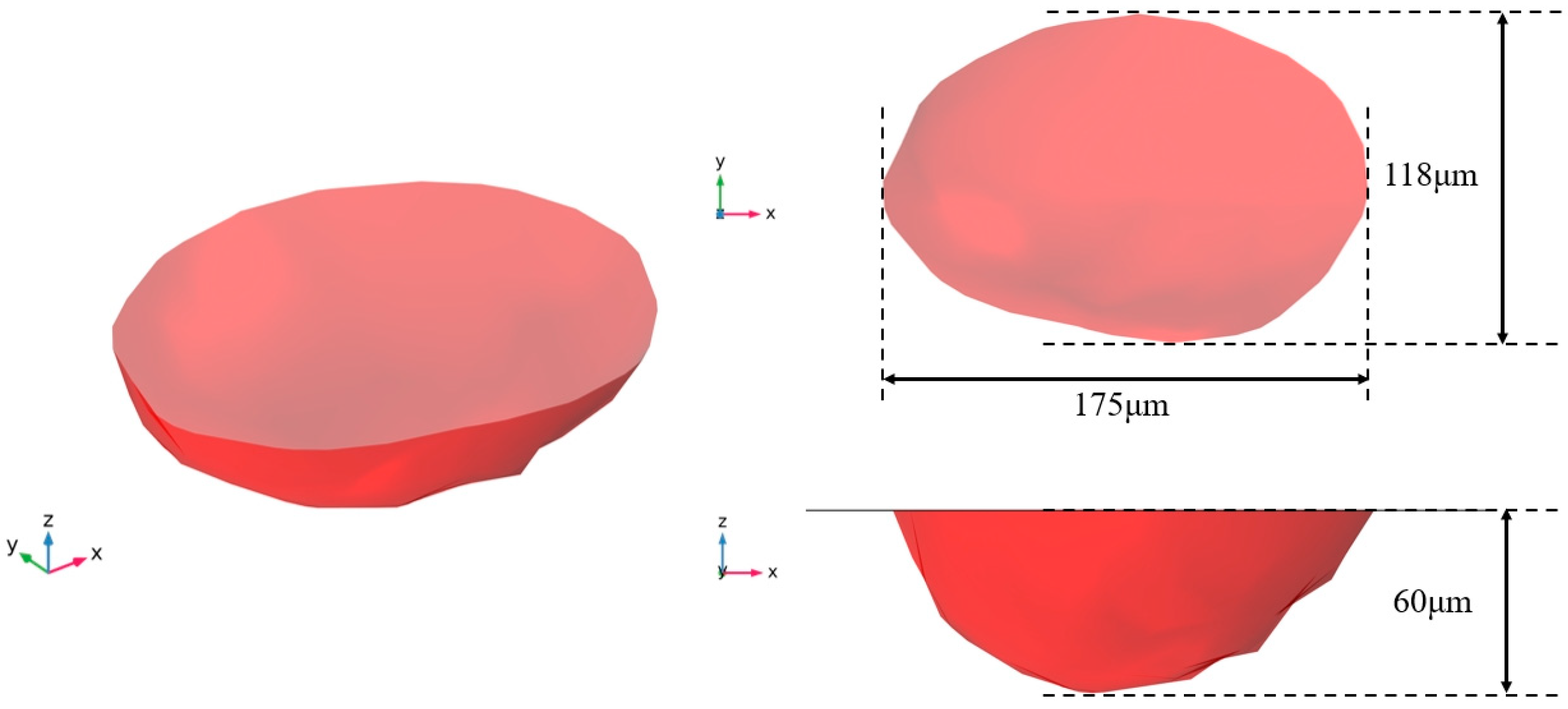
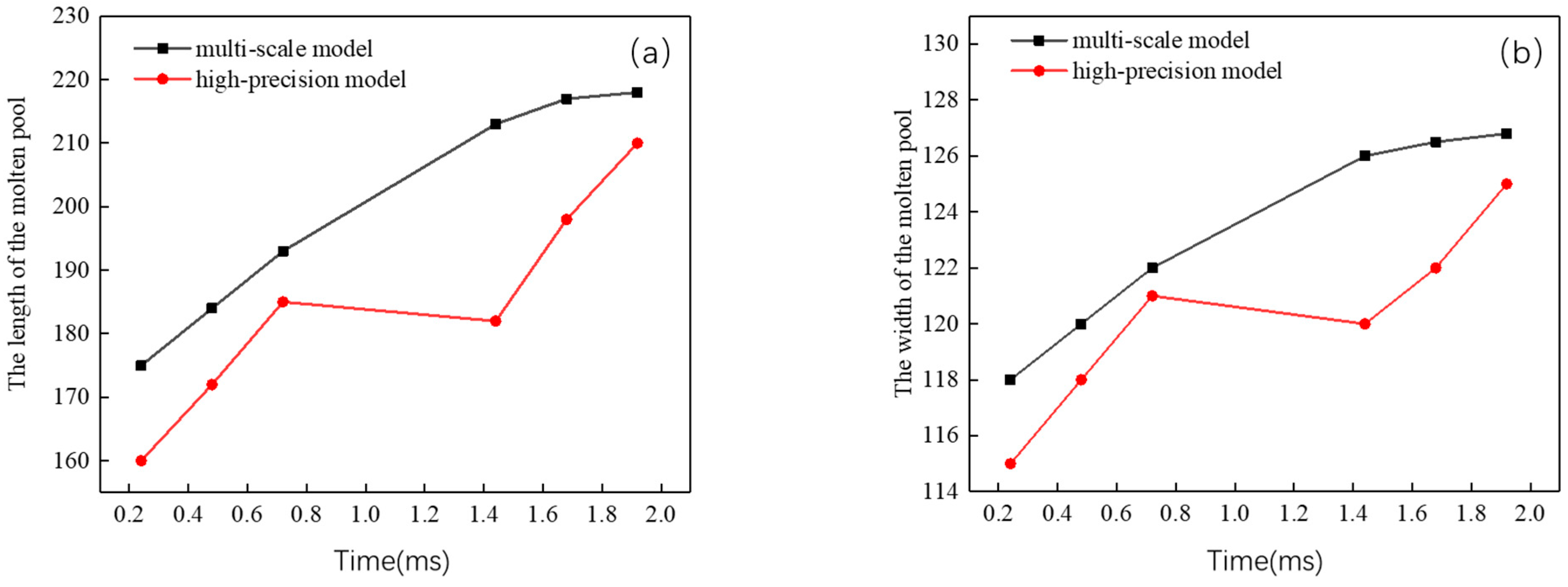
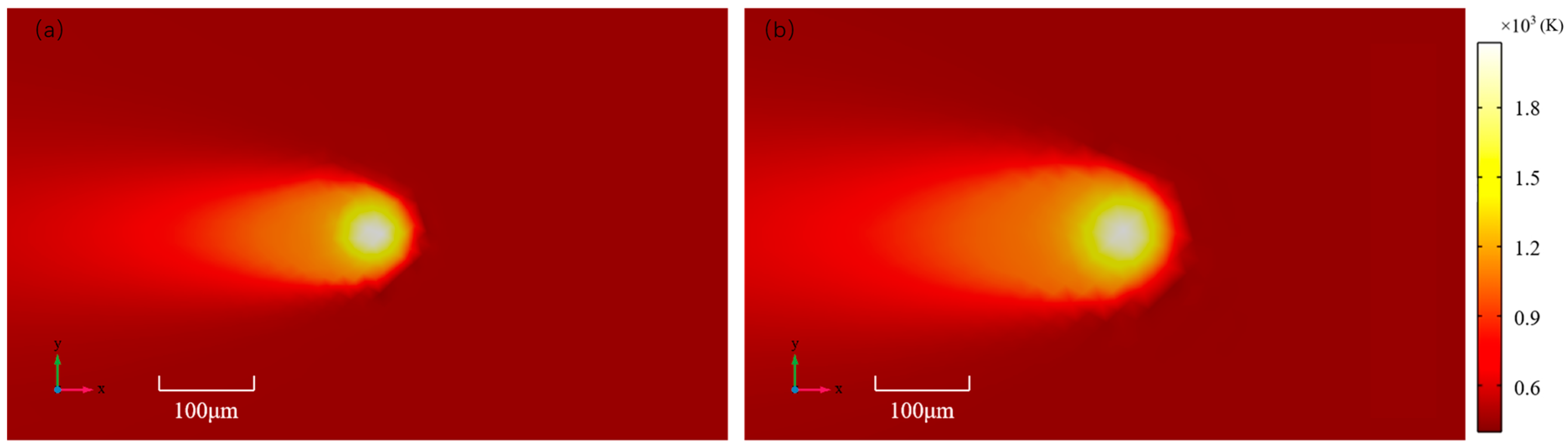
3.5. Validation of Numerical Simulation of SLM Multiscale Melt Channel Formation
4. Analysis of Heat Transfer Process in SLM Multiscale Melt Channel Formation
4.1. Liquidity Equivalence Characterisation
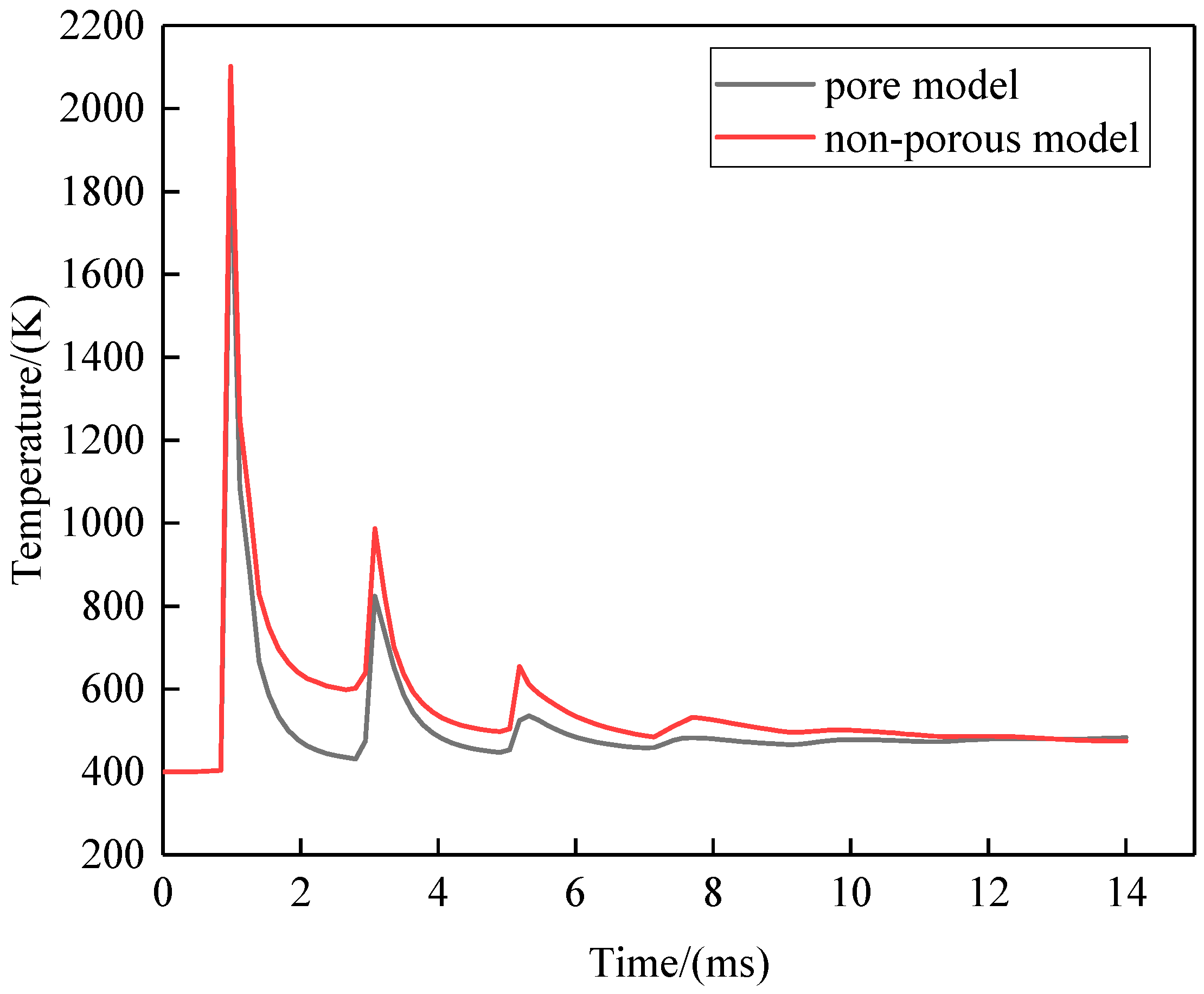
4.2. Pore Model Characterisation
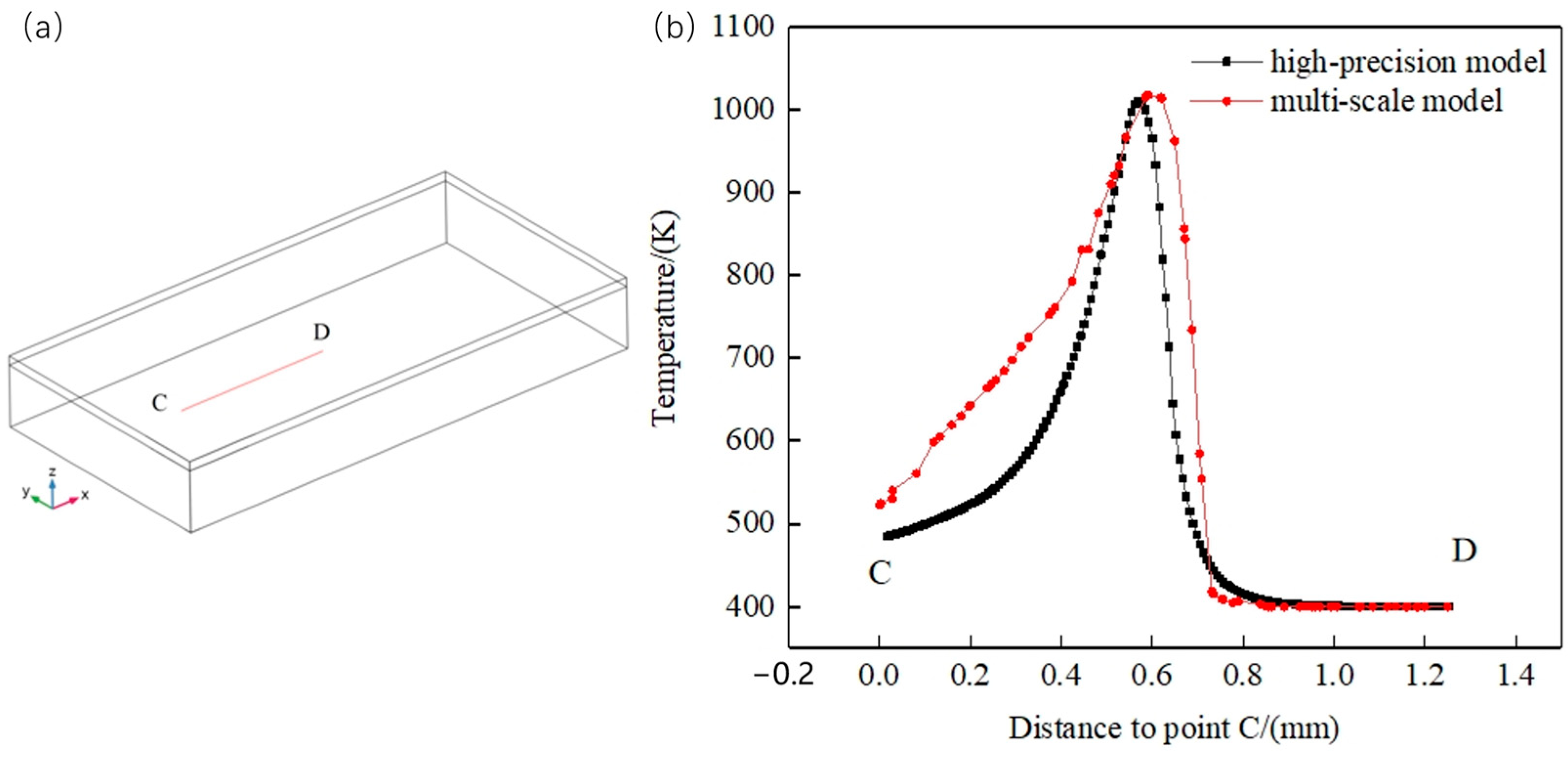
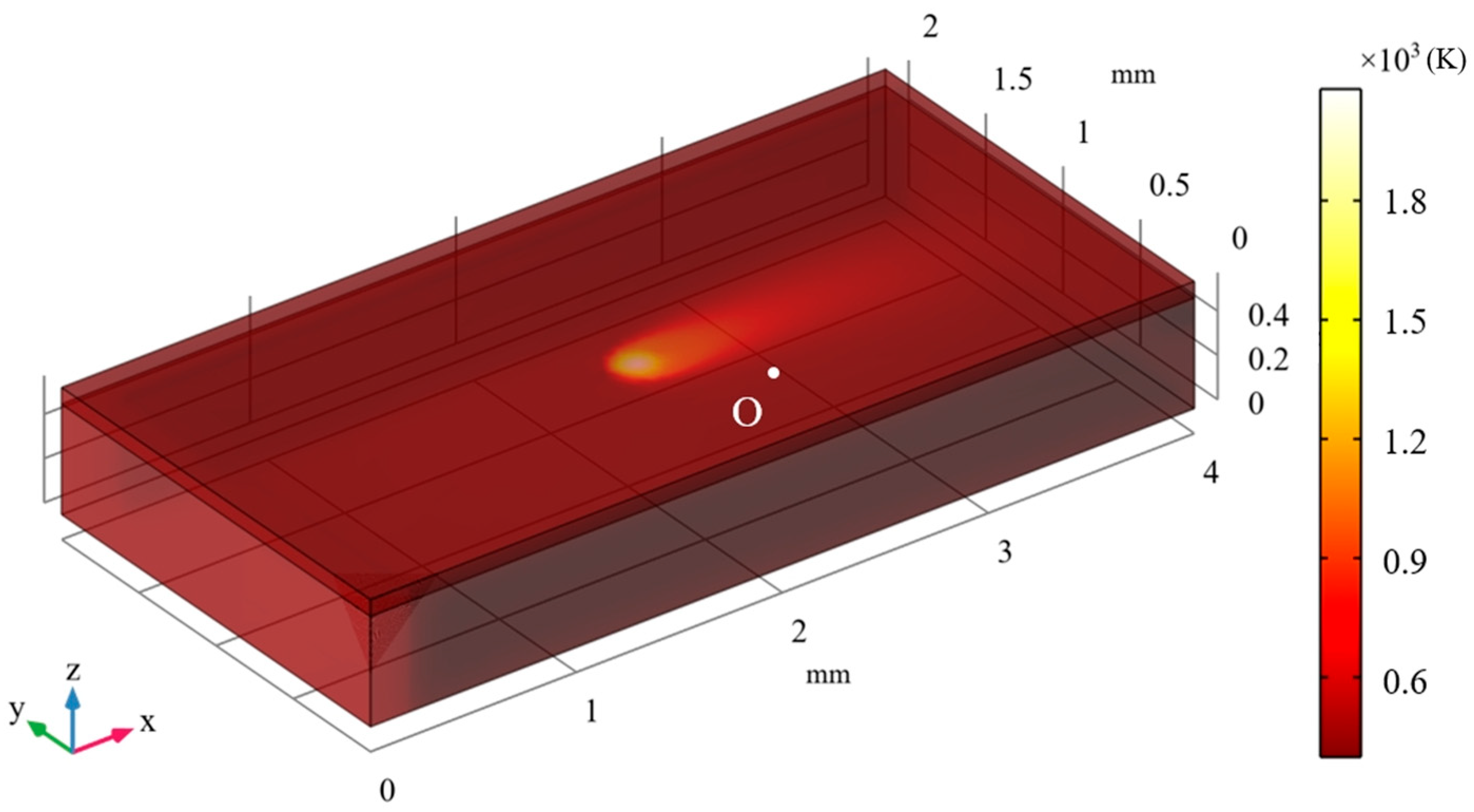
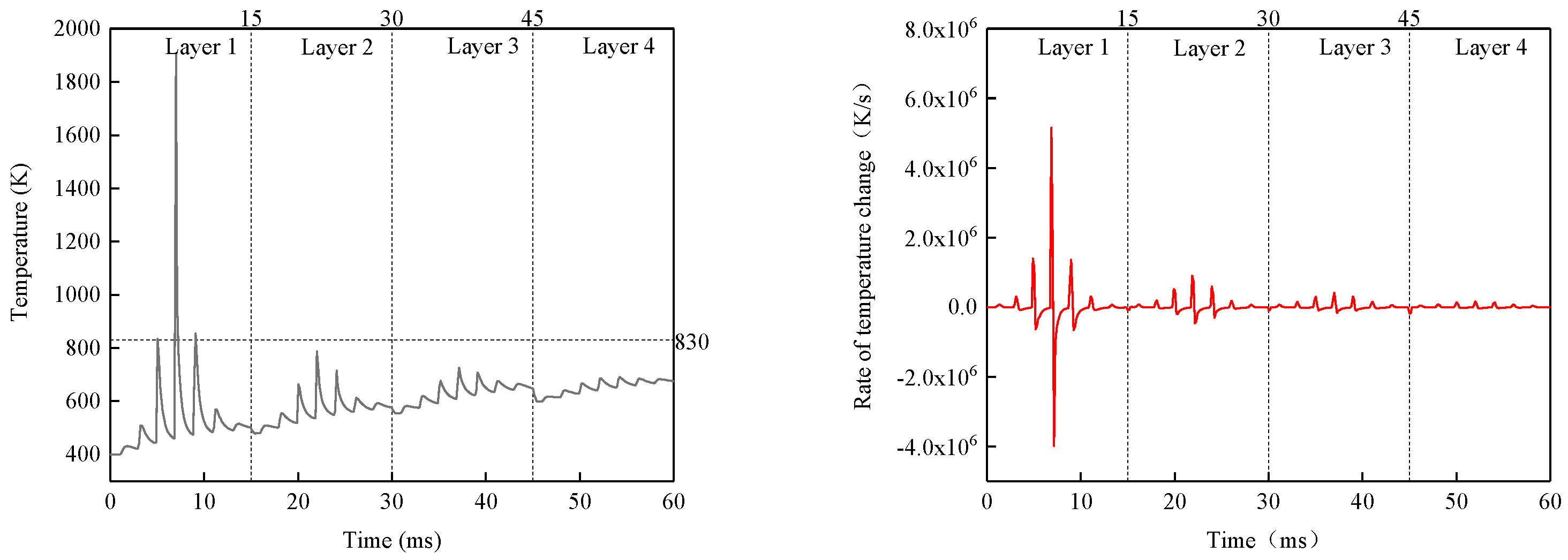
4.3. Evolution of Temperature Field in Multilayer Melt Channel Formation
4.4. Evolution of Melt Pool Characteristics
5. Conclusions
- (1)
- A numerical model of SLM single-layer melt-channel-forming process is constructed based on hydrodynamic theory for AlSi10Mg metallic materials, and the evolution of melt pool morphology during the SLM formation process of AlSi10Mg materials is investigated, and the validity of the numerical simulation method is verified through the melt-channel-forming experiments.
- (2)
- A more computationally efficient multiscale numerical model is established for the SLM multilayer melt-channel-forming process, and a binarised spatial stochastic function is used to simulate the formation of pores in the deposition region, and the simulation errors on the melt pool dimensions are small, with an average error on the melt pool length of 6.77% and an average error on the melt pool width of 1.69%.
- (3)
- The Marangoni convection effect increases the melt pool size, and the presence of pores significantly affects the evolution of the temperature field in the powder bed. With laser scanning and powder bed stacking, the peak melt pool temperature in the centre of the powder bed grows from 1643 K in the first layer to 2310 K in the fourth layer, and the melt pool length, width, and height dimensions increase by 44.9%, 21.7%, and 33.8%, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Glodez, S.; Klemenc, J.; Zupanic, F.; Vesenjak, M. High-cycle fatigue and fracture behaviours of SLM AlSi10Mg alloy. Trans. Nonferrous Met. Soc. China 2020, 30, 2577–2589. [Google Scholar] [CrossRef]
- Buchanan, C.; Gardner, L. Metal 3D printing in construction: A review of methods, research, applications, opportunities and challenges. Eng. Struct. 2019, 180, 332–348. [Google Scholar] [CrossRef]
- Zhang, J.; Song, B.; Wei, Q.; Bourell, D.; Shi, Y. A review of selective laser melting of aluminum alloys: Processing, microstructure, property and developing trends. J. Mater. Sci. Technol. 2019, 35, 270–284. [Google Scholar] [CrossRef]
- Wu, J.; Wang, X.Q.; Wang, W.; Attallah, M.M.; Loretto, M.H. Microstructure and strength of selectively laser melted AlSi10Mg. Acta Mater. 2016, 117, 311–320. [Google Scholar] [CrossRef]
- Gatto, A.; Cappelletti, C.; Defanti, S.; Fabbri, F. The Corrosion Behaviour of Additively Manufactured AlSi10Mg Parts Compared to Traditional Al Alloys. Metals 2023, 13, 913. [Google Scholar] [CrossRef]
- Li, B.-Q.; Li, Z.; Bai, P.; Liu, B.; Kuai, Z. Research on Surface Roughness of AlSi10Mg Parts Fabricated by Laser Powder Bed Fusion. Metals 2018, 8, 524. [Google Scholar] [CrossRef]
- Li, Z.; Kuai, Z.; Bai, P.; Nie, Y.; Fu, G.; Liu, W.; Yang, S. Microstructure and Tensile Properties of AlSi10Mg Alloy Manufactured by Multi-Laser Beam Selective Laser Melting (SLM). Metals 2019, 9, 1337. [Google Scholar] [CrossRef]
- Pelevin, I.A.; Ozherelkov, D.Y.; Nalivaiko, A.Y.; Bodyakova, A.I.; Chernyshikhin, S.V.; Zotov, B.O.; Korshunov, A.V.; Gromov, A.A. AlSi10Mg/AlN Interface Grain Structure after Laser Powder Bed Fusion. Metals 2022, 12, 2152. [Google Scholar] [CrossRef]
- Buchbinder, D.; Meiners, W.; Pirch, N.; Wissenbach, K.; Schrage, J. Investigation on reducing distortion by preheating during manufacture of aluminum components using selective laser melting. J. Laser Appl. 2014, 26, 012004. [Google Scholar] [CrossRef]
- Louvis, E.; Fox, P.; Sutcliffe, C.J. Selective laser melting of aluminium components. J. Mater. Process. Technol. 2011, 211, 275–284. [Google Scholar] [CrossRef]
- Megahed, S.; Buehring, J.; Duffe, T.; Bach, A.; Schroeder, K.-U.; Schleifenbaum, J.H. Effect of Heat Treatment on Ductility and Precipitation Size of Additively Manufactured AlSi10Mg. Metals 2022, 12, 1311. [Google Scholar] [CrossRef]
- Awd, M.; Stern, F.; Kampmann, A.; Kotzem, D.; Tenkamp, J.; Walther, F. Microstructural Characterization of the Anisotropy and Cyclic Deformation Behavior of Selective Laser Melted AlSi10Mg Structures. Metals 2018, 8, 825. [Google Scholar] [CrossRef]
- Li, R.; Shi, Y.; Liu, J.; Yao, H.; Zhang, W. Effects of processing parameters on the temperature field of selective laser melting metal powder. Powder Metall. Met. Ceram. 2009, 48, 186–195. [Google Scholar] [CrossRef]
- Ye, J.; Khairallah, S.A.; Rubenchik, A.M.; Crumb, M.F.; Matthews, M.J. Energy Coupling Mechanisms and Scaling Behavior Associated with Laser Powder Bed Fusion Additive Manufacturing. Adv. Eng. Mater. 2019, 21, 1900185. [Google Scholar] [CrossRef]
- Roberts, I.A.; Wang, C.J.; Esterlein, R.; Stanford, M.; Mynors, D.J. A three-dimensional finite element analysis of the temperature field during laser melting of metal powders in additive layer manufacturing. Int. J. Mach. Tools Manuf. 2009, 49, 916–923. [Google Scholar] [CrossRef]
- Zhanyong, Z.; Liang, L.; Le, T.; Peikang, B.; Jing, L.; Liyun, W.; Haihong, L.; Yahui, C. Simulation of Stress Field during the Selective Laser Melting Process of the Nickel-Based Superalloy, GH4169. Materials 2018, 11, 1525. [Google Scholar] [CrossRef] [PubMed]
- Körner, C.; Attar, E.; Heinl, P. Mesoscopic simulation of selective beam melting processes. J. Mater. Process. Technol. 2011, 211, 978–987. [Google Scholar] [CrossRef]
- Khairallah, S.A.; Anderson, A. Mesoscopic simulation model of selective laser melting of stainless steel powder. J. Mater. Process. Technol. 2014, 214, 2627–2636. [Google Scholar] [CrossRef]
- Ly, S.; Rubenchik, A.M.; Khairallah, S.A.; Guss, G.; Matthews, M.J. Metal vapor micro-jet controls material redistribution in laser powder bed fusion additive manufacturing. Sci. Rep. 2017, 7, 4085. [Google Scholar] [CrossRef]
- Qiu, C.; Panwisawas, C.; Ward, M.; Basoalto, H.C.; Brooks, J.W.; Attallah, M.M. On the role of melt flow into the surface structure and porosity development during selective laser melting. Acta Mater. 2015, 96, 72–79. [Google Scholar] [CrossRef]
- Panwisawas, C.; Qiu, C.; Anderson, M.J.; Sovani, Y.; Turner, R.P.; Attallah, M.M.; Brooks, J.W.; Basoalto, H.C. Mesoscale modelling of selective laser melting: Thermal fluid dynamics and microstructural evolution. Comput. Mater. Sci. 2017, 126, 479–490. [Google Scholar] [CrossRef]
- Shrestha, S.; Chou, K. A build surface study of Powder-Bed Electron Beam Additive Manufacturing by 3D thermo-fluid simulation and white-light interferometry. Int. J. Mach. Tools Manuf. 2017, 121, 37–49. [Google Scholar] [CrossRef]
- Tang, C.; Tan, J.L.; Wong, C.H. A numerical investigation on the physical mechanisms of single track defects in selective laser melting. Int. J. Heat Mass Transf. 2018, 126, 957–968. [Google Scholar] [CrossRef]
- Klassen, A.; Scharowsky, T.; Koerner, C. Evaporation model for beam based additive manufacturing using free surface lattice Boltzmann methods. J. Phys. D Appl. Phys. 2014, 47, 275303. [Google Scholar] [CrossRef]
- Wang, L.; Yan, W. Thermoelectric Magnetohydrodynamic Model for Laser-Based Metal Additive Manufacturing. Phys. Rev. Appl. 2021, 15, 064051. [Google Scholar] [CrossRef]
- Yin, J.; Zhu, H.; Ke, L.; Lei, W.; Dai, C.; Zuo, D. Simulation of temperature distribution in single metallic powder layer for laser micro-sintering. Comput. Mater. Sci. 2012, 53, 333–339. [Google Scholar] [CrossRef]
- Lampa, C.; Kaplan, A.F.; Powell, J.; Magnusson, C. An analytical thermodynamic model of laser welding. J. Phys. D Appl. Phys. 1997, 30, 1293. [Google Scholar] [CrossRef]
- Nikam, S.H.; Jain, N.K. Three-dimensional thermal analysis of multi-layer metallic deposition by microplasma transferred arc process using finite element simulation. J. Mater. Process. Technol. 2017, 249, 264–273. [Google Scholar] [CrossRef]
- Nikam, S.H.; Quinn, J.; McFadden, S. A simplified thermal approximation method to include the effects of Marangoni convection in the melt pools of processes that involve moving point heat sources. Numer. Heat Transf. Part A Appl. 2021, 79, 537–552. [Google Scholar] [CrossRef]
- du Plessis, A. Effects of process parameters on porosity in laser powder bed fusion revealed by X-ray tomography. Addit. Manuf. 2019, 30, 100871. [Google Scholar] [CrossRef]



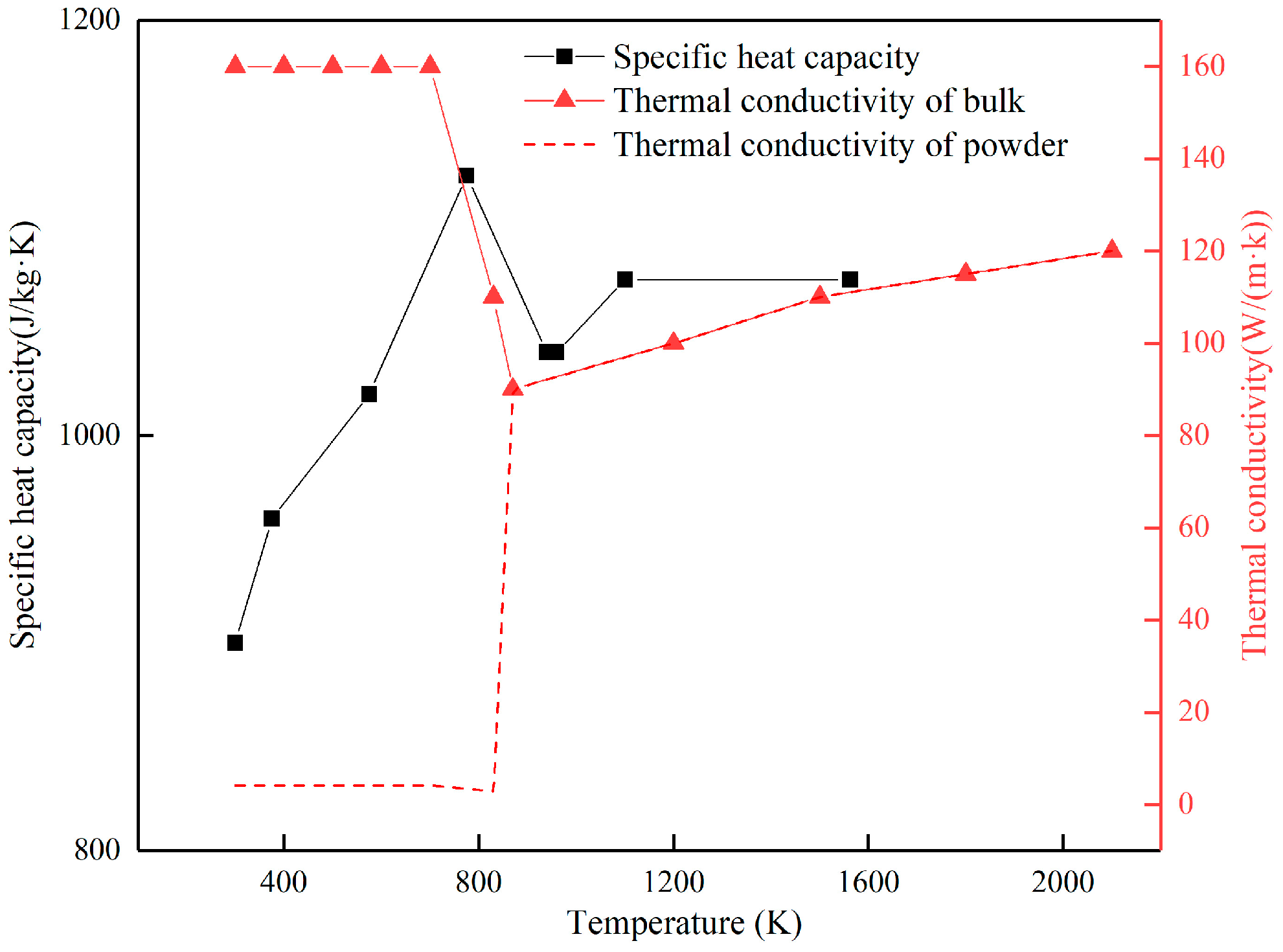
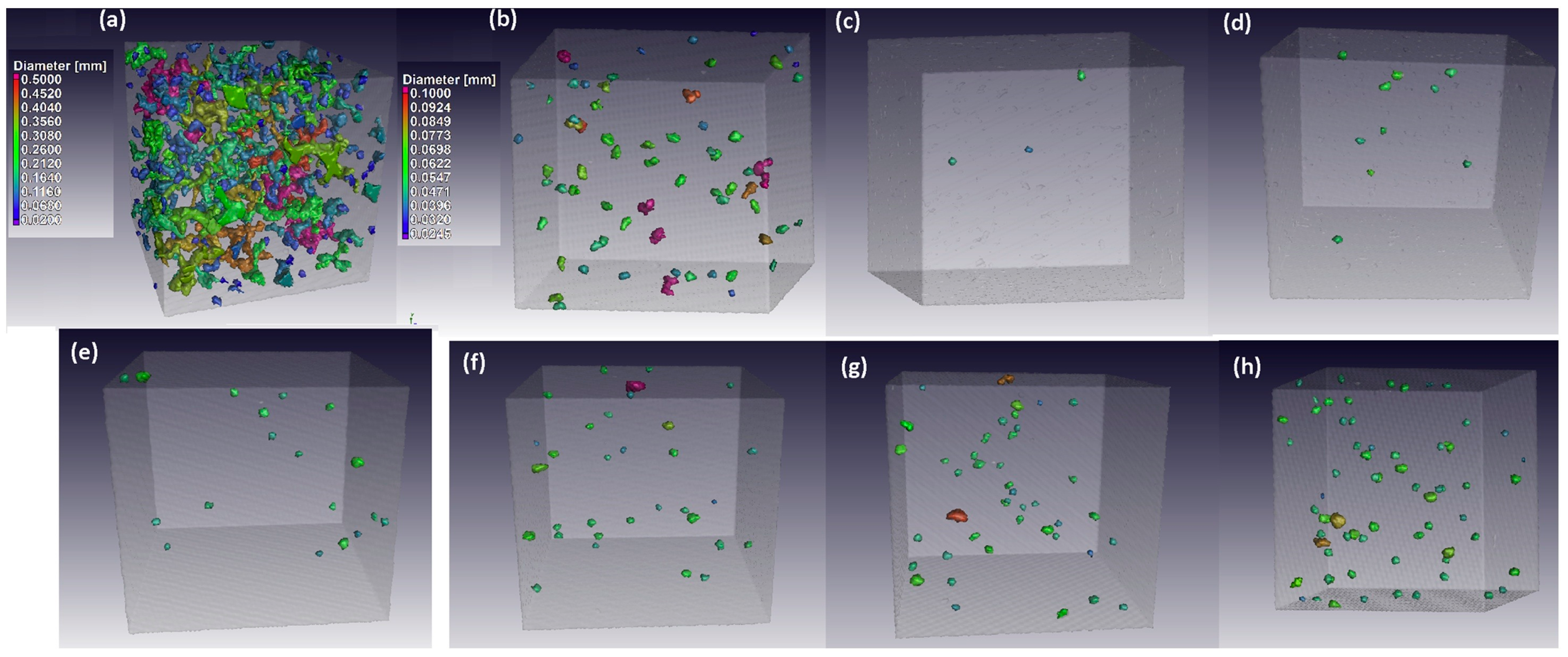
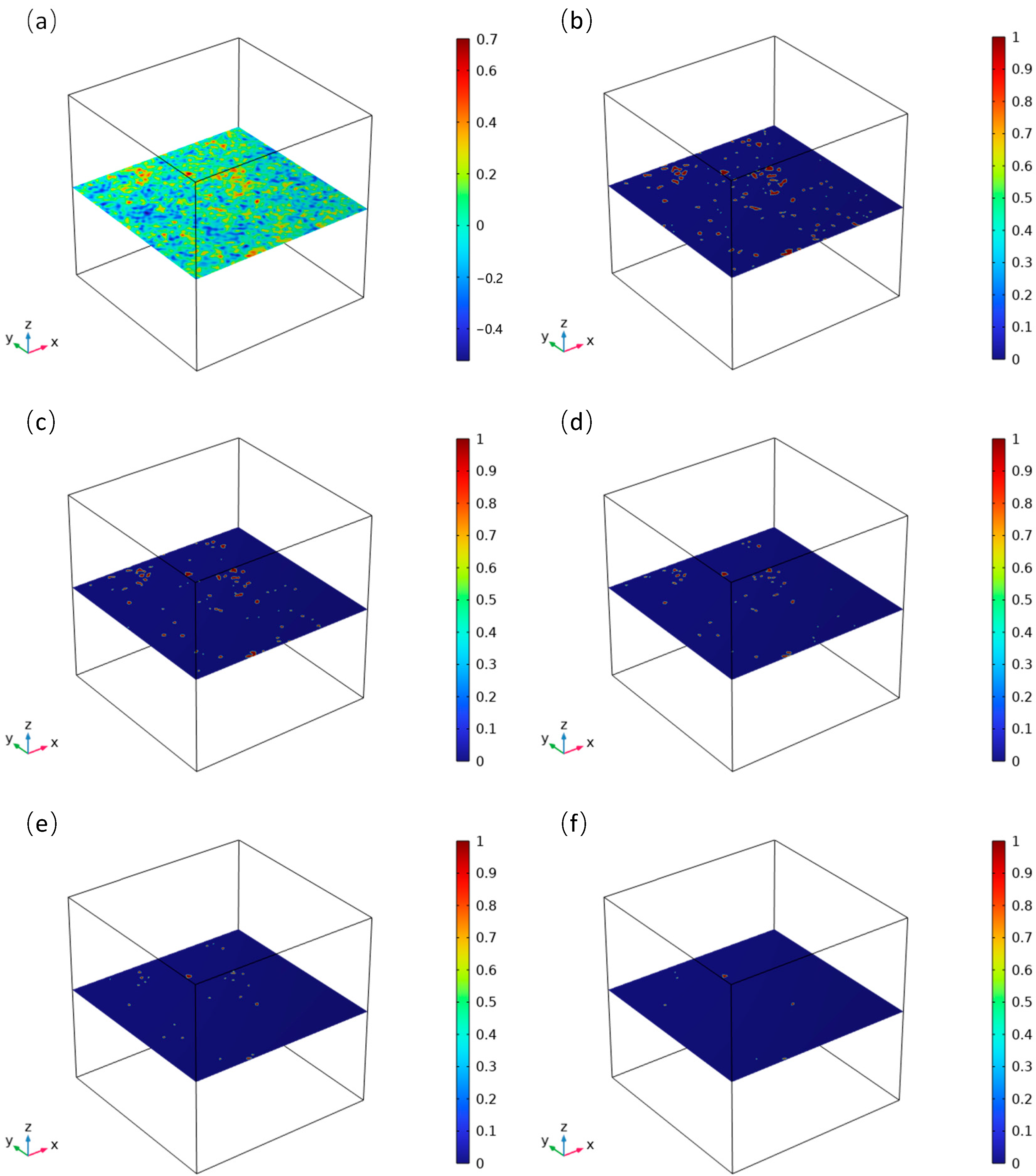
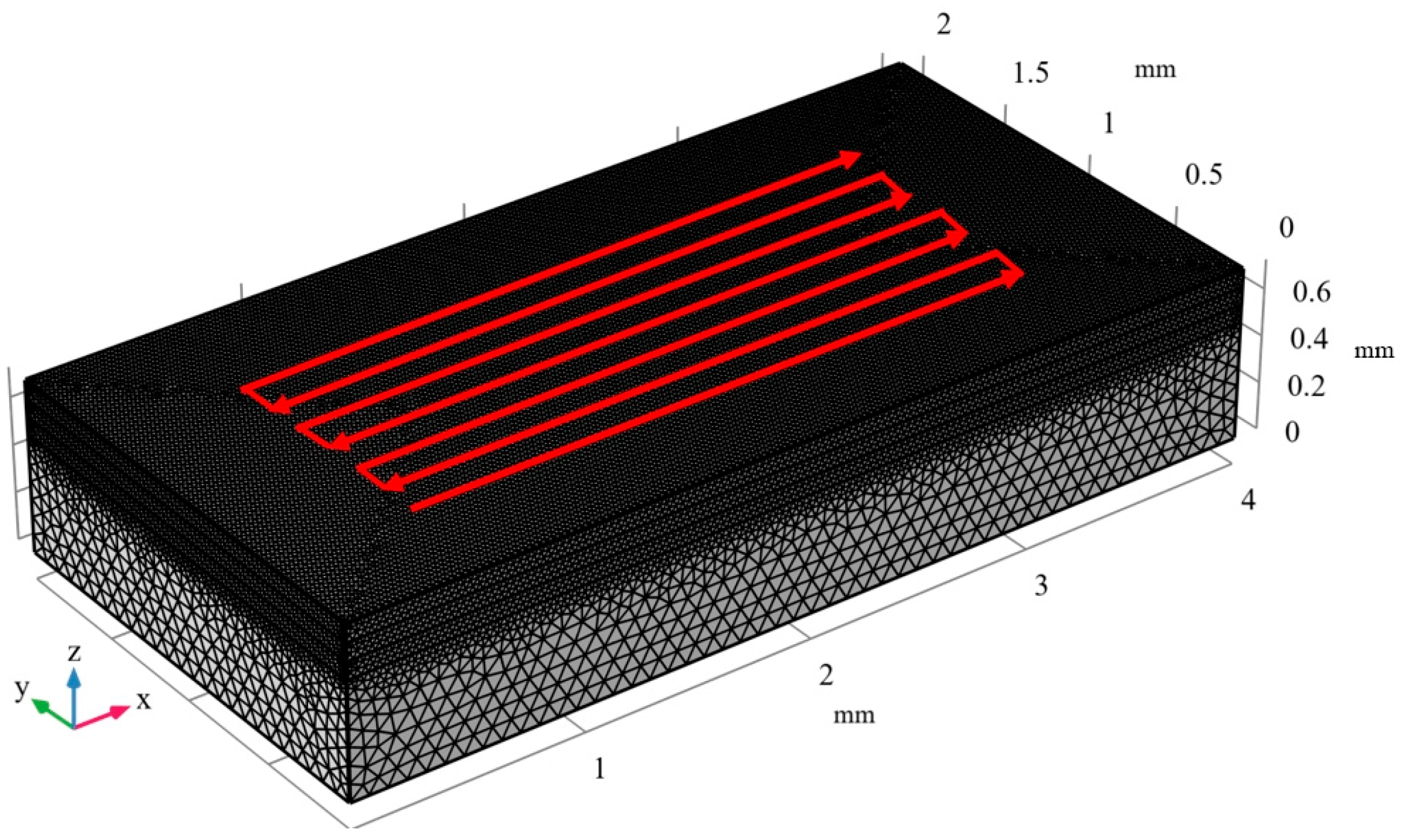



| Property | Value |
|---|---|
| Solidus temperature (Ts, K) | 830 |
| Liquidus temperature (Tl, K) | 870 |
| Boiling temperature (T1v, K) | 2743 |
| Latent heat of melting (ΔH, J/kg) | 3.89 × 105 |
| Latent heat of evaporation (ΔHv, J/kg) | 1.07 × 107 |
| Saturated vapor pressure (Pe, Pa) | 1.013 × 105 (Tb = 2743 K) |
| Surface tension coefficient (σ0, N/m) | 1.02 |
| Temperature sensitivity of surface tension (σT, N/(m·K)) | −3.1 × 10−4 |
| Convective heat transfer coefficient (hc, W/(m2·K)) | 82 |
| Radiation emissivity (ε) | 0.4 |
| Al | Si | Mg | Cu | Ni | V | Fe | Mn | Ti | Zn |
|---|---|---|---|---|---|---|---|---|---|
| rest | 10.3 | 0.35 | 0.20 | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 |
| Laser Power (W) | Powder Layer Thickness (μm) | Laser Radius (μm) | Scan Speed (mm/s) | Linear Energy Density (J/m) | Energy Density (J/mm3) | Melt Gap (μm) |
|---|---|---|---|---|---|---|
| 300 | 50 | 45 | 700 | 429 | 85.7 | 130 |
| 300 | 1000 | 300 | 60 | 130 | ||
| 300 | 1500 | 200 | 40 | 130 | ||
| 100 | 200 | 500 | 111 | 80 | ||
| 100 | 500 | 200 | 44.4 | 80 | ||
| 100 | 800 | 125 | 27.8 | 80 | ||
| 100 | 1000 | 100 | 22.2 | 80 |
| Characterisation | Length/(μm) | Width/(μm) | ||||
|---|---|---|---|---|---|---|
| Juncture/(ms) | 0.24 | 0.48 | 0.72 | 0.24 | 0.48 | 0.72 |
| Multiscale modelling of melt pools | 175 | 184 | 193 | 118 | 120 | 122 |
| High-precision model melting pool | 160 | 172 | 185 | 115 | 118 | 121 |
| Absolute error/(μm) | 15 | 12 | 8 | 3 | 2 | 1 |
| Relative error/(%) | 9.375 | 6.977 | 4.324 | 2.609 | 1.695 | 0.826 |
| Average relative error/(%) | 6.77 | 1.69 | ||||
| Position | First Layer | Second Layer | Third Floor | Fourth Floor |
|---|---|---|---|---|
| Peak temperature (K) | 1643 | 1920 | 2127 | 2310 |
| Raise temperature (K) | 277 | 207 | 183 | |
| Growth rate (%) | 16.9 | 10.8 | 8.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, F.; Yao, S.; Dong, Y.; Zheng, X.; Xie, M.; Yang, L.; Wang, D. Research on Multiscale Numerical Simulation Method for SLM Melting Process. Metals 2024, 14, 825. https://doi.org/10.3390/met14070825
Zou F, Yao S, Dong Y, Zheng X, Xie M, Yang L, Wang D. Research on Multiscale Numerical Simulation Method for SLM Melting Process. Metals. 2024; 14(7):825. https://doi.org/10.3390/met14070825
Chicago/Turabian StyleZou, Fan, Shuguang Yao, Yunhui Dong, Xin Zheng, Minhan Xie, Lei Yang, and Dongtao Wang. 2024. "Research on Multiscale Numerical Simulation Method for SLM Melting Process" Metals 14, no. 7: 825. https://doi.org/10.3390/met14070825
APA StyleZou, F., Yao, S., Dong, Y., Zheng, X., Xie, M., Yang, L., & Wang, D. (2024). Research on Multiscale Numerical Simulation Method for SLM Melting Process. Metals, 14(7), 825. https://doi.org/10.3390/met14070825





