Research on Microstructural Evolution Behavior of Ni-Based Single-Crystal Alloy with Re Based on Non-Linear Ultrasonic Lamb Wave and Molecular Dynamics Method
Abstract
:1. Introduction
1.1. Research Background
1.2. Research Status of Propagation Characteristics of Lamb Wave in NSC
1.3. Research Status of MD Simulation
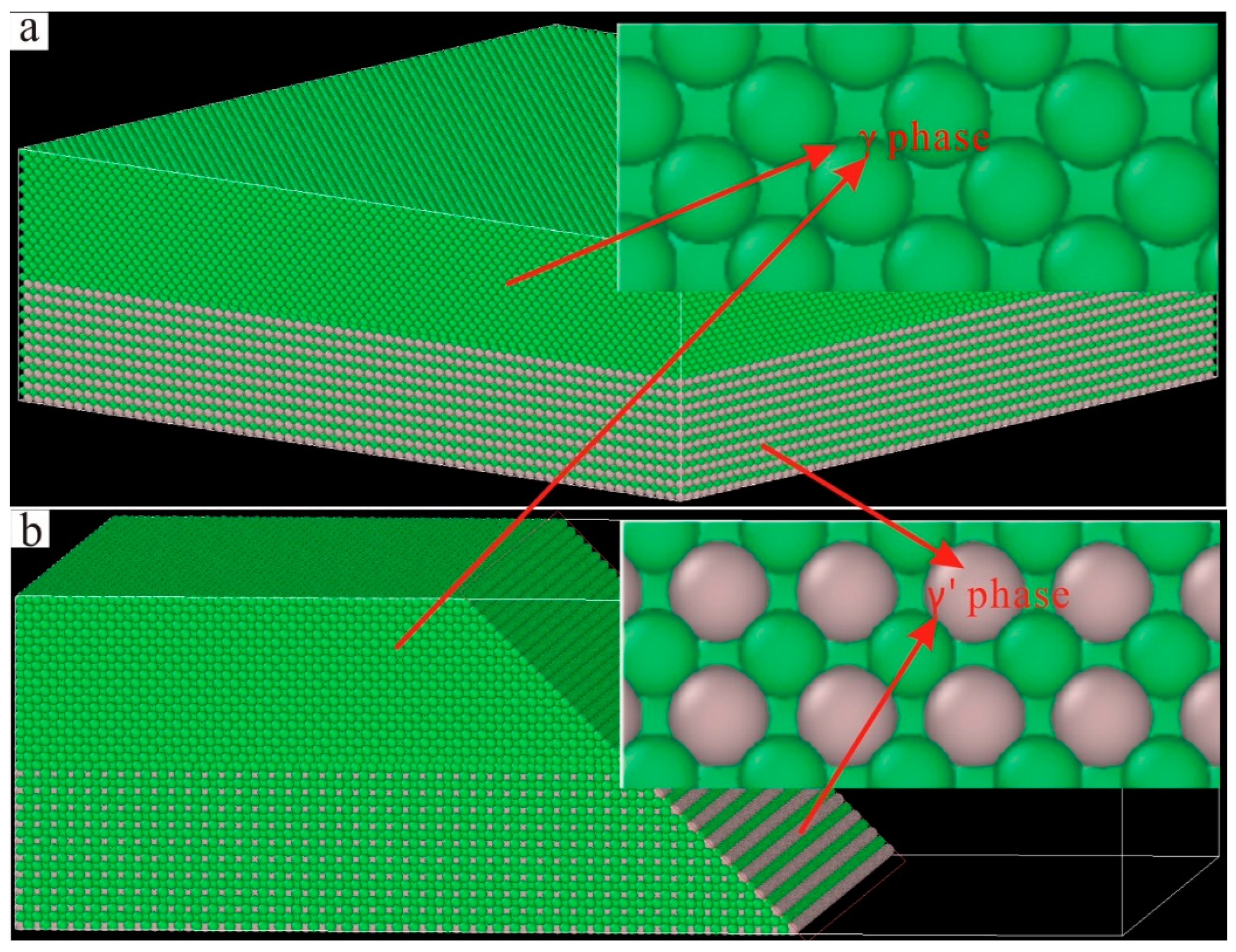
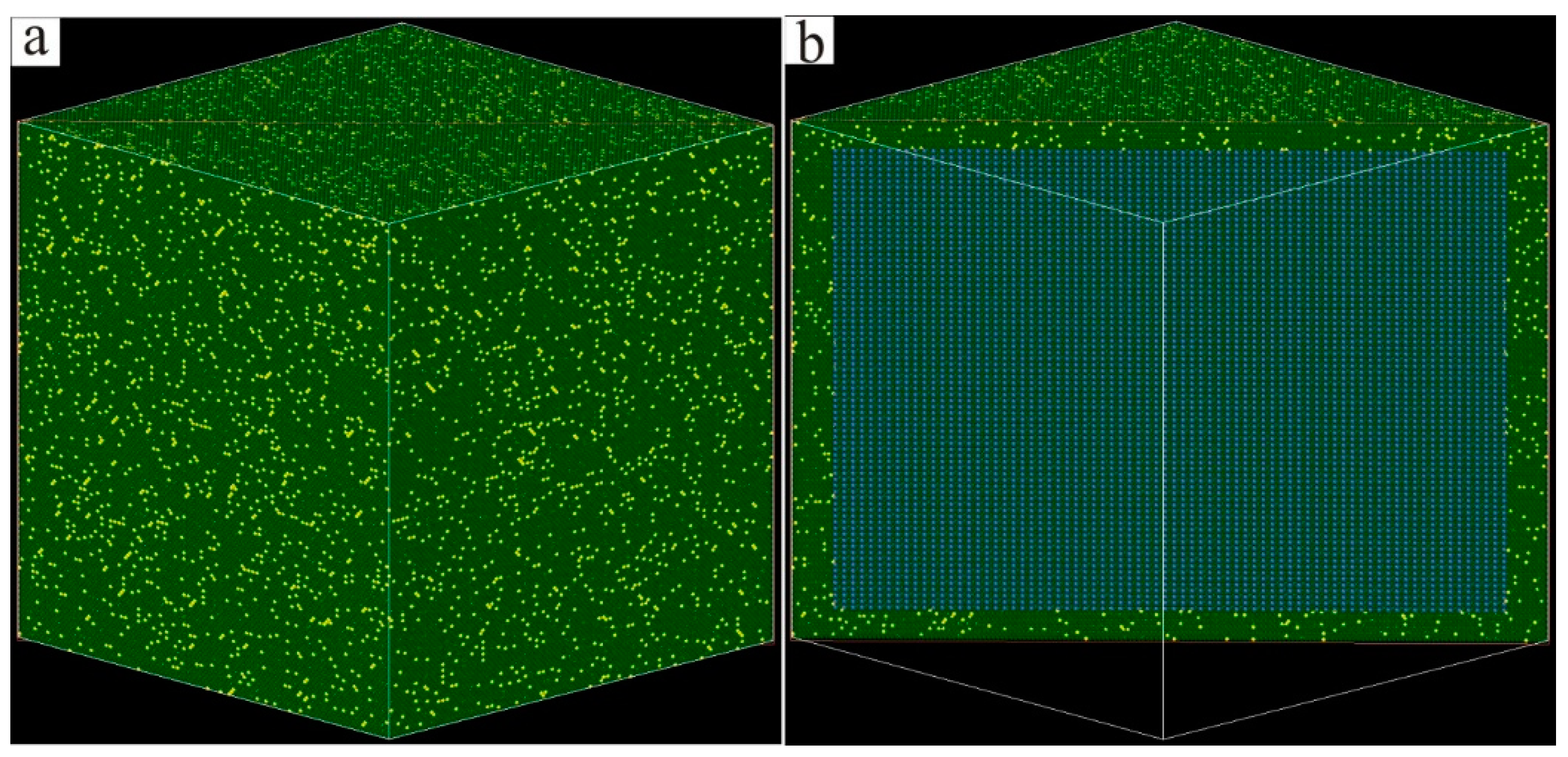
2. Research Methods
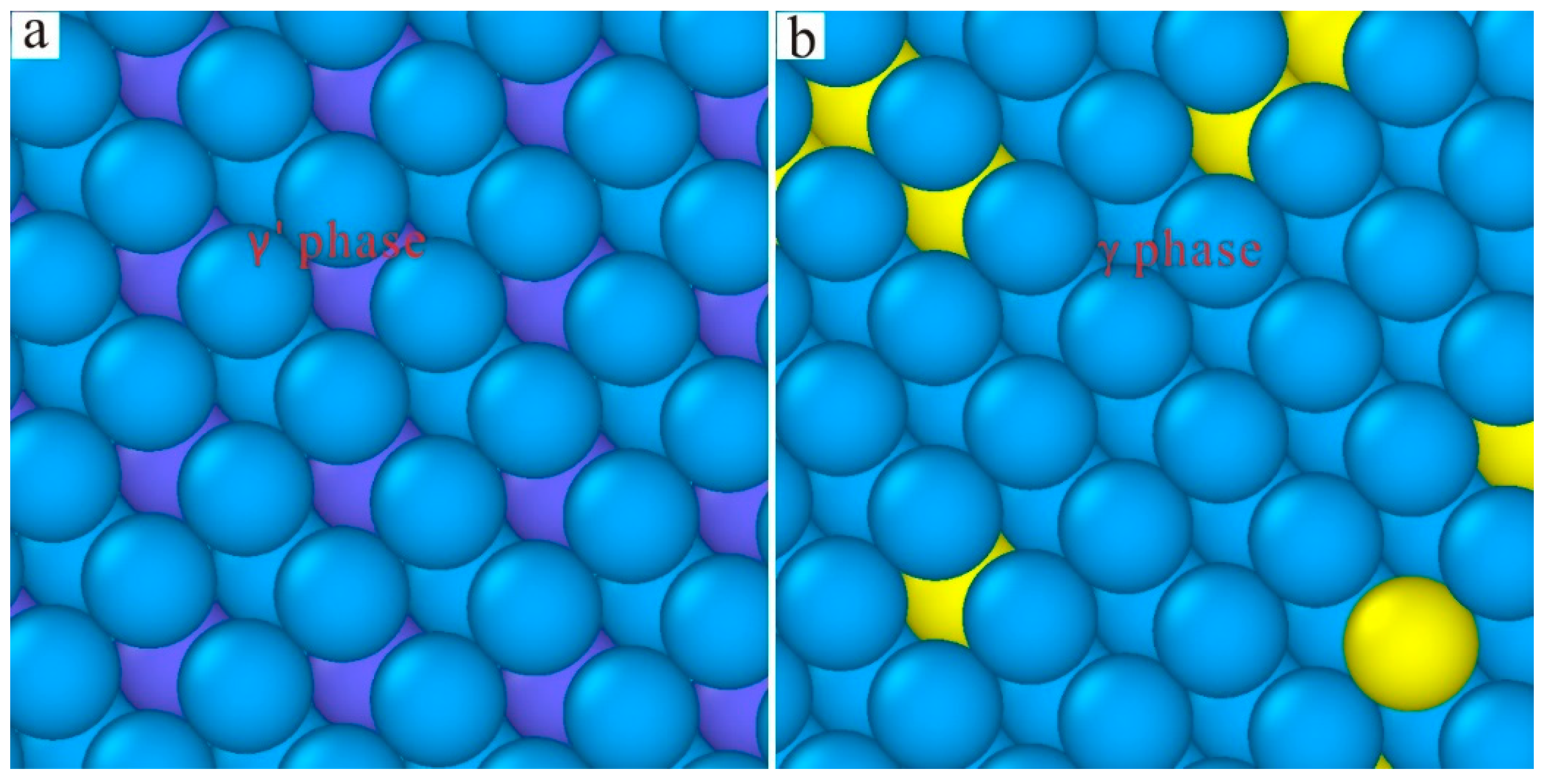
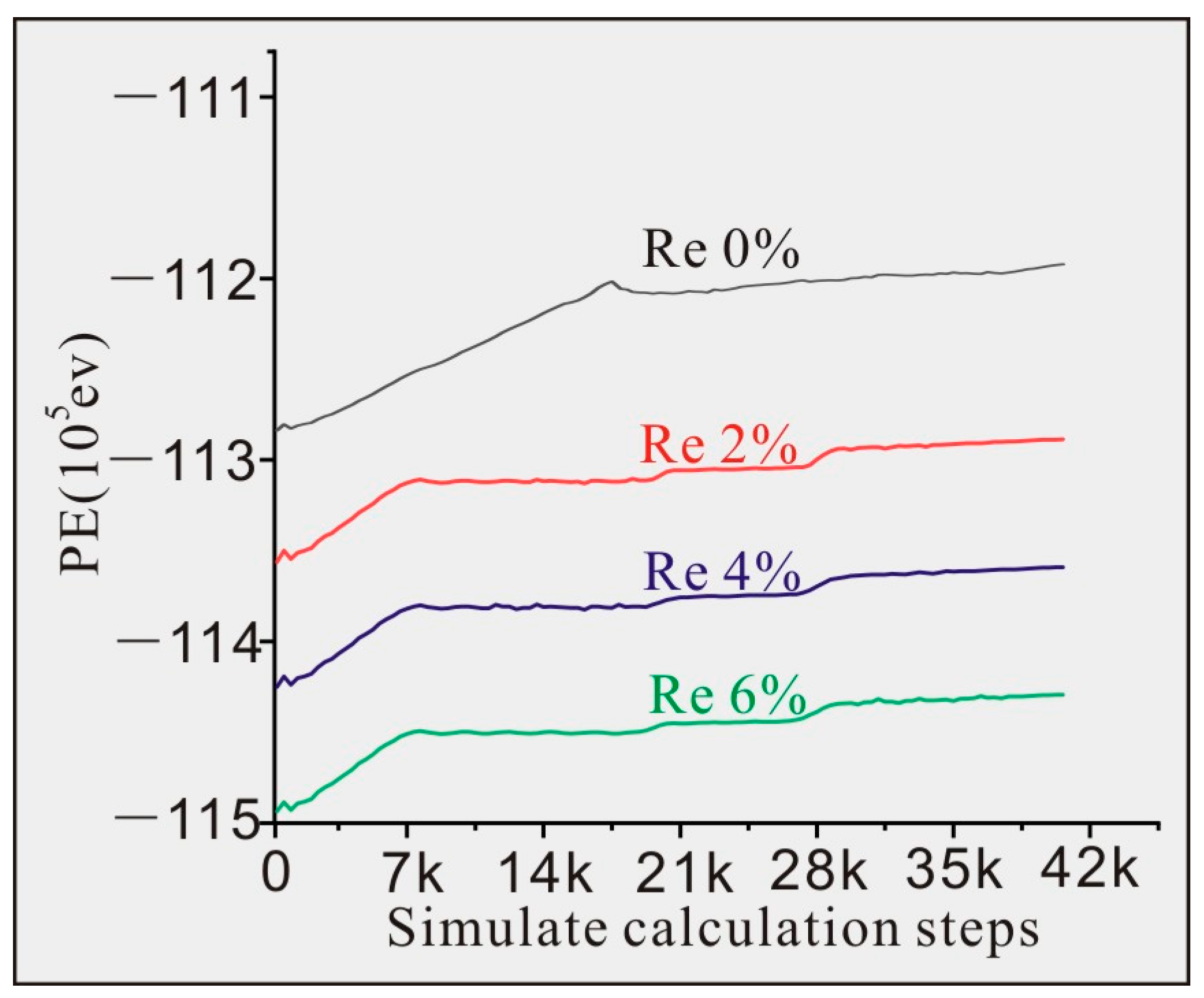
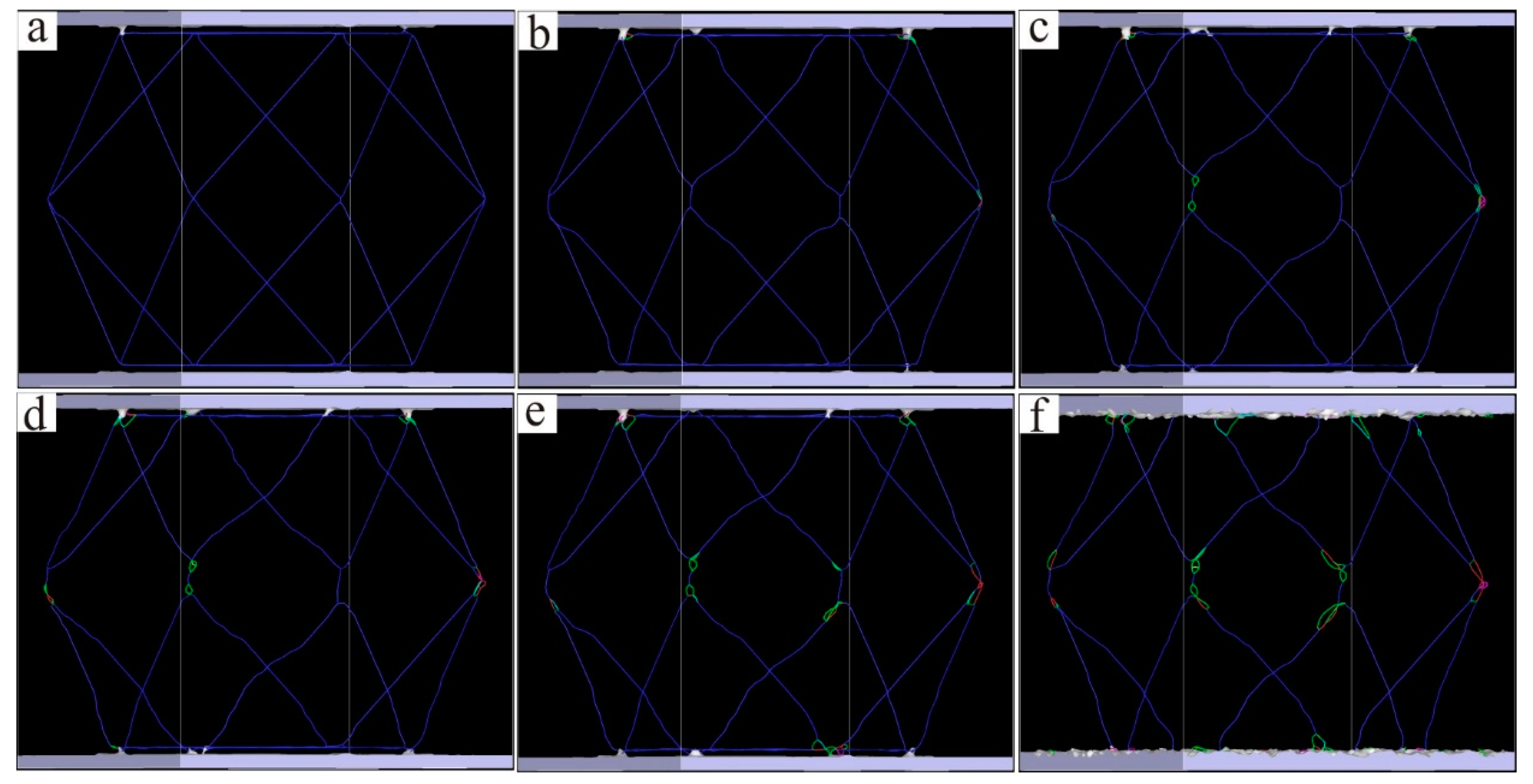
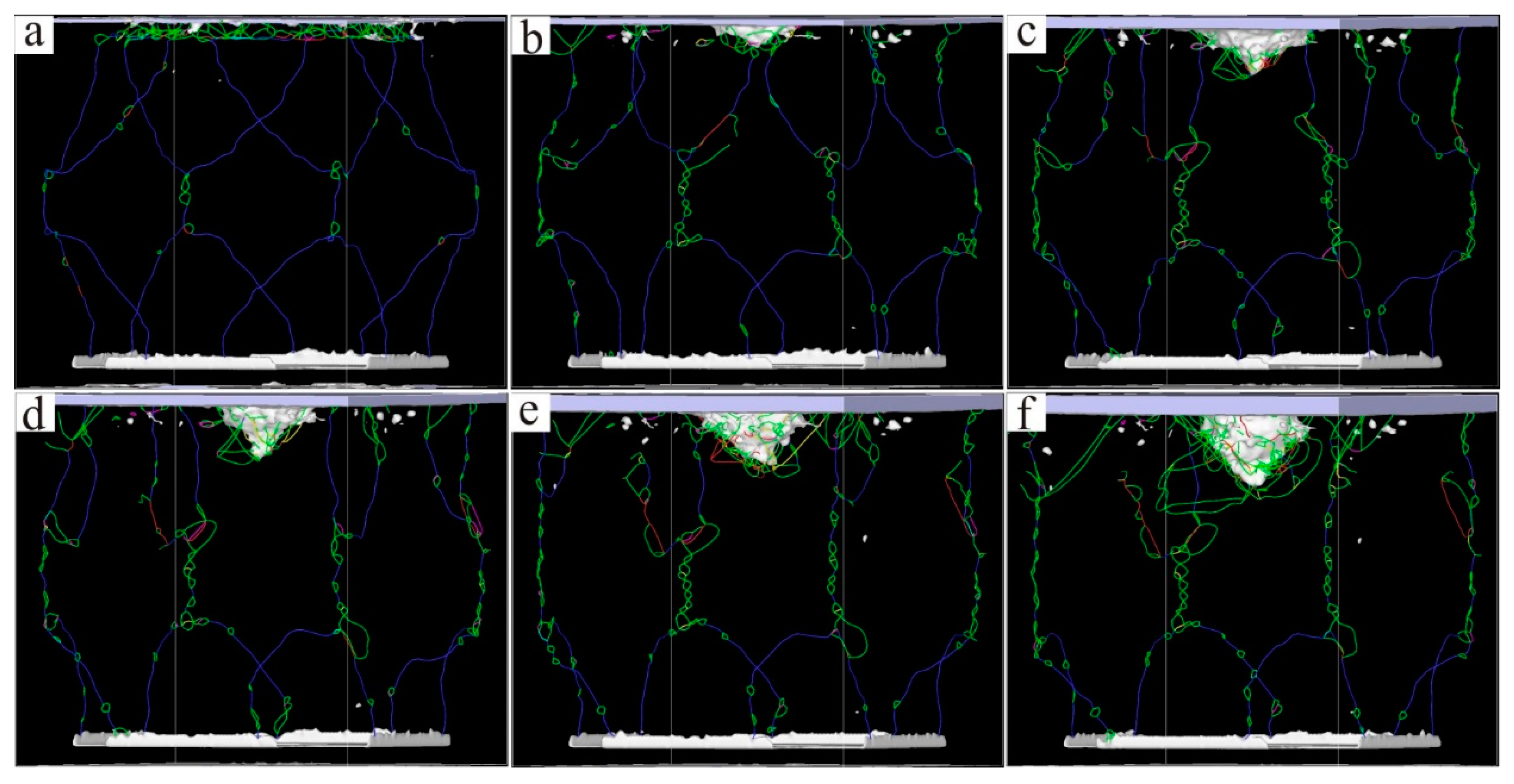
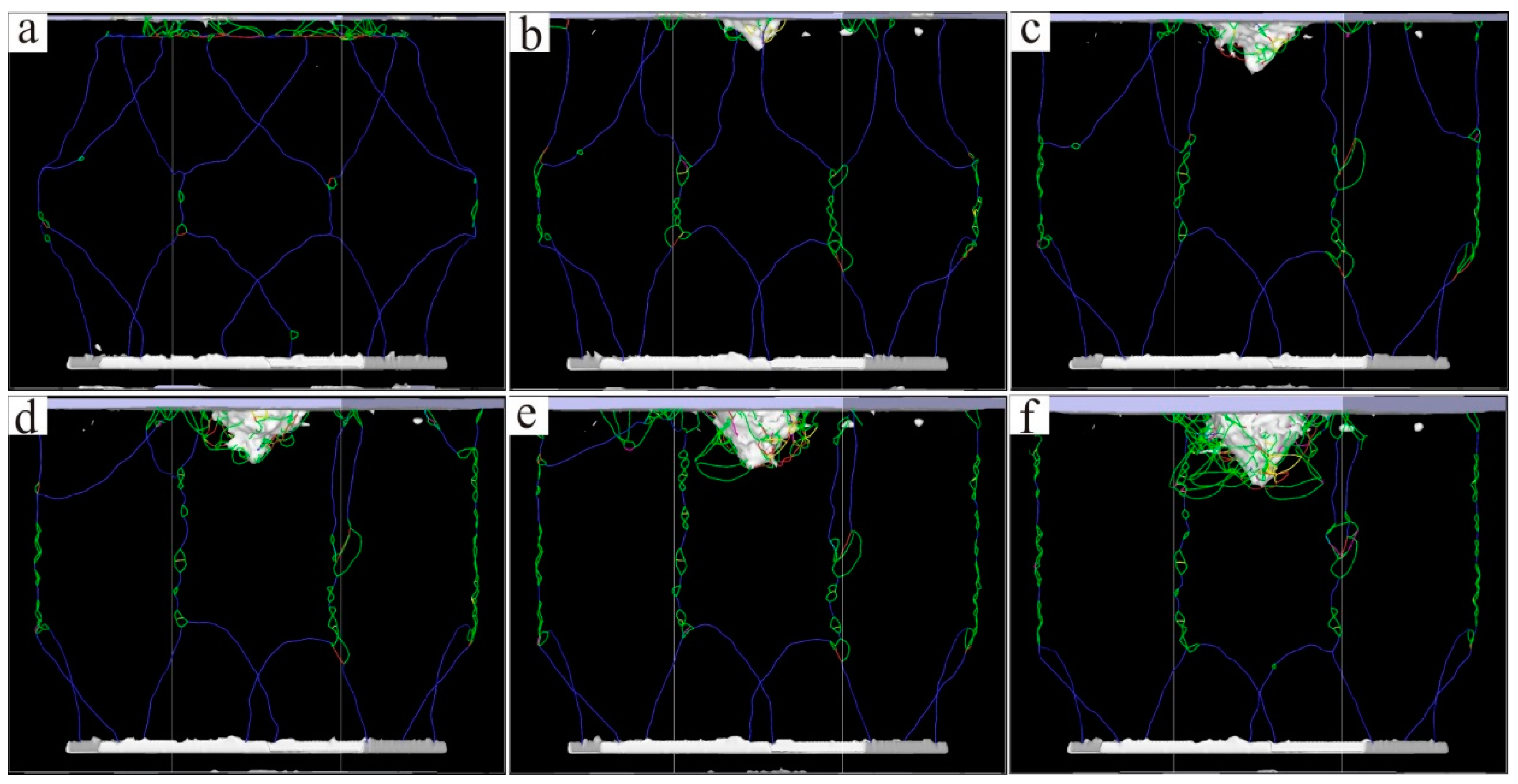
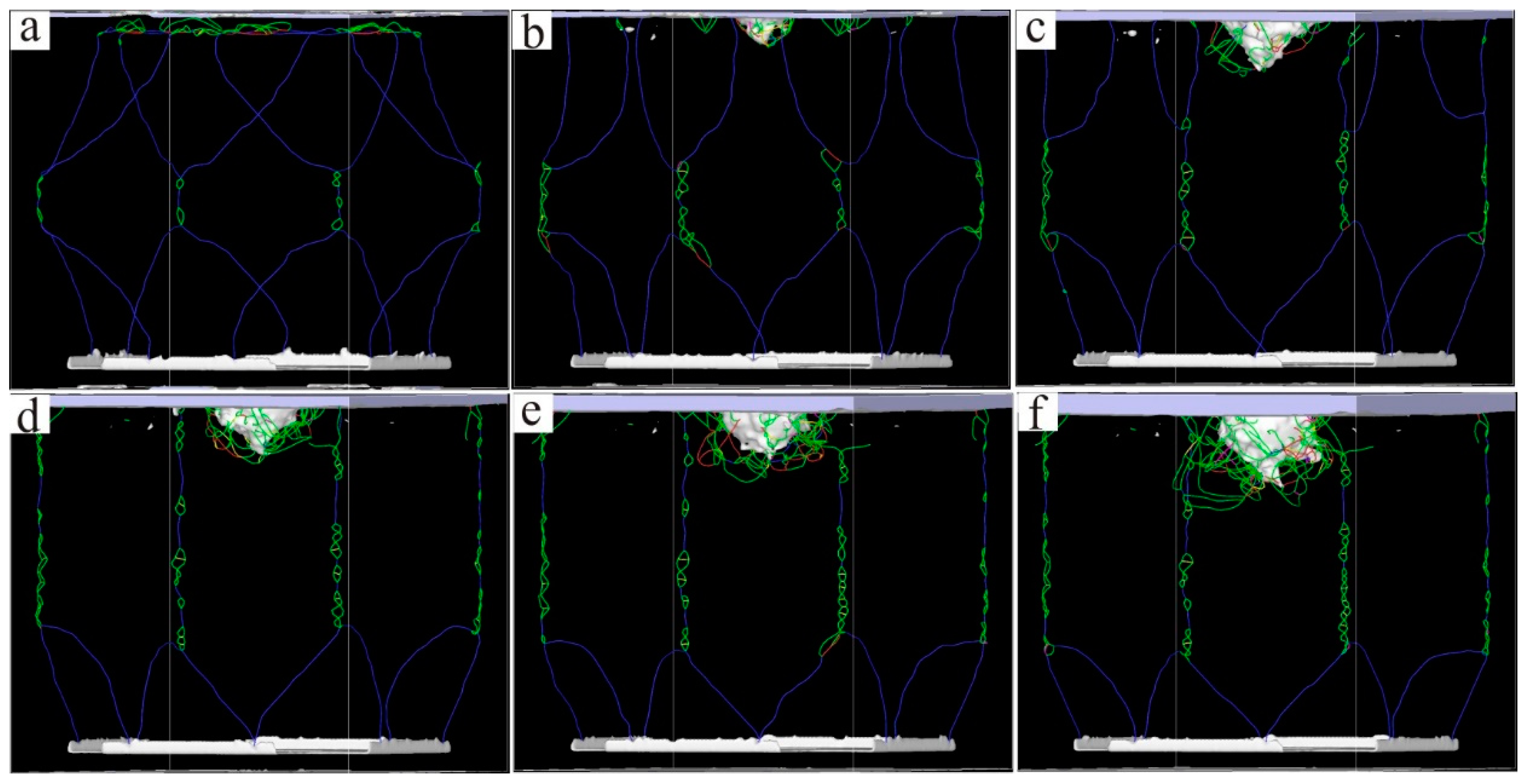
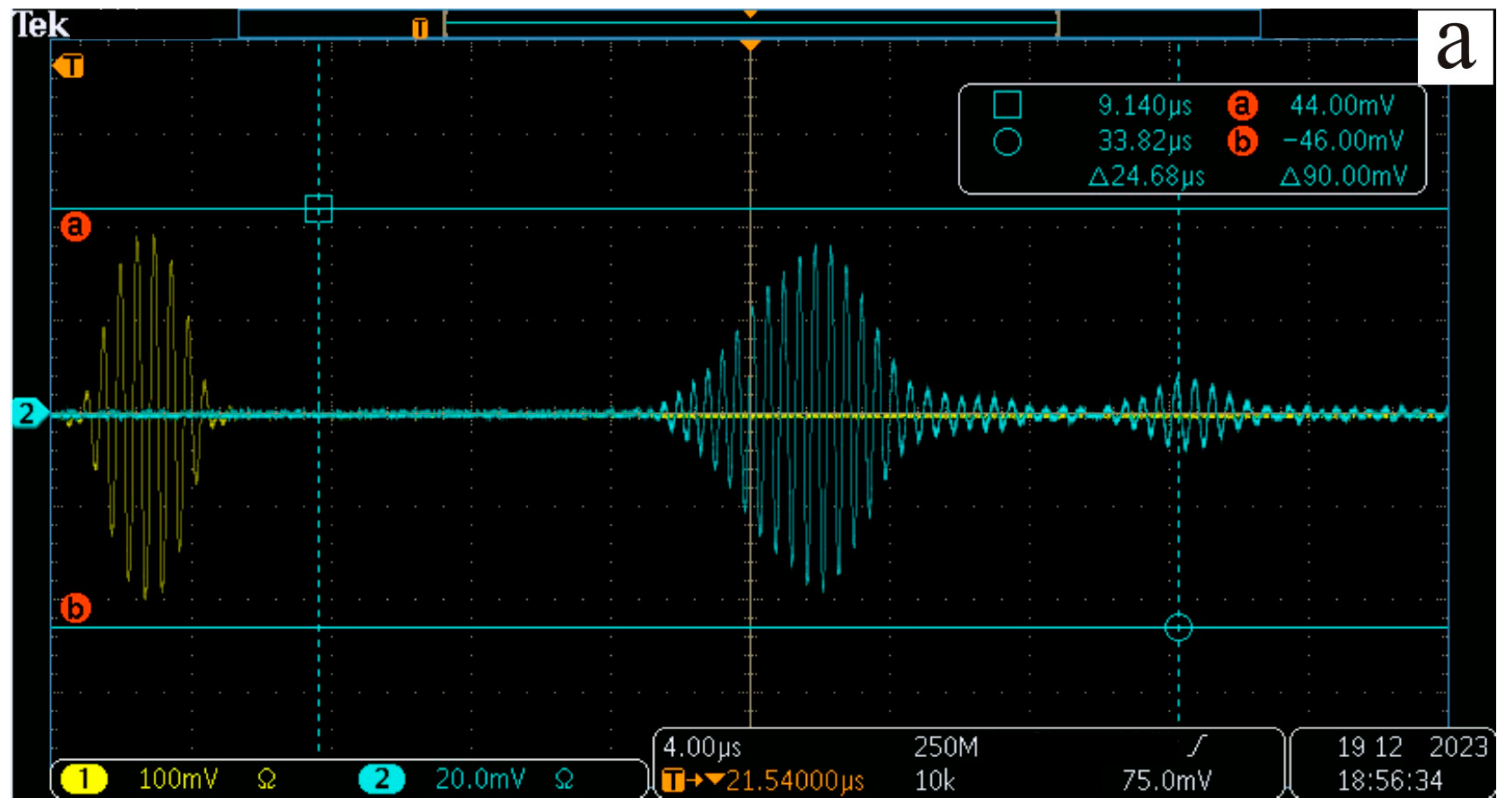
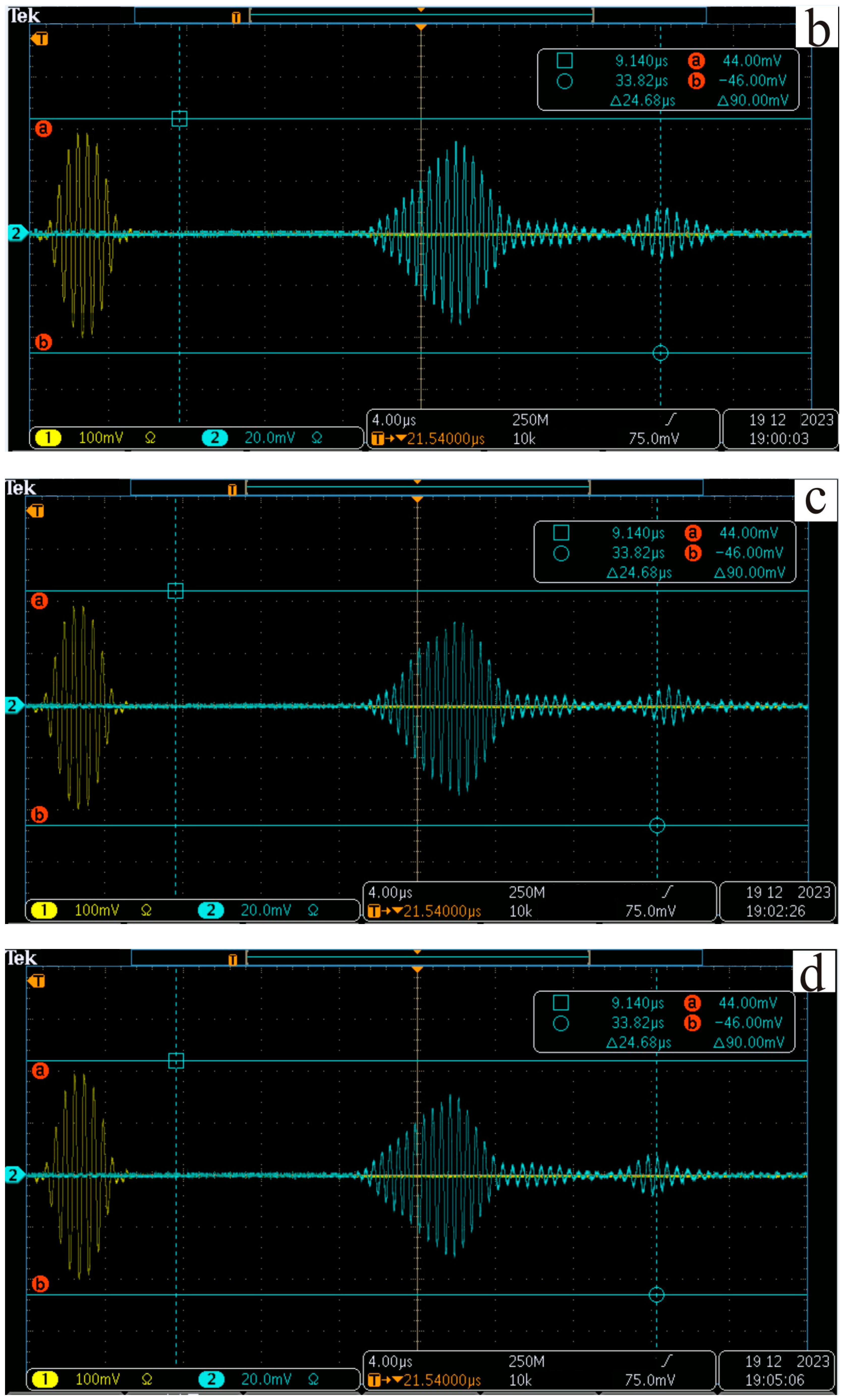
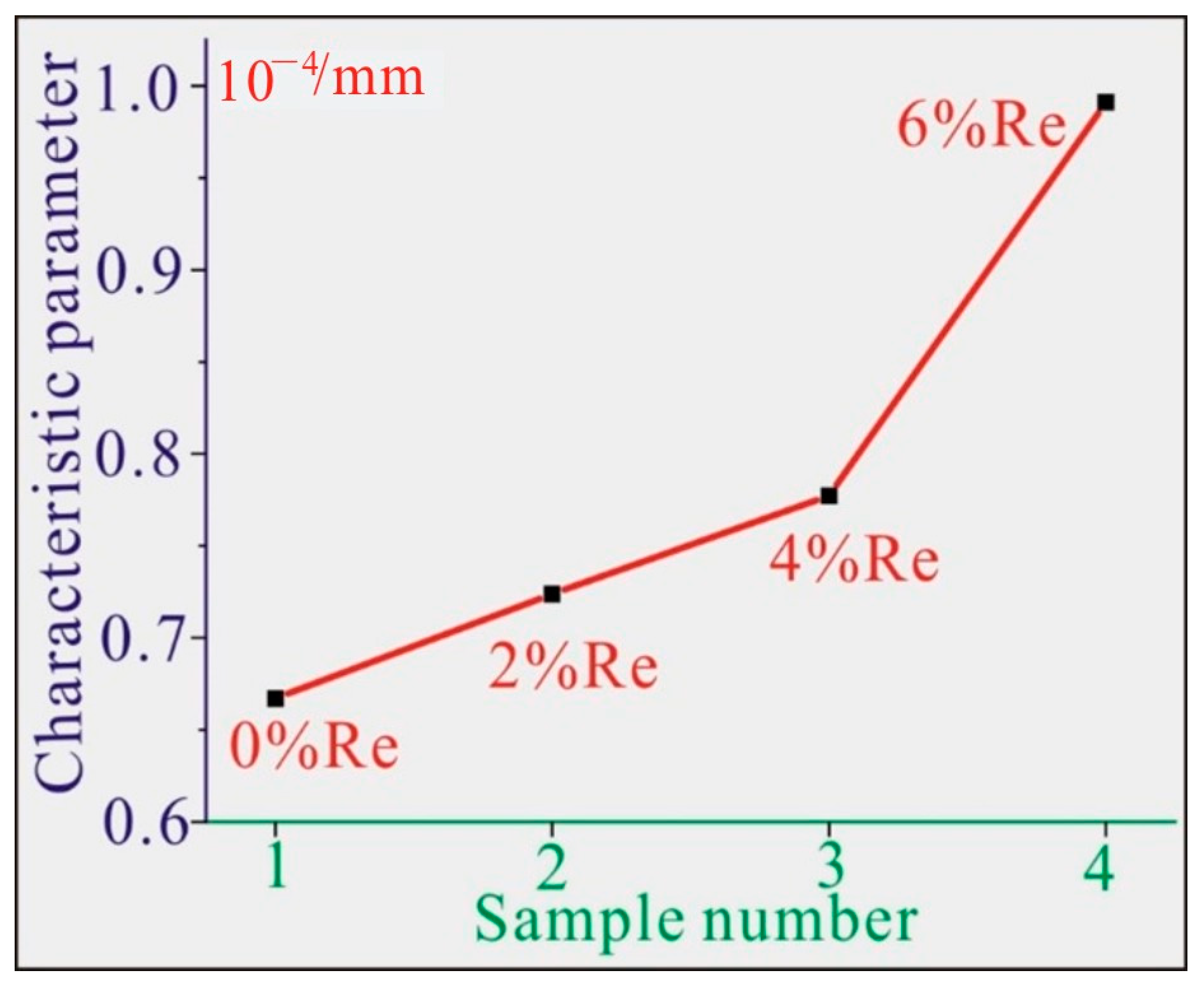
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pismennyi, V. Methods and techniques used in increasing gas temperature in front of the gas turbine engine turbine. Proc. High. Educ. Inst. Machine Build. 2023, 6, 108–118. [Google Scholar] [CrossRef]
- Dada, M.; Popoola, P.; Mathe, N. Recent advances of high entropy alloys for aerospace applications: A review. World J. Eng. 2023, 20, 43–74. [Google Scholar] [CrossRef]
- Holtham, N.; Davami, K. A Review of Laser Peening Methods for Single Crystal Ni-Based Superalloys. Metals 2022, 12, 1414. [Google Scholar] [CrossRef]
- Venkat, Y.; Choudary, K.R.; Chatterjee, D.; Das, D.K.; Pandey, A.K.; Singh, S. Development of mullite-alumina ceramic shells for precision investment casting of single-crystal high-pressure turbine blades. Ceram. Int. 2022, 48, 28199–28206. [Google Scholar] [CrossRef]
- Shi, Z.X.; Liu, S.Z.; Yue, X.D.; Hu, L.J.; Yang, W.P.; Wang, X.G.; Li, J.R. Effect of cellular recrystallization on tensile properties of a nickel-based single crystal superalloy containing Re and Ru. J. Iron Steel Res. Int. 2017, 24, 1059–1064. [Google Scholar] [CrossRef]
- Tian, S.G.; Qian, B.J.; Su, Y.; Yu, H.C.; Yu, X.F. Influence of Stacking Fault Energy on Creep Mechanism of a Single Crystal Nickel-Based Superalloy Containing Re. Mater. Sci. Forum 2012, 706 Pt 4, 2474–2479. [Google Scholar] [CrossRef]
- Yan, H.; Tian, S.; Zhao, G.; Tian, N.; Zhang, S.; Liu, L. Deformation features and affecting factors of a Re/Ru-containing single crystal nickel-based superalloy during creep at elevated temperature. Mater. Sci. Eng. A 2019, 768, 138437. [Google Scholar] [CrossRef]
- Shu, D.L.; Tian, S.G.; Wu, J.; Zhang, B.; Liang, S. Creep Behavior of a 4.5%Re/3.0%Ru Containing Single Crystal Nickel-based Superalloy at Elevated Temperature. J. Mater. Eng. 2017, 45, 41–46. [Google Scholar]
- Tian, S.; Zeng, Z.; Zhang, C.; Liu, C.; Li, B. Creep Behavior and Its Effect Factors of a Single Crystal Nickel-Based Superalloy Containing 4.5%Re at Medium Temperature. Rare Met. Mater. Eng. 2013, 42, 494–499. [Google Scholar]
- Rahul, A.; Gururaja, S.; Nandam, S.R.; Singh, K.K. Parametric evaluation of chip formation in peripheral milling of single crystal Ni-based superalloy. Int. J. Adv. Manuf. Technol. 2024, 132, 2293–2313. [Google Scholar]
- Morales, A.V.; Mauget, F.; Larrouy, B.; Villechaise, P.; Cormier, J. Very high cycle fatigue of a notched Ni-based single crystal superalloy at high temperature. Int. J. Fatigue 2024, 186, 108379. [Google Scholar] [CrossRef]
- Yoo, J.; Kwon, H.; Song, S.; Do, J.; Yun, D.W.; Kim, H.S.; Lee, S.G.; Kim, I.S.; Choi, B.G. Effects of lattice misfit of γ/γ′ phases on hydrogen embrittlement behavior in Ni-based single crystal superalloy. J. Mater. Res. Technol. 2024, 30, 5040–5055. [Google Scholar] [CrossRef]
- Lin, C.; Singh, J.; Hogan, M.; Yamamoto, N. Solid-State Joining of Dissimilar Single Crystal and Polycrystalline Ni-Based Superalloys Using Field-Assisted Sintering Technology. Metall. Mater. Trans. A 2024, 55, 1271–1283. [Google Scholar] [CrossRef]
- Esakkiraja, N.; Vishwakarma, A.; Makineni, S.K.; Jayaram, V.; Hickel, T.; Divinski, S.V.; Paul, A. Diffusion-controlled growth and microstructural evolution between Pt and Pd containing B2-NiAl bondcoats and Ni-based single crystal superalloy. Acta Mater. 2024, 266, 119687–119700. [Google Scholar] [CrossRef]
- Li, B.; Liu, R.; Zhu, W.; Zhang, Q.; Yu, J.; Xiang, Y.; Zhou, H. Research on the interaction between surface laser-pit of NSC and Lamb wave under micro-conditions. Appl. Surf. Sci. 2019, 483, 840–848. [Google Scholar] [CrossRef]
- Tang, Y.Q.; Kumar, A.; Chen, D.L.; Li, D.Y.; Li, Q.Y.; Li, W. Bauschinger effect on wear of cold-worked Cu and Mg—A study combining MD modeling and experimental investigation. Wear 2023, 522, 204726. [Google Scholar] [CrossRef]
- Zhang, L.; Jing, Y.; Qu, P.; Wang, W.; Yao, X. MD simulations of the microscopic mechanism of thermal conductivity enhancement of ethylene Glycol-Water-Au nanofluids. Appl. Surf. Sci. 2023, 609, 155389. [Google Scholar] [CrossRef]
- Jabraoui, H.; Estève, A.; Hong, S.; Rossi, C. Initial stage of titanium oxidation in Ti/CuO thermites: A MD study using ReaxFF forcefields. Phys. Chem. Chem. Phys. 2023, 25, 11268–11277. [Google Scholar] [CrossRef]
- Wang, G.; Li, B.; Yang, P.; Andersson, D.A. Ab-Initio MD simulations of binary NaCl-ThCl4 and ternary NaCl-ThCl4-UCl3 molten salts. J. Mol. Liq. 2023, 385, 121837. [Google Scholar] [CrossRef]
- Karaseov, P.A.; Karabeshkin, K.V.; Mongo, E.E.; Titov, A.I.; Ullah, M.W.; Kuronen, A.; Djurabekova, F.; Nordlund, K. Experimental study and MD simulation of damage formation in GaN under atomic and molecular ion irradiation. Vacuum 2016, 129, 166–169. [Google Scholar] [CrossRef]
- Erban, R.; Togashi, Y. Asymmetric Periodic Boundary Conditions for All-Atom MD and Coarse-Grained Simulations of Nucleic Acids. J. Phys. Chem. B 2023, 127, 8257–8267. [Google Scholar] [CrossRef] [PubMed]
- Yun, H.S.; Jaeyeong, P.; Koo, J.S.; Nahm, S.H. Deformation behavior and crack mechanism of a first generation single-crystal Ni-based superalloys under thermomechanical fatigue loading. Eng. Fract. Mech. 2024, 296, 109820. [Google Scholar]
- Ormastroni, L.M.B.; Kepa, T.; Cervellon, A.; Villechaise, P.; Pedraza, F.; Cormier, J. Very high cycle fatigue rupture mode at high temperatures of Ni-based superalloys coated with a slurry aluminide. Int. J. Fatigue 2024, 180, 108107. [Google Scholar] [CrossRef]
- Takahashi, Y.; Kobayashi, D.; Fujii, S.; Arai, S.; Takuma, M.; Saitoh, K.I.; Sato, T. Time-dependent subcritical crack growth and its mechanism in Ni-based single crystal superalloys at 500 °C. Mater. Sci. Eng. A 2024, 889, 145869. [Google Scholar] [CrossRef]
- Zhou, H.Y.; Li, B. Research on the Relationship between Surface Defects and Preparation Quality Evaluation of NSC. J. Mater. Eng. Perform. 2022, 32, 1612–1626. [Google Scholar] [CrossRef]
- Maffioli, L.; Ewen, J.P.; Smith, E.R.; Varghese, S.; Daivis, P.J.; Dini, D.; Todd, B.D. TTCF4LAMMPS: A toolkit for simulation of the non-equilibrium behaviour of molecular fluids at experimentally accessible shear rates. Comput. Phys. Commun. 2024, 300, 109205. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with ovito-the open visualization tool visualization and analysis of atomistic simulation data with OVITO-the open visualization tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Du, J.P.; Wang, C.Y.; Yu, T. Construction and application of multi-element EAM potential (Ni-Al-Re) in γ/γ′ Ni-based single crystal superalloys. Model. Simul. Mater. Sci. Eng. 2012, 21, 015007. [Google Scholar] [CrossRef]
- Wang, J.; Lu, H.; Wen, Z.; Lian, Y.; Wang, Y.; Yue, Z. Crystal plasticity theory coupled with meso-damage to predict the ratchetting behavior of nickel-based single crystal superalloy. Int. J. Fatigue 2022, 165, 107220. [Google Scholar] [CrossRef]
- Khoei, A.R.; Eshlaghi, G.T.; Shahoveisi, S. Atomistic simulation of creep deformation mechanisms in nickel-based single crystal superalloys. Mater. Sci. Eng. A 2021, 809, 140977. [Google Scholar] [CrossRef]
- Kumar, N.; Choubey, V.K. Comparative Evaluation of Oxidation Resistance of Detonation Gun-Sprayed Al2O3–40%TiO2 Coating on Nickel-Based Superalloys at 800 °C and 900 °C. High Temp. Corros. Mater. 2023, 99, 359–373. [Google Scholar] [CrossRef]
- Khoei, A.R.; Youzi, M.; Eshlaghi, G.T. Mechanical properties and γ/γ′ interfacial misfit network evolution: A study towards the creep behavior of Ni-based single crystal superalloys. Mech. Mater. 2022, 171, 104368. [Google Scholar] [CrossRef]








| Samples | Re | Ni | Ti | Cr | Co | Al | Mo | W | Ta |
|---|---|---|---|---|---|---|---|---|---|
| Sample 1 | 0 | 62.49 | 1.82 | 9.73 | 6.14 | 6.21 | 2.78 | 7.14 | 3.69 |
| Sample 2 | 2 | 60.49 | 1.82 | 9.73 | 6.14 | 6.21 | 2.78 | 7.14 | 3.69 |
| Sample 3 | 4 | 58.49 | 1.82 | 9.73 | 6.14 | 6.21 | 2.78 | 7.14 | 3.69 |
| Sample 4 | 6 | 56.49 | 1.82 | 9.73 | 6.14 | 6.21 | 2.78 | 7.14 | 3.69 |
| Calculation Steps | 0 wt.% Re | 2 wt.% Re | 4 wt.% Re | 6 wt.% Re | ||||
|---|---|---|---|---|---|---|---|---|
| HCP | OIS | HCP | OIS | HCP | OIS | HCP | OIS | |
| 200 | 95 | 40,446 | 89 | 40,003 | 73 | 39,921 | 0 | 39,222 |
| 5000 | 156 | 41,274 | 151 | 40,869 | 114 | 40,454 | 32 | 39,952 |
| 10,000 | 279 | 41,721 | 164 | 40,994 | 118 | 40,525 | 78 | 40,227 |
| 15,000 | 321 | 41,951 | 221 | 41,399 | 173 | 40,876 | 96 | 40,680 |
| 20,000 | 594 | 42,996 | 312 | 41,983 | 309 | 41,375 | 243 | 41,091 |
| 25,000 | 969 | 44,307 | 580 | 43,226 | 538 | 42,227 | 458 | 41,287 |
| Calculation Steps | 0 wt.% Re | 2 wt.% Re | 4 wt.% Re | 6 wt.% Re | ||||
|---|---|---|---|---|---|---|---|---|
| HCP | OIS | HCP | OIS | HCP | OIS | HCP | OIS | |
| 200 | 1683 | 63,027 | 1102 | 61,909 | 1080 | 57,631 | 817 | 54,442 |
| 5000 | 1715 | 63,425 | 1216 | 62,435 | 1207 | 59,275 | 1143 | 56,690 |
| 10,000 | 3205 | 65,899 | 2205 | 62,739 | 2106 | 61,877 | 2001 | 60,088 |
| 15,000 | 3620 | 69,421 | 2306 | 64,425 | 2232 | 62,496 | 2102 | 61,126 |
| 20,000 | 8318 | 70,125 | 6410 | 66,368 | 5056 | 63,798 | 5004 | 62,207 |
| 25,000 | 9781 | 73,118 | 9229 | 69,239 | 7386 | 67,802 | 7182 | 66,903 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Zhang, Y.; Zhou, H.; Li, X. Research on Microstructural Evolution Behavior of Ni-Based Single-Crystal Alloy with Re Based on Non-Linear Ultrasonic Lamb Wave and Molecular Dynamics Method. Metals 2024, 14, 1016. https://doi.org/10.3390/met14091016
Li B, Zhang Y, Zhou H, Li X. Research on Microstructural Evolution Behavior of Ni-Based Single-Crystal Alloy with Re Based on Non-Linear Ultrasonic Lamb Wave and Molecular Dynamics Method. Metals. 2024; 14(9):1016. https://doi.org/10.3390/met14091016
Chicago/Turabian StyleLi, Ben, Yilin Zhang, Hongyan Zhou, and Xuewu Li. 2024. "Research on Microstructural Evolution Behavior of Ni-Based Single-Crystal Alloy with Re Based on Non-Linear Ultrasonic Lamb Wave and Molecular Dynamics Method" Metals 14, no. 9: 1016. https://doi.org/10.3390/met14091016
APA StyleLi, B., Zhang, Y., Zhou, H., & Li, X. (2024). Research on Microstructural Evolution Behavior of Ni-Based Single-Crystal Alloy with Re Based on Non-Linear Ultrasonic Lamb Wave and Molecular Dynamics Method. Metals, 14(9), 1016. https://doi.org/10.3390/met14091016






