Effect of Atomic Ordering on Phase Stability and Elastic Properties of Pd-Ag Alloys
Abstract
1. Introduction
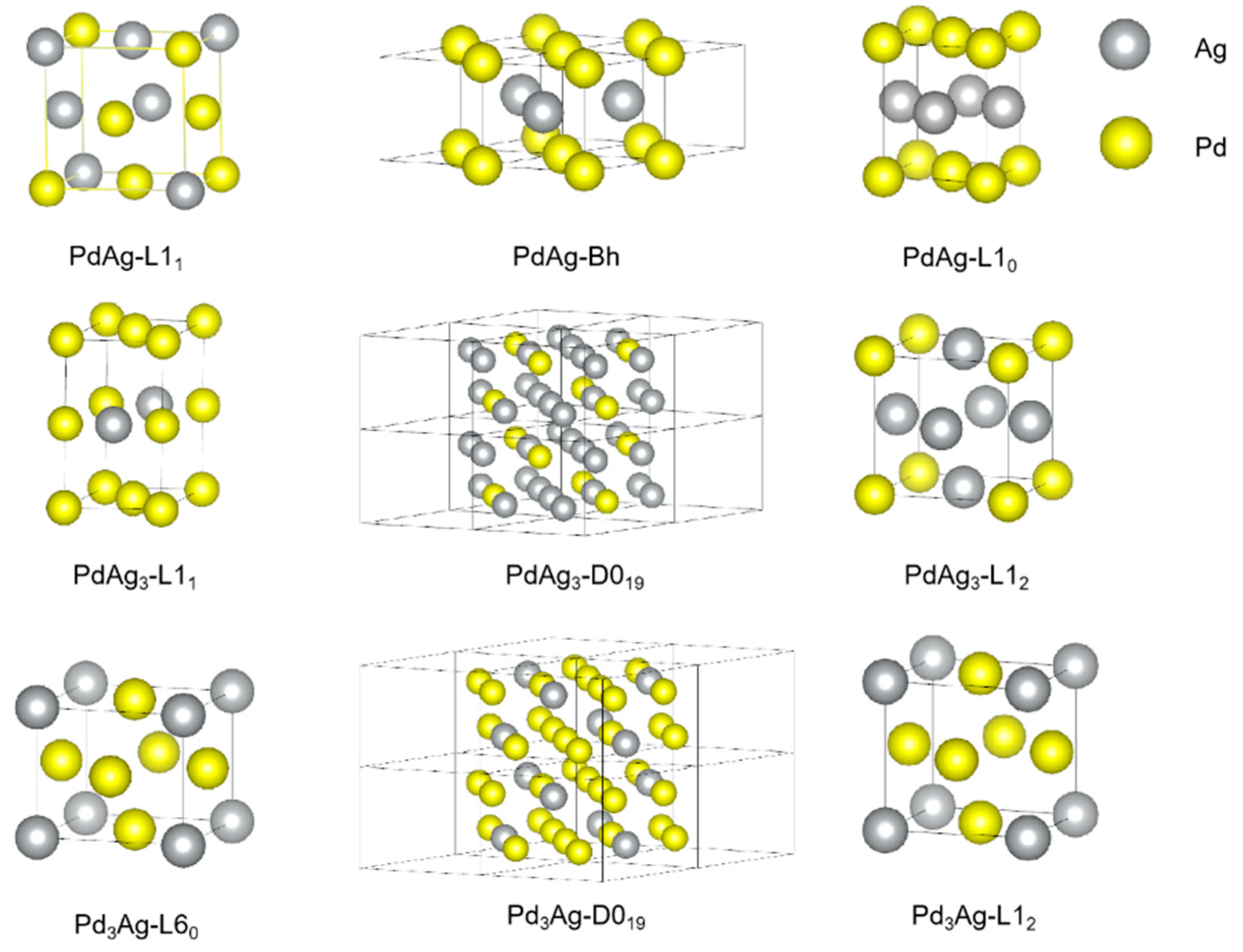
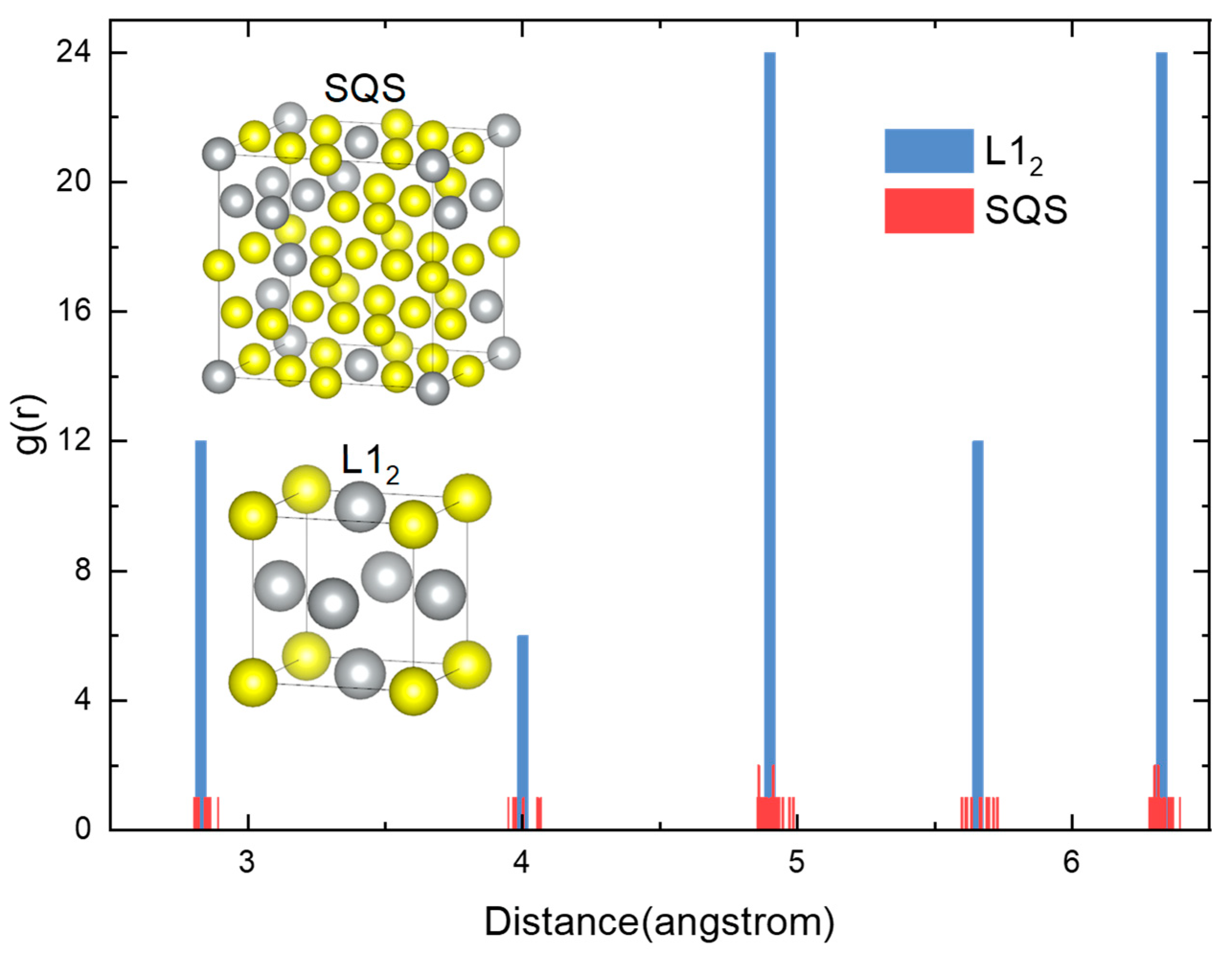
2. Methods and Details
3. Results and Discussion
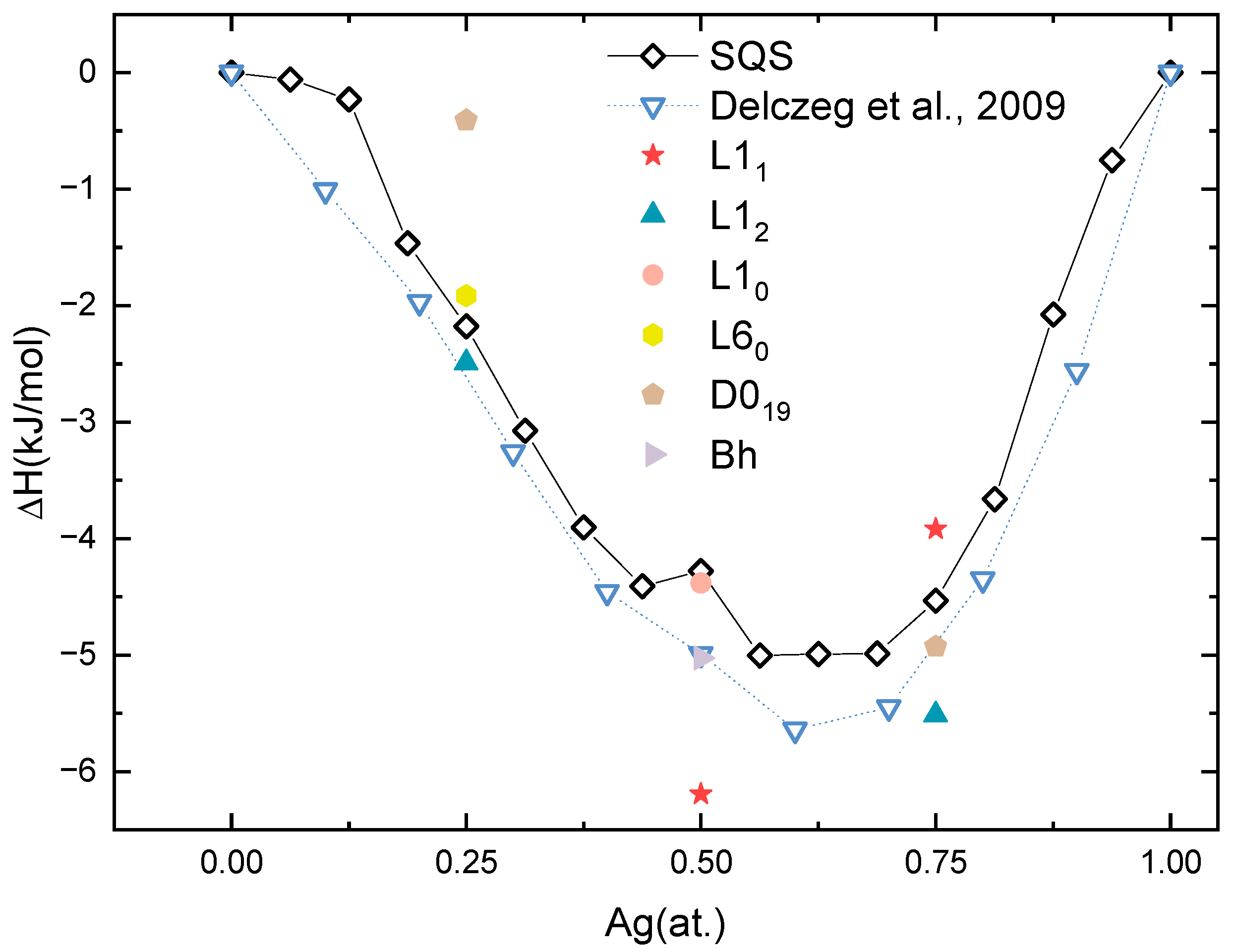
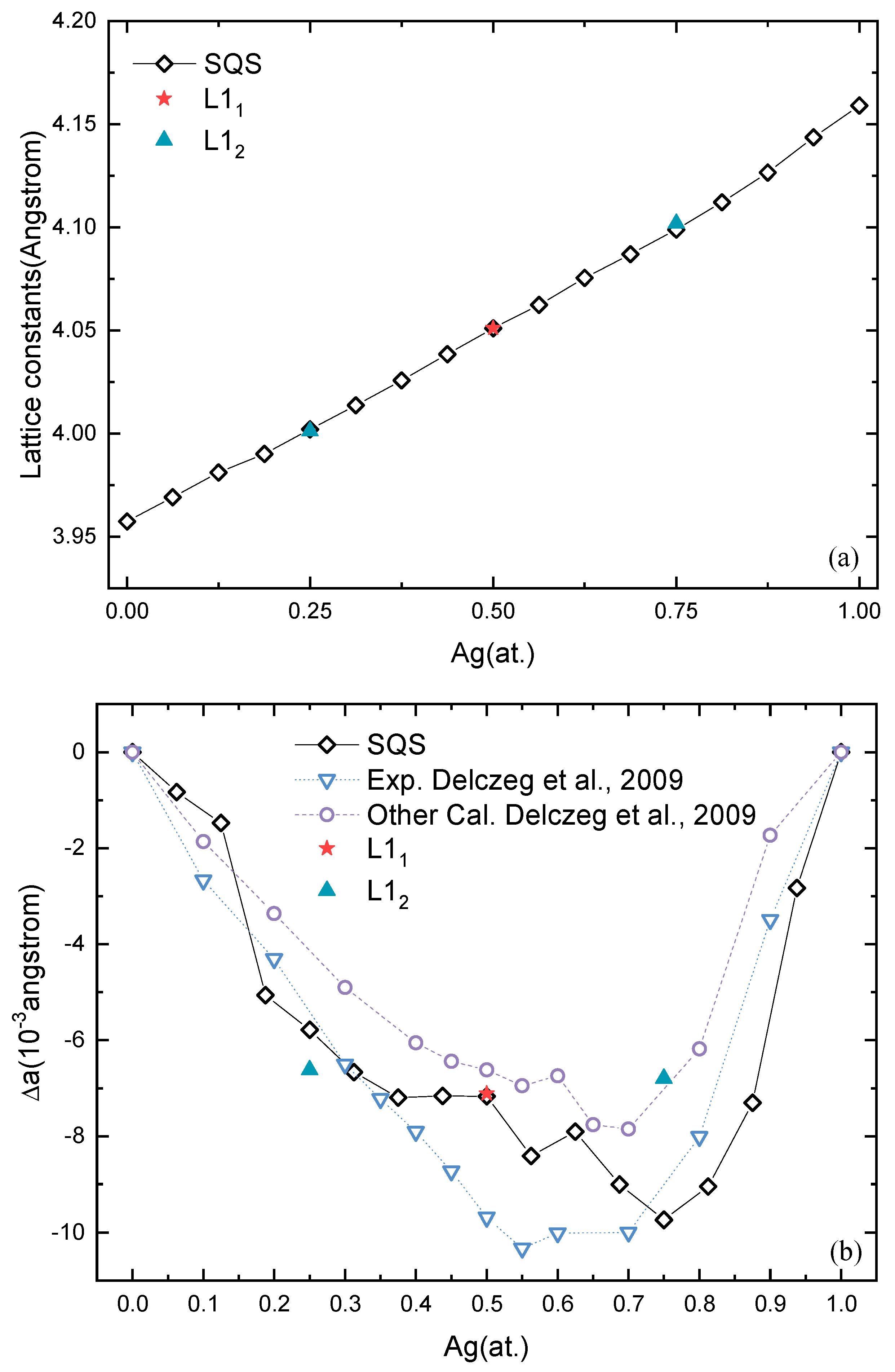
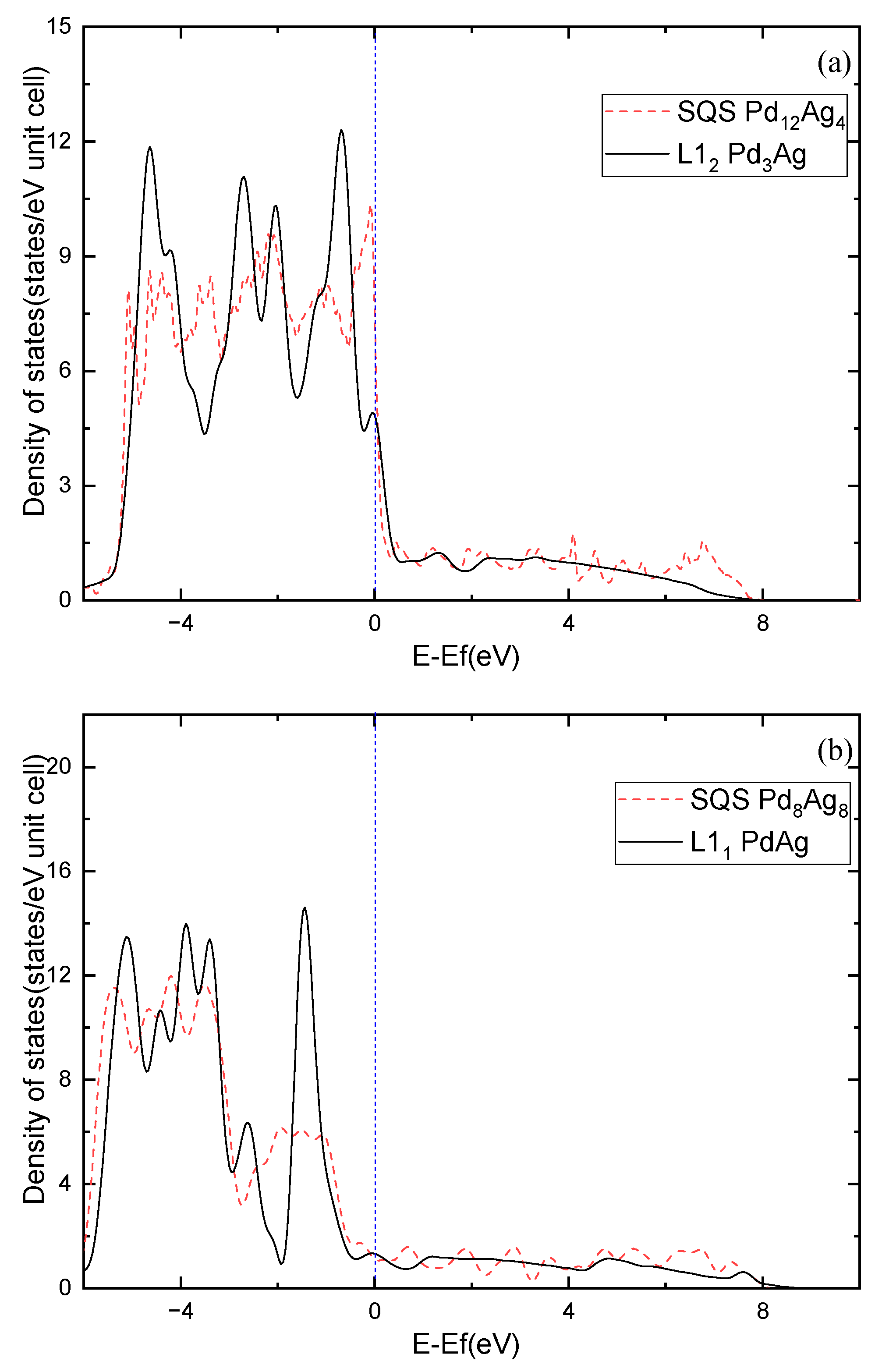
3.1. Phase Stability
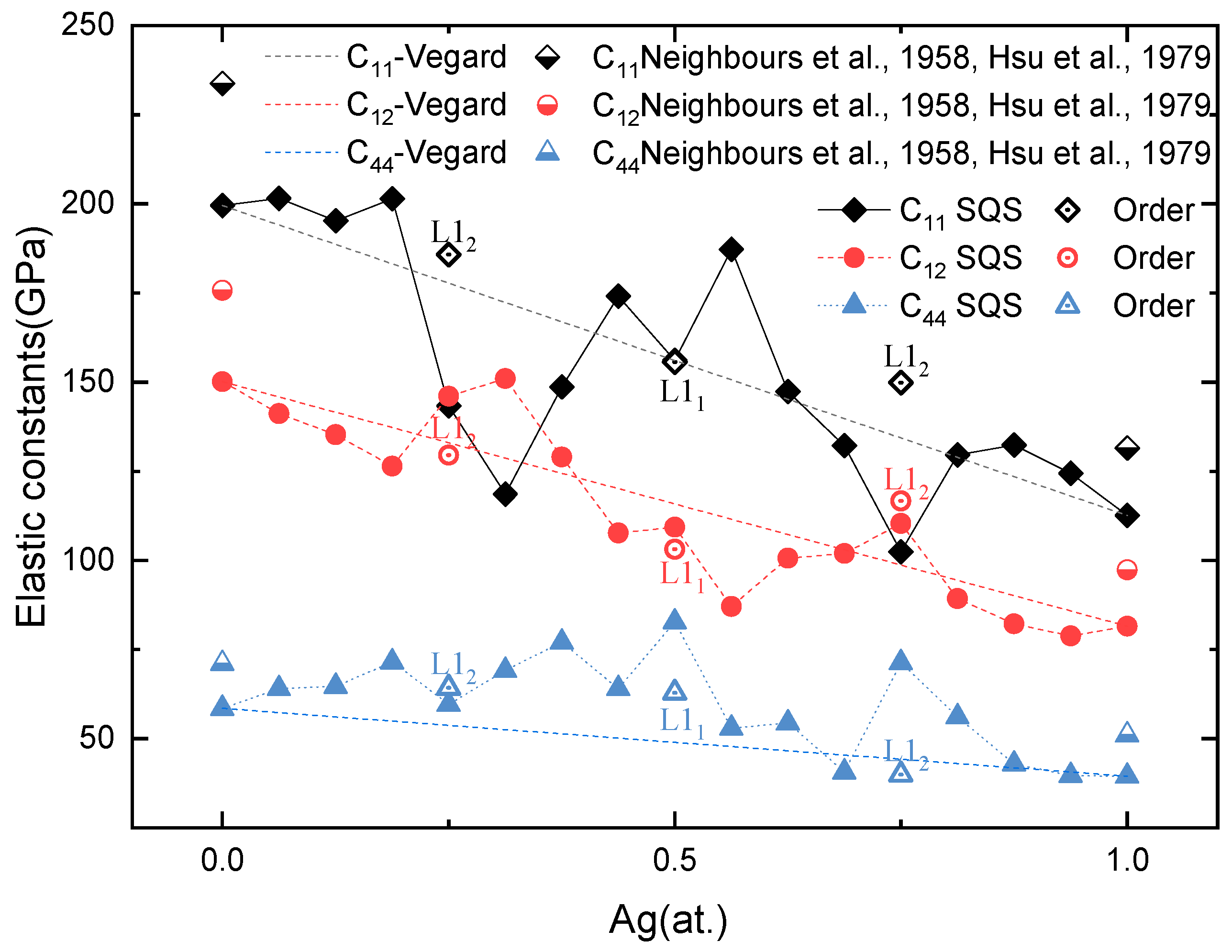
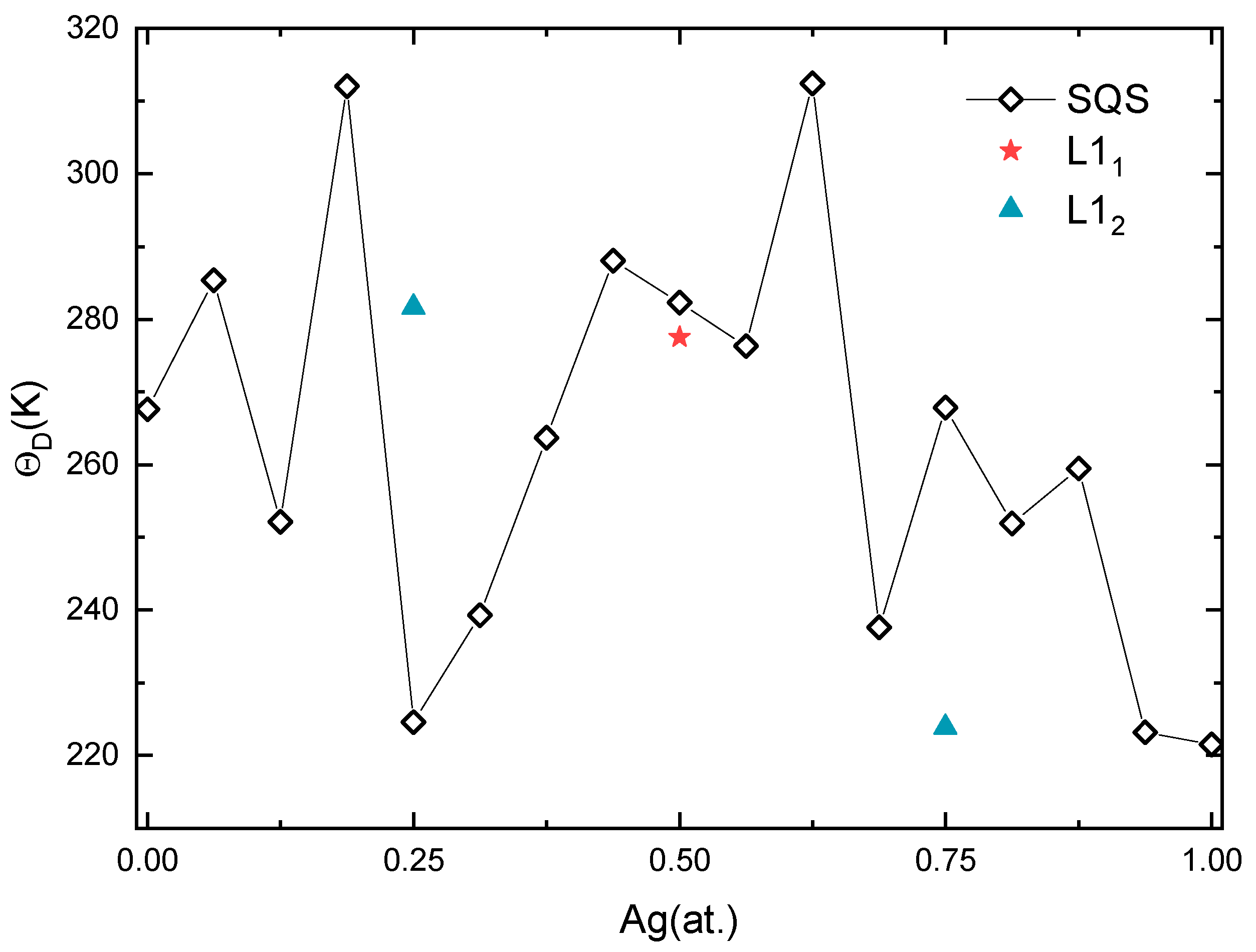
3.2. Mechanical Stability
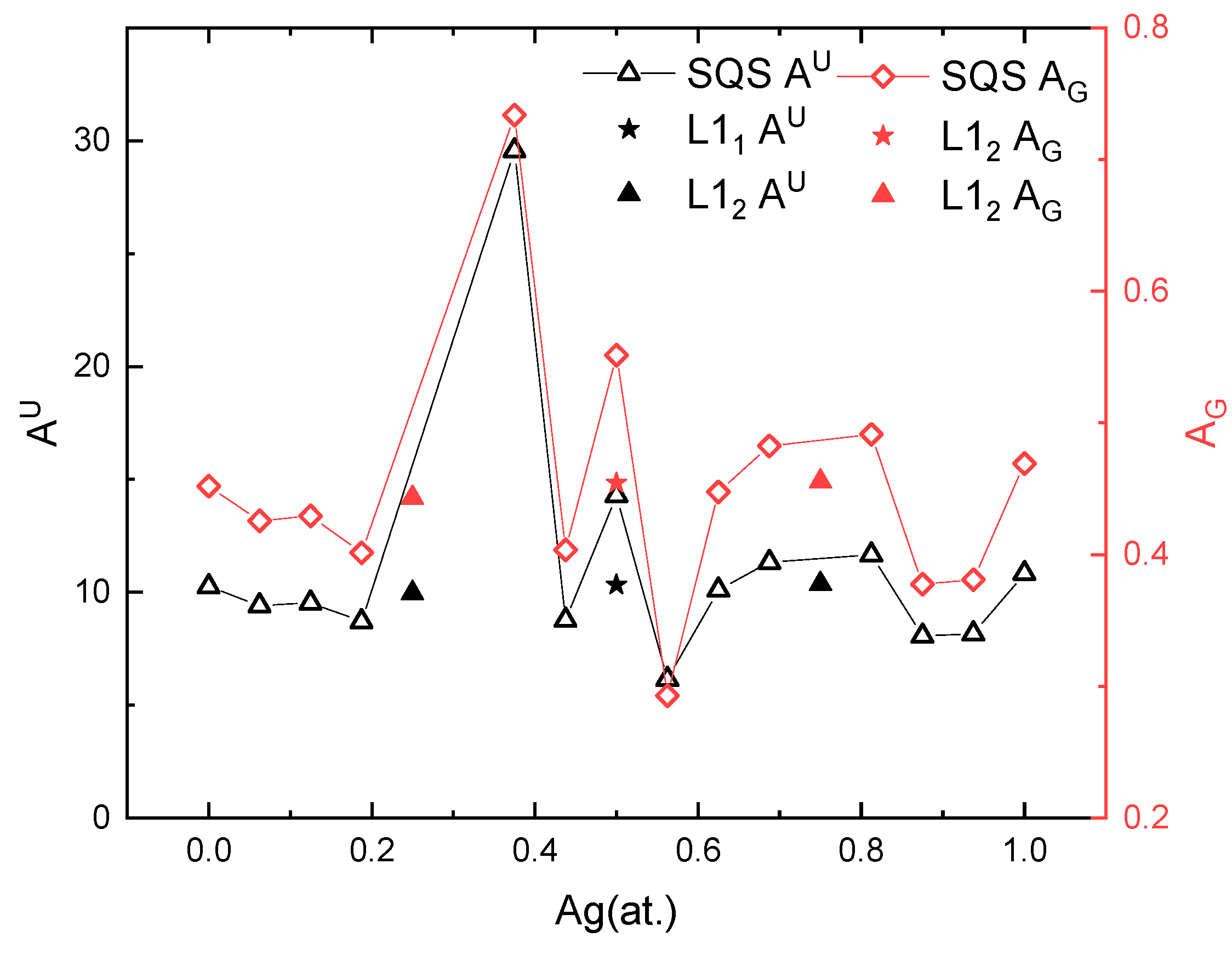
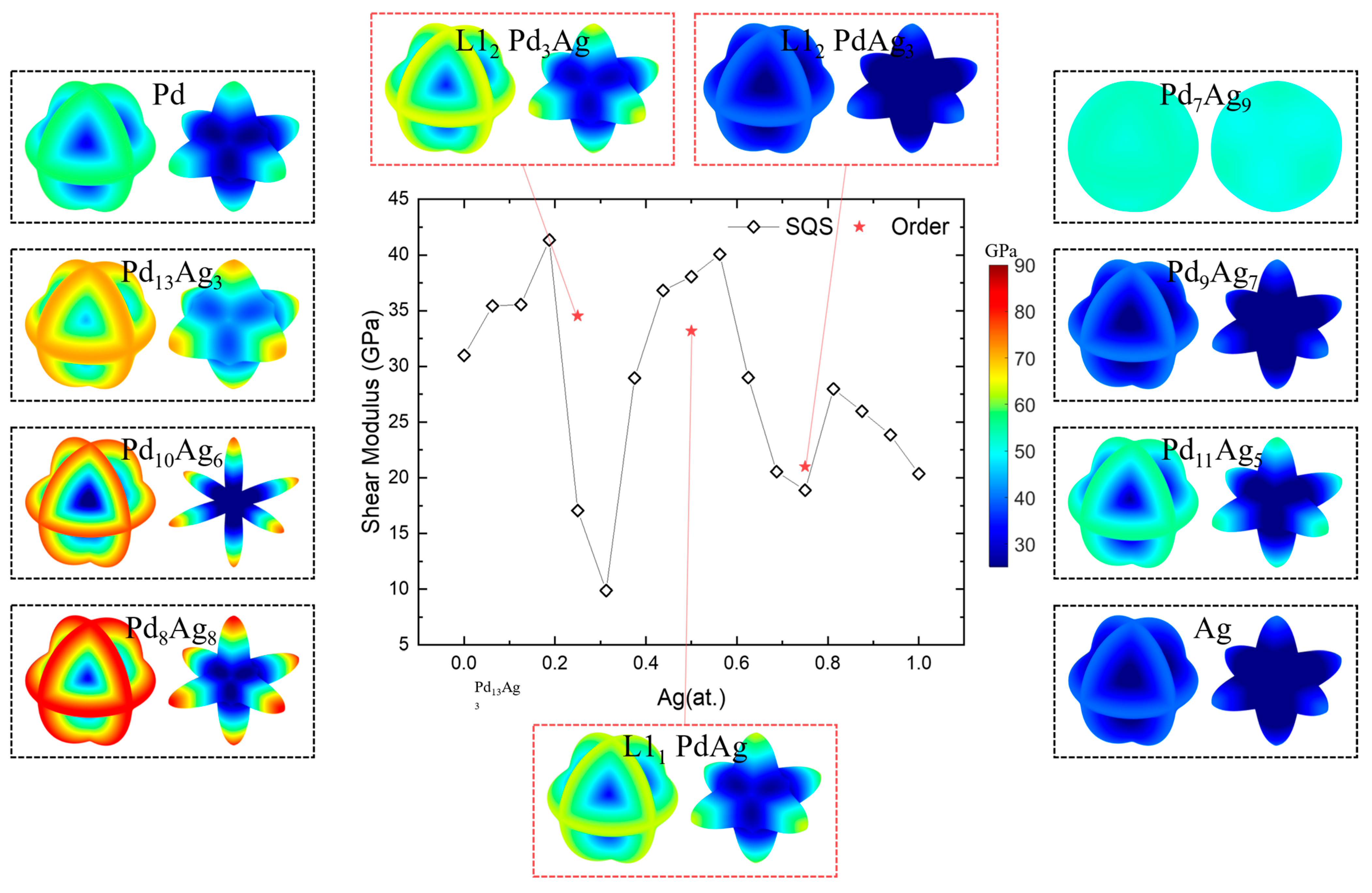
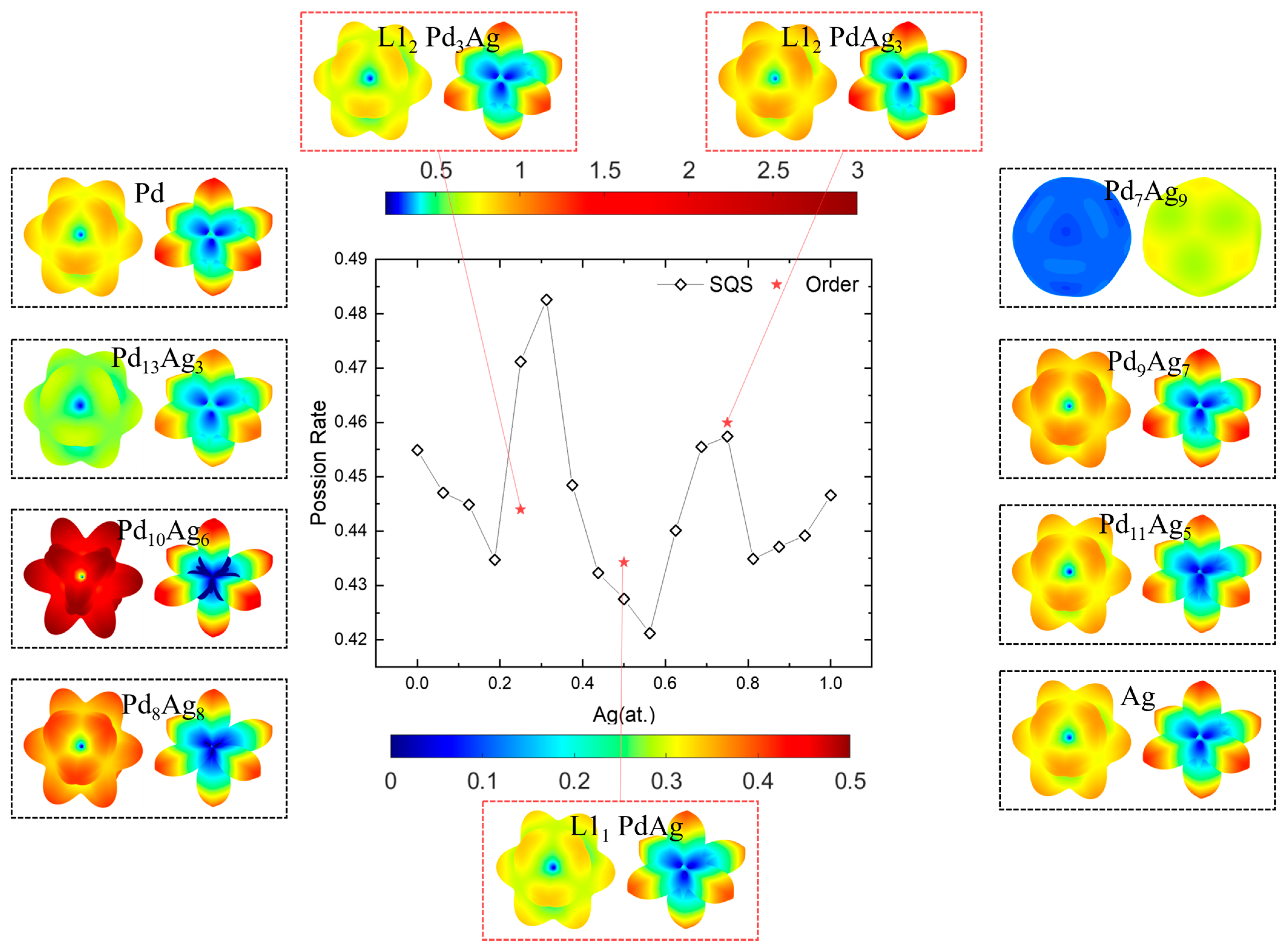
3.3. Mechanical Anisotropy
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Betancourt, L.E.; Rojas-Pérez, A.; Orozco, I.; Frenkel, A.I.; Li, Y.; Sasaki, K.; Senanayake, S.D.; Cabrera, C.R. Enhancing ORR Performance of Bimetallic PdAg Electrocatalysts by Designing Interactions between Pd and Ag. ACS Appl. Energy Mater. 2020, 3, 2342–2349. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, B.; Ling, L.; Zhang, R.; Fan, M. Probe into the Effects of Surface Composition and Ensemble Effect of Active Sites on the Catalytic Performance of C2H2 Semi-Hydrogenation over the Pd-Ag Bimetallic Catalysts. Chem. Eng. Sci. 2020, 218, 115549. [Google Scholar] [CrossRef]
- Mostashari, S.M.; Dehkharghani, R.A.; Afshar-Taromi, F.; Farsadrooh, M. A Straightforward One-Pot Synthesis of Pd–Ag Supported on Activated Carbon as a Robust Catalyst toward Ethanol Electrooxidation. Int. J. Hydrogen Energy 2021, 46, 9406–9416. [Google Scholar] [CrossRef]
- Shin, H.-J.; Kwon, Y.-H.; Seol, H.-J. Effect of Cooling Rate on Hardness and Phase Transformation of a Pd-Ag-Based Metal–Ceramic Alloy with or without Ice-Quenching. Metals 2021, 11, 680. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, Y.; Zhang, P.; Yang, X.; Chen, Y. Evolution of Interface Microstructure and Tensile Properties of AgPd30/CuNi18Zn26 Bilayer Laminated Composite Manufactured by Rolling and Annealing. Metals 2022, 12, 367. [Google Scholar] [CrossRef]
- Cao, X.; Jang, B.W.-L.; Hu, J.; Wang, L.; Zhang, S. Synthetic Strategies of Supported Pd-Based Bimetallic Catalysts for Selective Semi-Hydrogenation of Acetylene: A Review and Perspectives. Molecules 2023, 28, 2572. [Google Scholar] [CrossRef]
- Chen, W.-H.; Biswas, P.P.; Ong, H.C.; Hoang, A.T.; Nguyen, T.-B.; Dong, C.-D. A Critical and Systematic Review of Sustainable Hydrogen Production from Ethanol/Bioethanol: Steam Reforming, Partial Oxidation, and Autothermal Reforming. Fuel 2023, 333, 126526. [Google Scholar] [CrossRef]
- Chen, W.-H.; Li, S.-C.; Lim, S.; Chen, Z.-Y.; Juan, J.C. Reaction and Hydrogen Production Phenomena of Ethanol Steam Reforming in a Catalytic Membrane Reactor. Energy 2021, 220, 119737. [Google Scholar] [CrossRef]
- He, M.; Fang, Z.; Wang, P.; You, Y.; Li, Z. Recent Progress in Photocatalytic Chemical Fixation of Carbon Dioxide. ACS Sustain. Chem. Eng. 2023, 11, 12194–12217. [Google Scholar] [CrossRef]
- Razmgar, K.; Altarawneh, M.; Oluwoye, I.; Senanayake, G. Ceria-Based Catalysts for Selective Hydrogenation Reactions: A Critical Review. Catal. Surv. Asia 2021, 25, 27–47. [Google Scholar] [CrossRef]
- Rusinque, B.; Escobedo, S.; De Lasa, H. Hydrogen Production via Pd-TiO2 Photocatalytic Water Splitting under Near-UV and Visible Light: Analysis of the Reaction Mechanism. Catalysts 2021, 11, 405. [Google Scholar] [CrossRef]
- Wang, M.; Liang, L.; Liu, X.; Sun, Q.; Guo, M.; Bai, S.; Xu, Y. Selective Semi-Hydrogenation of Alkynes on Palladium-Selenium Nanocrystals. J. Catal. 2023, 418, 247–255. [Google Scholar] [CrossRef]
- Yang, J.-J.; Zhang, Y.; Xie, X.-Y.; Fang, W.-H.; Cui, G. Photocatalytic Reduction of Carbon Dioxide to Methane at the Pd-Supported TiO2 Interface: Mechanistic Insights from Theoretical Studies. ACS Catal. 2022, 12, 8558–8571. [Google Scholar] [CrossRef]
- Zhang, X.; Gu, Q.; Ma, Y.; Guan, Q.; Jin, R.; Wang, H.; Yang, B.; Lu, J. Support-Induced Unusual Size Dependence of Pd Catalysts in Chemoselective Hydrogenation of Para-Chloronitrobenzene. J. Catal. 2021, 400, 173–183. [Google Scholar] [CrossRef]
- Tucho, W.M.; Venvik, H.J.; Stange, M.; Walmsley, J.C.; Holmestad, R.; Bredesen, R. Effects of Thermal Activation on Hydrogen Permeation Properties of Thin, Self-Supported Pd/Ag Membranes. Sep. Purif. Technol. 2009, 68, 403–410. [Google Scholar] [CrossRef]
- Grashoff, G.J.; Pilkington, C.E.; Corti, C.W. The Purification of Hydrogen: A Review of the Technology Emphasising the Current Status of Palladium Membrane Diffusion. Platin. Met. Rev. 1983, 27, 157–169. [Google Scholar] [CrossRef]
- Opetubo, O.; Ibitoye, A.I.; Oyinbo, S.T.; Jen, T.-C. Analysis of Hydrogen Embrittlement in Palladium–Copper Alloys Membrane from First Principal Method Using Density Functional Theory. Vacuum 2022, 205, 111439. [Google Scholar] [CrossRef]
- Zhu, K.; Li, X.; Zhang, Y.; Zhao, X.; Liu, Z.; Guo, J. Tailoring the Hydrogen Transport Properties of Highly Permeable Nb51W5Ti23Ni21 Alloy Membrane by Pd Substitution. Int. J. Hydrogen Energy 2022, 47, 6734–6744. [Google Scholar] [CrossRef]
- Lin, W.-H.; Chang, H.-F. Characterizations of Pd–Ag Membrane Prepared by Sequential Electroless Deposition. Surf. Coat. Technol. 2005, 194, 157–166. [Google Scholar] [CrossRef]
- Zeng, G.; Goldbach, A.; Shi, L.; Xu, H. On Alloying and Low-Temperature Stability of Thin, Supported PdAg Membranes. Int. J. Hydrogen Energy 2012, 37, 6012–6019. [Google Scholar] [CrossRef]
- Ververs, W.J.R.; Arratibel Plazaola, A.; Di Felice, L.; Gallucci, F. On the Applicability of PdAg Membranes in Propane Dehydrogenation Processes. Int. J. Hydrogen Energy 2024, 50, 409–419. [Google Scholar] [CrossRef]
- Albano, M.; Madeira, L.M.; Miguel, C.V. Use of Pd-Ag Membrane Reactors for Low-Temperature Dry Reforming of Biogas—A Simulation Study. Membranes 2023, 13, 630. [Google Scholar] [CrossRef]
- Cechetto, V.; Agnolin, S.; Di Felice, L.; Pacheco Tanaka, A.; Llosa Tanco, M.; Gallucci, F. Metallic Supported Pd-Ag Membranes for Simultaneous Ammonia Decomposition and H2 Separation in a Membrane Reactor: Experimental Proof of Concept. Catalysts 2023, 13, 920. [Google Scholar] [CrossRef]
- Petriev, I.; Pushankina, P.; Andreev, G.; Ivanin, S.; Dzhimak, S. High-Performance Hydrogen-Selective Pd-Ag Membranes Modified with Pd-Pt Nanoparticles for Use in Steam Reforming Membrane Reactors. Int. J. Mol. Sci. 2023, 24, 17403. [Google Scholar] [CrossRef]
- Escalante, Y.; Tarditi, A.M. Thermally Stable Membranes Based on PdNiAu Systems with High Nickel Content for Hydrogen Separation. J. Membr. Sci. 2023, 676, 121581. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, P.; Yang, D.; Yang, P.; Liao, N. First-Principles Evaluation of Pd–Pt–Ag and Pd–Pt–Au Ternary Alloys as High Performance Membranes for Hydrogen Separation. Int. J. Hydrogen Energy 2024, 68, 607–613. [Google Scholar] [CrossRef]
- Ryu, S.; Badakhsh, A.; Oh, J.G.; Ham, H.C.; Sohn, H.; Yoon, S.P.; Choi, S.H. Experimental and Numerical Study of Pd/Ta and PdCu/Ta Composites for Thermocatalytic Hydrogen Permeation. Membranes 2022, 13, 23. [Google Scholar] [CrossRef]
- Savitskii, E.M.; Pravoverov, N.L. Kurnakov Phases in the Palladium-Silver System. Russ. J. Inorg. Chem. 1961, 6, 253–254. [Google Scholar]
- Müller, S.; Zunger, A. First-Principles Predictions of Yet-Unobserved Ordered Structures in the Ag-Pd Phase Diagram. Phys. Rev. Lett. 2001, 87, 165502. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Q.; Jiang, W.; Gong, H. Hydrogen Solubility in Pd3Ag Phases from First-Principles Calculation. Metals 2019, 9, 121. [Google Scholar] [CrossRef]
- Ruban, A.V.; Simak, S.I.; Korzhavyi, P.A.; Johansson, B. Theoretical Investigation of Bulk Ordering and Surface Segregation in Ag-Pd and Other Isoelectornic Alloys. Phys. Rev. B 2007, 75, 054113. [Google Scholar] [CrossRef]
- Svenum, I.-H.; Herron, J.A.; Mavrikakis, M.; Venvik, H.J. Adsorbate-Induced Segregation in a PdAg Membrane Model System: Pd3Ag(111). Catal. Today 2012, 193, 111–119. [Google Scholar] [CrossRef]
- Kitchin, J.R.; Reuter, K.; Scheffler, M. Alloy Surface Segregation in Reactive Environments: First-Principles Atomistic Thermodynamics Study of Ag3Pd(111) in Oxygen Atmospheres. Phys. Rev. B 2008, 77, 075437. [Google Scholar] [CrossRef]
- Tang, J.; Deng, L.; Deng, H.; Xiao, S.; Zhang, X.; Hu, W. Surface Segregation and Chemical Ordering Patterns of Ag–Pd Nanoalloys: Energetic Factors, Nanoscale Effects, and Catalytic Implication. J. Phys. Chem. C 2014, 118, 27850–27860. [Google Scholar] [CrossRef]
- Calvo, F. Thermodynamics of Nanoalloys. Phys. Chem. Chem. Phys. 2015, 17, 27922–27939. [Google Scholar] [CrossRef]
- Cui, M.; Yang, C.; Hwang, S.; Yang, M.; Overa, S.; Dong, Q.; Yao, Y.; Brozena, A.H.; Cullen, D.A.; Chi, M.; et al. Multi-Principal Elemental Intermetallic Nanoparticles Synthesized via a Disorder-to-Order Transition. Sci. Adv. 2022, 8, eabm4322. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Chen, D.P.; Sang, X.; Unocic, R.R.; Skrabalak, S.E. Size-Dependent Disorder–Order Transformation in the Synthesis of Monodisperse Intermetallic PdCu Nanocatalysts. ACS Nano 2016, 10, 6345–6353. [Google Scholar] [CrossRef] [PubMed]
- Keuler, J.N.; Lorenzen, L. Developing a Heating Procedure to Optimise Hydrogen Permeance through Pd–Ag Membranes of Thickness Less than 2.2 Μm. J. Membr. Sci. 2002, 195, 203–213. [Google Scholar] [CrossRef]
- Wang, D.; Flanagan, T.B.; Shanahan, K. Diffusion of H through Pd-Ag Alloys (423–523 K). J. Phys. Chem. B 2008, 112, 1135–1148. [Google Scholar] [CrossRef]
- Tosti, S.; Borgognoni, F.; Santucci, A. Electrical Resistivity, Strain and Permeability of Pd–Ag Membrane Tubes. Int. J. Hydrogen Energy 2010, 35, 7796–7802. [Google Scholar] [CrossRef]
- Lindau, R.; Möslang, A. Mechanical and Microstructural Properties of Tritium Permeable PdAg Alloy after Helium Implantation. J. Nucl. Mater. 1992, 191, 178–182. [Google Scholar] [CrossRef]
- Luo, H.; Liu, W.; Ma, Y.; Xiao, D.; Liang, C. Unraveling L12Al3X (X = Ti, Zr, Hf) Nano-Precipitate Evolution in Aluminum Alloys via Multi-Scale Diffusion Simulation. J. Mater. Res. Technol. 2024, 30, 7104–7114. [Google Scholar] [CrossRef]
- Othman, P.N.A.M.; Karim, N.A.; Kamarudin, S.K. First Principle Study of the Electronic and Catalytic Properties of Palladium-Silver (PdAg) Alloys Catalyst for Direct Liquid Fuel Cells. Chem. Phys. 2023, 564, 111711. [Google Scholar] [CrossRef]
- Farberow, C.A.; Godinez-Garcia, A.; Peng, G.; Perez-Robles, J.F.; Solorza-Feria, O.; Mavrikakis, M. Mechanistic Studies of Oxygen Reduction by Hydrogen on PdAg(110). ACS Catal. 2013, 3, 1622–1632. [Google Scholar] [CrossRef]
- Li, Q.; Song, L.; Pan, L.; Chen, Y.; Ling, M.; Zhuang, X.; Zhang, X. Density Functional Theory Studies of Electronic Properties of PdAg/Pd Surface Alloys. Appl. Surf. Sci. 2014, 288, 69–75. [Google Scholar] [CrossRef]
- Zunger, A.; Wei, S.-H.; Ferreira, L.G.; Bernard, J.E. Special Quasirandom Structures. Phys. Rev. Lett. 1990, 65, 353–356. [Google Scholar] [CrossRef] [PubMed]
- Ding, J.; Zhu, W.; Ma, Y.; Liu, W.; Huang, Y.; Liang, C. Evaluation of Phase Relationship in W-Fe-C Ternary System through Symmetry Principles and First-Principles Calculation. Mater. Des. 2022, 224, 111376. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab Initio Molecular Dynamics for Liquid Metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, Molecules, Solids, and Surfaces: Applications of the Generalized Gradient Approximation for Exchange and Correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef]
- Liu, L.C.; Wang, J.W.; Qian, J.; He, Y.H.; Gong, H.R.; Liang, C.P.; Zhou, S.F. Fundamental Effects of Ag Alloying on Hydrogen Behaviors in PdCu. J. Membr. Sci. 2018, 550, 230–237. [Google Scholar] [CrossRef]
- Methfessel, M.; Paxton, A.T. High-Precision Sampling for Brillouin-Zone Integration in Metals. Phys. Rev. B 1989, 40, 3616–3621. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E.; Jepsen, O.; Andersen, O.K. Improved Tetrahedron Method for Brillouin-Zone Integrations. Phys. Rev. B 1994, 49, 16223–16233. [Google Scholar] [CrossRef]
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. 1952, 65, 349. [Google Scholar] [CrossRef]
- Reuss, A. Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. Z. Angew. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for Three-Dimensional Visualization of Crystal, Volumetric and Morphology Data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Hart, G.L.W.; Nelson, L.J.; Vanfleet, R.R.; Campbell, B.J.; Sluiter, M.H.F.; Neethling, J.H.; Olivier, E.J.; Allies, S.; Lang, C.I.; Meredig, B.; et al. Revisiting the Revised Ag-Pt Phase Diagram. Acta Mater. 2017, 124, 325–332. [Google Scholar] [CrossRef]
- Liang, J.; Xia, Y.; Liu, X.; Huang, F.; Liu, J.; Li, S.; Wang, T.; Jiao, S.; Cao, R.; Han, J.; et al. Molybdenum-doped Ordered L10-PdZn Nanosheets for Enhanced Oxygen Reduction Electrocatalysis. SusMat 2022, 2, 347–356. [Google Scholar] [CrossRef]
- Volkova, E.G.; Novikova, O.S.; Volkov, A.Y. Formation of the L12-Type Superstructure in Cu-5.9 at.%Pd and Cu-8 at%Pd Alloys. IOP Conf. Ser. Mater. Sci. Eng. 2018, 447, 012029. [Google Scholar] [CrossRef]
- Yu, G.; Cheng, T.; Zhang, X.; Gong, W. Pressure-Induced Two Magnetic Collapses in the Ferromagnetic L12-Fe3Pd Alloy and Related Elasticity and Lattice Dynamics Anomalies. J. Magn. Magn. Mater. 2021, 538, 168322. [Google Scholar] [CrossRef]
- Zharkov, S.M.; Moiseenko, E.T.; Altunin, R.R. L10 Ordered Phase Formation at Solid State Reactions in Cu/Au and Fe/Pd Thin Films. J. Solid State Chem. 2019, 269, 36–42. [Google Scholar] [CrossRef]
- Zhou, M.; Liu, J.; Ling, C.; Ge, Y.; Chen, B.; Tan, C.; Fan, Z.; Huang, J.; Chen, J.; Liu, Z.; et al. Synthesis of Pd3Sn and PdCuSn Nanorods with L12Phase for Highly Efficient Electrocatalytic Ethanol Oxidation. Adv. Mater. 2022, 34, 2106115. [Google Scholar] [CrossRef]
- Von Pezold, J.; Dick, A.; Friák, M.; Neugebauer, J. Generation and Performance of Special Quasirandom Structures for Studying the Elastic Properties of Random Alloys: Application to Al-Ti. Phys. Rev. B 2010, 81, 094203. [Google Scholar] [CrossRef]
- Delczeg-Czirjak, E.K.; Delczeg, L.; Ropo, M.; Kokko, K.; Punkkinen, M.P.J.; Johansson, B.; Vitos, L. Ab Initio Study of the Elastic Anomalies in Pd-Ag Alloys. Phys. Rev. B 2009, 79, 085107. [Google Scholar] [CrossRef]
- Hultgren, R.; Desai, P.D.; Hawkins, D.T.; Gleiser, M.; Kelley, K.K. Selected Values of the Thermodynamic Properties of the Elements; American Society for Metals: Metals Park, OH, USA, 1973; pp. 264–267. [Google Scholar]
- Yu, R.; Zhu, J.; Ye, H.Q. Calculations of Single-Crystal Elastic Constants Made Simple. Comput. Phys. Commun. 2010, 181, 671–675. [Google Scholar] [CrossRef]
- Neighbours, J.R.; Alers, G.A. Elastic Constants of Silver and Gold. Phys. Rev. 1958, 111, 707–712. [Google Scholar] [CrossRef]
- Hsu, D.K.; Leisure, R.G. Elastic Constants of Palladium and β-Phase Palladium Hydride between 4 and 300 K. Phys. Rev. B 1979, 20, 1339–1344. [Google Scholar] [CrossRef]
- Zener, C. Contributions to the Theory of Beta-Phase Alloys. Phys. Rev. 1947, 71, 846–851. [Google Scholar] [CrossRef]
- Nakashima, P.N.H.; Smith, A.E.; Etheridge, J.; Muddle, B.C. The Bonding Electron Density in Aluminum. Science 2011, 331, 1583–1586. [Google Scholar] [CrossRef]
- Anderson, O.L. A Simplified Method for Calculating the Debye Temperature from Elastic Constants. J. Phys. Chem. Solids 1963, 24, 909–917. [Google Scholar] [CrossRef]
- Lin, C.-K.; Lin, Y.-G.; Wu, T.; Barkholtz, H.M.; Lin, Q.; Wei, H.; Brewe, D.L.; Miller, J.T.; Liu, D.-J.; Ren, Y.; et al. Direct Synthesis of Bimetallic Pd3Ag Nanoalloys from Bulk Pd3Ag Alloy. Inorg. Chem. 2012, 51, 13281–13288. [Google Scholar] [CrossRef] [PubMed]
- Smirnova, N.S.; Baeva, G.N.; Markov, P.V.; Mashkovsky, I.S.; Bukhtiyarov, A.V.; Zubavichus, Y.V.; Stakheev, A.Y. In Situ FTIR Study of Surface Site Transformations in Pd3In/α-Al2O3 and Pd3Ag/α-Al2O3 Induced by CO Adsorption. Mendeleev Commun. 2022, 32, 807–809. [Google Scholar] [CrossRef]
- Santoveña-Uribe, A.; Maya-Cornejo, J.; Bahena, D.; Ledesma, J.; Pérez, R.; Esparza, R. Synthesis and Characterization of AgPd Bimetallic Nanoparticles as Efficient Electrocatalysts for Oxygen Reduction Reaction. Electrocatalysis 2020, 11, 536–545. [Google Scholar] [CrossRef]
- Hosseinian, E.; Gupta, S.; Pierron, O.N.; Legros, M. Size Effects on Intergranular Crack Growth Mechanisms in Ultrathin Nanocrystalline Gold Free-Standing Films. Acta Mater. 2018, 143, 77–87. [Google Scholar] [CrossRef]
- Liu, J.; Bellini, S.; De Nooijer, N.C.A.; Sun, Y.; Pacheco Tanaka, D.A.; Tang, C.; Li, H.; Gallucci, F.; Caravella, A. Hydrogen Permeation and Stability in Ultra-Thin Pd Ru Supported Membranes. Int. J. Hydrogen Energy 2020, 45, 7455–7467. [Google Scholar] [CrossRef]
- Wunsch, A.; Gapp, E.; Peters, T.; Pfeifer, P. Impact of Product Gas Impurities from Dehydrogenation of Perhydro-Dibenzyltoluene on the Performance of a 10 Μm PdAg-Membrane. J. Membr. Sci. 2021, 628, 119094. [Google Scholar] [CrossRef]
- Alí, M.L.; Crespo, E.A.; Ruda, M.; Bringa, E.M.; Ramos, S.B. Hydrogen Effects on the Mechanical Properties of Nanocrystalline Free-Standing Palladium Thin Films. Int. J. Hydrogen Energy 2020, 45, 15213–15225. [Google Scholar] [CrossRef]
- Wang, F.; Liu, H.; Tang, S.; Ma, Y.; Liu, W.; Liang, C. Effects of Order-Disorder Transition on Phase Relationship, Elastic Strength, and Mechanical Anisotropy of Al-Li Alloys. Materialia 2022, 24, 101483. [Google Scholar] [CrossRef]
- Ranganathan, S.I.; Ostoja-Starzewski, M. Universal Elastic Anisotropy Index. Phys. Rev. Lett. 2008, 101, 055504. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Wang, F.; Tang, S.; Ma, Y.; Liu, W.; Liang, C. Unraveling the Leverage Effect in Phases Stability and Mechanical Properties of Al-Zn-Mg-Cu Alloy. J. Alloys Compd. 2024, 982, 173763. [Google Scholar] [CrossRef]
- Wang, S.F.; Dougherty, J.P.; Huebner, W.; Pepin, J.G. Silver-Palladium Thick-Film Conductors. J. Am. Ceram. Soc. 1994, 77, 3051–3072. [Google Scholar] [CrossRef]
- Mandal, K. Time-Dependent Synthesis of Pd0.5Ag0.5 Nano-Catalysts and Their Catalytic Performance in the Decomposition of Formic Acid. J. Indian Chem. Soc. 2024, 101, 101137. [Google Scholar] [CrossRef]
- Liu, H.; Tang, S.; Ma, Y.; Liu, W.; Liang, C. Short-Range Ordering Governs Brittleness and Ductility in W-Ta Solid Solution: Insights from Pugh’s Shear-to-Bulk Modulus Ratio. Scr. Mater. 2021, 204, 114136. [Google Scholar] [CrossRef]
- Yan, Z.; Cui, L.; Shi, K.; Zhang, M.; Pang, Z.; Guo, J.; Gao, R.; Hao, H. Theoretical Study the Influence of Partial Substitute Noble Metal Pd/Ag of PdAg-Based Catalyst by Non-Noble Metal Ni/Cu for 1,3-Butadiene Hydrogenation. Appl. Surf. Sci. 2022, 588, 152897. [Google Scholar] [CrossRef]
- Marmier, A. ElAM: A Computer Program for the Analysis and Representation of Anisotropic Elastic Properties. Comput. Phys. Commun. 2010, 181, 2102–2115. [Google Scholar] [CrossRef]
- Sanders, P.G.; Eastman, J.A.; Weertman, J.R. Elastic and Tensile Behavior of Nanocrystalline Copper and Palladium. Acta Mater. 1997, 45, 4019–4025. [Google Scholar] [CrossRef]
- Trappeniers, N.J.; Biswas, S.N.; Ten Seldam, C.A. Effect of Pressure on the Shear Modulus of Polycrystalline Aluminium, Copper and Silver. Phys. BC 1976, 85, 20–32. [Google Scholar] [CrossRef]
- McCarthy, E.K.; Bellew, A.T.; Sader, J.E.; Boland, J.J. Poisson’s Ratio of Individual Metal Nanowires. Nat. Commun. 2014, 5, 4336. [Google Scholar] [CrossRef] [PubMed]
- Alimov, V.N.; Busnyuk, A.O.; Notkin, M.E.; Livshits, A.I. Pd–V–Pd Composite Membranes: Hydrogen Transport in a Wide Pressure Range and Mechanical Stability. J. Membr. Sci. 2014, 457, 103–112. [Google Scholar] [CrossRef]
- Bhargav, A.; Jackson, G.S.; Ciora, R.J., Jr.; Liu, P.T.K. Model Development and Validation of Hydrogen Transport through Supported Palladium Membranes. J. Membr. Sci. 2010, 356, 123–132. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Luo, G.; Cao, Y.; Liang, C. Effect of Atomic Ordering on Phase Stability and Elastic Properties of Pd-Ag Alloys. Metals 2024, 14, 1017. https://doi.org/10.3390/met14091017
Chen X, Luo G, Cao Y, Liang C. Effect of Atomic Ordering on Phase Stability and Elastic Properties of Pd-Ag Alloys. Metals. 2024; 14(9):1017. https://doi.org/10.3390/met14091017
Chicago/Turabian StyleChen, Xiaoli, Guangxiong Luo, Yuxuan Cao, and Chaoping Liang. 2024. "Effect of Atomic Ordering on Phase Stability and Elastic Properties of Pd-Ag Alloys" Metals 14, no. 9: 1017. https://doi.org/10.3390/met14091017
APA StyleChen, X., Luo, G., Cao, Y., & Liang, C. (2024). Effect of Atomic Ordering on Phase Stability and Elastic Properties of Pd-Ag Alloys. Metals, 14(9), 1017. https://doi.org/10.3390/met14091017




