Damping and Compressive Properties of SLM-Fabricated Rhombic Dodecahedron-Structured Ni–Ti Shape Memory Alloy Foams
Abstract
:1. Introduction
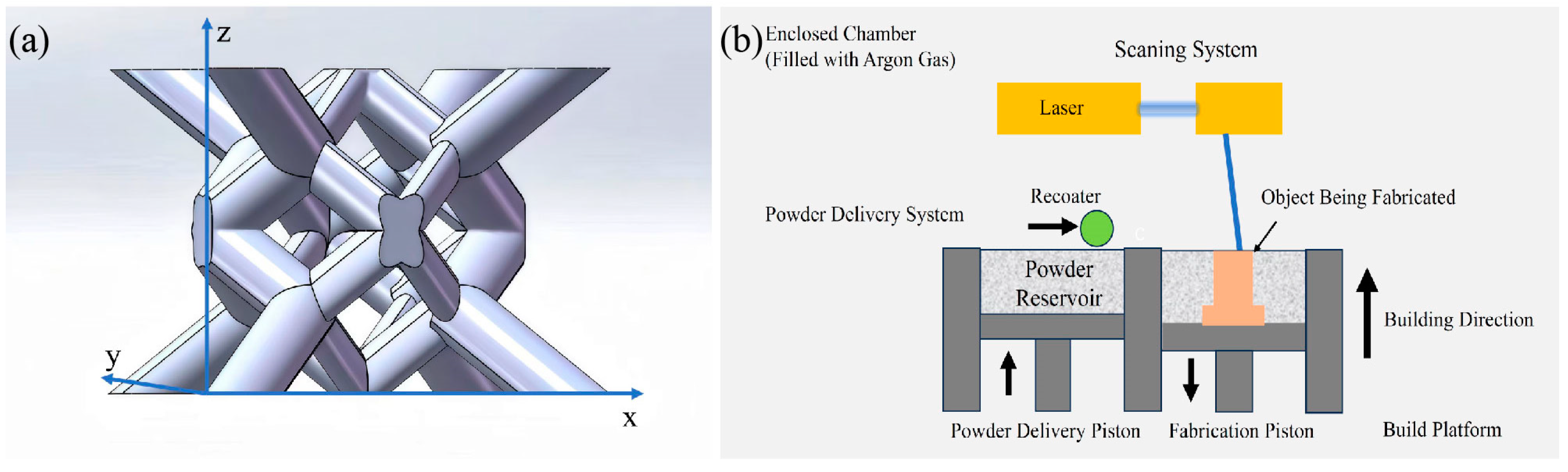
2. Materials and Methods
3. Results and Discussion
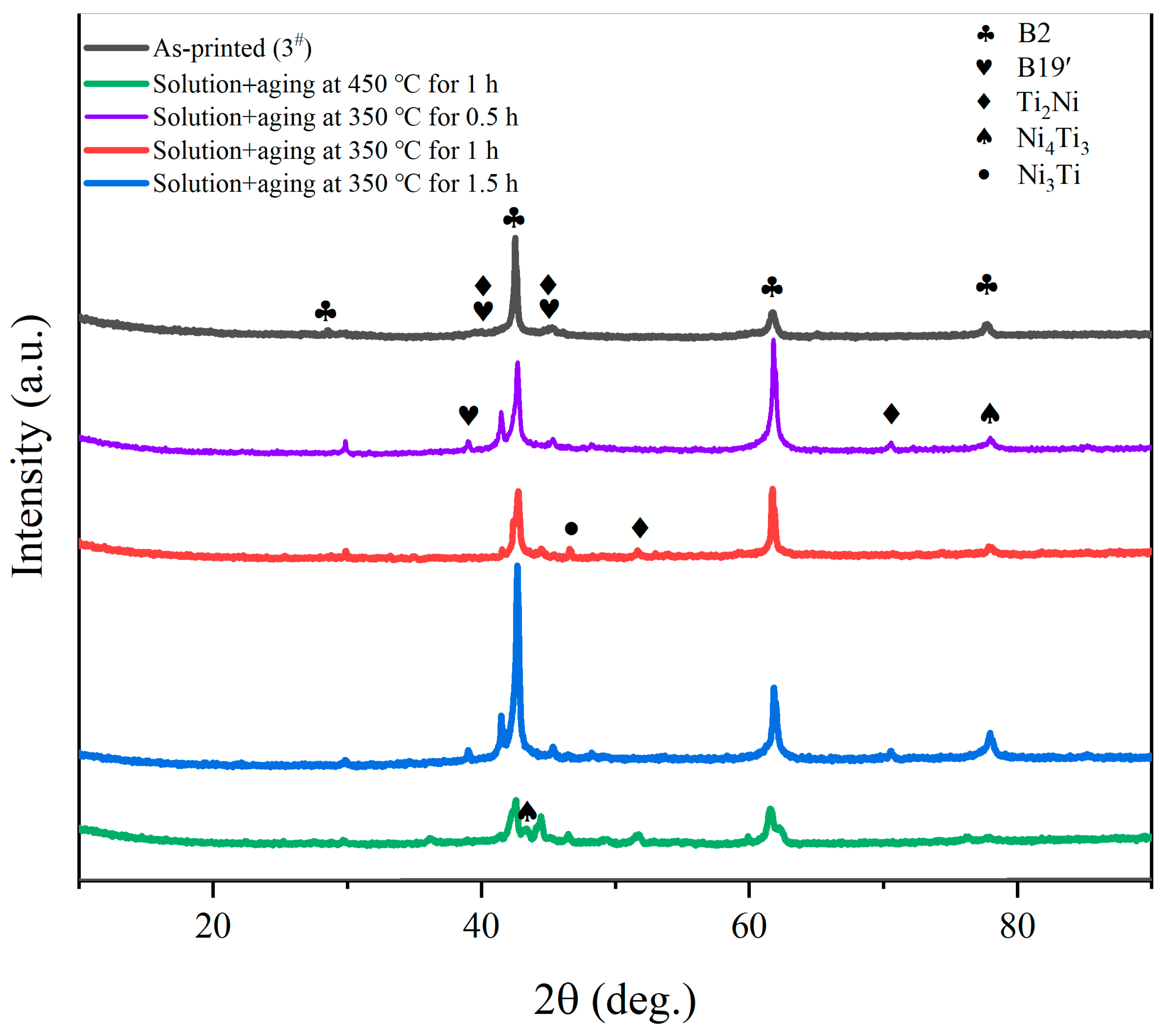
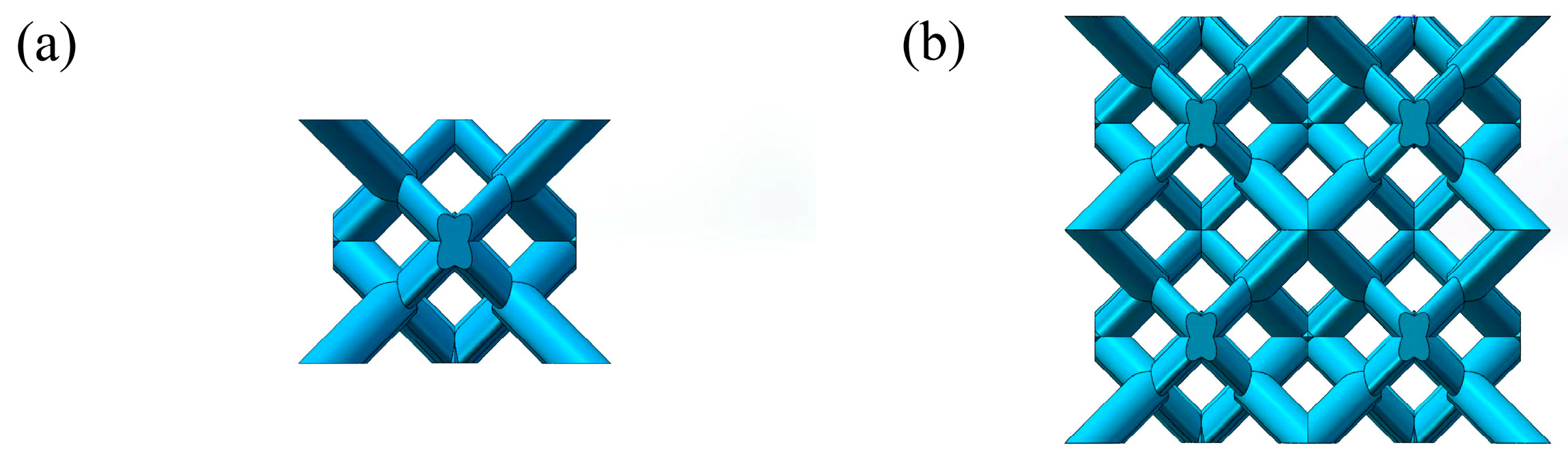
3.1. Characterization of Macroscopic Morphologies and Microstructures
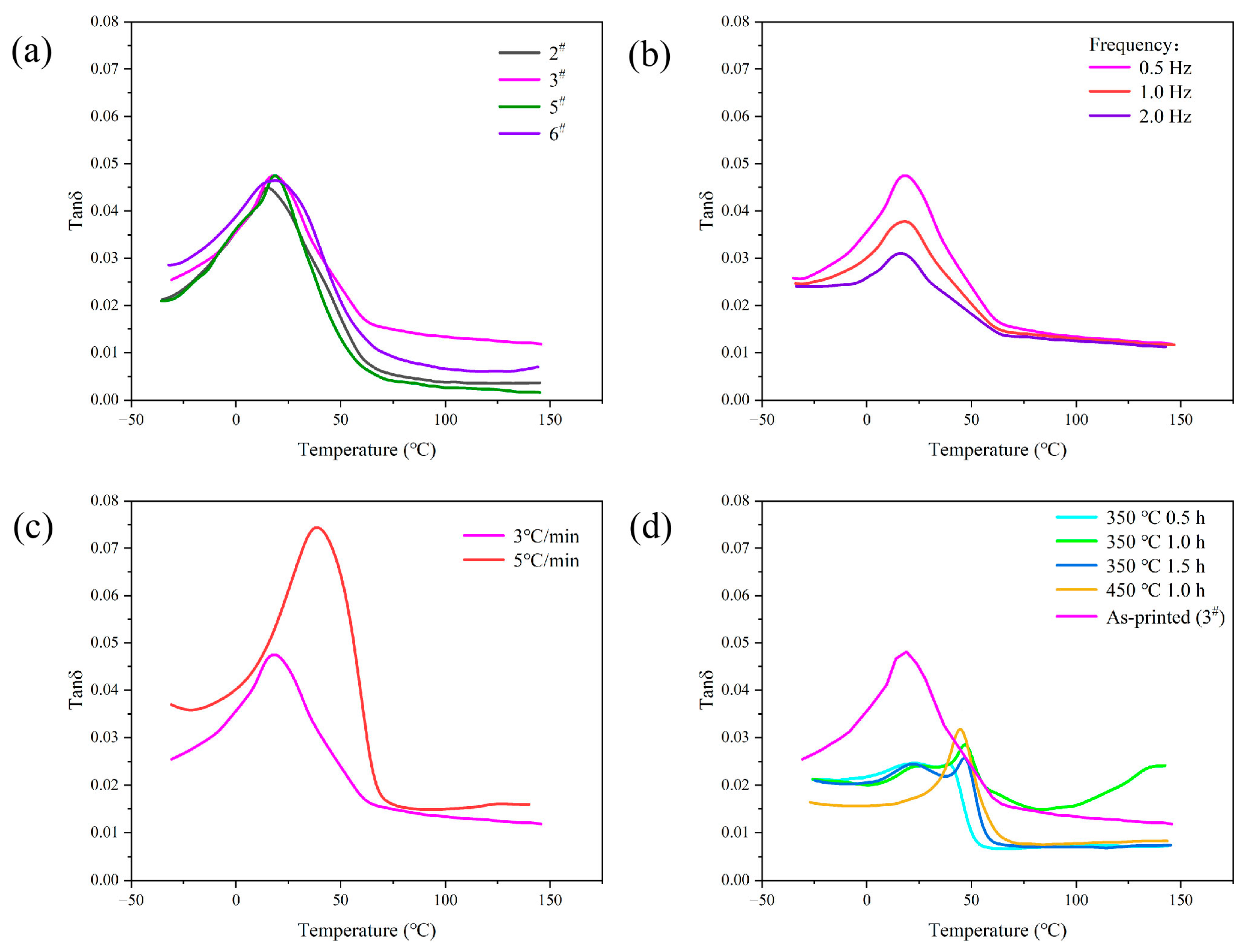
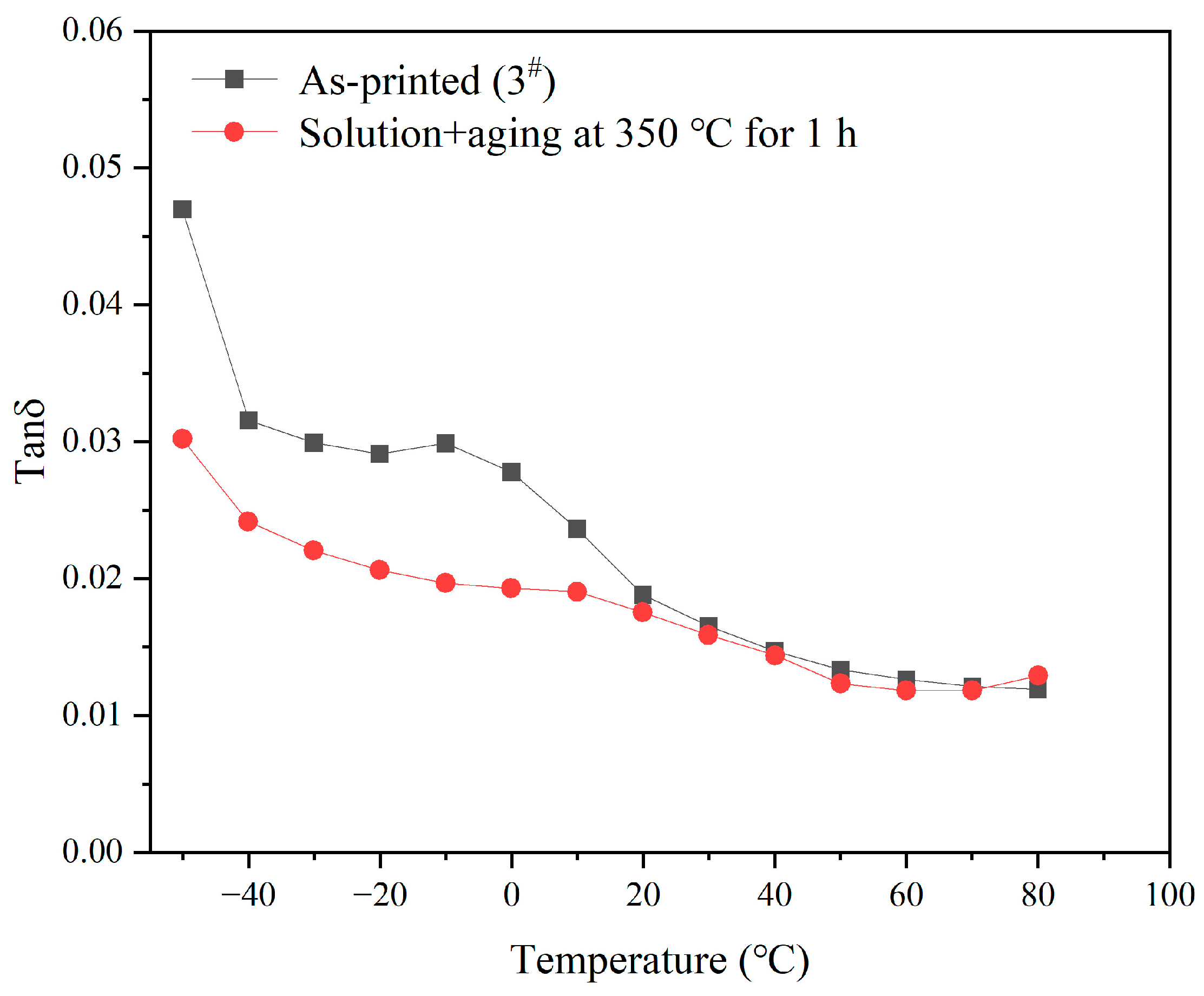
3.2. Property Tests and Mechanism Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, B.; Yu, C.; Wang, C.; Kan, Q.H.; Wang, Q.Y.; Kang, G.Z. Effect of pore on the deformation behaviors of NiTi shape memory alloys: A crystal-plasticity-based phase field modeling. Int. J. Plast. 2024, 175, 103931. [Google Scholar] [CrossRef]
- Hu, L.; Shen, Z.Y.; Chen, X.J.; Hu, K.Y.; Tang, M.; Wang, L. Microstructure characteristics of porous NiTi shape memory alloy synthesized by powder metallurgy during compressive deformation at room temperature. Metals 2023, 13, 1806. [Google Scholar] [CrossRef]
- Zhang, Y.T.; Wei, D.X.; Chen, Y.; Xie, L.C.; Wang, L.Q.; Zhang, L.C.; Lu, W.J.; Chen, G. Non-negligible role of gradient porous structure in superelasticity deterioration and improvement of NiTi shape memory alloys. J. Mater. Sci. Technol. 2024, 186, 48–63. [Google Scholar] [CrossRef]
- Sun, L.Q.; Chen, K.Y.; Geng, P.; Zhou, Y.; Wen, S.F.; Shi, Y.S. Mechanical and shape memory properties of NiTi triply periodic minimal surface structures fabricated by laser powder bed fusion. J. Manuf. Process. 2023, 101, 1091–1100. [Google Scholar] [CrossRef]
- Lai, T.; Xu, J.L.; Xiao, Q.F.; Tong, Y.X.; Huang, J.; Zhang, J.P.; Luo, J.M.; Liu, Y. Preparation and characterization of porous NiTi alloys synthesized by microwave sintering using Mg space holder. Trans. Nonferrous Met. Soc. China 2021, 31, 485–498. [Google Scholar] [CrossRef]
- Guo, W.; Kato, H. Submicron-porous NiTi and NiTiNb shape memory alloys with high damping capacity fabricated by a new top-down process. Mater. Des. 2015, 78, 74–79. [Google Scholar] [CrossRef]
- Andani, M.T.; Saedi, S.; Turabi, A.S.; Karamooz, M.R.; Haberland, C.; Karaca, H.E.; Elahinia, M. Mechanical and shape memory properties of porous Ni50.1Ti49.9 alloys manufactured by selective laser melting. J. Mech. Behav. Biomed. Mater. 2017, 68, 224–231. [Google Scholar] [CrossRef]
- Li, S.; Hassanin, H.; Attallah, M.M.; Adkins, N.J.E.; Essa, K. The development of TiNi-based negative Poisson’s ratio structure using selective laser melting. Acta Mater. 2016, 105, 75–83. [Google Scholar] [CrossRef]
- Bertheville, B. Porous single-phase Ni-Ti processed under Ca reducing vapor for use as a bone graft substitute. Biomaterials 2006, 27, 1246–1250. [Google Scholar] [CrossRef]
- Salvetr, P.; Pecenová, Z.; Školáková, A.; Novák, P. Innovative technology for preparation of seamless nitinol tubes using SHS without forming. Metall. Mater. Trans. A 2017, 48, 1524–1527. [Google Scholar] [CrossRef]
- Zhu, B.; Li, D.Y.; Du, C.H.; Wan, Z.C.; Zhou, Y.; Shu, C.; Luo, F.H.; Li, Y.M. Near-spherical micron-porous NiTi alloys with high performances fabricated via metal injection molding. Mater. Sci. Eng. A 2024, 892, 146114. [Google Scholar] [CrossRef]
- Meng, J.; Qiao, Y.; Chen, Y.; Liu, T.W.; Li, T.; Wang, H.Y.; Dai, L.H. A high-entropy alloy syntactic foam with exceptional cryogenic and dynamic properties. Mater. Sci. Eng. A 2023, 876, 145146. [Google Scholar] [CrossRef]
- Liu, J.A.; Liu, S.J.; Wang, B.; Sun, W.B.; Liu, X.J.; Han, Z.W. Compressive property and energy absorption characteristic of interconnected porous Mg-Zn-Y alloys with adjusting Y addition. J. Magnes. Alloys 2024, 12, 171–185. [Google Scholar] [CrossRef]
- Dmimitrova, R.; Simeonova, T.; Krastev, B.; Velikov, A.; Petkov, V.; Manolov, V. Al and A356 alloy foam castings modified with low concentrations of nano-aized particles: Structural study and compressive strength tests. Metals 2024, 14, 542. [Google Scholar] [CrossRef]
- Singh, P.; Shrivastava, V.; Abhash, A.; Yadav, B.N.; Singh, L.B.; Mondal, D.P. Compressive deformation and corrosion behaviour of moderate to highly porous Ti4Al4Co (wt%) alloy foam. Mater. Chem. Phys. 2021, 257, 123718. [Google Scholar] [CrossRef]
- Yang, X.; Ma, W.J.; Gu, W.P.; Zhang, Z.Y.; Wang, B.; Wang, Y.; Liu, S. Multi-scale microstructure high-strength titanium alloy lattice structure manufactured via selective laser melting. RSC Adv. 2021, 11, 22734. [Google Scholar] [CrossRef]
- Novak, N.; Al-Ketan, O.; Mauko, A.; Yilmaz, Y.E.; Opara, L.K.; Tanaka, S.; Hokamoto, K.; Rowshan, R.; Al-Rub, R.A.; Vesenjak, M.; et al. Impact loading of additively manufactured metallic stochastic sheet-based cellular material. Int. J. Impact Eng. 2023, 174, 104527. [Google Scholar] [CrossRef]
- Xue, Z.Y.; Hutchinson, J.W. A comparative study of impulse-resistant metal sandwich plates. Int. J. Impact Eng. 2004, 30, 1283–1305. [Google Scholar] [CrossRef]
- Gümrük, R.; Mines, R.A.W. Compressive behaviour of stainless steel micro-lattice structures. Int. J. Mech. Sci. 2013, 68, 125–139. [Google Scholar] [CrossRef]
- Yang, Z.L.; Liu, H.; Wu, Q.; Long, L. Study of energy absorption characteristics and deformation mechanism of stretching–bending synergistic lattices under dynamic compression. Adv. Eng. Mater. 2022, 25, 2201130. [Google Scholar] [CrossRef]
- Fallahi, H.; Sadighi, M.; Samandari, S.S. Compressive mechanical properties of open-cell cubic and rhombic dodecahedron lattice structures of variable cross section fabricated by fused deposition modeling. Mech. Mater. 2023, 184, 104712. [Google Scholar] [CrossRef]
- Ozdemir, Z.; Nava, E.H.; Tyas, A.; Warren, J.A.; Fay, S.D.; Goodall, R.; Todd, I.; Askes, H. Energy absorption in lattice structures in dynamics: Experiments. Int. J. Impact Eng. 2016, 89, 49–61. [Google Scholar] [CrossRef]
- Xiao, L.J.; Song, W.D.; Wang, C.; Tang, H.P.; Fan, Q.B.; Liu, N.; Wang, J.Z. Mechanical properties of open-cell rhombic dodecahedron titanium alloy lattice structure manufactured using electron beam melting under dynamic loading. Int. J. Impact Eng. 2017, 100, 75–89. [Google Scholar] [CrossRef]
- Xiao, L.J.; Song, W.D.; Wang, C.; Tang, H.P.; Fan, Q.B.; Liu, N.; Wang, J.Z. Mechanical behavior of open-cell rhombic dodecahedron Ti–6Al–4V lattice structure. Mater. Sci. Eng. A 2015, 640, 375–384. [Google Scholar] [CrossRef]
- Babaee, S.; Jahromi, B.H.; Ajdari, A.; Nayeb-Hashemi, H.; Vaziri, A. Mechanical properties of open-cell rhombic dodecahedron cellular structures. Acta Mater. 2012, 60, 2873–2885. [Google Scholar] [CrossRef]
- Babamiri, B.B.; Askari, H.; Hazeli, K. Deformation mechanisms and post-yielding behavior of additively manufactured lattice structures. Mater. Des. 2020, 188, 108443. [Google Scholar] [CrossRef]
- Epasto, G.; Palomba, G.; D’Andrea, D.; Bella, D.S.; Mineo, D.R.; Guglielmino, E.; Traina, F. Experimental investigation of rhombic dodecahedron micro-lattice structures manufactured by electron beam melting. Mater. Today 2019, 7, 578–585. [Google Scholar] [CrossRef]
- Yang, L.; Han, C.J.; Wu, H.; Hao, L.; Wei, Q.; Yan, C.; Shi, Y. Insights into unit cell size effect on mechanical responses and energy absorption capability of titanium graded porous structures manufactured by laser powder bed fusion. J. Mech. Behav. Biomed. Mater. 2020, 109, 103843. [Google Scholar] [CrossRef]
- Cao, X.F.; Duan, S.Y.; Liang, J.; Wen, W.B.; Fang, D. Mechanical properties of an improved 3D-printed rhombic dodecahedron stainless steel lattice structure of variable cross section. Int. J. Mech. Sci. 2018, 145, 53–63. [Google Scholar] [CrossRef]
- Cao, X.F.; Duan, S.Y.; Liang, J.; Wen, W.B.; Fang, D. Dynamic compressive behavior of a modified additively manufactured rhombic dodecahedron 316L stainless steel lattice structure. Thin-Walled Struct. 2020, 148, 106586. [Google Scholar] [CrossRef]
- Li, B.Q.; Wang, L.; Li, H.D.; Cui, G.; Su, B.X.; Yao, L.H.; Luo, L.S. Solidification characterization and its correlation with the mechanical properties and functional response of NiTi shape memory alloy manufactured by electron beam freeform fabrication. Addit. Manuf. 2021, 48, 102468. [Google Scholar] [CrossRef]
- Banhart, J.; Baumeister, J.; Weber, M. Damping properties of aluminium foams. Mater. Sci. Eng. A 1996, 205, 221–228. [Google Scholar] [CrossRef]
- Liu, Q.W.; Feng, Y.; Liu, B.C.; Xie, Q.; Zhou, J.J.; Zhang, G.H. Regulation of microstructure, phase transformation behavior, and enhanced high superelastic cycling stability in laser direct energy deposition NiTi shape memory alloys via aging treatment. Mater. Sci. Eng. A 2024, 915, 147207. [Google Scholar] [CrossRef]
- Lu, H.Z.; Liu, L.H.; Yang, C.; Luo, X.; Song, C.H.; Wang, Z.; Wang, J.; Su, Y.D.; Ding, Y.F.; Zhang, L.C.; et al. Simultaneous enhancement of mechanical and shape memory properties by heat-treatment homogenization of Ti2Ni precipitates in TiNi shape memory alloy fabricated by selective laser melting. J. Mater. Sci. Technol. 2022, 101, 205–216. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, D.; Bu, H.L.; Deng, L.L.; Liu, H.G.; Yuan, P.; Du, P.X.; Song, H.Z. XRD-based quantitative analysis of clay minerals using reference intensity ratios, mineral intensity factors, Rietveld, and full pattern summation methods: A critical review. Solid Earth Sci. 2018, 3, 16–29. [Google Scholar] [CrossRef]
- Zeng, C.Y.; Cao, S.; Li, Y.Y.; Zhao, Z.X.; Zhu, Z.W.; Wang, D.X.; Ma, X.; Zhang, X.P. Two-step constrained aging treatment enabled superior two-way shape memory effect and elevated R-phase transformation temperatures in a rapidly solidified Ni51Ti49 alloy. J. Alloys Compd. 2019, 785, 1180–1188. [Google Scholar] [CrossRef]
- Yi, J.C.; Wan, L.; Shu, T.; Zhang, X.W.; Liu, F.; Cheng, G.J. Unleashing multi-scale mechanical enhancement in NiTi shape memory alloy via annular intra-laser deposition with homogenized Ti2Ni nanoprecipitates. Acta Mater. 2024, 262, 119418. [Google Scholar] [CrossRef]
- Lee, T.J.; Kim, W.J. Effect of severe plastic deformation and post-deformation heat treatment on the microstructure and superelastic properties of Ti50.8Ni alloy. Materials 2022, 15, 7822. [Google Scholar] [CrossRef]
- Toker, G.P.; Saedi, S.; Acar, E.; Ozbulut, O.E.; Karaca, H.E. Loading frequency and temperature dependent damping capacity of NiTiHfPd shape memory alloy. Mech. Mater. 2020, 150, 103565. [Google Scholar] [CrossRef]
- Liu, S.; Zhu, J.; Lin, Y.; Wang, G.C.; Wang, X.B. Effect of stretching-bending deformation and aging treatment on phase transformation behavior and superelasticity of Ti-50.8 at.% Ni alloy. Intermetallics 2021, 129, 107051. [Google Scholar] [CrossRef]
- Pu, Z.; Du, D.; Zhang, D.Q.; Li, Z.X.; Xue, S.; Xi, R.; Wang, X.B.; Chang, B.H. Improvement of tensile superelasticity by aging treatment of NiTi shape memory alloys fabricated by electron beam wire-feed additive manufacturing. J. Mater. Sci. Technol. 2023, 145, 185–196. [Google Scholar] [CrossRef]
- Zhang, M.G.; Li, X.Z.; Wang, B.L.; Jiao, G.H.; Yang, Y.; Fang, X.W.; Huang, K. Prominent superelastic response induced by Ni4Ti3 phase in NiTi alloysfabricated via wire-arc directed energy deposition. Mater. Sci. Eng. A 2024, 897, 146366. [Google Scholar] [CrossRef]
- Sugimoto, K.; Mori, T.; Shiode, S. Effect of composition on the internal friction and Young’s modulus in γ-phase Mn-Cu alloys. Met. Sci. J. 1973, 7, 103–108. [Google Scholar] [CrossRef]
- Bidaux, J.E.; Schaller, R.; Beniot, W. Study of the h.c.p.-f.c.c. phase transformation in cobalt by acoustic measurements. Acta Metall. 1989, 37, 803–811. [Google Scholar] [CrossRef]
- Engene, B.; Yalçın, B. Experimental investigation on the mechanical properties of Ti6Al4V cellular structures produced with selective laser melting: Effects of rib thickness, unit cell type and orientation. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2024, 1–12. [Google Scholar] [CrossRef]
- Han, D.; Zhang, Y.; Zhang, X.Y.; Xie, Y.M.; Ren, X. Lightweight auxetic tubular metamaterials: Design and mechanical characteristics. Compos. Struct. 2023, 311, 116849. [Google Scholar] [CrossRef]
- Liu, H.Z.; Ma, H.W.; Cai, W.S.; Luo, X.; Wang, Z.; Song, C.H.; Yin, S.; Yang, C. Stable tensile recovery strain induced by a Ni4Ti 3 nanoprecipitate in a Ni50.4Ti49.6 shape memory alloy fabricated via selective laser melting. Acta Mater. 2021, 219, 117261. [Google Scholar] [CrossRef]
- Xu, J.L.; Bao, L.Z.; Liu, A.H.; Jin, X.F.; Luo, J.M.; Zhong, Z.C.; Zheng, Y.F. Effect of pore sizes on the microstructure and properties of the biomedical porous Ni-Ti SMAs prepared by microwave sintering. J. Alloys Compd. 2015, 645, 137–142. [Google Scholar] [CrossRef]
- Costanza, G.; Tata, M.E.; Libertini, R. Effect of temperature on the mechanical behavior of Ni-Ti shape memory sheets. In TMS2016 Annual Meeting Supplemental Proceedings; TMS, Ed.; The Minerals, Metals & Materials Society: Pittsburgh, PA, USA, 2016. [Google Scholar]










| Element | Ti | Ni | Fe | C | O | N |
| Content (wt.%) | 44.17 | 55.74 | 0.010 | 0.009 | 0.060 | 0.011 |
| Specimen Number | RDCS (x y z) | Rod Diameter (mm) |
|---|---|---|
| 1# | 2 mm × 2 mm × 2 mm | 0.2 |
| 2# | 2 mm × 2 mm × 2 mm | 0.4 |
| 3# | 2 mm × 2 mm × 2 mm | 0.6 |
| 4# | 3 mm × 3 mm × 3 mm | 0.2 |
| 5# | 3 mm × 3 mm × 3 mm | 0.4 |
| 6# | 3 mm × 3 mm × 3 mm | 0.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, D.; Wang, Q.; Liu, L.; Liu, S.; Cao, H.; Xie, J.; Yin, F. Damping and Compressive Properties of SLM-Fabricated Rhombic Dodecahedron-Structured Ni–Ti Shape Memory Alloy Foams. Metals 2025, 15, 335. https://doi.org/10.3390/met15030335
Guo D, Wang Q, Liu L, Liu S, Cao H, Xie J, Yin F. Damping and Compressive Properties of SLM-Fabricated Rhombic Dodecahedron-Structured Ni–Ti Shape Memory Alloy Foams. Metals. 2025; 15(3):335. https://doi.org/10.3390/met15030335
Chicago/Turabian StyleGuo, Di, Qingzhou Wang, Li Liu, Shuo Liu, Hao Cao, Jingxia Xie, and Fuxing Yin. 2025. "Damping and Compressive Properties of SLM-Fabricated Rhombic Dodecahedron-Structured Ni–Ti Shape Memory Alloy Foams" Metals 15, no. 3: 335. https://doi.org/10.3390/met15030335
APA StyleGuo, D., Wang, Q., Liu, L., Liu, S., Cao, H., Xie, J., & Yin, F. (2025). Damping and Compressive Properties of SLM-Fabricated Rhombic Dodecahedron-Structured Ni–Ti Shape Memory Alloy Foams. Metals, 15(3), 335. https://doi.org/10.3390/met15030335







