A Temperature Field Simulation of the Pressure Quenching Process of 18Cr2Ni2MoVNbA Gears
Abstract
:1. Introduction
2. Materials and Methods
2.1. Simulation Program
2.2. Mathematical Modeling
2.2.1. Governing Equations
2.2.2. Initial Conditions
2.2.3. Boundary Conditions
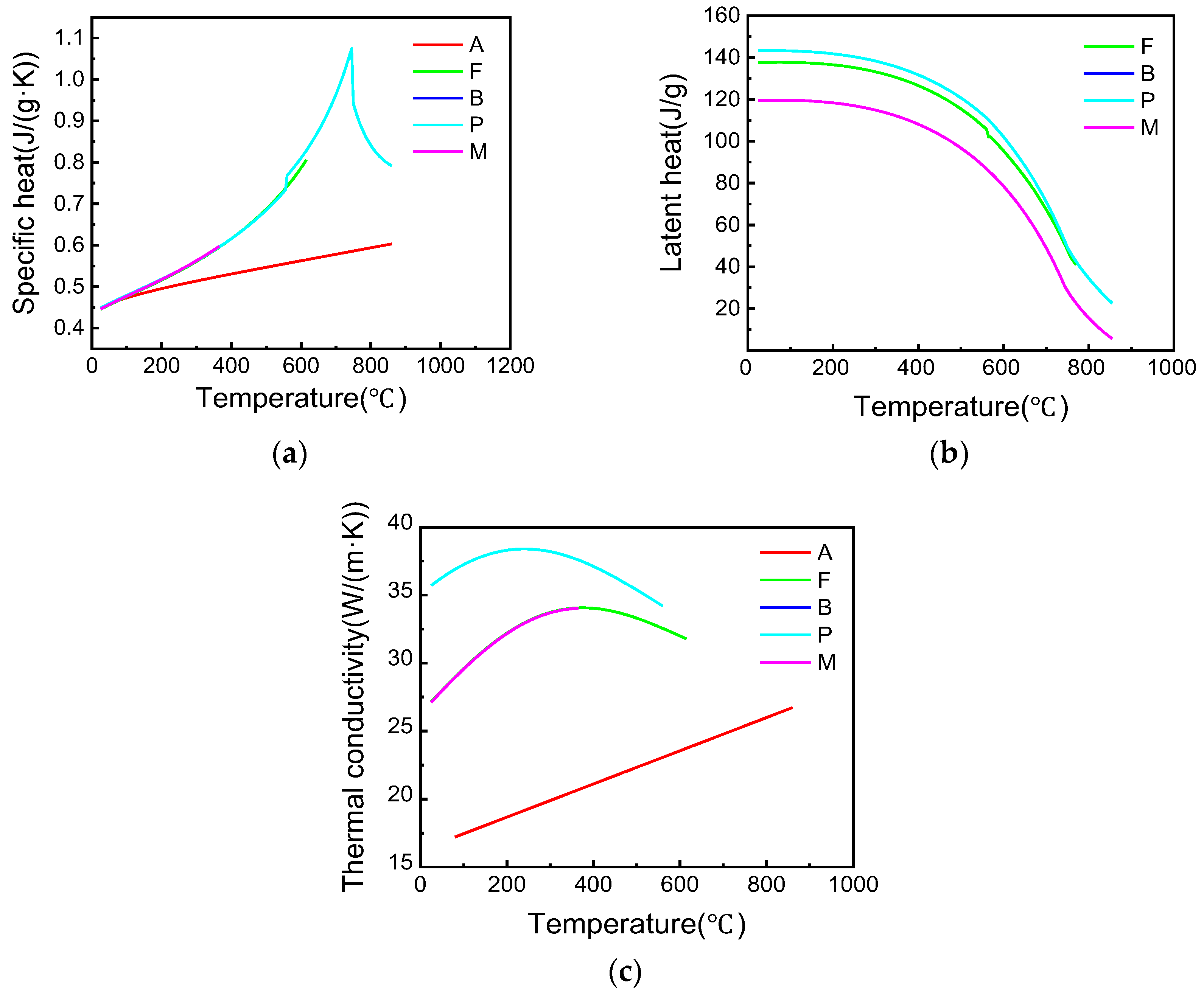
2.3. Determination of Material Parameters
2.3.1. Determination of the Rmophysical Parameters
2.3.2. Determination of the Heat Transfer Coefficient for Different Oil Flow Rates
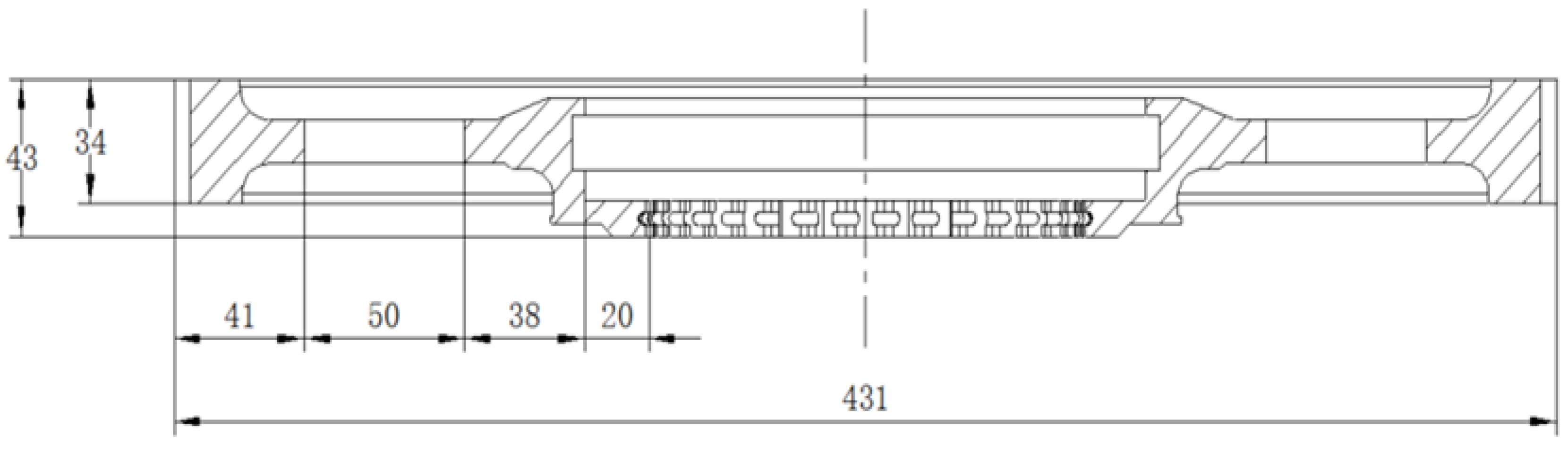
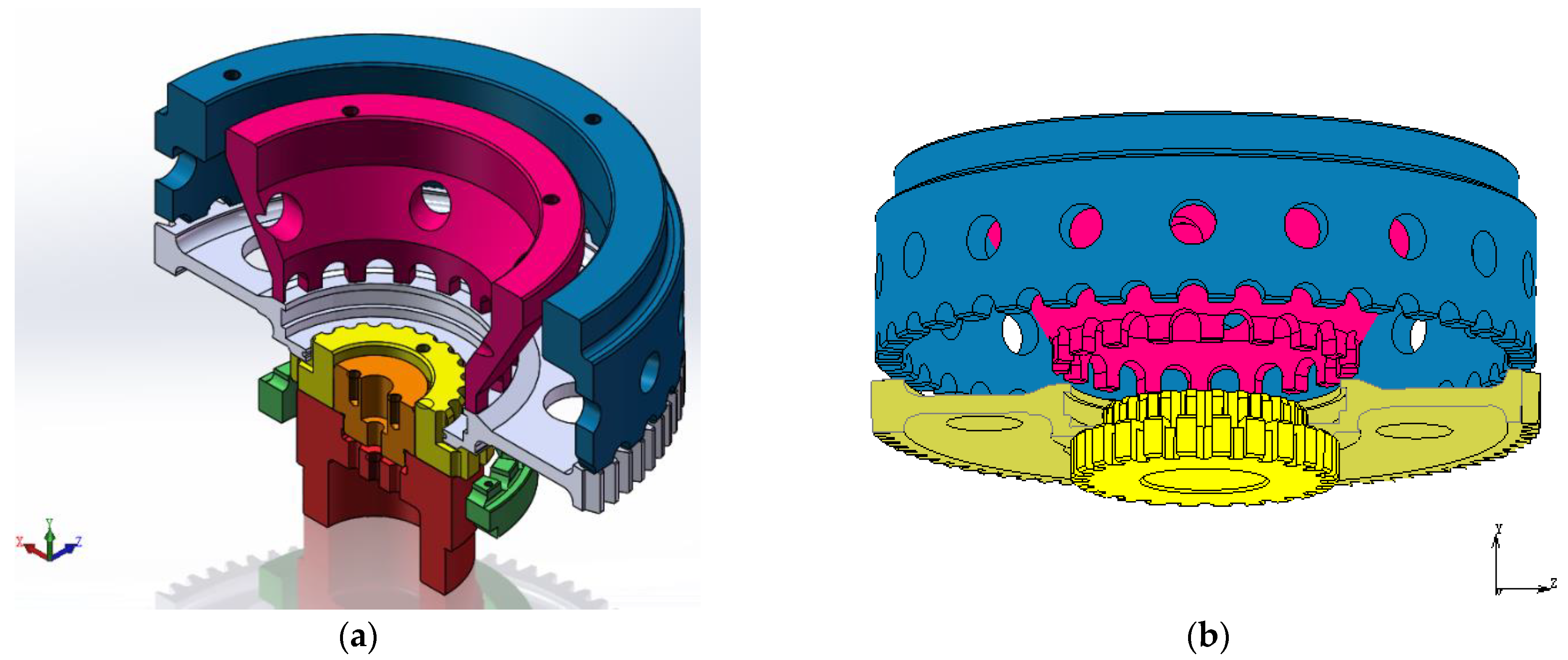
2.4. Finite Element Modeling
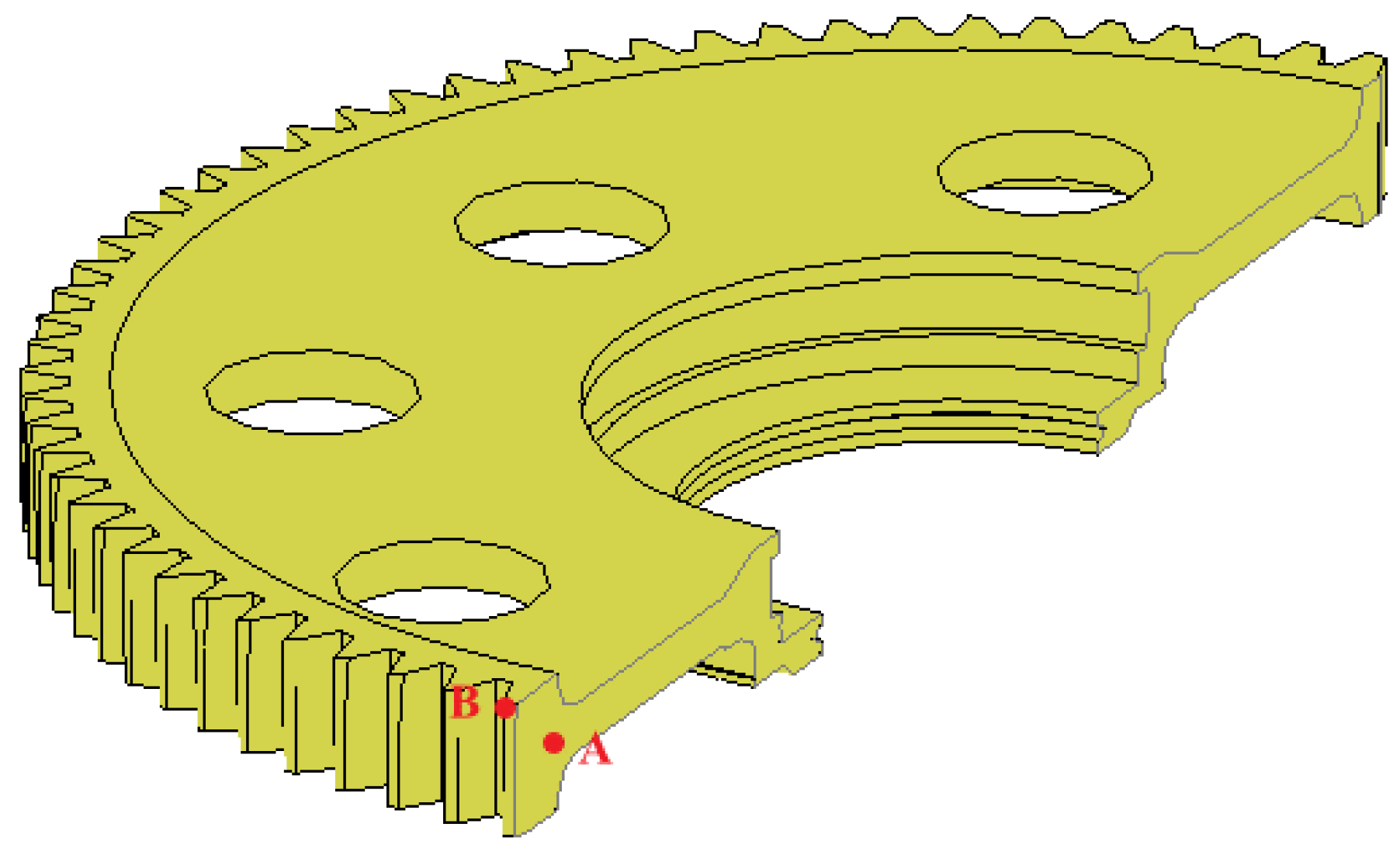
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yen, H.W.; Chiang, M.H.; Lin, Y.C.; Chen, D.; Huang, C.-Y.; Lin, H.-C. High-temperature tempered martensite embrittlement in quenched-and-tempered offshore steels. Metals 2017, 7, 253. [Google Scholar] [CrossRef]
- Liu, G.; Huang, C.; Zhao, B.; Wang, W.; Sun, S. Effect of Machined Surface Integrity on Fatigue Performance of Metal Workpiece: A Review. Chin. J. Mech. Eng. 2021, 34, 118. [Google Scholar] [CrossRef]
- Kiyak, M. Investigation of effects of cutting parameters on surface quality and hardness in the wire-EDM process. Int. J. Adv. Manuf. Technol. 2022, 119, 647–655. [Google Scholar] [CrossRef]
- Miao, S.; Ju, D.Y.; Chen, Y.; Liu, Y.-Q. Optimization based on orthogonal experiment design and numerical simulation for carburizing quenching process of helical gear. Mater. Perform. Charact. 2018, 8, 66–79. [Google Scholar] [CrossRef]
- Li, W.; Liu, B. Experimental investigation on the effect of shot peening on contact fatigue strength for carburized and quenched gears. Int. J. Fatigue 2018, 106, 103–113. [Google Scholar] [CrossRef]
- Zhi, L.; Jie, Y.; Li, S.-K.; Nie, W.-J.; Li, L.-X.; Wang, G. Study on inhomogeneous cooling behavior of extruded profile with unequal and large thicknesses during quenching using thermo-mechanical coupling model. Trans. Nonferrous Met. Soc. China 2020, 30, 1211–1226. [Google Scholar]
- Onishchenko, V. Investigation of tooth wears from scuffing of heavy duty machine spur gears. Mech. Mach. Theory 2015, 83, 38–55. [Google Scholar] [CrossRef]
- Shi, L.; Cui, X.; Li, J.; Jin, G.; Liu, J.; Tian, H. Improving the wear resistance of heavy-duty gear steels by cyclic carburizing. Tribol. Int. 2022, 171, 107576. [Google Scholar] [CrossRef]
- Iżowski, B.; Wojtyczka, A.; Motyka, M. Numerical Simulation of Low-Pressure Carburizing and Gas Quenching for Pyrowear 53 Steel. Metals 2023, 13, 371. [Google Scholar] [CrossRef]
- Li, X.; Ju, D.; Cao, J.; Wang, S.; Chen, Y.; He, F.; Li, H. Effect of Transformation Plasticity on Gear Distortion and Residual Stresses in Carburizing Quenching Simulation. Coatings 2021, 11, 1224. [Google Scholar] [CrossRef]
- Shao, W.; Yi, M.; Tang, J.; Sun, S. Prediction Minimization of the Heat Treatment Induced Distortion in 8620HSteel Gear: Simulation Experimental Verification. Chin. J. Mech. Eng 2022, 35, 126. [Google Scholar] [CrossRef]
- Pinheiro, P.M.; Junio, J.U.; Gonçalves, L.A.P.; da Costa, J.Â.P.; Ochoa, A.A.V.; Alves, K.G.B.; Leite, G.d.N.P.; Michima, P.S.A. Modeling and Simulation of the Induction Hardening Process: Evaluation of Gear Deformations and Parameter Optimization. Processes 2024, 12, 1428. [Google Scholar] [CrossRef]
- Liu, H.; Zhao, J.; Tang, J.; Shao, W.; Sun, B. Simulation and Experimental Verification of Die Quenching Deformation of Aviation Carburized Face Gear. Materials 2023, 16, 690. [Google Scholar] [CrossRef] [PubMed]
- Khan, D.; Gautham, B.P. Integrated modeling of carburizing-quenching-tempering of steel gears for an ICME framework. Integr. Mater. Manuf. Innov. 2018, 7, 28–41. [Google Scholar] [CrossRef]
- Li, J.; Feng, Y.; Zhang, H.; Min, N.; Wu, X. Thermomechanical Analysis of Deep Cryogenic Treatment of Navy C-Ring Specimen. J. Mater. Eng. Perform. 2014, 23, 4237–4250. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, G.; Shi, W.; Yang, L.; Li, Z. Modeling and Analysis of Deformation for Spiral Bevel Gear in Die Quenching Based on the Harden ability Variation. J. Mater. Eng. Perform. 2017, 26, 3034–3047. [Google Scholar] [CrossRef]
- Sun, Y.; Li, X.; Liu, C.; Deng, X.; Zhang, W.; Wang, J.; Zhang, Z.; Wen, T.; Song, T.; Ju, D. Development of an intelligent design and simulation aid system for heat treatment processes based on LLM. Mater. Des. 2024, 29, 113506. [Google Scholar] [CrossRef]
- Brokate, M.; Sprekels, J. Hysteresis and Phase Transitions; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1996. [Google Scholar]



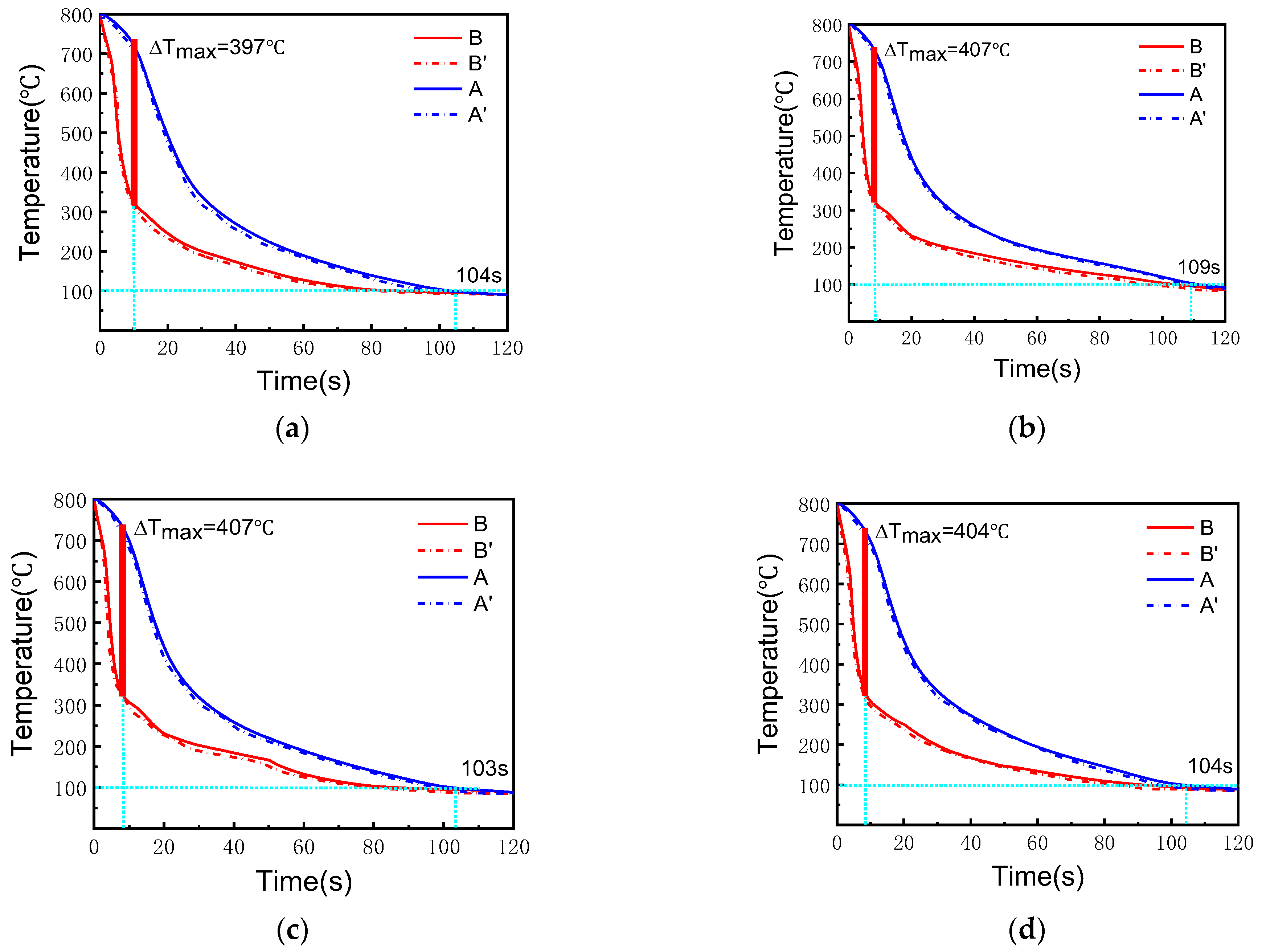
| The First Stage (20 s) | The Second Stage (30 s) | The Third Stage (70 s) | |
|---|---|---|---|
| condition 1 | A (189 L/min) | A-B-C (1136 L/min) | A-B-C (1136 L/min) |
| condition 2 | A-B-C (1136 L/min) | A (189 L/min) | A (189 L/min) |
| condition 3 | A-B-C (1136 L/min) | A (189 L/min) | A-B-C (1136 L/min) |
| condition 4 | B-C (1041 L/min) | C (965 L/min) | A-B (795 L/min) |
| C | Si | Mn | Cr | Ni | Mo | |
|---|---|---|---|---|---|---|
| 18Cr2Ni2MoVNbA | 0.2 | 0.18 | 0.58 | 1.69 | 1.59 | 0.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhao, Z.; Liu, J.; Tu, X.; Liu, S. A Temperature Field Simulation of the Pressure Quenching Process of 18Cr2Ni2MoVNbA Gears. Metals 2025, 15, 443. https://doi.org/10.3390/met15040443
Wang Y, Zhao Z, Liu J, Tu X, Liu S. A Temperature Field Simulation of the Pressure Quenching Process of 18Cr2Ni2MoVNbA Gears. Metals. 2025; 15(4):443. https://doi.org/10.3390/met15040443
Chicago/Turabian StyleWang, Yu, Ziheng Zhao, Jingang Liu, Xiaoxuan Tu, and Sisi Liu. 2025. "A Temperature Field Simulation of the Pressure Quenching Process of 18Cr2Ni2MoVNbA Gears" Metals 15, no. 4: 443. https://doi.org/10.3390/met15040443
APA StyleWang, Y., Zhao, Z., Liu, J., Tu, X., & Liu, S. (2025). A Temperature Field Simulation of the Pressure Quenching Process of 18Cr2Ni2MoVNbA Gears. Metals, 15(4), 443. https://doi.org/10.3390/met15040443





