A Novel Model for Transformation-Induced Plasticity and Its Performance in Predicting Residual Stress in Quenched AISI 4140 Steel Cylinders

Abstract

A better residual stress prediction model can lead to more accurate life assessments, better manufacturing process design and improved component reliability. Accurate modeling of transformation-induced plasticity (TRIP) is critical for improving residual stress simulation fidelity in advanced manufacturing processes. In this work, a novel TRIP model is implemented within a finite element framework to predict residual stress in quenched AISI 4140 steel cylinders. The proposed model incorporates a dual-exponential normalized saturation function to capture TRIP kinetics. Residual stress characterization through X-ray diffraction (XRD) is employed to validate the predictive capability of the finite element model that couples the new TRIP model. In addition, the performance of the new TRIP model in predicting residual stress is compared with traditional TRIP models such as Leblond and Desalos model. Systematic comparison of finite element models incorporating different TRIP models reveals that traditional TRIP models exhibit more deviations from the measurements, while the new TRIP model demonstrates more accurate predictive accuracy, with both the axial and hoop residual stress distribution curves showing a better degree of agreement with XRD results. The findings of this study provide a reliable numerical simulation tool for optimizing the quenching process, particularly for improving fatigue life predictions of critical components such as gears and bearings.

1. Introduction

With the rapid development of industry, carbon steels have gained widespread applications across engineering sectors due to their advantages of high strength, toughness and cost-effectiveness [1,2,3,4,5]. Quenching is a critical heat treatment process that enhances the comprehensive mechanical properties of medium-carbon alloy steels (such as AISI 4140 and 42CrMo), affecting the residual stress distribution, and, ultimately, the fatigue life and service reliability of steel components [6,7,8]. However, the quenching process involves complex transient heat transfer, phase transformation and stress couplings. Among the couplings existing between the three physical fields, five strong couplings are considered in this study: the latent heat released by phase transformations, the temperature-induced phase transformations, the thermal expansion/contraction, the phase transformation strain and the transformation-induced plasticity, as shown in Figure 1. High volumetric expansion induced by martensitic transformation combined with thermal gradients typically generate gradient residual stress fields within the components [9,10]. While a conventional X-ray diffraction (XRD) technique can measure static residual stress distributions after quenching [11,12], they are limited by challenges such as difficulty in stress measurement for complex parts (e.g., gears), time- and labor-intensive procedures and insufficient tracking of transient stress evolution. Finite element (FE) simulation technology, commonly used in quenching research, effectively addresses the inherent limitations of traditional experimental methods [13,14,15,16]. It allows for real-time tracking of transient temperature, microstructure and stress evolution during the quenching of complex-shaped components. With advances in computational technology, many commercial software packages, such as DEFORM [17], DANTE [18,19], SYSWELD [20] and ABAQUS [21,22], now enable the simulation of heat treatment processes.

Finite element simulations of heat treatment processes must solve critical issues such as determining the heat transfer coefficient [24], establishing phase transformation kinetics models [25] and defining stress–strain constitutive relationships [26]. In recent years, researchers have enhanced the accuracy of microstructure field calculations by refining phase transformation kinetics models, such as Jung’s critical transformation temperature correction [6] and Lee’s new proposed martensitic transformation equation [25]. Nevertheless, the adaptability of transformation-induced plasticity (TRIP) models remains a bottleneck for stress field prediction. TRIP refers to plastic strain observable during phase transformation under applied stress [27,28]. Unlike classical plasticity, the equivalent stress level required to trigger TRIP can be even lower than the yield strength of austenite, the softest phase. Existing studies indicate that the nonlinear characteristics of TRIP significantly influence the evolution of stress fields and the final residual stress distribution, necessitating its inclusion in stress–strain relationships [29]. There are two main approaches to incorporating TRIP effects into finite element simulation models: one involves artificially lowering the yield strength of the material during the phase transformation stage [30,31], and the other is to add an additional plastic strain term to the constitutive equation, which is more commonly used and has been extensively studied [9,26,29]. While Abrassart and Desalos have proposed equations to model the TRIP kinetics, these equations substantially underestimate experimental results [32]. Currently, TRIP modeling remains a pivotal challenge in finite element simulations of residual stress after quenching, and the mechanisms through which TRIP models influence the accuracy of residual stress predictions have yet to be fully understood.

Based on the experimental data on TRIP by Taleb et al. [32], this study proposes a dual-exponential normalized function to describe TRIP kinetics. Through thermo-mechanical coupled FE models incorporating various normalized saturation functions, this study systematically investigates the impact of these functions on the accuracy of residual stress predictions. By comparing the measured axial and hoop residual stress of quenched AISI 4140 cylinders with the simulation results, the model’s capability to predict residual stress is validated. The findings indicate that the proposed dual-exponential normalized function provides a better fit to the experimental data, resulting in more accurate predictions of the residual stress distribution. This research offers a reliable numerical simulation tool for optimizing and designing the quenching processes.

2. Materials and Methods

2.1. Experimental Methods

The chemical composition of the investigated steel AISI 4140, as determined through chemical analysis, is composed of 0.40%C, 0.27%Si, 0.58%Mn, 1.0%Cr, 0.17%Mo and 0.022%Ni, with the balance being Fe (all values in weight percentage). The thermal and mechanical properties used in this work are shown in

Table 1. Temperature-dependent thermal material properties.

Temperature (°C)	ρ (kg/m3)			Cp (J/(kg·K))			k (W/(m·K))
	A *	B *	M *	A	B	M	A	B	M
100	7900	7850	7800	594	488	594	27	43	27
200				594	523	594	27	40	27
300				594	566	594	27	38	27
400				594	617	594	27	36	27
500				594	684	594	27	34	27
600				594	781	594	27	33	27
700				594		594	27	32	27
800				594		594	27	32	27
900				605		605	28	32	27

* A, B, M denote austenite, bainite, and martensite, respectively.

and

Table 2. Temperature-dependent mechanical material properties.

Temperature (°C)	E (GPa)			Initial Yield Strength (MPa)			h (GPa)	Poisson’s Ratio
	A *	B 1 *	M 1 *	A	B	M	A, B, M	A, B, M
0	200	210	200	190	440	1600	8.47	0.3
300	175	193	185	110	330	1480	10.8
600	150	765	168	30	140	1260	0.06
900	124	120	-	20	30	-	-

* A, B, M denote austenite, bainite, and martensite, respectively. h is the isotropic hardening modulus.

. The cylindrical specimen employed for validation of the finite element models exhibited nominal dimensions of 50 mm diameter × 150 mm length. A precision-drilled cavity was created 1 mm beneath the cylinder’s surface into which a K-type thermocouple was inserted to capture the cooling curves during the quenching process.

The specimen was initially heated to 850 °C (1123 K) in a pit furnace, maintaining that temperature for 90 min to achieve complete austenitization. It was subsequently transferred and quenched in water at 18 °C for 5 min until its temperature dropped below 50 °C (323 K).

Residual stresses in the quenched cylinder were evaluated using an X-ray stress instrument (iXRD, PROTO, Waterloo, ON, Canada) operating at 20 KV and 4 mA. The testing followed the method ${\sin }^2\psi$ detailed in reference [33]. A Cr-Kα radiation source, with a wavelength of 0.2291 nm and 2 mm spot size, was utilized. Measurements were conducted using the iso-inclination method with the Fe {211} plane selected as the diffraction surface.

To obtain depth-dependent residual stress profiles, the outer layers of the cylinder were sequentially removed by turning and etched with a 15% nitric acid aqueous solution in 0.5 mm layers. Considering that the removal of the outer layer can lead to a redistribution of residual stress, the measured residual stress was corrected using Equations (1) and (2) as described in reference [34]:

$${\sigma }_{\mathrm{t}}\left(r\right)={\sigma }_{\mathrm{tm}}\left(r\right)-{\displaystyle \underset{r}{\overset{R}{\int }}{\sigma }_{\mathrm{tm}}\left(\xi \right)}\cdot {\displaystyle \frac{d\xi }{\xi }}$$

(1)

$${\sigma }_{\mathrm{z}}\left(r\right)={\sigma }_{\mathrm{zm}}\left(r\right)-2{\displaystyle \underset{r}{\overset{R}{\int }}{\sigma }_{\mathrm{zm}}\left(\xi \right)}\cdot {\displaystyle \frac{d\xi }{\xi }}$$

(2)

where ${\sigma }_{\mathrm{t}}\left(r\right)$ and ${\sigma }_{\mathrm{z}}\left(r\right)$ denote the corrected tangential and axial residual stresses at radius distance r, while ${\sigma }_{\mathrm{tm}}\left(r\right)$ and ${\sigma }_{\mathrm{zm}}\left(r\right)$ represent the measured tangential and axial residual stresses at radius distance r and R corresponds to the initial radius of the cylinder (25 mm).

2.2. Numerical Models

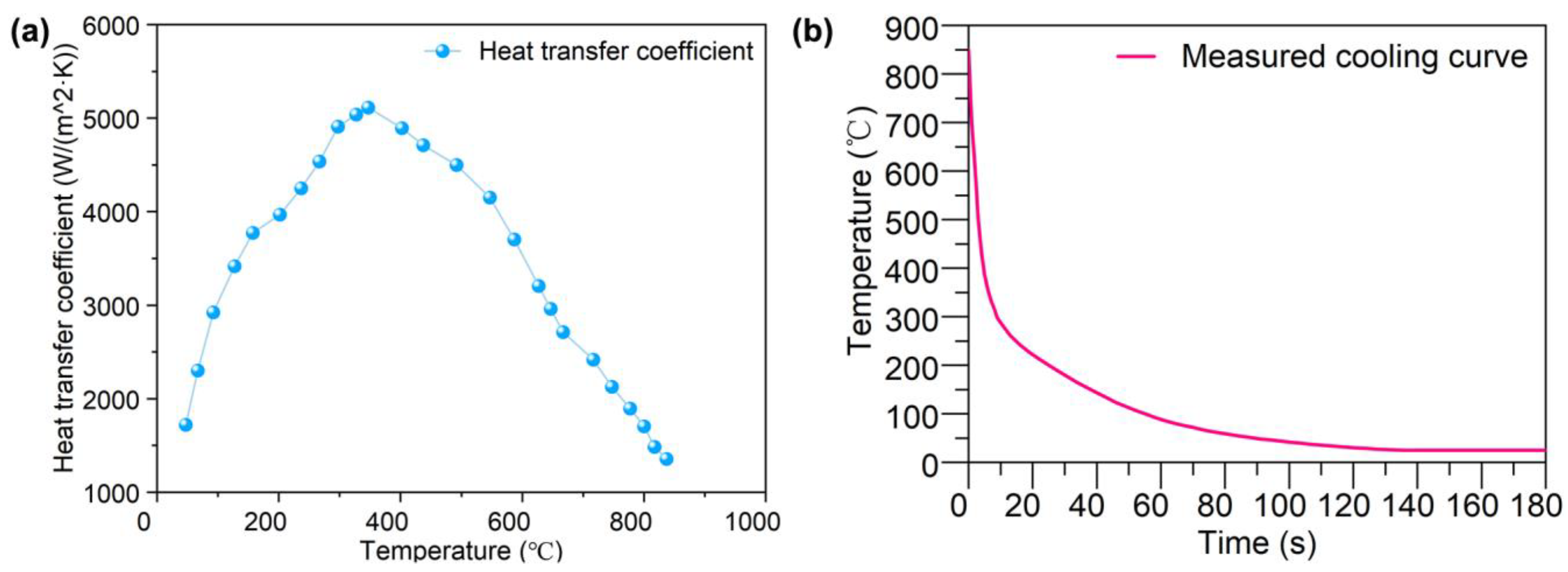
2.2.1. Temperature Distribution

To ensure accuracy in calculating quench-induced temperature fields, the latent heat of phase transformations must be considered. Compared to heat conduction effects, strain deformation energy contributes minimally to temperature variation (about 2 K) [35], thus being neglected in this study. The governing equation derived from the transient Fourier law is as follows:

$$\rho C_{\mathrm{p}}\dot{T}=\nabla \left(k\cdot \nabla T\right)+\dot{Q}$$

(3)

where $\rho$ is the density of the material, calculated as a linear weighted average of the densities of each phase; $C_{\mathrm{p}} \mathrm{and} k$ are temperature- and phase-dependent specific capacity and thermal conductivity, their data of each phase are taken from Kakhki et al. [36]; T is the temperature; $\dot{T}$ represents the time derivative of temperature; $\nabla$ denotes the gradient operator; $\dot{Q}$ represents the sum of the latent heat generation rate of phase transformations:

$$\dot{Q}={\displaystyle \sum _{j=2}^3\Delta H_k{\dot{\varphi }}_k}$$

(4)

here, $\Delta H_k$ represents the enthalpy change during the k-th phase transformation and ${\dot{\varphi }}_k$ denotes the transformation rate of the k-th phase (with k = 2 for bainite and k = 3 for martensite). The enthalpy changes associated with transformations to bainite and martensite are given by −5.12 × 10⁸ and −3.14 × 10⁸ J/m³.

The initial condition assumes complete and uniform austenitization at 850 °C. Additionally, film boundary conditions are imposed on the quenching surface:

$$-k\nabla T=h\left(T\right)\left(T_{\mathrm{s}}-T_{\mathrm{m}}\right)$$

(5)

where h(T) is the temperature-dependent heat transfer coefficient, T_s and T_m are surface and quenchant temperatures (291 K/18 °C). The h(T) profile (Figure 2) was determined from a thermocouple-measured cooling curve using an inverse heat transfer algorithm, with linear interpolation applied between discrete temperature nodes.

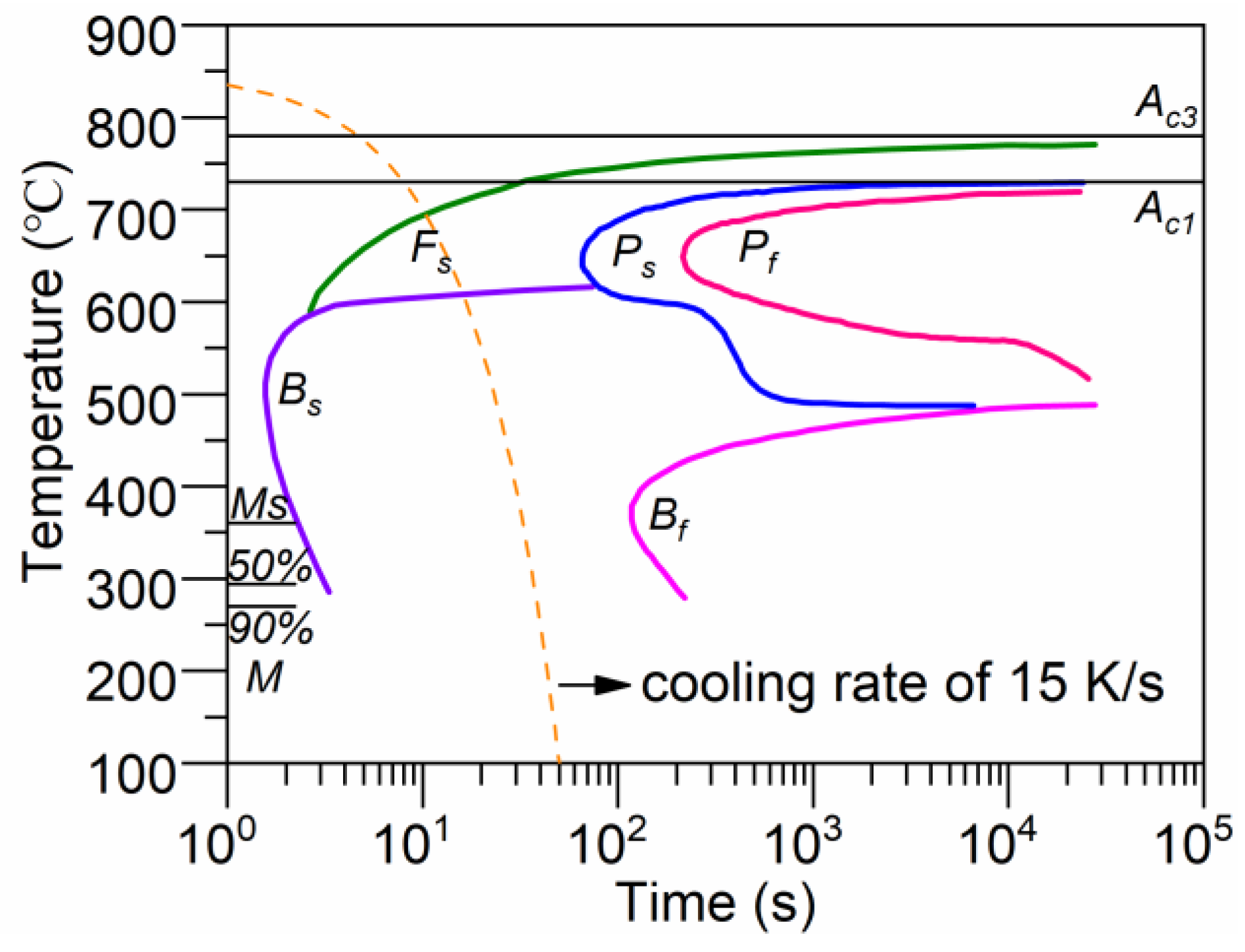
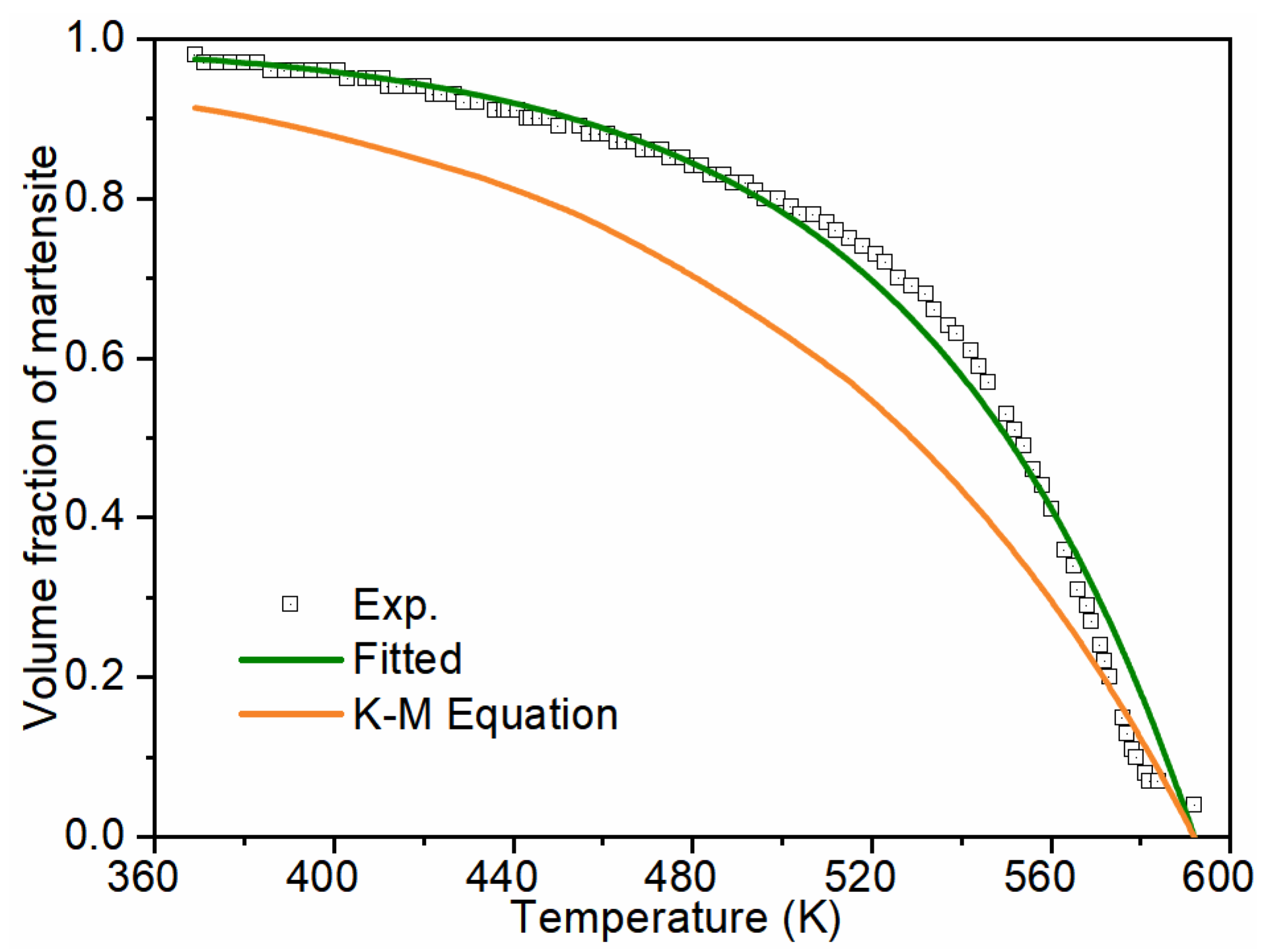
2.2.2. Phase Transformation Kinetics

Figure 3 shows the isothermal transformation diagram (TTT diagram) for AISI 4140 steel (Fe, 0.38%C, 0.64%Mn, 0.23%Si, 0.99%Cr, 0.16%Mo and 0.08%Ni) [37]. Since the slight difference in chemical composition between the steel used in this study and the steel used to determine the TTT diagram, the TTT curve was adjusted in this study. The parameters adjusted include the martensite start temperature (M_s), the bainite start temperature (B_s) and the overall TTT curve, with the correction method referenced from reference [38].

From the cooling curves of the cylinder, it can be observed that the slowest cooling rate occurs at the core of the cylinder, which is about 15 K/s. By combining this cooling rate with the corrected TTT curve, we conclude that for a 50 mm diameter cylinder made by AISI 4140 steel, no ferritic or pearlitic transformation occurs during quenching. Therefore, only bainitic and martensitic transformation should be considered in this study.

When the temperature drops below the bainite start temperature (B_s), bainite transformation occurs. In this work, the empirical formula proposed by Lee [39] is employed to determine the upper limit of the bainite transformation temperature Bs:

$$B_{\mathrm{s}}\left(°\mathrm{C}\right)=745-110\mathrm{C}-59\mathrm{Mn}-39\mathrm{Ni}-68\mathrm{Cr}-106\mathrm{Mo}+17\mathrm{MnNi}+6{\mathrm{Cr}}^2+29{\mathrm{Mo}}^2$$

(6)

Bainitic transformation is diffusion-controlled. The Johnson–Mehl–Avrami–Kolmogorov (JMAK) equation [40], combined with the additive rule, is the most widely used method for calculating diffusion-controlled transformations. However, the JMAK equation does not capture the slow termination characteristic of bainitic transformation [41]. When the temperature reaches B_s, the transformation proceeds at the following rate:

$${\displaystyle \frac{\mathrm{d}X}{\mathrm{d}t}}={\displaystyle \frac{2^{\left(G-1\right)/2}\cdot \Delta T^2\cdot \exp \left[-\frac{115115}{RT\left(t\right)}\right]\cdot X^{2\left(1-X\right)/3}\cdot {\left(1-X\right)}^{2X/3}}{\left(2.34+10.1\%\mathrm{C}+3.8\%\mathrm{Cr}+19\%\mathrm{Mo}\right)\cdot {10}^{-4}\cdot f\left(X,C_{\mathrm{i}}\right)}}$$

(7)

where

$$f\left(X,C_{\mathrm{i}}\right)=\exp \left[X^2\cdot \left(1.9\%\mathrm{C}+2.5\%\mathrm{Mn}+0.9\%\mathrm{Ni}+1.7\%\mathrm{Cr}+4\%\mathrm{Mo}-2.6\right)\right]$$

(8)

In Equation (7), ΔT is defined as the temperature difference between the current temperature and the bainite start temperature, X is the volume fraction of bainite, G is the ASTM grain size number; in this work, G is calculated as 9 based on the austenitization conditions, and R is the gas constant.

When the temperature drops below the martensite start temperature (M_s), martensitic transformation occurs independently with time. There are several empirical models for non-thermal martensitic transformation kinetics, and Lee [25] reviewed them. Among these, the following Koistinen and Marburger (K–M) equation [42] is the most widely used:

$$\begin{array}{r}{\xi }_{\mathrm{M}}=1-\exp \left[-0.011\cdot \left(M_{\mathrm{s}}-T_{\mathrm{q}}\right)\right]\\ M_{\mathrm{s}}>T_{\mathrm{q}}>193\mathrm{K} \left(-{80}^{\circ }\mathrm{C}\right)\end{array}$$

(9)

where ${\xi }_{\mathrm{M}}$ is volume fraction of the formed martensite and T_q corresponds to the minimum temperature reached during quenching process.

Equation (9) was originally developed for Fe-C binary alloys. When applied to AISI 4140, which contains additional alloying elements such as Cr, Mo and Mn, it may result in less accurate predictions of martensite volume fraction due to the influence of these elements on transformation kinetics and phase stability. To account for the effects of alloying elements, a modified K–M model is proposed as follows:

$${\xi }_{\mathrm{M}}=1-\exp \left[-K_{\mathrm{L}}\times (M_{\mathrm{s}}-T)\right]$$

(10)

where K_L is a function of the chemical composition. The value of K_L can be obtained by fitting the experimental data for martensitic transformation, as shown in Figure 4. The fitted value of K_L for AISI 4140 steel is 0.01663. As can be seen in Figure 4, the martensite volume fraction predicted by the K–M equation exhibits a significant deviation from the experimental data for AISI 4140. The martensite start temperature Ms used in the calculation was obtained using a thermodynamic-based model proposed in a previous study [43].

2.2.3. Analysis of Stress/Strain

Given the short duration of quenching, creep effects are neglected. The total strain increment decomposes into five components:

$$\Delta {\epsilon }_{ij}=\Delta {\epsilon }_{ij}^{\mathrm{el}}+\Delta {\epsilon }_{ij}^{\mathrm{pl}}+\Delta {\epsilon }_{ij}^{\mathrm{th}}+\Delta {\epsilon }_{ij}^{\mathrm{tr}}+\Delta {\epsilon }_{ij}^{\mathrm{trip}}$$

(11)

where $\Delta {\epsilon }_{ij}^{\mathrm{el}},\Delta {\epsilon }_{ij}^{\mathrm{pl}},\Delta {\epsilon }_{ij}^{\mathrm{th}},\Delta {\epsilon }_{ij}^{\mathrm{tr}} \mathrm{and} \Delta {\epsilon }_{ij}^{\mathrm{trip}}$ represent elastic, plastic, thermal, phase transformation and transformation-induced plasticity (TRIP) strain increments, respectively.

Thermal and phase transformation strains are isotropic, calculated as follows [44]:

$$\Delta {\epsilon }_{ij}^{\mathrm{th}}={\delta }_{ij}{\displaystyle \sum _{k=1}^3{\xi }_k}{\alpha }_k\Delta T$$

(12)

$$\Delta {\epsilon }_{ij}^{\mathrm{tr}}={\delta }_{ij}{\displaystyle \sum _{k=2}^3\Delta {\xi }_k}{\beta }_k$$

(13)

Here, k = 1, 2 and 3 correspond to austenite, bainite, and martensite, respectively. The parameters α_k and β_k represent the thermal expansion coefficient and the phase transformation expansion coefficients. The temperature-dependent transformation strain of austenite to bainite and austenite to martensite are $9\times {10}^{-3}$ to $9.5\times {10}^{-6}T$ and $9.5\times {10}^{-3}$ to $1.1\times {10}^{-5}T$, respectively; δ_ij is the Kronecker delta.

Table 3. Thermal expansion coefficients for each phase of AISI 4140.

Phase	Austenite	Bainite	Martensite
TEC * (10−5 K−1)	2.25	1.3	1.15

* TEC is the abbreviation for thermal expansion coefficient.

presents the thermal expansion coefficients of each phase utilized in this study.

Stress increments follow [45]:

$$\begin{array}{r}\Delta {\sigma }_{ij}=\lambda {\delta }_{ij}\Delta {\epsilon }_{kk}^{\mathrm{el}}+2\mu \Delta {\epsilon }_{ij}^{\mathrm{el}}+\Delta \lambda {\delta }_{ij}\Delta {\epsilon }_{kk}^{\mathrm{el}}+2\Delta \mu {\epsilon }_{ij}^{\mathrm{el}}\\ \lambda ={\displaystyle \frac{E}{1-2\nu }}-{\displaystyle \frac{E}{3\left(1+\nu \right)}}\\ \mu ={\displaystyle \frac{E}{2\left(1+\nu \right)}}\end{array}$$

(14)

where σ_ij is the Cauchy stress tensor; E and v are elastic modulus and Poisson’s ratio via linear mixture law.

The material exhibits rate-independent deformation behavior. Plasticity is described by the Von Mises yield criterion with isotropic hardening:

$$\sqrt{{\displaystyle \frac{3}{2}}\left(s_{ij}-{\alpha }_{ij}\right)\left(s_{ij}-{\alpha }_{ij}\right)}-{\sigma }_y=0$$

(15)

where s_ij denotes the deviatoric stress tensor, α_ij represents the deviatoric back stress tensor and σ_y is the yield strength of the material.

Many researchers [46,47,48,49,50] adopt the method of linear mixture law to calculate the yield strength when there are several phases coexisting in the material. However, traditional linear mixture law fails when phases exhibit order-of-magnitude hardness differences. The yield strength of the martensite phase is typically an order-of-magnitude higher than that of austenite, which can result in significant errors when applying a linear mixture law [23]. Therefore, a nonlinear mixture law is adopted in this study to more accurately calculate the material’s yield strength as follows:

$${\sigma }_{\mathrm{y}}=g\left({\xi }^{\gamma }\right){\sigma }_{\mathrm{y}}^{\gamma }+\left[1-g\left({\xi }^{\gamma }\right)\right]{\sigma }_{\mathrm{y}}^{\mathrm{bm}}$$

(16)

where ${\xi }^{\gamma }$ denotes the phase fraction of austenite; ${\sigma }_{\mathrm{y}}^{\gamma }$ is the yield strength of austenite; ${\sigma }_{\mathrm{y}}^{\mathrm{bm}}$ represents the yield strength of the mixed microstructure consisting of bainite and martensite and $g\left({\xi }^{\gamma }\right)$ is a normalized function of the austenite phase fraction, with the values obtained from reference [51].

The equivalent stress is initially evaluated assuming purely elastic behavior. When the elastic stress exceeds the yield strength σ_y, plastic flow is initiated. In such cases, Equations (14) and (15) are integrated using the backward Euler method.

Plastic strain in metals typically arises when deviatoric stress exceeds the material’s yield strength. However, a special case exists wherein plastic deformation occurs concurrently with phase transformation, even under relatively low external stress levels. This phenomenon is known as transformation-induced plasticity (TRIP). Unlike classical plasticity, TRIP does not rely on a yield criterion. Furthermore, the stress levels associated with TRIP are insufficient to produce conventional plastic deformation, even in the relatively soft austenite phase [42]. The incremental form of TRIP is expressed as follows:

$$\Delta {\epsilon }_{ij}^{\mathrm{trip}}={\displaystyle \frac{3}{2}}K{f}^{\prime }\left(\xi \right)h\left({\sigma }_{\mathrm{eq}},{\sigma }_{\mathrm{y}}\right)s_{ij}\Delta \xi$$

(17)

where K is the TRIP coefficient; $f\left(\xi \right)$ is a normalized saturation function; $f^{\prime }\left(\xi \right)$ represents the derivative of $f\left(\xi \right)$ with respect to the transformed phase fraction and $h\left({\sigma }_{\mathrm{eq}},{\sigma }_{\mathrm{y}}\right)$ is a function of the equivalent stress and the yield strength of the mixed microstructure. The introduction of $h\left({\sigma }_{\mathrm{eq}},{\sigma }_{\mathrm{y}}\right)$ accounts for the nonlinear effects induced by the applied stress. The expression for $h\left({\sigma }_{\mathrm{eq}},{\sigma }_{\mathrm{y}}\right)$ proposed by Leblond [41] is as follows:

$$h\left({\sigma }_{\mathrm{eq}},{\sigma }_{\mathrm{y}}\right)=\left\{\begin{array}{l}1,\mathrm{if}{\displaystyle \frac{{\sigma }_{\mathrm{eq}}}{{\sigma }_{\mathrm{y}}}}\le 0.5\\ 1+3.5\left({\displaystyle \frac{{\sigma }_{\mathrm{eq}}}{{\sigma }_{\mathrm{y}}}}-0.5\right),\mathrm{if}{\displaystyle \frac{{\sigma }_{\mathrm{eq}}}{{\sigma }_{\mathrm{y}}}}\ge 0.5\end{array}\right.$$

(18)

The TRIP coefficient K is obtained either experimentally or through theoretical calculations. In this work, the value of K is taken as $7\times {10}^{-5}$ MPa⁻¹.

The accuracy of predicting residual stress distribution after quenching using finite element simulations is influenced by three key factors: (1) the precision of temperature field calculations, (2) the accuracy of microstructural field calculations and (3) the correct modeling of TRIP. Among these, the accurate description of TRIP remains the most challenging.

Table 4. TRIP saturation functions.

Model	Expression
Abrassart	$\xi \left(3-2\sqrt{\xi }\right)$
Desalos	$\xi \left(2-\xi \right)$
Leblond	$\xi \left(1-\ln \left(\xi \right)\right) \mathrm{for} \xi >0.03, \mathrm{zero} \mathrm{otherwise}$
Tanaka	$\xi$

lists the commonly used TRIP saturation functions. Taleb [32] highlighted that the saturation functions proposed by Abrassart and Desalos significantly underestimated experimental results. To gain deeper insights into TRIP, this study analyzes the normalized function curve measured by Taleb et al., revealing the following characteristics: (1) during the initial stage of phase transformation, the normalized function increases rapidly and (2) in the final stage of phase transformation, the normalized function exhibits a slow, steady growth. Based on these observations, we propose a dual-exponential saturation function to capture these features. The unnormalized dual-exponential saturation function is as follows:

$$f\left(\xi \right)=A\cdot \exp \left(B\cdot \xi \right)+C\cdot \exp \left(D\cdot \xi \right)$$

(19)

The normalized type is as follows:

$$f\left(\xi \right)=A\cdot \exp \left(\log \left({\displaystyle \frac{1}{A}}+\exp \left(C\right)\right)\cdot \xi \right)-A\cdot \exp \left(C\cdot \xi \right)$$

(20)

where parameters A and C are used for normalization. By fitting the experimental curve of Taleb et al. using Equation (20), A and C are determined to be A = 0.9971 and C = −6.344, respectively. Figure 5 presents a comparison between the experimental results of the normalized function and the computational results obtained using the formulas proposed by Abrassart, Desalos, Leblond, Tanaka and the approach developed in this study. The results demonstrate that the fitting curve based on the dual-exponential function proposed in this study aligns more closely with the curve measured by Taleb et al. than those obtained using the normalized functions proposed by Desalos, Leblond and Tanaka. This means that by calibrating the coefficients, the dual-exponential form of normalized saturation function can better describe the dynamic behavior of phase transition-induced plasticity.

To evaluate the effectiveness of different TRIP models in calculating quenching residual stresses, Equation (21) presents the incremental form of TRIP strain for each model, based on the normalized functions proposed by Desalos, Leblond, Tanaka and this study. The case of neglecting the effects of TRIP is also considered. The TRIP coefficient K for AISI 4140 steel is obtained from reference [52] as follows:

$$\begin{array}{l}\left(\mathrm{a}\right)\Delta {\epsilon }_{ij}^{\mathrm{trip}}=0\\ \left(\mathrm{b}\right)\Delta {\epsilon }_{ij}^{\mathrm{trip}}=3K\left(1-\xi \right)h\left({\sigma }_{\mathrm{eq}},{\sigma }_{\mathrm{y}}\right)s_{ij}\Delta \xi \\ \left(\mathrm{c}\right)\Delta {\epsilon }_{ij}^{\mathrm{trip}}=-{\displaystyle \frac{\Delta V}{V}}{\displaystyle \frac{1}{{\sigma }_{\mathrm{y},\mathrm{A}}}}\left(\ln \xi \right)h\left({\sigma }_{\mathrm{eq}},{\sigma }_{\mathrm{y}}\right)s_{ij}\Delta \xi \\ \left(\mathrm{d}\right)\Delta {\epsilon }_{ij}^{\mathrm{trip}}={\displaystyle \frac{3}{2}}Kh\left({\sigma }_{\mathrm{eq}},{\sigma }_{\mathrm{y}}\right)s_{ij}\Delta \xi \\ \left(\mathrm{e}\right)\Delta {\epsilon }_{ij}^{\mathrm{trip}}={\displaystyle \frac{3}{2}}K{f}^{\prime }\left(\xi \right)h\left({\sigma }_{\mathrm{eq}},{\sigma }_{\mathrm{y}}\right)s_{ij}\Delta \xi \end{array}$$

(21)

where (a) represents the case where TRIP strain is not considered. While (b), (c) and (d) correspond to the phase TRIP strains proposed by Desalos, Leblond and Tanaka, respectively. The (e) represents the TRIP strain based on the dual-exponential normalized function proposed in this work.

In addition, the U_LTS model proposed by Taleb [53] is also evaluated to assess its capability in predicting residual stress. The U_LTS model can be expressed as the following:

$$\Delta {\epsilon }_{ij}^{\mathrm{trip}}=\left\{\begin{array}{l}-{\displaystyle \frac{2\Delta {\epsilon }_{12}}{{\sigma }_{\mathrm{y},\mathrm{A}}}}\left(\ln {\xi }_l\right){\displaystyle \frac{3}{2}}\left(s_{ij}-X_{ij}\right)\left(1+\delta {\displaystyle \frac{〈{\sigma }^h〉}{{\sigma }^{eq}}}\right)\Delta \xi \hspace{1em}if\hspace{1em}\xi \le {\xi }_l\\ -{\displaystyle \frac{2\Delta {\epsilon }_{12}}{{\sigma }_{\mathrm{y},\mathrm{A}}}}\left(\ln \xi \right){\displaystyle \frac{3}{2}}\left(s_{ij}-X_{ij}\right)\left(1+\delta {\displaystyle \frac{〈{\sigma }^h〉}{{\sigma }^{eq}}}\right)\Delta \xi \hspace{1em}if\hspace{1em}\xi >{\xi }_l\end{array}\right\}$$

(22)

with,

$${\xi }_l={\displaystyle \frac{{\sigma }_{\mathrm{y},\mathrm{A}}}{2\Delta {\epsilon }_{12}}}{\displaystyle \frac{4\mu +3K}{9C\mu }}$$

(23)

and,

$$〈{\sigma }^h〉={\sigma }^h\hspace{1em}if\hspace{1em}{\sigma }^h<0\hspace{1em}and\hspace{1em}〈{\sigma }^h〉=0\hspace{1em}if\hspace{1em}{\sigma }^h\ge 0$$

(24)

Here, ${\xi }_l$ represents the volume fraction at which the entire parent phase undergoes plastic deformation. s_ij is the deviatoric stress tensor. X_ij denotes the back stress tensor. $\Delta {\epsilon }_{12}$ is the deformation of transformation. $C={\displaystyle \frac{E}{3\left(1-2\upsilon \right)}}$ is the compressibility modulus. $\delta$ is a material parameter close to unity.

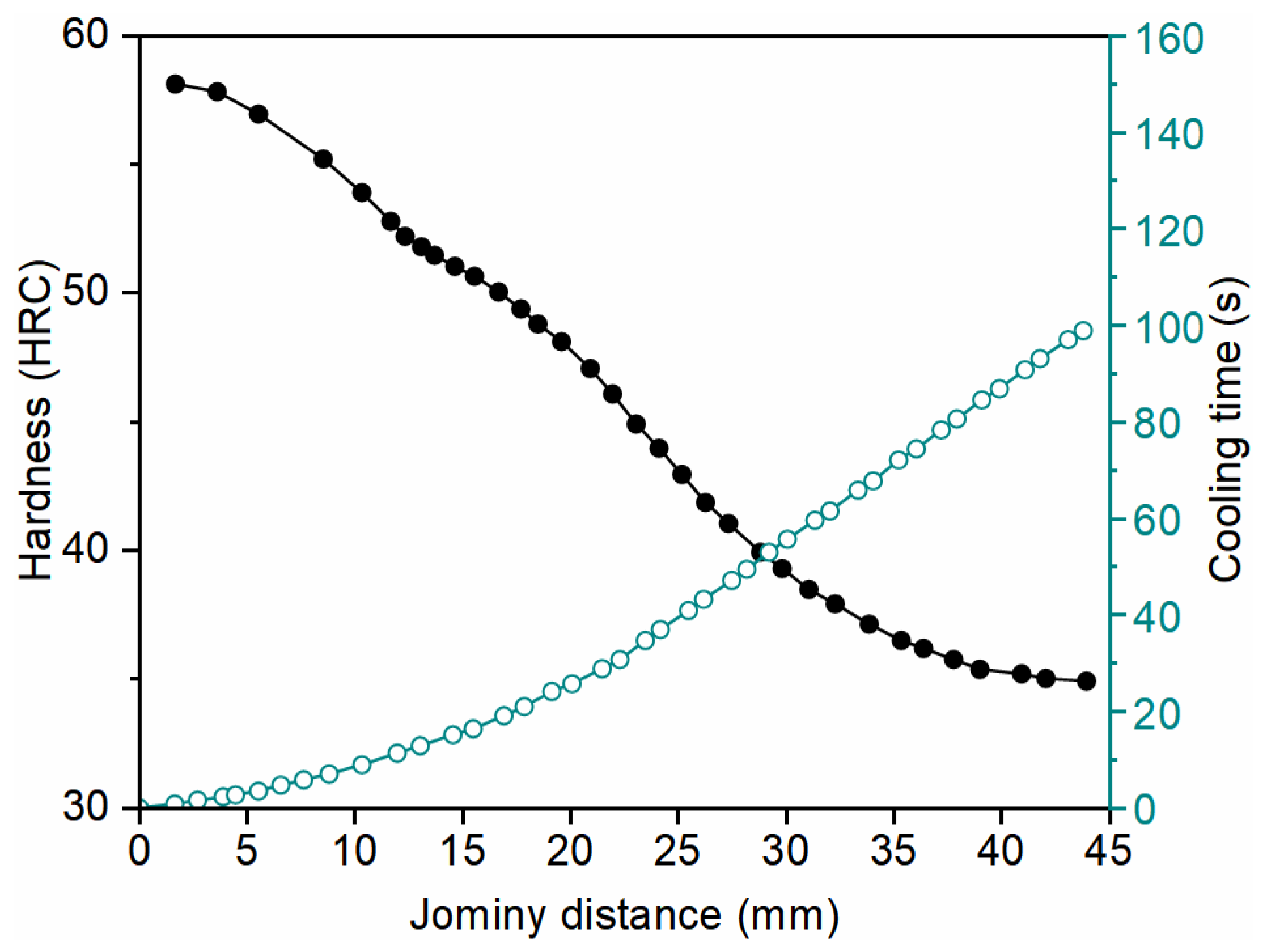
2.2.4. Calculation of Hardness

This study employs two methodologies to predict post-quench hardness distribution in the cylinder. The first approach utilizes an empirical regression formula developed by Creusot–Loire [54] combined with the linear mixture law to calculate hardness distribution. This method requires separate determination of phase-specific hardness values, where the Vickers hardness of individual phases correlates with chemical composition and critical cooling rates through the following relationships:

$${\mathrm{HV}}_{\mathrm{M}}=127+949\mathrm{C}+27\mathrm{Si}+11\mathrm{Mn}+8\mathrm{Ni}+16\mathrm{Cr}+21\log V$$

(25)

$$\begin{array}{l}{\mathrm{HV}}_{\mathrm{B}}=-323+185\mathrm{C}+330\mathrm{Si}+153\mathrm{Mn}+65\mathrm{Ni}+144\mathrm{Cr}+191\mathrm{Mo}\\ +\left(89+53\mathrm{C}-55\mathrm{Si}-22\mathrm{Mn}-10\mathrm{Ni}-20\mathrm{Cr}-33\mathrm{Mo}\right)\log V\end{array}$$

(26)

where HV_M and HV_B represent the Vickers hardness of martensite and bainite, respectively, and V denotes the characteristic cooling rate (the average cooling rate from 800 °C to 500 °C).

The relationship between Vickers hardness and Rockwell hardness is expressed as follows:

$$\begin{array}{l}HRC={\displaystyle \frac{100*HV-15100}{HV+223}},HV\ge 520\\ HRC={\displaystyle \frac{100*HV-13700}{HV+223}},200<HV<520\end{array}$$

(27)

The second hardness prediction methodology is based on Jominy hardenability curve and cooling time versus end-quench distance correlations. This approach involves three sequential steps: (1) calculate characteristic cooling time at target component locations; (2) determine equivalent end-quench distance via cooling time curve and (3) extract predicted hardness values from standard Jominy hardenability curve. The Jominy hardenability curve and cooling time curve employed in this study are illustrated in Figure 6.

2.2.5. Simulation Details

The meshing strategy used in this work contains 560 quadrilateral elements, with the elements in the surface region refined to capture the larger temperature gradient. Thermo-metallurgical-mechanical analysis is performed in this work. The total degrees-of-freedom of the FE analysis are 36,083. A scheme of “step-by-step time integration method” and “Newton–Raphson” method is employed in numerical calculation to deal with the time-dependent transient coupled equations. Because the heat transfer coefficient varies with the temperature on the heat transfer boundary, a non-uniform time step is used in the simulation.

3. Results

3.1. Cooling Curves

Figure 7 illustrates the temperature variation curves at different locations within the cylinder during the initial 180 s of cooling. The green, magenta and black solid lines in the graph represent the simulated cooling curves of the surface, mid-radius (1/2R) and core, respectively, while the hollow circles denote the cooling curve of the surface as measured by the thermocouple. The cooling curve calculated using the measured heat transfer coefficients as the thermal boundary conditions for the finite element model shows excellent agreement with the experimental results. As depicted in Figure 7, the cooling rates at different parts of the cylinder decrease in the following order: surface, mid-radius and core. The characteristic cooling rates (average cooling rate from 800 °C to 500 °C) for the surface, mid-radius and core of the cylinder are 116.2 K/s, 12.9 K/s and 12.4 K/s, respectively. Notably, the cooling curve for the core in Figure 7 significantly slows down between 30 and 40 s, forming a “plateau”, primarily due to the influence of latent heat in phase transformation. A comparison between the simulated and experimentally measured cooling curve of the surface reveals a slight discrepancy. This inconsistency may be attributed to heat transfer losses or inaccuracies in data acquisition between the thermocouple and the drilled specimen. Consequently, the simulated curve is slightly lower than the measured curve.

3.2. Microstructure Distribution

Figure 8 presents the simulation results of the microstructure distribution along the radial direction within the cylinder after quenching. Due to the rapid cooling rate at the surface, the primary microstructure after quenching is martensite, while the core, which cools more slowly, contains both martensite and bainite. As illustrated in Figure 8, the martensite phase fraction exhibits a gradual decrease from the surface toward the core of the cylinder. Specifically, the martensite content at the surface, mid-radius (1/2R) and core is 97.3%, 35.2% and 34.9%, respectively. In contrast, the bainite phase fraction increases with depth, reaching 1.9%, 64.5% and 64.8% at the corresponding locations. Notably, at a depth of 4.5 mm beneath the surface, the phase fractions of martensite and bainite are equal, making a transitional point in the microstructural distribution.

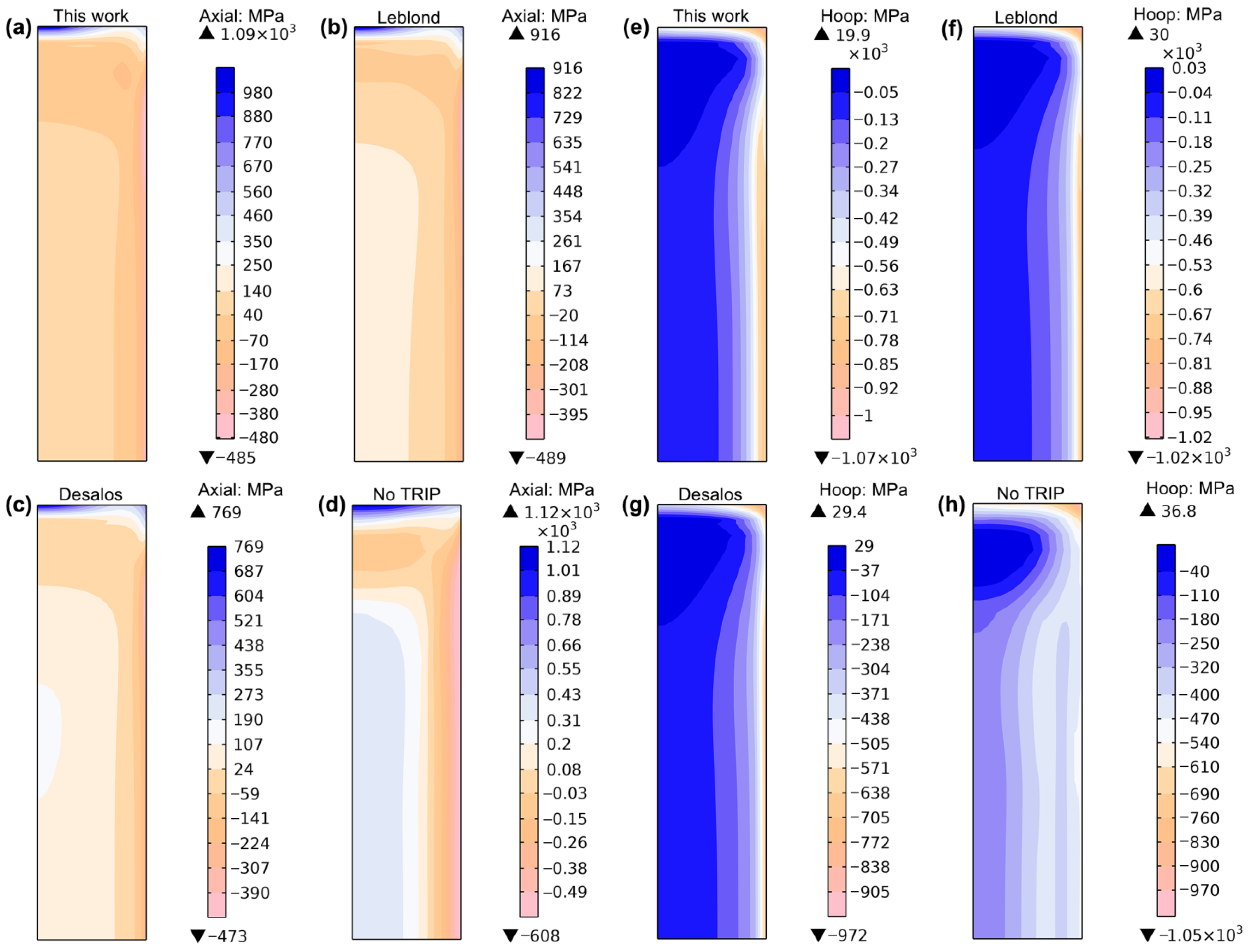
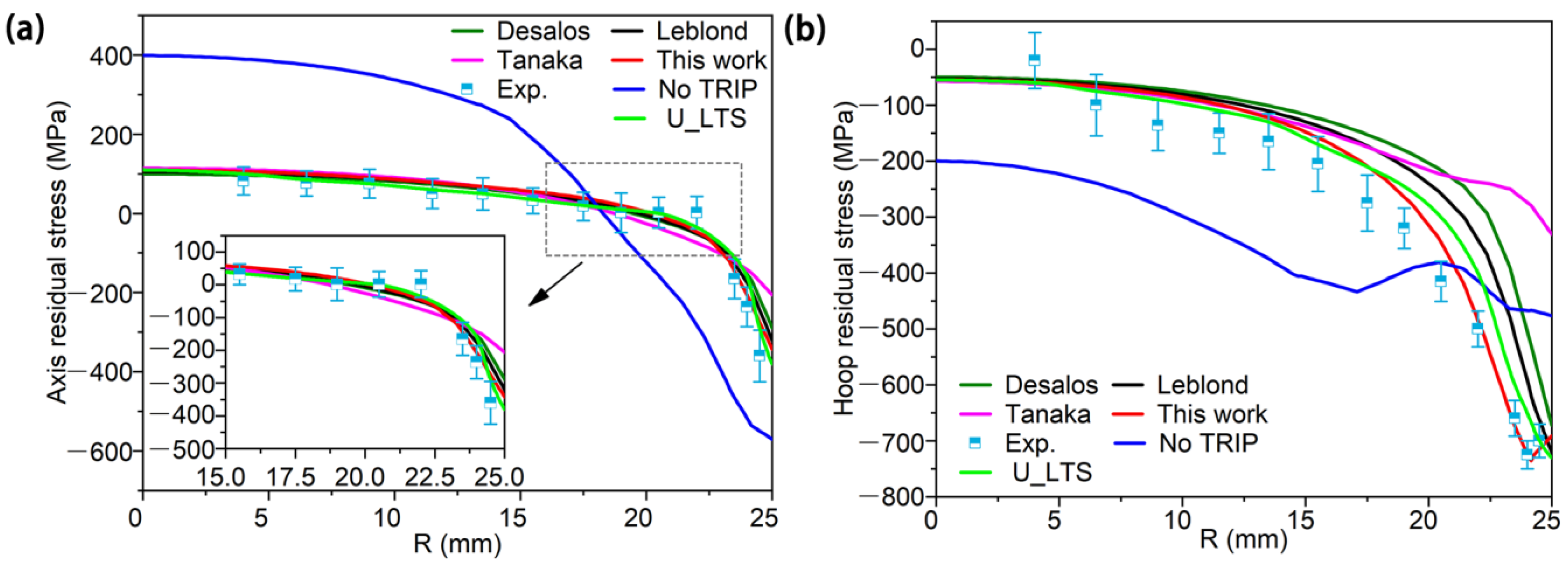
3.3. Residual Stress Distribution

Figure 9 shows the finite element counter plots of axial residual stress calculated using different TRIP models. Subfigures (a), (b), (c) and (d) in Figure 9 correspond to the results obtained using the proposed dual-exponential model, the Leblond TRIP model, the Desalos TRIP model and the TRIP-neglected model, respectively. As observed in the figure, the maximum tensile stress is located at the center of the cylinder’s top surface for all models, although in the TRIP-neglected case, this maximum shifts slightly to the right. The maximum compressive stress is consistently found on the outer surface of the cylinder, approximately 20 mm below the top surface. The maximum residual tensile stress amplitude is greatest for the TRIP-neglected model. The residual tensile stress amplitude is smallest for the Desalos TRIP model. Additionally, the residual compressive stress amplitude is smallest for the Desalos TRIP model, smaller than that for the proposed model, while the largest amplitude occurs with the TRIP-neglected model. Therefore, although different models have minimal impact on the locations of the maximum tensile and compressive residual stresses, they significantly affect the magnitudes of these stresses.

4. Discussion

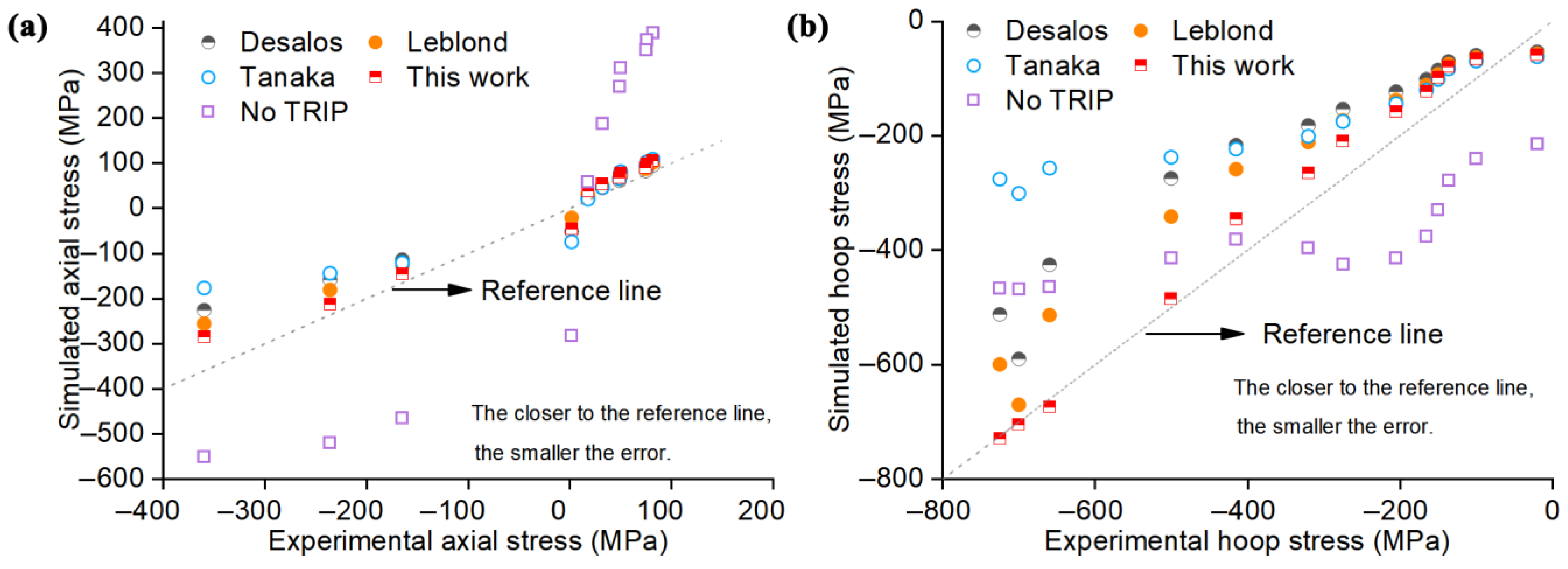
4.1. Performance of the New Model in Predicting Residual Stress

To assess the impact of the normalized functions on residual stress distribution, measured residual stresses were compared with those predicted by finite element simulations using the four aforementioned normalized functions (Equation (21)). Additionally, the residual stress distribution without considering TRIP effect was calculated. The results, depicted in Figure 10a,b, show axial and hoop residual stress distributions, respectively. A comparison with experimental data reveals that neglecting TRIP effect leads to significantly higher simulated maximum residual tensile and compressive stresses compared to the measured values. This discrepancy arises from the stress relaxation effect caused by exclusion of TRIP effect [55]. Furthermore, when compared to simulations using the normalized functions proposed by Desalos, Leblond and Tanaka, the residual stress distribution obtained with the dual-exponential normalized function shows a better match with XRD measurements. This improvement is primarily due to the dual-exponential function’s more accurate description of TRIP effect. The finite element model employing the dual-exponential normalized function thus provides a more reliable prediction of residual stress distribution, as it more effectively captures the trends observed in the experimental data. It is worth noting that the prediction capability of the U_LTS model is better than that of the Leblond model. The U_LTS model is based on the LTS model, while the LTS model was developed assuming that only the Greenwood–Johnson mechanism (GJM) was active. The improvement of the U_LTS model lies in its incorporation of the influence of back stress on the direction of plastic flow, allowing for a more accurate representation of transformation-induced plasticity kinetics than the Leblond model.

4.2. Evaluation of the New TRIP Model in Predicting Residual Stress

A coefficient of error (CE) is introduced to quantitatively evaluate the agreement between the simulated and experimental residual stresses. The CE is defined as follows:

$$CE={\displaystyle \frac{1}{N}}\cdot {\displaystyle \sum \left(\frac{\left|{\sigma }_{\exp }-{\sigma }_{\mathrm{cal}}\right|}{\left|{\sigma }_{\exp }\right|}\right)}$$

(28)

where N denotes the number of experimentally measured stress locations, ${\sigma }_{\exp }$ represents the measured residual stress and ${\sigma }_{\mathrm{cal}}$ is the corresponding calculated residual stress. The coefficient CE quantifies the average deviation between the measured and simulated residual stresses. A smaller CE value indicates better agreement between the simulation and experimental results, with a value approaching zero signifying a high level of accuracy.

Figure 11 compares the simulated residual stresses, obtained using different TRIP models, with the experimental values. Subplot (a) and (b), respectively, present comparative results of axial residual stress and hoop residual stress. In Figure 11a, the CE values for axial residual stress calculated using the Desalos TRIP model, Leblond TRIP model, Tanaka TRIP model, the model proposed in this study and TRIP-neglected model are 2.697, 1.337, 3.80, 2.551 and 15.793, respectively. In Figure 11b, the corresponding CE values are 0.491, 0.424, 0.556, 0.321 and 1.363. As shown in Figure 11, the residual stresses predicted by the model proposed in this study yield the lowest CE values among all models evaluated. This indicates that the finite element model incorporating the dual-exponential normalized function provides superior performance and more accurate prediction of residual stress distribution following quenching.

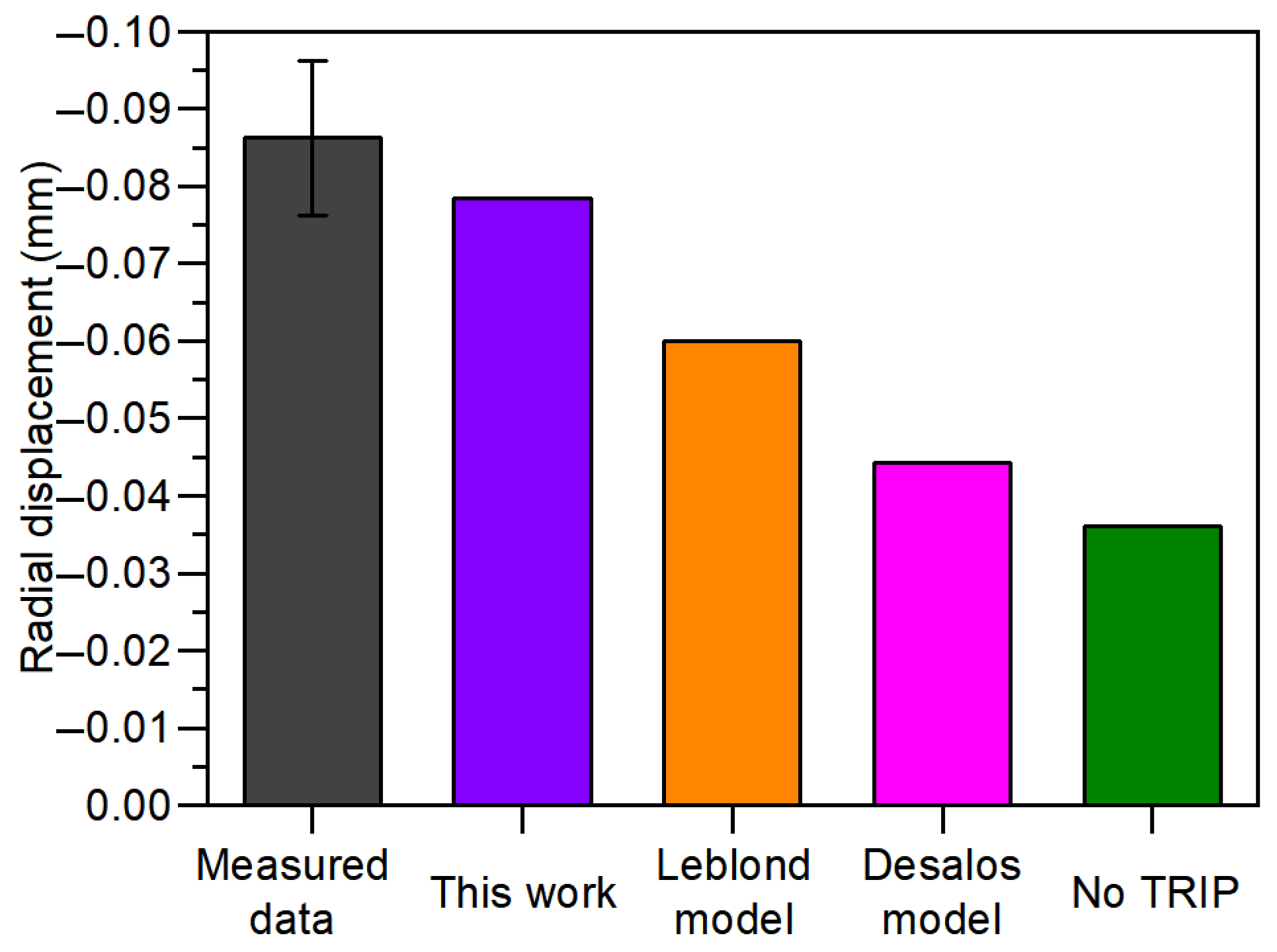
4.3. Performance of the New Model in Predicting Distortion After Quenching

The final dimensional changes in components after the quenching process play a critical role in ensuring dimensional stability. Figure 12 compares experimental measurements with simulation results of radial displacements of the quenched cylinder obtained from different TRIP models. Simulation results based on this work (violet bar), the Leblond model (orange bar), the Desalos model (magenta bar) and the TRIP-neglected model (olive bar) are presented. As shown in Figure 12, the finite element program implementing the new TRIP model demonstrates superior computational accuracy in predicting radial displacements of the quenched cylinder. Both the Leblond and Desalos models underestimate the radial displacements, while the TRIP-neglected model exhibits substantial deviations from experimental results. These results conclusively prove the necessity of considering transformation-induced plasticity effects in distortion prediction of quenched alloy steels.

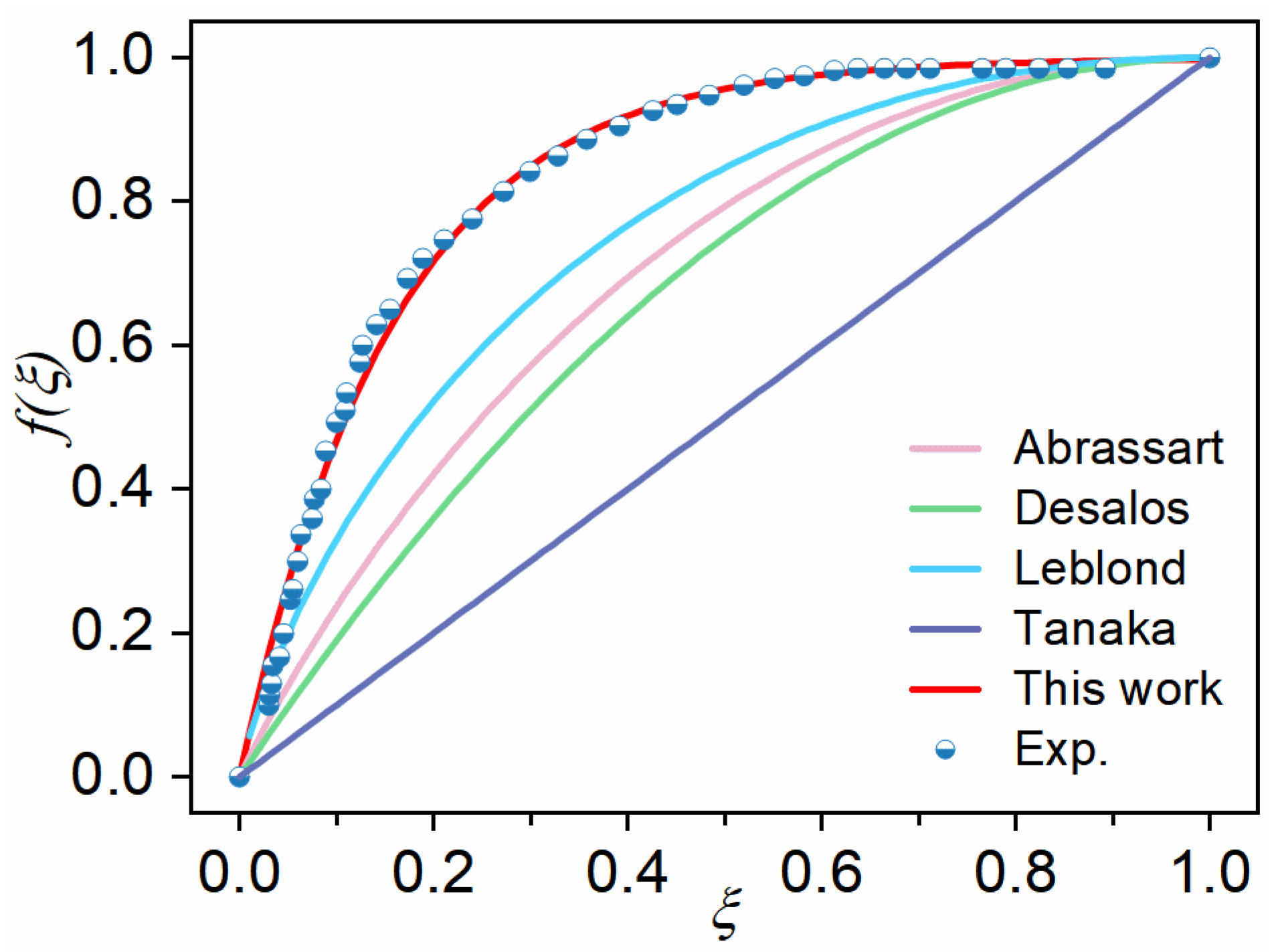
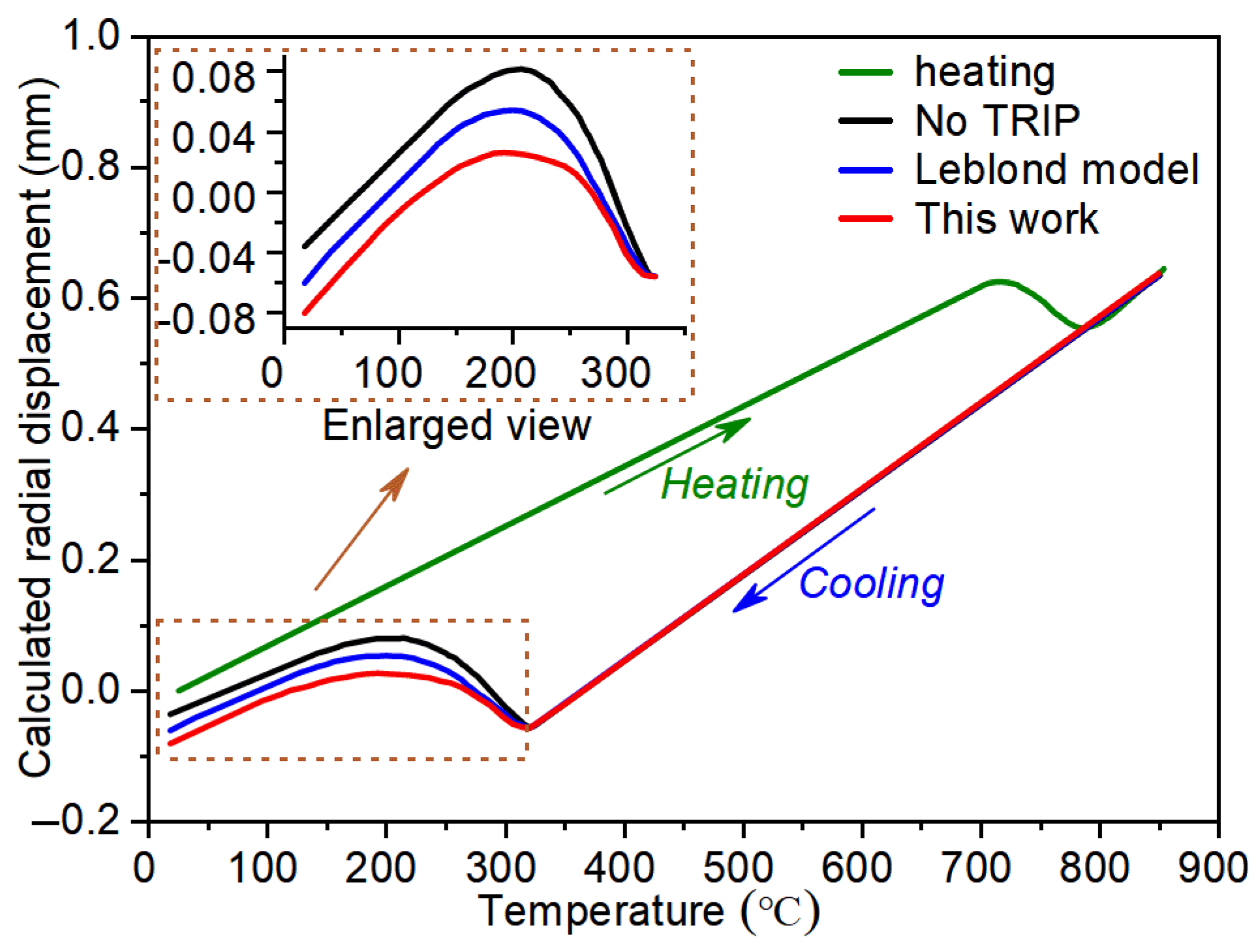
4.4. Dilatation Data Calculated Using Different TRIP Models

The comparative analysis of TRIP model performance in dilatation calculations is visualized in Figure 13. Figure 13 displays the radial displacements during heating and cooling obtained through simulations using three different TRIP models. The green curve in Figure 14 represents the radial displacements during the heating stage, while the red, blue and black curves, respectively, denote simulation results based on the new TRIP model, the Leblond TRIP model and the TRIP-neglected model. Figure 13 reveals linear thermal expansion/contraction characteristics in temperature ranges without phase transformations during heating/cooling processes. While nonlinear radial displacements in phase transformation stage are primarily attributed to atomic volume differences between face-centered cubic (FCC) and body-centered cubic (BCC) crystal structures. The magnified view demonstrates significant discrepancies among different TRIP models: predictions neglecting TRIP effects show smaller radial dimensional variations compared to both the new and Leblond models. Final simulation results exhibit ascending radial displacements in the order of TRIP-neglected model, the Leblond model and the new model. Cross-verification with experimental data in Section 4.4 confirms the best agreement between measurements and simulations using the TRIP model proposed in this work.

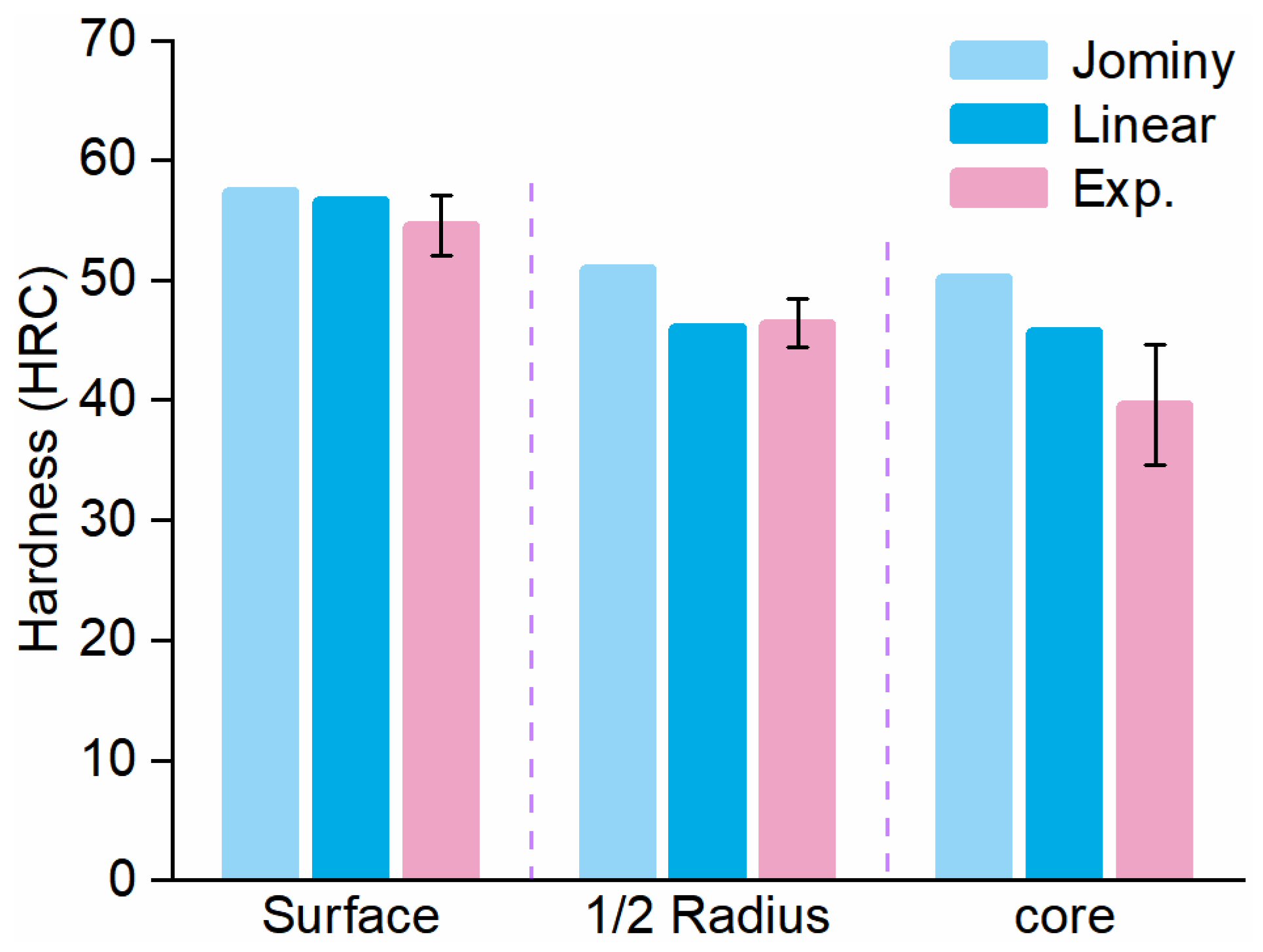
4.5. Hardness Prediction

Figure 14 comparatively presents the measured and simulated hardness profiles at three characteristic positions of the quenched cylinder: surface, mid-radius (1/2R) and core. The computational analysis was performed using both the Jominy hardenability curve method and the linear mixture law method. Both measured and simulated results demonstrate a sequential decrease in hardness from the surface to the core. As anticipated, the surface hardness is the highest (54.5 HRC), while the core has the lowest hardness (39.6 HRC). In Figure 14, “Jominy” denotes hardness values derived through the Jominy hardenability curve combined with the characteristic cooling time–Jominy distance correlation curve, while “Linear” refers to hardness values calculated using the individual hardness values of each phase coupled with the linear mixture law. The results indicate that both prediction methods overestimate hardness compared to experimental measurements. The linear mixture law method exhibits higher accuracy than the Jominy hardenability method. Two primary factors may account for the significant deviations in Jominy hardenability calculations: (1) chemical composition differences between the steel used in the standard Jominy test and the steel used in this study and (2) potential inaccuracies in the modified cooling time curve used to determine equivalent end-quench distances, leading to prediction–experiment discrepancies.

5. Conclusions

In this work, a novel TRIP model was implemented within a finite element framework to predict residual stress in quenched AISI 4140 steel cylinders. The performance of the new TRIP model in predicting residual stress was compared with traditional TRIP models such as Leblond and Desalos models. The predicted residual stress was compared with experimental data. The results show that the proposed dual-exponent model provides a more accurate prediction of residual stress, making it a valuable tool for optimizing the quenching process through finite element simulations. The main conclusions are as follows:

• Although the TRIP model has a minimal influence on the locations of the maximum axial tensile and compressive residual stresses, it has a significant impact on the magnitudes of these stresses.
• The finite element simulation with the TRIP model proposed in this work more accurately predicts the residual stress distribution after quenching. The CE values of the TRIP model proposed in this work for axial and hoop residual stress are 2.551 and 0.321.
• The transformation-induced plasticity (TRIP) must be incorporated in the finite element model when predicting the residual stress after quenching.
• The improvement of the U_LTS model lies in its incorporation of the influence of back stress on the direction of plastic flow, allowing for a more accurate representation of transformation-induced plasticity kinetics than the Leblond model.
• The linear mixture law demonstrates satisfactory performance in hardness calculations, while the accuracy of the Jominy hardenability curve method in hardness prediction is inherently dependent on the precision of experimental data.