Non-Equilibrium Solidification of Undercooled Metallic Melts
Abstract
:1. Introduction
2. Crystallization
2.1. Crystal Nucleation
2.1.1. Homogeneous Nucleation

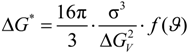
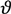 ) the catalytic potency factor for heterogeneous nucleation with
) the catalytic potency factor for heterogeneous nucleation with 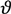 the wetting angle. In the case of homogeneous nucleation, f(
the wetting angle. In the case of homogeneous nucleation, f( 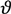 ) = 1.
) = 1.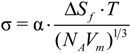


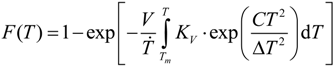
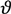 )1/3 = 0.61 for Zr from the undercooling experiments in the ESL. In the literature, a great variety of dimensionless solid-liquid interfacial energies are reported from modelling work. From the present investigations, the different approaches of solid-liquid interface modelling are evaluated by comparing the modelling results with findings inferred from maximum undercooling of Zr in electrostatic levitation experiments. Since the prefactor, KV, is comparable in the order of magnitude to the value given by Turnbull for homogeneous nucleation, f(
)1/3 = 0.61 for Zr from the undercooling experiments in the ESL. In the literature, a great variety of dimensionless solid-liquid interfacial energies are reported from modelling work. From the present investigations, the different approaches of solid-liquid interface modelling are evaluated by comparing the modelling results with findings inferred from maximum undercooling of Zr in electrostatic levitation experiments. Since the prefactor, KV, is comparable in the order of magnitude to the value given by Turnbull for homogeneous nucleation, f( 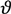 ) ≈ 1 is assumed. This leads to a lower limit of the dimensionless interfacial energy α ≥ 0.61. The comparison with the modelling results shows that the negentropic model, with α = 0.70 [16], gives the best agreement with the present experiment. Density-functional theory yields α = 0.46 and α = 0.48 [19] and molecular dynamics simulations yield α = 0.29, α = 0.32, and α = 0.36, respectively [20], depending on the potentials used for the simulations. All these values underestimate the solid-liquid interfacial energy inferred from the experiments. Only the negentropic model by Spaepen is in agreement with the experiments. More details are given in [21].
) ≈ 1 is assumed. This leads to a lower limit of the dimensionless interfacial energy α ≥ 0.61. The comparison with the modelling results shows that the negentropic model, with α = 0.70 [16], gives the best agreement with the present experiment. Density-functional theory yields α = 0.46 and α = 0.48 [19] and molecular dynamics simulations yield α = 0.29, α = 0.32, and α = 0.36, respectively [20], depending on the potentials used for the simulations. All these values underestimate the solid-liquid interfacial energy inferred from the experiments. Only the negentropic model by Spaepen is in agreement with the experiments. More details are given in [21].
2.1.2. Catalysis of Metastable Phase Nucleation by External Triggering

2.1.3. Experimental Determination of Metastable Phase Diagrams

2.2. Crystal Growth
2.2.1. Sharp Interface Theory of Dendrite Growth

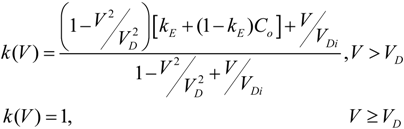
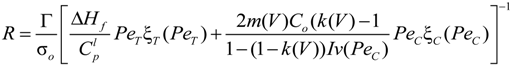
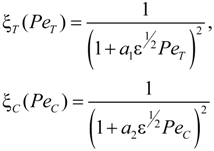
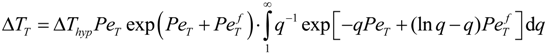
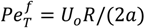 is the flow thermal Péclet number, with Uo the velocity of the uniformly forced flow far from the dendrite tip. We estimate the fluid flow velocity from the energy balance between the electromagnetic field, the gravitational field, and the viscous dissipation:
is the flow thermal Péclet number, with Uo the velocity of the uniformly forced flow far from the dendrite tip. We estimate the fluid flow velocity from the energy balance between the electromagnetic field, the gravitational field, and the viscous dissipation:
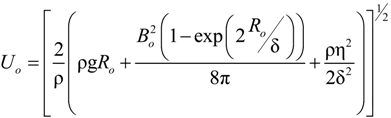
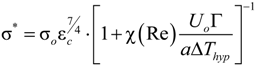
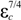 /σ* = 1.675 for the 3D upstream fluid flow imposed on the scale of a freely growing dendrite. Thus, from the two main Equations (6) and (14), the velocity V and the tip radius R of the dendrite can be calculated as a function of the initial undercooling ∆T.
/σ* = 1.675 for the 3D upstream fluid flow imposed on the scale of a freely growing dendrite. Thus, from the two main Equations (6) and (14), the velocity V and the tip radius R of the dendrite can be calculated as a function of the initial undercooling ∆T.
2.2.2. Influence of Forced Convection on Dendrite Growth Kinetics

2.2.3. Deviations from Local Equilibrium during Rapid Dendrite Growth in Pure Ni

2.2.4. Solute Trapping and Supersaturated Solid Solutions



2.2.5. Disorder Trapping and Disordered Superlattice Structure


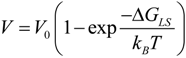

2.2.6. Dendrite Growth in Undercooled Glass-Forming Cu50Zr50 Alloy

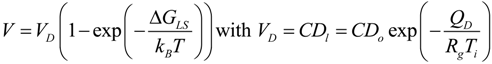
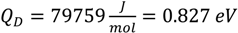 . Based upon these results, the dendrite growth velocity V is calculated as a function of the total undercooling ∆T. The results of these computations are presented by the solid line in Figure 14. The experimental results of the dendrite growth velocity are well reproduced. A maximum V = 0.227 m/s is found at ∆T = 209 K which is quite close to the experimental measurement of a maximum V = 0.025 m/s at ∆T = 200 K. It is interesting to note that using the temperature dependent viscosity does not lead to a matching of the experiments and the modelling [32], in contrast to the present work where the temperature dependent diffusion coefficient is used to take into account the mobility of the solid-liquid interface. This may be understood by the fact that the Einstein-Stokes relation does not hold for Zr-based glass forming alloys [78].
. Based upon these results, the dendrite growth velocity V is calculated as a function of the total undercooling ∆T. The results of these computations are presented by the solid line in Figure 14. The experimental results of the dendrite growth velocity are well reproduced. A maximum V = 0.227 m/s is found at ∆T = 209 K which is quite close to the experimental measurement of a maximum V = 0.025 m/s at ∆T = 200 K. It is interesting to note that using the temperature dependent viscosity does not lead to a matching of the experiments and the modelling [32], in contrast to the present work where the temperature dependent diffusion coefficient is used to take into account the mobility of the solid-liquid interface. This may be understood by the fact that the Einstein-Stokes relation does not hold for Zr-based glass forming alloys [78].
3. Levitation Techniques
3.1. Electromagnetic Levitation




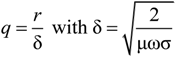
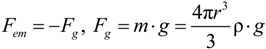

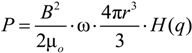
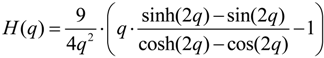
3.2. Electrostatic Levitation
 as:
as:

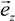 is the unit vector in z direction, i.e., parallel to the electrostatic field. A stable position of the sample is based on a local potential minimum at
is the unit vector in z direction, i.e., parallel to the electrostatic field. A stable position of the sample is based on a local potential minimum at  for all directions in space.
for all directions in space.
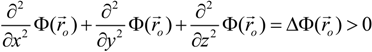
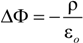
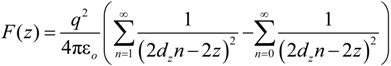

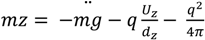

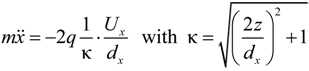

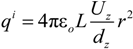
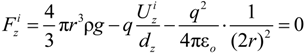
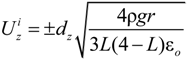
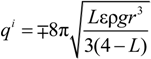
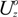 needed to keep the sample in the middle of the electrodes is calculated as:
needed to keep the sample in the middle of the electrodes is calculated as:
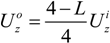
3.3. Electromagnetic Levitation in Reduced Gravity

4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Herlach, D.M.; Cochrane, R.F.; Egry, I.; Fecht, H.-J.; Greer, A.L. Containerless processing in the study of metallic melts and their solidification. Int. Mater. Rev. 1993, 6, 273–347. [Google Scholar]
- Herlach, D.M. Containerless undercooling and solidification of pure metals. Annu. Rev. Mater. Sci. 1991, 21, 23–44. [Google Scholar] [CrossRef]
- Rhim, W.-K.; Chung, S.K.; Barber, D.; Man, K.F.; Gutt, G.; Rulison, A.J.; Spjut, R.E. An electrostatic levitator for high temperature containerless materials processing in 1-g. Rev. Sci. Instrum. 1993, 64, 2961–2970. [Google Scholar] [CrossRef]
- Meister, T.; Werner, H.; Lohoefer, G.; Herlach, D.M.; Unbehauen, H. Gain-scheduled control of an electrostatic levitator. Eng. Pract. 2003, 11, 117–128. [Google Scholar] [CrossRef]
- Notthoff, C.; Franz, H.; Hanfland, M.; Herlach, D.M.; Holland-Moritz, D.; Petry, W. Energy-dispersive X-ray diffraction combined with electromagnetic levitation to study phase-selection in undercooled melts. Rev. Sci. Instrum. 2000, 71, 3791–3796. [Google Scholar] [CrossRef]
- Shuleshova, O.; Löser, W.; Holland-Moritz, D.; Herlach, D.M.; Eckert, J. Solidification and melting of high-temperature materials: In situ observations by synchrotron radiation. J. Mater. Sci. 2012, 47, 4497–4513. [Google Scholar] [CrossRef]
- Schenk, T.; Holland-Moritz, D.; Simonet, V.; Bellisent, R.; Herlach, D.M. Icosahedral short-range order in deeply undercooled metallic melts. Phys. Rev. Lett. 2002, 89, 075507. [Google Scholar] [CrossRef]
- Kelton, K.F.; Lee, G.W.; Gangopadhyay, A.K.; Hyers, R.W.; Rathz, T.; Rogers, J.; Robinson, M.B.; Robinson, D. First X-Ray Scattering Studies on Electrostatically Levitated Metallic Liquids: Demonstrated Influence of Local Icosahedral Order on the Nucleation Barrier. Phys. Rev. Lett. 2003, 90, 195504:1–195504:5. [Google Scholar] [CrossRef]
- Kelton, K.F.; Greer, A.L.; Herlach, D.M.; Holland-Moritz, D. The Influence of Order on the Nucleation Barrier. Mater. Res. Bull. 2004, 29, 940–944. [Google Scholar] [CrossRef]
- Notthoff, C.; Feuerbacher, B.; Frans, H.; Herlach, D.M.; Holland-Moritz, D. Direct determination of metastable phase diagram by synchrotron radiation experiments on undercooled metallic melts. Phys. Rev. Lett. 2001, 86, 1038–1041. [Google Scholar] [CrossRef]
- Funke, O.; Phanikumar, G.; Galenko, P.K.; Chernova, L.; Reutzel, S.; Kolbe, M.; Herlach, D.M. Dendrite growth velocity in levitated undercooled nickel melts. J. Cryst. Growth 2006, 297, 211–222. [Google Scholar] [CrossRef] [Green Version]
- Solidification of Containerless Undercooled Melts; Herlach, D.M.; Matson, D.M. (Eds.) Wiley-VCH: Weinheim, Germany, 2012.
- Skripov, V.P. Material Science, Crystal Growth and Materials; Pergamon Press: Amsterdam, The Netherlands, 1977. [Google Scholar]
- Christian, J.W. The Theory of Transformations in Metals and Alloys; Pergamon: Oxford, UK, 1975. [Google Scholar]
- Turnbull, D. Formation of Crystal Nuclei in Liquid Metals. J. Appl. Phys. 1950, 21, 1022–1028. [Google Scholar] [CrossRef]
- Nelson, D.R.; Spaepen, F. Polytetrahedral order in condensed matter. In Solid State Physics; Academic Press: New York, NY, USA, 1989. [Google Scholar]
- Turnbull, D. Under what conditions can a glass be formed? Contemp. Phys. 1969, 10, 473–488. [Google Scholar] [CrossRef]
- Dantzig, J.A.; Rappaz, M. Solidification; EPFL Press: Lausanne, Switzerland, 2009. [Google Scholar]
- Marr, D.W.; Gast, A.P. On the solid-fluid interface of adhesive spheres. J. Chem. Phys. 1993, 99, 2024–2030. [Google Scholar] [CrossRef]
- Sun, D.Y.; Asta, M.; Hoyt, J.J. Crystal-melt interfacial free energies and mobilities in fcc and bcc Fe. Phys. Rev. B 2004, 69, 174103:1–174103:9. [Google Scholar] [CrossRef]
- Klein, S.; Holland-Moritz, D.; Herlach, D.M. Crystal nucleation in undercooled liquid zirconium. Phys. Rev. B (BR) 2009, 80, 212202:1–212202:4. [Google Scholar] [CrossRef]
- Schleip, E.; Willnecker, R.; Herlach, D.M.; Görler, G.P. Measurements of ultra-rapid solidification rates in greatly undercooled bulk melts by a high speed photosensing device. Mater. Sci. Eng. A 1988, 98, 39–42. [Google Scholar] [CrossRef]
- Schleip, E.; Herlach, D.M.; Feuerbacher, B. External seeding of a metastable metallic phase. Europhys. Lett. 1990, 11, 751–756. [Google Scholar] [CrossRef]
- Cech, R.E. Evidence of solidification of a metastable phase in Fe-Ni alloys. Transactions AIME 1956, 206, 585–590. [Google Scholar]
- Cech, R.E.; Turnbull, D. Heterogeneous nucleation of the martensitic transformation. Transactions AIME 1956, 206, 124–130. [Google Scholar]
- Kim, Y.-W.; Lin, H.-W.; Kelly, T.F. Solidification structures in submicron spheres of iron-nickel: Experimental observations. Acta Metall. 1988, 36, 2525–2536. [Google Scholar] [CrossRef]
- Löser, W.; Garcia-Escorial, A.; Vinet, B. Metastable phase formation in eletromagnetic levitation, drop-tube and gas-atomization techniques: A comparative study. Int. J. Non-Equilib. Process. 1998, 11, 89–111. [Google Scholar]
- Galenko, P.K.; Sobolev, S. Local non-equilibrium effect on undercooling in rapid solidification of alloys. Phys. Rev. E 1997, 55, 343. [Google Scholar] [CrossRef]
- Galenko, P.K.; Danilov, D.A. Local non-equilibrium effect on rapid dendritic growth in binary alloy melt. Phys. Lett. A 1997, 235, 271–278. [Google Scholar] [CrossRef]
- Brener, E.; Melnikov, V.I. Pattern selection in two-dimensional dendrite growth. Adv. Phys. 1991, 40, 53–97. [Google Scholar] [CrossRef]
- Hoyt, J.J.; Asta, M.; Karma, A. Method for Computing the Anisotropy of the Solid-Liquid Interfacial Free Energy. Phys. Rev. Lett. 2001, 86, 5530–5533. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, L.-M.; Ma, M.Z.; Binder, S.; Volkmann, T.; Herlach, D.M.; Wang, J.S.; Xue, Q.G.; Tian, Y.J.; Liu, R.P. Diffusion-controlled crystal growth in deeply undercooled Zr50Cu50 melt on approaching the glass transition. Phys. Rev. B 2011, 83, 014202:1–014202:5. [Google Scholar] [CrossRef]
- Galenko, P. Extended thermodynamical analysis of a motion of the solid-liquid interface in a rapidly solidifying alloy. Phys. Rev. B 2002, 65, 144103:1–144103:8. [Google Scholar] [CrossRef]
- Galenko, P.K. Solute trapping and diffusionless solidification in a binary system. Phys. Rev. E 2007, 76, 031606:1–031606:9. [Google Scholar] [CrossRef]
- Kerrache, A.; Horbach, J.; Binder, K. Molecular-dynamics computer simulation of crystal growth and melting in Al50Ni50. Europhys. Lett. 2008, 81, 58001:1–58001:6. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Galenko, P.K. Selection criterion of stable dendritic growth at arbitrary Péclet numbers with convection. Phys. Rev. E 2013, 87, 062403:1–062403:5. [Google Scholar] [CrossRef]
- Herlach, D.M.; Galenko, P.K. Rapid solidification: In situ diagnostics and theoretical modeling. Mater. Sci. Eng. A 2007, 449–451, 34–41. [Google Scholar] [CrossRef]
- Lee, J.; Matson, D.M.; Binder, S.; Kolbe, M.; Herlach, D.M.; Hyers, R.W. Magnetohydrodynamic Modeling and Experimental Validation of Convection Inside Electromagnetically Levitated Co-Cu Droplets. Metall. Mater. Trans. B 2013, 44. [Google Scholar] [CrossRef]
- Bouissou, P.; Pelce, P. Effect of a forced flow on dendritic growth. Phys. Rev. A 1989, 40, 6673–6680. [Google Scholar] [CrossRef]
- Jeong, J.-H.; Goldenfeld, N.; Danzig, J.A. Phase field model for three-dimensional dendritic growth with fluid flow. Phys. Rev. E 2001, 64, 041602:1–041602:14. [Google Scholar]
- Karma, A.; Rappel, W.-J. Phase-field method for computationally efficient modeling of solidification with arbitrary interface kinetics. Phys. Rev. E 1996, 53, 3017–3021. [Google Scholar] [CrossRef]
- Beckermann, C.; Diepers, H.-J.; Steinbach, I.; Karma, A.; Tong, X. Modeling Melt Convection in Phase-Field Simulations of Solidification. J. Comput. Phys. 1999, 154, 468–496. [Google Scholar] [CrossRef]
- Reutzel, S.; Hartmann, H.; Galenko, P.K.; Schneider, S.; Herlach, D.M. Change of the kinetics of solidification and microstructure formation induced by convection in the Ni–Al system. Appl. Phys. Lett. 2007, 91, 041913:1–041913:3. [Google Scholar] [CrossRef] [Green Version]
- Barth, M.; Wei, B.; Herlach, D.M. Crystal growth in undercooled melts of the intermetallic compounds FeSi and CoSi. Phys. Rev. B 1995, 51, 3422–3428. [Google Scholar] [CrossRef]
- Hyers, R.W. Fluid flow effects in levitated droplets. Meas. Sci. Technol. 2005, 16, 394–401. [Google Scholar] [CrossRef]
- Coriell, S.R.; Turnbull, D. Relative roles of heat transport and interface rearrangement rates in the rapid growth of crystals in undercooled melts. Acta Metall. 1982, 30, 2135–2139. [Google Scholar] [CrossRef]
- Hoyt, J.J.; Asta, M.; Haxhimali, T.; Karma, A.; Napolitano, R.E.; Trivedi, R.; Laird, B.B.; Morris, J.R. Crystal-Melt Interfacers and Solidification Morphologies in Metals and Alloys. Mater. Res. Soc. Bull. 2004, 12, 935–939. [Google Scholar]
- Rozas, R.E.; Kuhn, P.; Horbach, J. Particle-Based Computer Simulation of Crystal Nucleation and Growth Kinetics in Undercooled Melts. In Solidification of Containerless Undercooled Melts; Herlach, D.M., Matson, D.M., Eds.; Wiley-VCH: Weinheim, Germany, 2012; pp. 381–401. [Google Scholar]
- Eckler, K.; Herlach, D.M. Measurements of dendrite growth velocities in undercooled pure Ni-melts—Some new results. Mater. Sci. Eng. A 1994, 178, 159–162. [Google Scholar] [CrossRef]
- Volkmann, T. Dendrite growth in undercooled nickel. unpublished results.
- Willnecker, R.; Herlach, D.; Feuerbacher, B. Evidence of nonequilibrium processes in rapid solidification of undercooled metals. Phys. Rev. Lett. 1989, 62, 2707–2710. [Google Scholar] [CrossRef]
- Eckler, K.; Cochrane, R.F.; Herlach, D.M.; Feuerbacher, B.; Jurisch, M. Evidence for a transition from diffusion- to thermally-controlled solidification in metallic alloys. Phys. Rev. B Brief Rep. 1992, 45, 5019–5022. [Google Scholar] [CrossRef]
- Arnold, C.B.; Aziz, M.J.; Schwarz, M.; Herlach, D.M. Parameter-free test of alloy dendrite-growth theory. Phys. Rev. B. 1999, 59, 334–343. [Google Scholar] [CrossRef]
- Galenko, P.K.; Reutzel, S.; Herlach, D.M.; Danilov, D.; Nestler, B. Modelling of dendritic solidification in undercooled dilute NiZr1alloy. Acta Mater. 2007, 55, 6834–6842. [Google Scholar] [CrossRef]
- Boettinger, W.J.; Aziz, M.J. Theory for the trapping of disorder and solute in intermetallic phases by rapid solidification. Acta Metall. 1989, 37, 3379–3391. [Google Scholar] [CrossRef]
- Aziz, M.J.; Boettinger, W.J. On the transition from short-range diffusion-limited to collision-limited growth in alloy solidification. Acta Metall. Mater. 1994, 42, 527–537. [Google Scholar] [CrossRef]
- Gandham, P.; Biswas, K.; Funke, O.; Holland-Moritz, D.; Herlach, D.M.; Chattopadhyay, K. Solidification of undercooled peritectic Fe–Ge alloy. Acta Mater. 2005, 53, 3591–3600. [Google Scholar] [CrossRef]
- Assadi, H.; Reutzel, S.; Herlach, D.M. Kinetics of solidification of B2 intermetallic phase in the Ni–Al system. Acta Mater. 2006, 54, 2793–2800. [Google Scholar] [CrossRef] [Green Version]
- Sutton, M.; Yang, Y.S.; Mainville, J.; Jordan-Sweet, J.L.; Ludwig, K.F., Jr.; Stephenson, G.B. Observation of a Precursor during the Crystallization of Amorphous NiZr2. Phys. Rev. Lett. 1989, 62, 288–291. [Google Scholar] [CrossRef]
- Greer, A.L.; Assadi, H. Rapid solidification of intermetallic compounds. Mater. Sci. Eng. A 1997, 226–228, 133–141. [Google Scholar] [CrossRef]
- Boettinger, W.J.; Bendersky, L.A.; Cline, J.; West, J.A.; Aziz, M.J. Disorder trapping in Ni2TiAl. Mater. Sci. Eng. A 1991, 133, 592–595. [Google Scholar] [CrossRef]
- Huang, Y.; Aziz, M.J.; Hutchinson, J.W.; Evans, A.G.; Saha, R.; Nix, W.D. Comparison of mechanical properties of Ni3Al thin films in disordered FCC and ordered L12 phases. Acta Mater. 2001, 49, 2853–2861. [Google Scholar] [CrossRef]
- Assadi, H.; Greer, A.L. The interfacial undercooling in solidification. J. Cryst. Growth 1997, 172, 249–258. [Google Scholar] [CrossRef]
- Hartmann, H.; Holland-Moritz, D.; Galenko, P.K.; Herlach, D.M. Evidence of the transition from ordered to disordered growth during rapid solidification of an intermetallic phase. Europhys. Lett. 2009, 87, 40007:1–40007:6. [Google Scholar] [CrossRef]
- Herlach, D.M.; Galenko, P.K.; Holland-Moritz, D. Metastable Solids from Undercooled Melts; Pergamon Materials Series; Cahn, R., Ed.; Elsevier: Oxford, UK, 2007; pp. 1–432. [Google Scholar]
- Greet, R.J.; Magill, J.H. An Empirical Corresponding-States Relationship for Liquid Viscosity. J. Phys. Chem. 1967, 71, 1746–1756. [Google Scholar] [CrossRef]
- Magill, J.H.; Plazek, D.J. Physical Properties of Aromatic Hydrocarbons. II. Solidification Behavior of 1,3,5-Tri-α-Naphthylbenzene. J. Chem. Phys. 1967, 46, 3757–3769. [Google Scholar] [CrossRef]
- Fuss, T.; Ray, C.S.; Lesher, C.E.; Day, D.E. Stress development and relaxation during crystal growth in glass-forming liquids. J. Non-Cryst. Solids 2006, 352, 434–443. [Google Scholar] [CrossRef]
- Fokin, V.M.; Nascimento, M.L.F.; Zanotto, E.D. Correlation between maximum crystal growth rate and glass transition temperature of silicate glasses. J. Non-Cryst. Solids 2005, 351, 789–794. [Google Scholar] [CrossRef]
- Wang, W. H.; Lewandowski, J. J.; Greer, A. L. Understanding the glass-forming ability of Cu50Zr50 alloys in terms of a metastable eutectic. J. Mater. Res. 2005, 20, 2307–2313. [Google Scholar]
- Oh, S.H.; Kauffmann, Y.; Scheu, C.; Kaplan, W.D.; Rühle, M. Ordered Liquid Aluminum at the Interface with Sapphire. Science 2005, 310, 661–663. [Google Scholar] [CrossRef]
- Oh, S.H.; Chisholm, M.F.; Kauffmann, Y.; Kaplan, W.D.; Luo, W.; Rühle, M.; Scheu, C. Oscillatory Mass Transport in Vapor-Liquid-Solid Growth of Sapphire Nanowires. Science 2010, 330, 489–493. [Google Scholar] [CrossRef]
- Jackson, K.A. The Interface Kinetics of Crystal Growth Processes. Interface Sci. 2002, 10, 159–169. [Google Scholar] [CrossRef]
- Ediger, M.D.; Harrowell, P.; Yu, L. Crystal growth kinetics exhibit a fragility-dependent decoupling from viscosity. J. Chem. Phys. 2008, 128, 034709:1–034709:6. [Google Scholar] [CrossRef]
- Hoyt, J.J.; Asta, M. Atomistic computation of liquid diffusivity, solid-liquid interfacial free energy, and kinetic coefficient in Au and Ag. Phys. Rev. B 2002, 65, 214106:1–214106:11. [Google Scholar] [CrossRef]
- Ashkenazy, Y.; Averback, R.S. Kinetic stages in the crystallization of deeply undercooled body-centered-cubic and face-centered-cubic metals. Acta Mater. 2010, 58, 524–530. [Google Scholar] [CrossRef]
- Herlach, D.M. Containerless Undercooling of Drops and Droplets. In Solidification of Containerless Undercooled Melts; Herlach, D.M., Matson, D.M., Eds.; Wiley-VCH: Weinheim, Germany, 2012. [Google Scholar]
- Brillo, J.; Pommrich, A.I.; Meyer, A. Relation between Self-Diffusion and Viscosity in Dense Liquids: New Experimental Results from Electrostatic Levitation. Phys. Rev. Lett. 2011, 107, 165902:1–165902:5. [Google Scholar] [CrossRef]
- Holland-Moritz, D.; Stüber, S.; Hartmann, H.; Unruh, T.; Meyer, A. Ni self-diffusion in Zr-Ni(-Al) melts. J. Phys.: Conf. Ser. 2009, 144, 012119:1–012119:4. [Google Scholar] [CrossRef]
- Tang, C.G.; Harrowell, P. Anomalously slow crystal growth of the glass-forming alloy CuZr. Nat. Mater. 2013, 12, 507–511. [Google Scholar] [CrossRef]
- Bragard, J.; Karma, A.; Lee, Y.H.; Plapp, M. Linking Phase-Field and Atomistic Simulations to Model Dendritic Solidification in Highly Undercooled Melts. Interface Sci. 2002, 10, 121–136. [Google Scholar] [CrossRef]
- Meyer, A.; Wuttke, J.; Petry, W.; Randl, O.G.; Schober, H. Slow Motion in a Metallic Liquid. Phys. Rev. Lett. 1998, 80, 4455–4457. [Google Scholar]
- Faupel, F.; Frank, W.; Macht, M.P.; Mehrer, H.; Naundorf, V.; Rätzke, K.; Schober, H.R.; Sharma, S.K.; Teichler, H. Diffusion in metallic glasses and supercooled melts. Rev. Mod. Phys. 2003, 75, 237–280. [Google Scholar] [CrossRef]
- Rony, P.R. The Electromagnetic Levitation of Metals; Technical Report UCRL-11411; Lawrence Radiation Laboratory/University of California: Berkeley, CA, USA, 1964. [Google Scholar]
- Earnshaw, S. On the nature of the molecular forces which regulate the constitution of the luminiferous ether. Trans. Camb. Philos. Soc. 1842, 7, 97–112. [Google Scholar]
- Rulison, A.J.; Watkins, J.L.; Zambrano, B. Electrostaic containerless processing system. Rev. Sci. Instrum. 1997, 68, 2856. [Google Scholar] [CrossRef]
- Meister, T. Aufbau und Regelung eines elektrostatischen Positionierers. Ph.D. Thesis, Ruhr-University, Bochum, Germany, 2000. [Google Scholar]
- Felici, N. Forces et charges de petits objets en contact avec une électrode affectée d’un champ électrique. Revue Générale d’Electricité 1966, 75, 1145–1160. [Google Scholar]
- Kordel, T.; Holland-Moritz, D.; Yang, F.; Peters, J.; Unruh, T.; Hansen, T.; Meyer, A. Neutron scattering experiments on liquid droplets using electrostatic levitation. Phys. Rev. B 2011, 83, 104205:1–104205:7. [Google Scholar]
- Piller, J.; Knauf, R.; Preu, P.; Lohöfer, G.; Herlach, D.M. Containerless positioning and inductive heating under micro-g conditions. In Proceedings of the 6th European Symposium on Materials Sciences under Microgravity, Bordeaux, France, 2–5 December 1986; ESA SP-256. pp. 437–444.
- Lohöfer, G. TEMPUS Space Station Vorentwicklung, SUPOS Spulenentwicklung, German Patent 38 36239 (1991) and DLR Internal Report 333. 2001; 76.
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Herlach, D.M. Non-Equilibrium Solidification of Undercooled Metallic Melts. Metals 2014, 4, 196-234. https://doi.org/10.3390/met4020196
Herlach DM. Non-Equilibrium Solidification of Undercooled Metallic Melts. Metals. 2014; 4(2):196-234. https://doi.org/10.3390/met4020196
Chicago/Turabian StyleHerlach, Dieter M. 2014. "Non-Equilibrium Solidification of Undercooled Metallic Melts" Metals 4, no. 2: 196-234. https://doi.org/10.3390/met4020196
APA StyleHerlach, D. M. (2014). Non-Equilibrium Solidification of Undercooled Metallic Melts. Metals, 4(2), 196-234. https://doi.org/10.3390/met4020196



