Isothermal Austenite–Ferrite Phase Transformations and Microstructural Evolution during Annealing in Super Duplex Stainless Steels

Abstract

Super Duplex Stainless Steels (SDSSs) are composed of α-ferrite and γ-austenite grains, the simultaneous presence of which forms an optimal microstructure to achieve the best combination of mechanical and corrosion resistance properties. Moreover, international quality standards are strict about the phase fraction ratio. The purpose of this work is the achievement of a better description of the phase ratio evolution taking place during annealing at 1080 °C in the super duplex stainless steels F53–S32750 and F55–S32760. The experimental results show a damped sinusoidal trend in the α/γ phase ratio evolution with the increase of the soaking time of thermal treatment. This can be described by coupling both the competitive coarsening growth regime and the concept of the local equilibrium phase transformations, pointing out a good correspondence with the experimental data. Further, recrystallization phenomena also play a major role. Finally, the additivity character of the observed processes has been proven.

1. Introduction

Duplex stainless steels are chromium-nickel-iron bi-phased alloys, in which the fraction of the constituent phases enables the optimization of the phases’ volume. Due to their ferritic-austenitic bi-phased microstructure, these steel grades are featured by a unique combination of high strength, toughness, ductility and corrosion resistance, overcoming the standard single-phase stainless steels (i.e., austenitic grades and ferritic grades).

If compared with the lower alloyed grades, the super duplex stainless steels (SDSSs) are characterized by a higher pitting corrosion resistance, which is ranked by the Pitting Resistance Equivalent Number (PREN). The duplex stainless steels featured by a PREN higher that 40 are indicated as super duplex. Molybdenum, tungsten and nitrogen are the main alloying additions to increase pitting corrosion performance and they are added in order to achieve a high PREN value [1]. Moreover, copper is added to improve corrosion resistance in acid solutions and to increase plastic formability, while the higher nickel concentrations enhance impact toughness [2]. On the other hand, such an increase of the alloying elements makes the microstructure more prone to the precipitation of the brittle intermetallic phases which is associated to an adverse effect on corrosion resistance and ductility [1,2].

Nowadays, the applications of duplex and super-duplex stainless steels are increasing continuously thanks to their outstanding mechanical properties, their corrosion resistance and their relatively low cost. Their use has grown drastically over the last fifteen years and, no doubt, there is great potential for a further volume increase, considering the numerous and consistent advantages offered by duplex stainless steels. This increasing market evolution involves both some consolidated industrial fields (i.e., oil and gas applications) and newly approached applications such as construction, desalinization plants and the nuclear power generation industry [3,4,5].

On the other hand, the growing trend featuring the market of the super-duplex stainless steels is limited by the precipitation of the brittle detrimental phases that can take place during the forming and the welding processes. Another undesired phenomenon that can take place during these processes is the uncontrolled change of the phase balance [6].

The present work has been performed on F53 (Cr 24–26 wt %, Ni 6–8 wt %, Mo 3–5 wt %, Cu < 0.5 wt %, Mn < 1.2 wt %, Si < 0.8 wt %, C < 0.03 wt %, N 0.24–0.32 wt % and Fe bal.) and F55 (Cr 24–26 wt %, Ni 6–8 wt %, Mo 3–4 wt %, W 0.5–1 wt %, Cu 0.5–1 wt %, Mn < 1 wt %, Si < 1 wt %, C < 0.03 wt %, N 0.2–0.3 wt % and Fe bal.) super-duplex stainless steels. It aims to describe the phase ratio evolution during annealing thermal treatment at 1080 °C, which is a typical hot working temperature for this steel grade. Nowadays, the assessment of such behavior is of significant importance, because it determines the quality of the products. In detail, standards are strict for the austenite content fork—the ideal microstructure is 50:50. Moreover, the comprehension of such a behavior is critical because it allows achievement of the desired microstructure after the forming step of the steel products or correction by heat treatment of a microstructure which does not fit the standard requirements. Finally, a deeper understanding of the phase ratio evolution would allow a better set up of the forming and welding processes, overcoming one of the main limitations affecting the diffusion of these steel grades [1,6].

The solid state phase transformations and, more precisely, the migration of the transformation interfaces have been an active field of research for over a century, focusing mainly on low-alloy steels [7]. However, previous work indicates that the precipitation of austenite in the stainless steel is comparable with the decomposition of austenite in low-alloy steels, implying that the direction of the f.c.c. ↔ b.c.c. transformation is irrelevant; thus, the models developed for low-alloy steels can be adopted in this context [8].

In the duplex stainless steels the phase transformation process is dynamic and its kinetics results mainly from the interactions between the diffusion fields in the bulk phases and the behavior of both carbon and alloying elements through the α-ferrite/γ-austenite interface.

The growth of a phase and consequently the interface migration can be treated by the Local Equilibrium (LE) model. This model considers a constant activity across the interfaces and the phase transformations are described under the hypothesis that the local equilibrium between the parent and the growing phases is maintained even at the migrating interfaces.

In the LE model, the interstitial and the substitutional elements partition are considered according to the local equilibrium assumptions, and this hypothesis implies that the chemical potential of each species across the interface should be constant, hence:

$${\mathsf{\mu }}_i^{\mathsf{\alpha }}={\mathsf{\mu }}_i^{\mathsf{\gamma }}$$

(1)

where ${\mathsf{\mu }}_i^{\mathsf{\alpha }}$ and ${\mathsf{\mu }}_i^{\mathsf{\gamma }}$ are the chemical potential of the element $i$ at the interface in the ferrite and the austenite phase, respectively. The Local Equilibrium assumption at the α/γ interface requires that the Equation (1) must be fulfilled for each component across the interface at any time.

Then, at the interface the mass balance law must be satisfied:

$$J_i^{\mathsf{\alpha }}-J_i^{\mathsf{\gamma }}=\frac{v}{V_m}(x_i^{\mathsf{\gamma }}-x_i^{\mathsf{\alpha }})$$

(2)

where $J_i^{\mathsf{\alpha }}$ and $J_i^{\mathsf{\gamma }}$ are the diffusion flux of $i$ in the ferrite and austenite phases respectively, $v$ is the interface migration velocity, $V_m$ corresponds to the molar volume and $x_i^{\mathsf{\gamma }}$ and $x_i^{\mathsf{\alpha }}$ are the molar fractions of the element $i$ in the ferrite and the austenite phase, respectively. Thus, in the LE model, it is necessary to solve Fick’s second law for all the alloying elements $i$ in both the austenite and ferrite phases $\mathsf{\phi }$:

$$\frac{\partial x_i^{\mathsf{\phi }}\left(r,t\right)}{\partial t}=\frac{1}{r^{k-1}}\frac{\partial }{\partial r}\left(r^{k-1}{D}_i^{\mathsf{\phi }}\left(x_i^{\mathsf{\phi }}\left(r,t\right)\right)\frac{\partial x_i^{\mathsf{\phi }}\left(r,t\right)}{\partial r}\right)$$

(3)

where $r$ is the radial coordinate, $t$ is time, $k=1,2,3$ is the geometry parameter (planar, cylindrical and spherical, respectively), $x_i^{\mathsf{\phi }}$ is the mole fraction of $i$ in $\mathsf{\phi }$, and $D_i^{\mathsf{\phi }}$ is the diffusion coefficients of the chemical species in the considered phase, which are dependent on the composition.

The boundary conditions for LE model can be written as:

$${\frac{\partial x_i^{\mathsf{\phi }}\left(r,t\right)}{\partial r}|}_{\begin{array}{c}r=0\\ r=\mathrm{L}\end{array}}=0$$

(4)

where $r=0$ and $r=\mathrm{L}$ signify the left and right boundary, respectively.

The equilibrium mole fractions at the interface in both the austenite and ferrite phases can be determined at every time step and then the position of the interface can be calculated as a function of time.

Due to the large difference in the diffusivities of the alloying elements, there are different partitioning modes that take place during the phase transformations. The situation becomes even more complex when a third element or further elements are added to the system. A case of particular interest is when an atom diffuses many orders of magnitude faster or slower than others. The transformation is controlled by the diffusion, but the rate of reaction can vary widely depending on whether the atoms are partitioned between the austenite and the ferrite. Also, the occurrence of a solute drag effect may play a crucial role in the interface mobility. The combination of these parameters results in three different growing modes: local equilibrium with partitioning (LEP), local equilibrium with negligible partitioning (LENP), and paraequilibrium (PE).

In detail, Super-Duplex-Stainless-Steels (SDSSs) have a very complex composition and the interaction between the different atoms is not easy to predict. Indeed, the Fe-C-Ni system can be seen as a paradigm of the simplest situation, in which the substitutional element has only a weak interaction with both C and the moving interface. In spite of this simplicity, in the Fe-C-Mo system the substitutional Mo atom interactions with both C and the moving phase interface (solute drag effect) are no longer expected to be negligible [7,9,10,11].

Further, a well-known problem of long standing interest about the formal kinetics is the conversion of isothermal kinetic data into predictions of the kinetics for various non-isothermal thermal treatments used in the real processes. This is often accomplished with the help of the additivity rule, which follows from Equation (5):

$${{\displaystyle \int }}_0^t\frac{\mathrm{d}t}{\mathsf{\tau }\left(X_0,T\right)}=1$$

(5)

where $\mathsf{\tau }\left(X_0,T\right)$ represents the isothermal transformation time for the transformed fraction $X=X_0$ at a temperature $T$ and $t$ is the total transformation time. Thus, an additive reaction implies that the total time to reach a special stage of transformation is obtained by adding the fractions formed by isothermal transformation in each time range and at each temperature until the sum reaches unity.

These phenomena and the isokinetic behavior that can rule the microstructure evolution have been extensively investigated for years. In spite of these efforts, the subject is still controversial because a full understanding of the physical limitations of the approach is lacking. Nevertheless, in industrial practice, isothermal kinetic behavior is frequently of less importance than its behavior during more complex thermal treatments. Thus, the additivity rule has been widely used in order to predict the phase transformation kinetics during thermal treatments. As a consequence, both theoretical and the experimental studies regarding the additivity rule have focused on its validation and on the limitations on nucleation, growth and transformation, in order to describe the kinetics of the transformation [12,13,14].

2. Experimental Procedure

Specimens with dimensions of approximately 30 mm × 20 mm × 15 mm were extracted from F53 and F55 forged ingots, featuring a 5:1 reduction ratio. A solution treatment at 1300 °C was then performed and the holding time was set for all the samples at 60 s per millimeter and the cooling step was realized by quenching, using stirred water. This initial heat treatment has been performed in order to obtain a duplex structure composed only by α-ferrite and γ-austenite, eliminating any previous secondary phase which could be present in the tested steels. Moreover, this thermal treatment aims to eliminate any residual stress and any deformation pattern, avoiding recrystallization phenomena. This thermal treatment allows achieving a supersaturation of γ-former elements within the α-ferritic phase. A holding temperature of 1300 °C was chosen to avoid any thermodynamic equilibrium between the metal matrix and any secondary phase; the soaking time was set as 60 s/mm so that a thermal and chemical homogenization would be assured [4].

Then, when the chemical homogenization was reached, the general chemical composition of the tested material was measured by optical emission spectroscopy.

A second isothermal annealing treatment was performed on the SDSSs specimens at 1080 °C at different holding times. This second heat treatment aimed at reproducing the temperature conditions experienced during the hot-working, avoiding the precipitation of the detrimental secondary phases. Different holding times were tested in order to point out the microstructural evolution of the tested alloys: 18, 36, 72, 145, 215, 285, 355, 425, 500, 570, 710, 850, 995, 1135 s/mm. The samples were water quenched at the end of the annealing heat treatment (Figure 1).

A third isothermal treatment was realized to refine the collected data, define the local kinetics of the microstructure evolution and prove that the behavior of the SDSSs during annealing thermal treatment follows the additivity rule. The temperature of this treatment was set at 1080 °C for 72 or 145 s per millimeter of the specimen thickness. The cooling was executed by water quench, also in this heat treatment (Figure 1).

The resulting specimens were treated for microstructural examination using Beraha’s tint etching (which selectively etches the ferritic phase) and oxalic acid electrolytic etching, as recommended by the standard ASTM E407-07. The quantitative metallographic analysis was performed following the standards to evaluate second-phase contents and grain sizes by automatic image analysis according to ASTM E1245-13 and ASTM E1382-10. Following the same procedure, the aspect ratios of the grains and the precipitation-free zone (PFZ) widths were measured. The local chemical composition analyses were performed using INCA Oxford Instrument (Tubney Woods, Abingdon, Oxon OX13 5QX, UK) SEM/EDS measurements on the different phases. Moreover, the crystallographic data were acquired through INCA Oxford Instrument (Tubney Woods, Abingdon, Oxon OX13 5QX, UK) SEM/EBSD analyses.

3. Results

Checking the general chemical composition through optical emission spectroscopy of the tested material after the solution thermal treatment, produced results in accordance with the standards. F53 SDSS had results composed of: Fe 61.90 wt %, Cr 25.16 wt %, Ni 6.34 wt %, Mo 4.58 wt %, Cu 0.33 wt %, Mn 0.81 wt %, Si 0.57 wt %, C 0.02 wt % and N 0.29 wt %. Further, the chemical composition measured for F55 SDSS resulted: Fe 61.74 wt %, Cr 24.63 wt %, Ni 6.68 wt %, Mo 3.86 wt %, W 0.73 wt %, Cu 0.76 wt %, Mn 0.74 wt %, Si 0.49 wt %, C 0.02 wt %, N 0.23 wt %.

The solution thermal treatment of the SDSSs formed a microstructure featured by γ-austenite grains, embedded in α-ferrite matrix that was supersaturated in γ-stabilizers elements. A consequence of this supersaturation was the segregation of γ-stabilizers elements, resulting in γ-austenite thick plates located at α-grain boundaries, which interconnected with the γ-austenitic grains.

The equilibrium phase fractions ratio, at temperatures below the solution thermal treatment temperature (1300 °C), moved to the ideal 50:50 equal proportion between α-ferrite and γ-austenite. This change in the equilibrium acts as driving force for further phase transformation. As a consequence, part of the α-ferrite, obtained during the homogenization heat treatment, was converted into γ-austenite via a solid state diffusion-controlled reaction, raising the γ-austenite content of the alloys (

Table 1. Phase ratio and aspect ratio of the γ-austenite phase during the isothermal annealing at 1080 °C.

Annealing Soaking Times [s/mm]		0	36	72	145	215	285	355	425	500	570	710	850	995	1135
F53–S32750	Phase Ratio	0.39	0.54	0.57	0.55	0.47	0.42	0.62	0.50	0.47	0.53	0.50	0.51	0.50	0.47
	Error	0.03	0.05	0.03	0.03	0.03	0.03	0.03	0.03	0.03	0.03	0.03	0.04	0.01	0.02
	γ Aspect Ratio	9.26	9.08	10.52	10.34	9.63	6.76	7.47	9.11	9.19	8.66	8.89	9.23	8.70	8.97
F55–S32760	Phase Ratio	0.36	0.49	0.54	0.54	0.40	0.44	0.54	0.51	0.45	0.52	0.41	0.40	0.44	0.41
	Error	0.03	0.02	0.05	0.03	0.00	0.04	0.01	0.04	0.03	0.05	0.04	0.01	0.07	0.02
	γ Aspect Ratio	9.33	10.87	9.17	11.61	10.21	7.78	8.21	9.92	8.38	9.09	10.27	9.56	9.64	8.89

, Figure 2 and Figure 3). This transformation is supported by the phase diagrams, by several computational models and by the experimental observations [8,15].

From a qualitative point of view, during the annealing thermal treatment two main processes occured. In the early stages, the generation of Widmanstätten saw-teeth structures, associated with Martensitic-shear nuclei and then with the sympathetic structures, took place and such transformation phenomena went on until the driving force was consumed. The thermodynamic driving force was provided by the deviation in the chemical composition from the phase equilibrium of the supersaturated α-matrix. Subsequently, the γ-nuclei growth started, following the principle of the minimization of the interfacial free-energy and such a γ-nuclei growth went on and caused the grains to coarsen (Figure 4). Since this phenomenon can be relevant to the grains’ shape, their aspect ratio has been calculated and reported in Table 1.

The formation of Widmanstätten γ- austenite occurs between 1200 °C and 650 °C by nucleation and growth and follows a C-curve kinetics. This ferrite to austenite transformation (α→γ) in duplex stainless steels is very similar to the transformation from austenite to the proeutectoid ferrite (γ→α) in hypoeutectoid low-alloy carbon steels. Initially, γ-austenite precipitates at the ferrite/ferrite grain boundaries and grows through the Widmanstätten morphology into the interior of the grains. Afterwards, austenite also precipitates as intra-granular side-plate islands. The rate of this reaction is very fast and the ferrite decomposition is fulfilled in a few minutes [6].

The occurrence of γ-precipitation phenomena during the cooling paths can be excluded, because of the absence of fine nuclei for the longest annealing times. Moreover, even in the early stages of the annealing thermal treatment the α-matrix experiences a loss of γ-stabilizer elements, which is the driving force for the γ-precipitation processes. As the soaking times of the annealing thermal treatment increases, the fine dispersion of γ-nuclei decreases and their larger average size witnesses the competitive character characterizing this growth stage (Figure 5) [1,8].

The phase ratio tends to reach a different equilibrium value after the application of the solution thermal treatment, since the existence field of the γ-austenite was extended by the lower annealing temperature. However, the intermediate stage of this transformation is characterized by strong fluctuations in the phase fractions. The variation of the phase fraction is not linear as a function of the treatment temperature as can be expected by quasi-equilibrium transformations. Both the analyzed SDSSs point out the same trend in the phase ratio evolution during the intermediate stage of the annealing thermal treatment. The phase ratio features broad oscillations around the equilibrium value (Figure 3).

This characteristic trend can be split in two contributing factors: a damping term and a sinusoidal term. Actually, the damping term corresponds to the loss of free-energy of the system at the equilibrium between the phases, so it is assisted by a long-range diffusion phenomena and it is ruled by the thermodynamic aspects. On the other hand, the sinusoidal oscillations are due to the local phase transformations and the local diffusive processes controlling the short-range diffusion kinetics.

At the annealing temperature the phase transformations are solid state diffusion-assisted reactions and they are ruled by the diffusion behavior of the alloying elements involved in a complex system, such as the investigated steels. The transport of α- and γ-stabilizers atoms plays a prominent role in the phase transformation reactions. Indeed, these elements are subjected to a strong partitioning within the two phases composing the alloys. Therefore, they are certainly responsible for the motion of the α/γ interfaces. In this case the phase transformations are mainly controlled by diffusive phenomena of the substitutional atoms (Ni as γ-former and Mo as α-stabilizer for this alloy), which produced the largest distortion in the lattice (Figure 6).

Related to the interface motion, another relevant phenomenon also occurs: the generation of a precipitation-free zone (PFZ) in the α-matrix, surrounding the γ-austenitic grains (Figure 7). The microstructure of the precipitation-free zone has a well-defined front. The growth rate of the γ-grains follows a $t^{1/3}$ kinetics, indication of the diffusion-limited competitive coarsening (Figure 7).

Moreover, the oscillating component of the phase fraction trend can be related to the local thermodynamic equilibrium at the moving interface and to the short-range diffusive phenomena that can also involve the recrystallization process. Thus, the upper and the lower limits of this oscillating trend are coupled respectively with the short-range diffusive phenomena and the reorganization of crystalline architecture and its periodicity is due to the diffusive competitive coarsening processes.

Regarding the lower limits of this oscillating trend, the occurrence of recrystallization was detected via SEM-EBSD analysis. The coincidence site lattice (CSL) model can be used as a standard for the characterization of the grain boundary structure of polycrystals.

The frequency of occurrence of a peculiar kind of CSL grain boundary is inherently associated with the newly recrystallized grains and forms a preferred crystallographic orientation relative to the parent grains. CSL boundaries Σ13 for f.c.c. lattices are associated with fast moving boundaries, testifying to the occurrence of nucleation and growth phenomena [16].

The CSL frequency of occurrence has been determined for γ-precipitates dispersed within the α-ferrite matrix. Thus, the increase in CSL boundaries Σ13 for f.c.c. γ-austenitic precipitates within α-ferrite grains proves the occurrence of the recrystallization phenomena. Such phenomena take place whenever the γ-austenite volume fraction reaches a minimum value in its broad oscillation during the isothermal annealing thermal treatment (Figure 8) [17,18,19].

Finally, the collected data on the phase ratio after the second isothermal annealing at 1080 °C thermal treatment show a robust correspondence with the phase fraction ratio evolution of the previous annealing treatment, not only in the trends but also quantitatively. Thus, the hypothesis of additivity for the investigated systems is validated (Figure 9).

4. Discussion

In this work, the phase ratio evolution during the annealing thermal treatment was investigated and its trend was seen as an oscillating curve damped to the equilibrium value. This trend can be observed even better whenever the grains’ shape is taken into account. Indeed, the presence of γ/γ internal interfaces and the twinning of interfaces into γ-austenite crystalline grains are caused by the coarsening phenomena that have taken place (Figure 10A). However, the formation of the typical lamellar microstructure at high temperatures is induced by the α/γ interface energy, which is lower than the α/α and γ/γ grain boundary energies [6,20].

As a consequence of the distribution of the γ-austenite grains in the α-ferrite matrix, a deviation from the round shape enhances the probability of the impingement among the austenite grains. Whenever this phenomenon occurs, the α/γ interfacial energy increases to a higher value featuring the γ/γ internal interfaces. Therefore, the increase in interfacial energy of the system provides free energy to support the α-ferrite to γ-austenite phase transformation.

Through simple geometrical considerations, the probability ratio of impingement depends on the aspect ratio (the ratio between the maximum and the minimum axis of the ellipse approximating the grain shape) of the γ-austenitic grains through the relationship expressed by Equation (6).

$$k=\frac{P{r}_n^{\mathrm{imp}}}{P{r}_0^{\mathrm{imp}}}=\frac{p_n}{p_0}=\frac{\sqrt{A{R}_0}\ast \left(A{R}_n+1\right)}{\sqrt{A{R}_n}\ast \left(A{R}_0+1\right)}$$

(6)

where $P{r}^{\mathrm{imp}}$ corresponds to the probability of grain impingement, $p$ is the perimeter γ-austenite grains and $AR$ corresponds to the aspect ratio of the γ-austenite grains.

Combining this equation with the experimental data on the variation of the aspect ratio featuring the γ-austenite grains, the calculation of the total surface energy variation is made possible and consequently the estimation of the further volume phase transformation can be performed. Thus, the distinction between the influence of grains geometry and the chemical aspects of the phase ratio evolution is possible. This can be achieved by the introduction of a correction factor $k=P{r}_n^{\mathrm{imp}}/P{r}_0^{\mathrm{imp}}$, calculated as shown in Equation (6), which takes into account the γ-austenitic grain aspect ratio. The results of phase ratio evolution can be rearranged applying the correction factor $k$ and they point out a sinusoidal damped behavior at the ongoing annealing thermal treatment (Table 1 and Figure 10B).

In order to completely define this sinusoidal damped trend of the phase ratio evolution with the soaking time of the annealing thermal treatment (Figure 3), the different aspects, featuring this behavior, will be discussed:

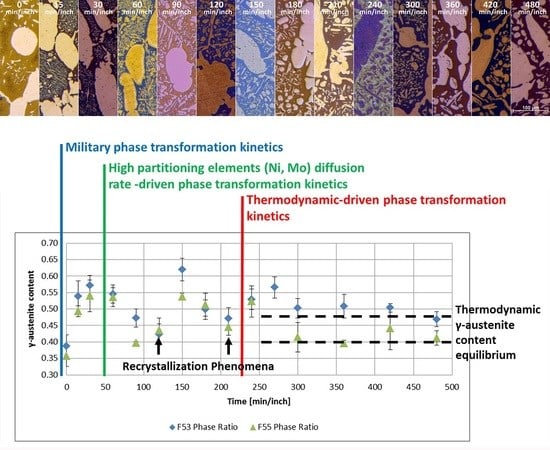
• The damping term is due to the loss of free-energy of the system near the thermodynamic equilibrium condition and it is associated with the thermodynamic aspects of the phase transformations induced by this thermal treatment.
  On the basis of the observations, the damping term of the phase fraction evolution follows an Arrhenius-type equation describing the driving force of the α-ferrite transformation into γ-austenite. The results confirm the lower activation energy of F53 (1.12 J/mol) if compared with F55 (2.25 J/mol), due to an initial wider deviation from the thermodynamic equilibrium as consequence of the higher concentration of γ-formers elements, as expected by the chemical composition standards [21].
  Because of the diffusive nature of this phase transformation, it is possible to define a diffusional relaxation time $\mathsf{\tau }$ after which the transformation closely approaches the full thermodynamic equilibrium, defined as:

  $$\mathsf{\tau }=a^2/D$$

  (7)

  where $a$ is the radius of the parent phase grains and $D$ is the diffusion coefficient of the substitutional solute atoms [22].
  The explicit formula of $D$ should be reported:

  $$D=D_0{e}^{-\frac{E_A}{k_{B}T}}$$

  (8)

  where $D_0$ is a temperature-independent pre-exponential term of diffusivity, $k_B$ is referred to the Boltzmann constant and $E_A$ corresponds to the activation energy of the diffusion [21,23]. The values used for the calculations are those reported by F. Ruffini et al. [23].
  Calculating $D$ for the motion of Ni atoms in α-ferrite, the faster substitutional element ruling the studied system, and obtaining the radius of the parent γ-phase grains ($a\approx 30\mathsf{\mu }\mathrm{m}$) from metallographic analysis (Figure 2), it is possible to calculate the diffusional relaxation time $\mathsf{\tau }=228\mathrm{s}/\mathrm{mm}$. The results are in good accordance with the experimental evidence for the longer soaking times of the annealing thermal treatment ($t>400\mathrm{s}/\mathrm{mm}$) (Figure 3 and Figure 10B).
• A robust deviation from the thermodynamic equilibrium and the Arrhenius-type trend of the phase ratio evolution occurs during the early stages of the annealing treatment. The explanation of this behavior can be ascribed to the military character of the ongoing γ-austenite nucleation. This assumes that local phase transformations would be much faster than the overall kinetics ruling the system, which is characterized by an intrinsically slower diffusion-controlled kinetics. As consequence of the military character of the ongoing γ-austenite nucleation processes, the transformation equilibrium is ruled by the local free-energies that exceed the overall reaction thermodynamic equilibrium (in the present case the supersaturation of α-matrix by γ-stabilizers elements). A clear picture of these phenomena can be provided by Widmanstätten precipitation processes: the nucleation is supported by a local supersaturation, generating grain boundaries’ saw-teeth structures but the transformation goes on until it is completed in the α-ferrite grains [24].
  This explanation can be supported by the observation of the local γ-nucleation processes, which are the cause of the fast increase of γ-austenite volume fraction at the early stages of the annealing thermal treatment (Figure 11).
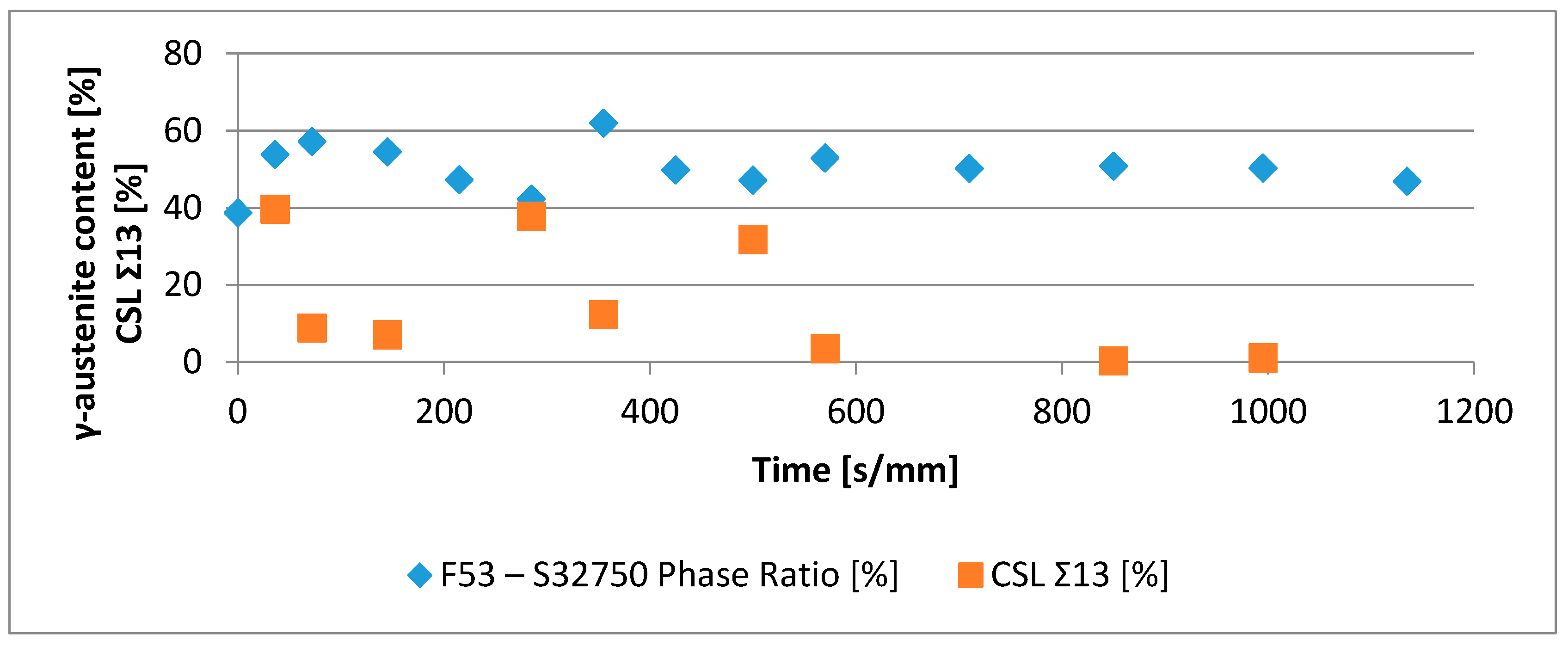
• The minima of the evolution of the phase ratio with the increase of the soaking time of the annealing thermal treatment are related to recrystallization phenomena. In these cases, the γ-austenitic grains show a primary recrystallization as testified by CSL data and, after that the recrystallization, γ-austenite can grow again. Moreover, in the literature it is reported that while γ-austenite shows a primary recrystallization, α-ferrite undergoes recovery due to its high stacking fault energy (SFE). Indeed, α-ferrite grains resemble the annealing texture of single phase ferritic steels, without revealing any influence performed by the concurrent second phase. So, the retarded nucleation and the reduced dislocation density, due to recovery, essentially suppress recrystallization, which is not detected for α-ferritic grains (Figure 8) [17,18,19].
• The maxima of the phase ratio evolution related to the ongoing of the annealing thermal treatment are related to the local thermodynamic equilibrium at the moving interfaces. This can be described using the Local Equilibrium model and it has been already demonstrated experimentally. This model points out the differences in the diffusive phenomena of the slow diffusing substitutional elements within the Fe-C system. Nickel interactions with the moving interface are expected to be weak and can treated by the local equilibrium model associated with the negligible partitioning (LENP) and paraequilibrium (PE) models. On the other hand, the interactions between molybdenum and the moving interfaces are much stronger. This can be interpreted by a model including the solute drag effect [10]. This effect grows as a function of the interface motion and, therefore, of the soaking time of the annealing thermal treatment. However, the strong drag effect would result in a robust increase of the molybdenum concentration at the moving interfaces (Figure 12) [25]. This instance proceeds up to the complete loss of chemical energy, promoting the interface motion and, consequently, up to the inversion of the α/γ interface motion.
• The periodicity of the oscillating component of the phase fraction evolution can be associated with the diffusive competitive coarsening processes. As extrapolated by the SEM line-scans (Figure 6), the motion of the α/γ interfaces is the result of the movements of the strong partitioned elements, as Mo (acting as α-stabilizer) and Ni (behaving as γ-former). However, the strong partition of these elements (due to the generated concentration gradients) promotes their motion into the other phase, respectively Mo towards γ-austenitic grains and γ-nuclei and Ni into the α-ferritic matrix. If compared with the diffusing paths of atoms the sizes of the grains are much larger, so the motion direction can be always assumed as perpendicular to the α/γ interface. Thus, the motion direction of both the diffusing species is the same, while the direction of their diffusive paths is opposed [10].
  Provided the diffusion-controlled nature of the solid-state transformation of α-ferrite into γ-austenite and under the hypothesis of the competitive growth regime and the identification of Ni and Mo as the main actors involved in these phenomena, a complete description of the sinusoidal term of the phase evolution can be achieved. The diffusion-controlled competitive coarsening kinetic appears modeled through the Equation (9):

  $$\{\begin{array}{c}{\langle R\left(t\right)\rangle }^3-{\langle R\left(t_0\right)\rangle }^3=\frac{8\widetilde{D_{\mathrm{Mo}}^{\mathsf{\alpha }}}{\mathsf{\gamma }}_{\mathsf{\alpha }/\mathsf{\gamma }}{\Omega }_{\mathrm{Mo}}^2{c}_{\mathrm{Mo}}^{\mathrm{eq}}(\infty )}{9k_{\mathrm{B}}T}\ast t\\ {\langle R\left(t\right)\rangle }^3-{\langle R\left(t_0\right)\rangle }^3=\frac{8\widetilde{D_{\mathrm{Ni}}^{\mathsf{\gamma }}}{\mathsf{\gamma }}_{\mathsf{\alpha }/\mathsf{\gamma }}{\Omega }_{\mathrm{Ni}}^2{c}_{\mathrm{Ni}}^{\mathrm{eq}}(\infty )}{9k_{\mathrm{B}}T}\ast t\end{array}$$

  (9)

  where $\langle R\rangle$ corresponds to the average grain size, $\tilde{D}$ is the chemical interdiffusivity, ${\mathsf{\gamma }}_{\mathsf{\alpha }/\mathsf{\gamma }}$ is the interface energy, $\Omega$ is the atomic volume, $c^{\mathrm{eq}}(\infty )$ is the solubility of the element in a phase for a system featured by a planar interface, $k_{\mathrm{B}}$ is the Boltzmann constant, $T$ is the temperature and $t$ is the time. Under the hypothesis of the same value for the growth of the average particle size, the system can be solved and the difference in the diffusion rates between Mo atoms, moving into α-ferrite, and Ni atoms, diffusing into γ-austenite, results in a delay in time for Ni atoms to cover the same diffusion path length. This calculated delay ($t=240.5\mathrm{s}/\mathrm{mm}$) corresponds also to a period of the sinusoidal term of the phase fraction ratio evolution, which has been observed by the experimental observation ($t\approx 250\mathrm{s}/\mathrm{mm}$) (Figure 3).
  The wide difference in the diffusion rates (100 times in α-ferrite than in γ-austenite) is related to the atomic packing factor of the b.c.c. α-ferritic structure that is lower than the f.c.c. γ-austenitic arrangement. Another consequence of this diffusive phenomenon, and according to the diffusion-controlled phase transformation models, is that the α-ferrite to γ-austenite transformation (α→γ) is approximately 1.9 times faster than the reverse austenite to ferrite transformation (γ→α) during the initial stages of the transformation. This occurs due to the absence of soft impingement phenomena (overlap of diffusion fields of the neighboring grains in the classic diffusion-controlled growth model, which slows the phase transformation kinetics) in the initial stages of the phase transformations [10].

A further confirmation of the description of these diffusive phenomena has been obtained considering the growth rate of the precipitation-free zones (PFZs) in the α-matrix surrounding the γ-austenitic grains (Figure 7). The literature reports that in binary alloys, the growth of the PFZs is related to the solute depletion, leading to a growth rate that is a function of the square root of the time, according to the competitive coarsening regime model [26,27].

In this work, the growth rate of the precipitation-free zone around the γ-grains follows a $t^{1/3}$ kinetics, which indicates a diffusion-limited competitive coarsening (Figure 7). These results indicate the coupled action of the simultaneous diffusion of both α-stabilizers and γ-formers elements. Thus, as a matter of fact, the precipitation-free zone is not just the consequence of the solute depletion but it is also related to the enrichment of α-formers atoms stabilizing the α-ferrite matrix.

Finally, the additivity hypothesis has been confirmed for the annealing thermal treatments of Super Duplex Stainless Steels. Since the additivity feature implies that overall time to reach a definite stage of transformation is obtained by adding the fractions of the time to reach this stage isothermally until the sum reaches unity [12]. The additivity concept has been associated to the diffusional growth, but the situation becomes much more complicated if the nucleation stage also is included, since transformations involving both the nucleation and the growth are not isokinetic [13].

In the present study, this statement can be easily confirmed by the evaluation of the phase fraction ratio and the consistency with the previous results of its evolution during the annealing treatment. This is also supported by the microstructure evolution processes, since the nucleation stage is terminated during the heating ramp of the first annealing thermal treatment, consuming the driving force deriving by the α-matrix supersaturation. Moreover, during the cooling paths, any significant phase transformation does not occur. Therefore, during the holding time at the annealing temperature, only the growth phenomena take place in the alloy and the isothermal character of the heat treatment ensures the additivity of the processes (Figure 9) [13].

The importance of the experimental confirmation of the additivity feature is related to the narrow fork of the phase fractions required by the quality standards. Under the hypothesis that additivity rule is valid, it is possible to tune the phase ratio and correct the unsatisfied parameters simply by a further annealing treatment [12].

5. Conclusions

This work aims to identify the microstructure variation of the studied F53–S32750 and F55–S32760 steels via different thermal treatments usually industrially performed. The main features of the overall phase transformations occurring in the considered super duplex stainless steels during the annealing thermal treatment at 1080 °C have been observed and described:

• The precipitation-free zone surrounding the γ- grains is featured by a growth rate as a function of $t^{1/3}$. This indicates the diffusion-limited competitive coarsening and the coupled action of the contemporary diffusions of both α-stabilizers and γ-formers elements.
• The evolution of the phase ratio α/γ results in a sinusoidal behavior damped to the equilibrium γ-austenite volume fraction. As consequence, the transformation process can be decomposed into two main contributions: the damping term (related to the thermodynamic aspects of the processes) due to the loss of free-energy of the system, and the sinusoidal oscillations associated to the diffusive processes in the alloys. This last aspect rules the kinetics of the reaction. The initial deviation from the thermodynamic equilibrium is caused by the military character of the α-intragranular γ nucleation.
• The thermodynamic factor is governed by an Arrhenius-type equation, resulting in lower activation energy for F53–S32750, as expected by the alloy composition. Discrepancies between the monotonic damping of the free-energy available for the phase transformation processes and the effective conversion of α-ferrite into γ-austenite are caused by different γ-grains aspect ratios. The sinusoidal kinetic component of the phase formation is ruled by the diffusive competitive coarsening processes. The periodicity is controlled by the diffusion rate of the high partitioning elements (i.e., nickel and molybdenum) in the different phases.
• The changes in the dominant transformation are due to the solute drag effect of Mo on the moving interfaces, as predicted by Local Equilibrium model, and to the recovery and recrystallization phenomena.
• The additivity character of the annealing thermal treatment has been proved. This result, coupled with the assessment of the phase fraction ratio evolution, represents a very powerful tool for the achievement of the desired and precise phase fraction ratio in the product realization.