Physical Modelling and Numerical Simulation of the Deep Drawing Process of a Box-Shaped Product Focused on Material Limits Determination
Abstract
1. Introduction
2. Materials and Methods
2.1. The Press-Die-Pressing System
2.2. Material
2.3. Numerical Simulation Model
2.3.1. Material Hardening Model
2.3.2. Material Yield Locus
2.3.3. Failure Criteria
2.3.4. Boundary Conditions
3. Results
4. Discussion
5. Conclusions
- The Hill 48 and Hill 90 yield locus mathematical models and the Hollomon and Krupkowski hardening law mathematical models for cold rolled low carbon aluminum-killed steel for enameling were determined from tensile tests at angles of 0°, 45°, and 90° to the rolling direction and bulge tests. Experimental Kosmalt 190 steel with a thickness of a0 = 0.5 mm showed extra deep drawing quality with rm = 1.57 and nm = 0.226.
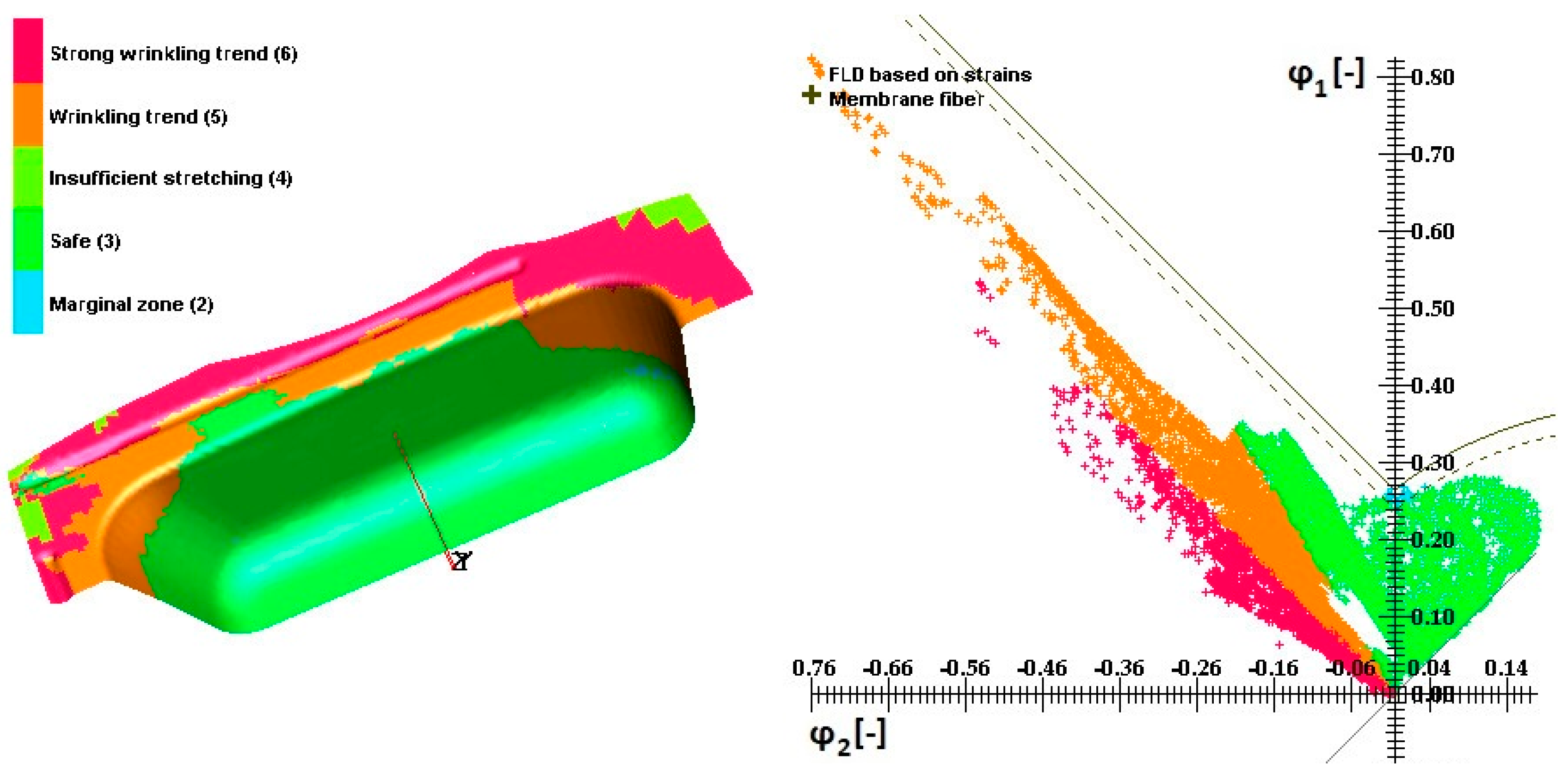
- In all numerical simulations and physical experiments, the bathtub model pressing was drawn free of fracture and wrinkles when simulated at the same blankholder force (340 kN) and friction (0.09) values. Keeler-Brazier’s mathematic model was used to define the forming limit curve and to determine material fracture in numerical simulations.
- The best yield locus/hardening law combination appeared to be Hill 48/Krupkowski. This was determined by comparing the wall thicknesses of model pressing in selected sections after simulations and physical experiments. The deviations at the local minima were 0.7% and −1.0% in section A-A (longitudinal) and 2.4% in section B-B (corner). The course of relative thickness change evaluated from numerical simulations and experimental measurements showed good conformity.
- The material’s anisotropy limits were found to be rm = 1.47 and nm = 0.23 when the model pressing free of fracture was drawn in a numerical simulation. Virtual materials were defined from experimentally measured values of the plastic strain ratio.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Menezes, L.F.; Teodosiu, C. Three-dimensional numerical simulation of the deep-drawing process using solid finite elements. J. Mater. Process. Technol. 2000, 97, 100–106. [Google Scholar]
- Thomas, W.; Oenoki, T.; Altan, T. Process simulation in stamping—Recent applications for product and process design. J. Mater. Process. Technol. 2000, 98, 232–243. [Google Scholar] [CrossRef]
- Spišák, E. Mathematical Modelling and Simulation of Technological Processes—Deep Drawing, 1st ed.; ELFA, Ltd.: Košice, Slovakia, 2000; p. 156. ISBN 80-7099-530-0. [Google Scholar]
- Jha, A.; Sedaghati, R.; Bhat, R. Dynamic Testing of Structures Using Scale Models. In Proceedings of the 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference, Austin, TX, USA, 18–21 April 2005; AIAA 2005-2259. American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2005. [Google Scholar]
- Langhaar, H.L. Dimensional Analysis and Theory of Models, 1st ed.; John Wiley & Sons: New York, NY, USA, 1951; ISBN 9780471516781. [Google Scholar]
- Szucz, E. Similitude and Modeling: Fundamental Studies in Engineering, 1st ed.; Elsevier: Amsterdam, The Netherlands, 1980; Volume 2. [Google Scholar]
- Coutinho, C.P.; Baptista, A.J.; Rodrigues, J.D. Reduced scale models based on similitude theory: A review up to 2015. Eng. Struct. 2016, 119, 81–94. [Google Scholar] [CrossRef]
- Sedov, L.I. Similarity and Dimensional Methods in Mechanics, 10th ed.; CRC Press: Boca Raton, FL, USA, 1993; p. 496. ISBN 9780849393082. [Google Scholar]
- Gronostajski, Z.; Hawryluk, M. Analysis of metal forming processes by using physical modeling and new plastic similarity condition. In Proceedings of the CP907, 10th ESAFORM Conference on Material Forming, Zaragoza, Spain, 18–20 April 2007. [Google Scholar]
- Davey, K.; Darvizeh, R.; Al-Tamimi, A. Finite Similitude in Metal Forming. In Proceedings of the NUMIFORM 2016: The 12th International Conference on Numerical Methods in Industrial Forming, Troyes, France, 4–7 July 2016. [Google Scholar]
- Al-Tamimi, A.; Darvizeh, R.; Davey, K. Experimental investigation into finite similitude for metal forming processes. J. Mater. Process. Technol. 2018, 262, 622–637. [Google Scholar] [CrossRef]
- Krishnamurthy, B.; Bylya, O.; Davey, K. Physical modelling for metal forming processes. Procedia Eng. 2017, 207, 1075–1080. [Google Scholar] [CrossRef]
- Keran, Z.; Piljek, P.; Ciglar, D. Metal forming similarity theory in numerical simulations. J. Technol. Plast. 2016, 41, 38–45. [Google Scholar]
- Ajiboye, J.S.; Jung, K.H.; Im, Y.T. Sensitivity study of frictional behavior by dimensional analysis in cold forging. J. Mech. Sci. Technol. 2010, 24, 115–118. [Google Scholar] [CrossRef]
- Roll, K. Simulation of sheet metal forming—Necessary developments in the future. In Proceedings of the NUMISHEET, 7th International Conference on Numerical Simulation of 3D Sheet Metal Forming Processes, Interlaken, Switzerland, 1–5 September 2008; ETH Zürich: Zürich, Switzerland, 2008; pp. 3–11. [Google Scholar]
- Silva, M.B.; Baptista, R.M.S.O.; Martins, P.A.F. Stamping of automotive components: A numerical and experimental investigation. J. Mater. Process. Technol. 2004, 155, 1489–1496. [Google Scholar] [CrossRef]
- Choudhury, I.A.; Lai, O.H.; Wong, L.T. PAM-STAMP in the simulation of stamping process of an automotive component. Simul. Model. Pract. Theory 2006, 14, 71–81. [Google Scholar] [CrossRef]
- Padmanabhan, R.; Oliveira, M.C.; Alves, J.L.; Menezes, L.F. Numerical simulation and analysis on the deep drawing of LPG bottles. J. Mater. Process. Technol. 2008, 200, 416–423. [Google Scholar] [CrossRef]
- Vafaeesefat, A. Finite Element Simulation for Blank Shape Optimization in Sheet Metal Forming. Mater. Manuf. Process. 2011, 26, 93–98. [Google Scholar] [CrossRef]
- Frącz, W.; Stachowicz, F.; Pieja, T. Aspects of verification and optimization of sheet metal numerical simulations process using the photogrammetric system. Acta Metall. Slovaca 2013, 19, 51–59. [Google Scholar] [CrossRef]
- Čada, R.; Tiller, P. Evaluation of Draw Beads Influence on Intricate Shape Stamping Drawing Process. Technol. Eng. 2014, 11, 5–10. [Google Scholar] [CrossRef][Green Version]
- Labergere, C.; Badreddine, H.; Msolli, S.; Saanouni, K.; Martiny, M.; Choquart, F. Modeling and numerical simulation of AA1050-O embossed sheet metal stamping. Procedia Eng. 2017, 207, 72–77. [Google Scholar] [CrossRef]
- Schrek, A.; Švec, P.; Brusilová, A.; Gábrišová, Z. Simulation process deep drawing of tailor welded blanks DP600 and BH220 materials in tool with elastic blankholder. J. Mech. Eng. Stroj. Caopis 2018, 68, 95–102. [Google Scholar] [CrossRef]
- Neto, D.M.; Oliveira, M.C.; Alves, J.L.; Menezes, L.F. Influence of the plastic anisotropy modelling in the reverse deep drawing process simulation. Mater. Des. 2014, 60, 368–379. [Google Scholar] [CrossRef]
- Neto, D.M.; Oliveira, M.C.; Santos, A.D.; Alves, J.L.; Menezes, L.F. Influence of boundary conditions on the prediction of springback and wrinkling in sheet metal forming. Int. J. Mech. Sci. 2017, 122, 244–254. [Google Scholar] [CrossRef]
- Mulidran, P.; Šiser, M.; Slota, J.; Spišák, E.; Sleziak, T. Numerical Prediction of Forming Car Body Parts with Emphasis on Springback. Metals 2018, 8, 435. [Google Scholar] [CrossRef]
- Chen, F.K.; Chiang, B.H. Analysis of die design for the stamping of a bathtub. J. Mater. Process. Technol. 1997, 72, 421–428. [Google Scholar] [CrossRef]
- Hojny, J.; Wozniak, D.; Glowacki, M.; Zaba, K.; Nowosielski, M.; Kwiatkowski, M. Analysis of die design for the stamping of a bathtub. Arch. Metall. Mater. 2015, 60, 661–666. [Google Scholar] [CrossRef]
- Sun, Q.; Xu, C.; Jiang, W. Study on the enameling properties of cold-rolled sheet steels containing different alloyed elements. Glass Enamel 2015, 6, 1–5. [Google Scholar]
- ESI Group. Pam-Stamp 2015 User’s Guide; ESI Group: Paris, France, 2015. [Google Scholar]
- Gerlach, J.; Kessler, L.; Linnepe, M. A study regarding material aspects for numerical modelling of mild steels. In Proceedings of the IDDRG 2009 Conference—Material Property Data for More Effective Numerical Analysis, Golden, CO, USA, 1–3 June 2009; pp. 351–360. [Google Scholar]
- Wang, L.; Lee, T.C. The effect of yield criteria on the forming limit curve prediction and the deep drawing process simulation. Int. J. Mach. Tools Manuf. 2006, 46, 988–995. [Google Scholar] [CrossRef]
- Hill, R.A. Theory of the yielding and plastic flow of anisotropic metals. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 193, 281–297. [Google Scholar]
- Hill, R. Constitutive modelling of orthotropic plasticity in sheet metals. J. Mech. Phys. Solids 1990, 38, 405–417. [Google Scholar] [CrossRef]
- Keeler, S.P.; Brazier, W.G. Relationship between Laboratory Material Characterization and Press-Shop Formability. Microalloying 1975, 75, 517–530. [Google Scholar]
- Hrivňák, A.; Evin, E. Formability of Steels, 1st ed.; Elfa: Košice, Slovakia, 2004; ISBN 80-89066-93-3. [Google Scholar]
- Pollák, L.; Tomáš, M.; Kuzmišin, J. Material formability and anisotropy of steel sheets for enamelling. In Proceedings of the 2005 International Scientific Conference on Structural Materials, Trnava, Slovakia, 22 June 2005; STU Bratislava: Bratislava, Slovakia, 2005; pp. 1–9. [Google Scholar]
- Beygelzimer, Y.; Kulagin, R.; Toth, L.S.; Ivanisenko, Y. The self-similarity theory of high pressure torsion. Beilstein, J. Nanotechnol. 2016, 7, 1267–1277. [Google Scholar] [CrossRef]
- Paul, S.K. Path independent limiting criteria in sheet metal forming. J. Manuf. Process. 2015, 20, 291–303. [Google Scholar] [CrossRef]
- Koc, M. Hydroforming for Advanced Manufacturing, 1st ed.; Woodhead Publishing: Amsterdam, The Netherlands, 2008; ISBN 9781845693282. [Google Scholar]
- Banabic, D. Sheet Metal. Forming Processes—Constitutive Modelling and Numerical Simulation, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Shaw, J.; Chen, M.; Watanabe, K. Metal Forming Characterization and Simulation of Advanced High Strength Steels. SAE Trans. 2001, 110, 926–935. [Google Scholar]
- Tisza, M.; Kovácx, Z.P. New methods for predicting the formability of sheet metals. Prod. Process. Syst. 2012, 5, 45–54. [Google Scholar]
- Denes, E.; Gergely, J.; Szabados, O.; Vero, B. A Comparative Study of the Properties of Low Carbon Aluminium-killed and Boron-microalloyed Steels for Enamelling. In Proceedings of the XXI International Enamellers Congress, Shanghai, China, 18–22 May 2008; pp. 274–281. [Google Scholar]
- Zhao, Y.; Huang, X.; Yu, B.; Chen, L.; Liu, X. Influence of boron addition on microstructure and properties of a low-carbon cold rolled enamel steel. Procedia Eng. 2017, 207, 1833–1838. [Google Scholar]
- Yi, Z.; Hongyan, W.; Linxiu, D. Effect of Continuous Annealing Process on Microstructure and Properties of Ultra-Low Carbon Cold Rolled Enamel Steel. In Proceedings of the 24th International Enamellers Congress, Chicago, IL, USA, 28 May–1 June 2018; pp. 115–122. [Google Scholar]
- Estrin, Y.; Beygelzimer, Y.; Kulagin, R. Design of Architectured Materials Based on Mechanically Driven Structural and Compositional Patterning. Adv. Eng. Mater. 2019. [Google Scholar] [CrossRef]
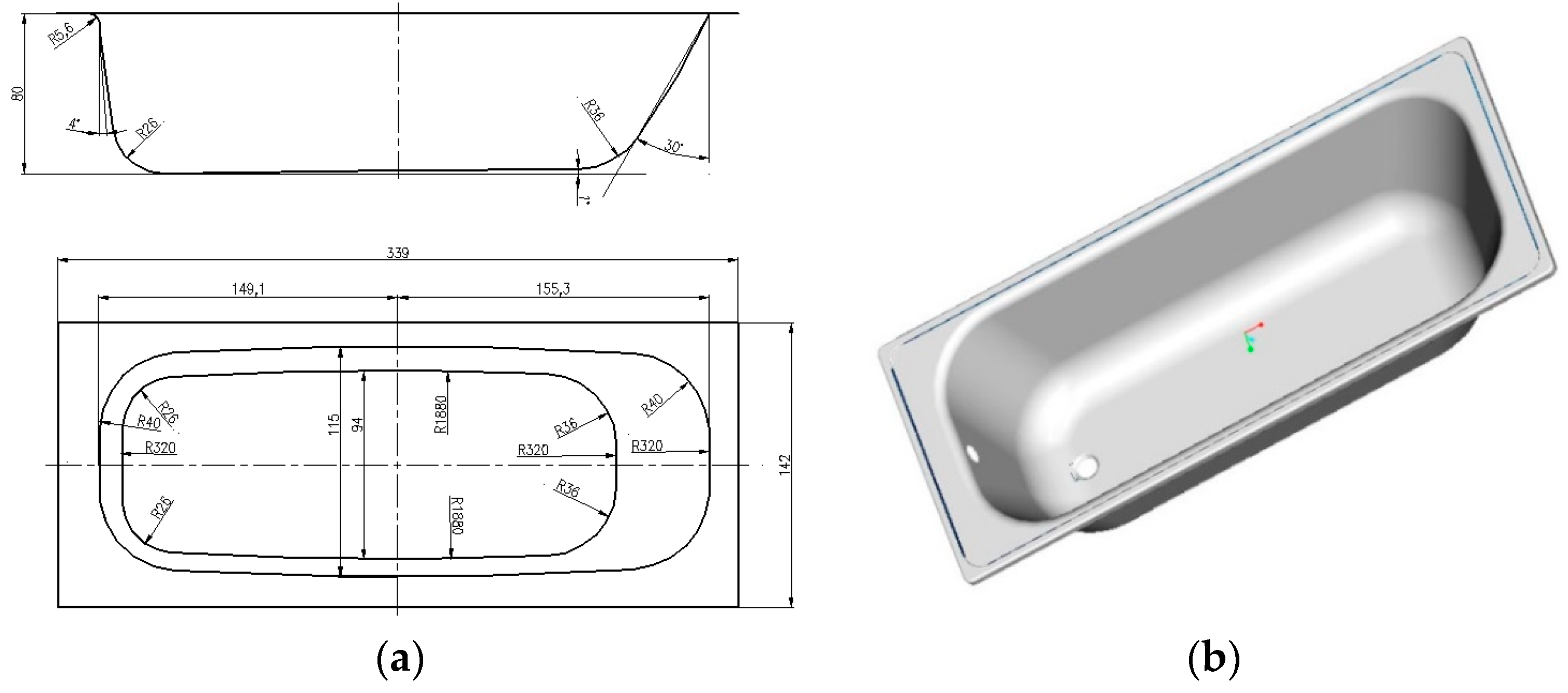

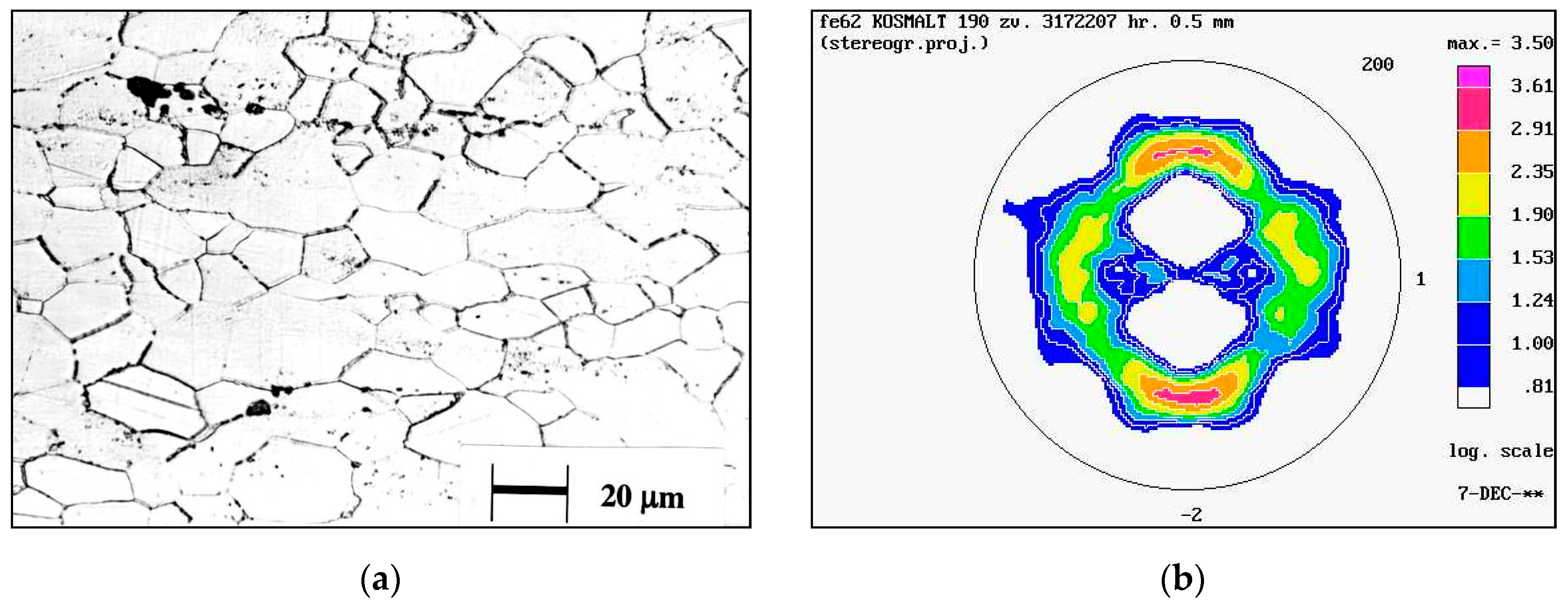
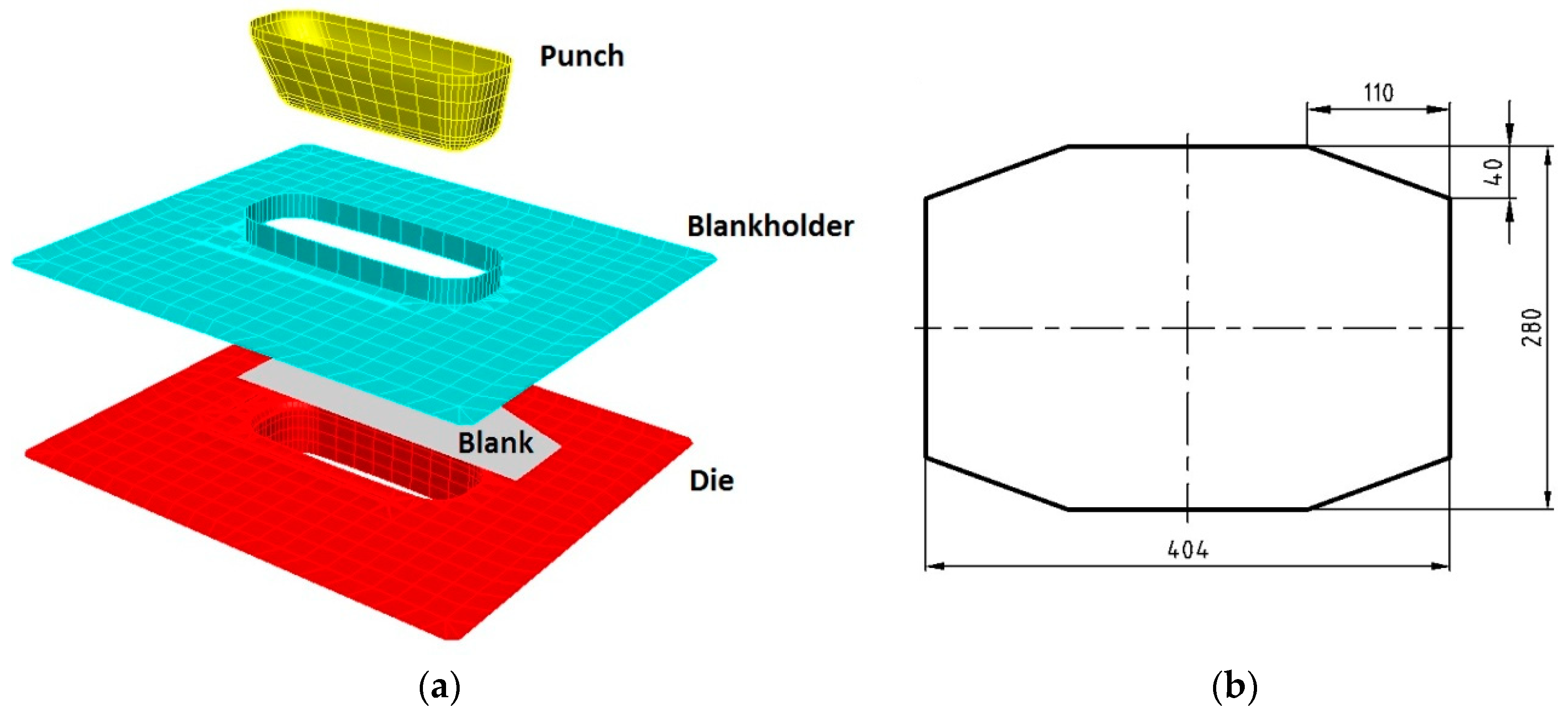





| Parameter | Real Bathtub | Bathtub Model |
|---|---|---|
| Geometry similarity (scale 1:5) | ||
| Length [mm] | 1695 | 339 |
| Width [mm] | 710 | 142 |
| Height [mm] | 400 | 80 |
| Wall to bottom radius [mm] (i.e., Punch radius [mm]) | 130 | 26 |
| Wall to flange radius [mm] (i.e., Die radius [mm]) | 28 | 5.6 |
| Mechanical similarity | ||
| Press | Hydraulic Fritz Muller BZE 2000 | Hydraulic Fritz Muller BZE 100 |
| Ram working velocity [mm·s−1] | 25 | 15 |
| Die and punch material | Cast steel | Cast steel |
| Physical similarity | ||
| Material | Enameling steel Kosmalt | Enameling steel Kosmalt |
| Lubricant | Vantol S | Vantol S |
| C | Mn | P | S | Al | N | Cu | Ni | Cr |
|---|---|---|---|---|---|---|---|---|
| 0.030 | 0.140 | 0.009 | 0.008 | 0.042 | 0.003 | 0.014 | 0.015 | 0.013 |
| Dir. [°] | Rp0.2 [MPa] | Rm [MPa] | A80 [%] | r [–] | rm [–] | Δr [–] | n [–] | nm [–] | Δn [–] |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 158 ±0.9 | 280 ±1.3 | 45.5 ±0.3 | 1.58 ±0.036 | 0.226 ±0.002 | ||||
| 45 | 159 ±1.1 | 286 ±0.9 | 42.4 ±0.5 | 1.33 ±0.032 | 1.57 | 0.47 | 0.227 ±0.001 | 0.226 | –0.001 |
| 90 | 155 ±1,0 | 279 ±0.5 | 45.4 ±0.5 | 2.02 ±0.052 | 0.225 ±0.001 |
| Model | K [MPa] | n [–] | φ0 [–] |
|---|---|---|---|
| Hollomon | 496 | 0.226 | - |
| Krupkowski | 505 | 0.248 | 0.00899 |
| Direction | Rp0.2 [MPa] | r [–] |
|---|---|---|
| 15 | 166 ±1.1 | 1.56 ±0.037 |
| 30 | 166 ±1.3 | 1.46 ±0.041 |
| 60 | 168 ±0.9 | 2.03 ±0.029 |
| 75 | 165 ±1.2 | 2.14 ±0.040 |
| α | β | γ | m |
|---|---|---|---|
| 1.56158 | 1.19317 | 20.2109 | 3.02902 |
| Simulation Number | Yield Locus/Hardening Law | Minimal Thickness [mm] | ||
|---|---|---|---|---|
| Section A-A | Section B-B | |||
| C-E | G-H | D-E | ||
| S1 | Hill 48/Hollomon | 0.421 | 0.330 | 0.380 |
| S2 | Hill 48/Krupkowski | 0.417 | 0.363 | 0.375 |
| S3 | Hill 90/Hollomon | 0.405 | 0.398 | 0.416 |
| S4 | Hill 90/Krupkowski | 0.412 | 0.396 | 0.417 |
| Experiment | 0.413 ± 0.006 | 0.368 ± 0.008 | 0.363 ± 0.006 | |
| Simulation Number | Section A-A | Section B-B | |
|---|---|---|---|
| C-E | G-H | D-E | |
| S1 | 1.7% | –7.6% | 3.4% |
| S2 | 0.7% | –1.0% | 2.4% |
| S3 | –1.7% | 5.9% | 10.6% |
| S4 | –0.3% | 5.7% | 10.8% |
| Material | r0 | r45 | r90 | rm | Result |
|---|---|---|---|---|---|
| Kosmalt 190 | 1.58 | 1.33 | 2.02 | 1.57 | Ok |
| Virtual B | 1.48 | 1.28 | 1.82 | 1.47 | Necking |
| Virtual C | 1.38 | 1.23 | 1.62 | 1.37 | Fracture |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tomáš, M.; Evin, E.; Kepič, J.; Hudák, J. Physical Modelling and Numerical Simulation of the Deep Drawing Process of a Box-Shaped Product Focused on Material Limits Determination. Metals 2019, 9, 1058. https://doi.org/10.3390/met9101058
Tomáš M, Evin E, Kepič J, Hudák J. Physical Modelling and Numerical Simulation of the Deep Drawing Process of a Box-Shaped Product Focused on Material Limits Determination. Metals. 2019; 9(10):1058. https://doi.org/10.3390/met9101058
Chicago/Turabian StyleTomáš, Miroslav, Emil Evin, Ján Kepič, and Juraj Hudák. 2019. "Physical Modelling and Numerical Simulation of the Deep Drawing Process of a Box-Shaped Product Focused on Material Limits Determination" Metals 9, no. 10: 1058. https://doi.org/10.3390/met9101058
APA StyleTomáš, M., Evin, E., Kepič, J., & Hudák, J. (2019). Physical Modelling and Numerical Simulation of the Deep Drawing Process of a Box-Shaped Product Focused on Material Limits Determination. Metals, 9(10), 1058. https://doi.org/10.3390/met9101058




