Numerical Study on the Formability of Metallic Bipolar Plates for Proton Exchange Membrane (PEM) Fuel Cells
Abstract
:1. Introduction
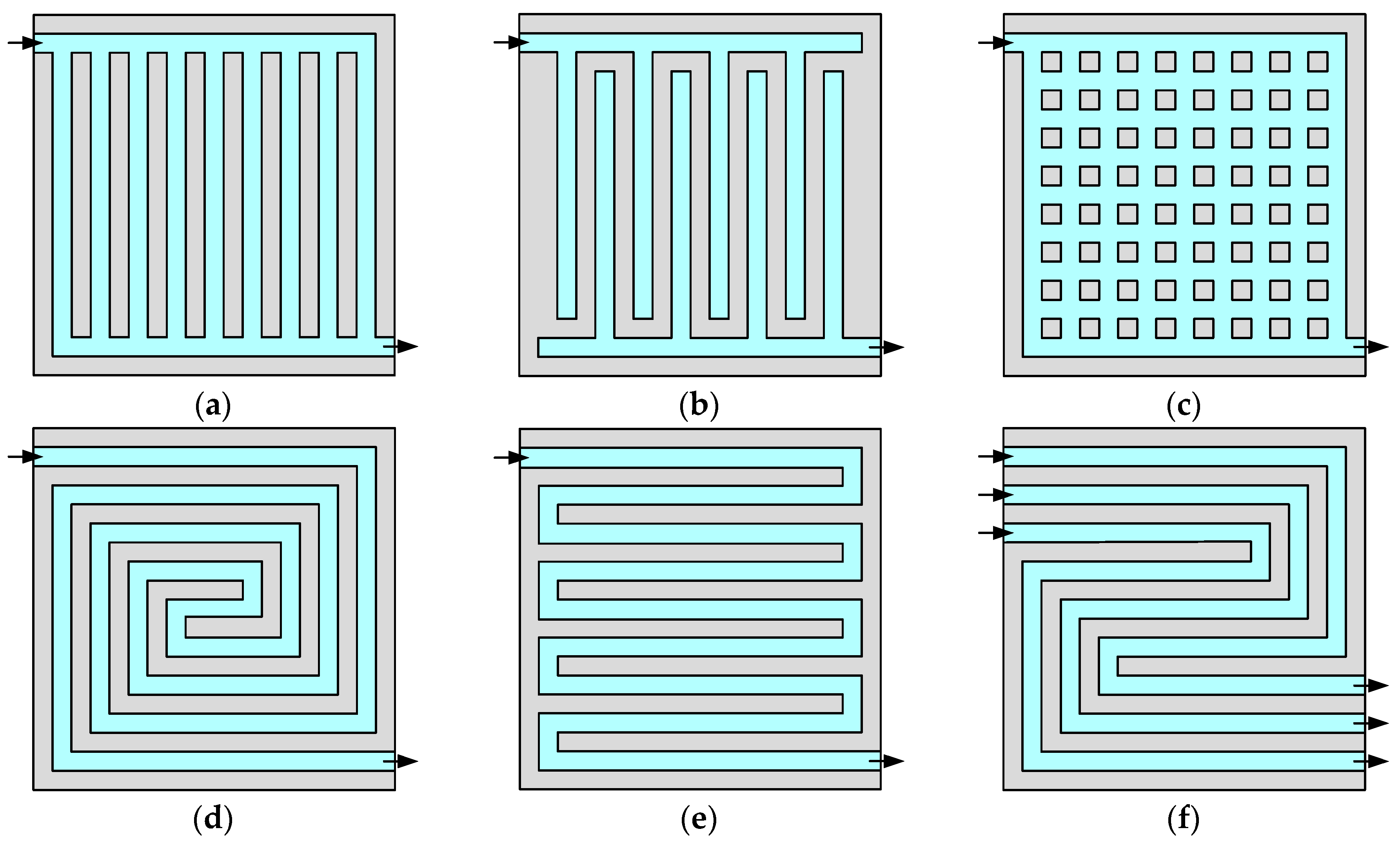
2. Flow Field Configurations
3. Finite Element Model
3.1. Material Properties
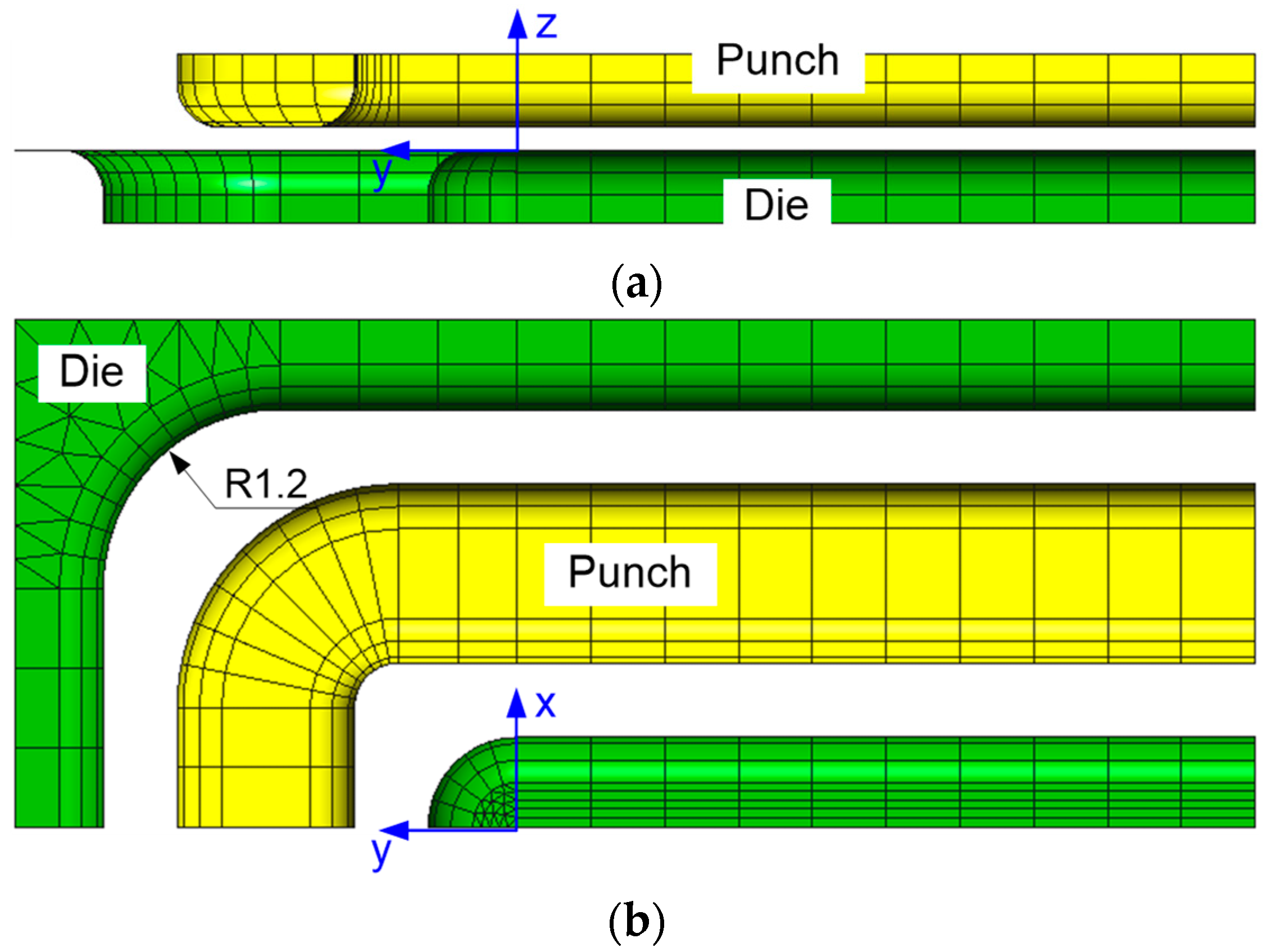
3.2. Stamping Process
4. Straight Channel Section
4.1. Multiple Channels
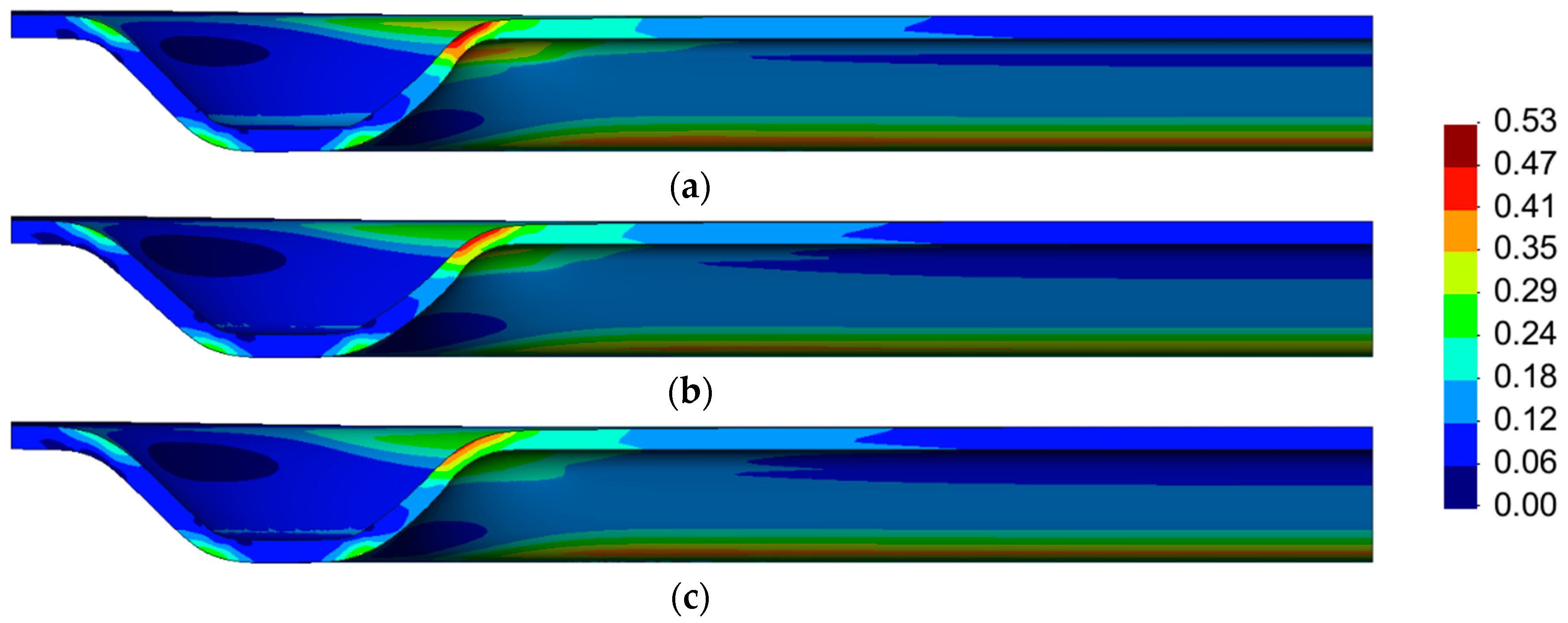
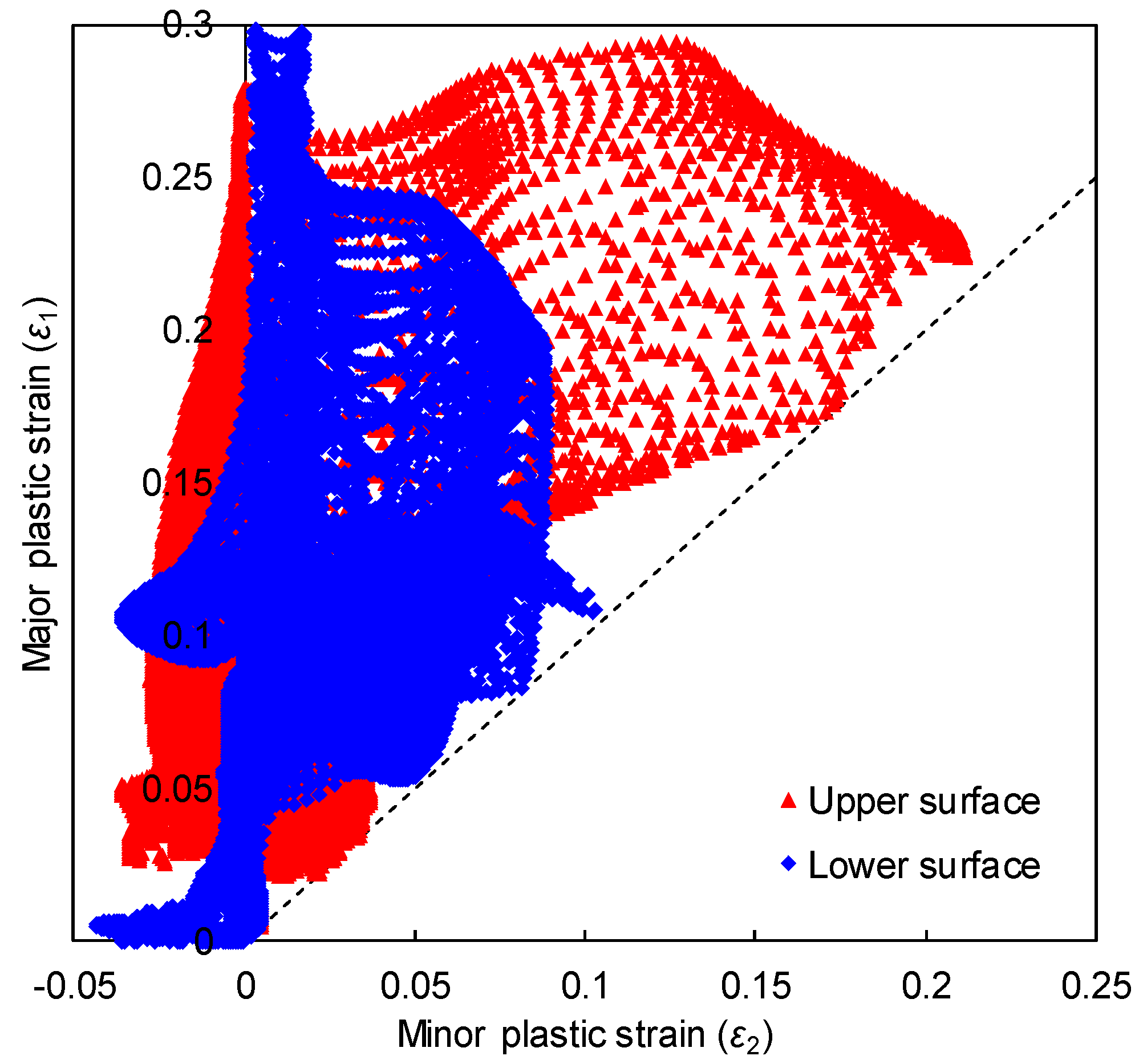
4.2. Single Channel
Effect of Tool Dimensions
5. U-bend Channel Section
5.1. Boundary Conditions
5.2. Bent Geometry
5.3. Effect of Tool Dimensions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dunn, S. Hydrogen futures: Toward a sustainable energy system. Int. J. Hydrogen Energy 2002, 27, 235–264. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, K.S.; Mishler, J.; Cho, S.C.; Adroher, X.C. A review of polymer electrolyte membrane fuel cells: Technology, applications, and needs on fundamental research. Appl. Energy 2011, 88, 981–1007. [Google Scholar] [CrossRef] [Green Version]
- Karimi, S.; Fraser, N.; Roberts, B.; Foulkes, F.R. A Review of Metallic Bipolar Plates for Proton Exchange Membrane Fuel Cells: Materials and Fabrication Methods. Adv. Mater. Sci. Eng. 2012, 2012, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Wang, J. Barriers of scaling-up fuel cells: Cost, durability and reliability. Energy 2015, 80, 509–521. [Google Scholar] [CrossRef]
- DOE. Hydrogen and Fuel Cell Activities, Progress, and Plans; DOE: New York, NY, USA, 2009.
- Hermann, A.; Chaudhuri, T.; Spagnol, P. Bipolar plates for PEM fuel cells: A review. Int. J. Hydrogen Energy 2005, 30, 1297–1302. [Google Scholar] [CrossRef]
- Peng, L.; Yi, P.; Lai, X. Design and manufacturing of stainless steel bipolar plates for proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2014, 39, 21127–21153. [Google Scholar] [CrossRef]
- Barbir, F. PEM Fuel Cells: Theory and Practice; Elsevier Academic: Cambridge, MA, USA, 2005. [Google Scholar]
- Taherian, R. A review of composite and metallic bipolar plates in proton exchange membrane fuel cell: Materials, fabrication, and material selection. J. Power Sources 2014, 265, 370–390. [Google Scholar] [CrossRef]
- Hu, Q.; Zhang, D.; Fu, H.; Huang, K. Investigation of stamping process of metallic bipolar plates in PEM fuel cell—Numerical simulation and experiments. Int. J. Hydrogen Energy 2014, 39, 13770–13776. [Google Scholar] [CrossRef]
- Peng, L.; Lai, X.; Liu, D.; Hu, P.; Ni, J. Flow channel shape optimum design for hydroformed metal bipolar plate in PEM fuel cell. J. Power Sources 2008, 178, 223–230. [Google Scholar] [CrossRef]
- Liu, Y.; Hua, L. Fabrication of metallic bipolar plate for proton exchange membrane fuel cells by rubber pad forming. J. Power Sources 2010, 195, 3529–3535. [Google Scholar] [CrossRef]
- Hung, J.C.; Chang, D.H.; Chuang, Y. The fabrication of high-aspect-ratio micro-flow channels on metallic bipolar plates using die-sinking micro-electrical discharge machining. J. Power Sources 2012, 198, 158–163. [Google Scholar] [CrossRef]
- Lee, S.J.; Lee, C.Y.; Yang, K.T.; Kuan, F.H.; Lai, P.H. Simulation and fabrication of micro-scaled flow channels for metallic bipolar plates by the electrochemical micro-machining process. J. Power Sources 2008, 185, 1115–1121. [Google Scholar] [CrossRef]
- Jin, C.; Jang, C.; Kang, C.; Jin, C.K.; Jang, C.H.; Kang, C.G. Vacuum Die Casting Process and Simulation for Manufacturing 0.8 mm-Thick Aluminum Plate with Four Maze Shapes. Metals 2015, 5, 192–205. [Google Scholar] [CrossRef] [Green Version]
- Antunes, R.A.; Oliveira, M.C.L.; Ett, G.; Ett, V. Corrosion of metal bipolar plates for PEM fuel cells: A review. Int. J. Hydrogen Energy 2010, 35, 3632–3647. [Google Scholar] [CrossRef]
- Koç, M.; Mahabunphachai, S. Feasibility investigations on a novel micro-manufacturing process for fabrication of fuel cell bipolar plates: Internal pressure-assisted embossing of micro-channels with in-die mechanical bonding. J. Power Sources 2007, 172, 725–733. [Google Scholar] [CrossRef]
- Mahabunphachai, S.; Cora, Ö.N.; Koç, M. Effect of manufacturing processes on formability and surface topography of proton exchange membrane fuel cell metallic bipolar plates. J. Power Sources 2010, 195, 5269–5277. [Google Scholar] [CrossRef]
- Kim, A.R.; Vinothkannan, M.; Yoo, D.J. Sulfonated fluorinated multi-block copolymer hybrid containing sulfonated (poly ether ether ketone) and graphene oxide: A ternary hybrid membrane architecture for electrolyte applications in proton exchange membrane fuel cells. J. Energy Chem. 2018, 27, 1247–1260. [Google Scholar] [CrossRef]
- Kim, A.R.; Park, C.J.; Vinothkannan, M.; Yoo, D.J. Sulfonated poly ether sulfone/heteropoly acid composite membranes as electrolytes for the improved power generation of proton exchange membrane fuel cells. Compos. Part B Eng. 2018, 155, 272–281. [Google Scholar] [CrossRef]
- André, J.; Antoni, L.; Petit, J.P.; De Vito, E.; Montani, A. Electrical contact resistance between stainless steel bipolar plate and carbon felt in PEFC: A comprehensive study. Int. J. Hydrogen Energy 2009, 34, 3125–3133. [Google Scholar] [CrossRef]
- Ge, J.; Higier, A.; Liu, H. Effect of gas diffusion layer compression on PEM fuel cell performance. J. Power Sources 2006, 159, 922–927. [Google Scholar] [CrossRef]
- Wlodarczyk, R.; Zasada, D.; Morel, S.; Kacprzak, A. A comparison of nickel coated and uncoated sintered stainless steel used as bipolar plates in low-temperature fuel cells. Int. J. Hydrogen Energy 2016, 41, 17644–17651. [Google Scholar] [CrossRef]
- Hung, Y.; EL-Khatib, K.M.; Tawfik, H. Corrosion-resistant lightweight metallic bipolar plates for PEM fuel cells. J. Appl. Electrochem. 2005, 35, 445–447. [Google Scholar] [CrossRef] [Green Version]
- Jin, C.K.; Koo, J.Y.; Kang, C.G. Fabrication of stainless steel bipolar plates for fuel cells using dynamic loads for the stamping process and performance evaluation of a single cell. Int. J. Hydrogen Energy 2014, 39, 21461–21469. [Google Scholar] [CrossRef]
- Park, W.T.; Jin, C.K.; Kang, C.G. Improving channel depth of stainless steel bipolar plate in fuel cell using process parameters of stamping. Int. J. Adv. Manuf. Technol. 2016, 87, 1677–1684. [Google Scholar] [CrossRef]
- Bong, H.J.; Lee, J.; Kim, J.H.; Barlat, F.; Lee, M.G. Two-stage forming approach for manufacturing ferritic stainless steel bipolar plates in PEM fuel cell: Experiments and numerical simulations. Int. J. Hydrogen Energy 2017, 42, 6965–6977. [Google Scholar] [CrossRef]
- Afshari, E.; Mosharaf-Dehkordi, M.; Rajabian, H. An investigation of the PEM fuel cells performance with partially restricted cathode flow channels and metal foam as a flow distributor. Energy 2017, 118, 705–715. [Google Scholar] [CrossRef]
- Wang, J. Theory and practice of flow field designs for fuel cell scaling-up: A critical review. Appl. Energy 2015, 157, 640–663. [Google Scholar] [CrossRef]
- Dhahad, H.A.; Alawee, W.H.; Hassan, A.K. Experimental study of the effect of flow field design to PEM fuel cells performance. Renew. Energy Focus 2019, 30, 71–77. [Google Scholar] [CrossRef]
- Kahraman, H.; Orhan, M.F. Flow field bipolar plates in a proton exchange membrane fuel cell: Analysis & modeling. Energy Convers. Manag. 2017, 133, 363–384. [Google Scholar]
- Arvay, A.; French, J.; Wang, J.C.; Peng, X.H.; Kannan, A.M. Nature inspired flow field designs for proton exchange membrane fuel cell. Int. J. Hydrogen Energy 2013, 38, 3717–3726. [Google Scholar] [CrossRef]
- Guo, N.; Leu, M.C.; Koylu, U.O. Bio-inspired flow field designs for polymer electrolyte membrane fuel cells. Int. J. Hydrogen Energy 2014, 39, 21185–21195. [Google Scholar] [CrossRef]
- Shimpalee, S.; Van Zee, J.W. Numerical studies on rib & channel dimension of flow-field on PEMFC performance. Int. J. Hydrogen Energy 2007, 32, 842–856. [Google Scholar]
- Hontañón, E.; Escudero, M.J.; Bautista, C.; García-Ybarra, P.L.; Daza, L. Optimisation of flow-field in polymer electrolyte membrane fuel cells using computational fluid dynamics techniques. J. Power Sources 2000, 86, 363–368. [Google Scholar] [CrossRef]
- Manso, A.P.; Marzo, F.F.; Mujika, M.G.; Barranco, J.; Lorenzo, A. Numerical analysis of the influence of the channel cross-section aspect ratio on the performance of a PEM fuel cell with serpentine flow field design. Int. J. Hydrogen Energy 2011, 36, 6795–6808. [Google Scholar] [CrossRef]
- Hu, P.; Peng, L.; Zhang, W.; Lai, X. Optimization design of slotted-interdigitated channel for stamped thin metal bipolar plate in proton exchange membrane fuel cell. J. Power Sources 2009, 187, 407–414. [Google Scholar] [CrossRef]
- Xu, Y.; Peng, L.; Yi, P.; Lai, X. Analysis of the flow distribution for thin stamped bipolar plates with tapered channel shape. Int. J. Hydrogen Energy 2016, 41, 5084–5095. [Google Scholar] [CrossRef]
- Menezes, L.F.; Teodosiu, C. Three-dimensional numerical simulation of the deep-drawing process using solid finite elements. J. Mater. Process. Technol. 2000, 97, 100–106. [Google Scholar] [CrossRef] [Green Version]
- Oliveira, M.C.; Alves, J.L.; Menezes, L.F. Algorithms and Strategies for Treatment of Large Deformation Frictional Contact in the Numerical Simulation of Deep Drawing Process. Arch. Comput. Methods Eng. 2008, 15, 113–162. [Google Scholar] [CrossRef] [Green Version]
- Menezes, L.F.; Neto, D.M.; Oliveira, M.C.; Alves, J.L. Improving Computational Performance through HPC Techniques: Case study using DD3IMP in-house code. AIP Conf. Proc. 2011, 1353, 1220–1225. [Google Scholar]
- Pham, C.H.; Thuillier, S.; Manach, P.Y. Prediction of flow stress and surface roughness of stainless steel sheets considering an inhomogeneous microstructure. Mater. Sci. Eng. A 2016, 678, 377–388. [Google Scholar] [CrossRef]
- Pham, C.H.; Thuillier, S.; Manach, P.Y. Mechanical Properties Involved in the Micro-forming of Ultra-thin Stainless Steel Sheets. Metall. Mater. Trans. A 2015, 46, 3502–3515. [Google Scholar] [CrossRef]
- Raj, A.K. Formability: Metastable Austenitic Stainless Steels; Lulu Press: Morrisville, NC, USA, 2015. [Google Scholar]
- Neto, D.M.; Oliveira, M.C.; Menezes, L.F.; Alves, J.L. Applying Nagata patches to smooth discretized surfaces used in 3D frictional contact problems. Comput. Methods Appl. Mech. Eng. 2014, 271, 296–320. [Google Scholar] [CrossRef]
- Neto, D.M.; Oliveira, M.C.; Menezes, L.F.; Alves, J.L. Nagata patch interpolation using surface normal vectors evaluated from the IGES file. Finite Elem. Anal. Des. 2013, 72, 35–46. [Google Scholar] [CrossRef]
- Hughes, T.J.R. Generalization of selective integration procedures to anisotropic and nonlinear media. Int. J. Numer. Methods Eng. 1980, 15, 1413–1418. [Google Scholar] [CrossRef]
- Li, K.P.; Carden, W.P.; Wagoner, R.H. Simulation of springback. Int. J. Mech. Sci. 2002, 44, 103–122. [Google Scholar] [CrossRef]
- Peng, L.; Liu, D.; Hu, P.; Lai, X.; Ni, J. Fabrication of Metallic Bipolar Plates for Proton Exchange Membrane Fuel Cell by Flexible Forming Process-Numerical Simulations and Experiments. J. Fuel Cell Sci. Technol. 2010, 7, 031009. [Google Scholar] [CrossRef]
- Xu, S.; Li, K.; Wei, Y.; Jiang, W. Numerical investigation of formed residual stresses and the thickness of stainless steel bipolar plate in PEMFC. Int. J. Hydrogen Energy 2016, 41, 6855–6863. [Google Scholar] [CrossRef]
- Koo, J.Y.; Jeon, Y.P.; Kang, C.G. Effect of stamping load variation on deformation behaviour of stainless steel thin plate with microchannel. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2013, 227, 1121–1128. [Google Scholar] [CrossRef]
- Liu, D.; Peng, L.; Lai, X. Effect of dimensional error of metallic bipolar plate on the GDL pressure distribution in the PEM fuel cell. Int. J. Hydrogen Energy 2009, 34, 990–997. [Google Scholar] [CrossRef]






















| Y0 (MPa) | K (MPa) | n |
|---|---|---|
| 255.02 | 1481.84 | 0.508 |
| w1 | w2 | S | r | R | d= (w2 + s)/2 |
|---|---|---|---|---|---|
| 1.2 mm | 2.2 mm | 1.2 mm | 0.3 mm | 0.3 mm | 1.7 mm |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neto, D.M.; Oliveira, M.C.; Alves, J.L.; Menezes, L.F. Numerical Study on the Formability of Metallic Bipolar Plates for Proton Exchange Membrane (PEM) Fuel Cells. Metals 2019, 9, 810. https://doi.org/10.3390/met9070810
Neto DM, Oliveira MC, Alves JL, Menezes LF. Numerical Study on the Formability of Metallic Bipolar Plates for Proton Exchange Membrane (PEM) Fuel Cells. Metals. 2019; 9(7):810. https://doi.org/10.3390/met9070810
Chicago/Turabian StyleNeto, Diogo M., Marta C. Oliveira, José L. Alves, and Luís F. Menezes. 2019. "Numerical Study on the Formability of Metallic Bipolar Plates for Proton Exchange Membrane (PEM) Fuel Cells" Metals 9, no. 7: 810. https://doi.org/10.3390/met9070810
APA StyleNeto, D. M., Oliveira, M. C., Alves, J. L., & Menezes, L. F. (2019). Numerical Study on the Formability of Metallic Bipolar Plates for Proton Exchange Membrane (PEM) Fuel Cells. Metals, 9(7), 810. https://doi.org/10.3390/met9070810








