Next Article in Journal
Reconstruction of Complex Zygomatic Bone Defects Using Mirroring Coupled with EBM Fabrication of Titanium Implant
Next Article in Special Issue
Fabrication of Two-Layered Aluminum Foam with Closed-Cell and Open-Cell Structures and Shaping of Closed-Cell Layer by Press Forming Immediately after Foaming
Previous Article in Journal
Flow Stress and Hot Deformation Activation Energy of 6082 Aluminium Alloy Influenced by Initial Structural State
Previous Article in Special Issue
Shaping of Aluminum Foam during Foaming of Precursor Using Steel Mesh with Various Opening Ratios
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Metals
Volume 9
Issue 12
10.3390/met9121249
metals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Influence of the Compaction Pressure and Sintering Temperature on the Mechanical Properties of Porous Titanium for Biomedical Applications

by
Sandra M. Castillo
,
Sergio Muñoz
*,
Paloma Trueba
,
Eduardo Díaz
and
Yadir Torres
Department of Engineering and Materials Science and Transportation, University of Seville, Av. Camino de los Descubrimientos s/n, 41092 Seville, Spain
*
Author to whom correspondence should be addressed.
Metals 2019, 9(12), 1249; https://doi.org/10.3390/met9121249
Submission received: 16 October 2019 / Revised: 16 November 2019 / Accepted: 20 November 2019 / Published: 22 November 2019
(This article belongs to the Special Issue Recent Developments in Porous Metals and Metallic Foams)
Browse Figures
Versions Notes

Abstract

:
In the present work, the use of porous titanium is proposed as a solution to the difference in stiffness between the implant and bone tissue, avoiding the bone resorption. Conventional powder metallurgical technique is an industrially established route for fabrication of this type of material. The results are discussed in terms of the influence of compaction pressure and sintering temperature on the porosity (volumetric fraction, size, and morphology) and the quality of the sintering necks. A very good agreement between the predicted values obtained using a simple 2D finite element model, the experimental uniaxial compression behavior, and the analytical model proposed by Nielsen, has been found for both the Young’s modulus and the yield strength. The porous samples obtained by the loose sintering technique and using temperatures between 1000 °C −1100 °C (about 40% of total porosity) are recommended for achieving a suitable biomechanical behavior for cortical bone partial replacement.

1. Introduction

Titanium and titanium alloys have been widely used as orthopedic implant materials due to their excellent mechanical and corrosion resistance, as well as their adequate biological behavior [1,2,3,4,5,6,7,8]. However, the stiffness of titanium is higher (100–110 GPa) than that of the cortical bone (20–25 GPa), which produces the stress-shielding phenomenon, promoting bone resorption surrounding the implant and compromising, in these cases, the implants reliability (clinical success). Despite the excellent advances, between 5% and 10% of bone implants can fail due to different causes during the five-year post-implantation period. Focusing on dental implants, after 10–15 years, survival rates over 89%, as well as a significant percentage of revision surgery (20%) to replace the failed implants (overload, peri-implantitis, etc.) have been reported [9]. Additionally, shorter recovery and loading times (e.g., immediate loading implants) are necessary to keep the quality of life of the patients. The design and manufacture of materials with a Young’s modulus close to that of cortical bone has been widely addressed in the scientific literature [10,11,12,13]. Among the possible solutions proposed are the use of metastable β-titanium alloys [14,15,16,17,18] and/or porous materials [19,20,21,22,23,24,25,26,27]. The bibliography includes up to 34 porous metal processing routes. All of them are summarized in the Doctoral Thesis of P. Trueba, and even a novel classification is proposed according to the state of the starting material [28]. In this context, some works show the limitations in controlling the quantity, size, distribution, and morphology of the pores by conventional techniques. Other works report the high cost and the difficulty in obtaining reproducible and versatile results using the new processing routes (laser sintering, spark plasma sintering, electron beam melting or selective laser melting, electric current activated/assisted sintering, etc.) [29,30,31]. However, the production of porous materials via the conventional powder metallurgy (PM) route can be cost-effective, flexible, and lead to the desired design foams by controlling the temperature and sintering time, as well as the compaction pressure. Low temperatures and compaction pressures are employed to obtained higher porosities and lower Young’s modulus. The loose sintering (compaction pressure is not applied) is the extreme case (maximum porosity) of the PM route [32,33,34]. However, an excessive porosity and/or deficient sinterability (quality of the necks) of titanium powder at low temperatures, may compromise the mechanical behavior [35,36,37,38,39].
On the other hand, several researchers have tried to develop finite element (FE) models to predict the mechanical properties of porous materials. Some of them have used very simplistic approximations with two-dimensional (2D) FE models based on periodically distributed circular pores geometries [40], while others have develop complex three-dimensional (3D) FE models based on microstructural information of the pore morphology [41,42], whose complexity makes their extensive use unfeasible. In order to overcome this difficulty, a 2D finite element model was proposed by these authors in previous work [43,44]. In this current work, a very comprehensive investigation has been carried out with the aim of achieving a better understanding of the powder metallurgy process. In this scenario, the influence of the compaction pressure and sintering temperature on the global performance of the porous samples has been experimentally analyzed, particularly the microstructure (size, type, and morphology of the pores and the percentage of porosity) and the mechanical properties (Young’s modulus and yield strength). Furthermore, our results are compared to numerical simulations of the mechanical response using the finite element method (FEM). The proposed FE model has been based on geometries generated from the pore morphology information obtained from image analysis.

2. Experimental Methods

2.1. Sample Processing

Titanium powder with an irregular morphology was obtained by a hydrogenation/dehydrogenation process. The particle size distribution, according to the supplier SE-JONG Materials Co. Ltd. (Gojan-dong, South Korea) showed a size lower that 9.7 μm (10 pct), 23.3 μm (50 pct), and 48.4 μm (90 pct), with a chemical composition equivalent to Grade 4 commercially pure titanium (c.p. Ti) ASTM F67-00. Powder metallurgy is a compaction process followed by sintering of the green compacts. Consequently, there are two essential processing variables to be evaluated: The pressure of compaction, Pc, and the sintering temperature, Ts. These variables have a great influence in the microstructure of the PM samples, for example their porosity (content, size, and morphology), the grain size and sinterability (quality of the necks between the metal particles), as well as their behavior in service (stiffness, yield stress, fatigue life and wear and corrosion resistance). The processing conditions used were chosen in order to obtain mechanical properties (Young’s modulus and yield strength) similar to those of the cortical bone (20–25 GPa and 150–180 MPa, respectively) [45,46,47,48].
The first series of samples was fabricated following the loose-sintering process [48]. First, the metal powder was poured into a mold and vibrated, with no compaction (Pc = 0). Then, the samples were heated to the corresponding sintering temperatures (1000 °C, 1100 °C, 1200 °C, and 1300 °C) for 2 h in a furnace with a ceramic horizontal tube (CARBOLYTE STF 15/75/450, Derbyshire, UK) under high vacuum (< 0.05 Pa = 5 × 10−4 mbar).
The second series of samples was obtained following the same sintering process, but with a previous compaction of the powder at two compacting pressures (Pc = 13 and 38.5 MPa). The implementation of very low compacting pressures required control of the applied load rate and a very sensitive load cell. This step was carried out by using an INSTRON 5505 universal machine (Instron, HighWycombe, UK). The deformation rate was 6 kN/s, the dwell time was 2 min, and the unloading time was 15 s for decreasing loads down to 15 kgf. Two compaction dies (tool steel material) were used: One of 8 mm (uniaxial compression test) and one of 12 mm (ultrasound measurements). To lubricate the sleeve walls, Ethlyne-Bis-Stearamide (EBS) wax was used during the compaction. The powder mass used to obtain the specimens with the suitable dimensions (height/diameter: 0.8 and 1.2) for compression and ultrasound tests were 5.14 and 13.21 g, respectively. These values were calculated taking into account the most unfavorable (no porosity) situation. At least three porous samples were manufactured for each condition.

2.2. Porosity Characterisation

The density measurements were performed using the Archimedes’ method with distilled water impregnation (ASTM C373-88). The total and interconnected porosity were calculated from the density measurement by using well-known mathematical expressions [49]. In addition, the total porosity (θ), the equivalent diameter (Deq), and the pore elongation factor (Fe, ratio between major and minor axis of ellipse equivalent to pore) were evaluated by image analysis, using an optical microscope Nikon Epiphot (Nikon, Tokyo, Japan) coupled with a camera Jenoptik Progres C3 (Jenoptik, Jena, Germany), and the suitable analysis software (Image-ProPlus 6.2, Mediacibernetic, Bethesda, MD, USA). To perform this study, a conventional metallographic preparation of the specimen was necessary, including resin mounting, grinding, and mechano-chemical polishing with magnesium oxide (MgO) and hydrogen peroxide (H2O2). Image analysis was performed using 5 pictures of 5x for each sample (one for each kind of material).

2.3. Mechanical Testing

The mechanical properties of the different porous materials were measured using two different methodologies. Firstly, through the uniaxial compression testing, according to the general Standard ASTM E9-89A and, particularly, the Standard for Mechanical testing of metals-ductility testing-compression test for porous and cellular metals (ISO 13314: 2011), with a height/diameter aspect ratio of 0.8. The tests were performed using a universal electromechanical Instron machine 5505 (Instron, HighWycombe, UK) by applying a strain rate of 0.005 mm/mm∙min. All tests were finished for a 50 pct strain and, afterwards, Young modulus (Ec) and yield strength (σy) were obtained. The Young’s modulus from the compression stress–strain curves was corrected with the testing machine stiffness (87.9 kN/mm). At least three different specimens were tested for each porous material under study. Furthermore, the value of dynamic Young’s modulus (Ed) was also evaluated through the ultrasound technique, using a Krautkramer USM 35 equipment (GE Measurement & Control Solutions, Minden, Germany). To evaluate longitudinal waves, a Panametrics S-NDT (Olympus, Tokyo, Japan) probe of 4 MHz and an ultrasonic couplant fluid (Sonotrace grade 30) was used, while for cross-sectional waves, a Panametric S-V153 probe of 1 MHz/.5 and a shear wave couplant (Panametric S-NDT, Olympus, Tokyo, Japan) was used. Finally, from the values obtained and by a proper mathematical expression, the dynamic Young’s modulus was calculated [50].

2.4. Finite Element Modelling

In the present work, a FE model previously proposed by the authors [43,44] was used. This numerical model combines the simplicity of a 2D periodic geometry with the complex information of the pore morphology extracted from experimentation. Thanks to the low computational cost of the FE model, a large number of simulations could be carried out in order to obtain more reliable results. The methodology to generate the 2D simulated microstructure is explained as follows (see Figure 1):
The baseline configuration consisted of a square matrix with a side length a, with a series of nxn pores periodically distributed inside. The number of pores along any direction, n, had to be chosen to ensure a minimum representative volume element (RVE), which gives reliable results in the simulations. On the other hand, the ratio between the side length and the average pore equivalent diameter (a/Deq) determined the total porosity of the simulated geometry. Once the defining parameters (Deq, a, n) were determined, the pores are generated in a uniform spatial distribution, but with a pore morphology (Deq and Fe) randomly generated following a normal distribution from the experimental data. In addition, the pore orientation was also randomly generated following a uniform distribution.
The simulated microstructure was comprised of two different phases: Titanium matrix and pores. The mechanical properties of grade IV c.p. Ti were used to describe the behavior of the titanium matrix [42]: Young’s Modulus, Edense = 110 GPa, yield strength, σy-dense = 650 MPa, and Poisson’s ratio, ν = 0.33. In order to describe the hardening plasticity behavior of titanium, an isotropic hardening with a very small tangent modulus ET = 1 GPa was used. To describe the pores, a linear elastic material with very low Young’s modulus (E = 10−7 GPa) and Poisson’s ratio (ν = 0.33) was used in order to avoid possible computational difficulties.
In the simulations, the boundary conditions were defined as follows: The bottom boundary is fixed in the y-direction; the left boundary is fixed in the x-direction; the right boundary with coupling constraint in the x-direction (all points of the right boundary have the same displacement in x-direction). A displacement boundary condition of up to 1% macroscopic strain was applied on the upper boundary in the y-direction. The use of displacement conditions allows an easy control of the calculation steps, being very helpful to obtain the stress/strain information. All 2D geometries had been meshed with eight-node biquadratic plane strain elements. All finite element simulations had been performed using the commercial finite element code ANSYS. Mesh convergence had been verified based on overall and local stress values.

3. Results and Discussion

3.1. Porosity Characterisation

The porosity distribution obtained from image analysis of the different porous samples studied are shown in Figure 2. The contents (vol.%) and morphological parameters of the pores (equivalent diameter (Deq) and pore elongation factor (Fe)), and the total and interconnected porosity (θ and θi, respectively) are summarized in Table 1. The porosity analysis reveals a clear influence of the pressure of compaction and the sintering temperature. Higher values of Pc and Ts lead to lower values of porosity (higher density) and to smaller pores (lower equivalent diameters), mostly isolated and rounded (higher elongation factor), as could be expected. It should be pointed out that the porosity values measured by the Archimedes’ method was reasonably in agreement with the porosity estimation done by image analysis. In addition, the interconnected porosity was always lower than the total porosity and showed a similar trend. In this context, a sintering temperature and a compacting pressure reduction produced the largest pores and more irregular shape because of the coalescence of the smaller ones. The pore sizes obtained by conventional PM routes at low pressures and loose sintering are insufficient to ensure the bone ingrowth requirements (interconnected porosity and sizes larger than 100 μm are required). However, previous studies have confirmed the role of surface roughness inside pores on cell differentiation and osteoblast adhesion [43,51,52,53]. The inner surfaces of pores obtained by loose sintering are less rough (adhesion of osteoblasts is poor) than those obtained by applying pressure during compaction. Inside the pores, osteoblast cells attached to the walls perceive higher load transfer and this local stress will promote cell differentiation and mineralization and, therefore, the potential implant osseointegration [54].

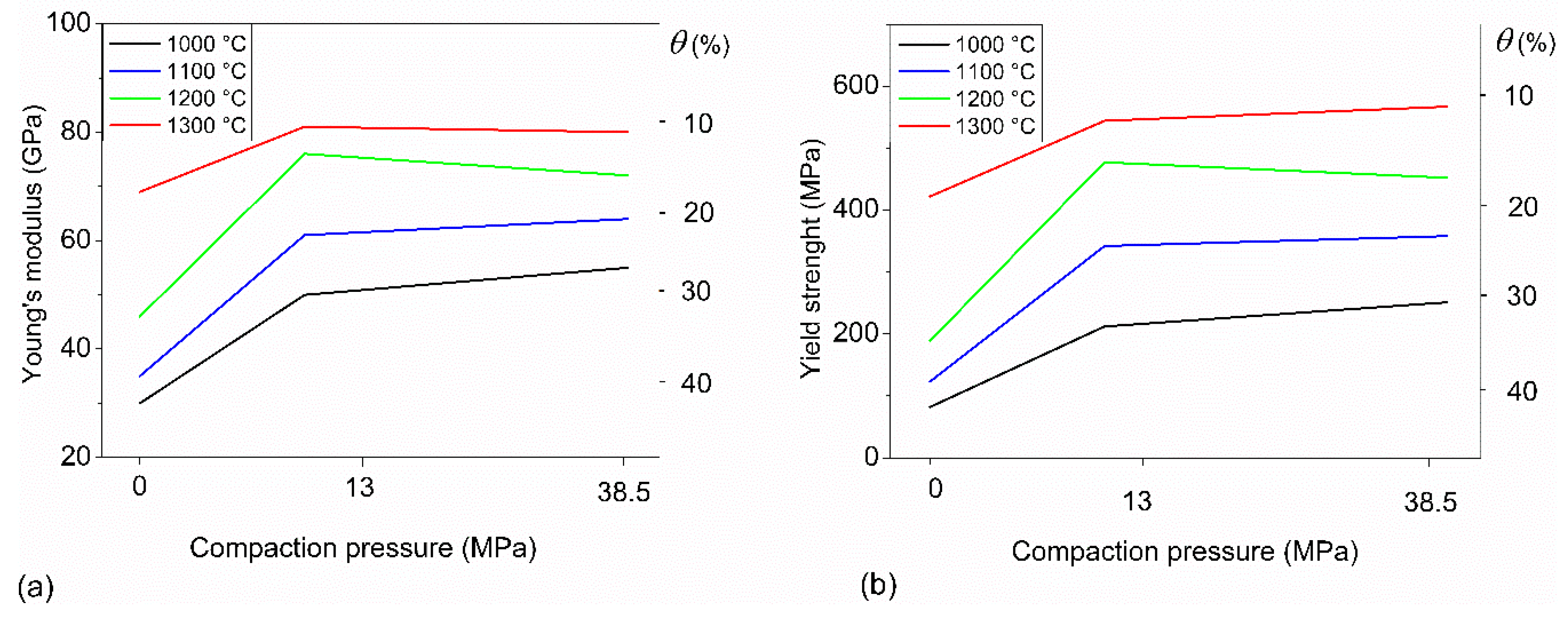
3.2. Mechanical Behavior

As it has been previously mentioned, the mechanical properties of the porous compacts have been measured using two different methodologies (see Table 2): The uniaxial compression test (Young’s modulus and yield strength) and the ultrasounds technique (dynamic Young’s module). As it has been pointed out by the authors in previous work [43,45,46], a discrepancy between the Young’s modulus obtained through both experimental approaches (compression test and ultrasounds) has been encountered. Greiner et al. (2005) [55] linked this to a super-elastic deformation within the linear-elastic range of NiTi materials; the stiffness measured by the ultrasonic technique decreases with increasing porosity, in agreement with elastic Eshelby-based theory for closed, spherical porosity. Torres et al. [46] reported a similar trend for others porous materials and related this difference to a stiffness testing machine effect in which the mechanical system and the sample were considered as two springs in series. Moreover, it must be remembered that the Ti matrix is different at each cross-section of the cylindrical sample during a compression test; the material collapse starts at the section with the lowest titanium content. However, in the ultrasonic technique, the Young’s modulus is estimated as a function of the wave velocity, which goes through all the sections of the sample. Therefore, a change in one of four parameters (time of transfer, attenuation, reflection, and frequency) associated with the high-frequency waves transition from side to side of the material, could be linked to variations of physical properties such as Young’s modulus, density, or homogeneity in the microstructure. In these works, the reliability and certainty of the ultrasound measurements were validated by comparing them to a well-known and accepted pore-elasticity model proposed by Nielsen [56], which includes porosity parameters experimentally determined. Consequently, the Young’s modulus obtained from the ultrasound technique seems to be more reliable than that obtained from compression tests. The porous samples obtained by loose sintering and 1100 °C have the most suitable biomechanical behavior in terms of guaranteeing the requirements of the cortical bone tissue (E = 20–25 GPa and σy = 150–180 MPa, respectively).
In order to clearly observe the influence of both processing variables (pressure of compaction, Pc, and sintering temperature, Ts) on the mechanical properties of the processed compacts, the experimental results summarized in Table 2 are plotted in Figure 3. With the aim of showing the influence of the total porosity, θ, on the mechanical properties, the values of this variable have also been included in the graphs.
In view of the results displayed in Figure 3, several conclusions can be drawn. On the one hand, the mechanical properties of the porous compacts depend on both processing variables (Pc and Ts), being the sintering temperature the more influential one. As it can be expected, both compression strength and Young’s modulus decrease as the porosity increases. It should be noted that, although the total porosity is the more influential porosity variable, there is also a noticeable influence of the other porosity variables related to the pore morphology (Deq and Fe) on the mechanical properties, especially on the yield strength. In this regard, the reduction in mechanical strength was more representative, as expected, for larger pores. This trend is related to the increasing titanium remaining in the matrix, as well as to softer pores contours (greater Ff), and to the better quality of the sintering necks, associated with a better cold welding of titanium powders and a decrease in surface energy (coalescence of titanium particles at higher sintering temperatures). The pores act like notches that produce stress concentrations (“notch strengthening”), besides reducing strength effective area. Within this context, it is expected that some changes from a close to an open porosity regime will generate a triaxial effect that can partially compensate for the strength loss associated with any increase of porous fraction. Therefore, under interconnected porosity conditions, yield strength will not be drastically reduced due to increments in porosity, which is the case when isolated porosity is increased. It can be concluded that, by varying the processing variables (Pc and Ts), the total porosity of the porous material can be carefully controlled, and thus, the desired mechanical properties.

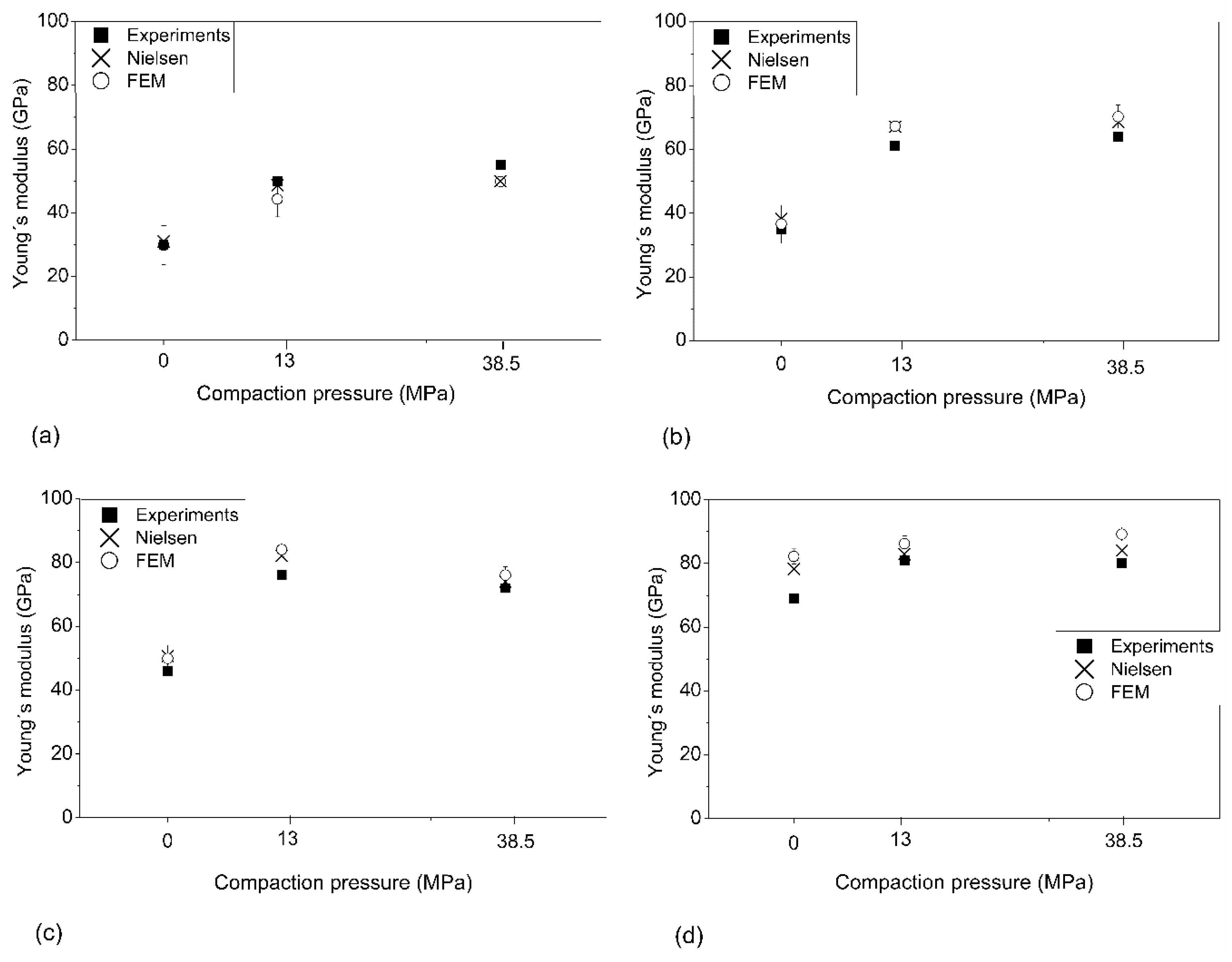
3.3. Finite Element Method Results

Following the methodology presented in Section 2.4 and making use of the main porosity characteristics shown in Table 1, several finite element geometries have been randomly generated for each porous material under study. Following this methodology, 60 different geometries (5 for each of the 12 porous materials under study) have been generated and used in simulations. One of the five geometries for each porous material under study has been chosen as “representative” and presented in Figure 4. Note that, for each geometry, the values of the total porosity (θ) and side length (a) have been included in the figure.
It is important to note that the porous geometries used in the numerical model (some of which have been presented in Figure 4) are not the same as the porous geometries extracted from the experiments (some of which have been presented in Figure 2). In fact, they do not need to be the exactly the same, but “statistically similar”, as is explained as follows. The FE geometries have been randomly generated following the statistical information of the porosity in real compacts by image analysis. This way, both geometries (FE and experimental one) have the same porosity level and the same statistical distribution of the main pore morphology characteristics (elongation factor and diameter). Consequently, both geometries are similar and can be expected to behave similarly.
Making use of the FE model, series of compression tests under displacement control up to 1% macroscopic strain have been simulated. From them, the predicted uniaxial stress–strain responses have been obtained and presented in Figure 5, for each of the 60 different simulations performed.
From the obtained stress–strain curves, the average response for each porous material is summarized in Table 3, where the predicted Young’s modulus and the 0.2% offset yield strength are listed in terms of overall average ± standard deviation. Notice that, in the results obtained from the simulations, the corresponding standard deviation for each case has been included. Thanks to the low computational cost of the proposed FE model, an important number of simulations can be carried out to obtain more feasible and representative predictions. As previously mentioned, five different geometries have been generated for each porous material under study. Consequently, from these five “virtual experiments”, we can obtain an average value and a standard deviation for each prediction.
From the results summarized in Table 3, several conclusions can be drawn. Firstly, one expected trend: An increase in the compaction pressure and sintering temperature leads to an increase in both material properties, Young’s modulus, and yield strength. These results can be easily explained in view of the porous geometries presented in Figure 4. At lower values of Pc and Ts, the porosity level increases and, therefore, the fraction of the matrix bearing stress also decreases. This is due to the fact that the stiffness of the porous material (Young’s modulus) decreases. Regarding the yield strength, the explanation is a bit more complex. At lower values of Pc and Ts, not only the level of porosity increases, but also the shape of the porous is sharper (lower values of elongation factor, see Table 1), which leads to higher level of stress concentration around pores. Both factors lead to greater probability of plastic deformation and, consequently, lower values of yield strength.
In order to illustrate this effect, the contour plots of the von Mises stress at 1% macroscopic strain, for two different cases are analyzed and presented in Figure 6. They are the extreme cases of the “representative” models presented in Figure 4, corresponding to the highest and the lowest porosity levels, respectively. The first case corresponds to processing variables of Ts = 1000 °C, Pc = 0 MPa, with a porosity level of θ = 43%, while the second case corresponds to processing variables of Ts = 1300 °C, Pc = 38.5 MPa, with a porosity level of θ = 12%. When comparing both cases, it can be seen that in the first case (with higher porosity), higher overall stress levels and higher stress concentration around the pores are found.
Secondly, regarding the dispersion of the obtained results, it can be concluded that the higher the Pc and Ts, the lower the dispersion in the values of the predicted Young’s modulus and yield strength are obtained.
In order to validate the proposed FE model, the results of the simulations are graphically presented in the following figures (Figure 7 and Figure 8). Firstly, regarding the Young’s modulus, the average predicted values (Table 3) are compared with the experimental results (Table 2) in Figure 7, for the different porous materials under study. Additionally, to corroborate the obtained results, the value of the Young’s modulus predicted using the Nielsen’s model has also been included. Note that in these graphs, the standard deviations of the simulated results by FEM have also been included.
The graphs show a very good agreement between the FE model predictions and the experiments. Furthermore, the results obtained using Nielsen’s model confirm the goodness of the proposed FE model. Secondly, regarding the yield strength, the average predicted values (Table 3) are compared with the experimental results (Table 2) in Figure 8 for the different porous materials under study. Standard deviation of the simulated results by FEM have also been included. Again, a relatively good agreement between the prediction and the experiments has been achieved. It must be taken into account the difficulty in predicting such a complex property as the yield strength. This mechanical property depends not only on the porosity level, but also—especially—on the distribution, size, and shape of the pores, which lead to important stress concentrations around pores and, consequently, to localized plastic strain.
Some authors have developed models in order to address the relationships between porosity and mechanical strength in sintered materials. One of those approaches [57] is based on the geometric relationship between the porosity and the effective area, by considering pores with a perfectly spherical geometry. Hyun et al. [58] validated their model with results obtained from porous copper by assuming cylindrical-shaped pores with a perpendicular orientation with respect to the direction of the applied load. Additionally, the “simple brick” model [59] assumes cubic pores and determines the relative strength according to the probability of finding a solid fraction of volume. Finally, the model of Griffiths et al. [60] considers porosity as a distribution of spheres and oval ellipsoids including a parameter that represents the pores shape factor.

4. Conclusions

The following general findings can be drawn from a detailed and extensive study of the influence of both the temperature and the compaction pressure, on the microstructural and mechanical properties of porous samples of commercially pure titanium for bone replacement.
The most suitable stiffness value close enough to the cortical bone (20–25 GPa) was achieved for the porous samples obtained by loose sintering and temperatures between 1000 °C–1100 °C (about 40% of total porosity), so it would become the recommended route considering the viability, feasibility, and implementation costs in the industrial sector. These parameters ensure the production of porous titanium while reducing the stress-shielding phenomenon. Although the mechanical resistance is compromised for these manufacturing conditions, the values obtained (123 MPa) are relatively acceptable (bone: 150–180 MPa). In general, the mechanical behavior of the porous materials obtained by PM routes depends on the content of the total and interconnected porosity, the quality of the sintering necks, as well as the equivalent diameter and the morphology (shape factor) of the pores.
Regarding the numerical work, an FE model that combines the simplicity of a 2D periodic geometry with the complex information of the pore morphology extracted from experiments has been used. By making use of this FE model, the different porous titanium materials under study have been simulated and their mechanical properties predicted. A very good agreement between predictions and experiments has been found for both mechanical properties, the Young’s modulus, and the yield strength. These good results have been confirmed using the analytical model proposed by Nielsen.

Author Contributions

Conceptualization, S.M. and Y.T.; investigation, P.T. and Y.T., methodology and software, S.M. and S.M.C.; validation, S.M., S.M.C., and E.D.; writing—original draft, S.M.C.; writing—review and editing, S.M.

Funding

This work was supported by Ministry of Economy and Competitiveness of the State General Administration of Spain under the grant MAT2015-71284-P.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

  1. Long, M.; Rack, H.J. Titanium alloys in total joint replacement—A materials science perspective. Biomaterials 1998, 19, 1621–1639. [Google Scholar] [CrossRef]
  2. Hayashi, Y.S.K.; Uenoyama, K.; Matsuguchi, N. Quantitative-analysis of invivo tissue responses to titanium-oxidecoated and hydroxyapatite-coated titanium-alloy. J. Biomed. Mater. Res. 1991, 25, 515–523. [Google Scholar] [CrossRef] [PubMed]
  3. Ning, C.; Zhou, L.; Tan, G. Fourth-generation biomedical materials. Mater. Today 2016, 19, 2–3. [Google Scholar] [CrossRef]
  4. Navarro, M.; Michiardi, A.; Castano, O.; Planell, J.A. Biomaterials in orthopaedics. J. R. Soc. Interface 2008, 5, 1137–1158. [Google Scholar] [CrossRef]
  5. Goriainov, V.; Cook, R.; Latham, J.M.; Dunlop, D.G.; Oreffo, R.O. Bone and metal: An orthopaedic perspective on osseointegration of metals. Acta Biomater. 2014, 10, 4043–4057. [Google Scholar] [CrossRef]
  6. Zhang, L.C.; Chen, L.Y. A Review on Biomedical Titanium Alloys: Recent Progress and Prospect. Adv. Eng. Mater. 2019, 21, 1801215. [Google Scholar] [CrossRef]
  7. Kaur, M.; Singh, K. Review on titanium and titanium based alloys as biomaterials for orthopaedic applications. Mat. Sci. Eng. C Mater. 2019, 102, 844–862. [Google Scholar] [CrossRef]
  8. Sola, A.; Belluci, D.; Cannillo, V. Functionally graded materials for orthopedic applications—An update on design and manufacturing. Biotechnol. Adv. 2016, 34, 504–531. [Google Scholar] [CrossRef]
  9. Norwsky, P.A.; Bumgardner, J.D. Biomaterial and antibiotic strategies for peri-implantitis: A review. J. Biomed. Mat. Res. 2009, 88, 530–543. [Google Scholar] [CrossRef]
  10. Naebe, M.; Shirvanimoghaddam, K. Functionally graded materials: A review of fabrication and properties. Appl. Mater. Today 2016, 5, 223–245. [Google Scholar] [CrossRef]
  11. Li, F.; Li, J.; Huang, T.; Kou, H.; Zhou, L. Compression fatigue behavior and failure mechanism of porous titanium for biomedical applications. J. Mech. Behav. Biomed. 2017, 65, 814–823. [Google Scholar] [CrossRef] [PubMed]
  12. Babaee, S.; Jahromi, B.H.; Ajdari, A.; Nayeb-Hashemi, H.; Vaziri, A. Mechanical properties of open-cell rhombic dodecahedron cellular structures. Acta Mater. 2012, 60, 2873–2885. [Google Scholar] [CrossRef]
  13. Özbilen, S.; Liebert, D.; Beck, T.; Bram, M. Fatigue behavior of highly porous titanium produced by powder metallurgy with temporary space holders. Mat. Sci. Eng. C Mater. 2016, 60, 446–457. [Google Scholar] [CrossRef] [PubMed]
  14. Yuhua, L.; Yang, C.; Zhao, H.; Qu, S.; Li, X.; Li, Y. New Developments of Ti-Based Alloys for Biomedical Applications. Materials 2014, 7, 1709–1800. [Google Scholar]
  15. O’Brien, B. Niobium Biomaterials. Charper in Advances in Metallic Biomaterials: Tissues, Materials and Biological Reactions; Niinomi, M., Narushima, T., Nakai, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
  16. Matsuno, H.; Yokoyama, A.; Watari, F.; Uo, M.; Kawasaki, T. Biocompatibility and osteogenesis of refractory metal implants, titanium, hafnium, niobium, tantalum and rhenium. Biomaterials 2001, 22, 1253–1262. [Google Scholar] [CrossRef]
  17. Niinomi, M.; Liu, Y.; Nakai, M.; Liu, H.; Li, H. Biomedical titanium alloys with Young’s moduli close to that of cortical bone. Regen. Biomater. 2016, 3, 173–185. [Google Scholar] [CrossRef]
  18. Liu, Y.J.; Li, S.J.; Zhang, L.C.; Hao, Y.L.; Sercombe, T.B. Early plastic deformation behaviour and energy absorption in porous β-type biomedical titanium produced by selective laser melting. Scr. Mater. 2018, 153, 99–103. [Google Scholar] [CrossRef]
  19. Pałka, K.; Pokrowiecki, R. Porous Titanium implants: A review. Adv. Eng. Mater. 2018, 20, 1700648. [Google Scholar] [CrossRef]
  20. Jin, Z.M.; Zheng, J.; Li, W.; Zhou, Z.R. Tribology of medical devices. Biosurface Biotribology 2016, 2, 173–192. [Google Scholar] [CrossRef]
  21. Reis, L.M.; Rodarte, Y.; Falchete, R.; Oliveira, L.G.; Alencastro, M.L.; Alves, C.A. Porous Titanium by Powder Metallurgy for Biomedical Application: Characterization, Cell Citotoxity and in vivo Tests of Osseointegration. In Charper 2 of Biomedical Engineering: Technical Applications in Medicine; Hudak, R., Ed.; InTech: Rijeka, Croatia, 2012. [Google Scholar]
  22. Khorasani, A.M.; Goldberg, M.; Doeven, E.H.; Littlefair, G. Titanium in biomedical applications—Properties and fabrication: A review. J. Biomater. Tiss. Eng. 2015, 5, 593–619. [Google Scholar] [CrossRef]
  23. Betts, C. Benefits of metal foams and developments in modelling techniques to assess their materials behaviour: A review. Mater. Sci. Technol. 2012, 28, 129–143. [Google Scholar] [CrossRef]
  24. Lee, W.H.; Hyun, C.Y. Fabrication of fully porous and porous-surfaced Ti-6Al-4V implants by electro-discharge-sintering of spherical Ti-6Al-4V powders in an one-step process. J. Mater. Process. Tech. 2007, 189, 219–223. [Google Scholar] [CrossRef]
  25. Su, Y.; Luo, C.; Zhang, Z.; Hermawan, H.; Zhu, D.; Huang, J.; Liang, Y.; Li, G.; Ren, L. Bioinspired surface functionalization of metallic biomaterials. J. Mech. Behav. Biomed. Mater. 2018, 77, 90–105. [Google Scholar] [CrossRef] [PubMed]
  26. Wu, S.; Liu, X.; Yeung, K.W.; Liu, C.; Yang, X. Biomimetic porous scaffolds for bone tissue engineering. Mat. Sci. Eng. 2014, 80, 1–36. [Google Scholar] [CrossRef]
  27. Singh, R.; Lee, P.D.; Dashwood, R.J.; Lindley, T.C. Titanium foams for biomedical applications: A review. Mater. Technol. 2010, 25, 127–136. [Google Scholar] [CrossRef]
  28. Trueba, P. Desarrollos de Titanio con Porosidad Gradiente Radial y Longitudinal Para Aplicaciones Biomédicas. Ph.D.; Thesis, University of Seville, Seville, Spain, 2017.
  29. Zhang, L.C.; Liu, Y.; Li, S.; Hao, Y. Additive Manufacturing of Titanium Alloys by Electron Beam Melting: A Review. Adv. Eng. Mater. 2018, 20, 1700842. [Google Scholar] [CrossRef]
  30. Singh, S.; Ramakrishna, S.; Singh, R. Material issues in additive manufacturing: A review. J. Manuf. Process. 2017, 25, 185–200. [Google Scholar] [CrossRef]
  31. Orrù, R.; Licheri, R.; Locci, A.M.; Cincotti, A.; Cao, G. Consolidation/synthesis of materials by electric current activated/assisted sintering. Mat. Sci. Eng. 2009, 63, 127–287. [Google Scholar] [CrossRef]
  32. Asaoka, K.; Kuwayama, N.; Okuno, O.; Miura, I. Mechanical properties and biomechanical compatibility of porous titanium for dental implants. J. Biomed. Mater. Res. 1985, 19, 699–713. [Google Scholar] [CrossRef]
  33. Wang, J.F.; Liu, X.Y.; Luan, B. Fabrication of Ti/polymer biocomposites for load-bearing implant applications. J. Mater. Process. Tech. 2008, 197, 428–433. [Google Scholar] [CrossRef]
  34. Oh, I.H.; Nomura, N.; Masahashi, N.; Hanada, S. Mechanical properties of porous titanium compacts prepared by powder sintering. Scr. Mater. 2003, 49, 1197–1202. [Google Scholar] [CrossRef]
  35. Jamshidinia, M.; Wangb, L.; Tong, W.; Ajlouni, R.; Kovacevic, R. Fatigue properties of a dental implant produced by electron beammelting (EBM). J. Mater. Process. Tech. 2015, 226, 255–263. [Google Scholar] [CrossRef]
  36. Ren, D.; Li, S.; Wang, H.; Hou, W.; Hao, Y.; Jin, W.; Yang, R.; Misra, R.D.K.; Murr, R.E. Fatigue behavior of Ti-6Al-4V cellular structures fabricated by additive manufacturing technique. J. Mater. Sci. Technol. 2019, 35, 285–294. [Google Scholar] [CrossRef]
  37. Zhao, D.; Huang, Y.; Ao, Y.; Han, C.; Wang, Q.; Li, Y.; Liu, J.; Wei, Q.; Zhang, Z. Effect of pore geometry on the fatigue properties and cell affinity of porous titanium scaffolds fabricated by selective laser melting. J. Mech. Behav. Biomed. 2018, 88, 478–487. [Google Scholar] [CrossRef]
  38. Zhao, S.; Li, S.J.; Wang, S.G.; Hou, W.T.; Li, Y.; Zhang, L.C. Compressive and fatigue behaviour of functionally graded Ti-6Al-4V meshes fabricated by electron beam melting. Acta Mater. 2018, 150, 1–15. [Google Scholar] [CrossRef]
  39. Yavari, S.A.; Ahmadi, S.M.; Wauthle, R.; Pouran, B.; Schrootene, J.; Weinans, H.; Zadpoor, A.A. Relationship between unit cell type and porosity and the fatigue behavior of selective laser melted meta-biomaterials. J. Mech. Behav. Biomed. 2015, 43, 91–100. [Google Scholar] [CrossRef]
  40. Li, H.; Oppenheimer, S.M.; Stupp, S.I.; Dunand, D.C.; Brinson, L.C. Effects of Pore Morphology and Bone Ingrowth on Mechanical Properties of Microporous Titanium as an Orthopaedic Implant Material. Mater. Trans. 2004, 45, 1124–1131. [Google Scholar] [CrossRef] [Green Version]
  41. Shen, H.; Oppenheimer, S.M.; Dunand, D.C.; Brinson, L.C. Numerical modeling of pore size and distribution in foamed titanium. Mech. Mater. 2006, 38, 933–944. [Google Scholar] [CrossRef] [Green Version]
  42. Shen, H.; Brinson, L.C. Finite element modeling of porous titanium. Int. J. Solids Struct. 2007, 44, 320–335. [Google Scholar] [CrossRef] [Green Version]
  43. Muñoz, S.; Pavón, J.J.; Rodríguez-Ortiz, J.A.; Civantos, A.; Allain, J.P.; Torres, Y. On the influence of space holder in the development of porous titanium implants: Mechanical, computational and biological evaluation. Mater. Charact. 2015, 108, 68–78. [Google Scholar] [CrossRef]
  44. Muñoz, S.; Castillo, S.M.; Torres, Y. Different models for simulation of mechanical behaviour of porous materials. J. Mech. Behav. Biomed. Mater. 2018, 80, 88–96. [Google Scholar] [CrossRef] [PubMed]
  45. Torres, Y.; Pavón, J.J.; Nieto, I.; Rodríguez, J.A. Conventional powder metallurgy process and characterization of porous titanium for biomedical applications. Met. Mater. Trans. B 2011, 42, 891–900. [Google Scholar] [CrossRef]
  46. Torres, Y.; Pavón, J.J.; Rodríguez, J.A. Processing and characterization of porous titanium for implants by using NaCl as space holder. J. Mater. Process. Technol. 2012, 212, 1061–1069. [Google Scholar] [CrossRef]
  47. Lascano, S.; Arévalo, C.; Montealegre-Melendez, I.; Muñoz, S.; Rodriguez-Ortiz, J.A.; Trueba, P.; Torres, Y. Porous titanium for biomedical applications: Evaluation of the conventional powder metallurgy frontier and space-holder technique. Appl. Sci. 2019, 9, 982. [Google Scholar] [CrossRef] [Green Version]
  48. Torres, Y.; Lascano, S.; Bris, J.; Pavón, J.J.; Rodriguez-Ortiz, J.A. Development of porous titanium for biomedical applications: A comparison between loose sintering and space-holder techniques. Mater. Sci. Eng. C 2014, 37, 148–155. [Google Scholar] [CrossRef] [PubMed]
  49. ASTM, C373-88. Standard Test Method for Water Absorption, Bulk Density, Apparent Porosity, and Apparent Specific Gravity of Fired Whiteware Products; AST International: West Conshohocken, PA, USA, 2006. [Google Scholar]
  50. Kikuchi, M.; Takahashi, M.; Okuno, O. Elastic moduli of cast Ti-Au, Ti-Ag, and Ti- Cu alloys. Dent. Mater. 2006, 22, 641–646. [Google Scholar] [CrossRef]
  51. Wen, C.E.; Yamada, Y.; Shimojima, K.; Chino, Y.; Asahina, T.; Mabuchi, M. Processing and mechanical properties of autogenous titanium implant materials. Mater. Sci. Mater. Med. 2002, 13, 397–401. [Google Scholar] [CrossRef]
  52. Dominguez, C.; Beltrán, A.M.; Garvi, M.D.; Salazar-Moya, A.; Lebrato, J.; Hickey, D.J.; Rodriguez-Ortiz, J.A.; Kamm, P.H.; Lebrato, C.; García-Moreno, F. Bacterial behavior on coated porous titanium substrate for biomedical applications. Surf. Coat. Technol. 2019, 357, 896–902. [Google Scholar] [CrossRef]
  53. Torres, Y.; Rodríguez-Ortiz, J.A.; Arias, S.; Echeverry, M.; Robledo, S.; Amigo, V.; Pavón, J.J. Processing, characterization and biological testing of porous titanium obtained by space-holder technique. J. Mater. Sci. 2012, 47, 6565–6576. [Google Scholar] [CrossRef]
  54. Civantos, A.; Domínguez, C.; Pino, R.J.; Setti, G.; Pavon, J.J.; Martínez-Campos, E.; Garcia-Garcia, F.J.; Rodriguez-Ortiz, J.A.; Allain, J.P.; Torres, Y. Designing bioactive porous titanium interfaces to balance mechanical properties and in vitro cells behavior towards increased osseointegration. Surf. Coat. Technol. 2019, 368, 162–174. [Google Scholar] [CrossRef]
  55. Greiner, C.; Oppenheimer, S.M.; Dunand, D.C. High strength, low stiffness, porous NiTi with superelastic properties. Acta Biomater. 2005, 1, 705–716. [Google Scholar] [CrossRef] [PubMed]
  56. Nielsen, L.F. Elasticity and damping of porous materials and impregnated. J. Am. Ceram. Soc. 1983, 67, 93–98. [Google Scholar] [CrossRef]
  57. Eudier, M. The mechanical properties of sintered low-alloy steels. Powder Met. 1962, 5, 278–290. [Google Scholar] [CrossRef]
  58. Hyun, S.; Murakami, K.; Nakajima, H. Anisotropic mechanical properties of porous copper fabricated by unidirectional solidification. Mater. Sci. Eng. A 2001, 299, 241–248. [Google Scholar] [CrossRef]
  59. Fleck, N.; Smith, R. Effect of Density on Tensile Strength, Fracture Toughness, and Fatigue Crack Propagation Behaviour of Sintered Steel. Powder Met. 1981, 3, 121–125. [Google Scholar] [CrossRef]
  60. Griffiths, T.J.; Davies, R.; Bassett, M.B. Analytical Study of Effects of Pore Geometry on Tensile Strength of Porous Materials. Powder Met. 1979, 22, 119–123. [Google Scholar] [CrossRef]
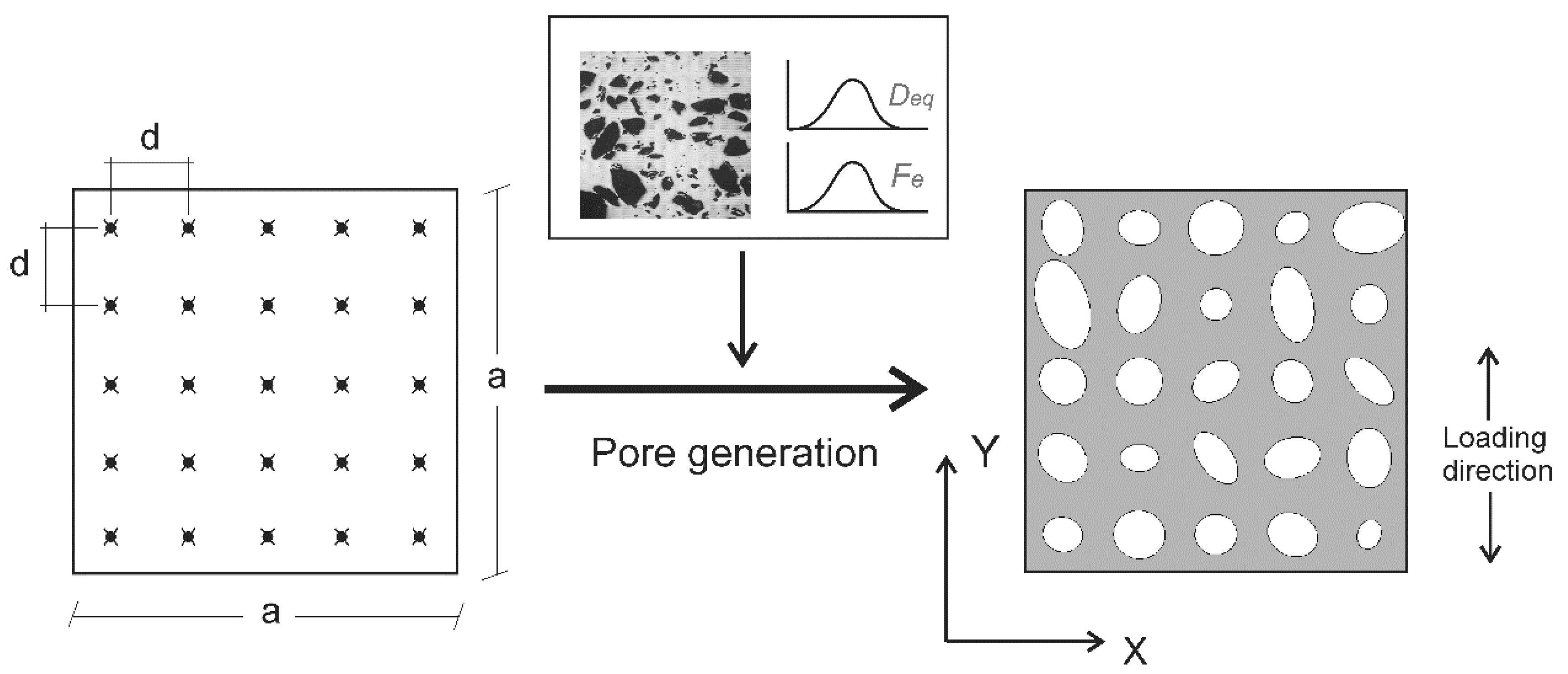
Metals 09 01249 g001 550
Figure 1. Geometry generation for finite element (FE) model.
Figure 1. Geometry generation for finite element (FE) model.
Metals 09 01249 g001
Metals 09 01249 g002 550
Figure 2. Optical images of the porous samples obtained with different compaction pressure and sintering temperature. Common scale bar.
Figure 2. Optical images of the porous samples obtained with different compaction pressure and sintering temperature. Common scale bar.
Metals 09 01249 g002
Metals 09 01249 g003 550
Figure 3. Experimental results of Young’s modulus (a) and yield strength (b), in terms of compaction pressure, for each sintering temperature. Values of total porosity, θ, are also included.
Figure 3. Experimental results of Young’s modulus (a) and yield strength (b), in terms of compaction pressure, for each sintering temperature. Values of total porosity, θ, are also included.
Metals 09 01249 g003
Metals 09 01249 g004 550
Figure 4. Representative geometries, for each porous material, with values of porosity (θ) and side length (a) included.
Figure 4. Representative geometries, for each porous material, with values of porosity (θ) and side length (a) included.
Metals 09 01249 g004
Metals 09 01249 g005 550
Figure 5. Macroscopic stress–strain response of porous titanium by FE model, for each sintering temperature: (a) 1000 °C; (b) 1100 °C; (c) 1200 °C; and (d) 1300 °C.
Figure 5. Macroscopic stress–strain response of porous titanium by FE model, for each sintering temperature: (a) 1000 °C; (b) 1100 °C; (c) 1200 °C; and (d) 1300 °C.
Metals 09 01249 g005
Metals 09 01249 g006 550
Figure 6. Von Mises stress distribution at 1% macroscopic strain, predicted by representative. FE models corresponding to (a) Ts = 1000 °C, Pc = 0 MPa, and (b) Ts = 1300 °C, Pc = 38.5 MPa.
Figure 6. Von Mises stress distribution at 1% macroscopic strain, predicted by representative. FE models corresponding to (a) Ts = 1000 °C, Pc = 0 MPa, and (b) Ts = 1300 °C, Pc = 38.5 MPa.
Metals 09 01249 g006
Metals 09 01249 g007 550
Figure 7. Experimental and simulated Young’s modulus in terms of compaction pressure, for each sintering temperature: (a) 1000 °C; (b) 1100 °C; (c) 1200 °C; and (d) 1300 °C.
Figure 7. Experimental and simulated Young’s modulus in terms of compaction pressure, for each sintering temperature: (a) 1000 °C; (b) 1100 °C; (c) 1200 °C; and (d) 1300 °C.
Metals 09 01249 g007
Metals 09 01249 g008 550
Figure 8. Experimental and simulated yield strength in terms of compaction pressure, for each sintering temperature: (a) 1000 °C; (b) 1100 °C; (c) 1200 °C; and (d) 1300 °C.
Figure 8. Experimental and simulated yield strength in terms of compaction pressure, for each sintering temperature: (a) 1000 °C; (b) 1100 °C; (c) 1200 °C; and (d) 1300 °C.
Metals 09 01249 g008
Table
Table 1. Influence of processing conditions on the characteristics of the obtained porosity.
Table 1. Influence of processing conditions on the characteristics of the obtained porosity.
Ts (°C)Pc (MPa)Density (g/cm3)Archimedes’ MethodImages Analysis
Total Porosity (%)Interconnected Porosity, θi (%)θ (%)Deq (µm)Fe
10000 (LS)2.47 ± 0.2341.4 ± 1.439.1 ± 1.743.0 ± 1.216.9 ± 3.10.59 ± 0.17
133.17 ± 0.0232.2 ± 0.728.27 ± 0.430.8 ± 1.613.8 ± 2.90.60 ± 0.17
38.53.31 ± 0.0329.4 ± 0.825.08 ± 0.929.5 ± 3.314.9 ± 2.10.57 ± 0.17
11000 (LS)2.79 ± 0.2237.4 ± 1.536.2 ± 1.536.9 ± 4.018.5 ± 3.90.57 ± 0.17
133.37 ± 0.3921.8 ± 0.6622.2 ± 1.920.7 ± 2.111.8 ± 2.60.64 ± 0.18
38.53.65 ± 0.0520.3 ± 0.414.9 ± 1.119.9 ± 2.511.0 ± 2.10.64 ± 0.18
12000 (LS)3.12 ± 0.1430.0 ± 0.627.9 ± 1.230.0 ± 6.915.2 ± 2.40.62 ± 0.18
133.88 ± 0.0213.6 ± 0.46.2 ± 0.713.2 ± 1.610.4 ± 1.50.70 ± 0.17
38.53.81 ± 0.0417.5 ± 0.610.1 ± 1.017.3 ± 2.112.8 ± 2.90.70 ± 0.17
13000 (LS)3.72 ± 0.0715.1 ± 0.213.8 ± 1.514.9 ± 1.813.7 ± 2.40.68 ± 0.18
133.96 ± 0.0813.4 ± 0.35.6 ± 0.912.8 ± 0.613.4 ± 2.80.75 ± 0.17
38.53.99 ± 0.0411.8 ± 0.35.4 ± 0.512.2 ± 1.313.0 ± 2.60.75 ± 0.17
Table
Table 2. Mechanical behavior: Young’s modulus and 0.2% offset yield strength.
Table 2. Mechanical behavior: Young’s modulus and 0.2% offset yield strength.
Ts (°C)Pc (MPa)Ultrasound TestCompression Test
Ed (GPa)Ec (GPa)σy (MPa)
10000 (LS)29.3 ± 2.213.4 ± 4.1123 ± 10
1349.5 ± 0.840.8 ± 3.6342 ± 8
38.554.6 ± 0.353.6 ± 5.2358 ± 7
11000 (LS)34.9 ± 0.927.9 ± 3.2189 ± 11
1361.2 ± 7.042.3 ± 4.4477 ± 12
38.563.8 ± 3.834.5 ± 2.8452 ± 9
12000 (LS)46.4 ± 5.840.2 ± 3.7422 ± 8
1376.3 ± 2.746.4 ± 3.2544 ± 8
38.572.1 ± 0.355.2 ± 4.2567 ± 10
13000 (LS)69.9 ± 2.233.2 ± 3.2467 ± 8
1381.3 ± 6.256.2 ± 5.2544 ± 7
38.580.7 ± 0.768.3 ± 5.4567 ± 8
Table
Table 3. Estimated values for elastic modulus and 0.2% offset yield strength by FE model.
Table 3. Estimated values for elastic modulus and 0.2% offset yield strength by FE model.
Ts (°C)Pc (MPa)E (GPa)σy (MPa)
10000 (LS)29.9 ± 6.1124.4 ± 31.5
1344.3 ± 5.5240.2 ± 56.0
38.549.8 ± 4.3275.1 ± 42.2
11000 (LS)36.6 ± 6.0201.3 ± 28.4
1367.3 ± 3.7434.4 ± 39.5
38.570.3 ± 3.6481.7 ± 49.1
12000 (LS)49.9 ± 4.1271.1 ± 38.9
1384.9 ± 2.2609.2 ± 21.4
38.576.9 ± 2.6526.5 ± 26.0
13000 (LS)82.2 ± 1.4575.8 ± 14.5
1386.2 ± 1.6615.1 ± 16.5
38.589.2 ± 1.4636.3 ± 14.0

Share and Cite

MDPI and ACS Style

Castillo, S.M.; Muñoz, S.; Trueba, P.; Díaz, E.; Torres, Y. Influence of the Compaction Pressure and Sintering Temperature on the Mechanical Properties of Porous Titanium for Biomedical Applications. Metals 2019, 9, 1249. https://doi.org/10.3390/met9121249

AMA Style

Castillo SM, Muñoz S, Trueba P, Díaz E, Torres Y. Influence of the Compaction Pressure and Sintering Temperature on the Mechanical Properties of Porous Titanium for Biomedical Applications. Metals. 2019; 9(12):1249. https://doi.org/10.3390/met9121249

Chicago/Turabian Style

Castillo, Sandra M., Sergio Muñoz, Paloma Trueba, Eduardo Díaz, and Yadir Torres. 2019. "Influence of the Compaction Pressure and Sintering Temperature on the Mechanical Properties of Porous Titanium for Biomedical Applications" Metals 9, no. 12: 1249. https://doi.org/10.3390/met9121249

APA Style

Castillo, S. M., Muñoz, S., Trueba, P., Díaz, E., & Torres, Y. (2019). Influence of the Compaction Pressure and Sintering Temperature on the Mechanical Properties of Porous Titanium for Biomedical Applications. Metals, 9(12), 1249. https://doi.org/10.3390/met9121249

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop