Exploring the Correlation between Subsurface Residual Stresses and Manufacturing Parameters in Laser Powder Bed Fused Ti-6Al-4V

Abstract

Subsurface residual stresses (RS) were investigated in Ti-6Al-4V cuboid samples by means of X-ray synchrotron diffraction. The samples were manufactured by laser powder bed fusion (LPBF) applying different processing parameters, not commonly considered in open literature, in order to assess their influence on RS state. While investigating the effect of process parameters used for the calculation of volumetric energy density (such as laser velocity, laser power and hatch distance), we observed that an increase of energy density led to a decrease of RS, although not to the same extent for every parameter variation. Additionally, the effect of support structure, sample roughness and LPBF machine effects potentially coming from Ar flow were studied. We observed no influence of support structure on subsurface RS while the orientation with respect to Ar flow showed to have an impact on RS. We conclude recommending monitoring such parameters to improve part reliability and reproducibility.

1. Introduction

The production of near net-shape metallic components with complex geometries, not achievable with conventional production method, is one of the main advantages of laser powder bed fusion (LPBF) additive manufacturing (AM) technique [1]. One of the well-studied materials for LPBF is Ti-6Al-4V alloy. This alloy is the most used titanium alloy and it is widely spread in aerospace [2]. LPBF allows building design-optimized structures, saving raw material, and reducing the weight of the component. Therefore, the aerospace industry aims at the development and certification of the AM process for this very alloy. Additionally, this alloy is widely used in the medical field, where AM techniques allow creating customized medical implants [3]. The presence of large residual stresses (RS) is a relevant issue in LPBF process since it may lead to detachment of support structure, cracking of the part or to geometrical distortion during manufacturing [4,5]. As reported in [6,7], the RS in LPBF have two dominating origins: the temperature gradient, and the cool-down phase of the molten top layer. As the result, high tensile RS are normally present in the surface and subsurface regions of LPBF materials [8,9] and they are balanced by compressive stress in the bulk [10]. Thus, every parameter influencing the thermal history of the part must influence the RS fields. The analysis of the influence of all manufacturing parameter sets and of the additional influence from the build chamber atmosphere on the RS state of AM parts is a formidable task. A design of experiment that encompasses all effects has never been attempted, and the present level of knowledge would not even benefit from a Taguchi approach [11]. Therefore, normally a multitude of parameters such as laser power (P), scanning velocity (v), hatch distance (h), or powder layer thickness (x) are bundled together in the volumetric energy density (E_v):

$$E_v=\frac{P}{v·h·x},$$

(1)

This parameter is normally used for porosity optimization (i.e., screening) in LPBF process. However, E_v represents a convolution of parameters and therefore simplifies the effect of each parameter. The same E_v, obtained as a combination of different parameters, can lead to different microstructures and properties of materials, as demonstrated in recent works [12,13].

Numerical simulations help to understand the RS distribution in parts built with different laser parameters and scanning strategies [14,15]. However, experimental data on RS in LPBF materials are still incomplete or even show contradictory trends depending on material and measurement method. For instance, in [16] the change of E_v of a fully dense AISI316L steel (density around 99.9%) has shown no impact on RS, measured by laboratory X-ray diffraction. In contrast, in our previous study, highly dense Ti-6Al-4V with different E_v has shown significant difference in RS along the building direction, obtained by synchrotron X-ray diffraction (SXRD) [13]. Additionally, it has been shown in [8] that SXRD allows building an RS profile along the depth (to around 100 µm for Ti-6Al-4V). The higher depth-resolved RS profiles (micrometer range) could be obtained by semi-destructive micro-hole drilling method [17].

As a further example, the rotating scanning strategy has been considered in many studies as the one giving the most homogeneous temperature distribution, hence, low RS [7,14]. However, in some studies the alternating 90° scanning strategy with stripe pattern has been recommended for minimization of RS [18]. The same disagreement can be found in case of support structures and their influence on RS. RS analysis of Ti-6Al-4V parts by X-ray diffraction in [19] has shown a reduction of stresses for a sample on support structure (with respect to sample built directly on the base plate). In contrast, in [20] a LPBF Al10SiMg sample built directly on the base plate (without support structures) has shown the lower RS, measured by hole drilling.

Not only laser parameters and scanning strategy [7,21] must be taken into account, but also other factors basically poorly explored in the open literature such as the position on the base plate, the laser path, or the Argon flow [13]. Those factors cannot always be captured by simulations and sometimes are not experimentally measurable. Therefore, RS studies should consider controllable manufacturing parameters as well as factors that do not appear, at first hand, to impact the manufacturing process. Moreover, all studies are material dependent. Therefore, they can be considered as unique cases. In such sparse knowledge matrix, any study focusing on explored or hidden parameters will bring a contribution to the general understanding of the process.

In this study, we explore the influence of parameters that have been (in the best case) partially neglected in previous studies. We show that this additional analysis complements the existing literature, bringing some missing bricks to the solution of the problem of RS assessment in AM parts, and allows corroborating (or contradicting) existing scenarios describing the origin of RS in AM parts. The work is therefore also targeted at generating further discussion on this highly complex topic.

2. Materials and Methods

2.1. Materials

18 cuboids, with a size of 5 × 5 × 15 mm³, were produced in a SLM Solutions 280^HL machine (SLM Solution Group AG, Lübeck, Germany) using plasma atomized Ti-6Al-4V ELI grade 23 powder from AP&C. The size distribution of the powder’s spherical particles was measured by laser diffraction (Beckman Coulter LS 13320 PIDS, Beckman Coulter GmbH, Krefeld, Germany), resulting in D-values D₁₀ = 22 µm, D₅₀ = 34 µm and D₉₀ = 46 µm.

Table 1. Processing parameters.

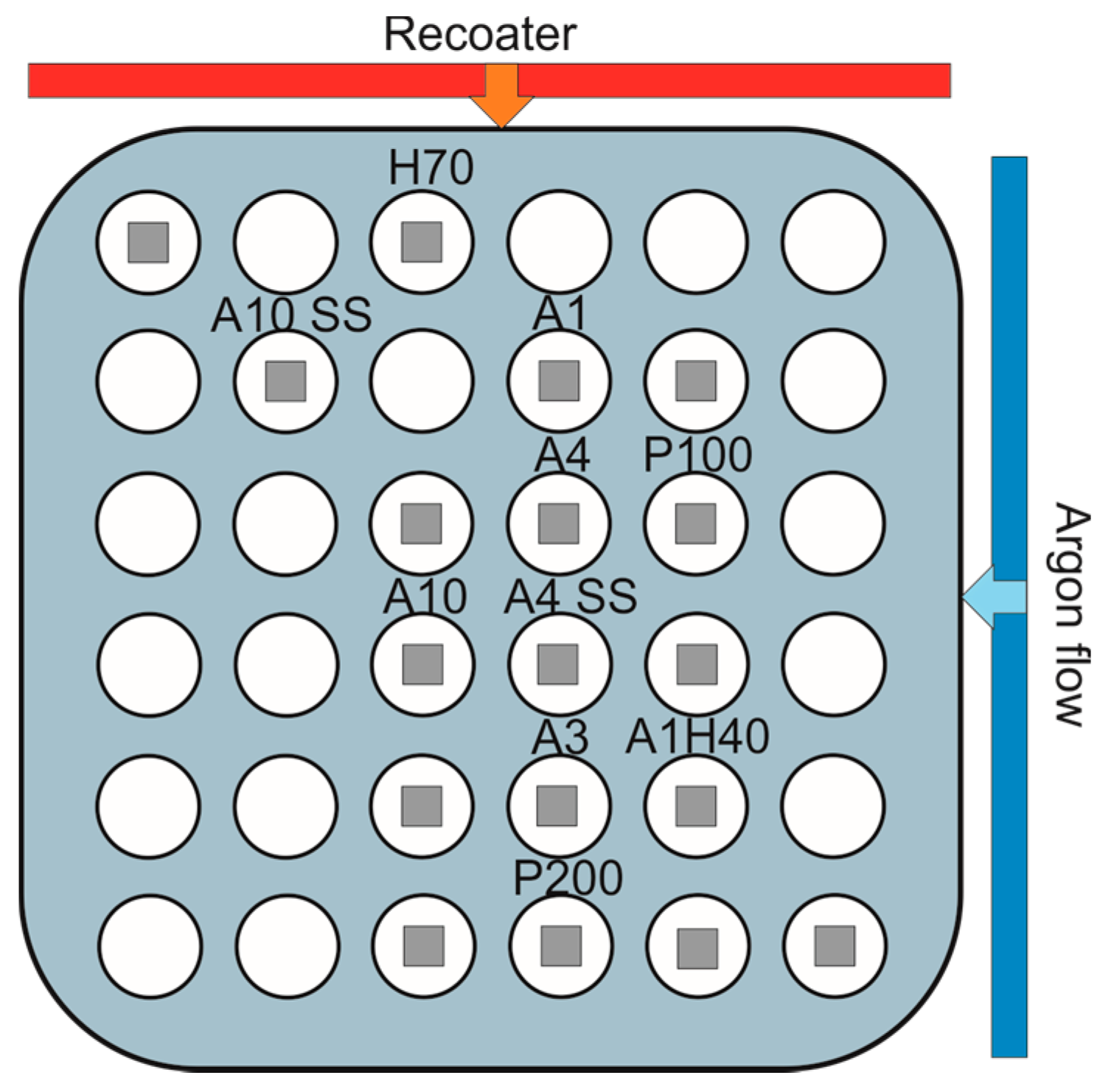
Sample Groups	Name	Power, p	Hatch Distance, h	Velocity, v	Volumetric Energy Density	Line Energy, p/v
		W	mm	mm/s	J/mm3	J/mm
Surface roughness	A4 *	175	0.1	500	116.7	0.35
	A4 without contour	175	0.1	500	116.7	0.35
Different surfaces	A4 *	175	0.1	500	116.7	0.35
Support structure	A4 *	175	0.1	500	116.7	0.35
	A4 SS	175	0.1	500	116.7	0.35
	A10	175	0.1	1100	53	0.16
	A10 SS	175	0.1	1100	53	0.16
Velocity variation	A1 *	175	0.1	200	291.7	0.88
	A3	175	0.1	400	145.8	0.44
	A4 *	175	0.1	500	116.7	0.35
	A10	175	0.1	1100	53.0	0.35
Power variation	P100	100	0.1	500	66.7	0.2
	A4 *	175	0.1	500	116.7	0.35
	P200	200	0.1	500	133.3	0.4
Hatch distance variation	A1H40 *	175	0.04	500	291.7	0.35
	H70	175	0.07	500	166.7	0.35
	A4 *	175	0.1	500	116.7	0.35

* Results for these samples were partially reported in [11].

shows the manufacturing parameters. Each sample was produced on a small round-shaped baseplate (Ø = 3 cm), which was screwed to a large baseplate 280 × 280 mm² preheated to 200 °C (see Figure 1). Since in our previous study [13] the position on the baseplate showed to be an important factor for RS, the location of each sample is uniquely defined (see Figure 1). Two samples were built on a 2 mm support structure (SS). The same powder layer thickness of 30 µm and a chessboard scan strategy with a minimum field size of 5 mm were chosen for all of them, while other processing parameters were varied. Also, for all samples, a set of two contours and one intermediate line (i.e., so called fill-contour line) were applied before the sample bulk was processed. In the contour scan, the same parameters, with 100 W laser power and 525 mm/s scan velocity, were used for all specimens. The microstructure and the RS for some cuboids from the same build job were partially discussed in [13]. The names of the parameter sets were kept the same as used in our previous studies [8,13,22,23] for consistency, and are indicated in Table 1. The A4 parameter set presents porosity-optimized conditions [23], and is always used as a reference.

2.2. Synchrotron X-ray Diffraction

The RS analysis was performed by SXRD at the synchrotron source BESSY II (Helmholtz Zentrum Berlin, Germany) at the EDDI beamline [24]. The energy dispersive diffraction technique allows obtaining the lattice spacing $d^{hkl}$ for different crystallographic planes $\left\{hkl\right\}$ in dependence of the energy $E_{hkl}$:

$$d^{hkl}\left(\mathsf{\AA }\right)=\frac{6.199}{\sin \mathsf{\theta }}\frac{1}{E_{hkl}\left(\mathrm{keV}\right)}$$

(2)

The EDDI beamline provided a white beam with an energy range of about 10 to 150 keV. The white beam allows probing different depths [25]. In fact, the penetration depth $\tau$ for the energy dispersive diffraction is determined by [24]:

$$\tau =\frac{\sin \mathsf{\theta }}{2\mathsf{\mu }\left(E_{hkl}\right)}\cos \psi ,$$

(3)

where $\mathsf{\mu }\left(E_{hkl}\right)$ is the linear absorption coefficient at the energy $E_{hkl}$. Therefore, different energies correspond to different $\tau$.

The experiment was performed in a reflection set-up with a fixed diffraction angle of 2θ = 8°. The prismatic gauge volume was defined by the intersection of the incoming (slits 500 × 500 μm²) and the diffracted beams towards the detector (vertical slits of 30 µm). Therefore, a gauge volume length of 3.8 mm was defined (Figure 2), although one has to bear in mind that more that 75% of the signal comes from central 50% of the length [26]. All samples were systematically measured on the surface opposite to the red line in Figure 1. During measurements all samples were attached to the baseplate, also support structures were not removed. All samples, except A4 without contour, were measured at the surface height identified by laser system (0 µm). Seven points along sample height were mapped to obtain the stress component along the building direction (BD, σ_z, Figure 2). The sin²ψ method was used assuming the normal stress component (σ_X) negligible at the surface. Diffraction peaks of six crystallographic planes of (α + α’) hexagonal Ti lattices were acquired. For the calculation of strains and stresses, diffraction elastic constants (DEC, reported in [8]) of α-Ti were used. The detailed description of experiment has been reported elsewhere [8,13].

2.3. Roughness Measurements

The roughness of selected specimen surfaces was measured using a confocal ZEISS LSM 700 laser scanning microscope from Zeiss AG, Oberkochen, Germany. For all specimens the same measurement parameters were used. The measurement position was at about 8 mm from the sample’s top. Images with a 100× magnification (objective EC Epiplan-Apochromat 10×/0.3 HD DIC M27) and a pixel size of 2.5 × 2.5 µm² were taken each 2.46 µm in height. The roughness values S_a (arithmetic mean height), S_q (root-mean-square height), S_z (maximum height) and S_p (maximum peak height) of an area of 2 × 2 mm² were calculated in the software ConfoMap (Version 7.4, ZEISS AG, Oberkochen, Germany) according to ISO25718.

3. Results and Discussion

LPBF materials are generally highly textured owing to the directional temperature gradient across the deposited layers that induce epitaxial growth along the building direction [27]. However, depending on the part usage, texture can be modified and reduced to some extent by changing scanning strategy [28] or modifying the alloy composition [29]. For the material investigated in the current study a difference in texture between contour region and bulk was observed. The diffractograms obtained by synchrotron X-ray diffraction of the porosity-optimized A4 sample in the subsurface region (in reflection mode) and in the bulk (transmission measurement) are shown in Figure 3a,b, respectively. The subsurface region presents similar intensities of the diffraction peaks for different ψ tilts, while in the bulk the peaks change intensity and even disappear for some orientations. This kind of behavior is well known for LPBF Ti-6Al-4V [30]. Texture is known to have an influence on strain measurements [4], which complicates RS analysis of such materials. Additionally, crystallographic plane-specific elastic constants can vary due to texture [31]. In the present study, only subsurface stresses (corresponding to contour regions) were considered. Also, only the 103 reflection is reported in the rest of the work, due to the presence of low intergranular stresses [32,33].

3.1. Effect of Surface Roughness

The contour scans are usually applied to reduce roughness of the sample, which is often dominated by the attached/partially unmolten powder particles [34]. However, in order to understand the effect of roughness on RS measurements one A4 sample without contour was investigated in this study. The A4 sample without contour scans was manufactured in a different build job but using the same bulk A4 parameters (Table 1). The surface roughness, obtained by confocal laser scanning microscopy, shows more than double S_q in case of the sample without contour scan compared to the one with contour (S_q = 33.3 µm vs. S_q = 13.2 µm, Figure 4a,b). Also, a higher maximum height S_z for the sample without contour scan (270 µm) compared to one with contour (102 µm) can be observed in the roughness maps. The surface alignment for RS measurements at the EDDI beamline is usually obtained by a laser system for each measurement point of the sample surface. In this way the surface waviness is taken into account. This surface alignment allowed obtaining a sufficient signal. The unmolten powder particles at the surface contribute to the diffraction signal but since they only are partially attached to the surface they do not contribute to macrostress formation, i.e., the RS value should be around zero. Therefore, for the sample without contour scan different depths from the surface, defined by the laser system, were measured (0 µm, 150 µm and 250 µm, see schematic sketch Figure 5a) to assess the influence of roughness on measurements. The 150 µm and 250 µm (Figure 1) correspond to the physical shift of the gauge volume inside the sample from the 0 µm position defined by the laser system. An increase of RS was observed (Figure 5b) by shifting the gauge volume deeper, as well as a decrease of experimental error which is related to the increase of the diffraction peaks intensity. Therefore, the surface RS of the sample without contour scan become close to those in the sample with contour scan at a shift of 250 µm. The stress profile along the sample height still fluctuates, possibly due to the inhomogeneous roughness/waviness. Additionally, the gradient of RS as a function of penetration depth shows that closer to the surface the partially attached powder particles contribute to the signal and reduce RS (Figure 5c) [8,9]. Therefore, the choice of the α-103 reflection minimized the influence of intergranular stresses, while it had the highest penetration, helping to overcome the problem of high roughness. The penetration depths of high energy X-ray into the material count from the center of the gauge volume (i.e., from 0, 150, 250 μm positions). Interestingly enough, for the sample without contour a RS value with gauge volume at 150 µm and the penetration depth of τ = 100 µm is approximately the same as the first RS value of gauge volume at 250 µm (τ ≈ 20 µm). Indeed, the combination of the RS profiles from Figure 5c, considering the physical shift from the surface and penetration depth of the X-ray beam, shows an increase of RS as function of depth (Figure 5d). This proves the concept of continuous RS gradient.

3.2. Effect of Sample Orientation with Respect to Ar Flow

For the comparability of results, the lateral surface opposite to the red line in Figure 1 and Figure 6 (named surface 1) was measured for all samples presented in this study. However, to check the distribution of RS at different sides of samples, all four lateral surfaces of cuboid A4 were measured (Figure 6). To avoid the effect of laser path and location of the sample on the baseplate (discussed in [13]) the sample was taken from the center of the baseplate, where we can assume negligible changes in laser orientation as it reaches the sample. The evolution of RS on the different surfaces shows the same tendency from the top of the sample to the mid-height (up to Z = 7 mm, see coordinate system in Figure 2), although with a scatter of about 100 MPa. However, in the lower part of the sample (Z > 7 mm) the curves split in two groups: Surfaces 1 and 3 show lower stresses (around 550 MPa) while surfaces 2 and 4 show higher values (up to 775 MPa). Thus, surfaces opposite to each other have similar RS, hence experience similar temperature distribution during production. Indeed, the surfaces 2 and 4 oriented perpendicular to Ar flow while 1 and 3 are parallel to it. After the contour scan, surfaces 2 and 4 may cool faster due to the larger surface cross section in contact with Ar flow, which results in a higher temperature gradient and hence higher RS (Figure 6b). Additionally, as observed by X-ray computed tomography, porosity distribution has not shown any pattern that can be related to stress relaxation (see Figure 5c in [13]). As shown in [35] for LPBF AlSi10Mg, the two surfaces facing Ar flow output (surface 2) and opposite to it (surface 4) have the highest difference in the roughness. In our case, roughness measurements were performed at each lateral surface and summarized in

Table 2. Roughness at different faces of cuboid A4.

Parameter	Surface 1	Surface 2	Surface 3	Surface 4
Sa, µm	11.2	9.68	9.87	9.08
Sq, µm	16.3	16.5	14.1	13.7
Sp, µm	64.7	54.8	64.6	70.2
Sz, µm	156	176	133	158

. The surface roughness values were similar for all surfaces of cuboid A4. This fact eliminates the effect of roughness on RS measurement in this case. Also, while the bulk scanning strategy was not the same for every side (since the chess pattern with rotation was used), it is difficult to assess any effect of the scanning strategy, since the rotation homogenizes the final temperature distribution. We can conclude that other factors influencing RS at different lateral faces of a sample, such as roughness and scanning strategy, seem to have a minor role with respect to Ar flow. Yet deeper investigations are needed together with a systematic analysis of the Ar flow paths.

3.3. Effect of Velocity Variation and of Support Structure

Support structures are an important part of the building process in LPBF since they help to build overhanging features [5]. They also facilitate heat dissipation, because loose powder has a poor thermal conductivity. Also, they can be used during design of the part to optimize RS and minimize distortion. For instance in [36], the use of support structure with more contact area near places with high RS has been recommended. While it has been shown for flat samples that support structures release some subsurface RS for IN718, by giving more flexibility to the sample free deformation, they cannot replace stress relieving heat treatment [9]. In the present study, we investigated samples with and without support structure, manufactured with the same parameters. Figure 7 shows that the use of the support structures does not affect RS: the RS profiles for Z > 6 mm is basically identical for samples produced with the same parameters set.

The effect of laser scan velocity was also investigated (c.f. [8,13], Figure 7b). The laser scan velocity is one of the most influential parameters affecting porosity [23]. For the sample A1 (v = 200 mm/s) the formation of an α + β microstructure, low RS and high volume fraction of pores (around 1%) have been reported in [13]. Although contour scan parameters were the same for all samples and only contour regions were probed by diffraction (up to 100 µm), the influence of bulk scanning parameters can be observed clearly: A decrease of subsurface RS occurs by decreasing laser velocity (Figure 7b). This confirms that that laser velocity has a larger impact on RS than the presence of support structures. The present results confirm previous studies: The same velocity variation has also been discussed in the case of more complicated sample geometry (bridge-shaped), where a similar tendency was found [8].

3.4. Effect of Power and Hatch Distance Variation

In our previous work [13], we have shown that the formation of the β-phase can be induced by intensified intrinsic heat treatment at 40 µm hatch distance (A1H40) conditions [37,38,39]. In this work a hatch distance of 70 µm (H70) was also evaluated to estimate the sensitivity of RS to hatch distance change. Figure 8a,b show the effect of laser power and hatch variations on RS, respectively. Increasing E_v by a factor of 2 (by increasing laser power) leads to a decrease of RS by about 100 MPa (sample P200 in Figure 8a). Increasing E_v by a factor of 2.5 by decreasing the hatch distance leads to a decrease of RS by more than 400 MPa (sample A1H40 in Figure 8b). This is due to the increased intrinsic laser energy input that also results in the formation of the β-phase [40]. This fact is also proved by diffractograms for P200 (133 J/mm³, Figure 8c) and H70 samples (167 J/mm³, Figure 8d): An increase of intensity of β-{110} peak can be observed for some ψ tilts in the case of H70 sample, indicating some texture in the β-phase (discussed in [40]). In [16], no dependence of RS on E_v was observed for fully dense AISI316L samples. This conclusion is only partially contradictory to ours: the authors of [16] have investigated only a small range of E_v (70 J/mm³–140 J/mm³). Indeed, in our study samples produced with E_v in the same range as [16] display similar RS. By significantly increasing E_v by hatch distance reduction, the RS decreases (Figure 7b) while keeping bulk porosity at a reasonable level [13].

4. Summary

Subsurface residual stresses (RS) were investigated in several LPBF Ti-6Al-4V cuboids by means of X-ray synchrotron diffraction. Since a texture difference between the bulk of the samples and the subsurface region was observed, we investigated the subsurface region (contour region), where the nearly random texture allowed us to use a conventional sin²ψ RS analysis. We also investigated the influences of roughness on subsurface RS measurements of AM parts, since the partially molten attached powder particles at the surface may lead to erroneous results and underestimation of RS. We conclude that additional sample preparation (e.g., sample polishing) or usage of non-destructive high energy X-ray or neutron diffraction is recommended to overcome this effect.

The volumetric energy density E_v, tracked in several process optimization studies, obviously influences the RS state, since it affects the thermal history of the part. We confirmed that an increase of E_v decreases RS, due to an increased intrinsic laser energy input into underlying layers. However, this RS decrease is only visible from a certain threshold value of E_v. This threshold E_v value can lie outside the process window for one of the parameters (such us laser power) and could be reached by varying other parameters (e.g., hatch distance). We showed that other factors (not contained in E_v) may also influence the RS state. For instance, we studied the influence of support structures and orientation of the sample with respect to Ar flow. The use of support structures did not show significant impact on RS for our simple sample geometry. In contrast, the orientation of the sample with respect to Ar flow had a larger impact. The discrepancy between RS at different faces of cuboid can be related to their orientation with respect to the Ar flow direction. Although all these factors cannot be fully tracked/measured in comprehensive design of experiment, it is recommended to consider them when implementing models or creating complex parts.