Study on the Effect of Laser Quenching on Fretting Fatigue Life
Abstract
:1. Introduction
2. Experiments and results
2.1. Specimen Materials
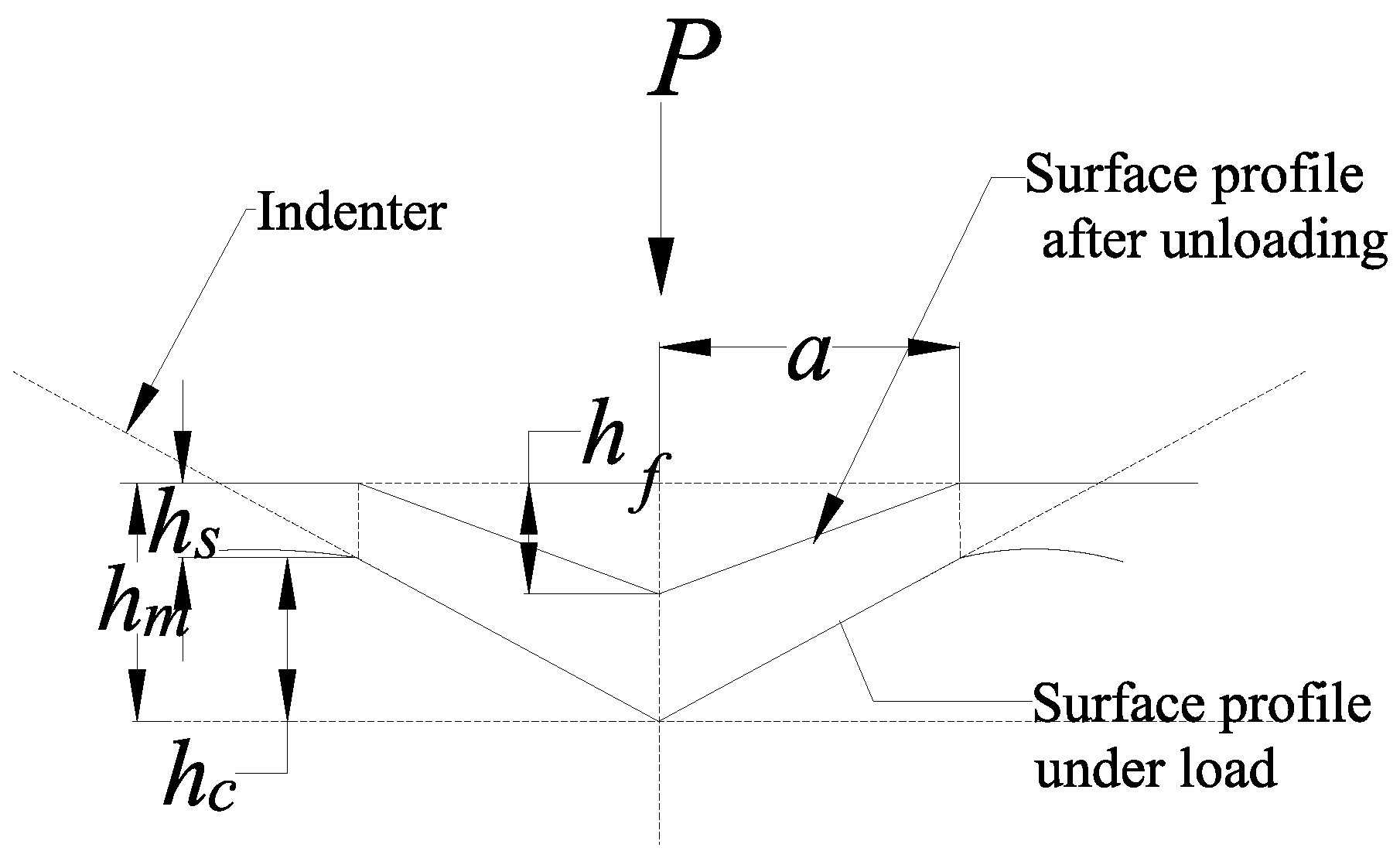
2.2. Hardness of TC11 Alloy after Hardening
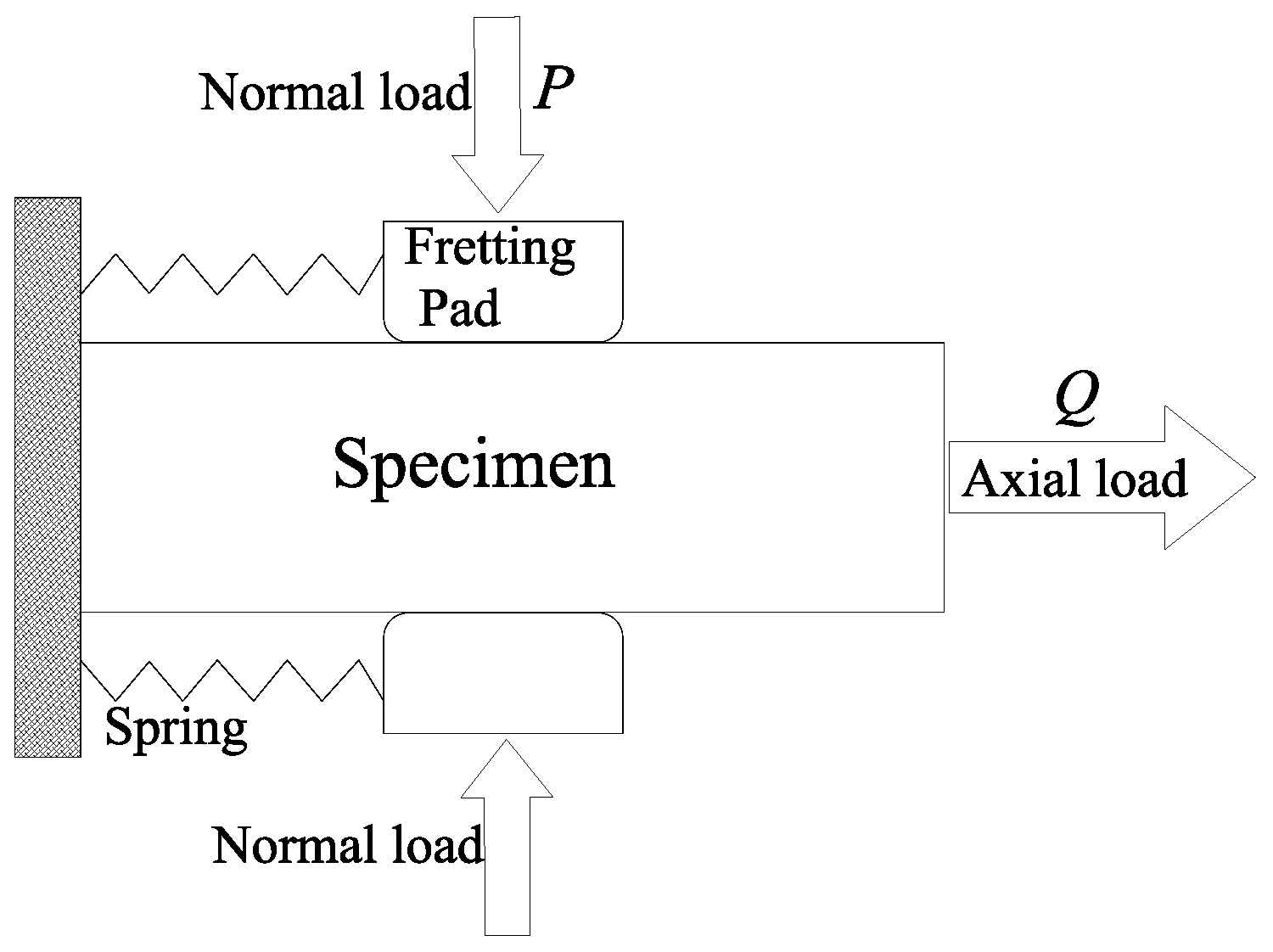
2.3. Fretting Fatigue Test
2.4. Fretting Fatigue Experimental Results
3. The Modified SWT Parameter
4. Simulation and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hills, D.A. Mechanics of fretting fatigue. Wear 1994, 175, 107–113. [Google Scholar] [CrossRef]
- Araújo, J.A.; Nowell, D. The effect of rapidly varying contact stress fields on fretting fatigue. Int. J. Fatigue 2002, 24, 763–775. [Google Scholar] [CrossRef]
- Nesládek, M.; Španiel, M.; Jurenka, J.; Růžička, J.; Kuželka, J. Fretting fatigue—Experimental and numerical approaches. Int. J. Fatigue 2012, 44, 61–73. [Google Scholar] [CrossRef]
- Rajasekaran, R.; Nowell, D. Fretting fatigue in dovetail blade roots: Experiment and analysis. Tribol. Int. 2006, 39, 1277–1285. [Google Scholar] [CrossRef]
- Golden, P.J.; Hutson, A.; Sundaram, V.; Arps, J.H. Effect of surface treatments on fretting fatigue of Ti–6Al–4V. Int. J. Fatigue 2007, 29, 1302–1310. [Google Scholar] [CrossRef]
- Vazquez, J.; Navarro, C.; Dominguez, J. Experimental results in fretting fatigue with shot and laser peened Al 7075-T651 specimens. Int. J. Fatigue 2012, 40, 143–153. [Google Scholar] [CrossRef]
- Srinivasan, S.; Garcia, D.B.; Gean, M.C.; Murthy, H.; Farris, T.N. Fretting fatigue of laser shock peened Ti–6Al–4V. Tribol. Int. 2009, 42, 1324–1329. [Google Scholar] [CrossRef]
- Liu, K.K.; Hill, M.R. The effects of laser peening and shot peening on fretting fatigue in Ti–6Al–4V coupons. Tribol. Int. 2009, 42, 1250–1262. [Google Scholar] [CrossRef]
- Dai, Z.D.; Wang CPan, S. Improving the fretting wear resistance of titanium alloy by laser beam quenching. Wear 1997, 213, 135–139. [Google Scholar] [CrossRef]
- Bhatti, N.A.; Wahab, M.A. Fretting fatigue crack nucleation: A review. Tribol. Int. 2018, 121, 121–138. [Google Scholar] [CrossRef]
- Araujo, J.A.; Nowell, D.; Vivacqua, R.C. The use of multiaxial fatigue models to predict fretting fatigue life of components subjected to different contact stress fields. Fatigue Fract. Eng. Mater. Struct. 2004, 27, 967–978. [Google Scholar] [CrossRef]
- Weber, B. Fatigue Multiaxiale des Structures Industrielles sous Chargement Quelconque [Enligne]. Ph.D. Thesis, Institut National des Sciences Appliquées de Lyon, Lyon, France, 1999. [Google Scholar]
- Romanowicz, P. Numerical assessment of fatigue load capacity of cylindrical crane wheel using multiaxial high-cycle fatigue criteria. Arch. Appl. Mech. 2017, 87, 1707–1726. [Google Scholar] [CrossRef]
- Bernasconi, A.; Filippini, M.; Foletti, S.; Vaudo, D. Multiaxial fatigue of a railway steel under non-proportional loading. Int. J. Fatigue 2006, 28, 663–672. [Google Scholar] [CrossRef]
- Smith, K.; Watson, N.; Topper, P.T. A stress strain function for the fatigue of metals. J. Mater. 1970, 5, 767–778. [Google Scholar]
- Hwang, D.H.; Cho, S. Mean stress effects in fretting fatigue life estimation method using fatigue damage gradient correction factor. J. Mech. Sci. Technol. 2017, 31, 4195–4202. [Google Scholar] [CrossRef]
- Bhatti, N.A.; Pereira, K.; Wahab, M.A. Effect of stress gradient and quadrant averaging on fretting fatigue crack initiation angle and life. Tribol. Int. 2019, 131, 212–221. [Google Scholar] [CrossRef]
- Aeronautical Manufacture Engineering Committee. Aeronautical Manufacture Engineering Handbook; Aerospace Industry Press: Beijing, China, 1997. [Google Scholar]
- Sum, W.S.; Williams, E.J.L. Finite element, critical-plane, fatigue life prediction of simple and complex contact configurations. Int. J. Fatigue 2005, 27, 403–416. [Google Scholar] [CrossRef]
- Bao, Y.W.; Wang, W.; Zhou, Y.C. Investigation of the relationship between elastic modulus and hardness based on depth-sensing indentation measurements. Acta Mater. 2004, 52, 5397–5404. [Google Scholar] [CrossRef]
- Shi, W.; Wen, W.D.; Cui, H.T. Prediction and Analysis on Fretting Fatigue Crack Initiation of Titanium Alloy TC11. Gas Turbine Exp. Res. 2014, 27, 37–40. [Google Scholar]












| Composition | Al | Mo | Zr | Si | Fe | Ti |
|---|---|---|---|---|---|---|
| Percent (wt. %) | 5.8–7.0 | 2.8–3.8 | 0.8–2.0 | 0.15–0.40 | 0.2–0.7 | Bal |
| E(GPa) | (MPa) | (MPa) | (MPa) | (MPa) | ||||
|---|---|---|---|---|---|---|---|---|
| 120 | 0.33 | 540 | 1130 | 854 | 2292 | −0.124 | 0.3584 | −0.692 |
| Series | P (MPa) | Qmax (kN) | Stress Ratio, r | Surface Treatment | Numbers of the Specimens |
|---|---|---|---|---|---|
| 1 | 0.65 | 30 | 0.1 | Laser quenching | 3 |
| 2 | 1.3 | 40 | 0.1 | Laser quenching | 3 |
| 3 | 0.65 | 30 | 0.1 | No treatment | 3 |
| 4 | 1.3 | 40 | 0.1 | No treatment | 3 |
| Load | Series 1 (Laser Quenching) | Series 3 (No Treatment) | ||
|---|---|---|---|---|
| Life (Cycles) | Average Life (Cycles) | Life (Cycles) | Average Life (Cycles) | |
| P = 0.65 MPa Qmax = 30 kN | 71210 | 54808 | 26991 | 26002 |
| 53782 | 23328 | |||
| 39431 | 27687 | |||
| Load | Series 2 (Laser quenching) | Series 4 (No treatment) | ||
| P = 1.3 MPa Qmax = 40 kN | 14605 | 15114 | 14489 | 12856 |
| 16601 | 13587 | |||
| 14135 | 10490 | |||
| Series | Maximum Equivalent Stress (MPa) | Maximum SWT Value (MPa) |
|---|---|---|
| 1 | 535 | 0.4327 |
| 2 | 982 | 0.8343 |
| 3 | 509 | 0.5966 |
| 4 | 917 | 1.3121 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Yang, X.; Cui, H.; Wen, W. Study on the Effect of Laser Quenching on Fretting Fatigue Life. Metals 2019, 9, 566. https://doi.org/10.3390/met9050566
Zhang H, Yang X, Cui H, Wen W. Study on the Effect of Laser Quenching on Fretting Fatigue Life. Metals. 2019; 9(5):566. https://doi.org/10.3390/met9050566
Chicago/Turabian StyleZhang, Hongjian, Xufeng Yang, Haitao Cui, and Weidong Wen. 2019. "Study on the Effect of Laser Quenching on Fretting Fatigue Life" Metals 9, no. 5: 566. https://doi.org/10.3390/met9050566
APA StyleZhang, H., Yang, X., Cui, H., & Wen, W. (2019). Study on the Effect of Laser Quenching on Fretting Fatigue Life. Metals, 9(5), 566. https://doi.org/10.3390/met9050566






