Modeling of Building Energy Consumption by Integrating Regression Analysis and Artificial Neural Network with Data Classification
Abstract
:1. Introduction
2. Methodology
2.1. Building Energy Data Collection and Operating Schedules
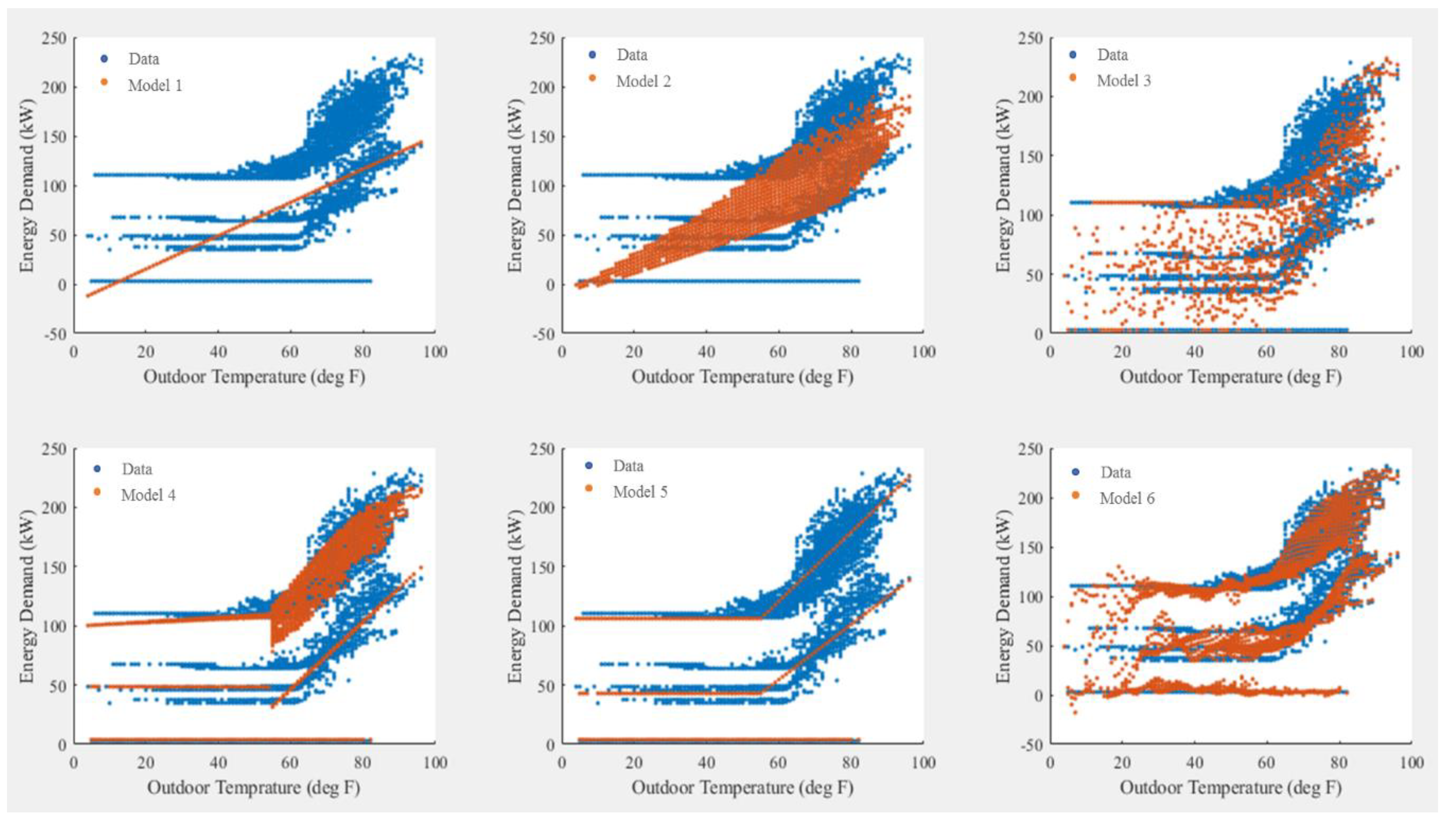
2.2. Building Energy Estimation Models
2.3. Conventional Regression Models
2.4. Data Classification and Proposed Models
2.5. Measurement of Correlation Coefficient r Values
2.6. Measurement of Root Mean Squared Error Values
3. Results
3.1. Energy Consumption of the Buildings and Data Trends
3.2. Training and Testing Data Sets for Models
3.3. Optimization of ANN Model
3.4. Evaluation of Correlation Coefficient r Values
3.5. Evaluation of RMSE Values
3.6. Performance of All Models
4. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- EIA. Consumption & Efficiency—U.S. Energy Information Administration. Available online: https://www.eia.gov/consumption/index.php (accessed on 8 July 2020).
- Zhao, H.; Magoulès, F. A review on the prediction of building energy consumption. Renew. Sustain. Energy Rev. 2012, 16, 3586–3592. [Google Scholar] [CrossRef]
- Yang, J.; Tan, K.K.; Santamouris, M.; Lee, S.E. Building energy consumption raw data forecasting using data cleaning and deep recurrent neural networks. Buildings 2019, 9, 204. [Google Scholar] [CrossRef] [Green Version]
- Fumo, N. A review on the basics of building energy estimation. Renew. Sustain. Energy Rev. 2014, 31, 53–60. [Google Scholar] [CrossRef]
- Runge, J.; Zmeureanu, R. Forecasting energy use in buildings using artificial neural networks: A review. Energies 2019, 12, 3254. [Google Scholar] [CrossRef] [Green Version]
- Lam, J.C.; Wan, K.K.W.; Liu, D.; Tsang, C.L. Multiple regression models for energy use in air-conditioned office buildings in different climates. Energy Convers. Manag. 2010, 51, 2692–2697. [Google Scholar] [CrossRef]
- ASHRAE. ASHRAE Handbook-Applications; American Society of Heating Refrigeration and Air Conditioning Engineers Inc.: Atlanta, GA, USA, 2015; Chapter 41. [Google Scholar]
- Nassif, N. Modeling and optimization of HVAC systems using artificial neural network and genetic algorithm. Build. Simul. 2013, 7, 237–245. [Google Scholar] [CrossRef]
- Seem, J.E. Using intelligent data analysis to detect abnormal energy consumption in buildings. Energy Build. 2007, 39, 52–58. [Google Scholar] [CrossRef]
- ASHRAE. ASHRAE Handbook—Energy Estimating and Modeling Methods; American Society of Heating Refrigeration and Air Conditioning Engineers Inc.: Atlanta, GA, USA, 2009; Chapter 19. [Google Scholar]
- Katipamula, S.; Claridge, D.E. Use of simplified system models to measure retrofit energy savings. J. Sol. Energy Eng. 1993, 115, 57–68. [Google Scholar] [CrossRef]
- ASHRAE. ASHRAE Handbook—Fundamentals; American Society of Heating Refrigeration and Air Conditioning Engineers Inc.: Atlanta, GA, USA, 2013; Chapter 19. [Google Scholar]
- Ji, Y.; Xu, P.; Ye, Y. HVAC terminal hourly end-use disaggregation in commercial buildings with Fourier series model. Energy Build. 2015, 97, 33–46. [Google Scholar] [CrossRef]
- Dhar, A.; Reddy, T.; Claridge, D. Modeling hourly energy use in commercial buildings with Fourier series functional forms. J. Sol. Energy Eng. 1998, 120, 217–223. [Google Scholar] [CrossRef]
- Fumo, N.; Rafe Biswas, M.A. Regression analysis for prediction of residential energy consumption. Renew. Sustain. Energy Rev. 2015, 47, 332–343. [Google Scholar] [CrossRef]
- Nassif, N. Single and multivariate regression models for estimating monthly energy consumption in schools in hot and humid climates. Energy Eng. 2013, 110, 33–54. [Google Scholar] [CrossRef]
- Korolija, I.; Zhang, Y.; Marjanovic-Halburd, L.; Hanby, V.I. Regression models for predicting UK office building energy consumption from heating and cooling demands. Energy Build. 2013, 59, 214–227. [Google Scholar] [CrossRef]
- Stein, J.; Hydeman, M.M. Development and testing of the characteristic curve fan model. ASHRAE Trans. 2004, 110, 347–356. [Google Scholar]
- Hydeman, M.; Webb, N.; Sreedharan, P.; Blanc, S. Development and testing of a reformulated regression-based electric chiller model. ASHRAE Trans. 2002, 108, 1118–1127. [Google Scholar]
- Mat Daut, M.A.; Hassan, M.Y.; Abdullah, H.; Rahman, H.A.; Abdullah, M.P.; Hussin, F. Building electrical energy consumption forecasting analysis using conventional and artificial intelligence methods: A review. Renew. Sustain. Energy Rev. 2017, 70, 1108–1118. [Google Scholar] [CrossRef]
- Chakraborty, D.; Elzarka, H. Advanced machine learning techniques for building performance simulation: A comparative analysis. J. Build. Perform. Simul. 2019, 12, 193–207. [Google Scholar] [CrossRef]
- Mohammadiziazi, R.; Bilec, M.M. Application of machine learning for predicting building energy use at different temporal and spatial resolution under climate change in USA. Buildings 2020, 10, 139. [Google Scholar] [CrossRef]
- Deb, C.; Zhang, F.; Yang, J.; Lee, S.E.; Shah, K.W. A review on time series forecasting techniques for building energy consumption. Renew. Sustain. Energy Rev. 2017, 74, 902–924. [Google Scholar] [CrossRef]
- Seyedzadeh, S.; Rahimian, F.P.; Glesk, I.; Roper, M. Machine learning for estimation of building energy consumption and performance: A review. Vis. Eng. 2018, 6, 5. [Google Scholar] [CrossRef]
- Foucquier, A.; Robert, S.; Suard, F.; Stéphan, L.; Jay, A. State of the art in building modeling and energy performance prediction: A review. Renew. Sustain. Energy Rev. 2013, 23, 272–288. [Google Scholar] [CrossRef] [Green Version]
- Nassif, N.; Arida, M.; Talib, R. Development and testing of building energy model using non-linear auto regression neural networks. In Proceedings of the ASHRAE Annual Conference, St Louis, MO, USA, 25–29 June 2016. [Google Scholar]
- Ekici, B.B.; Aksoy, U.T. Prediction of building energy consumption by using artificial neural networks. Adv. Eng. Softw. 2009, 40, 356–362. [Google Scholar] [CrossRef]
- Kalogirou, S.A. Artificial neural networks in energy applications in buildings. Int. J. Low-Carbon Technol. 2006, 1, 201–216. [Google Scholar] [CrossRef]
- Alam, A.G.; Baek, C.I.; Han, H. Prediction and analysis of building energy efficiency using artificial neural network and design of experiments. Appl. Mech. Mater. 2016, 819, 541–545. [Google Scholar] [CrossRef]
- Yokoyama, R.; Wakui, T.; Satake, R. Prediction of energy demands using neural network with model identification by global optimization. Energy Convers. Manag. 2009, 50, 319–327. [Google Scholar] [CrossRef]
- Ferlito, S.; Atrigna, M.; Graditi, G.; De Vito, S.; Salvato, M.; Buonanno, A.; Di Francia, G. Predictive models for building’s energy consumption: An artificial neural network (ANN) approach. In Proceedings of the 2015 XVIII Aisem Annual Conference, Trento, Italy, 3–5 February 2015; pp. 1–4. [Google Scholar]
- Hong, S.M.; Paterson, G.; Mumovic, D.; Steadman, P. Improved benchmarking comparability for energy consumption in schools. Build. Res. Inf. 2014, 42, 47–61. [Google Scholar] [CrossRef]
- Mena, R.; Rodríguez, F.; Castilla, M.; Arahal, M. A prediction model based on neural networks for the energy consumption of a bioclimatic building. Energy Build. 2014, 82, 142–155. [Google Scholar] [CrossRef]
- Azadeh, A.; Ghaderi, S.F.; Sohrabkhani, S. Annual electricity consumption forecasting by neural network in high energy-consuming industrial sectors. Energy Convers. Manag. 2008, 49, 2272–2278. [Google Scholar] [CrossRef]
- Hou, Z.; Lian, Z.; Yao, Y.; Yuan, X. Cooling-load prediction by the combination of rough set theory and an artificial neural-network-based on data-fusion technique. Appl. Energy 2006, 83, 1033–1046. [Google Scholar] [CrossRef]
- Ben-Nakhi, A.; Mahmoud, M. Energy conservation in buildings through efficient A/C control using neural networks. Appl. Energy 2002, 73, 5–23. [Google Scholar] [CrossRef]
- Nassif, N. Regression and artificial neural network models with data classifications for building energy predictions. ASHRAE Trans. 2018, 124, 52–60. [Google Scholar]
- Magoulès, F.; Zhao, H.; Elizondo, D. Development of an RDP neural network for building energy consumption fault detection and diagnosis. Energy Build. 2013, 62, 133–138. [Google Scholar] [CrossRef]
- Lee, W.Y.; House, J.M.; Kyong, N.H. Subsystem level fault diagnosis of a building’s air-handling unit using general regression neural networks. Appl. Energy 2004, 77, 153–170. [Google Scholar] [CrossRef]
- Hammad, A.W. Minimising the deviation between predicted and actual building performance via use of neural networks and BIM. Buildings 2019, 9, 131. [Google Scholar] [CrossRef] [Green Version]
- Taylor, C. How to Calculate the Correlation Coefficient. Thought Co. 28 January 2020. Available online: https://www.thoughtco.com/how-to-calculate-the-correlation-coefficient-3126228 (accessed on 9 August 2020).
- Stephanie, G. RMSE: Root Mean Square Error. Statistics How To. Available online: https://www.statisticshowto.com/probability-and-statistics/regression-analysis/rmse-root-mean-square-error/ (accessed on 17 October 2020).









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ridwana, I.; Nassif, N.; Choi, W. Modeling of Building Energy Consumption by Integrating Regression Analysis and Artificial Neural Network with Data Classification. Buildings 2020, 10, 198. https://doi.org/10.3390/buildings10110198
Ridwana I, Nassif N, Choi W. Modeling of Building Energy Consumption by Integrating Regression Analysis and Artificial Neural Network with Data Classification. Buildings. 2020; 10(11):198. https://doi.org/10.3390/buildings10110198
Chicago/Turabian StyleRidwana, Iffat, Nabil Nassif, and Wonchang Choi. 2020. "Modeling of Building Energy Consumption by Integrating Regression Analysis and Artificial Neural Network with Data Classification" Buildings 10, no. 11: 198. https://doi.org/10.3390/buildings10110198
APA StyleRidwana, I., Nassif, N., & Choi, W. (2020). Modeling of Building Energy Consumption by Integrating Regression Analysis and Artificial Neural Network with Data Classification. Buildings, 10(11), 198. https://doi.org/10.3390/buildings10110198





