Next Article in Journal
Seismic Acceleration and Displacement Demand Profiles of Non-Structural Elements in Hospital Buildings
Next Article in Special Issue
A Critical Review of Computational Creativity in Built Environment Design
Previous Article in Journal
Suitability of Seismic Isolation for Buildings Founded on Soft Soil. Case Study of a RC Building in Shanghai
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Buildings
Volume 10
Issue 12
10.3390/buildings10120242
buildings-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Creative Decision-Making Processes in Parametric Design

by
Ju Hyun Lee
and
Michael J. Ostwald
*
UNSW Built Environment, The University of New South Wales, Sydney, NSW 2052, Australia
*
Author to whom correspondence should be addressed.
Buildings 2020, 10(12), 242; https://doi.org/10.3390/buildings10120242
Submission received: 24 October 2020 / Revised: 10 December 2020 / Accepted: 12 December 2020 / Published: 15 December 2020
(This article belongs to the Special Issue Design Creativity in Architecture and Engineering)
Browse Figures
Versions Notes

Abstract

:
Decision-making in design is a cognitive process wherein alternatives are generated and evaluated, potentially enabling a more creative design process. In recent years parametric design’s heightened capacity for automatically generating and evaluating options has been celebrated by researchers and designers, but it has also placed an increased emphasis on decision-making activities which have not previously been studied in this context. This paper conducts the first in-depth protocol analysis of the decision-making process (DMP) in parametric design. Using empirical data, it identifies three parametric DMPs at the conceptual design stage: (i) “conclusive” DMP, (ii) “confirmative” DMP, and (iii) “simulative” DMP. The results of this research indicate that while conclusive DMP generates and evaluates design alternatives, its “forward incrementation” approach has only limited potential for creativity. The confirmative DMP develops three creative operation loops in parametric design, suggesting it may be an important creative process. The simulative DMP simultaneously addresses divergent and convergent thinking, also indicating potential creative operations and outcomes. The identification and analysis of these DMPs contributes to developing new knowledge about the processes used in parametric design and their capacity to support creative results.

1. Introduction

The design process involves a continuous series of decision-making activities that collectively shape a final outcome. Decision-making in design entails the processes of generating, evaluating, and determining a solution that satisfies given requirements or criteria. Decision-making is also influenced by a designer’s experience, preferences, and attitudes along with the specific design environment in which the work is undertaken. As such, decision-making in design is a cognitive process with both distinct “operations” and “contexts”. For example, in terms of operations, Jones [1] suggests an ASE (analysis–synthesis–evaluation) framework, while Stempfle and Badke-Schaub [2] identify four cognitive operations (generation, exploration, comparison, and selection) for the analysis of design team processes. Oxman [3], proposes a variation of these, presenting four classes of design operations (representation, generation, evaluation, and performance) for representing the basic cognitive components of both traditional (pen-and-paper) and digital design processes. Each of these models provide useful conceptual descriptions of micro-level decision-making process (DMP) in design. Thus, the DMPs which are the focus of this paper address individual cognitive processes (micro-cognition) wherein a design solution is determined from possible alternatives, potentially supporting creativity. Nonetheless, past research in this field has largely considered intelligent decision support tools [4,5,6], not the role of the DMP in design, or its connection to creativity. This last point, the connection to creativity, has, in recent years, been more closely associated with the context or environment in which design occurs, than to specific operations. This is especially the case with parametric design, a digital design environment which has been both linked to creativity and to more intensive DMPs.
While there are several definitions of parametric design, in this paper it is taken to describe a formative and generative design process using advanced algorithmic scripting of parameters and rules (e.g., Grasshopper™, CATIA™, and Generative Components™) for form-finding [7]. Its capacity to automatically generate multiple compliant solutions to a problem has been linked to creativity, both by way of cognitive patterns and the innovative or novel solutions it produces [8,9]. However, the number of alternatives generated by parametric software, coupled with a dual exploratory interface (geometrical and scripting) that drives constant evaluation, would logically be responsible for increasing the volume of DMPs needed. In other words, parametric design’s automated ideation, visualisation, and testing functions [10], require more frequent and complex DMPs for designers. The cognitive impacts of this are not only of interest in a practical sense, for improving our understanding of this specific design environment, but they have potential implications for creativity. Despite this situation, past cognitive research has not considered decision-making in parametric design. In addition, we do not know how parametric design processes might relate to creativity. Thus, the research question which this paper addresses is, “what kind of DMPs in parametric design can support creativity?” This paper responds to this question by conducting an in-depth analysis of cognitive activities in parametric design and of DMPs involved in solution generation and which have consequences for creative processes. Specifically, this paper reports the results of a protocol study of cognitive processes in parametric design.
This paper commences by reviewing literature on parametric design and decision-making processes and then describes the approach and results of a protocol study of cognitive activities in parametric design. Through a consideration of recursive cognitive patterns before/after a generative activity, this paper identifies three creative DMPs in parametric design: (i) conclusive DMP, (ii) confirmative DMP, and (iii) simulative DMP.

2. Parametric Design Processes

Parametric tools have been widely employed in the design domain over the past two decades, becoming well known for delivering creative or novel works [11,12,13]. From a practical perspective, the most original feature of parametric design is its algorithmic scripting process. While not every parametric operation could be regarded as “design”, the controlled application of parametric scripting (or algorithmic) tools to the generation of solutions to defined problems, has been accepted in recent years as constituting a type of design process: “parametric design”. Each algorithm in this process has two components, “parameter” and “rule”, which can be conceptualised, respectively, as either Roberto’s “variable” and “fixed” attributes [14] or Jones’ [15] “intuitive” and “rational”. From a cognitive perspective, however, they can be understood as serving “divergent” and “convergent” purposes.
In mathematics a parameter describes a range of variation [16], whereas in design, it defines the scope of design possibilities. Since the parameter is pivotal to the generation of design variations, it is often viewed as supporting divergent thinking, which is also closely associated with creativity [12,17]. Certainly, a design may already be heavily predetermined by controlling factors, and some parameters are sufficiently linear and reductive that they do not comply with the type discussed in this paper. Nevertheless, because the parameter defines a range of numeric values, it can produce a range of design alternatives. However, the properties or benefits of generated variations are sometimes too abstract or diffuse and the DMP for selecting a final solution from many hundreds of viable alternatives is a substantial problem for designers [18]. In contrast, a “rule” describes the resultant algorithmic functions as well as the relationships between components when generating variations [19,20]. Thus, rules might be understood as serving a convergent purpose in parametric design. Despite their apparent alignment to divergent and convergent purposes, which are typically mapped to creativity in design thinking, relatively little is known about the actual impacts of parameters and rules on creativity. It may well be that the scripting process is more akin to sketching in traditional design, which can be both an explorative (divergent) and a defining (convergent) process [21,22].
A small number of past studies have examined micro-cognitive processes in parametric design. Yu et al. [8], for example, capture “unexpected discoveries” in parametric design using Gero’s Function-Behaviour-Structure (FBS) coding scheme [23,24], which promotes continuous exploration in the design “solution space”. They also observe that designers often switch between the scripting interface and the geometry modelling interface to examine a model after changing parameters or rules (see Figure 1). The scripting interface enables the composition of visual (e.g., Grasshopper) or textual scripts (e.g., Python and Maya script editor) consisting of algorithmic components that define external geometries. The geometry modelling interface then represents the resultant forms or shapes, usually in the “3D modelling view” mode. These characteristics are also identified in a series of Lee et al.’s protocol studies [7,25,26,27]. The most recent, combining consensual assessment techniques (CAT) with protocol analysis, identifies four parametric design activities (changing parameters, perceiving geometries, introducing algorithmic ideas, and evaluating geometries) that can support creative problem-solving [27]. Results further suggest that “making generation” is critical for creative outcomes, because it reflects two well-known creative design strategies in parametric design, “problem-forwarding generative strategy” and “solution-reflecting generative strategy” [27].
Lee et al.’s [27] results provide two important directions for the present study. First, they identify solution-generating as an essential activity for characterising the generative aspects of parametric design. The present paper also treats generative activity as a core indicator of a DMP in parametric design, because it acts as a connection between divergent and convergent thinking. Second, Lee et al. [27] identify two micro-processes as supporting creativity in parametric design. One is a cyclic design process pattern of “evaluating geometries–introducing algorithmic ideas–changing parameters–evaluating geometries”, which is reminiscent to Jones’ ASE framework. The other is an “evaluating geometries–changing parameters–evaluating geometries” cycle that serves as a “solution-reflecting” activity. In these results, the dual micro-processes are treated as having the capacity to support creativity, because the coding coverages of the identified design activities are consistent with the results of the product-based evaluation of creativity (CAT). Furthermore, these two creative micro-processes highlight the intersection of algorithmic and geometric activities and the co-evolution of modifying parameters and rules. The present paper extends these two ideas through an in-depth protocol study to examine creative DMPs in parametric design.

3. Decision-Making and Creativity

Decision-making is the process of selecting, “a preferred option or a course of actions from among a set of alternatives on the basis of given criteria or strategies” [28] (p.73). Since early research on decision-making was published in game theory and economics [29], hundreds of studies have investigated decision-making across fields as diverse as cognitive science [30,31,32], computer science [33], psychology [34,35,36], business [37,38,39], decision science [40], management science [41], and artificial intelligence [42,43]. In the field of design, decision-making is also a critical topic, although only a few studies have considered it in detail. Vliegen and Mal [44], for example, use rational decision-making to structure a design meeting. They identify three stages in the decision-making cycle, (i) strategy (recognition and diagnosis), (ii) tactics (search, design, judgment, analysis, and review), and (iii) execution (authorisation), for an industrial automation project. They argue that tactics is useful for describing decision-making as part of the process of researching alternatives to select an optimal solution. Nikander and Liikkanen [45] investigate preference in design concept evaluation, advocating for a normative model comprising concept generation, evaluation, and selection. The concept generation process is divergent in nature, while the others are convergent. Ullman [46] also lists six decision-making steps for engineering design—brief decision-makers, delineate issues, identify criteria, generate options, evaluate options, and determine outcome. However, there is little empirical evidence about decision-making processes in design in this past research.
In contrast to the relative paucity of design research about decision making, there are multiple models of, and extensive past research about, the creative process. Wallas [47], for instance, proposes a four-stage creative process model (preparation, incubation, illumination, and verification), while Guilford’s [48] Structure of Intellect (SI) theory identifies five categories of mental operations (cognition, memory, convergent and divergent thinking, and evaluation) from cognitive experiments. Hayes [49] also categorises five cognitive processes in creativity (preparation, goal determination, representation, solution-finding, and revision). In terms of problem and solution spaces, Stempfle and Badke-Schaub [2] present four basic cognitive operations: “generation” and “exploration” for divergence; “comparison” and “selection” for convergence. Significantly, Sternberg [50] considers the development of creativity as a type of decision-making process. His “propulsion model” [50,51] suggests there are eight types of creative contributions: “replication, redefinition, forward incrementation, advance forward incrementation, redirection, reconstruction/redirection, reinitiating, and integration”. These contributions are used to explain the ways creative individuals make creative decisions. Although the propulsion model deals with creative movements of a field from one to another, the eight types of contributions can be employed to capture both micro and macro levels of cognition. That is, compared to the other models, Sternberg’s model not only clearly suggests creative operations, but it is also useful for investigating micro-cognitive DMPs. However, replication and integration only rarely occur in individual micro-cognition. “Advance forward incrementation” and “reinitiating” are also hard to distinguish from “forward incrementation” and “redirection”, respectively, in the laboratory setting. Thus, the present paper adopts four types of creative operations from Sternberg [50] for interpreting results (Table 1).
In summary, past research treats decision-making as a core creative process because it involves generation or modification of alternatives [52]. Furthermore, generating a set of viable solutions or options is itself, potentially a creative act [53]. Importantly, decision-making frequently requires combinations of divergent and convergent thinking and creativity is thought to emerge through the correspondence between the two [54]. Divergent thinking widens the scope of consideration of an issue, adding additional elements, options, and reactions. In contrast, convergent thinking reduces the breadth of possibilities, emphasising potential solutions [27]. The latter involves decision-making strategies for evaluating design alternatives to find the best solution. In this context, the making of a decision (or DMP) is regarded as a creative problem-solving activity. In parametric design, the scripted parameter defines the level of divergence, while the rule defines the required convergence. That is, through the use of algorithms (parameters and rules), which allow for rapid exploration of design alternatives, parametric design supports creativity [7,11,26,55,56].

4. Protocol Study

Protocol analysis is the most widely accepted research method for analysing design processes in detail [57,58]. It develops rigorous and rich results from small numbers of participants in design experiments, typically under laboratory conditions. Although there may be a gap between the results of micro-cognitive (laboratory) and macro-cognitive (naturalistic or real-world) approaches [59,60,61], the micro-cognitive ones provide the most controlled, repeatable, and consistent basis for studying and understanding designers’ DMPs. Furthermore, starting with a micro level pilot study of cognitive mechanisms underlying the creative process [62] provides a foundation for developing complementary results from macro-scale settings [63]. Thus, for this first study of this topic, a controlled laboratory setting is preferable [64].

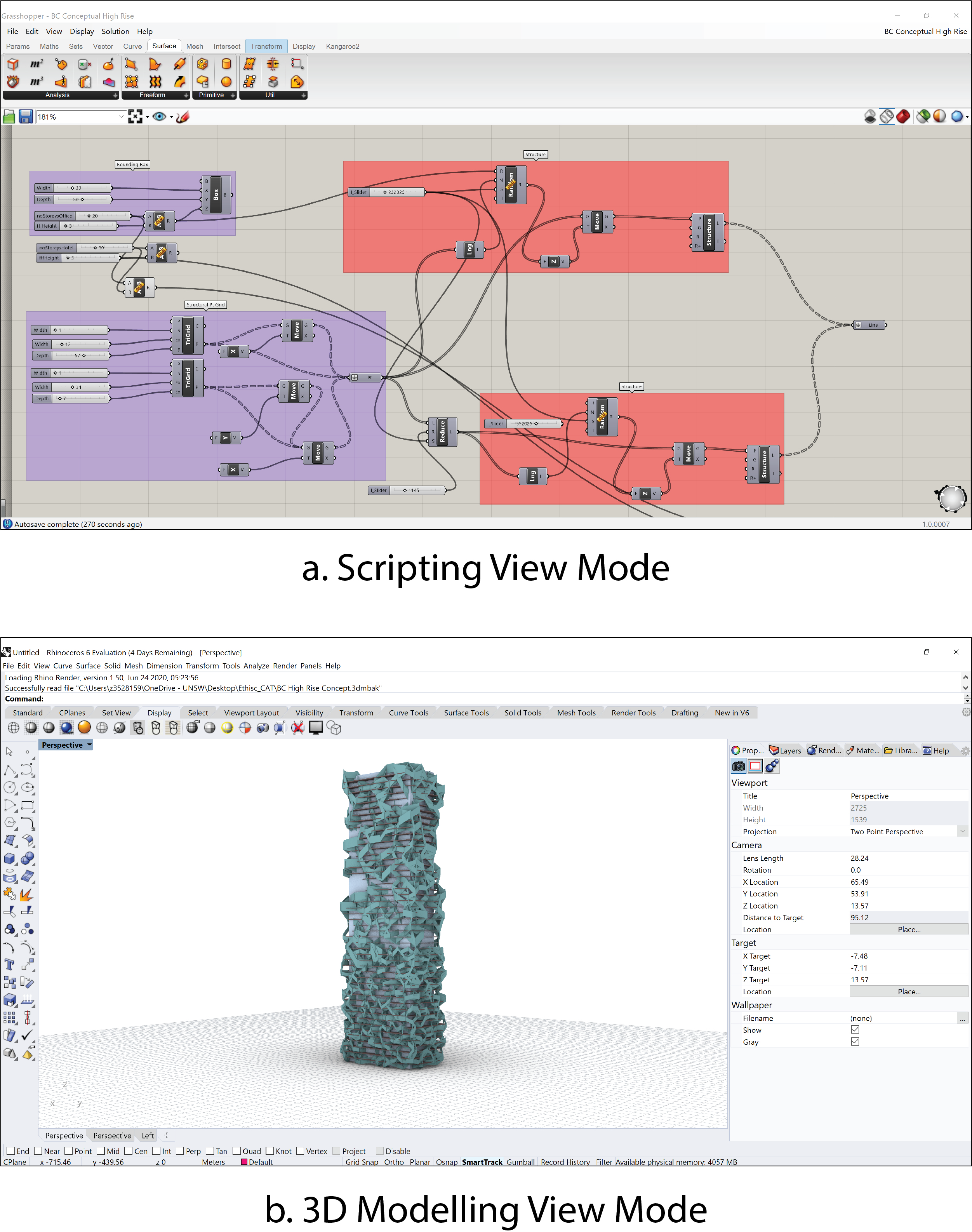
4.1. Research Procedure

Postgraduate architectural students, each with experience in parametric design, were recruited for the experiment. In order to explore DMPs in parametric design, six architectural designers—two with over five years’ parametric design experience (A, C) and the others with one year of experience (B, D, E, F)—participated in a design experiment. The designers were asked to work for approximately one hour to complete a concept design task for a high-rise building. However, taking into account the need for trouble-shooting scripts, and processing and rendering delays, the actual time taken varied. Participants were asked to accommodate five requirements in their concept designs: (a) two main functional types, office, and hotel; (b) a maximum floor area of 2500 square metres per floor; (c) the height is over 40 stories; (d) visually reflect structural forces using external data, and (e) intended to form a regional landmark.
The designers were given a free choice of parametric modelling tools. Four (A, B, E, F) selected graphical algorithm editors (Grasshopper) and two (C, D) selected text-based editors (Python and Maya script editor, respectively). All six used Rhinoceros 3D for visualising the geometric outputs of their algorithms. While their experiments were being videorecorded, designers were asked to “think aloud” and these thoughts were recorded and transcribed as a concurrent protocol. Before the experiments commenced, the participants practiced thinking aloud, and upon completion of the experiment, they took part in an interview (retrospective protocol) wherein they had an opportunity to elucidate any activities or thought processes that occurred during the experiments.
Design sessions were transcribed using NVivo software and then segmented into episodes. Each segment comprises something that changes a design (a step, an act, or an operation) [27,65] and which is encoded using a pre-defined scheme (Table 2). From the creative process models discussed in the third section, five categories (goal setting, representation, generation, evaluation, and revision) are suggested. Hayes’ five creative acts [49] are mainly used for the categorisation because they were developed to explore cognitive processes in creativity. However, there is no Hayes’ “preparation” act, but “generation” and “evaluation” categories are closely related to Hayes’ “searching for solution” act. Two subcategories (geometry and algorithm) are used to identify geometric and algorithmic modes in parametric designing. Lee et al.’s [27] coding scheme considers both geometric and algorithmic modes and three categories of conceptual activities (problem-finding, solution-generating, and solution-evaluating). Their categorisation and subclasses are selectively adopted in the present paper to develop the coding scheme for exploring creative DMPs (Table 2). Geometric modes represent the direct modelling processes for generating digital form and shape on the 3D modelling interface, while algorithmic modes encapsulate the generative processes that define the parameters and rules on the scripting interface. The generation category has no subcategory and only one code “G” that combines both geometric and algorithmic behaviours to generate one or more alternative(s).
To ensure consistency and validity of the results, the final protocol data was confirmed using an arbitration process. There were two rounds of encoding processes. In the first round two researchers who had professional experience in both cognitive research and protocol analysis transcribed, segmented, and encoded the data. In the second, and after a three-month interval, a post-doc fellow in design computing and cognition, conducted the encoding process. Table 3 presents the results of time duration, segmentation, and intercoder reliability of each protocol. Designers were given a notional one-hour timeframe to complete the design task, but they could continue beyond this if required. As a result, the average time duration of the design protocol was 76 min 20.8 s. The average number of segments was 309.0 (A: 220, B: 319, C: 364, D: 287, E: 360, F: 303) and the average time per segment was 14.8 s. With one exception (B), over 90% of each protocol was encoded using the coding scheme, regardless of the two types of applications, graphical algorithm editor (A, B, E, F) or text-based algorithm editor (C, D). On average, 92.2% of segments were encoded in the coding scheme, which confirms that it effectively captures the set of parametric design activities. Furthermore, the average percent agreement satisfies the target of 80%. Specifically, Krippendorff’s α values, which are used for measuring intercoder reliability seek results were α ≥ 0.800 [66,67]. Thus, these measures indicate the reliability of the coding results.
Three designers (A, E, F) completed the experiment in the recommended time. For the other three, additional time was taken up by troubleshooting or waiting for generative or visualisation processes to be completed. Although the participants had experience in parametric design, scripting is still a challenge for designers. Furthermore, visual scripting is typically much easier than textual scripting, and thus B had the smallest percentage of encoded segments (86.8%), spending non-encoded time for trouble-shooting software, or searching for and arranging rules. However, since this research undertakes an in-depth analysis of micro-cognitive activities and the sequential transitions of encoded segments, the different lengths of protocols and/or non-encoded segments have little impact on the results. Figure 2 illustrates of the high-rise building concept designs generated by the participants.

4.2. Coding Results

Because the length of each design protocol varies, to construct a comparison the results presented here refer to the percentage of the frequency, weighted by time duration of each code (Figure 3). This normalisation provides the capacity to compare the time devoted to each design process, category for each designer. On average, evaluation behaviours dominate the parametric design process, accounting for 39.0% (geometry: 17.4%, algorithm: 21.6%). Since parametric design develops geometric forms and shapes using algorithms, their visual outcomes may be unpredictable and designers regularly evaluate this in both the 3D modelling view and the scripting view [7,27]. This switching between views pattern is closely related to “creative micro-processes” [27] and “co-evolutionary processes” between design spaces and modes [27,68]. The next most frequent category is representation, which accounts for 26.7% (geometry: 2.4%, algorithm: 24.3%) and revision is the third. Algorithmic representations and revisions could be an ideal mode for undertaking parametric design, producing parameters and/or rules and then varying them, which might be akin to the traditional design process in a pen-and-paper environment.
These results illuminate several differences between the designers, including the fact that five tended to create new algorithms (RA) rather than revising existing ones (RVA), while designer D spent more time on algorithmic revision (27.9%). The average time of coded segments of D’s protocol was the highest, although D’s “goal setting” activities were of a lower magnitude. These results are consistent with a “trial-and-error design procedure” or a “novice problem-solver” profile, suggesting a person who lacks advanced analytical strategies or skills. C, who was more experienced, also employed both trial-and-error and “backward reasoning”, but his generative synthesis (G) was higher than the others. In contrast, designers who used the graphical editors (A, B, E, F) were more likely to record geometric modes in the goal setting and representation categories, than those using text-based scripting (C, D). Acknowledging the very small sample size, the graphical editor is likely to lead to more geometry-based modes.
Designer A, who was also one of the more experienced, applied well-organized, step-by-step rules from the initial problem space (goal setting), producing the second highest values of both GSG as well as G among the six designers. This design strategy is an example of a “problem-forwarding generative strategy”, which divides the “initial goals (ideas) into both geometric and algorithmic goals and then synthesising them with step-by-step generations to reach an overarching solution” [27] (p. 64). In contrast, the other experienced designer C, demonstrated increased proportions of generative and evaluation activities (at the algorithm level). C’s strategy, using the highest frequency coverage of G, may have provided an advantage in generating creative design variations, which is followed by co-evolutionary revision activities. Importantly, a generation-oriented strategy like this has been linked to creative outcomes [7,69].

4.3. Decision-Making Patterns

Divergent thinking in parametric design is closely related to the generation of design alternatives, i.e., G with decision-making activities arising from this activity. Previous decision-making research in design identifies “generation” as a functional precursor to evaluation or selection [45,46]. In this context, the results of this paper highlight the use of design activities around G to identify creative DMPs in parametric design. Theoretically, a sequential pattern, Goal Setting–Representation–Generation–Evaluation–Revision (e.g., GSG–RA–G–EG–RVA), might be expected, although an in-depth protocol study of the type undertaken in this paper, can capture additional significant DMP patterns. To analyse the patterns of sequences of cognitive activities around decision-making, a pair of segments preceding and following each segment encoded as G in a protocol were analysed to identify patterns in sequential relationships. If two segments are encoded by the same code, one more segment is investigated. There are 111 decision-making activities including G across the six protocols (A: 4, B: 4, C: 55, D: 20, E: 19, F: 9). Interestingly, these decision-making activities in the parametric design can be categorised into three significant decision-making patterns, (i) conclusive, (ii) confirmative and (ii) simulative activities. Table 4 describes the sequential patterns of the decision-making activities. Major patterns are originally developed from patterns having greater than or equal to three occurrences, while the simulative considers patterns which occurred twice, due to its limited recurrence.
The first type of DMP pattern, conclusive, looks like the traditional decision-making process that selects an optimal solution among alternatives, but this process, interestingly, tends to conclude by introducing geometric ideas (GSG). In addition to this pattern, four designers concluded their sessions with conclusive decision-making patterns. In this case, G is followed only by EG and/or EA. Twenty conclusive patterns were observed in the design experiments and there were two recursive patterns, EA–RVA–G–EG–GSG (f = 4) and G–EG–G–EG–GSG (f = 3) in Table 4. EG–RVA–G–EG–GSG (starting with “evaluating geometries”) which follows a similar pattern to the first, also occurred twice. Thus, EA or EG–RVA–G–EG–GSG would be the major conclusive decision-making pattern, which is partly supported by a cyclic pattern, G–EG–G.
The confirmative pattern of decision making involves revisiting an idea (or algorithm) to validate that it fulfils the chosen criteria. In parametric design it is the dominant DMP, closely related to EG, wherein the designer visually evaluates the outcome of algorithms (Figure 3). EA also frequently follows EG in the protocol data for the validation of design algorithms in the confirmative DMP (Table 4). In total, 74 instances of the confirmative pattern occurred in the protocols, with the two designers (C, D) producing more confirmative patterns, 49 and 15, respectively, because of a cognitive gap between the development of algorithms and their capacity to visualise the results. That is, these designers had to more frequently produce EG and EA after G, to confirm their algorithms (or scripts). This pattern may also be related to their trouble-shooting processes because another designer, who also had difficulty with his algorithms, produced three confirmative instances out of the four decision-making patterns in his design session. As a result, designers have developed three decision-making patterns, EA–RVA–G–EG–EA (f = 9), EG–EA–G–EG–EA (f = 4), and EA–RVA–G–G–EG (f = 3).
The simulative DMP, which involves both generation and selection during G, was frequently adopted by the designers using graphical algorithm editors. In their design sessions, design alternatives were simultaneously generated using a number slider system with a range of values. In this way, parameters support activities that enable divergence in design and generation of variations. Unlike the other patterns, the simulative DMP is not followed by EG, because designers had already examined their algorithms during G. Thus, it is frequently followed by algorithmic revision. Despite this, no strong patterns were observed. Nonetheless, the simulative process potentially supports creative design processes because its generative behaviour clearly develops both divergent and convergent thinking at the same time. The next section illustrates the three decision-making patterns in creative DMPs in parametric design

5. Creative DMPs in Parametric Design

Decision-making in design is typically defined as the process of generating alternatives and selecting one as the final outcome. Thus, with some variations, most DMP models in design involve a simple pair of generation and evaluation activities [1,3]. The present paper extends this way of looking at DMPs to a micro level, where specific sequences of activities which make up a DMP are identified. Following past research [27] into creative micro-processes in design, this paper identifies three creative DMPs in parametric design, (i) conclusive, (ii) confirmative, and (ii) simulative.

5.1. Conclusive DMP

In the conclusive DMP, designers confirm that generated alternatives meet the given design criteria or requirements. This DMP enables finalising the current design task and progressing to the next design goal or step. The primary version of this pattern, EA–RVA–G–EG–GSG (Table 4; Figure 4), starts by “evaluating geometries” or “evaluating algorithms” before “revising algorithms” triggers the generative activity. Sequentially, designers evaluate the visualised alternatives in the 3D view mode, deciding if the solutions meet the intended design goals. The iterative sequences of activities echo Stempfle’s and Badke-Schaub’s “process 1”, which entails a series of solution ideas leading to evaluation [2]. If the conditions are satisfied, the designer continues by “working forward”, frequently introducing new geometric goals or ideas, i.e., G–EG–GSG. In addition, the conclusive DMP tends to occur at the completion of the design session, with selecting an overarching solution.
The conclusive DMP may be a core part of the classic working forward problem-solving techniques, “hill climbing” and “divide-and-conquer”, setting up detailed and directed goals before developing solutions. It typically includes the setting of sub-goals and segmentation or decomposition of problems, and then solves sub-goals through a staged, iterative “step-by-step” process, before initiating a solution. In this context, the conclusive DMP is clearly part of the problem-forwarding generative strategy that supports creativity in parametric design [27]. Moreover, it also leads to “forward incrementation”, which is a creative DMP operation (Table 1) in parametric design. If the solution is not satisfied, the conclusive DMP may be able to undertake a cyclic redefinition process, G–EG–G, but this additional process is more closely related to the other two creative DMPs.

5.2. Confirmative DMP

The confirmative DMP is associated with staged decision making and is strongly related to algorithmic revision (RVA) and generative activities (Table 4). While the conclusive DMP can also be associated with revision activities, this happened only as a precursor to making generation (see Figure 4). In contrast, the confirmative DMP continues to examine geometries or algorithms, or more revision or generation activities, before or after decision-making. Based on the micro-pattern, EA–RVA–G–EG–EA (Table 4), the DMP process in Figure 5 starts by evaluating algorithms and then revising algorithms triggers the generative activity. Sequentially, designers evaluate the outcome of the revised algorithms in the 3D view mode, deciding if they are properly developed to represent intended geometries. Although the outcome may be satisfied, the designers then introduce new algorithmic goals (GSA) or algorithms (RA), redirecting the search for decisions to the solution space. This differs from the conclusive DMP which moves forwards to introducing new geometric goals GSG. However, this creative operation (“redirection”) is not one of the most common patterns. Table 4 indicates that the major confirmative DMP pattern is related to working backward problem-solving techniques, including “trial and error”, “solution-reflecting”, or “backward reasoning” [7,27,70]. There are three major processes, G–EG–EA (f = 33), G–EG–RVA (f = 23) and G–EG–G (f = 8), after the confirmative decision-making in Table 4.
The micro-pattern G–EG–EA is also frequently followed by EA–RVA–G, which is also the most common before the confirmative. That is a cyclic pattern (e.g., EA–RVA–G–EG–EA) of evaluating algorithms, revising algorithms, making generation, evaluating geometries, and then again evaluating algorithms. This process is akin to the reconstruction operation, returning the “field” to its original position, and then moving it in a new direction. In contrast, G–EG–RVA and G–EG–G develop the short cyclic patterns in Figure 5, suggesting a rapid change or redefinition. These creative operations might be related to Nikander and Liikkanen’s argument that concept rejection can lead to revision or new generation phases [52]. Collectively, the confirmative DMP involves three creative operations, redirection, reconstruction, and redefinition, based on solution-reflecting activities.

5.3. Simulative DMP

The simulative DMP is a variation of the confirmative DMP wherein the integrated activity of generation, evaluation and selection is followed by a revising activity (RVA). The protocol data pertaining to this trend is not, however, as strong as the other DMPs and there is no dominant micro-pattern. Nonetheless, unlike the other DMPs, the simulative DMP has a unique decision-making process that involves both divergent and convergent thinking concurrently. Once again, in contrast to Nikander’s and Liikkanen’s sequential generation, evaluation, and selection [45] process, in the simulative DMP they happen at the same time. Indeed, the generative activity is the decision-making activity in this type. Based on the data in Table 4, the simulative DMP can be illustrated with only one cyclic pattern (Figure 6), combining RVA–EG–G and G–RVA–EG. Thus, the simulative DMP has one creative operation (reconstruction), which is identically observed in the confirmative DMP. Although the cyclic pattern may be the only major pattern, Figure 6 suggests two more minor patterns that can contribute to the development of creative operations in this specific DMP—see the possible flows in Figure 6. After the decision-making, designers can move into an alternative revision process (revising algorithm 2 in Figure 6), which promotes redefinition—see also G–RVA–G in Table 4. If designers think they have found appropriate solutions, then the process may follow a G–GSA pattern, relating to redirection. Thus, the simulative DMP potentially suggests two more creative operations.

6. Discussion

6.1. Creative DMPs in Sketching, Computer-Aided Design, and Parametric Design

Traditionally, sketching has been linked to creativity, because it often supports the restructuring of a problem, through its flexible and intuitive application [71,72]. There is an assumption that in a co-evolutionary sketching processes there will more implicit/explicit decisions that facilitate most of subprocesses seen in creative process models [73]. In contrast, conventional computer-aided design (CAD) is regarded as an inhibitor to creativity because it has limited innate potential to support problem-solving [74]. Haapasalo [75], for example, states CAD interfaces are inflexible in sketching and there is a weak connection between the hand and the drawings on the screen. Whilst many researchers have tried to address this user interface barrier to intuitive designing [76], CAD has become largely accepted as a documentation tool, enabling routine tasks and recording final decisions. As such, investment in cognitive effort in CAD could hinder creativity in the design process. Interestingly, parametric design, although it requires an additional scripting interface, appears to involve creative problem-solving activities [7]. This perception might be caused by the fact that parametric design is not only enabling the generative capacity, but also supporting the restructuring of components [72] and regulating elements into an overall solution [77]. In addition, non-routine patterns of decisions, (e.g., leap, loop, and cycle) described in Badke-Schaub and Gehrlicher’s work [78] are often found in parametric design.
Decision-making in design used to be regarded as a conclusive activity, separate from problem-solving [78,79], where the final solution is selected from generated alternatives. In contrast, the three creative DMPs uncovered in the protocol data in this paper highlight the significance of step-by-step problem-forwarding, as well as revisiting generative components in parametric design. That is, decision-making is not one step in problem-solving, but a process. In particular, solution-reflecting activities result in three cyclic operations, redirection, reconstruction, and redefinition, which support creativity in the DMPs. This finding offers an unexpected new understanding of creative DMPs in parametric design.
The conclusive and simulative DMPs identified in this paper can also be used to conceptualise decision-making patterns that involve additional analytic tools or plug-ins. However, parametric design processes are frequently combined with various design analysis and simulation stages that support decision-making in practice [4,5,6]. Moreover, designers in parametric environments sometimes, use traditional design tools like pen-and-pencil, to explore visual representations at the conceptual design stage. These switching behaviours could lead to important creative DMPs, which the present paper will not capture, because the experiment required designers to work with an algorithm editor and 3D modelling tool. Nonetheless, the coding scheme exploring creative DMPs in this study is useful for capturing both algorithmic and geometric modes and their repetitive processes in parametric design environments. Chusllp and Jin’s three iterations (problem redefinition, idea stimulation, and concept reuse loops) in the traditional design environment [80] also help to conceptualise these DMPs in mixed design environments. In particular, the “problem redefinition loop” enables us to research decision-making activities in the problem space as well as “co-evolution” (e.g., “problem leads to solution” and “solution refocusses the problem” [68]).
Despite these new findings, there are several limitations to the approach taken in this paper. For example, this study considers only four creative operations from the eight creative contributions identified in Sternberg’s propulsion model [50]. That is, the other creative operations, such as replication and integration may be able to develop additional creative DMPs. Computational models of creative design processes (combination, transformation, analogy, emergence, and first principles) [81,82], can also be regarded as creative operations. Furthermore, parametric design involves different mental imagery and external representation from the other design processes (sketching and CAD). Thus, the 5R’s Model of sensational thinking (readiness, reception, reflection, revelation, and recreation) [83] can be applied to identify particular decision-making patterns in parametric design. However, these creative processes cannot be captured in the coding scheme in this paper. To explore these additional creative DMPs in parametric design requires additional coding schemes as well as different experimental settings. Collectively, the creative DMPs presented in this paper are limited to exploring individual conceptual parametric design processes.

6.2. Creative DMPs in Teamwork and Macro-Cognitive Approaches

While this paper only deals with individual DMPs in conceptual parametric design, they are reminiscent of DMPs in design collaboration. For example, Stempfle’s and Badke-Schaub’s “process 1” not only involves a conclusive DMP, but also supports both confirmative and simulative DMPs in terms of their redefinition operation. However, the combination of analysis and evaluation ideas, process 2, proposed by their study is not captured in the present research in any detail. This may be because the experiments in this paper have a well-defined design problem space and the project complexity was also limited. That is, the three DMPs in parametric design would be better applied to simple, well-defined problems at the conceptual design stage. Wong and Siu [84] also highlight the non-liner and the loop-back processes in the creative design process model of analysis-generation-evaluation. They identify three variations of the model, considering divergent and convergent thinking processes at the analysis (information) and/or evaluation (decision) state. There are also two looping-back routes that foster creativity at synthesis and evaluation. These features are similar to redefinition and redirection operations in our confirmative and simulative DMPs. In this way, the convergent and circular processes of Wong’ and Siu’s model can be applied to understand creative decision-making in individual design processes. As another interesting application of Jones’ ASE framework, Martinec [85] presents a cycle of synthesis and evaluation for innovative design that can lead to new problem entities. Martinec also highlights implicit decomposition (problem) strategies emerging through the innovative conceptual design processes, but the analysis state appears only in the adaptive design. Ensici et al. [86] further investigate the decision-making components in design teamwork, identifying used and rejected decisions as well as iterations between the components. Considering problem-solving phases, they present seven decision-making components (goal, knowledge, alternative, criterion, idea development, solution, and decision) and then explore decision topics during three design phases (conceptual, preliminary, and detail). Furthermore, rejected decisions in their study not only narrow the solution space, but also decrease the complexity of the problem space. Thus, their model could be used for a follow-up study, building on the work in the present paper, on DMPs in problem space. The analysis activities are rarely captured in individual laboratory experiments with simple design problems, while decision-making as a creative thinking process at the analysis stage should be considered in the context of design education and practice. Consequently, although the present research does not cover all the components and design phases of Ensici et al.’s model, individual DMPs in this paper can be useful for understanding many of micro-decisions that occur in design collaboration involving various types of designers as well as their innate psychological creativities (see Boden’s “P-creativity” [87]).
A final limitation with the present research is that a micro-cognition approach was chosen [2], and a macro-cognition approach could identify different patterns, and perhaps with a higher level of confidence, but also at the expense of adding substantial confounding factors. For example, Jensen and Ahmed-Kristensen [88] found that iterative and jumping processes are micro level patterns of the decision meeting, while they view a macro level pattern as a complex process in three problem-solving phases: criteria phase, conceptualisation phase, and selection phase. Klein et al. [40] argue that naturalistic decision-making has four features: the conditions are (i) dynamic and evolving, (ii) occurring in real-time, (iii) the goals are ill-defined, and the tasks are ill-structured, and (iv) expert users are involved. Thus, decision-making needs to consider complex sociotechnical contexts as well as cognitive operations [60]. In contrast, a micro-cognitive approach treats, “decision-making as an ingredient of control processes, either manual or supervisory, in man-machine systems” [59] (p. 331). Importantly, micro-cognition and macro-cognition are complementary, although the latter is closer to naturalistic decision-making [64]. Obviously, micro-cognitive decision-making can also be scaled-up to macro-cognition [89]. Taking an information-processing approach, for example, Cacciabue and Hollnagel [90] indicate that micro-cognition is useful for investigating how cognition takes place in the human mind. In this way, the present study has extended the tradition of experimental decision-making research into the field of design, where designers always deal with ill-defined goals and ill-structured tasks even in the artificial settings. As such, this research fundamentally addresses micro-cognitive deign processes which can be scaled to consider aspects of macro-cognitive design processes.

7. Conclusions

This paper has presented a detailed investigation of parametric design activities and illustrated three distinct creative DMPs, (i) conclusive, (ii) confirmative, and (iii) simulative DMPs, in the concept stage of a design. Through a rigorous protocol study, this paper has not only correlated creative DMP flowcharts with empirical evidence, but also conducted the first study into the development of creative DMPs using recursive decision-making patterns in design. Whilst the sample size of this study might be limited, the in-depth protocol analysis has enabled the identification of creative DMPs as well as four creative operations among a hundred of sequential processes, including solution generation in the study. The findings may be expanded to illuminate other parametric design processes supporting creativity. Moreover, the cyclic patterns of operations involving geometric and algorithmic modes have the potential to support “unexpected discoveries” and also mixed design representations at decision-making moments, and through these, support heightened creativity
As discussed, the results of any study under laboratory conditions cannot perfectly model all designers’ macro-cognitive activities or individual idiosyncrasies. The findings are also unintentionally inclined towards solution-oriented activities because the study addresses DMPs which generate solution. For this reason, a study of decision-making patterns in the problem space would be valuable follow-up study. In addition, a few computational models could also be used for further identification of creative DMPs in parametric design. Nevertheless, this paper contributes to new knowledge about the ways designers make decisions in parametric environments, and how such DMPs contribute to creative operations in design

Author Contributions

Data curation, J.H.L.; Formal analysis, M.J.O.; Investigation, M.J.O.; Methodology, J.H.L.; Writing–original draft, J.H.L.; Writing–review & editing, M.J.O. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Jones, J.C. A Method of Systematic Design. In Conference on Design Methods; Jones, J.C., Thornley, D.G., Eds.; Pergamon Press: Oxford, UK, 1963; pp. 53–73. [Google Scholar]
  2. Stempfle, J.; Badke-Schaub, P. Thinking in design teams—An analysis of team communication. Des. Stud. 2002, 23, 473–496. [Google Scholar] [CrossRef]
  3. Oxman, R. Digital architecture as a challenge for design pedagogy: Theory, knowledge, models and medium. Des. Stud. 2008, 29, 99–120. [Google Scholar] [CrossRef]
  4. Ochoa, C.E.; Capeluto, I.G. Strategic decision-making for intelligent buildings: Comparative impact of passive design strategies and active features in a hot climate. Build. Environ. 2008, 43, 1829–1839. [Google Scholar] [CrossRef]
  5. Chan, F.T.S.; Jiang, B.; Tang, N.K.H. The development of intelligent decision support tools to aid the design of flexible manufacturing systems. Int. J. Prod. Econ. 2000, 65, 73–84. [Google Scholar] [CrossRef]
  6. Hopfe, C.J.; Augenbroe, G.L.M.; Hensen, J.L.M. Multi-criteria decision making under uncertainty in building performance assessment. Build. Environ. 2013, 69, 81–90. [Google Scholar] [CrossRef] [Green Version]
  7. Holzer, D.; Hough, R.; Burry, M. Parametric Design and Structural Optimisation for Early Design Exploration. Int. J. Archit. Comput. 2007, 5, 625–643. [Google Scholar] [CrossRef]
  8. Lee, J.H.; Gu, N.; Ostwald, M.J. Creativity and parametric design? Comparing designer’s cognitive approaches with assessed levels of creativity. Int. J. Des. Creat. Innov. 2015, 3, 78–94. [Google Scholar] [CrossRef]
  9. Yu, R.; Gu, N.; Lee, J.H. Comparing designers’ behavior in responding to unexpected discoveries in parametric design environments and geometry modeling environments. Int. J. Archit. Comput. 2013, 11, 393–414. [Google Scholar] [CrossRef]
  10. Woodbury, R. Elements of Parametric Design; Routledge: London, UK; New York, NY, USA, 2010. [Google Scholar]
  11. Blosiu, J.O. Use of Synectics as An Idea Seeding Technique to Enhance Design Creativity. In Proceedings of the Systems, Man, and Cybernetics IEEE SMC 99 Conference Proceedings, Tokyo, Japan, 12–15 October 1999; Volume 1003, pp. 1001–1006. [Google Scholar]
  12. Iordanova, I. Teaching Digital Design Exploration: Form Follows. Int. J. Archit. Comput. 2007, 5, 685–702. [Google Scholar] [CrossRef]
  13. Iordanova, I.; Tidafi, T.; Guité, M.; Paoli, G.D.; Lachapelle, J. Parametric methods of exploration and creativity during architectural design: A Case study in the design studio. In Proceedings of the 13th International Conference, Montreal, QC, Canada, 17–19 June 2009; pp. 423–439. [Google Scholar]
  14. Barrios Hernandez, C.R. Thinking parametric design: Introducing parametric Gaudi. Des. Stud. 2006, 27, 309–324. [Google Scholar] [CrossRef]
  15. Jones, J.C. Design Methods; John Wiley & Sons Inc.: New York, NY, USA, 1992. [Google Scholar]
  16. Cardenas, C.A. Modeling Strategies: Parametric Design for Fabrication in Architectural Practice; Harvard University: Cambridge, NJ, USA, 2008. [Google Scholar]
  17. Kolarevic, B. (Ed.) Architecture in the Digital Age: Design and Manufacturing; Spon Press-Taylor & Francis Group: New York, NY, USA; London, UK, 2003. [Google Scholar]
  18. Hanna, S.; Turner, A. Teaching Parametric Design in Code and Construction. In Proceedings of the SiGraDi2006/Educacion y Desarrollo Academico, Santiago, Chile, 21–23 November 2006; pp. 158–161. [Google Scholar]
  19. Sutherland, I.E. Sketch pad: A man-machine graphical communication system. In Proceedings of the AFIPS Spring Joint Computer Conference, Detroit, MI, USA, 21–23 May 1963; pp. 329–346. [Google Scholar]
  20. Lee, J.Y.; Kim, K. Geometric reasoning for knowledge-based parametric design using graph representation. Comput. Aided Des. 1996, 28, 831–841. [Google Scholar] [CrossRef]
  21. Salim, F.; Burry, J. Software Openness: Evaluating Parameters of Parametric Modeling Tools to Support Creativity and Multidisciplinary Design Integration. In Computational Science and Its Applications—ICCSA 2010; Taniar, D., Gervasi, O., Murgante, B., Pardede, E., Apduhan, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6018, pp. 483–497. [Google Scholar]
  22. Burry, M. Scripting Cultures: Architectural Design and Programming; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
  23. Gero, J.S.; Neill, T.M. An approach to the analysis of design protocols. Des. Stud. 1998, 19, 21–61. [Google Scholar] [CrossRef]
  24. Gero, J.S. Design Prototypes: A Knowledge Representation Schema for Design. Ai Mag. 1990, 11. [Google Scholar] [CrossRef]
  25. Lee, J.H.; Gu, N.; Ostwald, M.J.; Jupp, J. Understanding Cognitive Activities in Parametric Design. In Global Design and Local Materialization; Zhang, J., Sun, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 38–49. [Google Scholar]
  26. Lee, J.H.; Gu, N.; Williams, A. Parametric design strategies for the generation of creative designs. Int. J. Archit. Comput. 2014, 12, 263–282. [Google Scholar] [CrossRef]
  27. Lee, J.H.; Ostwald, M.J.; Gu, N. Design Thinking: Creativity, Collaboration and Culture; Springer International Publishing: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
  28. Wang, Y.; Ruhe, G. The Cognitive Process of Decision Making. Int. J. Cogn. Inform. Nat. Intell. 2007, 1, 73–85. [Google Scholar] [CrossRef] [Green Version]
  29. Von Neumann, J.; Morgenstern, O. Theory of Games and Economic Behavior; Princeton University Press: Princeton, NJ, USA, 1947. [Google Scholar]
  30. Frederick, S. Cognitive Reflection and Decision Making. J. Econ. Perspect. 2005, 19, 25–42. [Google Scholar] [CrossRef] [Green Version]
  31. Crozier, R.; Ranyard, R. Cognitive process models and explanations of decision making. In Decision Making: Cognitive Models and Explanations; Crozier, R., Ranyard, R., Svenson, O., Eds.; Routledge: London, UK; New York, NY, USA, 2002; pp. 5–20. [Google Scholar]
  32. Harte, J.M.; Koele, P. Psychometric and methodological aspects of process tracing research. In Decision Making: Cognitive Models and Explanations; Crozier, R., Ranyard, R., Svenson, O., Eds.; Routledge: London, UK; New York, NY, USA, 2002; pp. 21–34. [Google Scholar]
  33. Stirling, W.C. Satisficing Games and Decision Making: With Applications to Engineering and Computer Science; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
  34. Janis, I.L.; Mann, L. Decision Making: A Psychological Analysis of Conflict, Choice, and Commitment; Free Press: New York, NY, USA, 1977. [Google Scholar]
  35. Isen, A.M. Positive affect and decision making. In Handbook of Emotions; The Guilford Press: New York, NY, USA, 1993; pp. 261–277. [Google Scholar]
  36. Plous, S. The Psychology of Judgment and Decision Making; McGraw-Hill Education: New York, NY, USA, 1993. [Google Scholar]
  37. Bazerman, M.H.; Moore, D.A. Judgment in Managerial Decision Making; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
  38. Huber, G.P. A Theory of the Effects of Advanced Information Technologies on Organizational Design, Intelligence, and Decision Making. Acad. Manag. Rev. 1990, 15, 47–71. [Google Scholar] [CrossRef] [Green Version]
  39. Eisenhardt, K.M.; Zbaracki, M.J. Strategic Decision Making. Strateg. Manag. J. 1992, 13, 17–37. [Google Scholar] [CrossRef] [Green Version]
  40. Klein, G.A.; Orasanu, J.; Calderwood, R.; Zsambok, C.E. Decision Making in Action: Models and Methods; Ablex Publishing: Norwood, NJ, USA, 1993. [Google Scholar]
  41. Bellman, R.E.; Zadeh, L.A. Decision-Making in a Fuzzy Environment. Manag. Sci. 1970, 17. [Google Scholar] [CrossRef]
  42. Jarrahi, M.H. Artificial intelligence and the future of work: Human-AI symbiosis in organizational decision making. Bus. Horiz. 2018, 61, 577–586. [Google Scholar] [CrossRef]
  43. Duan, Y.; Edwards, J.S.; Dwivedi, Y.K. Artificial intelligence for decision making in the era of Big Data—Evolution, challenges and research agenda. Int. J. Inf. Manag. 2019, 48, 63–71. [Google Scholar] [CrossRef]
  44. Vliegen, H.J.W.; Mal, H.H.V. Rational decision making: Structuring of design meetings. IEEE Trans. Eng. Manag. 1990, 37, 185–190. [Google Scholar] [CrossRef]
  45. Nikander, J.B.; Liikkanen, L.A.; Laakso, M. The preference effect in design concept evaluation. Des. Stud. 2014, 35, 473–499. [Google Scholar] [CrossRef]
  46. Ullman, D.G. Robust decision-making for engineering design. J. Eng. Des. 2001, 12, 3–13. [Google Scholar] [CrossRef]
  47. Wallas, G. The Art of Thought; Harcourt Brace: New York, NY, USA, 1926. [Google Scholar]
  48. Guilford, J.P. The Nature of Human Intelligence; McGraw-Hill: New York, NY, USA, 1967. [Google Scholar]
  49. Hayes, J.R. Cognitive processes in Creativity. In Handbook of Creativity. Perspectives on Individual Differences; Glover, J.A., Ronning, R.R., Reynolds, C.R., Eds.; Plenum Press: New York, NY, USA, 1989; pp. 135–145. [Google Scholar]
  50. Sternberg, R.J. The development of creativity as a decision-making process. In Creativity and Development; Sawyer, R.K., John-Steiner, V., Moran, S., Sternberg, R.J., Feldman, D.H., Nakamura, J., Csikszentmihalyi, M., Eds.; Oxford University Press: New York, NY, USA, 2003; Volume 91–138. [Google Scholar]
  51. Sternberg, R.J.; Kaufman, J.C.; Pretz, J.E. The Propulsion Model of Creative Contributions Applied to the Arts and Letters. J. Creat. Behav. 2001, 35, 75–101. [Google Scholar] [CrossRef]
  52. Montgomery, H. The search for a dominance structure in decision making: Examining the evidence. In Decision Making in Action: Models and Methods; Klein, G.A., Orasanu, J., Calderwood, R., Zsambok, C.E., Eds.; Ablex Publishing: Norwood, NJ, USA, 1993; pp. 182–187. [Google Scholar]
  53. Doherty, M.E. A laboratory scientist’s view of naturalistic decision making. In Decision Making in Action: Models and Methods; Klein, G.A., Orasanu, J., Calderwood, R., Zsambok, C.E., Eds.; Ablex Publishing: Norwood, NJ, USA, 1993; pp. 362–388. [Google Scholar]
  54. Lawson, B. How Designers Think; Eastview Editions; Architectural Press: Westfield, NY, USA, 1980. [Google Scholar]
  55. SHoP (Sharples, Holden Pasquarelli), Versioning: Evolutionary techniques in Architecture; Wiley: London, UK, 2002.
  56. Spiller, N. Digital Architecture Now: A Global Survey of Emerging Talent; Thames and Hudson: London, UK, 2008. [Google Scholar]
  57. Chai, K.-H.; Xiao, X. Understanding design research: A bibliometric analysis of Design Studies (1996–2010). Des. Stud. 2012, 33, 24–43. [Google Scholar] [CrossRef]
  58. Coley, F.; Houseman, O.; Roy, R. An introduction to capturing and understanding the cognitive behaviour of design engineers. J. Eng. Des. 2007, 18, 311–325. [Google Scholar] [CrossRef]
  59. Johannsen, G. Architecture of Man—Machine Decision Making Systems. In Lntelligent Decision Support in Process Environments; Hollnagel, E., Mancini, G., Woods, D.D., Eds.; Springer: Berlin/Heidelberg, Germany, 1986; pp. 327–339. [Google Scholar]
  60. Schraagan, J.M.; Klein, G.; Hoffman, R.R. The Macrocognition Framework of Naturalistic Decision Making. In Naturalistic Decision Making and Macrocognition; Schraagan, J.M., Militello, L.G., Ormerod, T., Lipshitz, R., Eds.; Ashgate Publishing: Aldershot, UK, 2008; pp. 3–25. [Google Scholar]
  61. Klein, G. Naturalistic Decision Making. Hum. Factors 2008, 50, 456–460. [Google Scholar] [CrossRef] [Green Version]
  62. Botella, M.; Zenasni, F.; Lubart, T. What Are the Stages of the Creative Process? What Visual Art Students Are Saying. Front. Psychol. 2018, 9. [Google Scholar] [CrossRef]
  63. Hoffman, R.R.; McNeese, M.D. A History for Macrocognition. J. Cogn. Eng. Decis. Mak. 2009, 3, 110–197. [Google Scholar] [CrossRef]
  64. Klein, G.; Ross, K.G.; Moon, B.M.; Klein, D.E.; Hoffman, R.R.; Hollnagel, E. Macrocognition. IEEE Intell. Syst. 2003, 18, 81–85. [Google Scholar] [CrossRef]
  65. Goldschmidt, G. The designer as a team of one. Des. Stud. 1995, 16, 189–209. [Google Scholar] [CrossRef]
  66. Krippendorff, K. Agreement and information in the reliability of coding. Commun. Methods Meas. 2011, 5, 93–112. [Google Scholar] [CrossRef] [Green Version]
  67. Krippendorff, K. Content Analysis: An Introduction to Its Methodology; Sage publications: Thousand Oaks, CA, USA, 2018. [Google Scholar]
  68. Maher, M.L.; Poon, J. Modeling Design Exploration as Co-Evolution. Comput. Aided Civ. Infrastruct. Eng. 1996, 11, 195–209. [Google Scholar] [CrossRef]
  69. Kruger, C.; Cross, N. Solution driven versus problem driven design: Strategies and outcomes. Des. Stud. 2006, 27, 527–548. [Google Scholar] [CrossRef]
  70. Ahmed, S.; Wallace, K.M.; Blessing, L.M. Understanding the differences between how novice and experienced designers approach design tasks. Res. Eng. Des. 2003, 14, 1–11. [Google Scholar] [CrossRef]
  71. Bilda, Z.; Demirkan, H. An insight on designers’ sketching activities in traditional versus digital media. Des. Stud. 2003, 24, 27–50. [Google Scholar] [CrossRef] [Green Version]
  72. Verstijnen, I.M.; van Leeuwen, C.; Goldschmidt, G.; Hamel, R.; Hennessey, J.M. Sketching and creative discovery. Des. Stud. 1998, 19, 519–546. [Google Scholar] [CrossRef]
  73. Lubart, T.I. Models of the Creative Process: Past, Present and Future. Creat. Res. J. 2001, 13, 295–308. [Google Scholar] [CrossRef]
  74. Ibrahim, R.; Pour Rahimian, F. Comparison of CAD and manual sketching tools for teaching architectural design. Autom. Constr. 2010, 19, 978–987. [Google Scholar] [CrossRef]
  75. Haapasalo, H. Creative Computer Aided Architectural Design: Internal Approach to the Design Process; Department of Industrial Engineering, University of Oulu: Oulu, Finland, 2000. [Google Scholar]
  76. Fjeld, M.; Bichsel, M.; Rauterberg, M. BUILD-IT: An intuitive design tool based on direct object manipulation. In Gesture and Sign Language in Human-Computer Interaction; Springer: Berlin/Heidelberg, Germany, 2012; pp. 297–308. [Google Scholar]
  77. Akin, O.; Moustapha, H. Strategic use of representation in architectural massing. Des. Stud. 2004, 25, 31–50. [Google Scholar] [CrossRef]
  78. Badke-Schaub, P.; Gehrlicher, A. Patterns of decisions in design: Leaps, loops, cycles, sequences and meta-processes. In Proceedings of the 14th International Conference on Engineering Design, ICED 03, Stockholm, Sweden, 19–21 August 2003; pp. 313–314. [Google Scholar]
  79. Simon, H.A. Decision Making and Problem Solving. In Decision Making: Alternatives to Rational Choice Models; Zey, M., Ed.; Sage: Newbury Park, CA, USA, 1992; pp. 32–53. [Google Scholar]
  80. Chusllp, P.; Jin, V. Cognitive modeling of iteration in conceptual design. In Proceedings of the ASME Design Engineering Technical Conference, Salt Lake City, UT, USA, 28 September–2 October 2004; Volume 3, pp. 473–485. [Google Scholar]
  81. Rosenman, M.A.; Gero, J.S. Creativity in design using a design prototype approach. In Modeling Creativity and Knowledge-Based Creative Design; Gero, J.S., Maher, M.L., Eds.; Lawrence Erlbaum: Hillsdale, NJ, USA, 1993; pp. 119–148. [Google Scholar]
  82. Gero, J.S. Computational Models of Innovative and Creative Design Processes. Technol. Forecast. Soc. Chang. 2000, 64, 183–196. [Google Scholar] [CrossRef]
  83. Hasirci, D.; Demirkan, H. Understanding the effects of cognition in creative decision making: A creativity model for enhancing the design studio process. Creat. Res. J. 2007, 19, 259–271. [Google Scholar] [CrossRef]
  84. Wong, Y.L.; Siu, K.W.M. A model of creative design process for fostering creativity of students in design education. Int. J. Technol. Des. Educ. 2012, 22, 437–450. [Google Scholar] [CrossRef]
  85. Martinec, T. A Model of Information Processing and Interactions in Teams Developing Technical Systems; University of Zagreb: Zagreb, Croatia, 2019. [Google Scholar]
  86. Ensici, A.; Badke-Schaub, P.; Bayazıt, N.; Lauche, K. Used and rejected decisions in design teamwork. CoDesign 2013, 9, 113–131. [Google Scholar] [CrossRef]
  87. Boden, M.A. The Creative Mind: Myths and Mechanisms; Routledge: London, UK; New York, NY, USA, 2004. [Google Scholar]
  88. Jensen, A.R.V.; Ahmed-Kristensen, S. Identifying knowledge in decision-making processes: A case study. In Proceedings of the 11th International Design Conference, DESIGN 2010, Dubrovnik, Croatia, 17–20 May 2010; pp. 1543–1552. [Google Scholar]
  89. West, R.L.; Somers, S. Scaling up from Micro Cognition to Macro Cognition: Using SGOMS to build Macro Cognitive Models of Sociotechnical Work in ACT-R. Cogn. Sci. 2011, 33, 1788–1793. [Google Scholar]
  90. Cacciabue, P.C.; Hollnagel, E. Simulation of cognition: Applications. In Expertise and Technology: Cognition and Human Computer Cooperation; Hoc, J.M., Cacciabue, P.C., Hollnagel, E., Eds.; Erlbaum: Hillsdale, NJ, USA, 1995; pp. 55–73. [Google Scholar]
Buildings 10 00242 g001 550
Figure 1. Two working modes (interfaces) in parametric design.
Figure 1. Two working modes (interfaces) in parametric design.
Buildings 10 00242 g001
Buildings 10 00242 g002 550
Figure 2. Conceptual models generated by six designers (A–F) in the experiment
Figure 2. Conceptual models generated by six designers (A–F) in the experiment
Buildings 10 00242 g002
Buildings 10 00242 g003 550
Figure 3. The distributions of the coding results of six designers’ protocols (A–F) (percentage of time duration).
Figure 3. The distributions of the coding results of six designers’ protocols (A–F) (percentage of time duration).
Buildings 10 00242 g003
Buildings 10 00242 g004 550
Figure 4. The conclusive DMP to support creativity.
Figure 4. The conclusive DMP to support creativity.
Buildings 10 00242 g004
Buildings 10 00242 g005 550
Figure 5. The confirmative DMP to support creativity.
Figure 5. The confirmative DMP to support creativity.
Buildings 10 00242 g005
Buildings 10 00242 g006 550
Figure 6. The simulative DMP to support creativity.
Figure 6. The simulative DMP to support creativity.
Buildings 10 00242 g006
Table
Table 1. Four creative operations adapted from [50].
Table 1. Four creative operations adapted from [50].
Creative OperationDescription
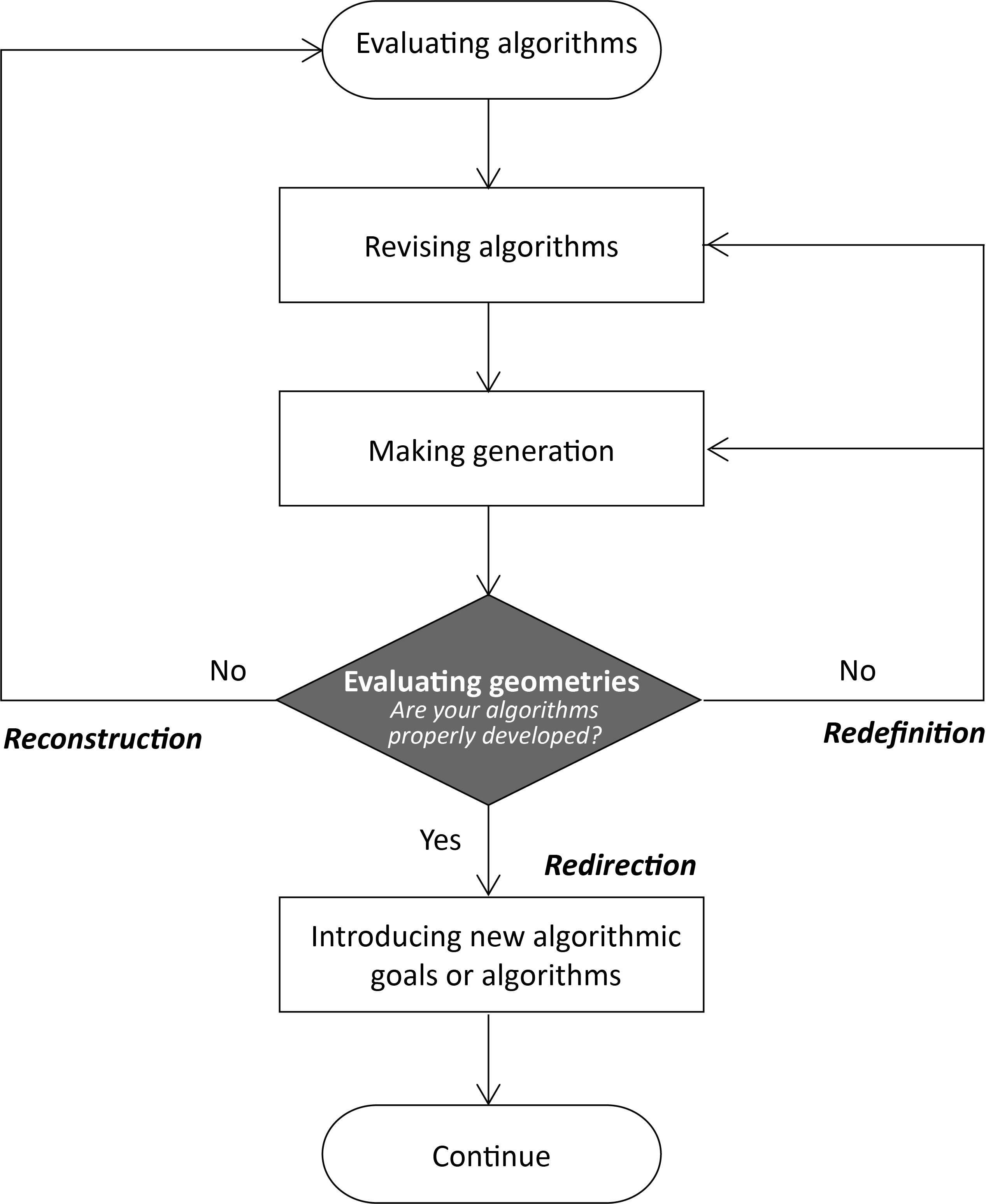
RedefinitionA change in perception as to where the situation is currently located.
Forward incrementationMoving the situation forward, from a point in the space of contributions and in the direction the work is already going.
RedirectionTaking the situation from where it is at a given time, and then moving it in a new direction
ReconstructionReturning the situation to a point where it previously was, and then shifting it in a new direction.
Table
Table 2. Coding scheme used for investigating creative DMPs in parametric design.
Table 2. Coding scheme used for investigating creative DMPs in parametric design.
CategorySubcategoryCodeDescription
Goal SettingGeometryGSGintroduce new geometric goals or ideas
AlgorithmGSAintroduce new algorithmic goals or ideas
RepresentationGeometryRGcreate geometries without an algorithm
AlgorithmRAcreate initial parameters and/or rules
Generation -Gmake generation or alternatives (e.g., executing or running scripts to create alternatives)
EvaluationGeometryEGevaluate primitives or existing geometries
AlgorithmEAevaluate existing parameters and/or rules
RevisionGeometryRVGrevise existing geometries
AlgorithmRVArevise existing algorithms (parameters and/or rules)
Table
Table 3. Results of time duration, segmentation, and intercoder reliability of each protocol.
Table 3. Results of time duration, segmentation, and intercoder reliability of each protocol.
Protocol CodeTime DurationNum. of SegmentsAverage Time of SegmentsCoded SegmentsIntercoder Reliability
Percent AgreementKrippendorff’s Alpha
A47 min 54.7 s22013.1 s208 (94.5%)92.0%0.904
B87 min 8 s31916.4 s277 (86.8%)84.7%0.825
C102 min 2 s36416.8 s334 (91.8%)97.3%0.969
D93 min 26 s28719.5 s265 (92.0%)97.0%0.964
E64 min 22 s36010.7 s347 (96.4%)87.7%0.857
F63 min 12 s30312.5 s278 (91.7%)81.9%0.800
Mean76 min 20.8 s308.814.8 s284.8 (92.2%)90.1%0.887
SD20 min 56.6 s53.23.3 s50.4 (3.2%)6.4%0.071
Table
Table 4. Sequential patterns of the decision-making activities including G in the design experiments (f: frequency).
Table 4. Sequential patterns of the decision-making activities including G in the design experiments (f: frequency).
Decision–Making TypeTotal f of OccurrencesMajor Pattern (f)On/Before ‘G’ (f)On/After ‘G’ (f)
Conclusive20EA–RVA–G–EG–GSG (4)
G–EG–G–EG–GSG (3)		EA–RVA–G (7)
EG–RVA–G (4)
EG–EA–G (3)
G–EG–G (3)		G–EG–GSG (8)
Confirmative74EA–RVA–G–EG–EA (9)
EG–EA–G–EG–EA (4)
EA–RVA–G–G–EG (3)		EA–RVA–G (19)
EG–EA–G (6)
RVA–EA–G (6)
G–EG–G (5)
RVA–EA–G (5)
EA–RA–G (3)
G–EA–G (3)
GSA–RVA–G (3)
RVA–G–G (3)
RVA–EG–G (3)		G–EG–EA (33)
G–EG–RVA (23)
G–EG–G (8)
G–EG–GSA (3)
G–EG–RA (3)
G–G–EG (3)
Simulative17-RVA–EG–G (3)
EG–EA–G (2)
GSG–EG–G (2)		G–RVA–EG (3)
G–GSA–RA (2)
G–RVA–EA (2)
G–RVA–G (2)
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Lee, J.H.; Ostwald, M.J. Creative Decision-Making Processes in Parametric Design. Buildings 2020, 10, 242. https://doi.org/10.3390/buildings10120242

AMA Style

Lee JH, Ostwald MJ. Creative Decision-Making Processes in Parametric Design. Buildings. 2020; 10(12):242. https://doi.org/10.3390/buildings10120242

Chicago/Turabian Style

Lee, Ju Hyun, and Michael J. Ostwald. 2020. "Creative Decision-Making Processes in Parametric Design" Buildings 10, no. 12: 242. https://doi.org/10.3390/buildings10120242

APA Style

Lee, J. H., & Ostwald, M. J. (2020). Creative Decision-Making Processes in Parametric Design. Buildings, 10(12), 242. https://doi.org/10.3390/buildings10120242

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop