Observation and Interpretation of Closely Spaced Fundamental Modes of a High-Rise Building
Abstract
:1. Introduction
2. Full-Scale Measurements
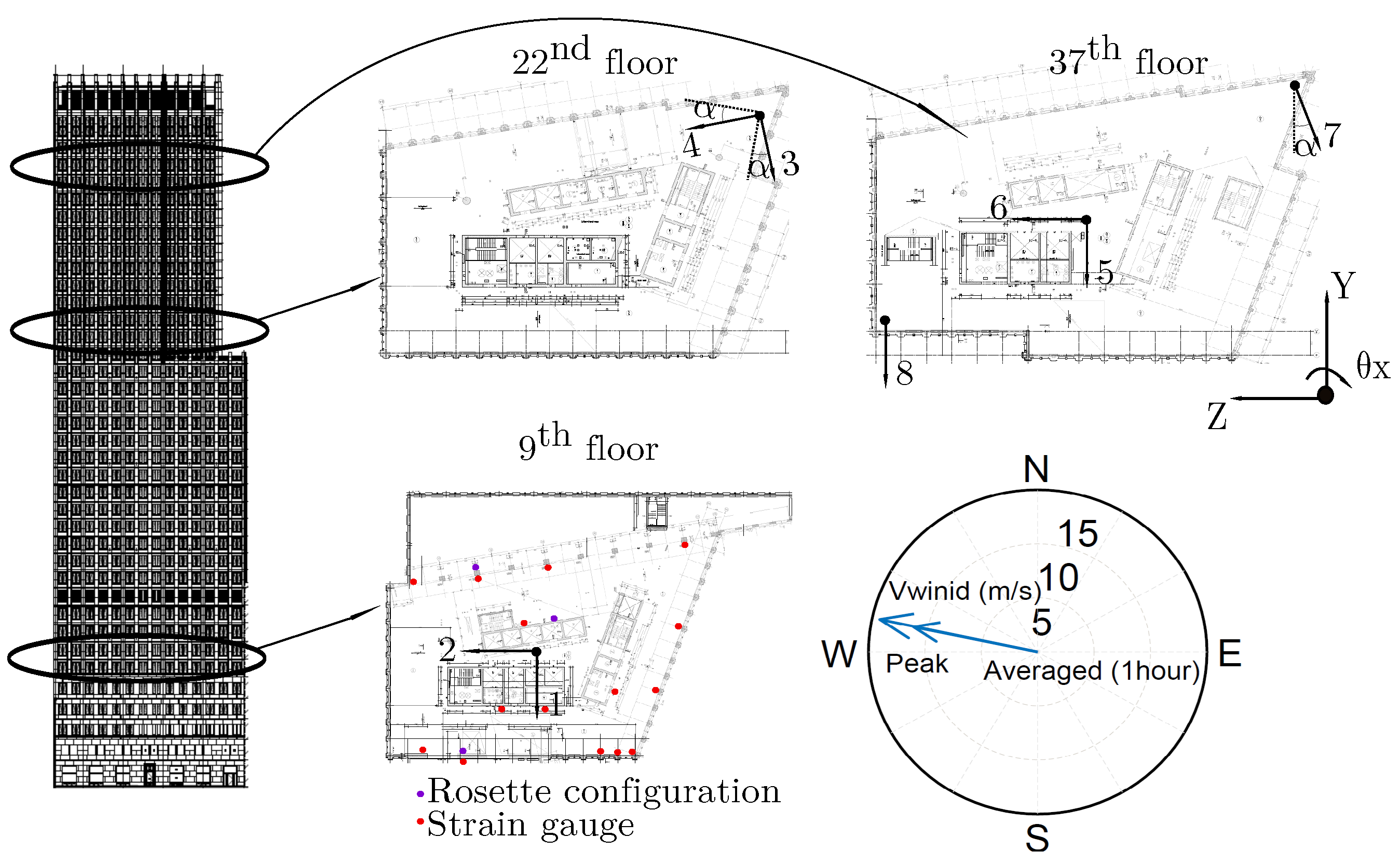
2.1. Building Description
2.2. Instrumentation Strategy and Experimental Results
3. Modelling Approach
A Model
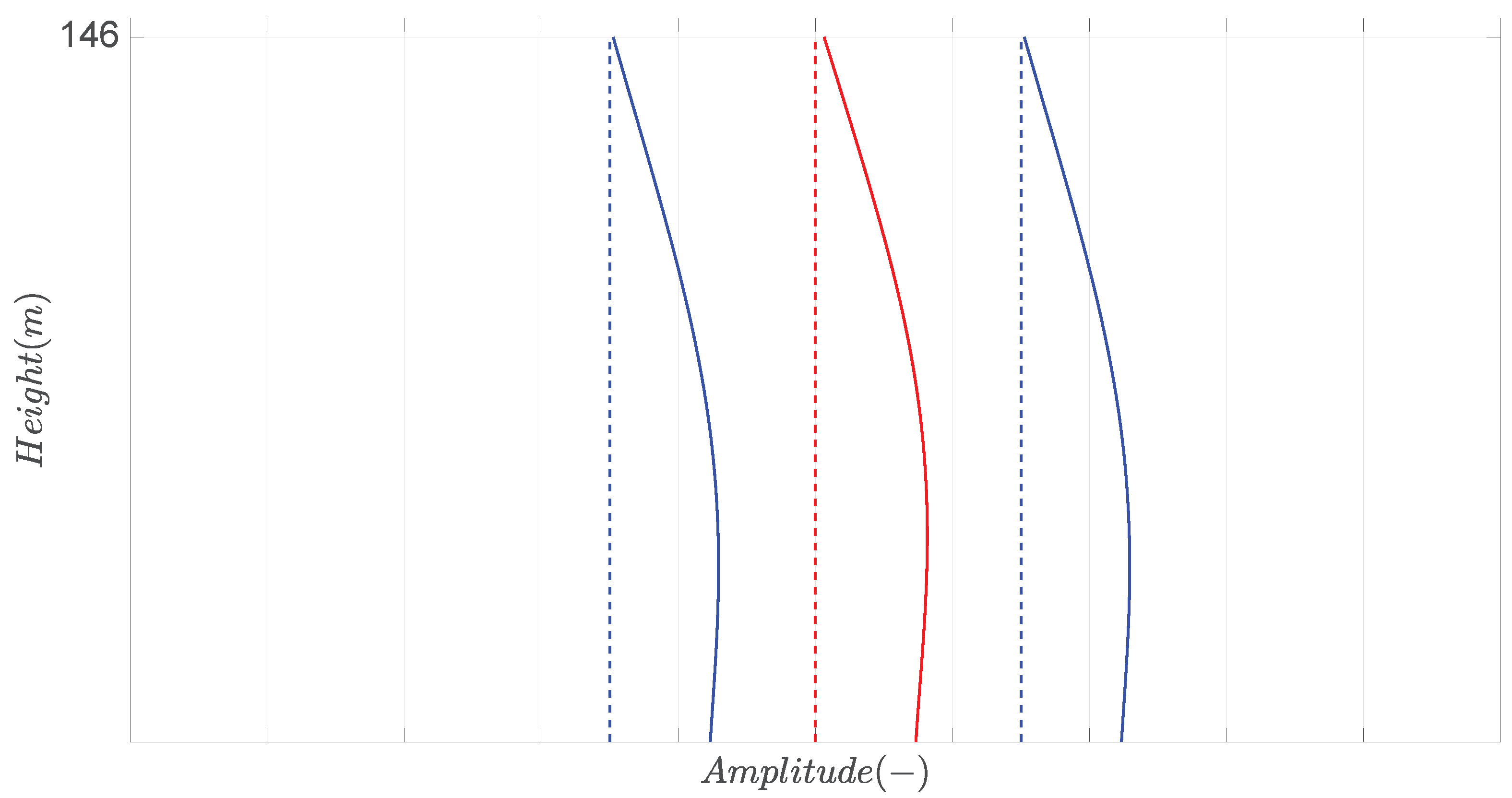
4. Comparison of the Experimental and Modelling Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Gentile, C.; Poggi, C.; Ruccolo, A.; Vasic, M. Vibration-Based Assessment of the Tensile Force in the Tie-Rods of the Milan Cathedral. Int. J. Archit. Herit. 2019, 13, 411–424. [Google Scholar] [CrossRef]
- Seelig, J.M.; Hoppmann, W.H. Impact On An Elastically Connected Double-beam System. J. Appl. Mech. 1963, 31, 31. [Google Scholar]
- Seelig, J.M.; Hoppmann, W.H. Normal mode vibrations of systems of elastically connected parallel bars. J. Acoust. Soc. Am. 1963, 36, 30. [Google Scholar]
- Dublin, M.; Friedrich, H.R. Forced Responses of Two Elastic Beams Interconnected by Spring-Damper Systems. J. Aeronaut. Sci. 1956, 23, 824–829. [Google Scholar] [CrossRef]
- Rao, S. Natural vibrations of systems of ellastically conected Timoshenko beams. J. Acoust. Soc. Am. 1974, 55, 1232–1237. [Google Scholar] [CrossRef]
- Chonan, S. Dynamical Behaviors of Elastically Connected Double-Beam Systems Subjected to an Impulsive Load. Trans. Jpn. Soc. Mech. Eng. 1975, 41, 2815–2824. [Google Scholar] [CrossRef]
- Hamada, T.R.; Nakayama, H.; Hayashi, K. Free And Forced Vibrations Of Elastically Connected Double-beam Systems. Bull. JSME 1983, 26, 1936–1942. [Google Scholar] [CrossRef] [Green Version]
- Dougla, B.E.; Yang, J.C.S. Transverse compressional damping in the vibratory response of elastic-viscoelastic- elastic beams. AIAA J. 1978, 16, 925–930. [Google Scholar] [CrossRef]
- Irie, T.; Yamada, G.; Kobayashi, Y. The steady-state response of an internally damped double-beam system interconnected by several springs. J. Acoust. Soc. Am. 1982, 71, 1155–1162. [Google Scholar] [CrossRef]
- Vu, H.; Ordoñez, A.; Karnopp, B. Vibration of a double-beam system. J. Sound Vib. 2000, 229, 807–822. [Google Scholar] [CrossRef]
- Oniszczuk, Z. Damped vibration analysis of an elastically connected complex double-string system. J. Sound Vib. 2003, 264, 253–271. [Google Scholar] [CrossRef]
- Li, Y.X.; Sun, L.Z. Transverse Vibration of an Undamped Elastically Connected Double-Beam System with Arbitrary Boundary Conditions. J. Eng. Mech. 2015, 142, 04015070. [Google Scholar]
- Gómez, S.S.; Metrikine, A.V. The Energy Flow Analysis as a Tool for Identification of Damping in Tall Buildings Subjected to Wind: Contributions of the Foundation and the Building Structure. J. Vib. Acoust. 2018, 141, 011013. [Google Scholar] [CrossRef]
- Sánchez Gómez, S. Energy Flux Method for Identification of Damping in High-Rise Buildings Subject to Wind. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2019. [Google Scholar]












| Weak-dir | 0.39 | 0.46 | 1.65 |
| Strong-dir | 0.55 | 0.62 | |
| Torsional-dir | 1.0 | 2.5 |
| Natural Frequencies in the Weak Direction | ||
|---|---|---|
| Exp.Identified [rad/s] | Model [rad/s] | |
| 2.5 | 2.5 | |
| 2.9 | 2.9 | |
| 10.3 | 10.3 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sanchez Gómez, S.; Metrikine, A.V. Observation and Interpretation of Closely Spaced Fundamental Modes of a High-Rise Building. Buildings 2020, 10, 132. https://doi.org/10.3390/buildings10070132
Sanchez Gómez S, Metrikine AV. Observation and Interpretation of Closely Spaced Fundamental Modes of a High-Rise Building. Buildings. 2020; 10(7):132. https://doi.org/10.3390/buildings10070132
Chicago/Turabian StyleSanchez Gómez, Sergio, and Andrei V. Metrikine. 2020. "Observation and Interpretation of Closely Spaced Fundamental Modes of a High-Rise Building" Buildings 10, no. 7: 132. https://doi.org/10.3390/buildings10070132




