Moisture Redistribution in Full-Scale Wood-Frame Wall Assemblies: Measurements and Engineering Approximation
Abstract
1. Introduction
2. Experimental Methods
2.1. Wall Assemblies and Wetting System
2.2. Moisture Content, Temperature, and Relative Humidity Measurements
2.3. Load Cell and Counter-Balance System
3. Experimental Results
4. Moisture Transfer Model
4.1. Basic Moisture Transfer Mechanisms and Approximations
4.2. Moisture Transfer Model for the Whole Wall and for the Water Injection Site
5. Modeling Results and Discussion
5.1. Modeling versus Measured Drying Curves
5.1.1. Results for Poly Walls
5.1.2. Results for Non-Poly Walls
5.2. Water Vapor Pressure and Component Moisture Flows
5.3. The Shape of the Redistribution Function
5.4. Further Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Load Cell Drift and Temperature Correction

Appendix B. Calibration of Simple Sorption Model
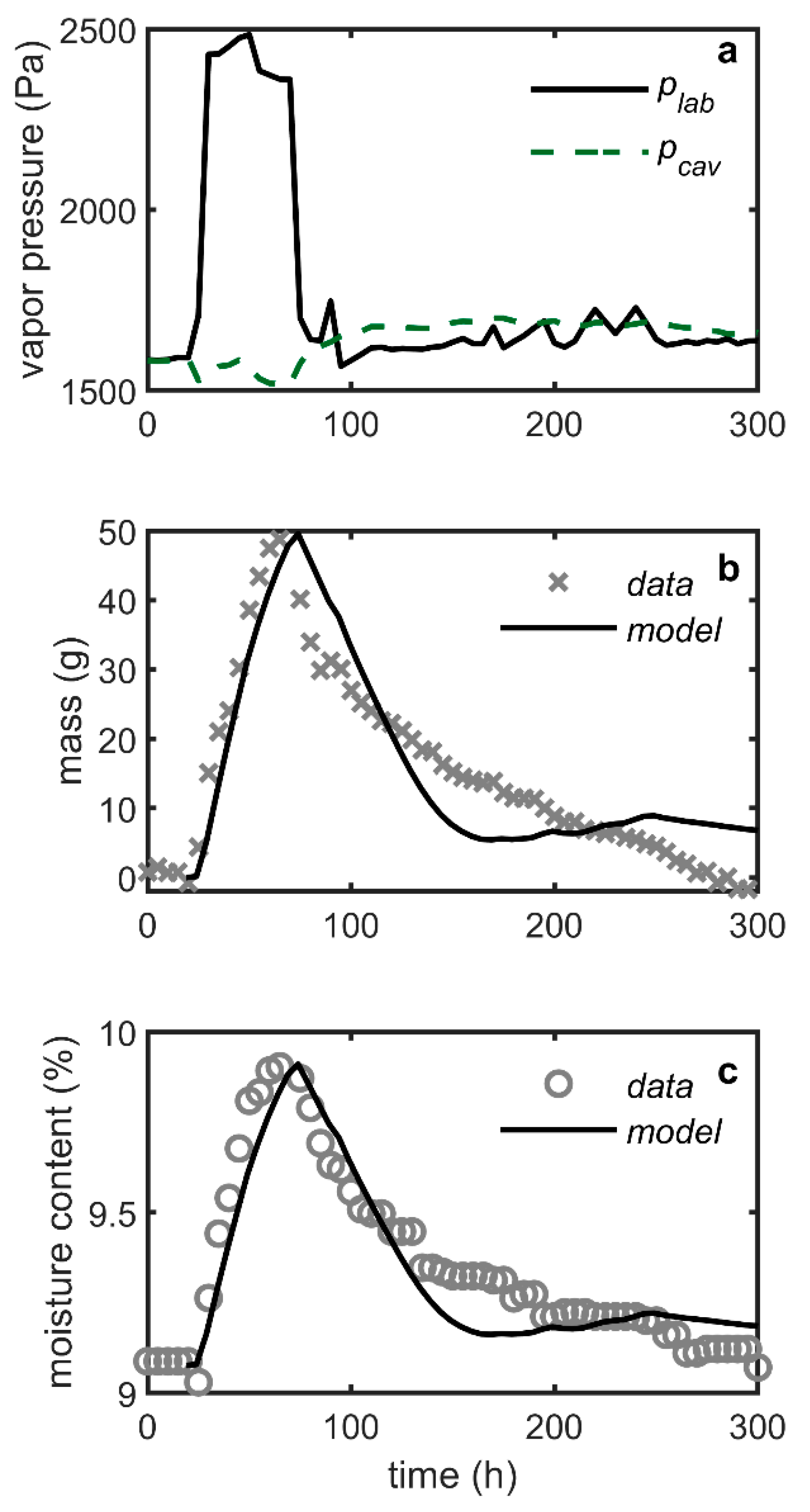
Appendix C. Vapor Pressure Coordination with Room Vapor Pressure

| Number | Label | Vapor Pressure Correction (Pa) | ||
|---|---|---|---|---|
| - | - | pcav | pwet | pnw |
| 1 | Poly, w/o XPS | 201 | 340 | 327 |
| 2 | Poly, w/ XPS | 153 | 273 | 297 |
| 3 | Wood, w/o XPS | 145 | 327 | 216 |
| 4 | Wood, w/ XPS | 253 | 430 | 346 |
| 5 | Paint, w/o XPS | 203 | 398 | 403 |
| 6 | Paint, w/ XPS | 144 | 311 | 278 |
References
- Tenwolde, A.; Rose, W.B. Moisture control strategies for the building envelope. J. Therm. Insul. Build. Envel. 1996, 19, 206–214. [Google Scholar] [CrossRef]
- Lstiburek, J. Understanding vapor barriers. ASHRAE J. 2004, 46, 40–50. [Google Scholar]
- Saber, H.H.; Maref, W. Field research study for investigating wetting and drying characteristics in wood-framing walls subjected to cold climate. J. Build. Phys. 2019, 174425911989118. [Google Scholar] [CrossRef]
- Van Belleghem, M.; Steeman, M.; Janssens, A.; De Paepe, M. Heat, air and moisture transport modelling in ventilated cavity walls. J. Build. Phys. 2014, 38, 317–349. [Google Scholar] [CrossRef]
- Tariku, F.; Simpson, Y.; Iffa, E. Experimental investigation of the wetting and drying potentials of wood frame walls subjected to vapor diffusion and wind-driven rain loads. Build. Environ. 2015, 92, 368–379. [Google Scholar] [CrossRef]
- Lstiburek, J.W.; Mitchell, J. Water & walls. ASHRAE J. 2013, 55, 72–80. [Google Scholar]
- Lstiburek, J.W. Double, double toil and trouble: Macbeth does vapor barriers. ASHRAE J. 2013, 55, 56–62. [Google Scholar]
- Boardman, C.R.; Glass, S.V.; Lebow, P.K. Simple and accurate temperature correction for moisture pin calibrations in oriented strand board. Build. Environ. 2017, 112, 250–260. [Google Scholar] [CrossRef]
- Boardman, C.R.; Glass, S.V.; Munson, R.; Yeh, B.; Chow, K. Field Moisture Performance of Wood-Framed Walls with Exterior Insulation in a Cold Climate; U.S. Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2019; pp. 1–42.
- Van Straaten, R. Measurement of Ventilation and Drying of Vinyl Siding and Brick Clad Wall Assemblies. Master’s Thesis, University of Waterloo, Department of Civil Engineering, Waterloo, ON, Canada, 2004. [Google Scholar]
- Smegal, J.; Lstiburek, J.; Straube, J.; Grin, A. Moisture-related durability of walls with exterior insulation in the Pacific Northwest. In Proceedings of the Thermal Performance of the Exterior Envelopes of Whole Buildings XII International Conference, Clearwater Beach, FL, USA, 1–5 December 2013. [Google Scholar]
- Ojanen, T. Improving the drying efficiency of timber frame walls in cold climates by using exterior insulation. In Proceedings of the Thermal Performance of the Exterior Envelopes of Buildings VII International Conference, Clearwater Beach, FL, USA, 6–10 December 1998. [Google Scholar]
- Hazleden, D.G.; Morris, P.I. The influence of design on drying of wood-frame walls under controlled conditions. In Proceedings of the Performance of Exterior Envelopes of Whole Buildings VIII International Conference, Clearwater Beach, FL, USA, 2–7 December 2001. [Google Scholar]
- Schumacher, C.J.; Shi, X.; Davidovich, D.; Burnett, E.F.; Straube, J.F. Ventilation drying in wall systems. In Proceedings of the Second International Conference on Building Physics, Leuven, Belgium, 14–18 September 2003. [Google Scholar]
- Teasdale-St-Hilaire, A.; Derome, D.; Fazio, A. Behavior of wall assemblies with different wood sheathings wetted by simulated rain penetration. In Proceedings of the Performance of Exterior Envelopes of Whole Buildings IX International Conference, Clearwater Beach, FL, USA, 5–10 December 2004. [Google Scholar]
- Derome, D.; Desmarais, G.; Thivierge, C. Large-scale experimental investigation of wood-frame walls exposed to simulated rain penetration in a cold climate. In Proceedings of the Performance of the Exterior of Whole Buildings X International Conference, Clearwater Beach, FL, USA, 2–7 December 2007. [Google Scholar]
- Maref, W.; Lacasse, M.A.; Krouglicof, N. A precision weighing system for helping assess the hygrothermal response of full-scale wall assemblies. In Proceedings of the Performance of Exterior Envelopes of Whole Buildings VIII International Conference, Clearwater Beach, FL, USA, 2–7 December 2001. [Google Scholar]
- Straube, J.; Smegel, J. Modeled and Measured Drainage, Storage and Drying Behind Cladding Systems; Building Science Corporation: Somerville, MA, USA, 2009. [Google Scholar]
- Derome, D.; Saneinejad, S. Inward vapor diffusion due to high temperature gradients in experimentally tested large-scale wall assemblies. Build. Environ. 2010, 45, 2790–2797. [Google Scholar] [CrossRef]
- Smegal, J.; Lstiburek, J. Hygric Redistribution in Insulated Assemblies: Retrofitting Residential Envelopes without Creating Moisture Issues; U.S. Department of Energy: Oak Ridge, TN, USA, 2013.
- Finch, G.; Straube, J. Ventilated wall claddings: Review, field performance, and hygrothermal modeling. In Proceedings of the Thermal Performance of the Exterior Envelopes of Whole Buildings X International Conference, Clearwater Beach, FL, USA, 2–7 December 2007. [Google Scholar]
- Pallin, S.; Hun, D.; Boudreax, P. Simulating air leakage in walls and roofs using indoor and outdoor boundary conditions. In Proceedings of the Thermal Performance of the Exterior of Envelopes of Whole Buildings XIII International Conference, Clearwater Beach, FL, USA, 4–8 December 2016. [Google Scholar]
- Boardman, C.R.; Glass, S.V.; Chow, K.; Yeh, B. Hygrothermal modeling of wall drying after water injection. In Proceedings of the Thermal Performance of the Exterior Envelopes of Whole Buildings XIV International Conference, Clearwater Beach, FL, USA, 9–12 December 2019. [Google Scholar]
- ANSI. Voluntary Product Standard PS 2-10. In Performance Standard for Wood-Based Structural-Use Panels; National Institute of Standards and Technology, U.S. Department of Commerce: Washington, DC, USA, 2011. [Google Scholar]
- Buck, A.L. New equations for computing vapor pressure and enhancement factor. J. Appl. Meteorol. Climatol. 1981, 20, 1527–1532. [Google Scholar] [CrossRef]
- Straube, J.F.; Burnett, E.F. Building Science for Building Enclosures; Building Science Press: Westford, MA, USA, 2005; ISBN 978-0-9755127-4-6. [Google Scholar]
- Whitehead, L.; Whitehead, R.; Valeur, B.; Berberan-Santos, M. A simple function for the description of near-exponential decays: The stretched or compressed hyperbola. Am. J. Phys. 2009, 77, 173–179. [Google Scholar] [CrossRef]
- Tenwolde, A. Ventilation, humidity and condensation in manufactured houses during winter. ASHRAE Trans. 1994, 100, 103–115. [Google Scholar]
- Boardman, C.R.; Glass, S.V. Basement radon entry and stack driven moisture infiltration reduced by active soil depressurization. Build. Environ. 2015, 85, 220–232. [Google Scholar] [CrossRef]
- Standard Methods for Water Vapor Transmission of Materials. In ASTM E96/E96M—16; ASTM International: West Conshohocken, PA, USA, 2016.
- Kumaran, M.K.; Trechsel, H.R. Hygrothermal Properties Of Building Materials. In Moisture Analysis and Condensation Control in Building Envelopes; ASTM International: West Conshohocken, PA, USA, 2001; pp. 29–65. ISBN 978-0-8031-2089-1. [Google Scholar]
- Kumaran, M.K.; Lackey, J.C.; Normandin, N.; Tariku, F.; van Reenen, D. A Thermal and Moisture Transport Property Database for Common Building and Insulating Materials: Final Report from ASHRAE Research Project 1018-RP; American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc.: Atlanta, GA, USA, 2002. [Google Scholar]
- Ojanen, T.; Ahonen, J.; Simonson, C.J.; Fazio, P.; Ge, H.; Rao, J.; Desmarais, G. Moisture performance characteristics of OSB and spruce plywood exterior sheathing products. In Research in Building Physics and Building Engineering, Proceedings of the Third International Building Physics Conference, Montreal, QC, Canada, 28–31 August 2006; Fazio, P., Ge, H., Rao, J., Desmarais, G., Eds.; Taylor & Francis: London, UK, 2006; pp. 97–105. ISBN 978-0-415-41675-7. [Google Scholar]
- Timusk, P.C.; Pressnail, K.D.; Cooper, P.A. The effects of board density, resin content and component layers on the permeability properties of mill-fabricated oriented strandboard. In Proceedings of the 12th Canadian Conference of Building Science and Technology, Montreal, QC, Canada, 6–8 May 2009; Quebec Building Envelope Council: Montreal, QC, Canada, 2009; pp. 325–334. [Google Scholar]
- Kumaran, M.K. Material Properties; Heat, Air and Moisture Transport; Laboratorium, Katholieke University, Bouwfysica: Leuven, Belgium, 1996. [Google Scholar]
- Alsayegh, G.; Mukhopadhyaya, P.; Wang, J.; Zalok, E.; Van Reenen, D. Preliminary Characterization of Physical Properties of Cross-Laminated-Timber (CLT) Panels for Hygrothermal Modelling. Adv. Civ. Eng. Mater. 2013, 2, 20120048. [Google Scholar] [CrossRef]
- Kordziel, S.; Glass, S.V.; Boardman, C.R.; Munson, R.A.; Zelinka, S.L.; Pei, S.; Tabares-Velasco, P.C. Hygrothermal characterization and modeling of cross-laminated timber in the building envelope. Build. Environ. 2020, 177, 106866. [Google Scholar] [CrossRef]













| Number | Label | Water Injection (g) | XPS Thickness (mm) | Lab RH Stability | Lumber Covering |
|---|---|---|---|---|---|
| 1 | Poly, w/o XPS | 160 | 0 | fair | Poly |
| 2 | Poly, w/ XPS | 160 | 50.8 | good | Poly |
| 3 | Wood, w/o XPS | 300 | 0 | good | None |
| 4 | Wood, w/ XPS | 160 | 25.4 | good | None |
| 5 | Paint, w/o XPS | 160 | 0 | poor | Paint |
| 6 | Paint, w/ XPS | 160 | 50.8 | fair | Paint |
| Rosb | Rxps | Rwood | Rsorp | Rair | Rpnt |
|---|---|---|---|---|---|
| 2619 | 1954 | 3941 | 550 | 11 | 7 |
| Parameter | Wood, w/o XPS | Wood, w/ XPS | Paint, w/o XPS | Paint, w/ XPS | Average |
|---|---|---|---|---|---|
| c | 0.43 | 1.13 | 1.59 | 2.63 | 1.44 |
| τmrd (h) | 287 | 199 | 89 | 98 | 168 |
| Model | Poly, w/o XPS | Poly, w/ XPS | Wood, w/o XPS | Wood, w/ XPS | Paint, w/o XPS | Paint, w/ XPS |
|---|---|---|---|---|---|---|
| nexp | 0.49 | 0.61 | 0.65 | 0.37 | 0.19 | 0.30 |
| exp | 0.15 | 0.21 | 0.54 | 0.40 | 0.22 | 0.21 |
| log | 0.72 | 0.76 | - | - | 0.70 | 0.59 |
| linear | 1.47 | 1.42 | - | - | 1.22 | 1.11 |
| diff | 1.50 | 2.03 | - | - | 1.46 | 1.34 |
| Model | Poly, w/o XPS | Poly, w/ XPS | Wood, w/o XPS | Wood, w/ XPS | Paint, w/o XPS | Paint, w/ XPS |
|---|---|---|---|---|---|---|
| nexp | 0.50 | 1.34 | 1.07 | 0.43 | 0.22 | 0.60 |
| exp | 1.38 | 2.17 | 0.81 | 0.98 | 1.16 | 1.50 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boardman, C.R.; Glass, S.V.; Zelinka, S.L. Moisture Redistribution in Full-Scale Wood-Frame Wall Assemblies: Measurements and Engineering Approximation. Buildings 2020, 10, 141. https://doi.org/10.3390/buildings10080141
Boardman CR, Glass SV, Zelinka SL. Moisture Redistribution in Full-Scale Wood-Frame Wall Assemblies: Measurements and Engineering Approximation. Buildings. 2020; 10(8):141. https://doi.org/10.3390/buildings10080141
Chicago/Turabian StyleBoardman, Charles R., Samuel V. Glass, and Samuel L. Zelinka. 2020. "Moisture Redistribution in Full-Scale Wood-Frame Wall Assemblies: Measurements and Engineering Approximation" Buildings 10, no. 8: 141. https://doi.org/10.3390/buildings10080141
APA StyleBoardman, C. R., Glass, S. V., & Zelinka, S. L. (2020). Moisture Redistribution in Full-Scale Wood-Frame Wall Assemblies: Measurements and Engineering Approximation. Buildings, 10(8), 141. https://doi.org/10.3390/buildings10080141







