Integrated Cost-Analysis Approach for Seismic and Thermal Improvement of Masonry Building Façades
Abstract
:1. Introduction
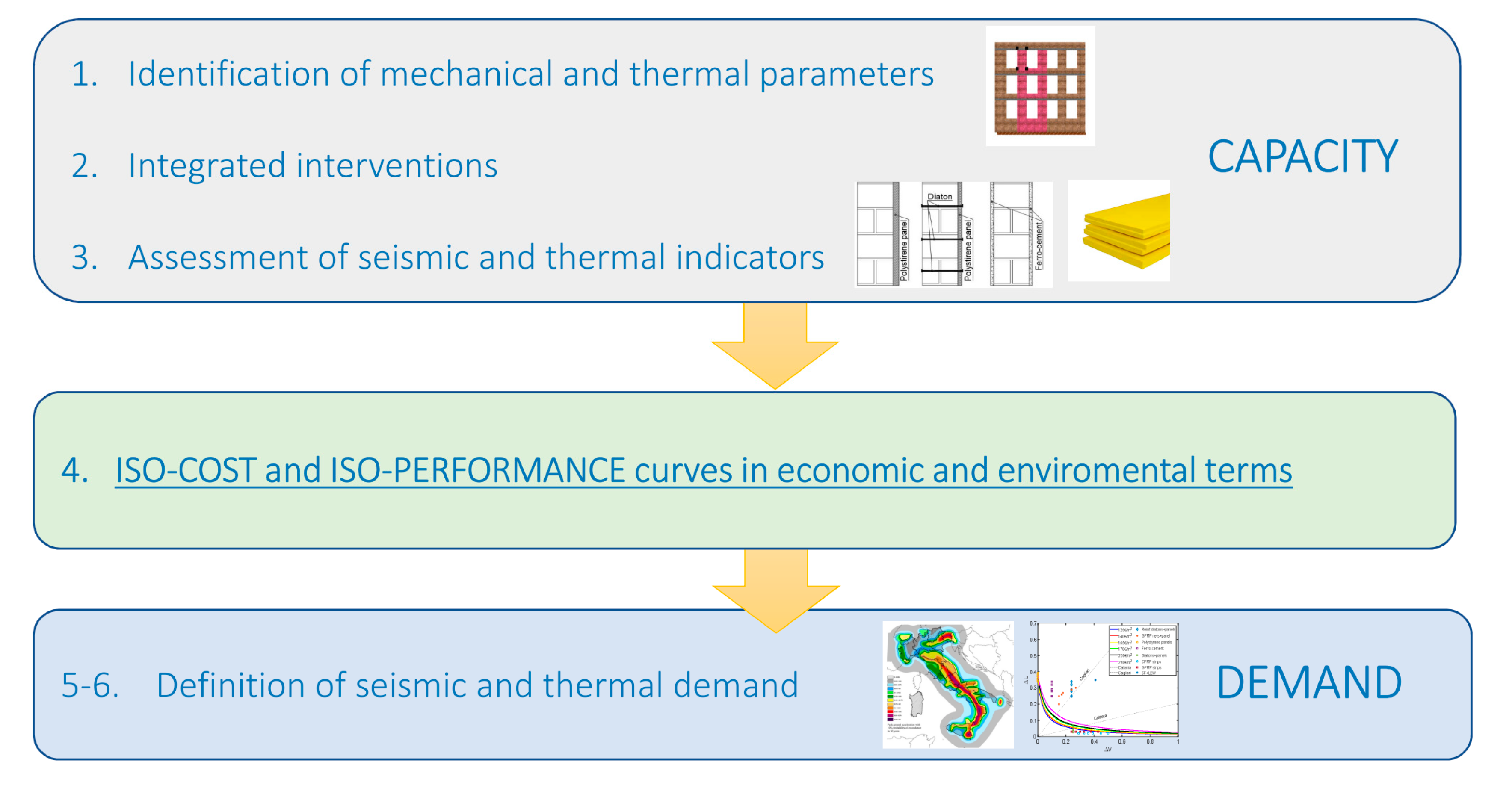
2. Integrated Approach at the Mesoscale Level
2.1. Procedure
- Acquisition of the structural and thermal parameters needed for the analysis (mechanical parameters, such as tensile strength, shear strength, etc. and thermal parameters, such as thermal conductivity, thicknesses, etc.)
- Definition of a set of integrated interventions, namely retrofitting strategies that have positive effects on either the seismic response, or the thermal performance or both of them.
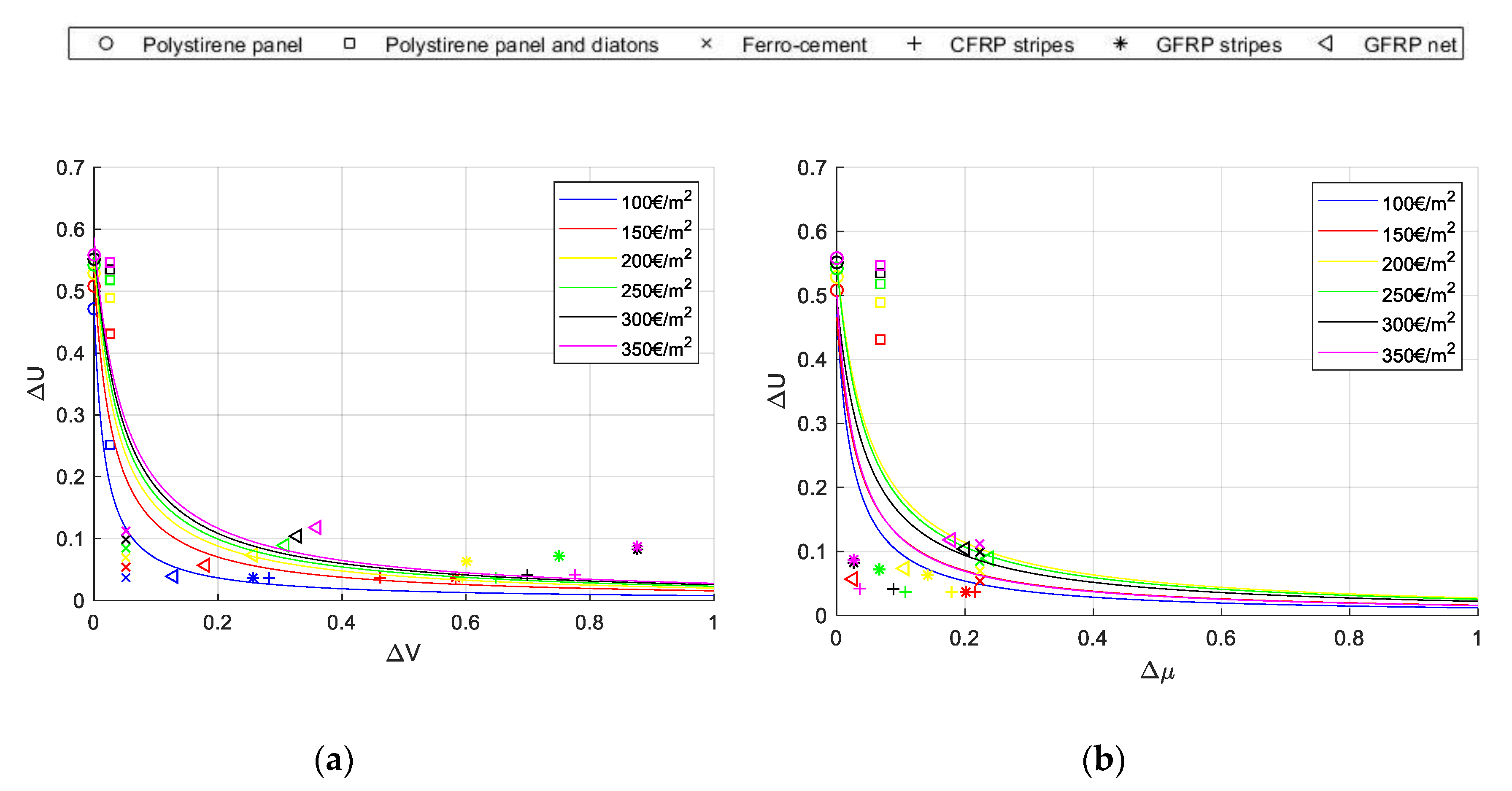
- Identification of a performance indicator at mesoscale level: as for the structural behavior, the variation of base shear capacity and the corresponding variation of ductility capacity are considered, defined by well-known methods (non-linear static analysis); as for the thermal side, the variation of thermal transmittance is taken into account.
- Economic and environmental iso-cost curves representing the relationships between the thermal capacity indicator () and the structural capacity indicators ( or . For each integrated intervention, after an economic budget (investment) or an environmental impact in terms of CO2eq are fixed, one can calculate, as explained in Section 2.2 and Section 2.3, the corresponding pair of capacity indicators. That represents a single point in the graphs − or −. By varying the economic budget or the environmental impact, several points are obtained. Finally, the curves fitting these points can be regarded as iso-cost curves. Moreover, the iso-performance curves, that will be the subject of future work, will express, for the same seismic or energetic performance, the economic investment needed or the environmental impact caused by each integrated intervention.
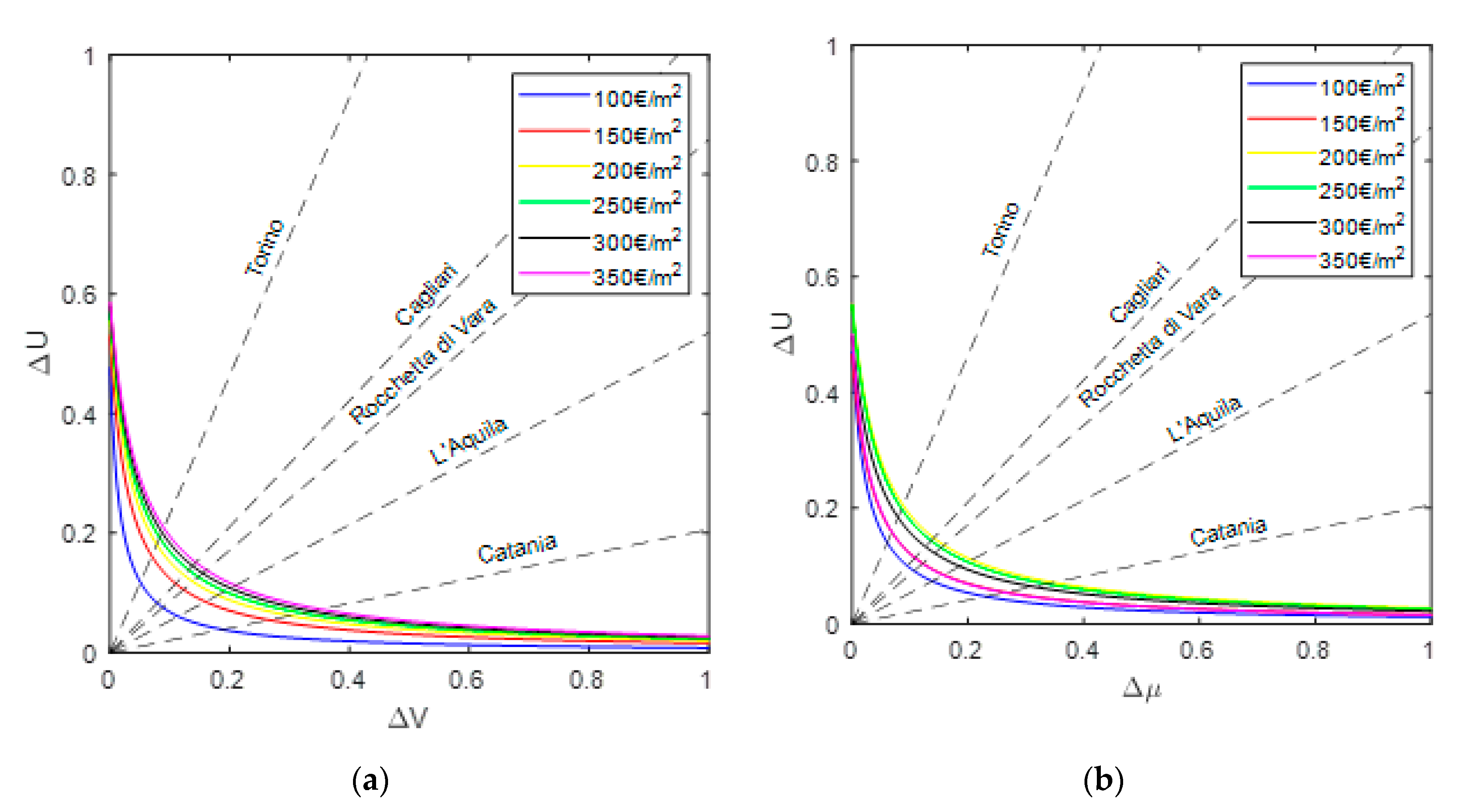
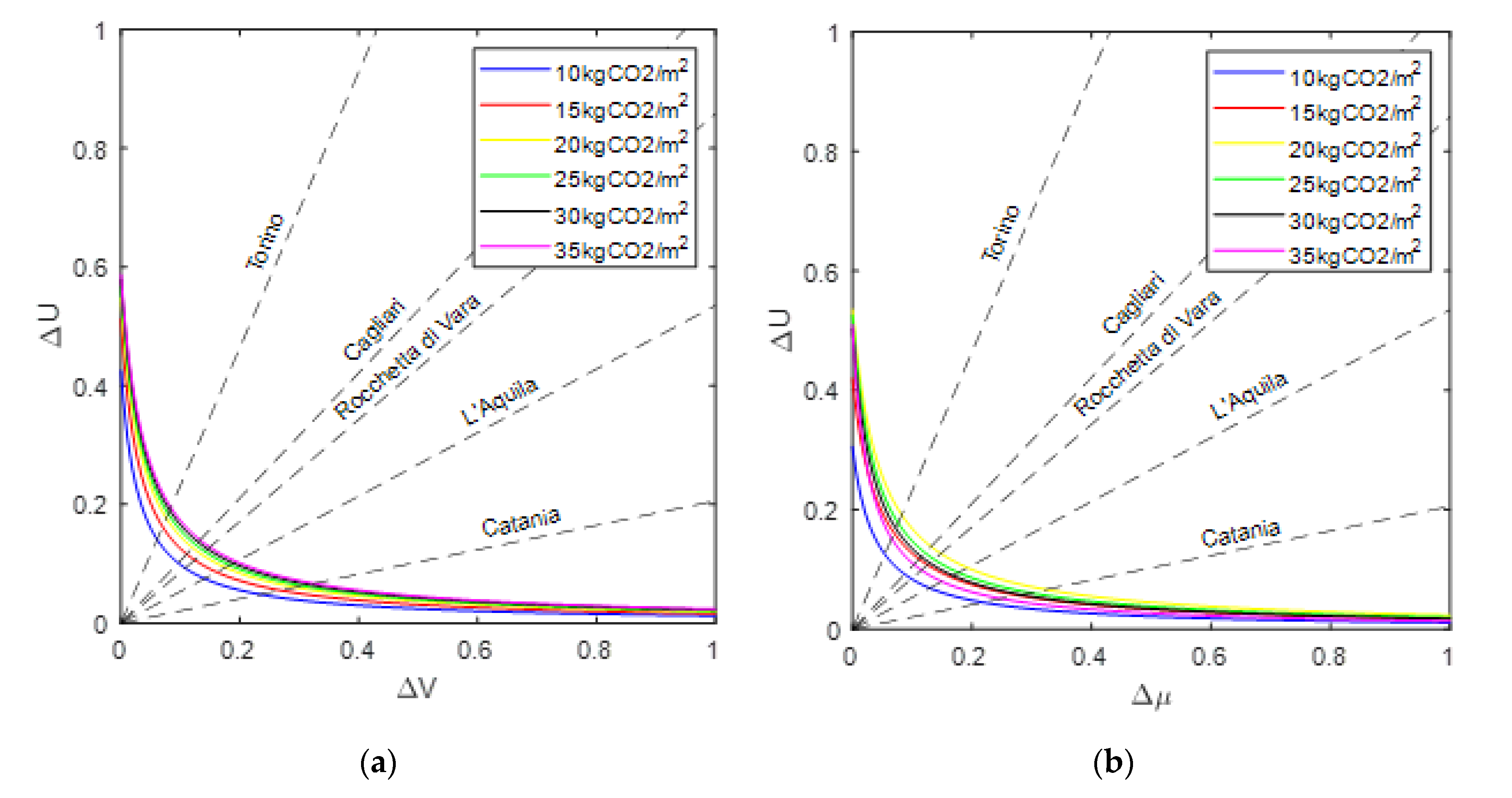
- Definition of dimensionless parameters and , defined in [28], to identify the demand for thermal and seismic performances respectively, with the expressions:where is the seismic peak ground acceleration at the site, is the maximum value in all the Italian regions (or any other reference zone in the world); is the degree day value of the site and the maximum Italian value. They are given for the different construction sites respectively by [30,31].
- The hypothesis of a correlation between energy efficiency demand and seismic demand, through demand curves identified by these analytical expressions:
2.2. Thermal Performance Indicator
- is the thermal resistance of the internal surface,
- is the resistance of the i-th layer,, where is the thickness of the i-th wall layer ;
- is the resistance of the external surface,.
- is the glass area [];
- is the glass heat transmission [];
- is the area of the support [];
- is the support heat transmission [];
- is the glass perimeter [];
- is the spacer heat transmission [].
- (a)
- select the thermal characteristics of the frame support ;
- (b)
- select the thermal characteristics of the glass ;
- (c)
- cross the values of and by selecting the percentage of the support with respect to the entire opening and find the value of of the opening with the chosen characteristics.
- is the area of the masonry element [];
- is the thermal transmittance of the masonry portion [];
- is the area of the window [];
- is the thermal transmittance of the window [];
- is the perimeter of the wall [];
- is the linear thermal transmittance [].
2.3. Structural Performance Indicators
3. Application of the Integrated Approach at Mesoscale Level
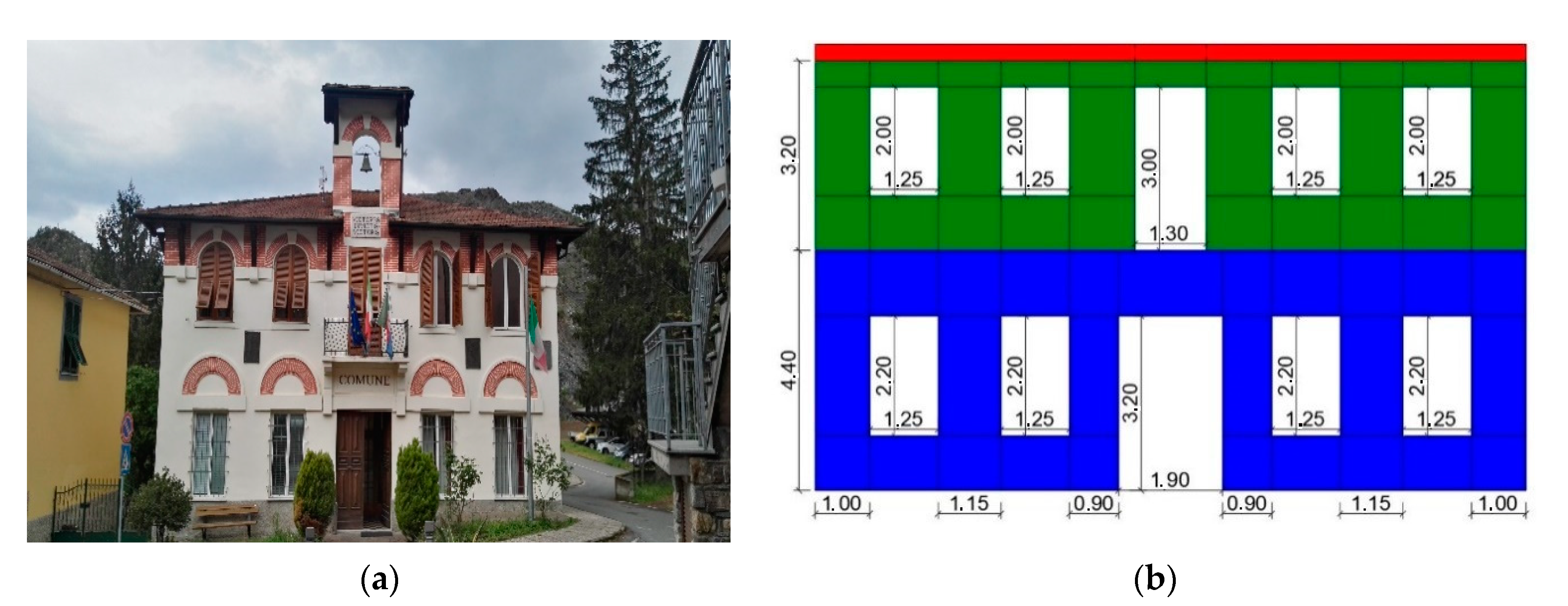
3.1. Case of Study
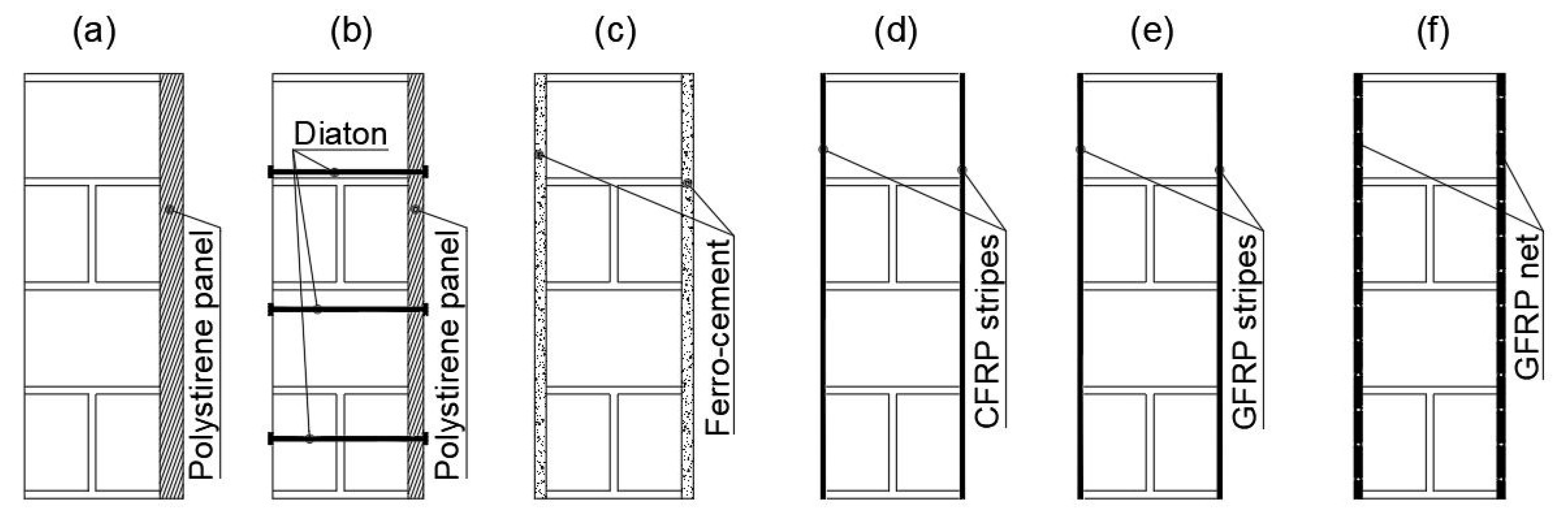
3.2. Assumptions on the Integrated Interventions
3.3. The Procedure of Estimation of the Varied Mechanical and Thermal Properties
- is the wall thickness;
- are the reinforcement area placed in horizontal and vertical direction per unit of length;
- are the spacings between horizontal or vertical strips.
3.4. Cost Analysis
3.4.1. Economic Cost Analysis
3.4.2. Environmental Cost Analysis
4. Definition of Demand Curves and Discussion of Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- De Falco, A.; Giresini, L.; Sassu, M. Temporary Preventive Seismic Reinforcements on Historic Churches: Numerical Modeling of San Frediano in Pisa. Appl. Mech. Mater. 2013, 351, 1393–1396. [Google Scholar] [CrossRef]
- Casapulla, C.; Maione, A.; Argiento, L.U. Seismic analysis of an existing masonry building according to the multi-level approach of the italian guidelines on cultural heritage. Ing. Sismica 2017, 34, 40–59. [Google Scholar]
- Casapulla, C.; Argiento, L.U. In-plane frictional resistances in dry block masonry walls and rocking-sliding failure modes revisited and experimentally validated. Compos. Part B Eng. 2018, 132, 197–213. [Google Scholar] [CrossRef]
- Alecci, V.; De Stefano, M.; Galassi, S.; Lapi, M.; Orlando, M. Evaluation of the American Approach for Detecting Plan Irregularity. Adv. Civ. Eng. 2019, 2019, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Alecci, V.; De Stefano, M. Building irregularity issues and architectural design in seismic areas. Frat. Integrità Strutt. 2018, 13, 161–168. [Google Scholar] [CrossRef]
- Gattesco, N.; Boem, I.; Dudine, A. Diagonal compression tests on masonry walls strengthened with a GFRP mesh reinforced mortar coating. Bull. Earthq. Eng. 2014, 13, 1703–1726. [Google Scholar] [CrossRef]
- Giresini, L.; Sassu, M.; Butenweg, C.; Alecci, V.; De Stefano, M. Vault macro-element with equivalent trusses in global seismic analyses. Earthq. Struct. 2017, 12, 409–423. [Google Scholar] [CrossRef]
- Giresini, L.; Solarino, F.; Paganelli, O.; Oliveira, D.V.; Froli, M. One-sided rocking analysis of corner mechanisms in masonry structures: Influence of geometry, energy dissipation, boundary conditions. Soil Dyn. Earthq. Eng. 2019, 123, 357–370. [Google Scholar] [CrossRef]
- Giresini, L.; Casapulla, C.; Denysiuk, R.; Matos, J.C.; Sassu, M. Fragility curves for free and restrained rocking masonry façades in one-sided motion. Eng. Struct. 2018, 164, 195–213. [Google Scholar] [CrossRef]
- Giresini, L. Design strategy for the rocking stability of horizontally restrained masonry walls. In Proceedings of the COMPDYN 2017, 6th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Rhodes Island, Greece, 15–17 June 2017. [Google Scholar]
- Alecci, V.; Stipo, G.; La Brusco, A.; De Stefano, M.; Rovero, L. Estimating elastic modulus of tuff and brick masonry: A comparison between on-site and laboratory tests. Constr. Build. Mater. 2019, 204, 828–838. [Google Scholar] [CrossRef]
- Giresini, L.; Sassu, M.; Sorrentino, L. In situ free-vibration tests on unrestrained and restrained rocking masonry walls. Earthq. Eng. Struct. Dyn. 2018, 47, 3006–3025. [Google Scholar] [CrossRef]
- Giresini, L.; Puppio, M.L.; Taddei, F. Experimental pull-out tests and design indications for strength anchors installed in masonry walls. Mater. Struct. 2020, 53, 1–16. [Google Scholar] [CrossRef]
- Goncalves, M. Insulating Solid Masonry Walls. Available online: www.cebq.org (accessed on 26 May 2020).
- Schiavi, A.; Cellai, G.; Secchi, S.; Brocchi, F.; Grazzini, A.; Prato, A.; Mazzoleni, F. Stone masonry buildings: Analysis of structural acoustic and energy performance within the seismic safety criteria. Constr. Build. Mater. 2019, 220, 29–42. [Google Scholar] [CrossRef]
- Sassu, M.; Giresini, L.; Bonannini, E.; Puppio, M.L. On the Use of Vibro-Compressed Units with Bio-Natural Aggregate. Buildings 2016, 6, 40. [Google Scholar] [CrossRef] [Green Version]
- Mistretta, F.; Piras, M.V.; Fadda, M.L. A Reliable Visual Inspection Method for the Assessment of R.C. Structures Through Fuzzy Logic Analysis. In Life-Cycle of Structural Systems: Design, Assessment, Maintenance and Management—Proceedings of the 4th International Symposium on Life-Cycle Civil Engineering, Tokyo, Japan, 14–16 November 2014; Taylor & Francis Group: London, UK, 2015; pp. 1154–1160. [Google Scholar]
- Andreini, M.; Sassu, M. Mechanical behaviour of full unit masonry panels under fire action. Fire Saf. J. 2011, 46, 440–450. [Google Scholar] [CrossRef] [Green Version]
- Meloni, P.; Mistretta, F.; Stochino, F.; Carcangiu, G. Thermal Path Reconstruction for Reinforced Concrete Under Fire. Fire Technol. 2019, 55, 1451–1475. [Google Scholar] [CrossRef]
- Kumar, R.; Gardoni, P. Renewal theory-based life-cycle analysis of deteriorating engineering systems. Struct. Saf. 2014, 50, 94–102. [Google Scholar] [CrossRef]
- Biswas, W. Carbon footprint and embodied energy consumption assessment of building construction works in Western Australia. Int. J. Sustain. Built Environ. 2014, 3, 179–186. [Google Scholar] [CrossRef] [Green Version]
- Sharma, N.; Tabandeh, A.; Gardoni, P. Resilience analysis: A mathematical formulation to model resilience of engineering systems. Sustain. Resilient Infrastruct. 2017, 3, 49–67. [Google Scholar] [CrossRef] [Green Version]
- Galadanci, A.S.; Ianakiev, A.; Kromanis, R.; Robinson, J. Energy investigation framework: Understanding buildings from an energy perspective view. J. Build. Eng. 2020, 28, 101046. [Google Scholar] [CrossRef]
- Ma, Z.; Cooper, P.; Daly, D.; Ledo, L. Existing building retrofits: Methodology and state-of-the-art. Energy Build. 2012, 55, 889–902. [Google Scholar] [CrossRef]
- Calvi, G.; Sousa, L.; Ruggeri, C. Energy Efficiency and Seismic Resilience: A Common Approach. In Multi-Hazard Approaches to Civil Infrastructure Engineering; Gardoni, P., LaFave, J.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 165–208. [Google Scholar]
- Global Alliance for Buildings and Construction. Global Status Report. 2018. Available online: https://www.unenvironment.org/resources/report/global-status-report-2018 (accessed on 23 July 2020).
- Sassu, M.; Stochino, F.; Mistretta, F. Assessment Method for Combined Structural and Energy Retrofitting in Masonry Buildings. Buildings 2017, 7, 71. [Google Scholar] [CrossRef] [Green Version]
- Mistretta, F.; Stochino, F.; Sassu, M. Structural and thermal retrofitting of masonry walls: An integrated cost-analysis approach for the Italian context. Build. Environ. 2019, 155, 127–136. [Google Scholar] [CrossRef]
- Hasik, V.; Escott, E.; Bates, R.; Carlisle, S.; Faircloth, B.; Bilec, M.M. Comparative whole-building life cycle assessment of renovation and new construction. Build. Environ. 2019, 161, 106218. [Google Scholar] [CrossRef]
- Italian Institute of Geophysics and Volcanology: Map of Seismic Hazard. Available online: https.www.ingv.it (accessed on 26 May 2020).
- EN ISO 15927-6 Hygrothermal Performance of Buildings—Calculation and Presentation of Climatic Data—Part 6: Accumulated Temperature Differences (Degree-Days); International Organization for Standardization: Geneva, Switzerland, 2007; pp. 1–13.
- UNI EN ISO 6946:2008. Componenti ed Elementi per Edilizia—Resistenza Termica e Trasmittanza Termica—Metodo di Calcolo; International Organization for Standardization: Geneva, Switzerland, 2008; pp. 1–28. [Google Scholar]
- UNI 10351:1994. Building Materials. Thermal Conductivities and Vapour Permeabilities; International Organization for Standardization: Geneva, Switzerland, 1994; pp. 1–21. [Google Scholar]
- EN ISO 10077-1:2006. Thermal Performance of Windows, Doors and Shutters—Calculation of Thermal Transmittance; International Organization for Standardization: Geneva, Switzerland, 2006; pp. 1–35. [Google Scholar]
- UNI EN ISO 10211:2008. Thermal Bridge in Buildings—Thermal Flow and Surface Temperatures—Calculation Methods; International Organization for Standardization: Geneva, Switzerland, 2008; pp. 1–55. [Google Scholar]
- UNI EN ISO 14683:2008. Thermal Bridges in Building Construction—Linear Thermal Transmittance—Simplified Methods and Default Values; International Organization for Standardization: Geneva, Switzerland, 2008; pp. 1–27. [Google Scholar]
- Gruppo Sismica, s.r.l. 3D MACRO—Computer Program for Modelling the Seismic Behavior of Masonry Buildings. Modellazione di Pannelli Murari Rinforzati nel Piano con Reti Fibrenet in GFRP e Malta di Calce; Gruppo Sismica s.r.l.: Catania, Italy, 2020. [Google Scholar]
- Pantò, B.; Giresini, L.; Sassu, M.; Calio, I. Non-linear modeling of masonry churches through a discrete macro-element approach. Earthq. Struct. 2017, 12, 223–236. [Google Scholar] [CrossRef]
- Ministero delle Infrastrutture e dei Trasporti. Circolare Applicativa 21 Gennaio 2019, n. 7; Ministero delle Infrastrutture e dei Trasporti: Codroipo, Italy, 2019.
- National Research Council. CNR-DT 200/2004: Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Existing Structures; National Research Council: Rome, Italy, 2004; pp. 80–110. [Google Scholar]
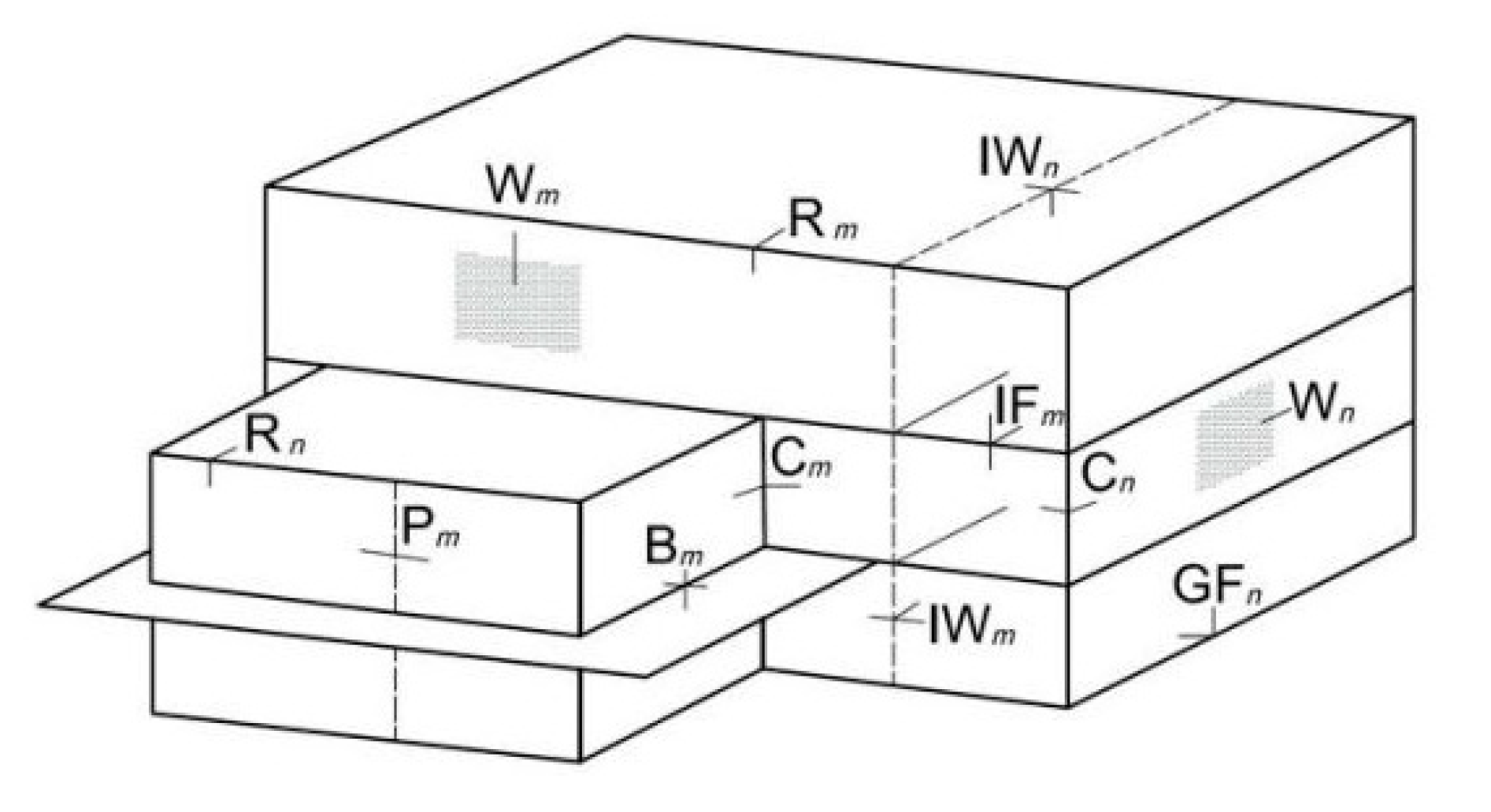

| R | Connections Between External Elements | Corners Between Vertical Walls and Roof |
| B | Corners between vertical walls and projecting elements | |
| C | Corners between vertical walls | |
| GF | Corner between vertical walls and floors | |
| IF | Corners between external vertical walls and intermediate floors | |
| IW | Corners between inner vertical walls and external elements | |
| P | Presence of external columns | |
| W | Presence of doors and windows | |
| fm,k | τ0 | E | G | w | λ |
|---|---|---|---|---|---|
| [N/mm2] | [N/mm2] | [N/mm2] | [N/mm2] | [kN/m3] | [W/mK] |
| 3.20 | 0.065 | 1740.00 | 580.00 | 21.00 | 2.30 |
| Type of Intervention | Investment | |||||
|---|---|---|---|---|---|---|
| 100 €/m2 | 150 €/m2 | 200 €/m2 | 250 €/m2 | 300 €/m2 | 350 €/m2 | |
| Polystyrene panel | 1.753 | 1.660 | 1.608 | 1.574 | 1.551 | 1.534 |
| Polystyrene panel + diatons | 2.305 | 1.854 | 1.708 | 1.636 | 1.593 | 1.564 |
| Ferro-cement | 2.845 | 2.802 | 2.762 | 2.725 | 2.689 | 2.656 |
| CFRP strips | 2.845 | 2.845 | 2.845 | 2.845 | 2.835 | 2.832 |
| GFRP strips | 2.845 | 2.845 | 2.779 | 2.757 | 2.730 | 2.718 |
| GFRP net | 2.839 | 2.794 | 2.753 | 2.713 | 2.676 | 2.641 |
| Type of Intervention | Emissions | |||||
|---|---|---|---|---|---|---|
| 10 kgCO2eq/m2 | 15 kgCO2eq/m2 | 20 kgCO2eq/m2 | 25 kgCO2eq/m2 | 30 kgCO2eq/m2 | 35 kgCO2eq/m2 | |
| Polystyrene panel | 1.933 | 1.729 | 1.642 | 1.593 | 1.562 | 1.540 |
| Polystyrene panel + diatons | 1.950 | 1.735 | 1.645 | 1.595 | 1.563 | 1.541 |
| Ferro-cement | 2.915 | 2.893 | 2.872 | 2.851 | 2.831 | 2.812 |
| CFRP strips | 2.845 | 2.845 | 2.845 | 2.845 | 2.834 | 2.832 |
| GFRP strips | 2.845 | 2.845 | 2.766 | 2.741 | 2.730 | 2.718 |
| GFRP net | 2.848 | 2.808 | 2.769 | 2.733 | 2.699 | 2.666 |
| Type of Intervention | Investment | |||||
|---|---|---|---|---|---|---|
| 100 €/m2 | 150 €/m2 | 200 €/m2 | 250 €/m2 | 300 €/m2 | 350 €/m2 | |
| Polystyrene panel | 446.803 | 446.803 | 446.803 | 446.803 | 446.803 | 446.803 |
| Polystyrene panel + diatons | 458.259 | 458.259 | 458.259 | 458.259 | 458.259 | 458.259 |
| Ferro-cement | 469.716 | 469.716 | 469.716 | 469.716 | 469.716 | 469.716 |
| CFRP strips | 572.824 | 653.019 | 712.169 | 736.157 | 759.093 | 793.436 |
| GFRP strips | 561.367 | 707.326 | 715.263 | 781.991 | 838.286 | 838.286 |
| GFRP net | 504.085 | 562.998 | 561.367 | 584.280 | 595.737 | 607.193 |
| Type of Intervention | Emissions | |||||
|---|---|---|---|---|---|---|
| 10 kgCO2/m2 | 15 kgCO2/m2 | 20 kgCO2/m2 | 25 kgCO2/m2 | 30 kgCO2/m2 | 35 kgCO2/m2 | |
| Polystyrene panel | 446.803 | 446.803 | 446.803 | 446.803 | 446.803 | 446.803 |
| Polystyrene panel + diatons | 458.259 | 458.259 | 458.259 | 458.259 | 458.259 | 458.259 |
| Ferro-cement | 469.716 | 469.716 | 469.716 | 469.716 | 469.716 | 469.716 |
| CFRP strips | 607.193 | 690.176 | 715.270 | 736.182 | 770.554 | 793.436 |
| GFRP strips | 687.389 | 726.755 | 759.086 | 816.354 | 838.286 | 838.286 |
| GFRP net | 504.085 | 515.541 | 561.367 | 572.000 | 595.737 | 607.193 |
| Type of Intervention | Investment | |||||
|---|---|---|---|---|---|---|
| 100 €/m2 | 150 €/m2 | 200 €/m2 | 250 €/m2 | 300 €/m2 | 350 €/m2 | |
| Polystyrene panel | 2.633 | 2.633 | 2.633 | 2.633 | 2.633 | 2.633 |
| Polystyrene panel + diatons | 2.811 | 2.811 | 2.811 | 2.811 | 2.811 | 2.811 |
| Ferro-cement | 3.220 | 3.220 | 3.220 | 3.220 | 3.220 | 3.220 |
| CFRP strips | 3.338 | 3.201 | 3.104 | 2.915 | 2.866 | 2.727 |
| GFRP strips | 3.235 | 3.163 | 3.006 | 2.808 | 2.563 | 2.563 |
| GFRP net | 2.477 | 2.566 | 2.911 | 3.258 | 3.260 | 3.302 |
| Type of Intervention | Emissions | |||||
|---|---|---|---|---|---|---|
| 10 kgCO2/m2 | 15 kgCO2/m2 | 20 kgCO2/m2 | 25 kgCO2/m2 | 30 kgCO2/m2 | 35 kgCO2/m2 | |
| Polystyrene panel | 2.633 | 2.633 | 2.633 | 2.633 | 2.633 | 2.633 |
| Polystyrene panel + diatons | 2.811 | 2.811 | 2.811 | 2.811 | 2.811 | 2.811 |
| Ferro-cement | 3.220 | 3.220 | 3.220 | 3.220 | 3.220 | 3.220 |
| CFRP strips | 2.914 | 3.253 | 3.002 | 2.947 | 2.802 | 2.727 |
| GFRP strips | 2.812 | 2.969 | 2.875 | 2.738 | 2.563 | 2.563 |
| GFRP net | 2.603 | 2.690 | 2.911 | 2.923 | 3.260 | 3.285 |
| Material | Cost |
|---|---|
| Polystyrene panel | 1517 €/m3 |
| Diatons | 80 €/m2 |
| Ferro-cement | 2080 €/m3 |
| CFRP stripes | 2160 €/m3 |
| GFRP stripes | 1723 €/m3 |
| GFRP nets | 4667 €/m3 |
| Economic Investment | α0 | α1 |
|---|---|---|
| 100 €/m2 | 0.0079 | 0.0166 |
| 150 €/m2 | 0.0162 | 0.0305 |
| 200 €/m2 | 0.0209 | 0.0376 |
| 250 €/m2 | 0.0240 | 0.0421 |
| 300 €/m2 | 0.0267 | 0.0460 |
| 350 €/m2 | 0.0291 | 0.0497 |
| Economic Investment | α0 | α1 |
|---|---|---|
| 100 €/m2 | 0.0121 | 0.0258 |
| 150 €/m2 | 0.0165 | 0.0353 |
| 200 €/m2 | 0.0287 | 0.0519 |
| 250 €/m2 | 0.0265 | 0.0482 |
| 300 €/m2 | 0.0231 | 0.0465 |
| 350 €/m2 | 0.0160 | 0.0319 |
| Material | Emissions of CO2eq |
|---|---|
| Polystyrene panel | 138 kgCO2eq/m3 |
| Diatons | 0.25 kgCO2eq/m2 |
| Ferro-cement | 450 kgCO2eq/m3 |
| CFRP stripes | 87,140 kgCO2eq/m3 |
| GFRP stripes | 15,062 kgCO2eq/m3 |
| GFRP nets | 520 kgCO2eq/m3 |
| Environmental Impact | α0 | α1 |
|---|---|---|
| 5 kgCO2eq/m2 | 0.0128 | 0.0301 |
| 10 kgCO2eq/m2 | 0.0166 | 0.0325 |
| 20 kgC kgCO2eq/m2 | 0.0199 | 0.0364 |
| 30 kgCO2eq/m2 | 0.0216 | 0.0381 |
| 40 kgCO2eq/m2 | 0.0232 | 0.0401 |
| 50 kgCO2eq/m2 | 0.0245 | 0.0417 |
| Environmental Impact | α0 | α1 |
|---|---|---|
| 5 kgCO2eq/m2 | 0.0155 | 0.0377 |
| 10 kgCO2eq/m2 | 0.0182 | 0.0434 |
| 20 kgCO2eq/m2 | 0.0246 | 0.0460 |
| 30 kgCO2eq/m2 | 0.0206 | 0.0392 |
| 40 kgCO2eq/m2 | 0.0185 | 0.0367 |
| 50 kgCO2eq/m2 | 0.0142 | 0.0279 |
| Site | PGAi | cR | DDi | cU |
|---|---|---|---|---|
| Rocchetta di Vara | 0.120 | 0.436 | 1934 | 0.374 |
| Torino | 0.060 | 0.218 | 2617 | 0.507 |
| L’Aquila | 0.250 | 0.909 | 2514 | 0.487 |
| Catania | 0.215 | 0.782 | 833 | 0.161 |
| Cagliari | 0.050 | 0.182 | 990 | 0.192 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giresini, L.; Paone, S.; Sassu, M. Integrated Cost-Analysis Approach for Seismic and Thermal Improvement of Masonry Building Façades. Buildings 2020, 10, 143. https://doi.org/10.3390/buildings10080143
Giresini L, Paone S, Sassu M. Integrated Cost-Analysis Approach for Seismic and Thermal Improvement of Masonry Building Façades. Buildings. 2020; 10(8):143. https://doi.org/10.3390/buildings10080143
Chicago/Turabian StyleGiresini, Linda, Simona Paone, and Mauro Sassu. 2020. "Integrated Cost-Analysis Approach for Seismic and Thermal Improvement of Masonry Building Façades" Buildings 10, no. 8: 143. https://doi.org/10.3390/buildings10080143






