The Effect of Sand Type on the Rheological Properties of Self-Compacting Mortar
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Particle Shape Measurements
2.3. Paste Rheological Threshold Theory
2.4. Mortar Rheology Threshold Theory
3. Results
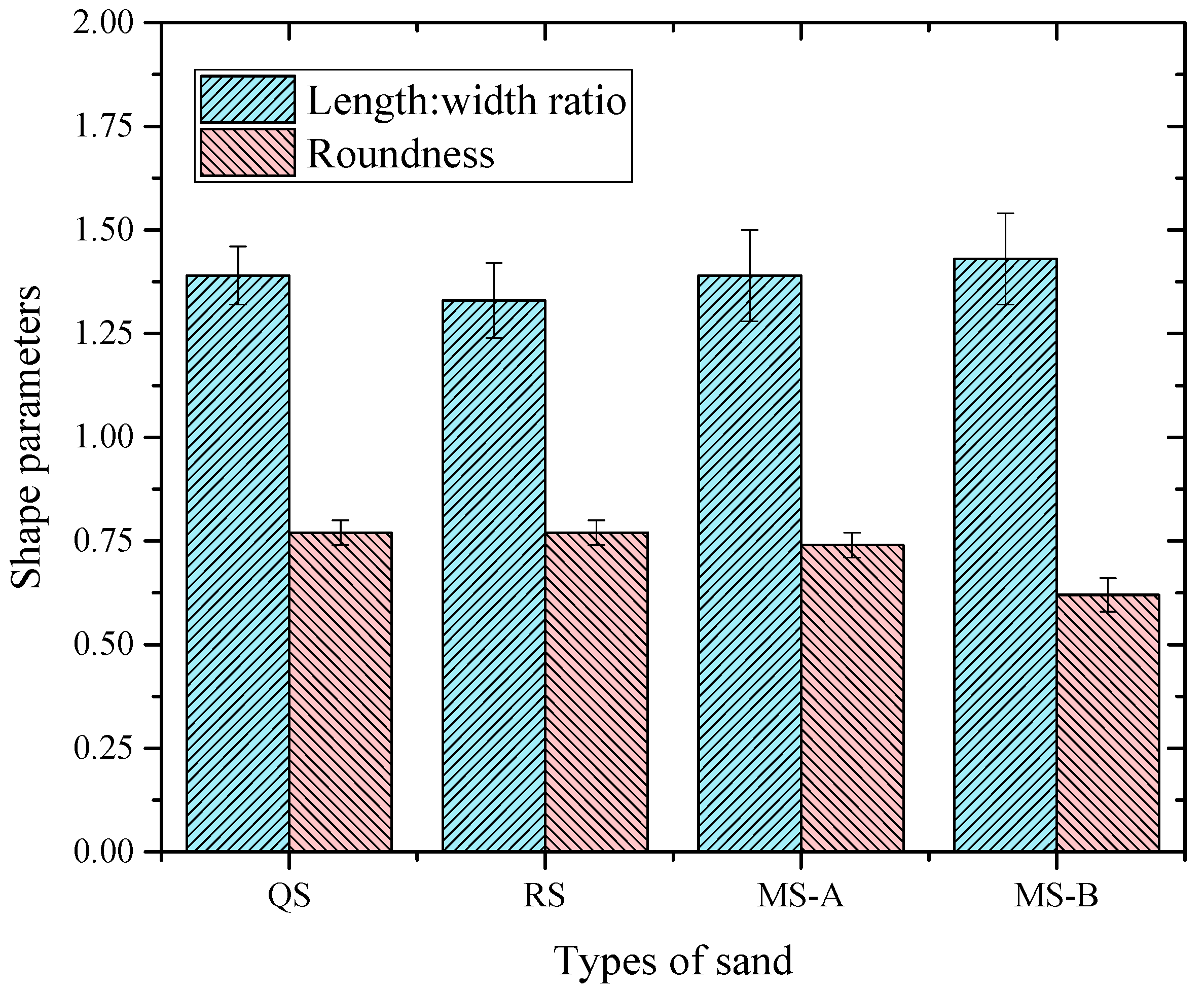
3.1. Particle Shape Parameters
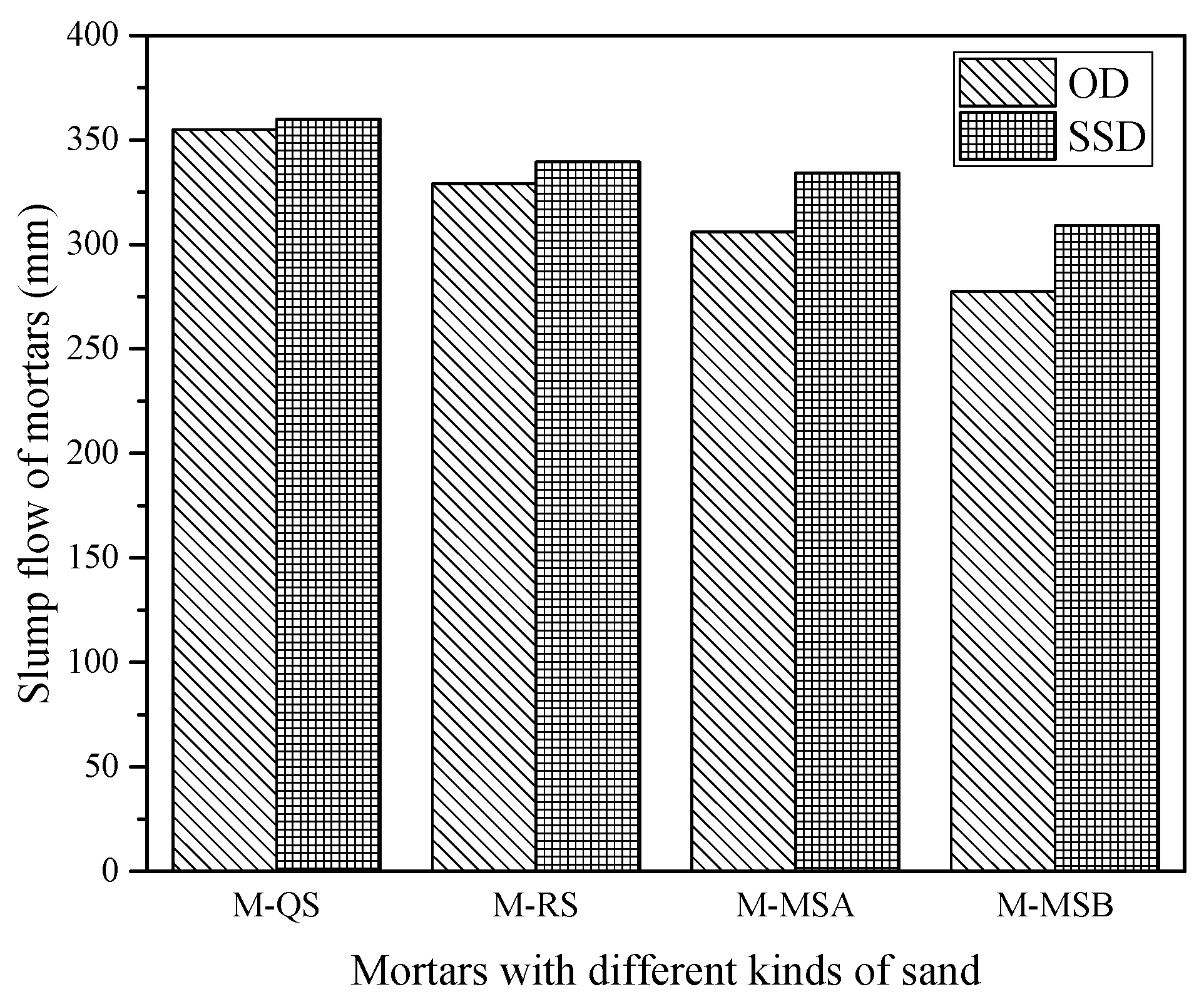
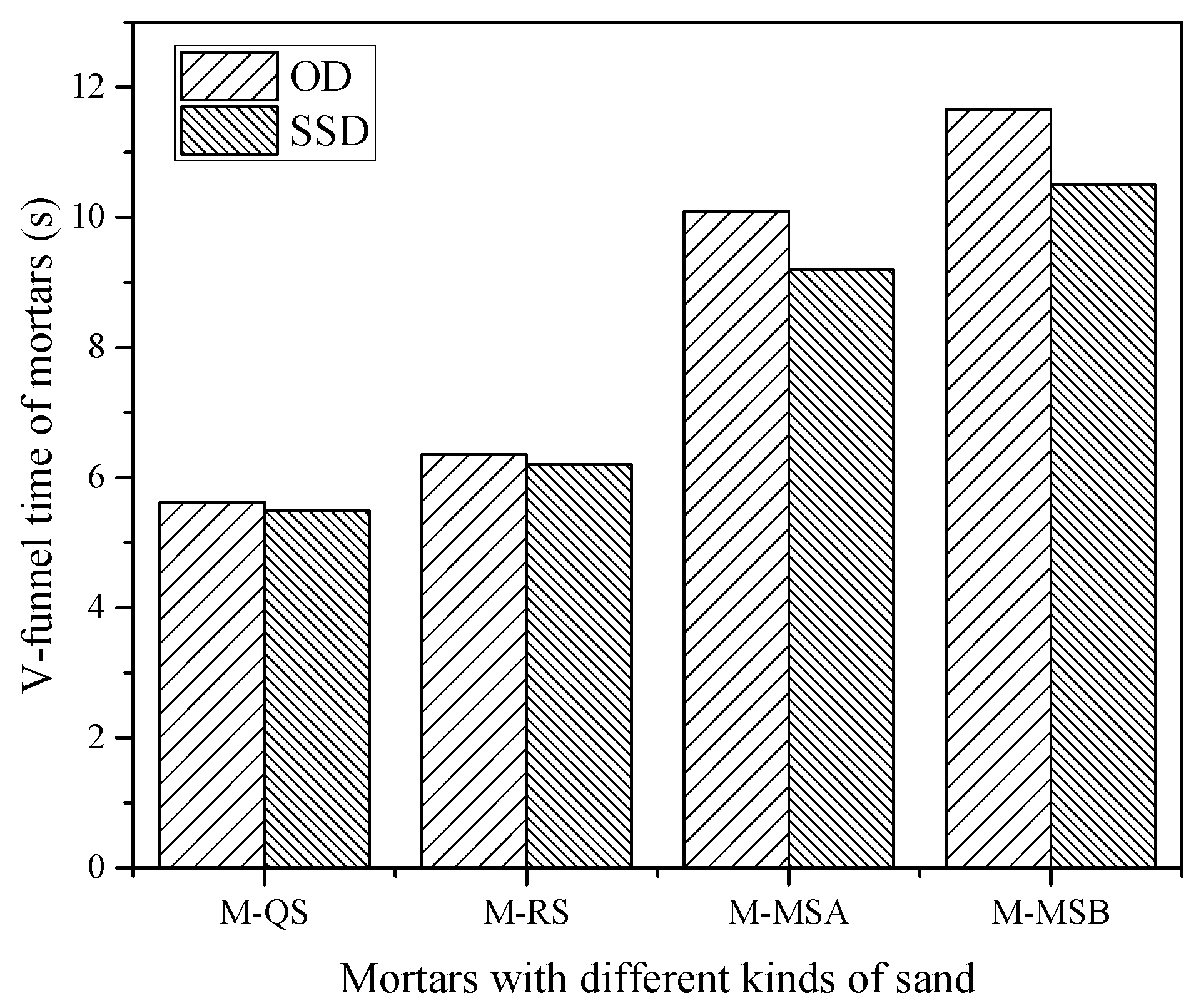
3.2. Mortars with Four Kinds of Sands
3.3. Pastes and Mortars with RS and MS-A in SSD Conditions
4. Analysis and Discussion
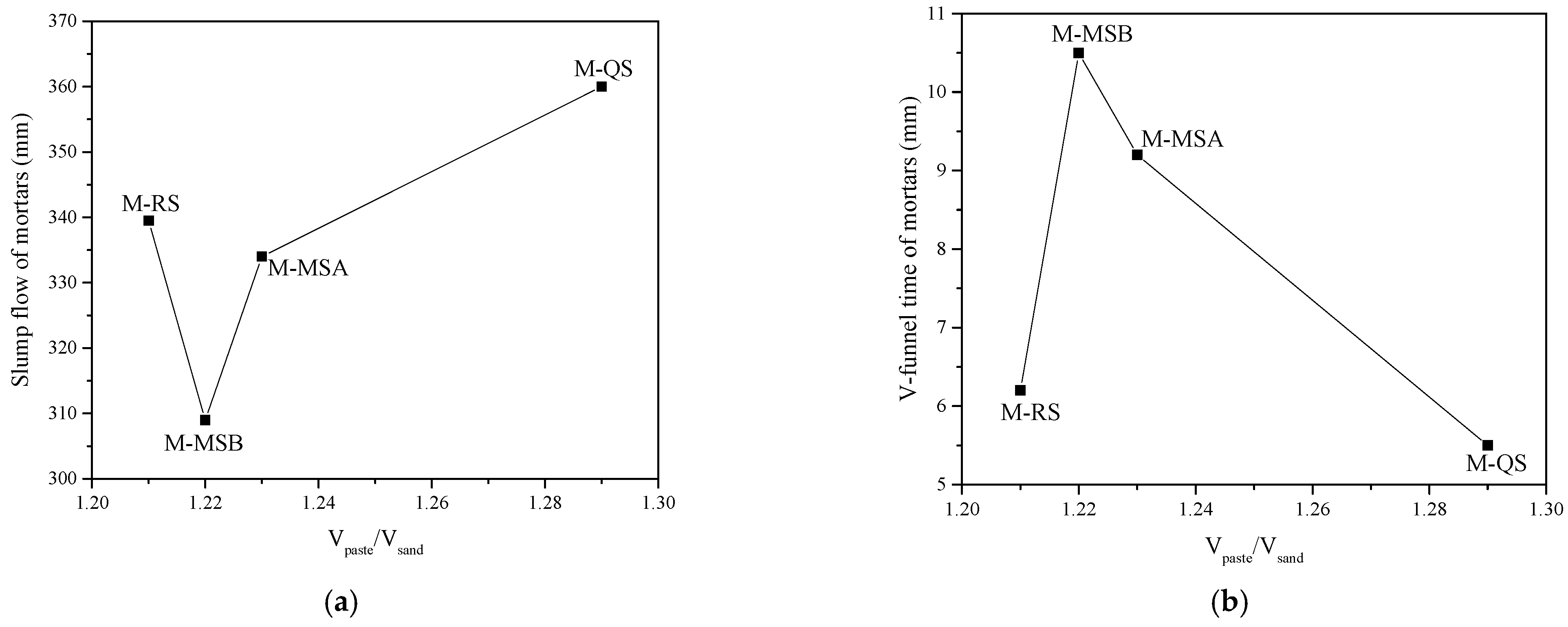
4.1. Effect of Sand Water Absorption on Mortar Rheological Properties
4.2. Effect of Sand Density on Mortar Rheological Properties
4.3. Relationship between Mortar Rheological Results and Shape–Weight Parameters
4.4. Comparison of SCP Zone and SCM Zones
4.5. Prediction of SCM Zone
5. Conclusions
- The changing trends in slump flows and V-funnel times of different mortars in the SSD conditions are similar to those in the OD conditions. The slump flow of mortar for the same sand in SSD conditions is greater than that in OD conditions, whereas the V-funnel time of mortar for the same sand in SSD conditions is less than that in OD conditions. The effect of different water absorption of different sands on mortar rheology can be eliminated by conducting tests in SSD conditions;
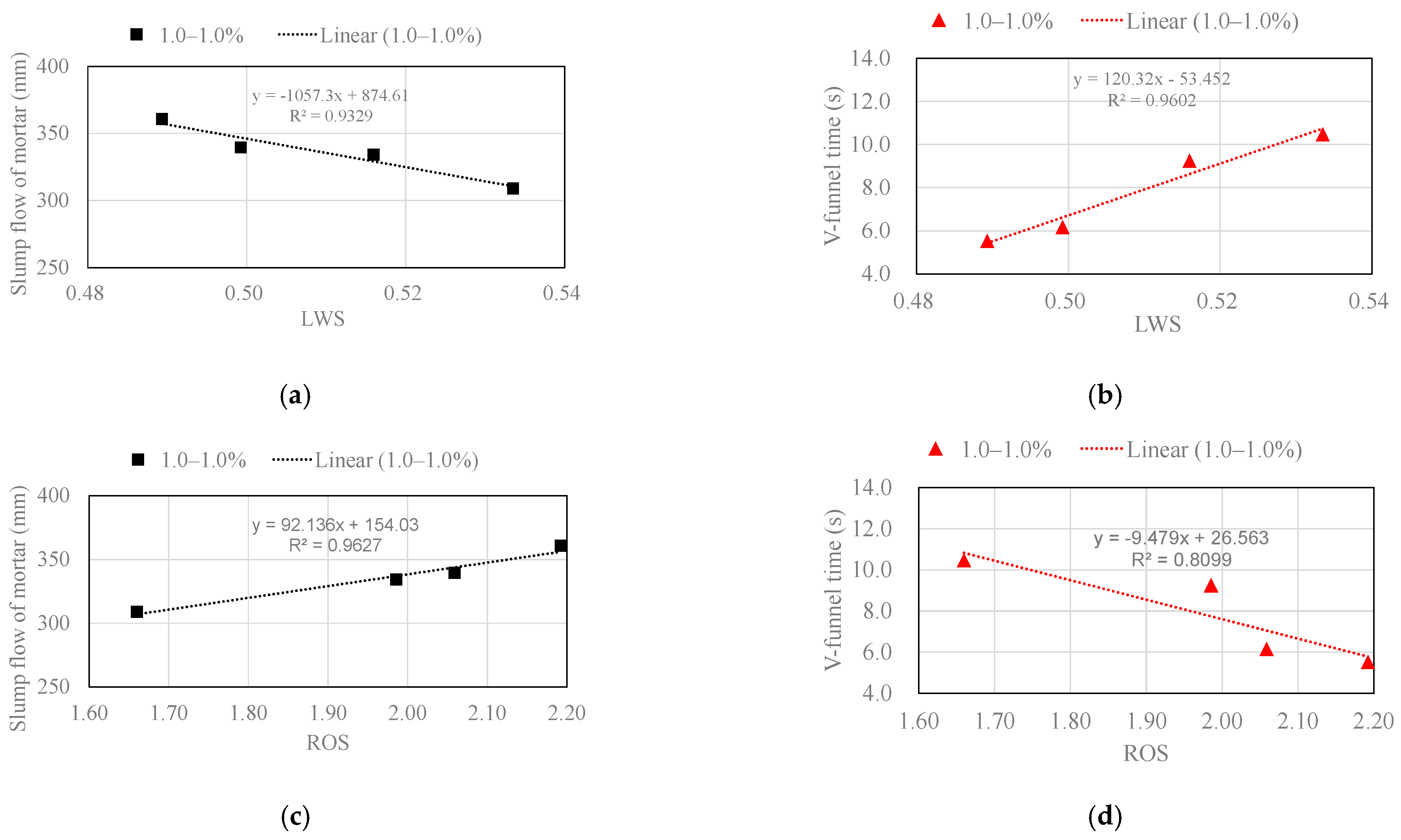
- LWS and ROS were selected to quantify the compound effects of sand type on mortar rheology. Regression analysis showed an excellent linear correlation between slump flow and LWS, with R2 = 0.9863, or ROS, with R2 = 0.9286. A very good linear correlation also existed between V-funnel time and LWS, with R2 = 0.9625, or ROS, with R2 = 0.8159;
- The substantial overlap between the SCP zone and the SCM zone for RS indicated the validity of paste rheological threshold theory and mortar rheological threshold theory for obtaining the SCM zone;
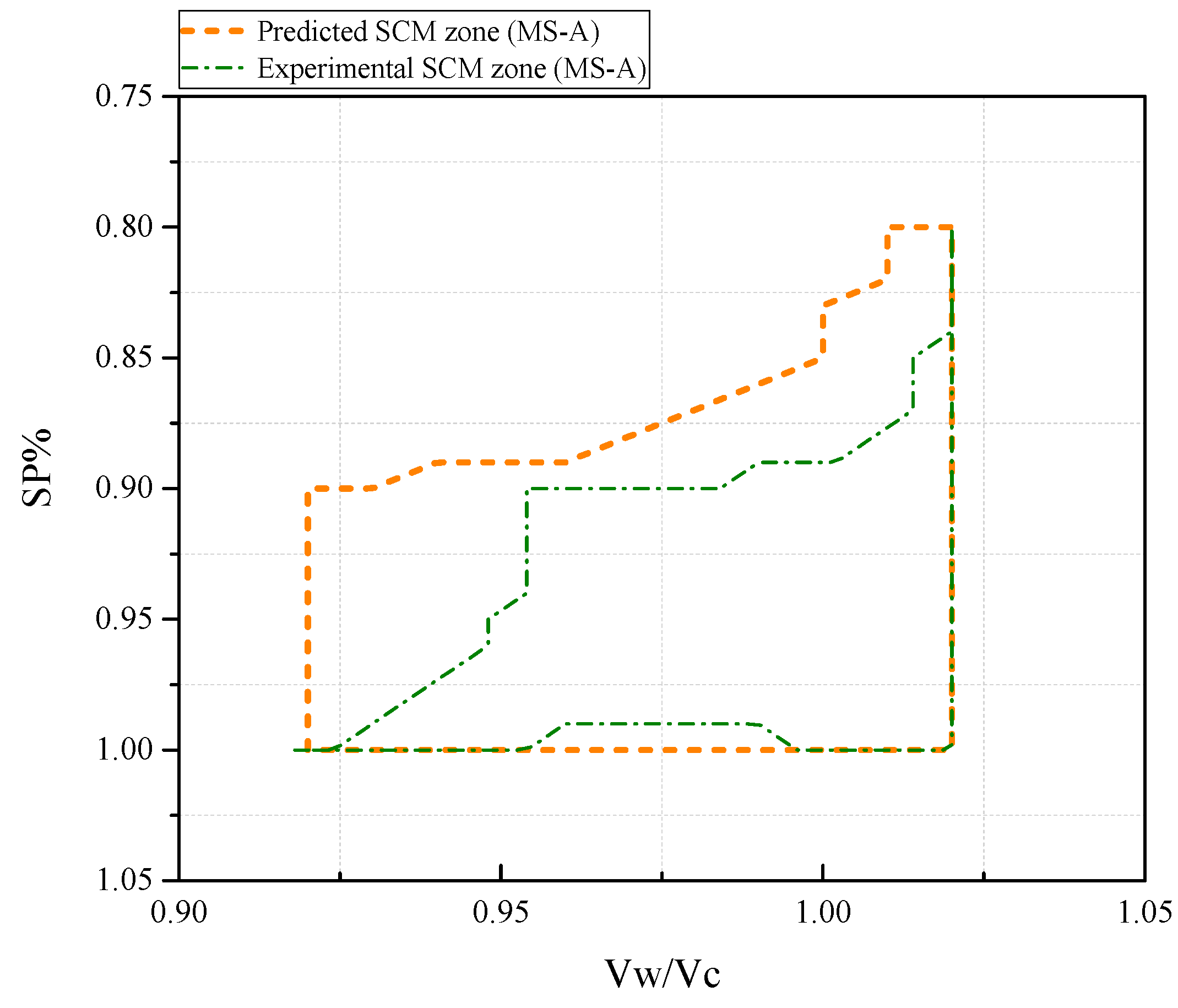
- Based on the particle shape–weight parameters, the rheological properties of mortars could be predicted. Based on the mortar rheological threshold theory, the SCM zone can be drawn. The predicted SCM zone overlapped considerably with the experimental SCM zone for MS-A.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Okamura, H.; Ouchi, M. Self-compacting concrete. J. Adv. Concr. Technol. 2003, 1, 5–15. [Google Scholar] [CrossRef]
- An, X.; Wu, Q.; Jin, F.; Huang, M.; Zhou, H.; Chen, C.; Liu, C. Rock-filled concrete, the new norm of SCC in hydraulic engineering in China. Cem. Concr. Compos. 2014, 54, 89–99. [Google Scholar] [CrossRef]
- Banfill, P.F.G. Rheology of Fresh Cement and Concrete: Proceedings of an International Conference. Liverpool, 1990; CRC Press: Boca Raton, FL, USA, 1990. [Google Scholar]
- Saak, A.W.; Jennings, H.M.; Surendra, P.S. New Methodology for Designing Self-Compacting Concrete. Mater. J. 2001, 98, 429–439. [Google Scholar]
- Bui, V.K.; Akkaya, Y.; Shah, S.P. Rheological Model for Self-Consolidating Concrete. Mater. J. 2002, 99, 549–559. [Google Scholar]
- Roussel, N. A Theoretical Frame to Study Stability of Fresh Concrete. Mater. Struct. 2006, 39, 81–91. [Google Scholar] [CrossRef]
- Chidiac, S.E.; Mahmoodzadeh, F. Plastic viscosity of fresh concrete—A critical review of predictions methods. Cem. Concr. Compos. 2009, 31, 535–544. [Google Scholar] [CrossRef]
- Hu, J.; Wang, K. Effect of coarse aggregate characteristics on concrete rheology. Constr. Build. Mater. 2011, 25, 1196–1204. [Google Scholar] [CrossRef]
- Wu, Q.; An, X. Development of a mix design method for SCC based on the rheological characteristics of paste. Constr. Build. Mater. 2014, 53, 642–651. [Google Scholar] [CrossRef]
- Zhang, J.; An, X.; Nie, D. Effect of fine aggregate characteristics on the thresholds of self-compacting paste rheological properties. Constr. Build. Mater. 2016, 116, 355–365. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, J.; An, X.; Qi, B.; Shen, D.; Lv, M. Effects of fly ash and limestone powder on the paste rheological thresholds of self-compacting concrete. Constr. Build. Mater. 2021, 281, 122560. [Google Scholar] [CrossRef]
- Li, P.; Zhang, T.; An, X.; Zhang, J. An enhanced mix design method of self-compacting concrete with fly ash content based on paste rheological threshold theory and material packing characteristics. Constr. Build. Mater. 2020, 234, 117380. [Google Scholar] [CrossRef]
- Li, P.; Ran, J.; Nie, D.; Zhang, W. Improvement of mix design method based on paste rheological threshold theory for self-compacting concrete using different mineral additions in ternary blends of powders. Constr. Build. Mater. 2021, 276, 122194. [Google Scholar] [CrossRef]
- Geiker, M.R.; Brandl, M.; Thrane, L.N.; Nielsen, L.F. On the effect of coarse aggregate fraction and shape on the rheological properties of self-compacting concrete. Cem. Concr. Aggreg. 2002, 24, 3–6. [Google Scholar]
- Hu, J.; Wang, K. Effects of Size and Uncompacted Voids of Aggregate on Mortar Flow Ability. J. Adv. Concr. Technol. 2007, 5, 75–85. [Google Scholar] [CrossRef] [Green Version]
- Li, P.; Lu, W.; An, X.; Zhou, L.; Du, S. Effect of Epoxy Latexes on the Mechanical Behavior and Porosity Property of Cement Mortar with Different Degrees of Hydration and Polymerization. Materials 2021, 14, 517. [Google Scholar] [CrossRef] [PubMed]
- Bajad, M.N.; Sakhare, S. Influence of artificial sand on the properties of concrete and mortar. Int. J. Civ. Eng. Technol. 2018, 9, 447–454. [Google Scholar]
- Cortes, D.D.; Kim, H.K.; Palomino, A.M.; Santamarina, J.C. Rheological and mechanical properties of mortars prepared with natural and manufactured sands. Cem. Concr. Res. 2008, 38, 1142–1147. [Google Scholar] [CrossRef]
- Harini, M.; Shaalini, G.; Dhinakaran, G. Effect of size and type of fine aggregates on flowability of mortar. KSCE J. Civ. Eng. 2011, 16, 163–168. [Google Scholar] [CrossRef]
- Zeghichi, L.; Benghazi, Z.; Baali, L. The Effect of the Kind of Sands and Additions on the Mechanical Behaviour of S.C.C. Phys. Procedia 2014, 55, 485–492. [Google Scholar] [CrossRef] [Green Version]
- Ling, S.K.; Kwan, A.K.H. Adding ground sand to decrease paste volume, increase cohesiveness and improve passing ability of SCC. Constr. Build. Mater. 2015, 84, 46–53. [Google Scholar] [CrossRef]
- De Oliveira Haddad, L.D.; Neves, R.R.; De Oliveira, P.V.; Dos Santos, W.J.; De Carvalho Junior, A.N. Influence of particle shape and size distribution on coating mortar properties. J. Mater. Res. Technol. 2020, 9, 9299–9314. [Google Scholar] [CrossRef]
- Ren, Q.; De Schutter, G.; Jiang, Z.; Chen, Q. Multi-level diffusion model for manufactured sand mortar considering particle shape and limestone powder effects. Constr. Build. Mater. 2019, 207, 218–227. [Google Scholar] [CrossRef]
- Ren, Q.; Tao, Y.; Jiao, D.; Jiang, Z.; Ye, G.; De Schutter, G. Plastic viscosity of cement mortar with manufactured sand as influenced by geometric features and particle size. Cem. Concr. Compos. 2021, 122, 104163. [Google Scholar] [CrossRef]
- Wang, L.; Guo, F.; Lin, Y.; Yang, H.; Tang, S.W. Comparison between the effects of phosphorous slag and fly ash on the CSH structure, long-term hydration heat and volume deformation of cement-based materials. Constr. Build. Mater. 2020, 250, 118807. [Google Scholar] [CrossRef]
- Wang, L.; Jin, M.; Zhou, S.; Tang, S.; Lu, X. Investigation of microstructure of CSH and micro-mechanics of cement pastes under NH4NO3 dissolution by 29Si MAS NMR and microhardness. Measurement 2021, 185, 110019. [Google Scholar] [CrossRef]
- Tang, S.; Wang, Y.; Geng, Z.; Xu, X.; Yu, W.; Chen, J. Structure, fractality, mechanics and durability of calcium silicate hydrates. Fractal Fract. 2021, 5, 47. [Google Scholar] [CrossRef]
- Shen, D.; Wang, W.; Li, Q.; Yao, P.; Jiang, G. Early-age behaviour and cracking potential of fly ash concrete under restrained condition. Mag. Concr. Res. 2020, 72, 246–261. [Google Scholar] [CrossRef]
- Shen, D.; Liu, X.; Zhou, B.; Zeng, X.; Du, J. Influence of initial cracks on the frequency of a 60-year-old reinforced-concrete box beam. Mag. Concr. Res. 2021, 73, 121–134. [Google Scholar] [CrossRef]
- Shen, D.; Jiao, Y.; Kang, J.; Feng, Z.; Shen, Y. Influence of ground granulated blast furnace slag on early-age cracking potential of internally cured high performance concrete. Constr. Build. Mater. 2020, 233, 117083. [Google Scholar] [CrossRef]
- Mora, C.; Kwan, A.; Chan, H. Particle size distribution analysis of coarse aggregate using digital image processing. Cem. Concr. Res. 1998, 28, 921–932. [Google Scholar] [CrossRef]
- Kwan, A.K.; Mora, C.; Chan, H. Particle shape analysis of coarse aggregate using digital image processing. Cem. Concr. Res. 1999, 29, 1403–1410. [Google Scholar] [CrossRef]
- Mora, C.; Kwan, A. Sphericity, shape factor, and convexity measurement of coarse aggregate for concrete using digital image processing. Cem. Concr. Res. 2000, 30, 351–358. [Google Scholar] [CrossRef]
- Rao, C.; Tutumluer, E.; Kim, I.T. Quantification of coarse aggregate angularity based on image analysis. Transp. Res. Rec. 2002, 1787, 117–124. [Google Scholar] [CrossRef]
- Fletcher, T.; Chandan, C.; Masad, E.; Sivakumar, K. Aggregate imaging system for characterizing the shape of fine and coarse aggregates. Transp. Res. Rec. 2003, 1832, 67–77. [Google Scholar] [CrossRef] [Green Version]
- Marinoni, N.; Pavese, A.; Foi, M.; Trombino, L. Characterisation of mortar morphology in thin sections by digital image processing. Cem. Concr. Res. 2005, 35, 1613–1619. [Google Scholar] [CrossRef]
- Bouquety, M.N.; Descantes, Y.; Barcelo, L.; De Larrard, F.; Clavaud, B. Experimental study of crushed aggregate shape. Constr. Build. Mater. 2007, 21, 865–872. [Google Scholar] [CrossRef]
- Shen, D.; Liu, C.; Wang, M.; Kang, J.; Li, M. Effect of polyvinyl alcohol fiber on the cracking risk of high strength concrete under uniaxial restrained condition at early age. Constr. Build. Mater. 2021, 300, 124206. [Google Scholar] [CrossRef]
- Podczeck, F. A shape factor to assess the shape of particles using image analysis. Powder Technol. 1997, 93, 47–53. [Google Scholar] [CrossRef]
- Fernlund, J.M.R. Image analysis method for determining 3-D shape of coarse aggregate. Cem. Concr. Res. 2005, 35, 1629–1637. [Google Scholar] [CrossRef]
- Fernlund, J.M.R. 3-D image analysis size and shape method applied to the evaluation of the Los Angeles test. Eng. Geol. 2005, 77, 57–67. [Google Scholar] [CrossRef]
- Lin, C.L.; Miller, J.D. 3D characterization and analysis of particle shape using X-ray microtomography (XMT). Powder Technol. 2005, 154, 61–69. [Google Scholar] [CrossRef]
- Cepuritis, R.; Wigum, B.J.; Garboczi, E.J.; Mørtsell, E.; Jacobsen, S. Filler from crushed aggregate for concrete: Pore structure, specific surface, particle shape and size distribution. Cem. Concr. Compos. 2014, 54, 2–16. [Google Scholar] [CrossRef]
- Jamkar, S.S.; Rao, C.B.K. Index of Aggregate Particle Shape and Texture of coarse aggregate as a parameter for concrete mix proportioning. Cem. Concr. Res. 2004, 34, 2021–2027. [Google Scholar] [CrossRef]
- Westerholm, M.; Lagerblad, B.; Silfwerbrand, J.; Forssberg, E. Influence of fine aggregate characteristics on the rheological properties of mortars. Cem. Concr. Compos. 2008, 30, 274–282. [Google Scholar] [CrossRef]
- Hafid, H.; Ovarlez, G.; Toussaint, F.; Jezequel, P.H.; Roussel, N. Effect of particle morphological parameters on sand grains packing properties and rheology of model mortars. Cem. Concr. Res. 2016, 80, 44–51. [Google Scholar] [CrossRef]
- Shen, W.; Yang, Z.; Cao, L.; Cao, L.; Liu, Y.; Yang, H.; Lu, Z.; Bai, J. Characterization of manufactured sand: Particle shape, surface texture and behavior in concrete. Constr. Build. Mater. 2016, 114, 595–601. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, L. Effect of Particle Shape of Limestone Manufactured Sand and Natural Sand on Concrete. Procedia Eng. 2017, 210, 87–92. [Google Scholar]
- Estephane, P.; Garboczi, E.J.; Bullard, J.W.; Wallevik, O.H. Three-dimensional shape characterization of fine sands and the influence of particle shape on the packing and workability of mortars. Cem. Concr. Compos. 2019, 97, 125–142. [Google Scholar] [CrossRef]
- Zhang, J.; An, X.; Yu, Y.; Nie, D. Effects of coarse aggregate content on the paste rheological thresholds of fresh self-compacting concrete. Constr. Build. Mater. 2019, 208, 564–576. [Google Scholar] [CrossRef]
- Toutou, Z.; Roussel, N. Multi Scale Experimental Study of Concrete Rheology: From Water Scale to Gravel Scale. Mater. Struct. 2006, 39, 189–199. [Google Scholar] [CrossRef]
- Krieger, I.M.; Dougherty, T.J. A mechanism for non-Newtonian flow in suspensions of rigid spheres. Trans. Soc. Rheol. 1959, 3, 137–152. [Google Scholar] [CrossRef]
- Roussel, N.; Stefani, C.; Leroy, R. From mini-cone test to Abrams cone test: Measurement of cement-based materials yield stress using slump tests. Cem. Concr. Res. 2005, 35, 817–822. [Google Scholar] [CrossRef]
- Chidiac, S.E.; Maadani, O.; Razaqpur, A.G.; Mailvaganam, N.P. Controlling the quality of fresh concrete—A new approach. Mag. Concr. Res. 2000, 52, 353–363. [Google Scholar] [CrossRef] [Green Version]
- Nie, D.; An, X. Optimization of SCC mix at paste level by using numerical method based on a paste rheological threshold theory. Constr. Build. Mater. 2016, 102, 428–434. [Google Scholar] [CrossRef]
- Nie, D.; An, X. Mini slump flow measurement tool based on self phase image processing. J. Tsinghua Univ. 2016, 56, 1249–1254. [Google Scholar]
- Zhang, J.; An, X.; Li, P. Research on a mix design method of self-compacting concrete based on a paste rheological threshold theory and a powder equivalence model. Constr. Build. Mater. 2020, 233, 117292. [Google Scholar] [CrossRef]
- Zhang, J.; Lv, M.; An, X.; Shen, D.; He, X.; Nie, D. Improved Powder Equivalence Model for the Mix Design of Self-Compacting Concrete with Fly Ash and Limestone Powder. Adv. Mater. Sci. Eng. 2021, 2021, 1–12. [Google Scholar]
- Chai, H.W. Design and testing of self-compacting concrete. Ph.D. Thesis, University of London, London, UK, 1998. [Google Scholar]
- Şahmaran, M.; Christianto, H.A.; Yaman, İ.Ö. The effect of chemical admixtures and mineral additives on the properties of self-compacting mortars. Cem. Concr. Compos. 2006, 28, 432–440. [Google Scholar] [CrossRef]
- Adjoudj, M.; Ezziane, K.; Kadri, E.H.; Soualhi, H. Study of the Rheological Behavior of Mortar with Silica Fume and Superplasticizer Admixtures According to the Water Film Thickness. KSCE J. Civ. Eng. 2018, 22, 2480–2491. [Google Scholar] [CrossRef]




| Mix ID * | [VW/VC]OD | SP% | Cement (g) | Water (g) | SP (g) | Sand (g) | SF (mm) | Vt (s) |
|---|---|---|---|---|---|---|---|---|
| M-QS(OD) | 1.0 | 1.0 | 1108.3 | 348.5 | 11.08 | 1579.5 | 355 | 5.62 |
| M-RS(OD) | 1.0 | 1.0 | 1108.3 | 348.5 | 11.08 | 1579.5 | 329 | 6.36 |
| M-MSA(OD) | 1.0 | 1.0 | 1108.3 | 348.5 | 11.08 | 1579.5 | 306 | 10.10 |
| M-MSB(OD) | 1.0 | 1.0 | 1108.3 | 348.5 | 11.08 | 1579.5 | 277.5 | 11.66 |
| Mix ID | [VW/VC]SSD | SP% | Cement (g) | Water + Additional Water (g) | SP (g) | Sand (g) | SF (mm) | Vt (s) |
|---|---|---|---|---|---|---|---|---|
| M-QS(SSD) | 1.0 | 1.0 | 1108.3 | 348.5 + 5.5 | 11.08 | 1579.5 | 360.0 | 5.50 |
| M-RS(SSD) | 1.0 | 1.0 | 1108.3 | 348.5 + 11.1 | 11.08 | 1579.5 | 339.5 | 6.20 |
| M-MSA(SSD) | 1.0 | 1.0 | 1108.3 | 348.5 + 30.0 | 11.08 | 1579.5 | 334.0 | 9.20 |
| M-MSB(SSD) | 1.0 | 1.0 | 1108.3 | 348.5 + 36.3 | 11.08 | 1579.5 | 309.0 | 10.50 |
| [VW/VC]SSD | SP% | Paste Rheological Properties | M-RS(SSD) | M-MSA(SSD) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| SF (mm) | T200 (s) | τthreshold (Pa) | ηthreshold (Pa·s) | τpaste (Pa) | ηpaste (Pa·s) | SFmortar (mm) | Vt (s) | SFmortar (mm) | Vt (s) | ||
| 0.90 | 0.80 | 298 | 4.24 | 1.20 | 17.2 | 0.62 | 55.4 | 239 | 14.98 | 115 | 44.84 |
| 0.90 | 0.90 | 289 | 3.96 | 1.20 | 17.2 | 0.72 | 51.7 | 293 | 10.53 | 144 | 30.24 |
| 0.90 | 1.00 | 306 | 3.44 | 1.20 | 17.2 | 0.54 | 44.9 | 303 | 10.11 | 169 | 18.08 |
| 0.96 | 0.80 | 288 | 3.81 | 1.19 | 18.3 | 0.72 | 49.1 | 298 | 8.32 | 145 | 21.23 |
| 0.96 | 0.90 | 313 | 3.00 | 1.19 | 18.3 | 0.50 | 38.8 | 323 | 7.81 | 231 | 10.36 |
| 0.96 | 1.00 | 338 | 2.02 | 1.19 | 18.3 | 0.35 | 26.2 | 325 | 6.90 | 286 | 8.90 |
| 1.02 | 0.80 | 290 | 3.22 | 1.18 | 19.3 | 0.71 | 40.9 | 311 | 6.54 | 229 | 6.49 |
| 1.02 | 0.90 | 331 | 2.26 | 1.18 | 19.3 | 0.34 | 28.6 | 330 | 6.32 | 279 | 6.70 |
| 1.02 | 1.00 | 353 | 1.17 | 1.18 | 19.3 | 0.25 | 14.9 | 336 | 5.97 | 316 | 7.11 |
| [VW/VC]SSD | SP% | Sand Type | Length:Width Ratio | Roundness | Specific Gravity | LWS | ROS | SFmortar (mm) | Vt (s) |
|---|---|---|---|---|---|---|---|---|---|
| 1.0 | 1.0 | QS | 1.39 | 0.77 | 2.84 | 0.489 | 2.19 | 360.0 | 5.50 |
| 1.0 | 1.0 | RS | 1.33 | 0.77 | 2.67 | 0.499 | 2.06 | 339.5 | 6.20 |
| 1.0 | 1.0 | MS-A | 1.39 | 0.74 | 2.70 | 0.516 | 1.99 | 334.0 | 9.20 |
| 1.0 | 1.0 | MS-B | 1.43 | 0.62 | 2.68 | 0.534 | 1.66 | 309.0 | 10.50 |
| [VW/VC]SSD | SP% | τpaste (Pa) | ηpaste (Pa·s) | LWS | ROS | SFmortar (mm) | Vt (s) |
|---|---|---|---|---|---|---|---|
| 0.90 | 0.80 | 0.62 | 55.4 | 0.499 | 2.06 | 239 | 14.98 |
| 0.90 | 0.90 | 0.72 | 51.7 | 0.499 | 2.06 | 293 | 10.53 |
| 0.90 | 1.00 | 0.54 | 44.9 | 0.499 | 2.06 | 303 | 10.11 |
| 0.96 | 0.80 | 0.72 | 49.1 | 0.499 | 2.06 | 298 | 8.32 |
| 0.96 | 0.90 | 0.50 | 38.8 | 0.499 | 2.06 | 323 | 7.81 |
| 0.96 | 1.00 | 0.35 | 26.2 | 0.499 | 2.06 | 325 | 6.90 |
| 1.02 | 0.80 | 0.71 | 40.9 | 0.499 | 2.06 | 311 | 6.54 |
| 1.02 | 0.90 | 0.34 | 28.6 | 0.499 | 2.06 | 330 | 6.32 |
| 1.02 | 1.00 | 0.25 | 14.9 | 0.499 | 2.06 | 336 | 5.97 |
| 0.90 | 0.80 | 0.62 | 55.4 | 0.516 | 1.99 | 115 | 44.84 |
| 0.90 | 0.90 | 0.72 | 51.7 | 0.516 | 1.99 | 144 | 30.24 |
| 0.90 | 1.00 | 0.54 | 44.9 | 0.516 | 1.99 | 169 | 18.08 |
| 0.96 | 0.80 | 0.72 | 49.1 | 0.516 | 1.99 | 145 | 21.23 |
| 0.96 | 0.90 | 0.50 | 38.8 | 0.516 | 1.99 | 231 | 10.36 |
| 0.96 | 1.00 | 0.35 | 26.2 | 0.516 | 1.99 | 286 | 8.90 |
| 1.02 | 0.80 | 0.71 | 40.9 | 0.516 | 1.99 | 229 | 6.49 |
| 1.02 | 0.90 | 0.34 | 28.6 | 0.516 | 1.99 | 279 | 6.70 |
| 1.02 | 1.00 | 0.25 | 14.9 | 0.516 | 1.99 | 316 | 7.11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Zhang, J.; An, X.; Qi, B.; Li, W.; Shen, D.; Li, P.; Lv, M. The Effect of Sand Type on the Rheological Properties of Self-Compacting Mortar. Buildings 2021, 11, 441. https://doi.org/10.3390/buildings11100441
Yang S, Zhang J, An X, Qi B, Li W, Shen D, Li P, Lv M. The Effect of Sand Type on the Rheological Properties of Self-Compacting Mortar. Buildings. 2021; 11(10):441. https://doi.org/10.3390/buildings11100441
Chicago/Turabian StyleYang, Song, Jingbin Zhang, Xuehui An, Bing Qi, Wenqiang Li, Dejian Shen, Pengfei Li, and Miao Lv. 2021. "The Effect of Sand Type on the Rheological Properties of Self-Compacting Mortar" Buildings 11, no. 10: 441. https://doi.org/10.3390/buildings11100441
APA StyleYang, S., Zhang, J., An, X., Qi, B., Li, W., Shen, D., Li, P., & Lv, M. (2021). The Effect of Sand Type on the Rheological Properties of Self-Compacting Mortar. Buildings, 11(10), 441. https://doi.org/10.3390/buildings11100441







