Floor Acceleration Demands in a Twelve-Storey RC Shear Wall Building
Abstract
1. Introduction
2. Description of the Analysed Structure
3. Analysis Overview
3.1. Properties of the Considered Structural and NSC Models
3.1.1. Structural Model
3.1.2. NSC Model
3.2. Seismic Inputs for the RHA and Direct Method
3.3. A Brief Summary of the Method for the Direct Determination of PFAs and FRS
- Initial calculations in terms of the elastic modal analysis have to be conducted, in order to determine the following dynamic properties of the structure: natural periods Tp,i, mode shapes ϕij and modal participation factors Γi (i denotes the mode and j denotes the floor).
- In the case of nonlinear structural behaviour, the method needs to be used in conjunction with the N2 method, as integrated into Eurocode 8 (for more details on the N2 method see Fajfar [33,34]). It is therefore assumed that nonlinear behaviour applies only to the fundamental mode. A mode shape {ϕ1} is represented by the inelastic deformation shape, and all higher modes are treated as linear elastic. Nonlinear structural behaviour is taken into account through a ductility dependent reduction factor Rµ proposed by Vidic et al. [35]:
- 3.
- FRS at considered floors and for individual modes taken into account should be determined as:
- 4.
- The resulting FRS should be determined by combining the FRS values obtained for individual modes. In the range of the periods of NSCs from Ts = 0 up to and including the end of the plateau of the resonance region of the fundamental mode (Ts = Tp,1), the SRSS or Complete Quadratic Combination (CQC) modal combination rules are used. In the post-resonance region of the fundamental mode, the algebraic sum (ALGSUM) should be applied, with the relevant signs of individual modes taken into account. The upper limit of the resulting floor spectrum calculated from the ALGSUM is represented by the plateau obtained for the resonance region of the fundamental mode by using the SRSS or CQC rules.
3.4. A Step-by-Step Application of the Direct Method
3.4.1. Elastic Modal Analysis
3.4.2. Pushover Analysis of the Structure
3.4.3. Determination of PFAs and FRS
3.4.4. Resulting PFAs and FRS
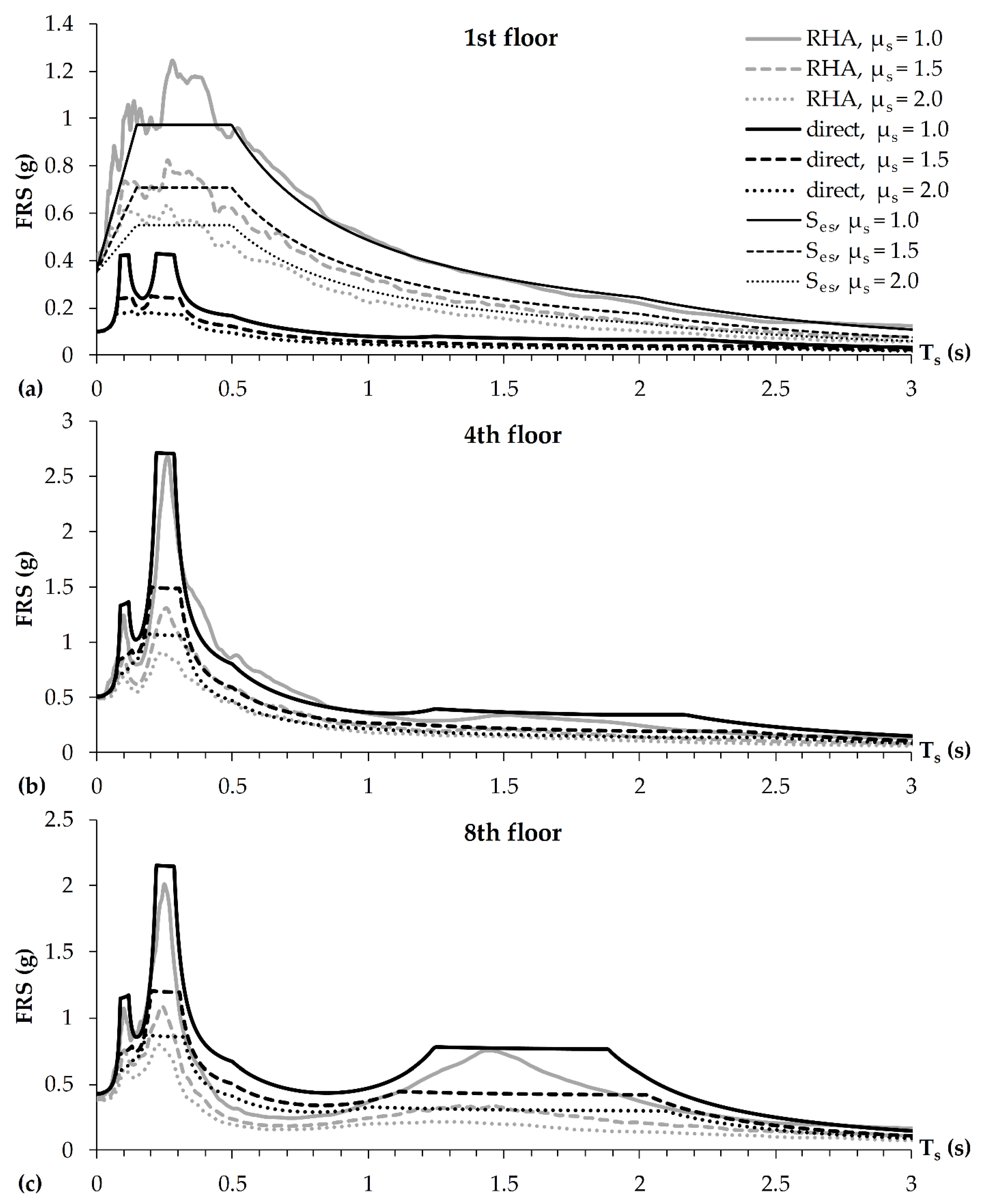
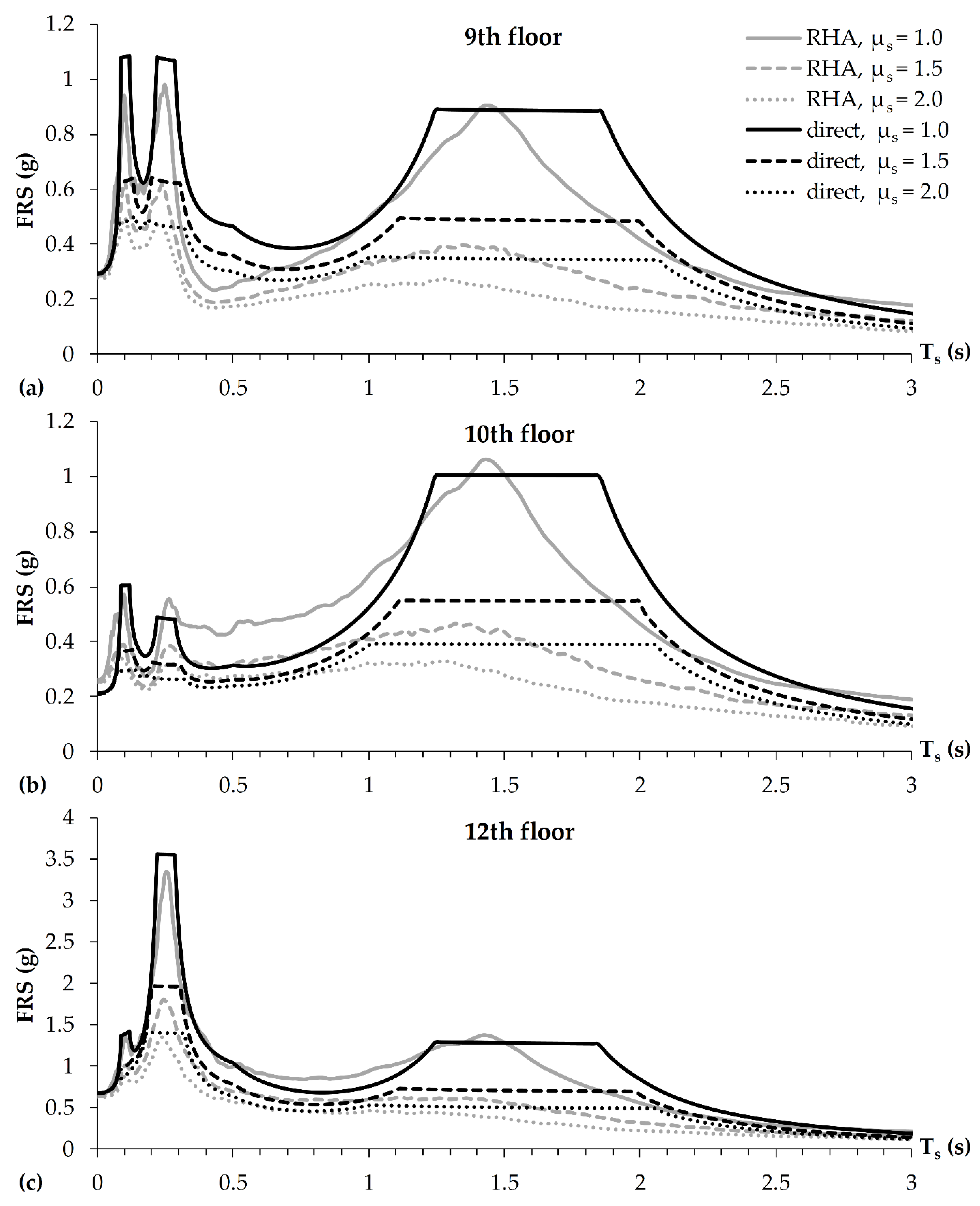
4. Results and Discussion
4.1. Peak Floor Accelerations
4.2. Floor Response Spectra
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Petrone, C.; Magliulo, G.; Manfredi, G. Seismic demand on light acceleration-sensitive nonstructural components in European reinforced concrete buildings. Earthq. Eng. Struct. Dyn. 2015, 44, 1203–1217. [Google Scholar] [CrossRef]
- Petrone, C.; Magliulo, G.; Manfredi, G. Floor response spectra in RC frame structures designed according to Eurocode 8. Bull. Earthq. Eng. 2016, 14, 747–767. [Google Scholar] [CrossRef]
- Vukobratović, V.; Fajfar, P. A method for the direct determination of approximate floor response spectra for SDOF inelastic structures. Bull. Earthq. Eng. 2015, 13, 1405–1424. [Google Scholar] [CrossRef]
- Vukobratović, V.; Fajfar, P. A method for the direct estimation of floor acceleration spectra for elastic and inelastic MDOF structures. Earthq. Eng. Struct. Dyn. 2016, 45, 2495–2511. [Google Scholar] [CrossRef]
- Lucchini, A.; Franchin, P.; Mollaioli, F. Uniform hazard floor acceleration spectra for linear structures. Earthq. Eng. Struct. Dyn. 2017, 46, 1121–1140. [Google Scholar] [CrossRef]
- Kothari, P.; Parulekar, Y.M.; Reddy, G.R.; Gopalakrishnan, N. In-structure response spectra considering nonlinearity of RCC structures: Experiments and analysis. Nucl. Eng. Des. 2017, 322, 379–396. [Google Scholar] [CrossRef]
- Anajafi, H.; Medina, R.A. Evaluation of ASCE 7 equations for designing acceleration-sensitive nonstructural components using data from instrumented buildings. Earthq. Eng. Struct. Dyn. 2018, 47, 1075–1094. [Google Scholar] [CrossRef]
- Surana, M.; Singh, Y.; Lang, D.H. Floor Spectra of Inelastic RC Frame Buildings Considering Ground Motion Characteristics. J. Earthq. Eng. 2018, 22, 488–519. [Google Scholar] [CrossRef]
- Filiatrault, A.; Perrone, D.; Merino, R.J.; Calvi, G.M. Performance-based seismic design of nonstructural building elements. J. Earthq. Eng. 2018, 1–33. [Google Scholar] [CrossRef]
- Merino, R.J.; Perrone, D.; Filiatrault, A. Consistent floor response spectra for performance-based seismic design of non-structural elements. Earthq. Eng. Struct. Dyn. 2020, 49, 261–284. [Google Scholar] [CrossRef]
- Kazantzi, A.K.; Vamvatsikos, D.; Miranda, E. Evaluation of seismic acceleration demands on building nonstructural elements. ASCE J. Struct. Eng. 2020, 146, 1–15. [Google Scholar] [CrossRef]
- Gabbianelli, G.; Perrone, D.; Brunesi, E.; Monteiro, R. Seismic acceleration and displacement demand profiles of non-structural elements in hospital buildings. Buildings 2020, 10, 243. [Google Scholar] [CrossRef]
- Vukobratović, V. The Influence of Nonlinear Seismic Response of Structures on the Floor Acceleration Spectra. Ph.D. Thesis, University of Ljubljana, Ljubljana, Slovenia, 2015. Available online: http://drugg.fgg.uni-lj.si/5153/ (accessed on 10 November 2020).
- Kelly, T.E. Floor response of yielding structures. Bull. N. Z. Natl. Soc. Earth Eng. 1978, 11, 255–272. Available online: http://www.nzsee.org.nz/db/Bulletin/Archive/11(4)0255.pdf (accessed on 10 November 2020).
- Hadjian, A.H. Seismic response of structures by the response spectrum method. Nucl. Eng. Des. 1981, 66, 179–201. [Google Scholar] [CrossRef]
- Rodriguez, M.E.; Restrepo, J.I.; Carr, A.J. Earthquake-induced floor horizontal accelerations in buildings. Earthq. Eng. Struct. Dyn. 2002, 31, 693–718. [Google Scholar] [CrossRef]
- Viti, G.; Olivieri, M.; Travi, S. Development of non-linear floor response spectra. Nucl. Eng. Des. 1981, 64, 33–38. [Google Scholar] [CrossRef]
- Adam, C.; Fotiu, P.A. Dynamic analysis of inelastic primary-secondary systems. Eng. Struct. 2000, 22, 58–71. [Google Scholar] [CrossRef]
- Villaverde, R. Simple method to estimate the seismic nonlinear response of nonstructural components in buildings. Eng. Struct. 2006, 28, 1209–1221. [Google Scholar] [CrossRef]
- Chaudhuri, S.R.; Villaverde, R. Effect of building nonlinearity on seismic response of nonstructural components: A parametric study. ASCE J. Struct. Eng. 2008, 134, 661–670. [Google Scholar] [CrossRef]
- Tamura, I.; Matsuura, S.; Shimazu, R. Yield strength reduction factor of nonlinear SDOF systems on the supporting structures. In Proceedings of the ASME 2016 Pressure Vessels and Piping Conference (PVP 2016), Vancouver, BC, Canada, 17–21 July 2016. [Google Scholar] [CrossRef]
- Vukobratović, V.; Fajfar, P. Code-oriented floor acceleration spectra for building structures. Bull. Earthq. Eng. 2017, 15, 3013–3026. [Google Scholar] [CrossRef]
- Obando, J.C.; Lopez-Garcia, D. Inelastic displacement ratios for nonstructural components subjected to floor accelerations. J. Earthq. Eng. 2018, 22, 569–594. [Google Scholar] [CrossRef]
- Anajafi, H.; Medina, R.A.; Santini-Bell, E. Inelastic floor spectra for designing anchored acceleration-sensitive nonstructural components. Bull. Earthq. Eng. 2020, 18, 2115–2147. [Google Scholar] [CrossRef]
- Kazantzi, A.K.; Miranda, E.; Vamvatsikos, D. Strength-reduction factors for the design of light nonstructural elements in buildings. Earthq. Eng. Struct. Dyn. 2020, 49, 1329–1343. [Google Scholar] [CrossRef]
- Taghavi, S.; Miranda, E. Response spectrum method for estimation of peak floor acceleration demand. In Proceedings of the ATC and SEI Conference on Improving the Seismic Performance of Existing Buildings and Other Structures, San Francisco, CA, USA, 9–11 December 2009. [Google Scholar] [CrossRef]
- Pozzi, M.; Der Kiureghian, A. Response spectrum analysis for floor acceleration. Earthq. Eng. Struct. Dyn. 2015, 44, 2111–2127. [Google Scholar] [CrossRef]
- Eurocode 8. Design of structures for earthquake resistance—Part 1: General rules, seismic actions and rules for buildings. In European Standard EN 1998-1; European Committee for Standardization: Brussels, Belgium, 2004.
- Eurocode 2. Design of concrete structures—Part 1-1: General rules and rules for buildings. In European Standard EN 1992-1-1; European Committee for Standardization: Brussels, Belgium, 2004.
- ASCE 4-98. Seismic Analysis of Safety-Related Nuclear Structures and Commentary; American Society of Civil Engineers: Reston, VA, USA, 2000.
- Eurocode 8. Design of structures for earthquake resistance—Part 3: Assessment and retrofitting of buildings. In European Standard EN 1998-3; European Committee for Standardization: Brussels, Belgium, 2005.
- Ambraseys, N.; Smit, P.; Sigbjörnsson, R.; Suhadolc, P.; Margaris, B. Internet-Site for European Strong-Motion Data; European Commission, Research-Directorate General, Environment and Climate Programme: Brussels, Belgium, 2002; Available online: http://isesd.hi.is/ (accessed on 26 November 2020).
- Fajfar, P. Capacity spectrum method based on inelastic demand spectra. Earthq. Eng. Struct. Dyn. 1999, 28, 979–993. [Google Scholar] [CrossRef]
- Fajfar, P. A nonlinear analysis method for performance based seismic design. Earthq. Spectr. 2000, 16, 573–592. [Google Scholar] [CrossRef]
- Vidic, T.; Fajfar, P.; Fischinger, M. Consistent inelastic design spectra: Strength and displacement. Earthq. Eng. Struct. Dyn. 1994, 23, 507–521. [Google Scholar] [CrossRef]
- Sullivan, T.J.; Calvi, P.M.; Nascimbene, R. Towards improved floor spectra estimates for seismic design. Earthq. Struct. 2013, 4, 109–132. [Google Scholar] [CrossRef]
- Fajfar, P.; (University of Ljubljana, Ljubljana, Slovenia); Vukobratović, V.; (University of Novi Sad, Novi Sad, Serbia). Personal communication, 2018.
- Pinkawa, M.; Hoffmeister, B.; Feldmann, M. A critical review of current approaches on the determination of seismic force demands on nonstructural components. In Proceedings of the 9th International Conference on Structural Dynamics (EURODYN 2014), Porto, Portugal, 30 June–2 July 2014. [Google Scholar]
- U.S. Nuclear Regulatory Commission. Combining modal responses and spatial components in seismic response analysis. In Regulatory Guide 1.92; U.S. Nuclear Regulatory Commission: Washington, DC, USA, 2006. [Google Scholar]
- U.S. Nuclear Regulatory Commission. Damping values for seismic design of nuclear power plants. In Regulatory Guide 1.61; U.S. Nuclear Regulatory Commission: Washington, DC, USA, 2007. [Google Scholar]
- Phipps, M.; Gillengerten, J.; Lizundia, B.; Medina, R.; Miranda, E.; Pekelnicky, R. Improved seismic design of nonstructural components and systems (ATC-120). In Proceedings of the SEAOC 2017 Convention, San Diego, CA, USA, 13–15 September 2017. [Google Scholar]





| Mode | T (s) | MX (%) | MY (%) |
|---|---|---|---|
| 1X | 1.52 | 64.5 | 0 |
| 2Y | 1.45 | 0 | 64.6 |
| 3torsion | 1.21 | 0 | 0 |
| 4X | 0.26 | 20.6 | 0 |
| 5Y | 0.25 | 0 | 20.6 |
| 6torsion | 0.21 | 0 | 0 |
| 7X | 0.10 | 7.2 | 0 |
| 8Y | 0.10 | 0 | 7.0 |
| 9torsion | 0.08 | 0 | 0 |
| Mode (i) | 1 (elastic) | 2 (elastic) | 3 (elastic) | 1 (nonlinear) |
|---|---|---|---|---|
| Tp,i (s) | 1.45 | 0.25 | 0.10 | 1.54 |
| ϕi1 | 0.01 | −0.11 | 0.36 | 0.04 |
| ϕi2 | 0.05 | −0.32 | 0.82 | 0.10 |
| ϕi3 | 0.10 | −0.55 | 1.11 | 0.16 |
| ϕi4 | 0.17 | −0.76 | 1.06 | 0.24 |
| ϕi5 | 0.25 | −0.89 | 0.66 | 0.32 |
| ϕi6 | 0.34 | −0.91 | 0.05 | 0.41 |
| ϕi7 | 0.44 | −0.82 | −0.55 | 0.51 |
| ϕi8 | 0.55 | −0.60 | −0.92 | 0.60 |
| ϕi9 | 0.66 | −0.28 | −0.91 | 0.70 |
| ϕi10 | 0.77 | 0.11 | −0.50 | 0.80 |
| ϕi11 | 0.89 | 0.55 | 0.20 | 0.90 |
| ϕi12 | 1.0 | 1.0 | 1.0 | 1.0 |
| Γi | 1.47 | −0.70 | 0.35 | 1.47 |
| Mode (i) | 1 | 2 | 3 | SRSS Comb. |
|---|---|---|---|---|
| Sep,i (g) | 0.28 | 0.87 | 0.57 | - |
| Rµ | 1.9 | 1.0 | 1.0 | - |
| PFAi1 (g) | 0.01 | 0.07 | 0.07 | 0.10 |
| PFAi2 (g) | 0.02 | 0.19 | 0.16 | 0.25 |
| PFAi3 (g) | 0.03 | 0.33 | 0.22 | 0.40 |
| PFAi4 (g) | 0.05 | 0.46 | 0.21 | 0.51 |
| PFAi5 (g) | 0.07 | 0.54 | 0.13 | 0.56 |
| PFAi6 (g) | 0.09 | 0.55 | 0.01 | 0.56 |
| PFAi7 (g) | 0.11 | 0.50 | −0.11 | 0.52 |
| PFAi8 (g) | 0.13 | 0.37 | −0.18 | 0.43 |
| PFAi9 (g) | 0.15 | 0.17 | −0.18 | 0.29 |
| PFAi10 (g) | 0.17 | −0.07 | −0.10 | 0.21 |
| PFAi11 (g) | 0.19 | −0.33 | 0.04 | 0.38 |
| PFAi12 (g) | 0.22 | −0.61 | 0.20 | 0.68 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vukobratović, V.; Ruggieri, S. Floor Acceleration Demands in a Twelve-Storey RC Shear Wall Building. Buildings 2021, 11, 38. https://doi.org/10.3390/buildings11020038
Vukobratović V, Ruggieri S. Floor Acceleration Demands in a Twelve-Storey RC Shear Wall Building. Buildings. 2021; 11(2):38. https://doi.org/10.3390/buildings11020038
Chicago/Turabian StyleVukobratović, Vladimir, and Sergio Ruggieri. 2021. "Floor Acceleration Demands in a Twelve-Storey RC Shear Wall Building" Buildings 11, no. 2: 38. https://doi.org/10.3390/buildings11020038
APA StyleVukobratović, V., & Ruggieri, S. (2021). Floor Acceleration Demands in a Twelve-Storey RC Shear Wall Building. Buildings, 11(2), 38. https://doi.org/10.3390/buildings11020038







