Advanced Multi-Body Modelling of DCCSS Isolators: Geometrical Compatibility and Kinematics
Abstract
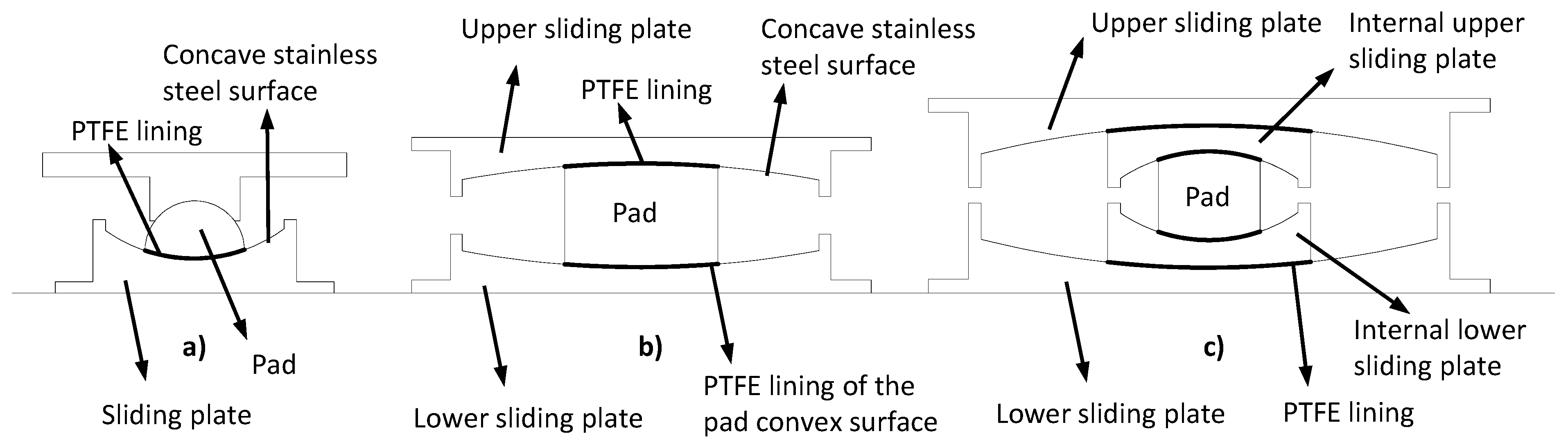
:1. Introduction
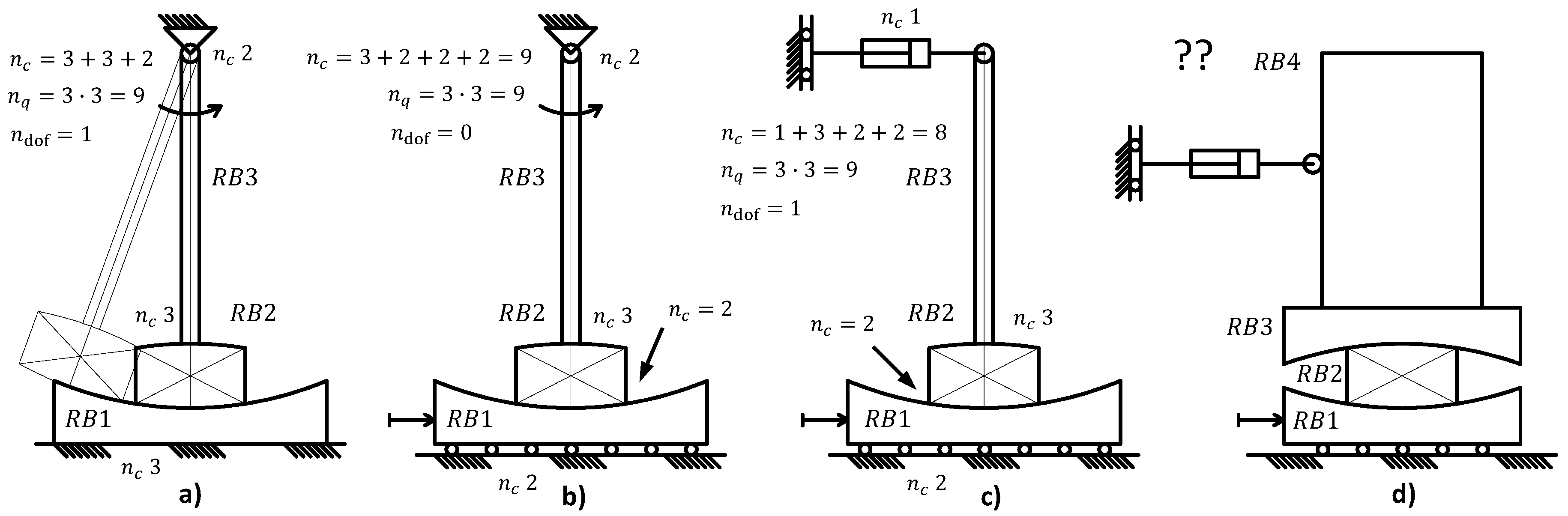
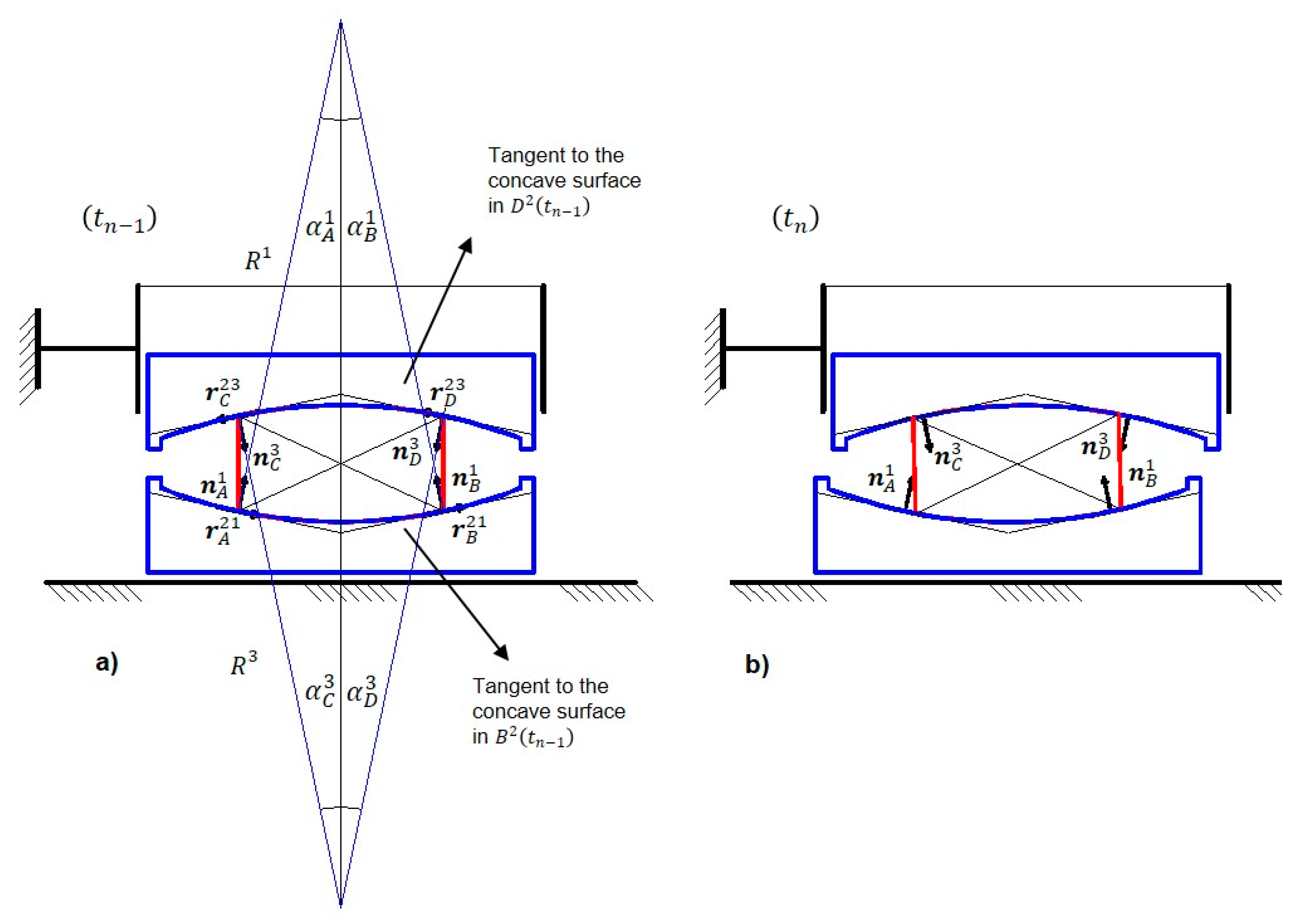
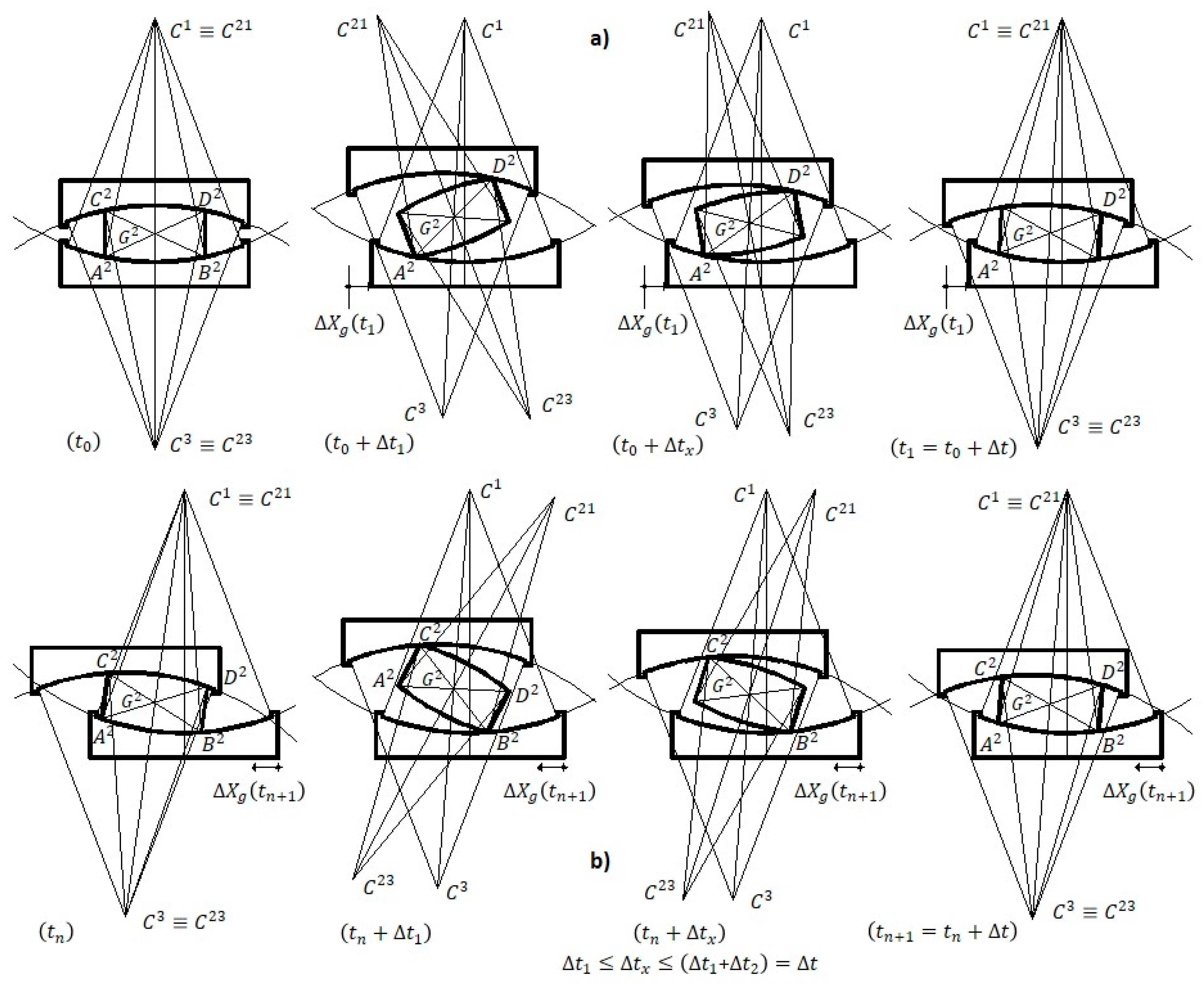
2. Research Motivation: Can We Always Speak about Pendulum?
3. Supposed Compliant Sliding
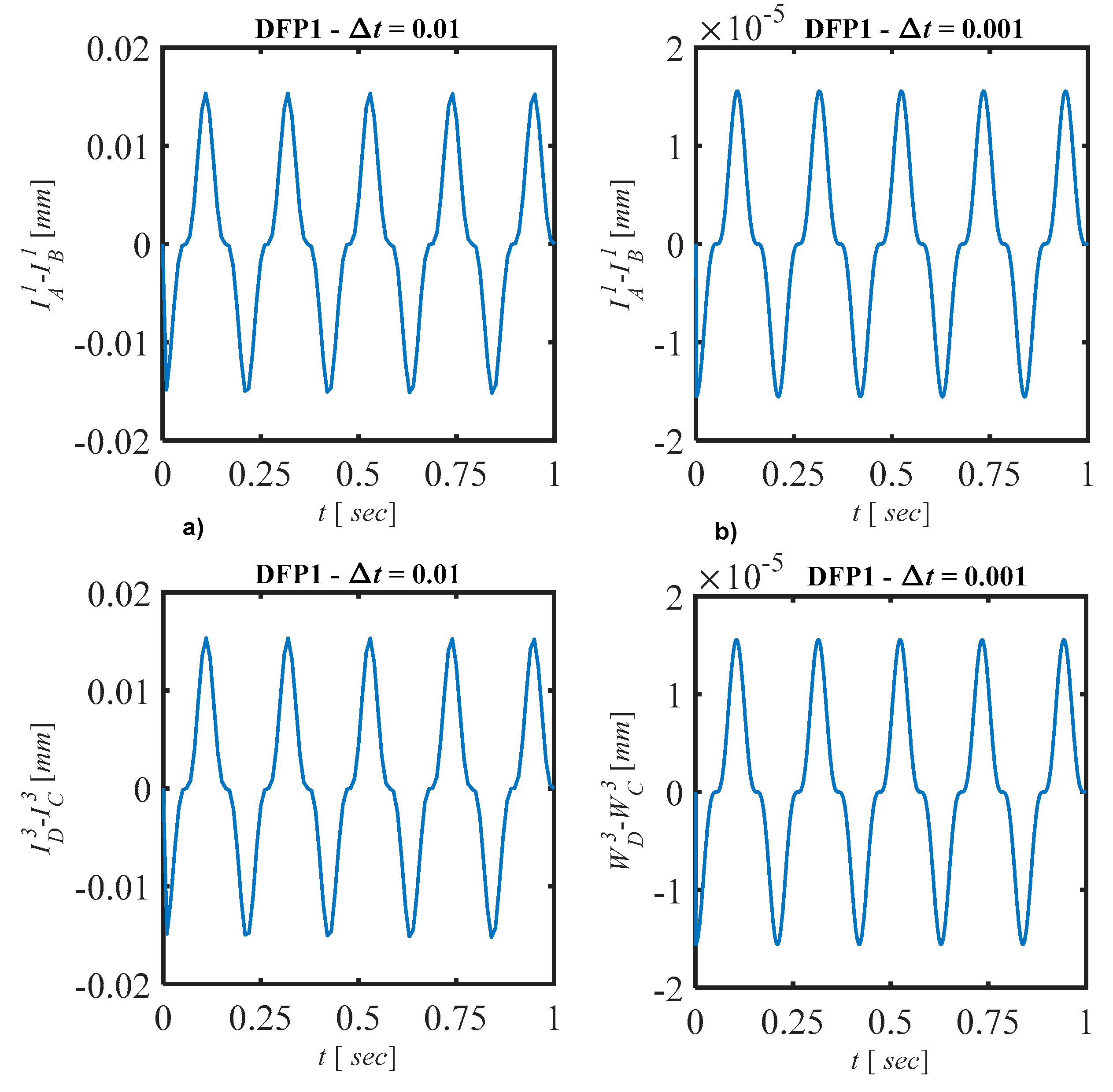
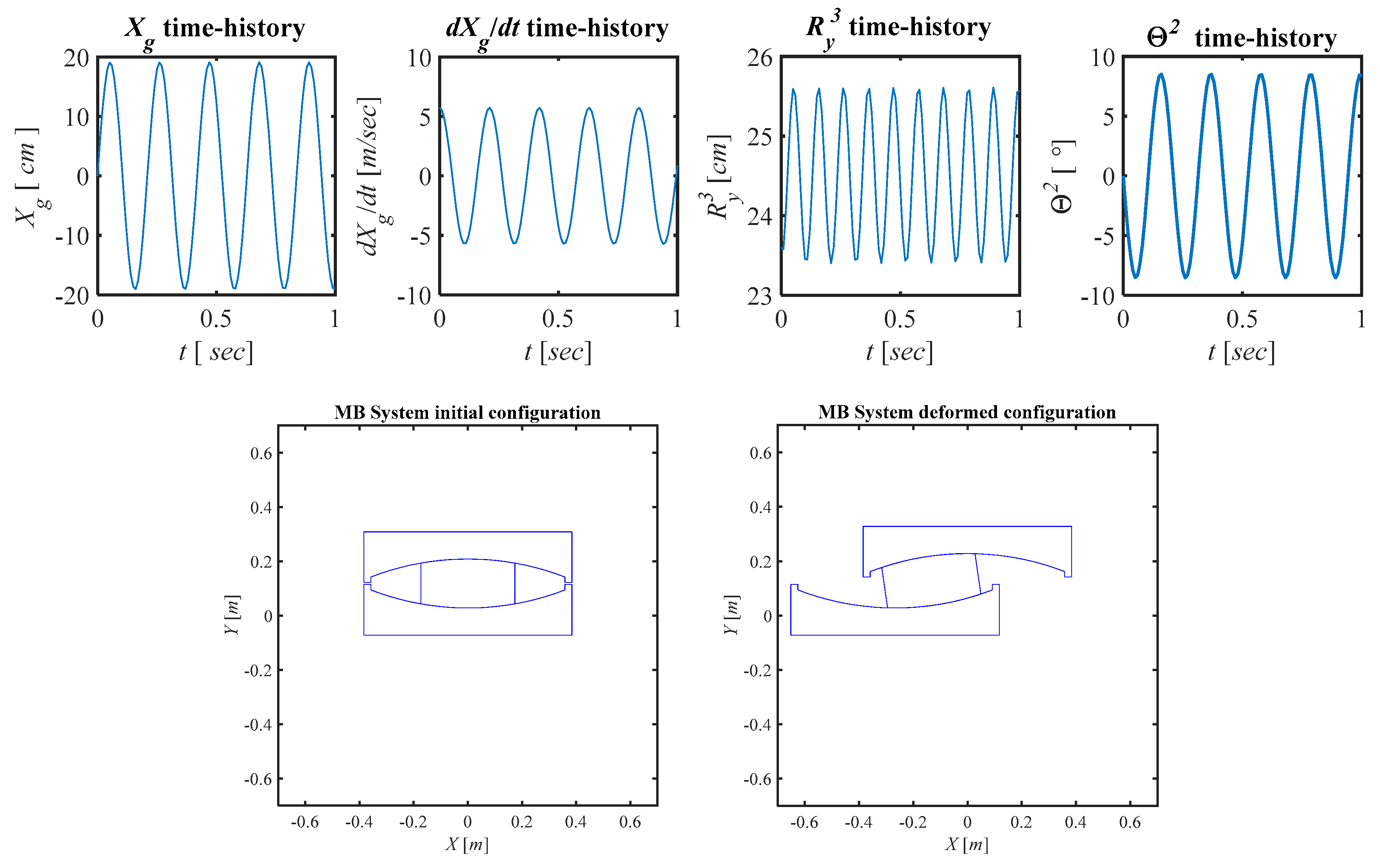
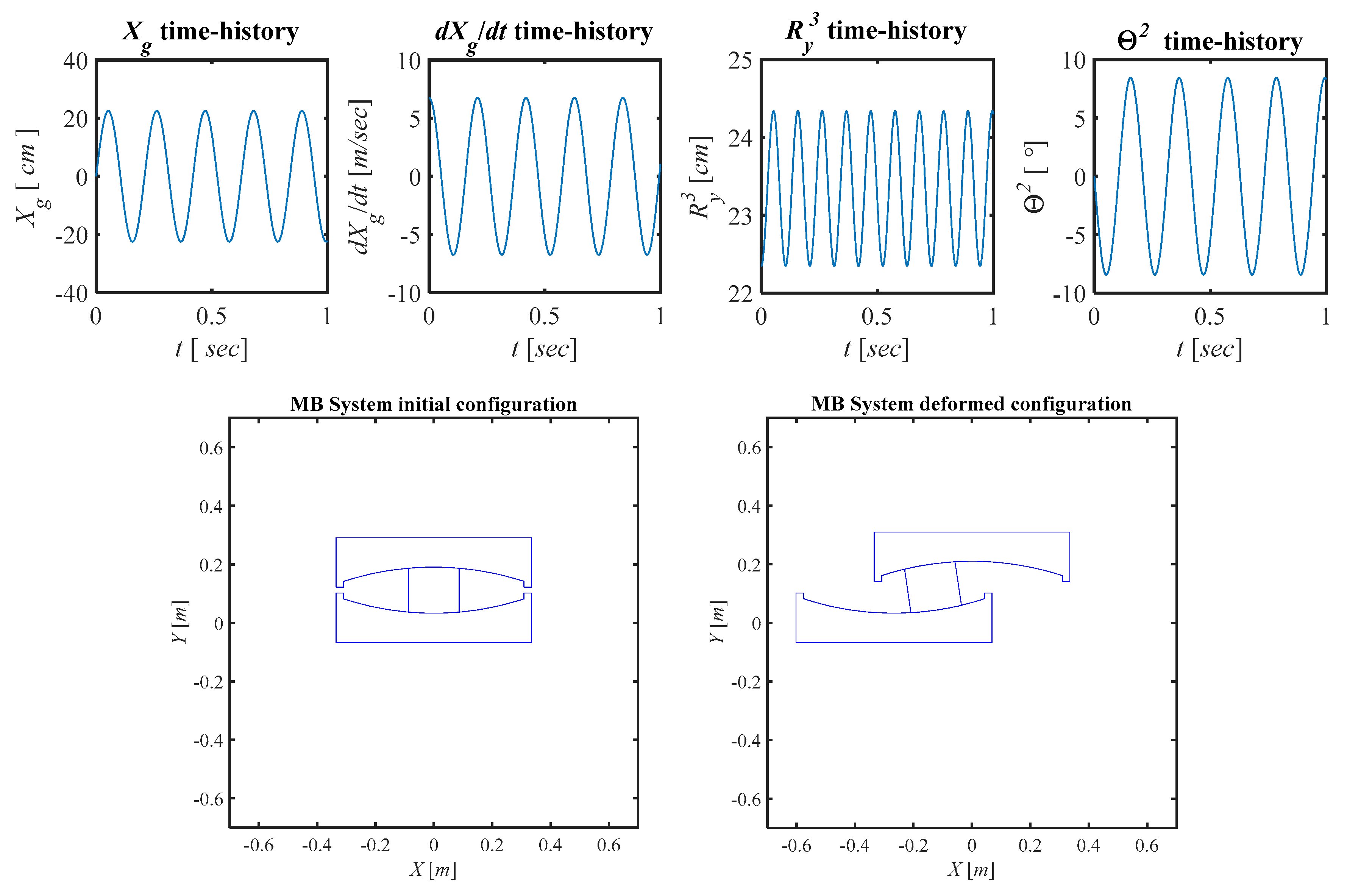
3.1. Numerical Details
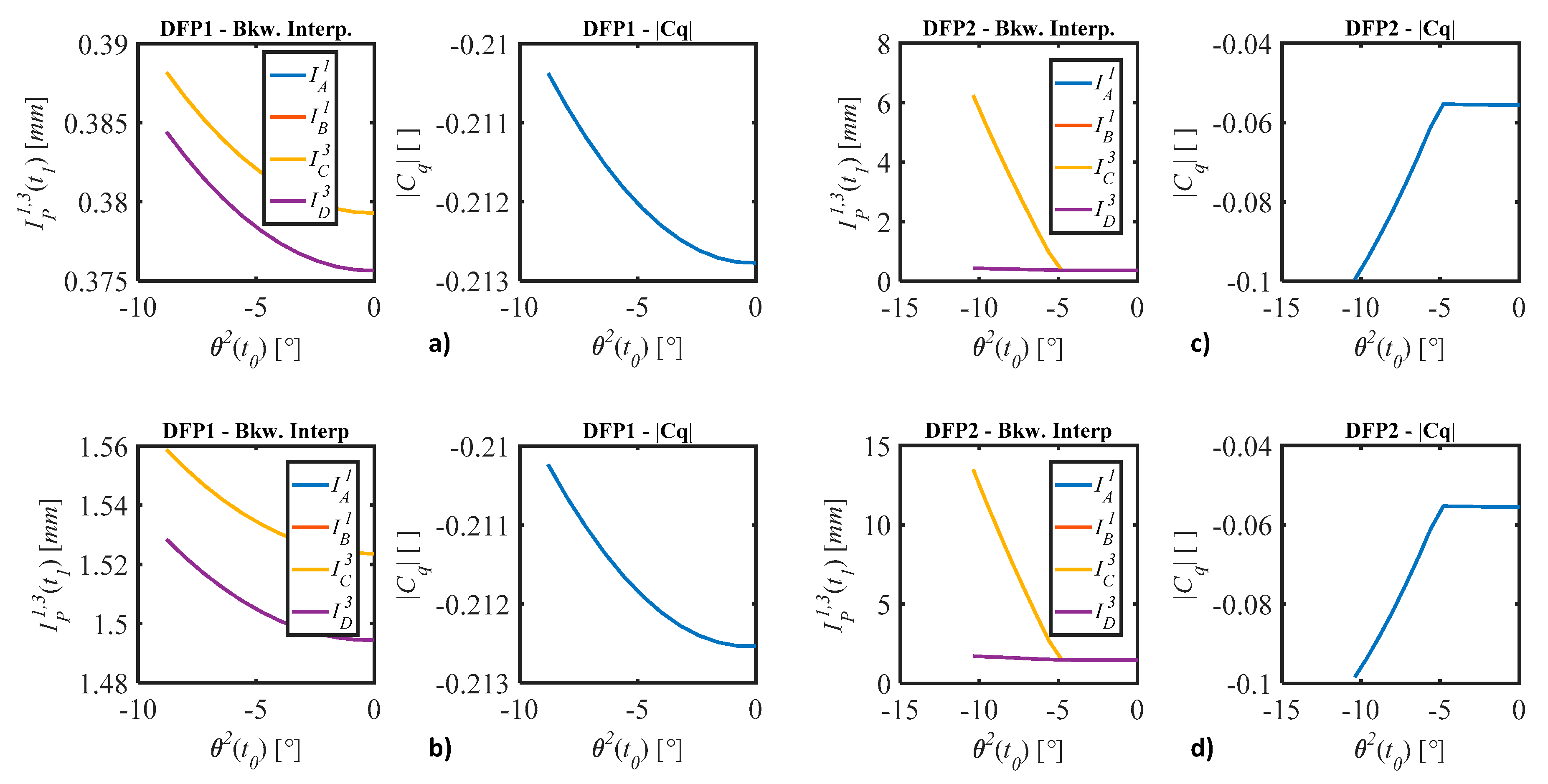
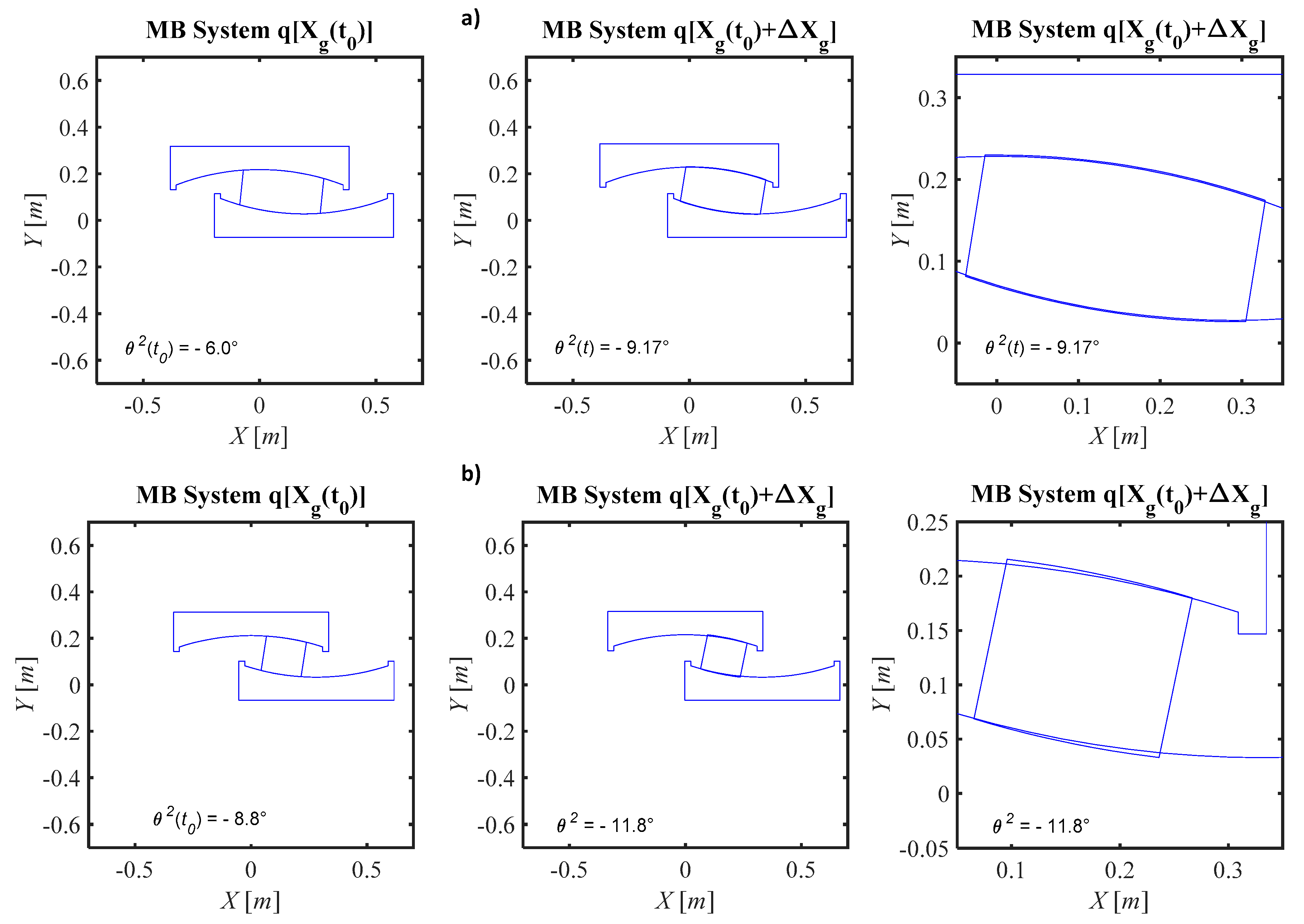
3.2. Results: The First Time-Step t1 of Sliding
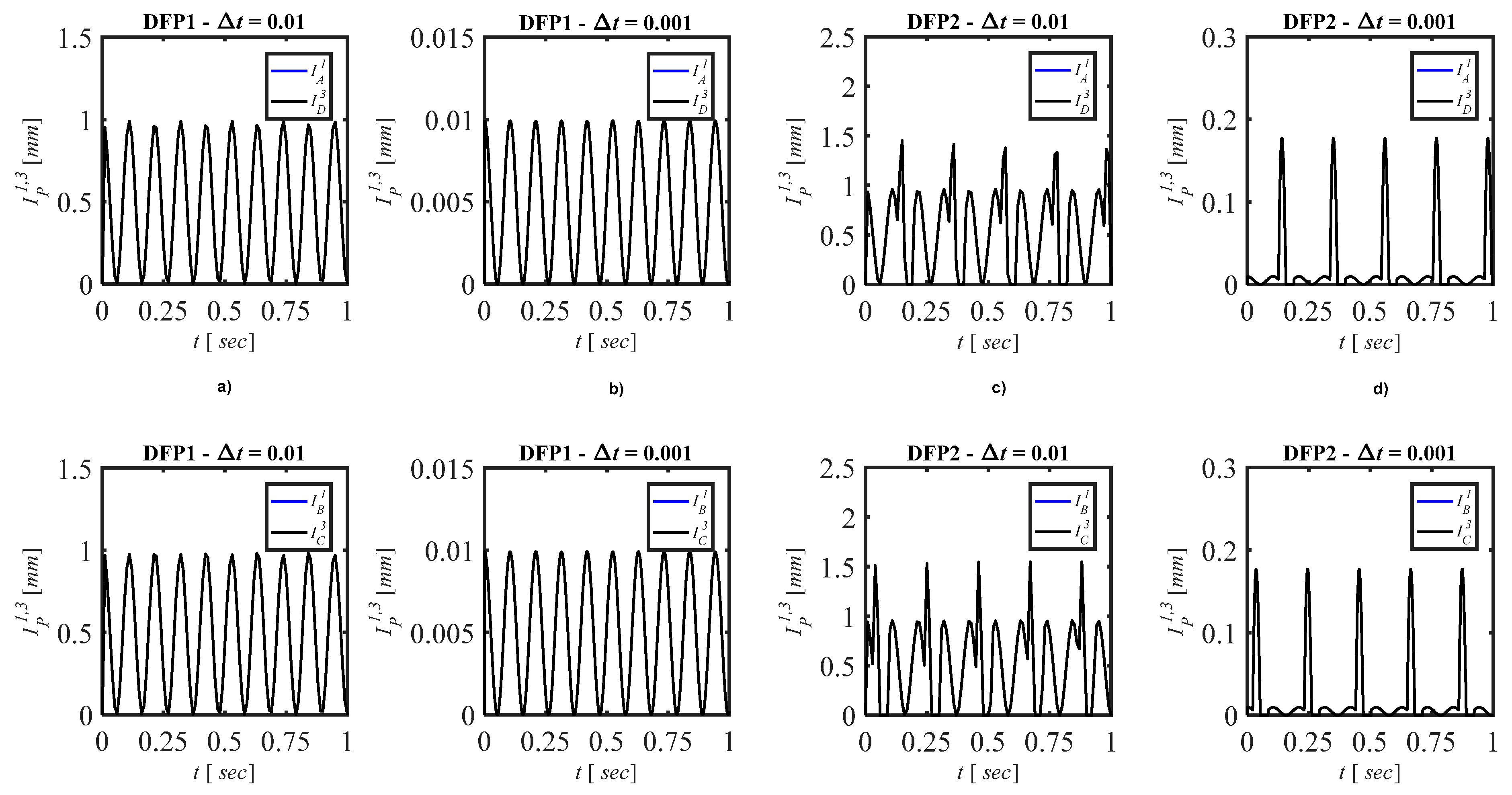
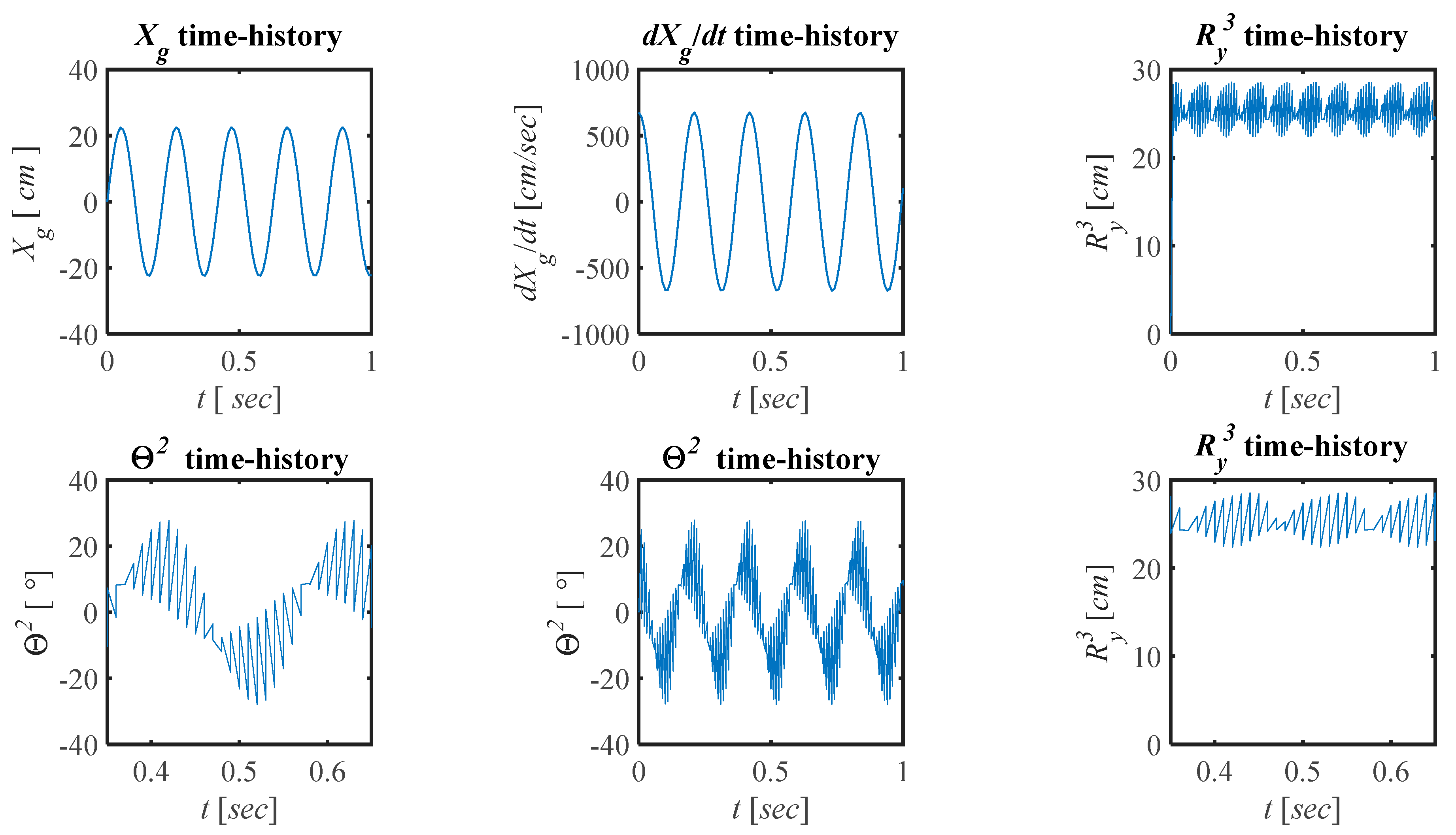
3.3. Results: The Time Histories
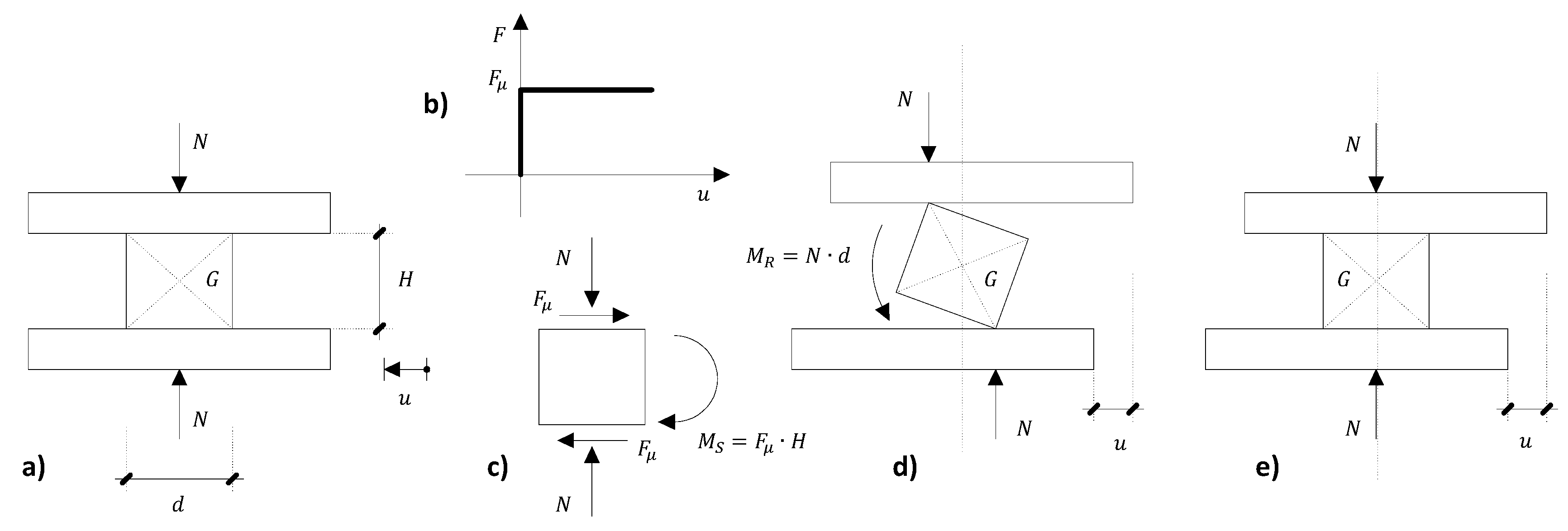
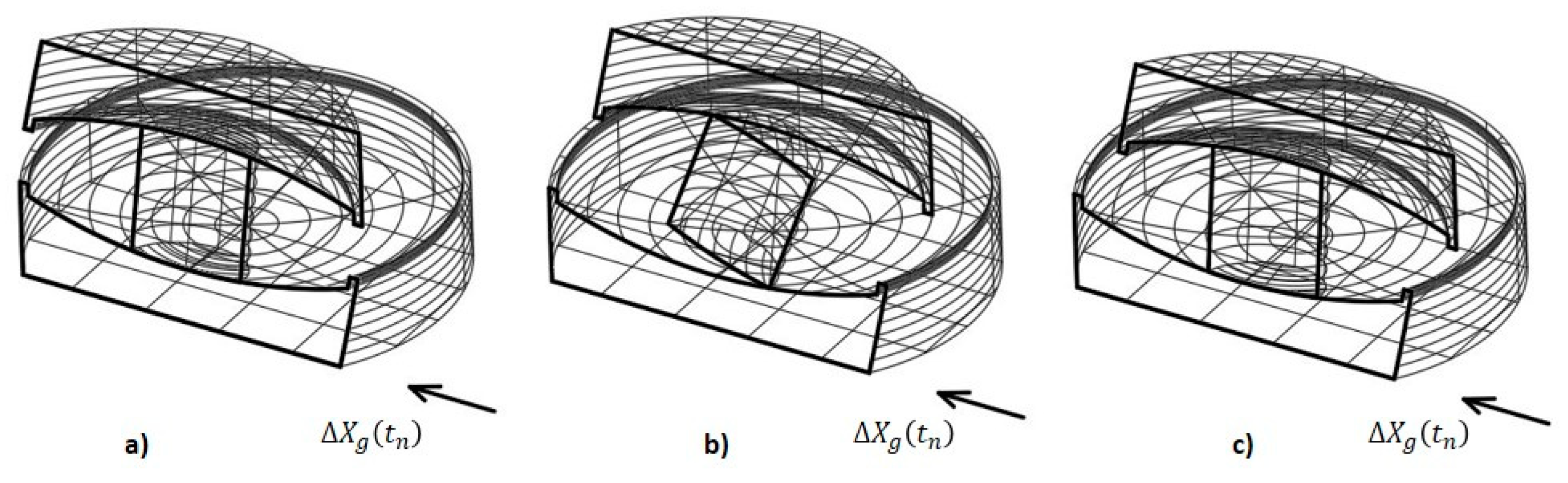
4. Inspiring Physical Observation
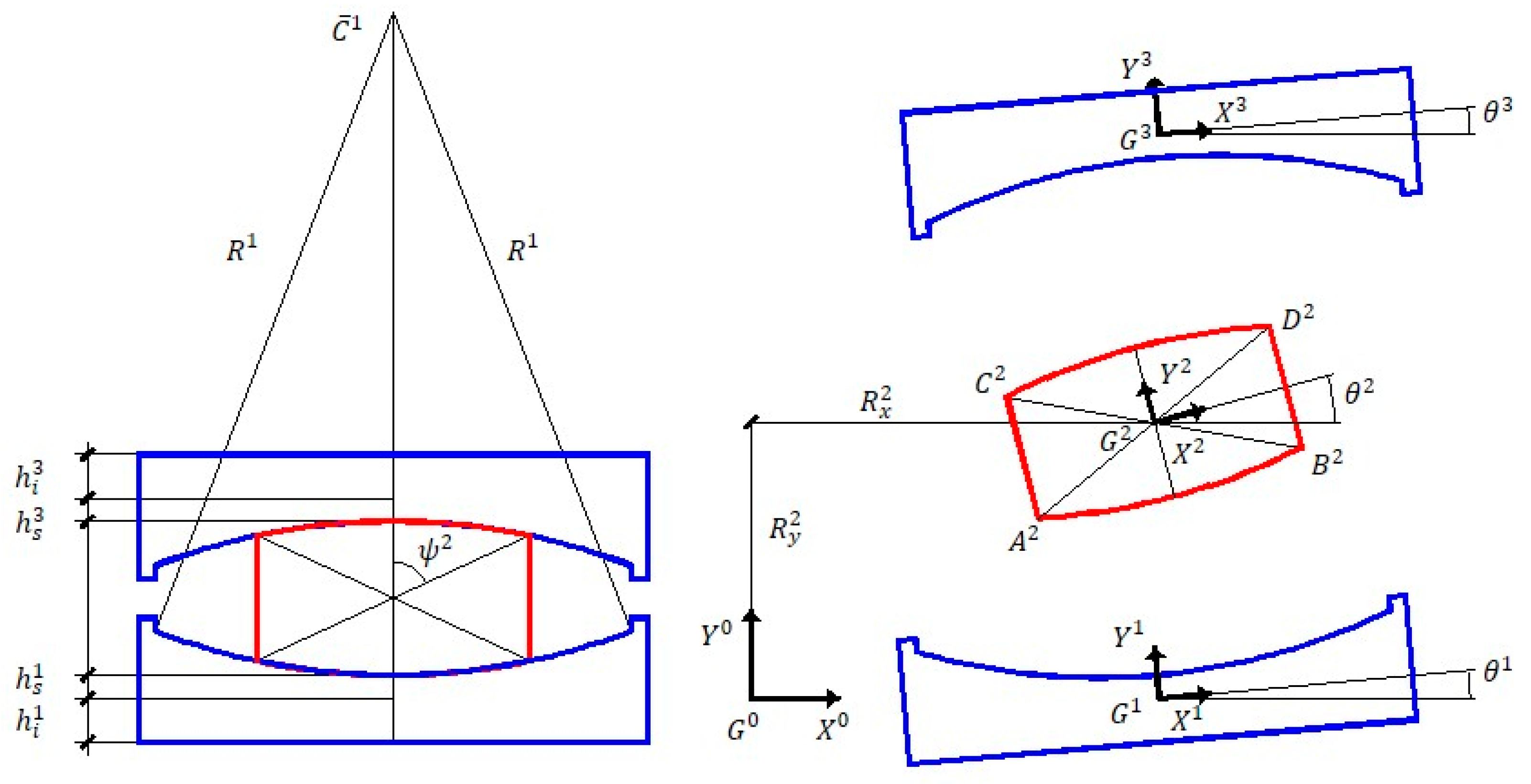
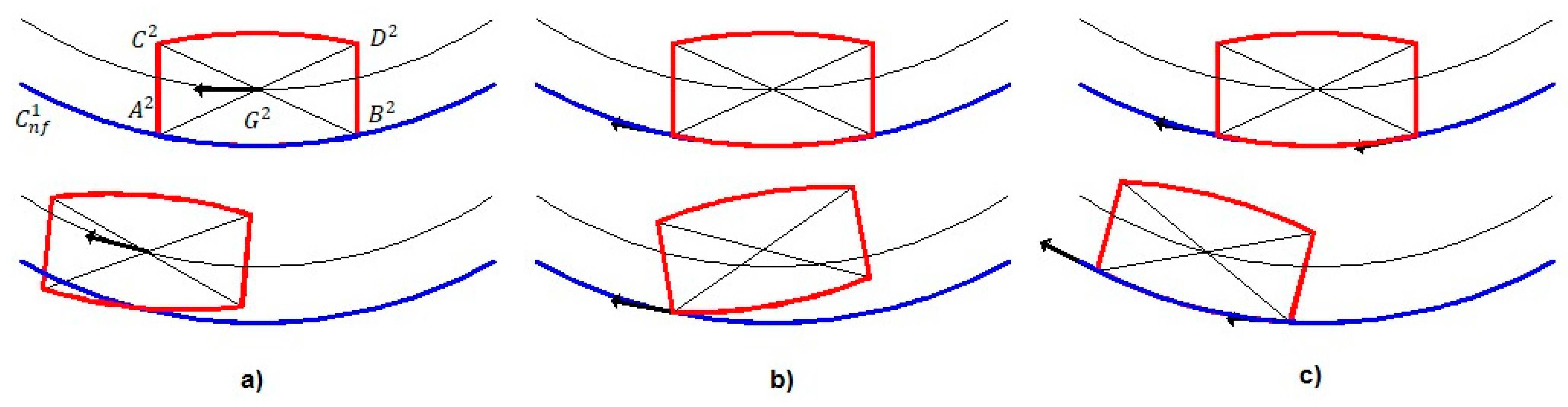
Geometrical Compatibility
5. Proposed Stick-Slip Modelling Strategy
5.1. Sticking Phase
5.2. Slipping Phase
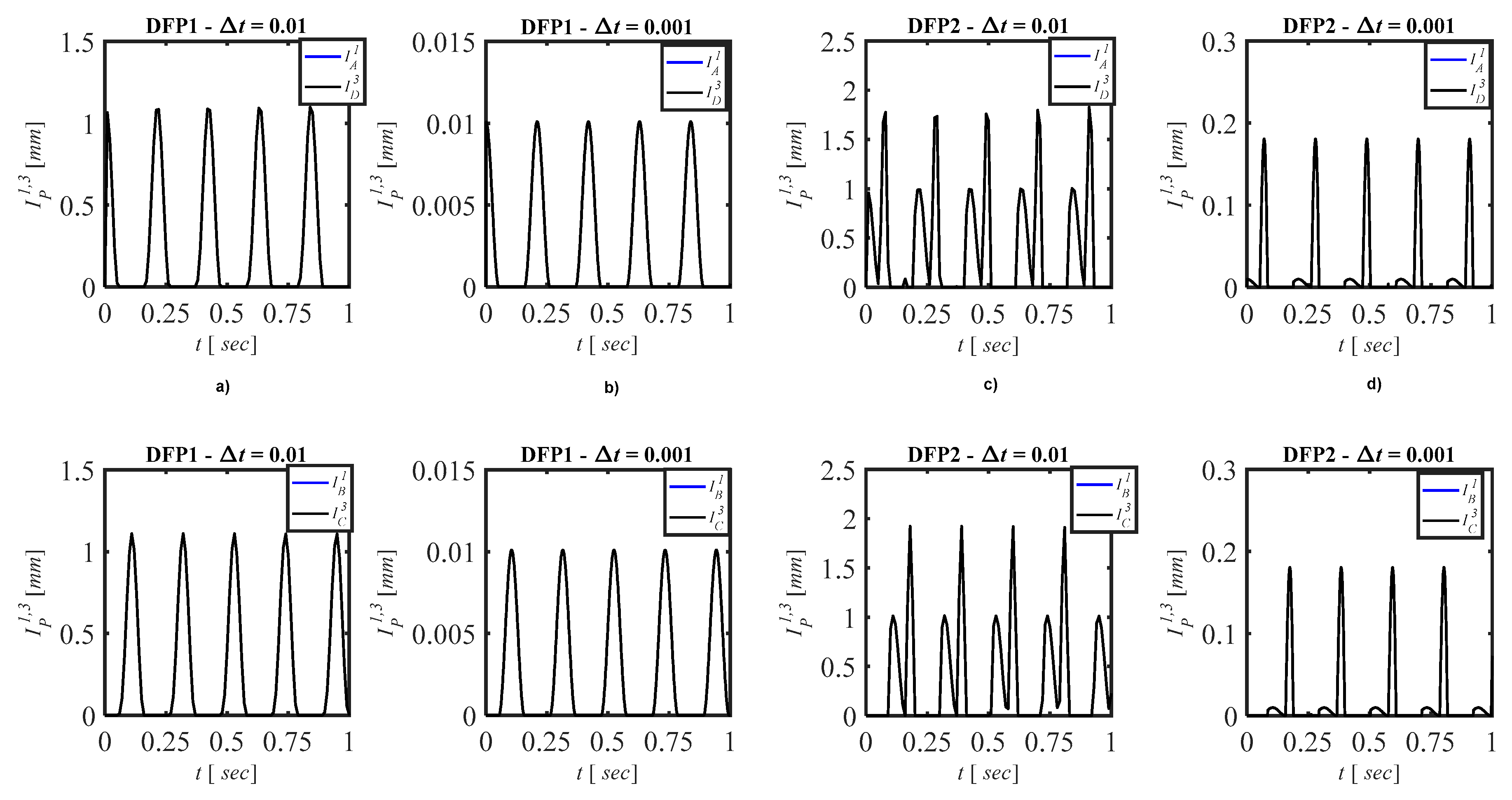
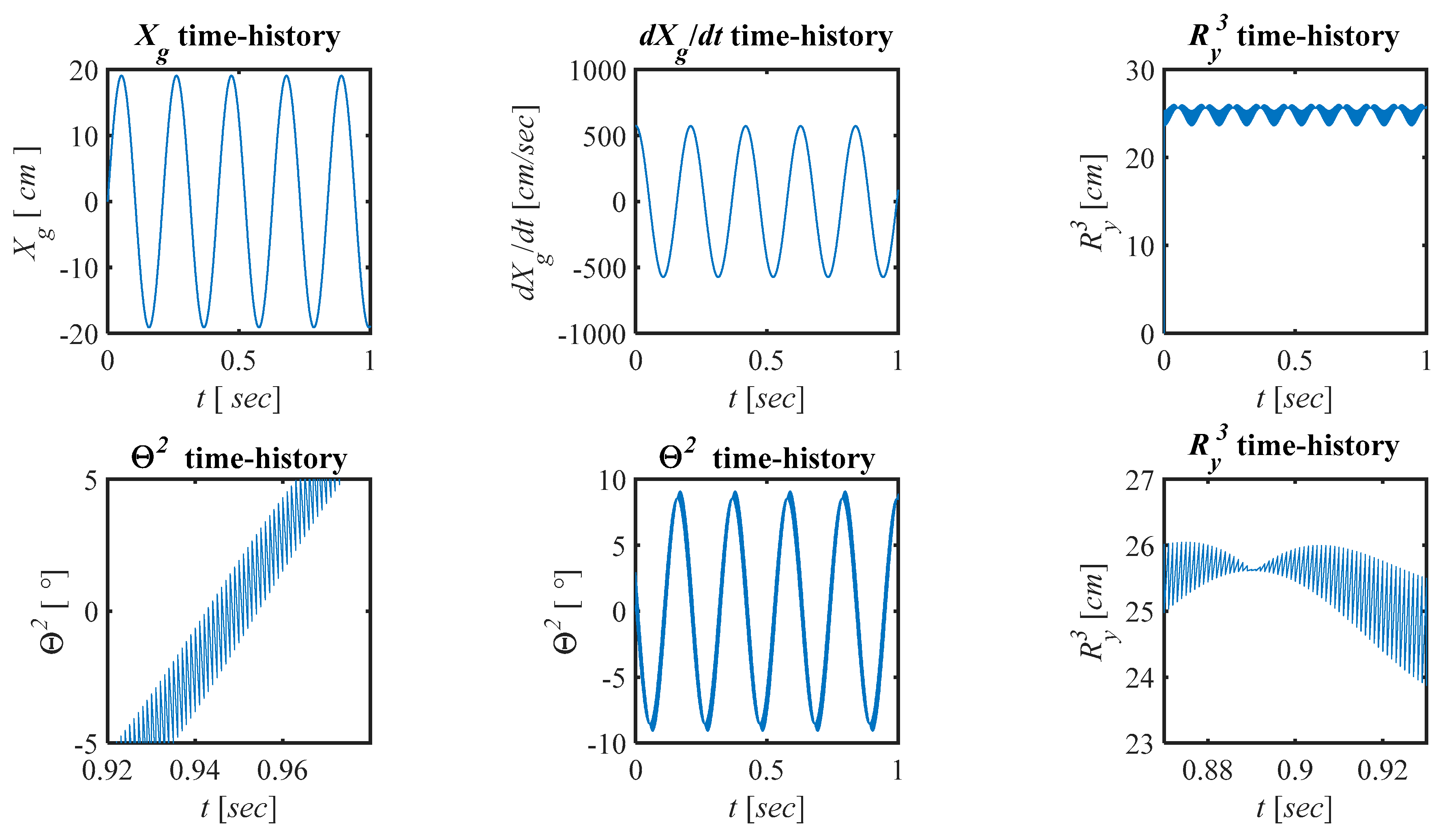
5.3. Numerical Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| , | Geometrical quantities defining the pad cross section |
| , | Circumferences characterizing the lower and upper plates concave plates, RB1 and RB3 |
| , | Center of the two concave surfaces of RB1 and RB3, respectively |
| , | Circumferences characterizing the lower and upper convex surfaces of RB2 |
| , | Center of the 2 convex surfaces of RB2, coupled with and , respectively |
| Centroid of the i-th RB | |
| Intersection of the i-th RB circumference and the radius passing through | |
| Intersection of the i-th RB circumference and either one of the straight sides of the pad | |
| , | Radius of the concave surface belonging to RB1 and RB3, respectively |
| , | Radius of the convex surface, of RB2, and coupled with RB1 or RB3, respectively |
| Global abscissa of the local reference system of the i-th RB | |
| Global ordinate of the local reference system of the i-th RB | |
| Initial interpenetration in correspondence of point , along the concave surface of the i-th RB | |
| Time-history of interpenetration in correspondence of point P, along the surface of the i-th RB | |
| i-th RB coordinates transformation matrix | |
| Non-linear kinematic constraints written in vector format | |
| Non-linear kinematic constraints Jacobian Matrix | |
| Vector of the global coordinates of the centroid of the i-th RB | |
| Versor with origin in point P and normal to the i-th RB | |
| Vector of the multi-body system generalized coordinates | |
| Vector of the generalized coordinates of the i-th RB | |
| Global position vector of point P belonging to the i-th Rigid Body | |
| Displacement vector of point P belonging to the i-th RB, with respect to the j-th RB | |
| Local position vector of point P in the reference system of the i-th Rigid Body | |
| Element at the i-th row and j-th column of the Jacobian Matrix | |
| Length of the diagonal of the pad | |
| , | Height of the retaining ring of RB1 and RB3, respectively |
| , | Height of the concave plate, either RB1 or RB3, between most depressed point and opposite flat face |
| Time duration of the ground-imposed time history | |
| Generic time integration instant | |
| , | Thickness of the retaining ring of RB1 and RB3, respectively |
| Local abscissa of point P in the reference system of the j-th RB | |
| Local ordinate of point P in the reference system of the j-th RB | |
| Integration time step | |
| First part (Sticking) of the time step | |
| Second part (slipping) of the time step | |
| Ground-imposed time history | |
| Maximum amplitude of the ground-imposed time-history | |
| , | Half opening angle defining the extension of concave plates RB1 and RB3, respectively |
| , | Opening angle of the convex face of RB2 coupled with either RB1 or RB3 |
| , | Angle between the radius passing through either or , and local axis |
| , | Angle between the radius passing through either or5 , and local axis |
| Counter-clockwise angle formed by the local reference axis with respect to | |
| Angle defining the size of the straight cylinder constituting the pad | |
| Circular frequency of the ground-imposed time history | |
| Vector of the Newton differences |
References
- Zayas, V.A.; Low, S.S.; Mahin, S.A. The FPS Earthquake Resisting System; Report No. 87-01; Earthquake Engineering Research Center: Berkley, CA, USA, 1987. [Google Scholar]
- Mokha, A.; Constantinou, M.C.; Reinhorn, A. Teflon Bearings in Base Isolation, I: Testing. ASCE J. Struct. Eng. 1990, 116, 438–454. [Google Scholar] [CrossRef]
- Constantinou, M.C.; Mokha, A.; Reinhorn, A. Teflon Bearings in Base Isolation, II: Modeling. ASCE J. Struct. Eng. 1990, 116, 455–474. [Google Scholar] [CrossRef]
- Fenz, D.M.; Constantinou, M.C. Behavior of the Double Concave Friction Pendulum Bearing. Earthq. Eng. Struct. Dyn. 2006, 35, 1403–1424. [Google Scholar] [CrossRef]
- Fenz, D.M.; Constantinou, M.C. Spherical Sliding Isolation Bearings with Adaptive Behavior: Experimental Verification. Earthq. Eng. Struct. Dyn. 2008, 37, 185–205. [Google Scholar] [CrossRef]
- Becker, T.C.; Mahin, S.A. Experimental and Analytical Study of the Bi-directional Behavior of the Triple Friction Pendulum Isolator. Earthq. Eng. Struct. Dyn. 2012, 41, 355–373. [Google Scholar] [CrossRef]
- Becker, T.C.; Mahin, S.A. Correct Treatment of Rotation of Sliding Surfaces in Kinematic Model of the Triple Friction Pendulum Bearing. Earthq. Eng. Struct. Dyn. 2012, 42, 311–317. [Google Scholar] [CrossRef]
- Tsai, C.S.; Lin, Y.C.; Su, H.C. Characterization and Modeling of Multiple Friction Pendulum System with Numerous Sliding Interfaces. Earthq. Eng. Struct. Dyn. 2010, 39, 1463–1491. [Google Scholar] [CrossRef]
- Nagarajaiah, S.; Reinhorn, A.M.; Constantinou, M.C. Nonlinear Dynamic Analysis of 3D Base Isolated Structures. ASCE J. Struct. Eng. 1991, 117, 2035–2054. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z.; Du, X.; Xu, C.; Han, R. Numerical analyses of seismic performance of underground and aboveground structures with friction pendulum bearings. Soil Dyn. Earthq. Eng. 2020, 130, 105967. [Google Scholar] [CrossRef]
- Habieb, A.B.; Valente, M.; Milani, G. Effectiveness of different base isolation systems for seismic protection: Numerical insights into an existing masonry bell tower. Soil Dyn. Earthq. Eng. 2019, 125, 105752. [Google Scholar] [CrossRef]
- Almazán, J.L.; De La LLera, J.C.; Inaudi, J.A. Modelling aspects of structures isolated with the friction pendulum system. Earthq. Eng. Struct. Dyn. 1998, 27, 845–867. [Google Scholar] [CrossRef]
- Almazán, J.L.; De La LLera, J.C. Accidental torsion due to overturning in nominally symmetric structures isolated with the FPS. Earthq. Eng. Struct. Dyn. 2003, 32, 919–948. [Google Scholar] [CrossRef]
- Almazán, J.L.; De la Llera, J.C. Analytical model of structures with frictional pendulum isolators. Earthq. Eng. Struct. Dyn. 2011, 31, 305–332. [Google Scholar] [CrossRef]
- Lomiento, G.; Bonessio, N.; Benzoni, G. Friction Model for Sliding Bearings under Seismic Excitation. J. Earthq. Eng. 2013, 17, 1162–1191. [Google Scholar] [CrossRef]
- Sarlis, A.A.; Constantinou, M.A. A model of triple friction pendulum bearing for general geometric and frictional parameters. Earthq. Eng. Struct. Dyn. 2016, 45, 1837–1853. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G.; Benzoni, G. Analytical and finite element investigation on the thermo-mechanical coupled response of friction isolators under bidirectional excitation. Soil Dyn. Earthq. Eng. 2018, 106, 131–147. [Google Scholar] [CrossRef]
- Quaglini, V.; Gandelli, E.; Dubini, P. Numerical investigation of curved surface sliders under bidirectional orbits. Ing. Sismica 2019, 36, 118–136. [Google Scholar]
- Ponzo, F.C.; Di Cesare, A.; Leccese, G.; Nigro, D. Standard requirements for the recentering capability of curved surface sliders. Ing. Sismica 2019, 36, 95–106. [Google Scholar]
- Quaglini, V.; Dubini, P.; Poggi, C. Experimental assessment of sliding materials for seismic isolation systems. Bull. Earthq. Eng. 2012, 10, 717–740. [Google Scholar] [CrossRef]
- Ponzo, F.C.; Di Cesare, A.; Leccese, G.; Nigro, D. Shake table testing on restoring capability of double concave friction pendulum seismic isolation systems. Earthq. Eng. Struct. Dyn. 2017, 46, 2337–2353. [Google Scholar] [CrossRef]
- Pavese, A.; Furinghetti, M.; Casarotti, C. Experimental assessment of the cycle response of friction-based isolators under bidirectional motions. Soil Dyn. Earthq. Eng. 2018, 114, 1–11. [Google Scholar] [CrossRef]
- Pigouni, E.A.; Castellano, M.G.; Infanti, S.; Colato, G.P. Full-scale dynamic testing of pendulum isolators (Curved surface sliders). Soil Dyn. Earthq. Eng. 2019, 130. [Google Scholar] [CrossRef]
- Popov, V. Contact Mechanics and Friction-Physical Principles and Applications; Springer: Berlin, Germany, 2010; pp. 175–230. [Google Scholar]
- Belfiore, N.P.; Di Benedetto, A.; Pennestrì, E. Foundations of Mechanics Applied to Machines; Casa Editrice Ambrosiana: Milano, Italy, 2000; pp. 153–194. (In Italian) [Google Scholar]
- Shabana, A.A. Dynamics of Multibody Systems; John Wiley & Sons: New York, NY, USA, 1989; pp. 195–240. [Google Scholar]
- Shabana, A.A. Computational Dynamics; John Wiley & Sons: New York, NY, USA, 2001; pp. 295–378. [Google Scholar]
- Nikravesh, P.E. Planar Multibody Dynamics-Formulation, Programming with MATLAB, and Applications; CRC Press, Taylor & Francis Group: New York, NY, USA, 2018; pp. 355–382. [Google Scholar]
- Bianco, V.; Bernardini, D.; Mollaioli, F.; Monti, G. Modeling of the temperature rises in multiple friction pendulum bearings by means of thermomechanical rheological elements. Arch. Civ. Mech. Eng. 2019, 19, 171–185. [Google Scholar] [CrossRef]
- Bianco, V.; Monti, G.; Belfiore, N.P. New approach to model the mechanical behavior of multiple friction pendulum devices. In Proceedings of the 5th International Conference Integrity-Reliability-Failure, IRF2016, Porto, Portugal, 24–28 July 2016. [Google Scholar]
- Bianco, V.; Monti, G.; Belfiore, N.P. Complete analytical thermo-mechanical model of double friction pendulum devices. In Proceedings of the COMPDYN 2017, 6th ECCOMAS Thematic Conference on Computational methods in Structural Dynamics and Earthquake Engineering, Rhodes Island, Greece, 15–17 June 2017. [Google Scholar]
- Bianco, V.; Monti, G.; Belfiore, N.P. Mechanical Modelling of Friction Pendulum Isolation Devices. In Proceedings of Italian Concrete Days 2016, Lecture Notes in Civil Engineering; Di Prisco, M., e Menegotto, M., Eds.; Springer: Cham, Switzerland, 2018; pp. 133–146. [Google Scholar]
- Bianco, V.; Monti, G.; Belfiore, N.P. Fine-tuning of modelling strategy to simulate thermo-mechanical behavior of double friction pendulum seismic isolators. NED Univ. J. Res. 2020, 3. [Google Scholar] [CrossRef]
- Mariti, L.; Belfiore, N.P.; Pennestrì, E.; Valentini, P.P. Comparison of Solution Strategies for Multibody Dynamics Equations. Int. J. Numer. Methods Eng. 2011, 88, 637–656. [Google Scholar] [CrossRef]
- Italian Ministry of Infrastructures and Transport. Italian Technical Regulations, Technical Standards for Construction (NTC2018); Italian Ministry of Infrastructures and Transport: Rome, Italy, 2018. [Google Scholar]
- European Committee for Standardization (CEN). Eurocode 8. Design of Structures for Earthquake Resistance-Part 1: General Rules, Seismic Actions and Rules for Buildings (UNI EN 1998-1); European Committee for Standardization (CEN): Brussels, Belgium, 2004. [Google Scholar]
- CEN. European Standard EN 15129:2009:E Anti-Seismic Devices; CEN: Brussels, Belgium, 2009. [Google Scholar]



| Label | cm | m | ° | cm | cm | cm | ° | cm | cm | rad/s | ° | s | s |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DFP 1 | 2 | 1 | 21 | 15 | 10 | 2.58 | 10 | 5–10 * | 19.08 | 30 | 2 | 0.01–0.001 | 1 |
| DFP 2 | 2 | 1 | 18 | 15 | 10 | 2.58 | 5 | 5–10 * | 22.5 | 30 | 0.5–10 | 0.01–0.001 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bianco, V.; Monti, G.; Belfiore, N.P. Advanced Multi-Body Modelling of DCCSS Isolators: Geometrical Compatibility and Kinematics. Buildings 2021, 11, 50. https://doi.org/10.3390/buildings11020050
Bianco V, Monti G, Belfiore NP. Advanced Multi-Body Modelling of DCCSS Isolators: Geometrical Compatibility and Kinematics. Buildings. 2021; 11(2):50. https://doi.org/10.3390/buildings11020050
Chicago/Turabian StyleBianco, Vincenzo, Giorgio Monti, and Nicola Pio Belfiore. 2021. "Advanced Multi-Body Modelling of DCCSS Isolators: Geometrical Compatibility and Kinematics" Buildings 11, no. 2: 50. https://doi.org/10.3390/buildings11020050
APA StyleBianco, V., Monti, G., & Belfiore, N. P. (2021). Advanced Multi-Body Modelling of DCCSS Isolators: Geometrical Compatibility and Kinematics. Buildings, 11(2), 50. https://doi.org/10.3390/buildings11020050








