Quantification of Air Change Rate by Selected Methods in a Typical Apartment Building
Abstract
:1. Introduction
- Vinf—volume of infiltrated air in the room with natural airflow (m3),
- Vm—room volume (m3),
- il,v—gap permeability coefficient (m3/(m·s·Pa0.67)),
- l—length of the gap (m),
- Δpc—total air pressure difference (Pa).
- -
- by quantification of total aerodynamic coefficient Cp = Cpe − Cpi—“aerodynamic quantification of building”, which accepts the variability of climatic parameters, takes into account the wind influence with building parameters and the air permeability of the building;
- -
- based on experimental measurements of carbon dioxide in the selected reference room in an apartment building.
1.1. Aerodynamic Quantification of Building
1.1.1. Quantification of Total Aerodynamic Coefficient Cp
- h0—height from the neutral pressure plane NPP (m),
- ρae, ρai—outdoor and indoor air density (kg/m3),
- Cp—total aerodynamic coefficient (-),
- v—wind speed (m/s).
- Cp—total aerodynamic coefficient (-),
- Cpe—coefficient of external pressure (-),
- Cpi—coefficient of internal pressure (-).
1.1.2. External Aerodynamic Coefficient
1.1.3. Internal Aerodynamic Coefficient
- Cpi—the aerodynamic coefficient of internal pressure (-),
- A(+)—the real equivalent area of openings on the windward side of the building (m2),
- A(−)—the real equivalent area of openings on the other sides of the building (m2).
- L(+)—the sum of the lengths of the openings’ gaps on the windward side of a building (m),
- L(−)—the sum of the lengths of the openings gaps on the leeward and lateral sides of a building (m).
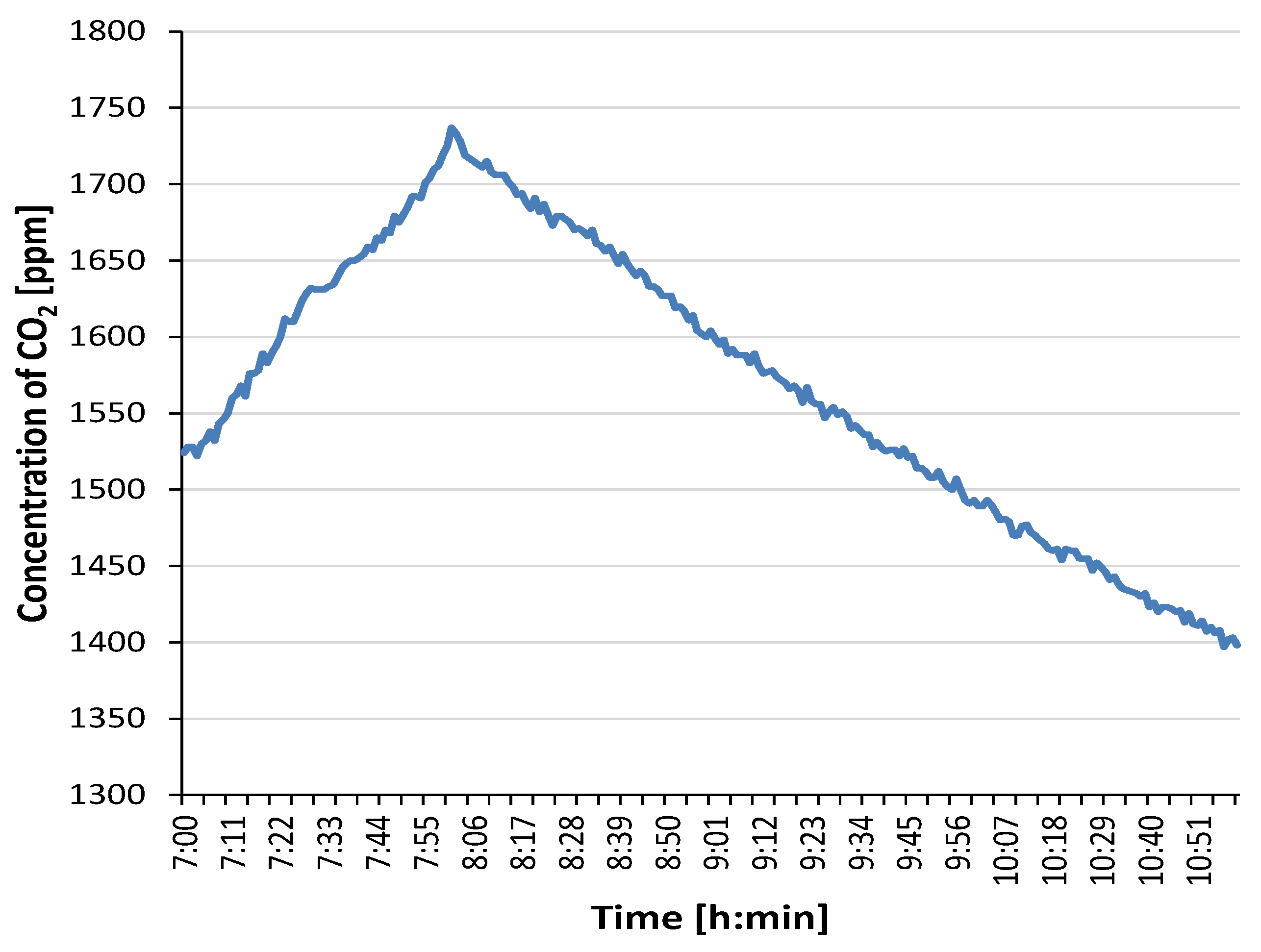
1.2. Measurement of Carbon Dioxide Concentration Values
- n—air change rate (1/s),
- CIDA,S—CO2 concentration in the room at the start of the decrease of concentration (mg/m3);
- CIDA,E—CO2 concentration in the room at the end of the decrease of concentration (mg/m3);
- CSUP—CO2 concentration in the outdoor air at time t; t (s) is duration of the decrease of CO2 concentration (mg/m3).
2. Materials and Methods
2.1. Description of the Reference Building
- ▪
- the medium height building with a height 15 m < h = 36.4 m < 50 m → buildings to 15 floors
- ▪
- the geometry is of the ground plan l/b = 25.2/12.3 ≈ 2—the plate type building with spatial proportionality: 1.5 ≤ h/b = 36.4/12.3 = 2.9 ≤ 6.0 and with area proportionality: 1.5 ≤ l/b = 25.2/12.3 = 2.04 ≤ 4.0
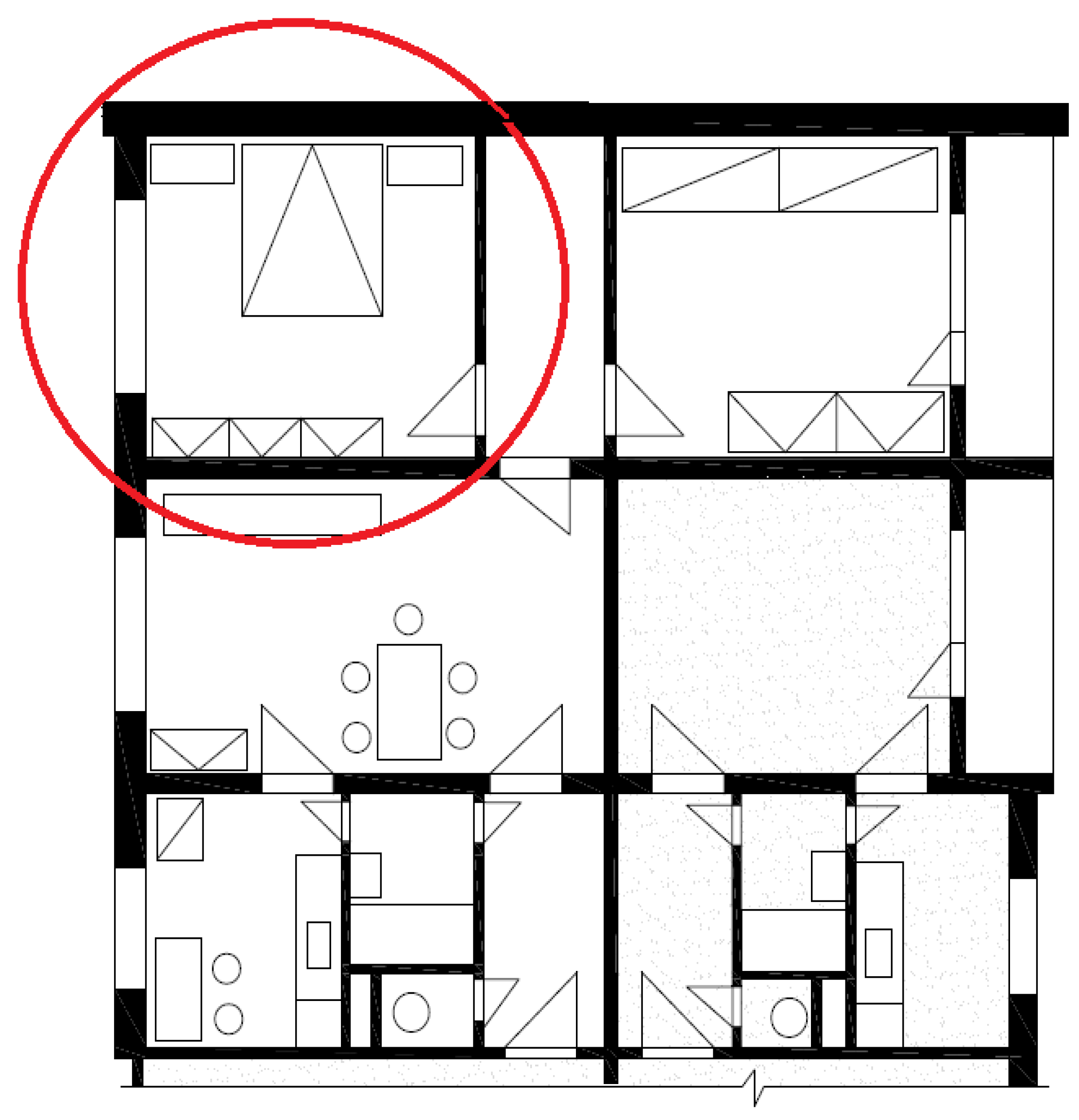
2.2. Reference Room in Selected Apartment Building
2.3. Research Flowchart
- ▪
- Calculation of air change rate without considering of openings
- ▪
- Calculation of air change rate with considering of openings
- ▪
- Calculation of air change rate on the basis of measured concentrations of carbon dioxide
- ▪
- Comparison and verification of individual two methods
3. Measurement and Calculation Analysis
3.1. Measurement and Description of the External Climatic and Internal Parameters
- v10,met—wind speed measured at hydro-meteorological stations at 10 m height (m/s),
- k—coefficient-indicating the impact of terrain categories and the height above the ground (-).
3.2. Prediction of Air Change Rate Using Quantifying of Total Aerodynamic Coefficient Cp
3.3. Determination of Air Change Rate on the Basis of Measured Values of Carbon Dioxide Concentration
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Bornehag, C.G.; Sundell, J.; Hagerhed-Engman, L.; Sigsgaard, T. Association between ventilation rates in 390 Swedish homes and allergic symptoms in children. Indoor Air 2005, 15, 275–280. [Google Scholar] [CrossRef] [PubMed]
- Sundell, J.; Levin, H.; Nazaroff, W.W.; Cain, W.S.; Fisk, W.J.; Grimsrud, D.T.; Gyntelberg, F.; Li, Y.; Persily, A.K.; Pickering, A.C.; et al. Ventilation rates and health: Multidisciplinary review of the scientific literature. Indoor Air 2011, 21, 191–204. [Google Scholar] [CrossRef] [PubMed]
- Wargocki, P.; Sundell, J.; Bischof, W.; Brundrett, G.; Fanger, P.O.; Gyntelberg, F.; Hanssen, S.O.; Harrison, P.; Pickering, A.; Seppanen, O.; et al. Ventilation and health in non-industrial indoor environments: Report from a European Multidisciplinary Scientific Consensus Meeting (EUROVEN). Indoor Air 2002, 12, 113–128. [Google Scholar] [CrossRef]
- Asikainen, A.; Hänninen, O.; Brelih, N.; Bischof, W.; Hartmann, T.; Carrer, P.; Wargocki, P. The Proportion of Residences in European Countries with Ventilation Rates below the Regulation Based Limit Value. Int. J. Vent. 2013, 12, 129–134. [Google Scholar] [CrossRef]
- Slovak Republic Office of Standards, Metrology and Testing. STN 73 4301—Dwelling Buildings; Slovak Republic Office of Standards, Metrology and Testing: Bratislava, Slovakia, 2005.
- Chmúrny, I. Tepelná Ochrana Budov; JAGA: Bratislava, Slovakia, 2003. [Google Scholar]
- Aynsley, R.M.; Melbourne, W.; Vickery, B.J. Architectural Aerodynamics; Applied Science Publishers Ltd.: London, UK, 1977; ISBN 0-85334-698-4. Available online: https://www.worldcat.org/title/architectural-aerodynamics/oclc/569295778 (accessed on 12 January 2021).
- Meroney, R.N.; Neff, D.E.; Birdsall, J.B. Wind-tunnel simulation of infiltration across permeable building envelopes: Energy and air pollution exchange rates. In Proceedings of the 7th International Symposium on Measurement and Modeling of Environmental Flows International Mechanical Enginnering Conference, San Francisco, CA, USA, 12–17 November 1995; Available online: https://www.osti.gov/biblio/435757 (accessed on 12 January 2021).
- Székyová, M.; Bodo, R.; Ihradský, J. Vetranie; STU Bratislava: Bratislava, Slovakia, 2002; ISBN 80-227-1681-2. [Google Scholar]
- Kleiven, T. Natural Ventilation in Buildings; Norwegian University of Science and Technology: Trondheim, Norway, 2003; Available online: https://ntnuopen.ntnu.no/ntnu-xmlui/handle/11250/231090 (accessed on 20 January 2021).
- Bielek, M.; Bielek, B. Vplyv stavebných materiálov a konštrukcií na kvalitu života. Parametrizovanie energeticko-environmentálneho hodnotenia stavebných konštrukcií a budov. In Aerodynamika Budov pre Kvantifikáciu ich Prirodzeného Vetrania; PROFING: Bratislava, Slovakia, 2005. [Google Scholar]
- Drkal, F.; Lain, M.; Schwarzer, J.; Zmrhal, V. Vzduchotechnika; Evropský Sociální Fond: Praha, Czech Republic, 2009. [Google Scholar]
- Katunsky, D.; Katunská, J.; Bullová, I. Solution of the air flow in the ventilated facade and its effect on the thermal characteristics of the peripheral wall. In Proceedings of the 18th International Multidisciplinary Scientific GeoConference, SGEM 2018, Albena, Bulgaria, 2–8 July 2018; ISBN 978-619-7408-52-2. [Google Scholar] [CrossRef]
- Muehleisen, R.T.; Patrizi, S. A new parametric equation for the wind pressure coefficient for low-rise buildings. Energy Build. 2013, 57, 245–249. [Google Scholar] [CrossRef]
- Ginger, J.D. Internal Pressures and Cladding Net Wind Loads on Full-Scale Low-Rise Building. J. Struct. Eng. 2000, 126, 538–543. [Google Scholar] [CrossRef]
- Chen, J.H.; Chen, C.H. A Study on the Wind Pressures of the Partial Enclosed Buildings in the View of Net Pressures. In Proceedings of the Seventh Asia-Pacific Conference on Wind Engineering 2009, Taipei, Taiwan, 8–12 November 2009; Available online: http://14.139.190.172/cgi-bin/koha/opac-detail.pl?biblionumber=6583&shelfbrowse_itemnumber=6583 (accessed on 21 January 2021).
- Thampi, H.; Dayal, V.; Sarkar, P.P. Finite Element Modeling of Interaction of Tornado with a Low-Rise Timber Building. In Proceedings of the Fifth International Symposium on Computational Wind Engineering, Chapel Hill, NC, USA, 23–27 May 2010; Available online: https://www.researchgate.net/profile/Vinay_Dayal/publication/267545369_Finite_element_modeling_of_interaction_of_tornado_with_a_low-rise_timber_building/links/5464bb840cf2a8cf007bffed.pdf (accessed on 15 January 2021).
- Cóstola, D.; Blocken, B.; Hensen, J.L.M. Overview of pressure coefficient data in building energy simulation and airflow network programs. Build. Environ. 2009, 44, 2027–2036. [Google Scholar] [CrossRef] [Green Version]
- Montazeri, H.; Blocken, B. CFD simulation of wind-induced pressure coefficients on buildings with and without balconies: Validation and sensitivity analysis. Build. Environ. 2013, 60, 137–149. [Google Scholar] [CrossRef]
- STN EN 1991-1-4: 2007, Eurocode 1: Actions on Structures. Part 1–4: General Actions. Wind Actions. Available online: https://www.phd.eng.br/wp-content/uploads/2015/12/en.1991.1.4.2005.pdf (accessed on 25 January 2021).
- Richards, P.; Hoxey, R. Wind loads on the roof of a 6 m cube. J. Wind. Eng. Ind. Aerodyn. 2008, 96, 984–993. [Google Scholar] [CrossRef]
- Bitsuamlak, G.; Tecle, A.S. Full-Scale External and Internal Pressure Measurements for a Low-Rise Building. Florida Internation-al University. 2009. Available online: http://www.ihrc.fiu.edu/wpcontent/uploads/2012/05/HLMP (accessed on 11 January 2021).
- Doudak, G.; McClure, G.; Smith, I.; Stathopoulos, T. Comparison of Field and Wind Tunnel Pressure Coefficients for a Light-Frame Industrial Building. J. Struct. Eng. 2009, 135, 1301–1304. [Google Scholar] [CrossRef]
- Al Zoubi, F.; Li, Z.; Wei, Q.; Sun, Y. Wind tunnel test and numerical simulation of wind pressure on a high-rise building. J. Chongqing Univ. 2010. Available online: http://www.cnki.com.cn/Article/CJFDTotal-CQDX201001008.htm (accessed on 12 February 2021).
- Amin, J.; Ahuja, A. Experimental study of wind-induced pressures on buildings of various geometries. Int. J. Eng. Sci. Technol. 2011, 3, 68562. Available online: https://www.ajol.info/index.php/ijest/issue/view/8314 (accessed on 12 January 2021). [CrossRef]
- Amin, J.A.; Ahuja, A.K. Effects of Side Ratio on Wind-Induced Pressure Distribution on Rectangular Buildings. J. Struct. 2013, 2013, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Bielek, M.; Černík, P.; Tajmír, M. Aerodynamika Budov. Fyzikálne Problémy Účinkov Vetra na Budovy a Ich Okolie; ALFA: Bratislava, Slovakia, 1990; ISBN 80-05-00632-2. [Google Scholar]
- Ginger, J.; Letchford, C. Net pressures on a low-rise full-scale building. J. Wind. Eng. Ind. Aerodyn. 1999, 83, 239–250. [Google Scholar] [CrossRef]
- Holmes, J. Mean and fluctuating internal pressures induced by wind. In Proceedings of the Wind Engineering; Elsevier BV: Amsterdam, The Netherlands, 1980; pp. 435–450. Available online: https://www.aivc.org/sites/default/files/members_area/medias/pdf/Airbase/airbase_00824.pdf (accessed on 10 February 2021).
- Bielek, M.; Bielek, B. Aerodynaická kvantifikácia budovy pre určenie prietoku vzduchu a energetického režimu prirodzeného fyzikálního medzipriestoru. In Proceedings of the 7th Vedecká Konferencia Budova a Energia 2007, Podbanské, Slovakia, 5–7 December 2007. [Google Scholar]
- EN ISO 12569: Thermal Performance of Buildings and Materials—Determination of Specific Airflow Rate in Buildings—Tracer Gas Dilution Method 2017. Available online: https://www.iso.org/standard/69817.html (accessed on 10 February 2021).
- Benedettelli, M.; Naticchia, B.; Carbonari, A.; Pascucci, M. Testing of a Tracer Gas Based Measurement Procedure to Assess Air Change Rates in Buildings. ISARC Proc. Int. Symp. Autom. Robot. Constr. 2015, 32, 1–7. [Google Scholar]
- Sherman, M. Tracer-gas techniques for measuring ventilation in a single zone. Build. Environ. 1990, 25, 365–374. [Google Scholar] [CrossRef]
- Persily, A.K. Evaluating Building IAQ and Ventilation with Indoor Carbon Dioxide; ASHRAE Transactions: Boston, MA, USA, 1997; Volume 103, Part 2; Available online: https://www.aivc.org/sites/default/files/airbase_10530.pdf (accessed on 12 January 2021).
- Kisilewicz, T.; Nowak-Dzieszko, K. Low airflow measurements by means of gas tracing method. IOP Conf. Ser. Mater. Sci. Eng. 2018, 415, 012030. [Google Scholar] [CrossRef]
- Nowak, K.; Nowak-Dzieszko, K.; Marcinowski, A. Analysis of ventilation air exchange rate and indoor air quality in the office room using metabolically generated CO2. IOP Conf. Ser. Mater. Sci. Eng. 2018, 415, 012028. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, L.; Ji, Z.; Ma, L.; Hui, Y. Test on Ventilation Rates of Dormitories and Offices in University by the CO2 Tracer Gas Method. Procedia Eng. 2015, 121, 662–666. [Google Scholar] [CrossRef] [Green Version]
- Cui, S.; Cohen, M.; Stabat, P.; Marchio, D. CO2 tracer gas concentration decay method for measuring air change rate. Build. Environ. 2015, 84, 162–169. [Google Scholar] [CrossRef]
- Laussmann, D.; Helm, D. Air Change Measurements Using Tracer Gases: Methods and Results. Significance of air change for indoor air quality. Chemistry, Emission Control, Radioactive Pollution and Indoor Air Quality; SP. ED1—Nicolas Mazzeo: Rijeka, Croatia, 2011. [Google Scholar] [CrossRef] [Green Version]
- Katunský, D.; Nemec, M.; Kamenský, M. Airtightness of Buildings in Slovakia. Adv. Mater. Res. 2013, 649, 3–6. [Google Scholar] [CrossRef]
- Ferdyn-Grygierek, J.; Baranowski, A.; Blaszczok, M.; Kaczmarczyk, J. Thermal Diagnostics of Natural Ventilation in Buildings: An Integrated Approach. Energies 2019, 12, 4556. [Google Scholar] [CrossRef] [Green Version]
- Weerasuriya, A.; Zhang, X.; Gan, V.J.; Tan, Y. A holistic framework to utilize natural ventilation to optimize energy performance of residential high-rise buildings. Build. Environ. 2019, 153, 218–232. [Google Scholar] [CrossRef]
- Craig, S. The optimal tuning, within carbon limits, of thermal mass in naturally ventilated buildings. Build. Environ. 2019, 165, 106373. [Google Scholar] [CrossRef]
- Conceição, E.; Gomes, J.; Awbi, H. Influence of the Airflow in a Solar Passive Building on the Indoor Air Quality and Thermal Comfort Levels. Atmosphere 2019, 10, 766. [Google Scholar] [CrossRef] [Green Version]
- Raji, B.; Tenpierik, M.J.; Bokel, R.; van den Dobbelsteen, A. Natural summer ventilation strategies for energy-saving in high-rise buildings: A case study in the Netherlands. Int. J. Vent. 2019, 19, 25–48. [Google Scholar] [CrossRef] [Green Version]
- Alomirah, H.F.; Moda, H.M. Assessment of Indoor Air Quality and Users Perception of a Renovated Office Building in Manchester. Int. J. Environ. Res. Public Health 2020, 17, 1972. [Google Scholar] [CrossRef] [Green Version]
- Tam, C.; Zhao, Y.; Liao, Z.; Zhao, L. Mitigation Strategies for Overheating and High Carbon Dioxide Concentration within Institutional Buildings: A Case Study in Toronto, Canada. Buildings 2020, 10, 124. [Google Scholar] [CrossRef]
- Lu, C.-Y.; Lin, J.-M.; Chen, Y.-Y.; Chen, Y.-C. Building-Related Symptoms among Office Employees Associated with Indoor Carbon Dioxide and Total Volatile Organic Compounds. Int. J. Environ. Res. Public Health 2015, 12, 5833–5845. [Google Scholar] [CrossRef] [PubMed]
- Stabile, L.; Massimo, A.; Canale, L.; Russi, A.; Andrade, A.; Dell’Isola, M. The Effect of Ventilation Strategies on Indoor Air Quality and Energy Consumptions in Classrooms. Buildings 2019, 9, 110. [Google Scholar] [CrossRef] [Green Version]











| Number of Measurement | Date and Hours of Measurement | CO2 Concentration | Air Temperature | Reduced Wind Speed v | ||||
|---|---|---|---|---|---|---|---|---|
| Starting CIDA,S | Ending CIDA,E | The Time of Decrease t | Indoor | Outdoor | ||||
| (-) | (d. m. y) | (h:m) | (ppm) | (ppm) | (min) | (°C) | (°C) | (m/s) |
| 1 | 5 March 2018 | 8:40 | 1151 | 1064 | 69 | 23.1 | −5.0 | 3.9 |
| 2 | 5 March 2018 | 10:30 | 1076 | 1019 | 69 | 23.1 | −6.0 | 3.9 |
| 3 | 17 March 2018 | 18:00 | 1133 | 891 | 52 | 25.5 | −12.3 | 9.4 |
| 4 | 17 March 2018 | 21:00 | 1440 | 1170 | 31 | 26.4 | −14.1 | 10.3 |
| 5 | 1 December 2018 | 21:00 | 945 | 874 | 42 | 23.0 | −4.0 | 2.7 |
| 6 | 2 December 2018 | 9:00 | 1326 | 1215 | 28 | 24.4 | −3.0 | 1.6 |
| 7 | 2 December 2018 | 14:00 | 964 | 896 | 38 | 23.2 | −3.0 | 1.6 |
| 8 | 25 January 2019 | 20:10 | 1200 | 1024 | 59 | 22.9 | −4.0 | 6.7 |
| 9 | 26 January 2019 | 9:10 | 1346 | 1206 | 29 | 24.4 | −5.0 | 3.4 |
| 10 | 26 January 2019 | 20:00 | 1353 | 1230 | 42 | 23.0 | −6.0 | 1.1 |
| 11 | 27 January 2019 | 15:10 | 841 | 771 | 57 | 23.0 | −2.0 | 1.6 |
| 12 | 2 February 2019 | 9:30 | 2052 | 1907 | 45 | 24.2 | 4.0 | 2.3 |
| 13 | 2 February 2019 | 13:30 | 1778 | 1698 | 32 | 23.6 | 5.0 | 2.7 |
| 14 | 2 February 2019 | 20:30 | 1400 | 1279 | 61 | 23.1 | 4.0 | 0.7 |
| 15 | 3 February 2019 | 9:30 | 1654 | 1525 | 60 | 24.0 | 7.0 | 2.0 |
| 16 | 4 February 2019 | 19:00 | 1375 | 1214 | 60 | 24.0 | 2.0 | 3.6 |
| 17 | 5 February 2019 | 10:00 | 1307 | 1180 | 60 | 24.1 | 2.0 | 2.0 |
| 18 | 25 March 2019 | 20:30 | 1740 | 1686 | 25 | 25.0 | 8.0 | 4.4 |
| 19 | 1 April 2019 | 20:30 | 1322 | 1276 | 15 | 25.1 | 8.3 | 6.3 |
| 20 | 8 April 2019 | 19:10 | 1751 | 1682 | 45 | 24.6 | 19.0 | 5.4 |
| 21 | 10 April 2019 | 20:10 | 1310 | 1210 | 30 | 24.5 | 10.0 | 8.3 |
| 22 | 11 April 2019 | 20:00 | 1121 | 0991 | 50 | 23.9 | 6.0 | 9.4 |
| 23 | 17 April 2019 | 20:20 | 1918 | 1789 | 45 | 24.1 | 11.0 | 4.7 |
| 24 | 6 May 2019 | 18:40 | 1251 | 1077 | 60 | 24.0 | 6.0 | 6.6 |
| No. (-) | n (1/h) | U (%) | No. (-) | n (1/h) | U (%) | No. (-) | n (1/h) | U (%) | No. (-) | n (1/h) | U (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.10 | 4.10 | 7 | 0.19 | 3.79 | 13 | 0.11 | 2.07 | 19 | 0.19 | 1.55 |
| 2 | 0.08 | 4.47 | 8 | 0.28 | 1.89 | 14 | 0.13 | 2.74 | 20 | 0.08 | 4.03 |
| 3 | 0.46 | 1.02 | 9 | 0.30 | 2.50 | 15 | 0.11 | 4.70 | 21 | 0.24 | 2.42 |
| 4 | 0.59 | 2.12 | 10 | 0.20 | 2.50 | 16 | 0.18 | 3.96 | 22 | 0.23 | 5.24 |
| 5 | 0.18 | 5.85 | 11 | 0.19 | 1.76 | 17 | 0.16 | 4.74 | 23 | 0.11 | 0.88 |
| 6 | 0.26 | 1.93 | 12 | 0.11 | 1.94 | 18 | 0.09 | 8.63 | 24 | 0.23 | 1.62 |
| Number of Measurements | The Air Change Rate, n | Difference between | |||||
|---|---|---|---|---|---|---|---|
| Cp = Cpe | Cp = Cpe − Cpi | Carbon Dioxide Method | |||||
| A | B | C | B–C | A–C | |||
| (-) | (1/h) | (1/h) | (1/h) | (1/h) | (%) | (1/h) | (%) |
| 3 | 0.57 | 0.45 | 0.46 | 0.02 | 3.5 | 0.10 | 17.9 |
| 4 | 0.63 | 0.50 | 0.59 | 0.09 | 18.2 | 0.04 | 7.0 |
| 8 | 0.32 | 0.25 | 0.28 | 0.03 | 10.5 | 0.04 | 12.8 |
| 18 | 0.18 | 0.14 | 0.09 | 0.05 | 34.6 | 0.09 | 49.5 |
| 19 | 0.25 | 0.17 | 0.19 | 0.02 | 10.0 | 0.06 | 23.4 |
| 20 | 0.16 | 0.10 | 0.08 | 0.02 | 20.2 | 0.09 | 53.3 |
| 21 | 0.33 | 0.21 | 0.24 | 0.03 | 14.0 | 0.09 | 26.8 |
| 22 | 0.39 | 0.25 | 0.23 | 0.02 | 8.6 | 0.16 | 40.7 |
| 23 | 0.18 | 0.13 | 0.11 | 0.02 | 14.3 | 0.07 | 37.6 |
| 24 | 0.27 | 0.23 | 0.23 | 0.04 | 19.6 | 0.04 | 15.9 |
| Number of Measurements | The Air Change Rate, n | Difference between | |||||
|---|---|---|---|---|---|---|---|
| Cp = Cpe | Cp = Cpe − Cpi | Carbon Dioxide Method | |||||
| A | B | C | B–C | A–C | |||
| (-) | (1/h) | (1/h) | (1/h) | (1/h) | (%) | (1/h) | (%) |
| 2 | 0.16 | 0.12 | 0.08 | 0.042 | 35.6 | 0.083 | 52.1 |
| 5 | 0.20 | 0.18 | 0.18 | 0.003 | 1.9 | 0.015 | 7.6 |
| 6 | 0.20 | 0.22 | 0.26 | 0.044 | 20.0 | 0.064 | 32.0 |
| 7 | 0.18 | 0.18 | 0.19 | 0.009 | 4.7 | 0.009 | 4.7 |
| 9 | 0.24 | 0.26 | 0.30 | 0.044 | 16.8 | 0.066 | 27.6 |
| 10 | 0.19 | 0.14 | 0.20 | 0.062 | 44.8 | 0.014 | 7.3 |
| 11 | 0.17 | 0.14 | 0.19 | 0.057 | 42.2 | 0.022 | 12.9 |
| 12 | 0.15 | 0.13 | 0.11 | 0.019 | 14.8 | 0.041 | 27.1 |
| 13 | 0.15 | 0.12 | 0.11 | 0.008 | 6.9 | 0.043 | 28.0 |
| 14 | 0.13 | 0.13 | 0.13 | 0.000 | 0.0 | 0.000 | 0.3 |
| 15 | 0.13 | 0.15 | 0.11 | 0.036 | 24.7 | 0.018 | 13.8 |
| 16 | 0.19 | 0.18 | 0.18 | 0.005 | 0.0 | 0.009 | 4.5 |
| 17 | 0.15 | 0.16 | 0.16 | 0.000 | 0.0 | 0.010 | 6.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bullová, I.; Kapalo, P.; Katunský, D. Quantification of Air Change Rate by Selected Methods in a Typical Apartment Building. Buildings 2021, 11, 174. https://doi.org/10.3390/buildings11040174
Bullová I, Kapalo P, Katunský D. Quantification of Air Change Rate by Selected Methods in a Typical Apartment Building. Buildings. 2021; 11(4):174. https://doi.org/10.3390/buildings11040174
Chicago/Turabian StyleBullová, Iveta, Peter Kapalo, and Dušan Katunský. 2021. "Quantification of Air Change Rate by Selected Methods in a Typical Apartment Building" Buildings 11, no. 4: 174. https://doi.org/10.3390/buildings11040174
APA StyleBullová, I., Kapalo, P., & Katunský, D. (2021). Quantification of Air Change Rate by Selected Methods in a Typical Apartment Building. Buildings, 11(4), 174. https://doi.org/10.3390/buildings11040174







