Deep Learning Optimal Control for a Complex Hybrid Energy Storage System

Abstract

Deep Reinforcement Learning (DRL) proved to be successful for solving complex control problems and has become a hot topic in the field of energy systems control, but for the particular case of thermal energy storage (TES) systems, only a few studies have been reported, all of them with a complexity degree of the TES system far below the one of this study. In this paper, we step forward through a DRL architecture able to deal with the complexity of an innovative hybrid energy storage system, devising appropriate high-level control operations (or policies) over its subsystems that result optimal from an energy or monetary point of view. The results show that a DRL policy in the system control can reduce the system operating costs by more than 50%, as compared to a rule-based control (RBC) policy, for cooling supply to a reference residential building in Mediterranean climate during a period of 18 days. Moreover, a robustness analysis was carried out, which showed that, even for large errors in the parameters of the system simulation models corresponding to an error multiplying factors up to 2, the average cost obtained with the original model deviates from the optimum value by less than 3%, demonstrating the robustness of the solution over a wide range of model errors.

1. Introduction

As building energy consumption accounts for a large percentage of the total energy consumption, an extensive work on new methods and strategies for more efficient control systems has been done. In this sense, many approaches have been proposed, from classical control theory to reinforcement learning, particularly related to heating, ventilation and air conditioning (HVAC) systems. The availability, ubiquity and performance of current digital systems, as well as their reduced cost, allow to devise control scenarios where many parameters can be easily monitored (i.e., batteries state, instant photovoltaic production, current consumption demand, etc.) and take real-time decisions according to different control techniques, always pursuing some predefined objectives such as lowest operating costs or better efficiencies, among others.

Even though the use of machine learning techniques is relatively recent, model predictive control (MPC) and all its flavors, produced a large number of publications in the field of optimal control for energy storage systems. A complete review on control of storage systems can be found in [1,2,3,4] with particular reference to MPC approaches. Even though MPC is able to reach optimal or quasi-optimal solutions, its implementation for complex systems is challenging. Aside from its computational requirements that can difficult a real-time control, MPC optimization problems usually require to be formulated as mixed integer non-linear programming (MINLP) problems [5,6], requiring specialized solvers to find optimal solutions as SCIP [7,8]. Current state-of-the-art solvers only deal with certain type of non-linearities, making it sometimes hard or impossible to express a complex system as a quasi-linear system. Not to mention its difficulty to adapting under uncertainty scenarios, especially arising from model inaccuracies.

In recent years, reinforcement learning (RL) has emerged as an efficient alternative to MPC. RL is based on a mathematical framework for experience-driven autonomous learning [9]. In essence, the learning process is established on a trial-and-error basis, interacting with either the real system or its model. Early RL algorithms, back to the 1980s, proved to solve a wide range of problems in different areas. Q-Learning was one of the most often recurred [10], being firstly used in the field of thermal storage control by Liu and Henze [11,12], and proving experimentally its feasibility. It was in that work where the RL drawbacks for optimal control were mentioned. An inaccurate model may lead to unexpected behavior and, as in all the RL approaches, the curse of dimensionality of the actions-state space arose, putting difficulties in future approaches for complex systems. It was at this point that neural networks came to the rescue, by substituting the time and memory consuming value tables in classical RL schemes and becoming deep reinforcement learning (DRL).

Since its appearance in 2013 [13], DRL has been applied successfully to many complex control problems and, particularly, was first used in HVAC control in [14]. A good review of RL for energy management can be found in [15,16,17], while [18] made an exhaustive analysis of DRL applications for HVAC systems. For the particular case of thermal energy storage (TES) systems, only a few studies were reported in [15,17]. Actually, [17] only identifies 6 publications related to the control of TES systems, all of them with a complexity degree of the TES system far below the one of this study. The study and experimentation by Liu and Henze [19] were the cornerstones of the application of RL to active and passive TES systems, proving the advantages of hybrid approaches that allow accelerating the learning phase by simulation. Later and distinct uses of RL are found in [20,21] describing the first use, to the authors knowledge, of RL techniques to phase change materials (PCM) storage.

The main contribution in this study is twofold. First, the use of DRL for optimal control under demand response in a complex and innovative system to reduce the energy demand for heating, cooling and domestic hot water of a standard single-family residential building is presented in detail. The system, proposed and developed within the H2020 research project, HYBUILD [22], integrates different subsystems such as photovoltaic (PV) panels, Fresnel solar thermal collector, a sorption chiller connected with a reversible heat pump and electrical and thermal energy storages. The application of DRL for optimal control of such a complex system is the first to the best of the authors knowledge. Second, a robustness analysis of the learning process was performed, showing that the learned model results are useful and accurate even for large deviations between the real and the simulated system, answering one of the open questions reported in [17] and proving that the model presented in this study and evaluated under a simulated scenario may fit the control requirements for the real test pilot plant.

2. Methodology

This section explains the details of the system and the approach used for system modelling and optimization.

2.1. System Description

The system considered in this study (Figure 1) was designed to ensure comfort indoor conditions and domestic hot water (DHW) in residential buildings, and specifically to reduce primary energy consumption of single-family houses located in Mediterranean climate regions. Therefore, the different system components were chosen and sized with the main purpose to meet most of the cooling demand using solar energy. To enhance the energy efficiency of the system and the share of renewable energy, it incorporates four different energy storage technologies: an electric battery connected to PV panels, a low-temperature phase change material (PCM) storage unit connected to the low-pressure side of the heat pump, a sorption chiller connected to the high-pressure side of the heat pump and a buffer water tank that stores the heat produced by the Fresnel solar collectors. The hot water stored in the buffer tank is used to drive the sorption chiller and also to contribute to heating and DHW supply.

The heat pump is fed with DC current by means of a DC-bus, which interconnects the PV panels, electric battery, heat pump and (by means of an AC/DC inverter) the power grid. Even though this type of connection enhances the complexity of the system, it also gives a high flexibility and improves the efficiency of the system by reducing the number of multiple stages of conversions from DC to AC and vice-versa.

To obtain the energy demand of the building, a single-family residential building located in Athens was considered as a reference building for Mediterranean climate regions. The building has a total surface of 100 m² distributed in two floors, each having a living surface area of 50 m², and it was assumed to be inhabited by four people. The ceiling/floor heights considered were 2.5 m/3.0 m, while the building width/depth were 6.5 m/8.0 m. The glazing ratio considered was of 20% on the south side, 10% on the north side and 12% on the east and west sides. The energy demand profile for cooling, heating and DHW of the building were obtained within the HYBUILD project [23] activities and it is out of the scope of this paper to present the details of energy demand calculations.

2.2. Components Models and Operating Modes Description

This subsection presents the main system components mathematical models along with the associated operating modes, which were implemented in the control strategies developed for the system.

2.2.1. Fresnel Collectors

The Fresnel collectors consist of flat mirrors that can rotate around a fixed horizontal axis oriented along the north-south direction. There are only two possible operating modes of this component: mode 1 (on) and mode 2 (off). In mode 1, the orientation of the mirrors is set by a controller in such a way that they focus the incident solar radiation to the receiver that is located on top of the mirrors to heat the water in the primary circuit up to 100 °C. The heat is transferred to the buffer tank by means of a heat exchanger (HEX1) and two circulation pumps (P1 and P2) installed in the primary and secondary circuits, respectively. No heat losses were considered in HEX1 for simplicity. In mode 2, no heat is harvested by the solar collectors and pumps P1 and P2 are switched off.

When operating in mode 1, the thermal power generated by the Fresnel collectors (${\dot{Q}}_{solar}$, in kW) is given by Equation (1), otherwise ${\dot{Q}}_{solar}=0$.

$$\begin{gathered} {\dot{Q}}_{solar}=\left[{\eta }_{opt}·{\eta }_{clean}·DNI-\left(4.8703-0.0981·T_m+9·{10}^{-4}·T_m^2\right)- \\ \left(\frac{(T_m-T_{amb})-80}{4}+29.043+1.0983·v_w+0.4188·v_w^2+4·{10}^{-5}·v_w^3\right)\right]· \\ {A}_{Fres}/1000, \end{gathered}$$

(1)

where ${\eta }_{opt}$ is the optical efficiency of the receiver, ${\eta }_{clean}=1$ is the mirror cleanness factor, DNI (in W/m²) is the direct normal irradiance at the specified location [24], $T_m=95$°C is the mean receiver temperature, $T_{amb}$ (in °C) is the ambient air temperature [24], $v_w$ (in m/s) is the wind speed [24] and $A_{Fres}=60$ m² is the total surface area of the solar collectors.

The values for the optical efficiency of the receiver (${\eta }_{opt}$) depend on the month of the year and on the geographic coordinates of the location, and were provided by the manufacturer within HYBUILD activities [22].

The overall electricity consumption of Fresnel collectors is the sum of the consumption of the circulation pumps P1 (34 W) and P2 (34 W), when the Fresnel collectors operate in mode 1, otherwise the electricity consumption of this component is zero.

2.2.2. PV Panels

The PV panels were assumed to face south and have a tilt angle of 30° with respect to the horizontal plane. The net power generated by the PV panels ($PV$, in kW) is given by Equation (2):

$$PV={\eta }_{PV}·E_{POA}·A_{PV},$$

(2)

where ${\eta }_{PV}=0.16$ [25] is the efficiency of the PV system, $E_{POA}$ (in W/m²) is the plan of array (POA) irradiance at the specified location and $A_{PV}=20.9$ m² is the PV panels surface area. The efficiency of auxiliary components related to the PV system (DC/DC converter, connections, etc.) was assumed to be accounted for in ${\eta }_{PV}$.

The value of the solar irradiance incident to the PV surface ($E_{POA}$, in W/m²) is the sum of three contributions, as shown in Equation (3):

$$E_{POA}=E_b+E_g+E_d,$$

(3)

where $E_b$ (in W/m²) is the POA beam component, $E_g$ (in W/m²) is the POA ground-reflected component and $E_d$ (in W/m²) is the POA sky-diffuse component.

The three contributions shown in the right-hand member of Equation (3) were obtained using Pysolar library [26] and Reindl model [27,28,29], and assuming an albedo of 0.2.

2.2.3. Heat Pump and PCM Tank

The heat pump (HP) is one of the core components of the system and it is mainly used to provide space cooling, although it can also provide space heating. On the one hand, the low-pressure circuit of the HP is connected to an innovative type of PCM tank, which can at the same time act as the evaporator of the heat pump. The main purpose of the PCM tank is to store the surplus of coolness produced by the HP during periods of low cooling demand and high PV production, when the electric battery is already completely charged. On the other hand, the high-pressure circuit of the HP (condenser) is connected, by means of a hydraulic loop, to the evaporator of a sorption chiller, so that the heat rejected by the HP condenser is absorbed by the evaporator of the sorption chiller. The objective of this connection is to increase the efficiency (EER) of the HP and reduce therefore the overall electricity consumption of the heat pump.

As shown in Figure 1, the hydraulic connections allow the HP and PCM tank to operate in different modes, either for cooling or heating purposes, as summarized in

Table 1. Operating modes of the HP and PCM tank.

Mode	Description	Active Pumps	Dry Cooler	Fan-Coils
Cooling 1	PCM tank is charged by the heat pump, no cooling is provided to the building	P5–P8 (if sorption is on) P7 and P8 (if sorption is off)	On	Off
Cooling 2	PCM tank is discharging to provide cooling to the building	P9 and P10	Off	On
Cooling 3	Cooling is provided by the HP through the PCM tank	P5–P10 (if sorption is on) P7–P10 (if sorption is off)	On	On
Cooling 4	Cooling is provided by the HP through the standard evaporator	P5–P10 (if sorption is on) P7–P10 (if sorption is off)	On	On
Heating	Heating is provided by the HP	P7 and P10	On	On
0	No cooling or heating is provided	None	Off	Off

.

The PCM tank consists of a compact three-fluids (refrigerant-PCM-water) heat exchanger, in which PCM is placed in an array of parallel channels containing aluminum fins, sandwiched between refrigerant and water channels in an alternating sequence. This configuration allows for efficient heat transfer between the three fluids in the same container, also made of aluminum, which allows for easy charging and discharging of the PCM, as well as direct heat transfer between the supply and demand circuits. An amount of 160 kg of the commercial RT4 PCM, which is a paraffin that melts around 5 °C, was considered in the PCM tank. A complete description of the HP and PCM tank model can be found in [30]. A slightly improved model for the PCM tank was used in this study to also consider the sensible contribution to the overall energy stored in the PCM tank, as well as energy losses to the ambient. The updated relation between the charging level of the PCM tank ($E_{PCM,t}$, in kJ) and the PCM temperature ($T_{PCM,t}$, in °C) at time t is shown in Equation (4):

$$\begin{gathered} E_{PCM,t}= \\ \left\{\begin{array}{c}43186.8,if{T}_{PCM,t}<-2°C\\ -211.75·T_{PCM,t}{}^2-2110.7·T_{PCM,t}+39812,if-2°\mathrm{C}\le T_{PCM,t}\le 3°C\\ -1270.5·T_{PCM,t}{}^2+3183·T_{PCM,t}+33460,if3°C<T_{PCM,t}<6°C\\ -1136.7·T_{PCM,t}+13640,if6°\mathrm{C}\&\le T_{PCM,t}\le 12°\mathrm{C}\\ 0,if{T}_{PCM,t}>12°\mathrm{C}\end{array}\right., \end{gathered}$$

(4)

Regardless the operating mode, the change in the energy stored in the PCM tank at time t is calculated from the charging level at the previous time slot ($E_{PCM,t-1}$, in kJ) and the net rate of coolness transfer to the PCM in the time interval $\Delta t$ (in seconds), as shown in Equation (5):

$$E_{PCM,t}=E_{PCM,t-\Delta t}+\left({\dot{Q}}_{PCM}-{\dot{Q}}_{losses}\right)·\Delta t,$$

(5)

where ${\dot{Q}}_{PCM}$(in kW) is the rate of coolness transfer to the PCM and ${\dot{Q}}_{losses}=\left(T_{amb,t}-T_{PCM,t-1}\right)/R_{PCM}$ (in kW) are the coolness losses from the PCM tank to the ambient air at temperature $T_{amb,t}$ (in °C). The thermal resistance of the PCM tank ($R_{PCM}$) was estimated to be equal to 424.5 K/kW.

The rate of coolness transfer to the PCM (${\dot{Q}}_{PCM}$) depends on the operating mode. When operating in cooling mode 1, the entire energy (coolness) generated by the HP (${\dot{Q}}_{evap}$, in kW) [30] is transferred to the PCM, so that ${\dot{Q}}_{PCM}={\dot{Q}}_{evap}$. In cooling mode 2, the PCM is discharged by the heat transfer fluid (HTF) of the building cooling circuit, and it was assumed to be equal (in absolute value) to the cooling demand, i.e., ${\dot{Q}}_{PCM}=-{\dot{Q}}_{cool,demand}$. In cooling mode 3, an energy balance is needed to determine the net rate of coolness transferred to the PCM because, on the one hand, the PCM is cooled down by the refrigerant and, on the other hand, it is heated up by the HTF. Therefore, in cooling mode 3, the PCM tank can actually be charging or discharging, depending on the charge level and the cooling demand. In cooling mode 4, the heat pump operates with the standard evaporator and the PCM tank is by-passed, and the same occurs when the heat pump operates in the heating mode. Therefore, ${\dot{Q}}_{PCM}=0$ in cooling mode 4 and in heating mode.

When the heat pump operates in heating mode, the sorption chiller is always off. The heat required by the building is taken from the ambient air through the dry cooler by activating pump P7 and by-passing HEX2, and it is delivered to the building heating loop connected to the condenser of the heat pump by activating P10 and by-passing HEX3.

Once the charging level of the PCM tank at time slot t ($E_{PCM,t}$) is calculated, the PCM temperature and the water temperature at condenser outlet ($T_{wc,out,t}$) can be updated. Moreover, the electricity consumption of the compressor of the heat pump (${\dot{Q}}_{comp}$), as well as the electricity consumption of all auxiliary equipment (pumps, dry cooler, fan-coils), can be calculated by taking into account what components are active in each operating mode according to Table 1. Only the compressor of the heat pump is driven by the DC-bus, while all other equipment uses electricity directly from the grid.

2.2.4. Sorption Chiller

The sorption chiller consists of two adsorbers based on a silica gel/water system, which switch periodically between adsorption and desorption operation in counter phase, a condenser and an evaporator. There are only two possible operating modes for the sorption chiller: mode 1 in which the sorption chiller is on and mode 2 in which it is off. In mode 1, the adsorption cycle is activated thanks to the hot water provided by the buffer tank. To work properly, the temperature of the hot water provided by the buffer tank ($T_{HT,in}$) should lie between 65 °C and 95 °C. At the evaporator side of the sorption chiller, heat is taken from the condenser of the HP. The waste heat produced by the sorption chiller is drained by the dry cooler to the ambient air at temperature $T_{amb}$.

The thermal coefficient of performance ($CO{P}_{th}$) of the sorption chiller is defined as $CO{P}_{th}={\dot{Q}}_{LT}/{\dot{Q}}_{HT}$, where ${\dot{Q}}_{LT}$ (in kW) is the cooling power (heat taken from the condenser of the HP) and ${\dot{Q}}_{HT}$ (in kW) is the thermal power extracted from the buffer tank. Experimental tests performed in the lab showed that $CO{P}_{th}$ can be considered constant and equal to 0.55 for a large range of operating conditions.

The cooling power of the sorption module (${\dot{Q}}_{LT}$) is a function of the water temperature at the evaporator inlet ($T_{LT,in}$, in °C), the water temperature that returns from the dry cooler ($T_{MT,in}$, in °C) and the water temperature that returns from the buffer tank ($T_{HT,in}$, in °C) [31], as shown in Equation (6):

$${\dot{Q}}_{LT}=4.559+1.36245·T_{LT,in}-1.64553·T_{MT,in}+0.47773·T_{HT,in},$$

(6)

The return water temperature from the dry cooler ($T_{MT,in}$) was assumed to be 5 K above the ambient temperature, i.e., $T_{MT,in}=T_{amb}+5$. The water temperature at the evaporator inlet ($T_{LT,in}$) was assumed to be equal to the water temperature at the outlet of the condenser of the HP evaluated at the previous time slot, i.e., $T_{LT,in,t}=T_{wc,out,t-1}$.

Therefore, the thermal power extracted from the buffer tank (${\dot{Q}}_{HT}$) can be calculated according to Equation (7) [31]:

$${\dot{Q}}_{HT}=\frac{{\dot{Q}}_{LT}}{CO{P}_{th}}=\frac{{\dot{Q}}_{LT}}{0.55},$$

(7)

Water temperature at the outlet of the adsorption module ($T_{HT,out,t}$, in °C) can be obtained using an energy balance as shown in Equation (8):

$$T_{HT,out,t}=T_{HT,in,t}-\frac{{\dot{Q}}_{HT}}{{\dot{m}}_{ad}·c_{p,w}},$$

(8)

where ${\dot{m}}_{ad}=0.694$ kg/s is the mass flow rate of the water in the loop that connects the buffer tank with the sorption chiller and $c_{p,w}=4.18$ kJ/(kg·K) is the specific heat capacity of the water.

Finally, the water temperature at the evaporator outlet ($T_{LT,out,t}$, in °C) can be obtained using an energy balance as shown in Equation (9):

$$T_{LT,out,t}=T_{LT,in,t}-\frac{{\dot{Q}}_{LT}}{{\dot{m}}_{wc}·c_{p,w}},$$

(9)

where ${\dot{m}}_{wc}=1.417$ kg/s is the mass flow rate of the water in the loop that connects the condenser of the HP with the evaporator of the sorption chiller.

In mode 2, the sorption chiller is off and the following values were assumed for the main variables related to the sorption chiller: ${\dot{m}}_{ad}={\dot{Q}}_{HT}={\dot{Q}}_{LT}=0$, $T_{HT,out,t}=T_{HT,in,t}=T_{buffer,top,t-1}$, $T_{LT,in,t}=T_{amb}+5$ and $T_{LT,out,t}=T_{LT,in,t}$, where $T_{buffer,top,t-1}$ (in °C) is the temperature of the water at the top part of the buffer tank at the previous time slot.

The overall electricity consumption of the sorption chiller in mode 1 is the sum of the electricity consumption of the dry cooler, pumps P5–P8 and the actuators of the hydraulic system and controller (around 200 W). In mode 2, the electricity consumption of the sorption chiller is zero. The electricity needed to feed the sorption module is taken from the grid.

2.2.5. Dry Cooler

The dry cooler switches on whenever there is a need to reject heat from the system to the ambient air, i.e., when the sorption chiller and/or the heat pump are on. The electricity consumption of the dry cooler (${\dot{W}}_{dc}$, in kW) depends on the part load of the dry cooler ($P{L}_{dc}$) and it is given in Equation (10) [32]:

$${\dot{W}}_{dc}=0.0176-0.1622·P{L}_{dc}+0.8781·P{L}_{dc}^2,$$

(10)

The part load ($P{L}_{dc}$) is defined as the actual thermal power to be rejected or absorbed by the dry cooler divided by its nominal thermal power (40 kW), i.e., $P{L}_{dc}={\dot{Q}}_{drycooler}/40$. The actual thermal power (${\dot{Q}}_{drycooler}$, in kW) depends on the operating modes of both the sorption chiller and the HP, as shown in Equation (11):

$$\begin{gathered} {\dot{Q}}_{drycooler}= \\ \left\{\begin{array}{c}{\dot{Q}}_{HT}+{\dot{Q}}_{LT},\mathrm{if}\mathrm{sorption}\mathrm{chiller}\mathrm{is}\mathrm{on}\\ {\dot{Q}}_{cond},\mathrm{if}\mathrm{sorption}\mathrm{chiller}\mathrm{is}\mathrm{off}\mathrm{and}\mathrm{HP}\mathrm{operates}\mathrm{in}\mathrm{cooling}\mathrm{mode}\\ {\dot{Q}}_{evap},\mathrm{if}\mathrm{HP}\mathrm{operates}\mathrm{in}\mathrm{heating}\mathrm{mode}\end{array}\right., \end{gathered}$$

(11)

where ${\dot{Q}}_{cond}$ (in kW) is the rate of heat rejected by the HP condenser and ${\dot{Q}}_{evap}$ (in kW) is the heat absorbed by the dry cooler from the ambient air.

2.2.6. DHW Tank

The DHW tank is used in the system to store a sufficient amount of hot water able to meet the DHW demand of the building at any moment. Therefore, the water stored in the tank should always be kept above a minimum temperature level. To achieve it, the DHW tank should be heated with hot water from the buffer tank. An electric heater can also be used as a backup in case the temperature in the buffer tank is not high enough to be able to charge the DHW tank. In case the water temperature inside the DHW tank lies within the required temperature range, no heat is provided to the DHW tank. This means that there are three possible operating modes for the DHW tank: mode 1, in which the DHW tank is heated by the buffer tank, mode 2, in which it is heated by the electric heater and mode 3, when no heat is provided to the DHW tank.

In mode 1, pump P3 is activated to circulate hot water from the top part of the buffer tank to heat the DHW tank. This mode can be activated whenever the temperature inside the DHW tank ($T_{DHW}$, in °C) is below a lower threshold ($T_{DHW}<T_{set,DHW}-5$) and the temperature of the water at the top part of the buffer tank ($T_{buffer,top}$, in °C) is above a given threshold ($T_{buffer,top}\ge T_{set,DHW}+10$). The DHW tank is heated by the water from the buffer tank until the water temperature inside the DHW reaches the upper threshold of the set-point temperature ($T_{DHW}\ge T_{set,DHW}+5$) or the buffer tank temperature is lower than the required threshold ($T_{buffer,top}<T_{set,DHW}+10$), whichever occurs first. The value considered for the set-point temperature of the DHW tank is $T_{set,DHW}=50$°C.

Mode 2 is activated when the temperature inside the DHW tank is below the set-point range ($T_{DHW}<T_{set,DHW}-5$) and the DHW tank is heated by the electric heater (instead of the buffer tank). Similar to mode 1, the electric heater is switched off when the water temperature reaches the upper threshold of the set-point temperature ($T_{DHW}\ge T_{set,DHW}+5$). In mode 3, water temperature inside the DHW tank lies within the required temperature range ($T_{set,DHW}-5<T_{DHW}<T_{set,DHW}+5$), so no heat is supplied to the DHW tank, although heat can be discharged from the DHW tank to meet the demand.

In all three modes, the temperature distribution inside the tank is considered homogeneous, and it can be calculated at any time t by means of an energy balance given in Equation (12):

$$\begin{gathered} a_1·{\dot{Q}}_{DHW,buffer}+a_2·{\dot{Q}}_{DHW,el}-{\dot{Q}}_{DHW,demand}-{\dot{Q}}_{loss,DHW}= \\ \frac{M_{DHW}·c_{p,w}·\left(T_{DHW,t}-T_{DHW,t-1}\right)}{\Delta t}, \end{gathered}$$

(12)

where $a_1=\left(1,0,0\right)$ and $a_2=\left(0,1,0\right)$ for DHW mode $=\left(1,2,3\right),$ respectively, ${\dot{Q}}_{DHW,buffer}$(in kW) is the heat extracted from the buffer tank, ${\dot{Q}}_{DHW,el}=2$ kW is the thermal power supplied by the electric heater, ${\dot{Q}}_{DHW,demand}$ (in kW) is the DHW demand, ${\dot{Q}}_{loss,DHW}$ (in kW) are the heat losses from the DHW tank to the ambient air, $M_{DHW}=250$ kg is the mass of the water inside the DHW tank and $T_{DHW,t-1}$(in °C) is the temperature of the water inside the DHW tank calculated in the previous time slot.

The heat extracted from the buffer tank (${\dot{Q}}_{DHW,buffer}$) depends on the temperature inside the DHW tank ($T_{DHW,t}$) as shown in Equation (13):

$${\dot{Q}}_{DHW,buffer}={\dot{m}}_{DHW}·c_{p,w}·\left(T_{DHW,in}-T_{DHW,t}\right),$$

(13)

where ${\dot{m}}_{DHW}=0.556$ kg/s is the water mass flow rate (displaced by pump P3) in the loop that charges the DHW tank and $T_{DHW,in}=60$°C is the set-point of water temperature at the DHW tank inlet.

Heat losses from the DHW tank to the ambient air (${\dot{Q}}_{loss,DHW}$) are calculated using Equation (14):

$${\dot{Q}}_{loss,DHW}=\frac{T_{DHW,t}-T_{amb,t}}{R_{DHW}},$$

(14)

where $R_{DHW}=830.8$ K/kW is the overall thermal resistance of the DHW tank.

The electricity consumption of the DHW tank from the grid is associated to the circulating pump P3 (only in mode 1) and the electric heater (only in mode 2). There is no electricity consumption in mode 3.

2.2.7. Buffer Tank

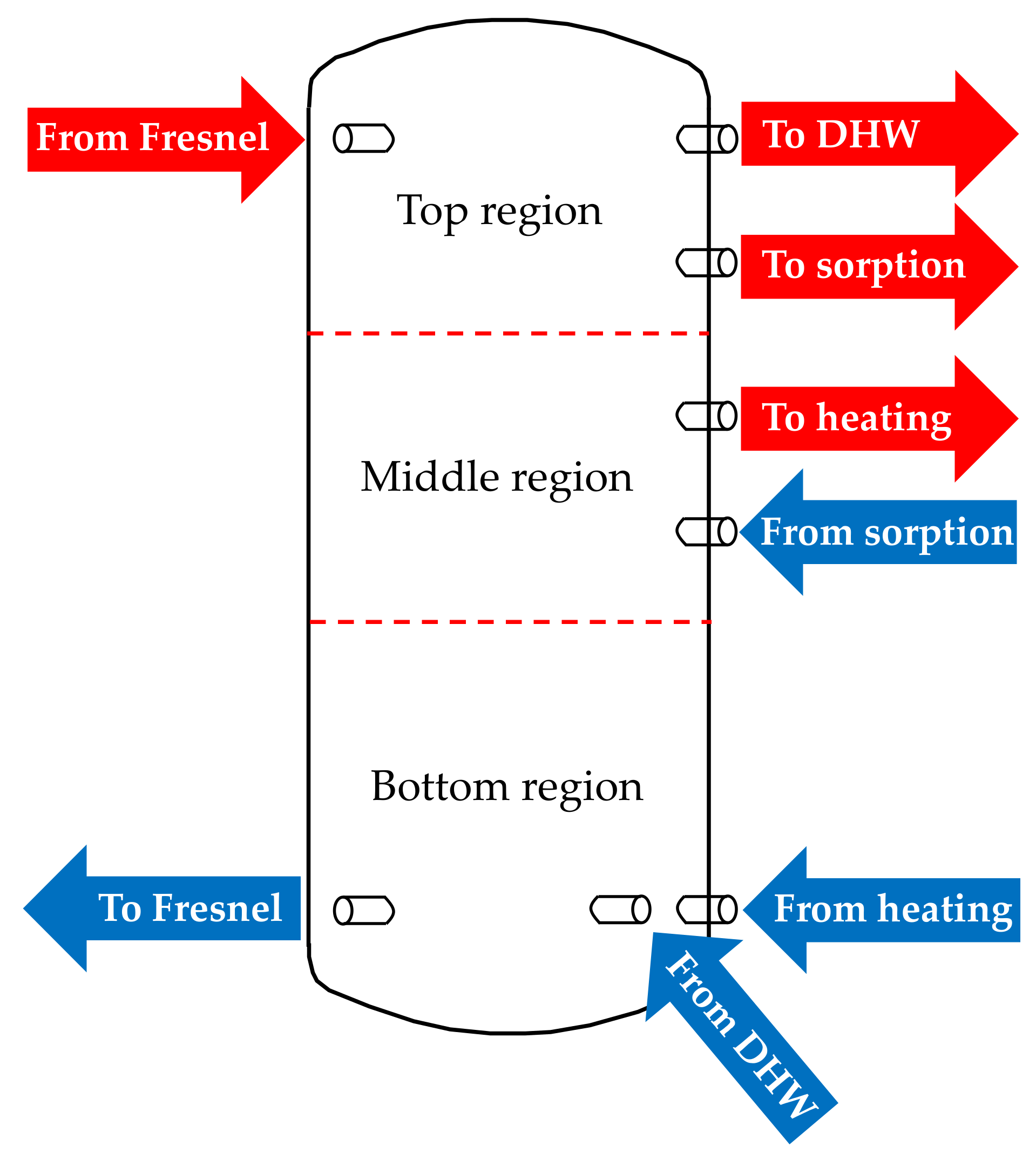
The buffer tank is modelled considering three different regions (volumes) and assuming a uniform water temperature distribution inside each volume (Figure 2) [33,34]. The temperature of the buffer tank at time slot t is calculated by applying an energy balance to each of the three different volumes of the tank. Heat transfer by conduction or natural convection between two adjacent regions is neglected and the only heat transfer mechanism considered is through mass transfer. The buffer tank charging is assumed to be done with hot water at constant inlet temperature of 95 °C coming from the Fresnel solar field. The heat generated by the solar collectors (${\dot{Q}}_{solar}$, in kW) is transferred to the buffer tank by means of a heat exchanger placed between the solar field loop and the buffer tank loop (HEX1 in Figure 1). Heat losses between the solar field and the buffer tank were neglected for simplicity. The mass flow rate of the water in the buffer tank loop (${\dot{m}}_{solar}$, in kg/s) is variable to maintain a constant water temperature at the buffer tank inlet.

For the top region, the energy balance is shown in Equation (15):

$$\begin{gathered} {\dot{m}}_{solar}·c_{p,w}·\left(T_{solar,in}-T_{buffer,top,t-1}\right)+\dot{m}{\prime }_{DHW}·c_{p,w}·\left(T_{buffer,mid,t-1}- \\ {T}_{buffer,top,t-1}\right)+{\dot{m}}_{ad}·c_{p,w}·\left(T_{buffer,mid,t-1}-T_{buffer,top,t-1}\right)- \\ \frac{\left(T_{buffer,top,t-1}-T_{amb}\right)}{R_{buffer,top}}=f_{top}·M_{buffer}·c_{p,w}·\frac{T_{buffer,top,t}-T_{buffer,top,t-1}}{\Delta t}, \end{gathered}$$

(15)

where $M_{buffer}$= 800 kg is the mass of the water inside the buffer tank, $f_{top}$= 0.3 is the mass fraction of the top part of the buffer tank, $T_{solar,in}$= 95 °C is the inlet temperature of the water flow coming from the Fresnel collectors,$T_{buffer,top,t-1}$(in °C) and $T_{buffer,mid,t-1}$(in °C) are the temperatures of water at the top and middle parts of the buffer tank in the previous time slot, respectively, and $\Delta t$ is the time step (in seconds). If sorption module is off, ${\dot{m}}_{ad}$= 0. The sorption module is automatically switched off when $T_{buffer,top,t}<$ 65 °C and it may be switched on again when $T_{buffer,top,t}\ge$ 68 °C (if the high-level controller decides it is best to do it, and whenever the heat pump is working in one of the cooling modes 1, 3 or 4).

The mass flow rate of the loop that connects the buffer tank with the solar field (${\dot{m}}_{solar}$, in kg/s) is given by Equation (16):

$${\dot{m}}_{solar}=\frac{{\dot{Q}}_{solar}}{c_{p,w}·\left(T_{solar,in}-T_{buffer,bot,t-1}\right)},$$

(16)

where $T_{buffer,bot,t-1}$(in °C) is the water temperature at the bottom part of the buffer tank evaluated at the previous time slot. When the water temperature at the top of the buffer tank reaches 94 °C during charging, the solar field is switched off and the charging of the buffer tank stops (${\dot{m}}_{solar}$= 0) until the water temperature at the top of the buffer tank decreases to 90 °C, when it may be switched on again if ${\dot{Q}}_{solar}>$ 0.

The water mass flow rate at the buffer tank outlet towards the DHW tank charging circuit ($\dot{m}{\prime }_{DHW}$, in kg/s) is given by Equation (17):

$$\dot{m}{\prime }_{DHW}=\frac{{\dot{m}}_{DHW}·\left(T_{DHW,in}-T_{DHW,t-1}\right)}{\left(T_{buffer,top,t-1}-T_{DHW,t-1}\right)},$$

(17)

where $T_{DHW,t-1}$(in °C) is the temperature inside the DHW tank at the previous time slot. Equation (17) only applies if the DHW tank works in mode 1 (charging with heat supplied from the buffer tank), otherwise $\dot{m}{\prime }_{DHW}$ = 0.

Heat losses from the top part of the buffer tank to the ambient air depend on the thermal resistance of this part of the tank ($R_{buffer,top}$, in K/kW), which can be calculated using Equation (18):

$$R_{buffer,top}=\frac{R_{buffer}·\left(A_{edge}+2·A_{base}\right)}{f_{top}·A_{edge}+A_{base}},$$

(18)

where $R_{buffer}$= 430.3 K/kW is the overall thermal resistance of the buffer tank, $A_{edge}$= 4.095 m² is the surface area of the buffer tank edge (lateral surface area) and $A_{base}$= 0.62 m² is the surface area of the base of the buffer tank.

For the middle part of the buffer tank, the energy balance is shown in Equation (19):

$$\begin{gathered} {\dot{m}}_{solar}·c_{p,w}·\left(T_{buffer,top,t-1}-T_{buffer,mid,t-1}\right)+\dot{m}{\prime }_{DHW}·c_{p,w}· \\ \left(T_{buffer,bot,t-1}-T_{buffer,mid,t-1}\right)+{\dot{m}}_{ad}·c_{p,w}·\left(T_{HT,out,t-1}-T_{buffer,mid,t-1}\right)+ \\ {\dot{m}}_{heat}·c_{p,w}·\left(T_{buffer,bot,t-1}-T_{buffer,mid,t-1}\right)-\frac{\left(T_{buffer,mid,t-1}-T_{amb}\right)}{R_{buffer,mid}}=f_{mid}· \\ {M}_{buffer}·c_{p,w}·\frac{T_{buffer,mid,t}-T_{buffer,mid,t-1}}{\Delta t}, \end{gathered}$$

(19)

where ${\dot{m}}_{heat}$= 0.63 kg/s is the mass flow rate of the building heating loop (circulated by pump P4), $f_{mid}$= 0.3 is the mass fraction of the middle part of the buffer tank and $T_{HT,out,t-1}$(in °C) is the temperature of the water returning from the adsorption module. If there is no heating demand (${\dot{Q}}_{heat,demand}$= 0) or heat is provided to the building by the heat pump working in heating mode, ${\dot{m}}_{heat}$= 0.

Heat losses from the middle part of the buffer tank to the ambient air depend on the thermal resistance of this part of the tank ($R_{buffer,mid}$, in K/kW), which can be calculated using Equation (20):

$$R_{buffer,mid}=\frac{R_{buffer}·\left(A_{edge}+2·A_{base}\right)}{f_{mid}·A_{edge}},$$

(20)

For the bottom region of the buffer tank, the energy balance equation is shown in Equation (21):

$$\begin{gathered} {\dot{m}}_{solar}·c_{p,w}·\left(T_{buffer,mid,t-1}-T_{buffer,bot,t-1}\right)+\dot{m}{\prime }_{DHW}·c_{p,w}·\left(T_{DHW,t-1}- \\ {T}_{buffer,bot,t-1}\right)+{\dot{m}}_{heat}·c_{p,w}·\left(T_{heat,out,t-1}-T_{buffer,bot,t-1}\right)- \\ \frac{\left(T_{buffer,bot,t-1}-T_{amb}\right)}{R_{buffer,bot}}=f_{bot}·M_{buffer}·c_{p,w}·\frac{T_{buffer,bot,t}-T_{buffer,bot,t-1}}{\Delta t}, \end{gathered}$$

(21)

where $f_{bot}$= 0.4 is the mass fraction of the bottom part of the buffer tank.

When the heating demand is satisfied by the buffer tank, water temperature returning from the building ($T_{heat,out,t-1}$, in °C) depends on the heating demand of the building (${\dot{Q}}_{heat,demand}$, in kW) and it is calculated according to Equation (22):

$$T_{heat,out,t-1}=T_{buffer,mid,t-1}-\frac{{\dot{Q}}_{heat,demand}}{{\dot{m}}_{heat}·c_{p,w}},$$

(22)

Otherwise, when there is no heating demand from the building (${\dot{Q}}_{heat,demand}$= 0) or heat is provided by the heat pump working in heating mode, ${\dot{m}}_{heat}$= 0 and $T_{heat,out,t-1}=T_{buffer,mid,t-1}$ (as an alternative to Equation (22)). In case that water temperature at the middle part of the buffer tank is below 45 °C ($T_{buffer,mid,t}<$ 45 °C), heat cannot be delivered to the building from the buffer tank, therefore pump P4 switches off (${\dot{m}}_{heat}$= 0).

Heat losses from the bottom part of the buffer tank to the ambient air depend on the thermal resistance of this part of the tank ($R_{buffer,bot}$, in K/kW), which can be calculated using Equation (23):

$$R_{buffer,bot}=\frac{R_{buffer}·\left(A_{edge}+2·A_{base}\right)}{f_{bot}·A_{edge}+A_{base}},$$

(23)

The overall electricity consumption associated to the buffer tank only consists of the electricity consumption of pump P4 (34 W) when the heating demand of the building is higher than zero and this demand is met by the buffer tank (${\dot{m}}_{heat}>$0) and not by the heat pump working in heating mode.

2.2.8. DC-Bus

The heat pump is driven by DC through a connection to the DC-bus. Electricity can be taken either from the PV panels and/or from the battery, depending on the PV production and the state of charge of the battery. Furthermore, in case that the power supplied by the battery and the PV panels is not enough to feed the heat pump, electricity can also be provided by the power grid through an AC/DC converter (not shown in Figure 1). Conversely, when the PV production is high and the battery is fully charged, surplus electricity can be delivered to the grid. The power generated by the PV panels ($PV$, in kW) was assumed to be always less than the maximum charging power of the battery ($PV<MaxB$) and the maximum discharging power of the battery ($MaxB$) was assumed to be always higher than the power demanded by the HP ($MaxB>HP$).

Three different operating modes were considered for the DC-bus, focusing on the control strategy of the battery, as summarized in

Table 2. Operating modes of the DC-bus and associated thresholds values.

Mode	Name	${\mathit{E}}_1(\%)$	${\mathit{E}}_2(\%)$
1	Charging	75	90
2	Discharging	10	25
3	Buffer	10	90

. Two thresholds, $E_1$ (in %) and $E_2$ (in %), were used to drive the DC-bus in one of the three possible operating modes.

Charging mode (mode 1) takes place if $E_{min}\le B_S\le E_1$, where $E_{min}=10\%$ is the lower charging level allowed for the battery, $B_S$ (in %) is the state of charge of the battery and $E_1$ (in %) is a threshold below which the battery is automatically charged (i.e., when $B_S\le E_1$). In this mode, the battery charges at a constant maximum rate ($B=MaxB=3$ kW) until $B_S=75\%$, after which the battery switches to buffer mode.

In charging mode, the power required by the heat pump (HP) can only be taken from the PV and/or from the grid (G), but not from the battery (Figure 3a).

The equations that describe the different energy streams in charging mode are shown in the set of Equation (24):

$$\left\{\begin{array}{c}H{P}_{PV}=\min \left(PV,HP\right)\\ B_{PV}=\max \left(0,PV-HP\right)\\ B_G=MaxB-B_{PV}\\ H{P}_G=\max \left(0,HP-PV\right)\\ G_{PV}=H{P}_B=0\end{array}\right.,$$

(24)

where $H{P}_{PV}$ (in kW) is the power supplied to the HP from the PV panels, $B_{PV}$ (in kW) is the power supplied to the battery from the PV panels, $B_G$ (in kW) is the power required from the grid to charge the battery at maximum power, $H{P}_G$ is the power required from the grid to feed the HP, $G_{PV}$ is the power coming from the PV panels that is delivered to the grid and $H{P}_B$ is the power supplied to the HP from the battery. The power exchanged between X and Y, where X and Y may refer to PV (PV panels), HP (heat pump), G (power grid) or B (battery), is assumed to be positive ($X_Y>0$) if energy is incoming to X from Y ($X\leftarrow Y$).

Discharging mode (mode 2) takes place if $E_2<B_S\le E_{max}$, where $E_2$ (in %) is a threshold above which the battery automatically discharges (i.e., when $B_S>E_2$) and $E_{max}=90\%$ is the upper threshold allowed for the charging level of the battery. In this mode, the battery is discharging at the maximum rate ($B=-MaxB=-3$ kW) towards both the HP and the grid (Figure 3b) until $B_S=25\%$, after which the battery switches to buffer mode.

The equations that describe the different energy streams in discharging mode are shown in the set of Equation (25):

$$\left\{\begin{array}{c}H{P}_{PV}=\min \left(PV,HP\right)\\ H{P}_B=\max \left(0,HP-PV\right)\\ B_G=-MaxB+H{P}_B\\ G_{PV}=\max \left(0,PV-HP\right)\\ H{P}_G=B_{PV}=0\end{array}\right.,$$

(25)

Buffer mode (mode 3) takes place if $E_1<B_S\le E_2$. Whenever the optimizer decides to switch to the buffer mode, the following values are assigned: $E_1=10\%$ and $E_2=90\%$. In this way, the battery will be forced to switch to buffer mode whatever the value of $B_S$ is.

In mode 3, the battery acts as a buffer, meaning that it charges if there is a surplus of electricity production from the PV panels or it discharges if the HP requires more power than is produced by the PV panels (Figure 3c). In this mode, there is no interaction between the battery and the grid, i.e., the battery cannot charge from the grid, neither can it deliver electricity to the grid.

The equations that describe the different energy streams in buffer mode are shown in the set of Equation (26):

$$\begin{gathered} H{P}_{PV}=\min \left(PV,HP\right) \\ {B}_G=0 \\ \mathrm{if}(-400\mathrm{W}<PV-HP<400\mathrm{W})\mathrm{then} \\ \left\{\begin{array}{c}{G}_{PV}=\max \left(0,PV-HP\right)\\ H{P}_G=\max \left(0,HP-PV\right)\\ B_{PV}=H{P}_B=0\end{array}\right. \\ \mathrm{else} \\ \left\{\begin{array}{c}{B}_{PV}=\max \left(0,PV-HP\right)\\ H{P}_B=\max \left(0,HP-PV\right)\\ G_{PV}=H{P}_G=0\end{array}\right., \end{gathered}$$

(26)

In this mode, the total power supplied to the grid (G) can be negative, positive or zero, depending on the relation between PV production and HP consumption. The total power supplied to the battery (B) can be positive if there is a surplus of PV generation, negative when the power demand of the HP cannot be met only from the PV panels, or zero, when the absolute difference between PV production and HP consumption is less than 400 W ($\left|PV-HP\right|<400\mathrm{W}$).

For all operating modes, the state of charge of the battery at time instant t ($B_{S,t}$) is given by Equation (27):

$$B_{S,t}=B_{S,t-1}+\frac{{\eta }_B·B·\Delta t/3600}{C_{B,max}},$$

(27)

where $B_{S,t-1}$ is the state of charge of the battery at the previous time slot, ${\eta }_B$ is the efficiency of battery charging/discharging process, $C_{B,max}=7.3$ kWh is the maximum storage capacity of the battery and $\Delta t$ (in seconds) is the time step of the simulation. For the sake of simplicity, the value of the efficiency of battery charging/discharging process (${\eta }_B$) was assumed to depend on the sign of B: ${\eta }_B=0.9$ if $B\ge 0$ (battery is charging) and ${\eta }_B=1$ if $B<0$ (battery is discharging).

2.2.9. Summary of the Main Model Parameters

The main model parameters considered for the training/testing scenarios that will be explained later are summarized below:

• Surface of the Fresnel solar collectors: 60 m².
• PV panels surface: 20.9 m².
• PV panels orientation: 0° (south).
• PV panels inclination: 30°.
• PCM tank storage capacity: $\approx 43,200$ kJ (12 kWh).
• DHW tank capacity: 250 L.
• DHW electric heater power: 2 kW.
• Buffer tank capacity: 800 L.
• Battery energy storage capacity: 7.3 kWh.
• Maximum battery charging/discharging power: 3 kW.

2.3. DRL Control Description

2.3.1. General Description

Reinforcement learning is a class of solution methods that optimizes a numerical reward by interaction with the environment [9], in which a learning agent takes actions that drive the environment to new states, provoking some reward being observed by the agent. It is in this context that Markov decision processes (MDP) provide a useful mathematical framework to solve the problem of learning from interaction to optimize a given goal [35]. In a finite and discrete MDP, the environment is represented at each time step as a state. Based on this state, the agent, according to a given policy, decides to execute an action, obtaining a reward from the environment and moving it to the next state. Considering stochastic environments, one can think on state-transition probabilities that characterize the MDP. Furthermore, as each transition gives a reward, each state may be associated to a state-value function that represents all the expected MDP rewards given a state. These representations are the basis for the Bellman optimality equations [36], which must be solved to achieve an optimal solution for the problem.

Expressing the MDP abstraction more formally, and considering a discrete time MDP with time step t = 0, 1, 2, …, the MDP consists of:

• A set of states $S$ that represents the environment, being $S_t\in S$ the environment state at time t.
• A set of actions $A$ that can be taken by the agent, being $A_t\in A\left(s\right)$ the action taken at time t from the subset of available actions at state $s$, $A\left(s\right)$.
• A numerical reward for the new visited state, $R_{t+1}\in ℝ$ that will depend on its trajectory: $S_0,A_0,R_0,S_1,A_1,R_1,$…, $S_t,A_t,R_t$.
• Assuming that the system dynamics is Markovian, random variables $S_t$ and $R_t$ will only depend on its previous values, with a probability distribution,$p(),$ which characterizes the system, defined as in Equation (28):

  $$p\left(s^{\prime },r|s,a\right)\dot{=}Pr\left\{S_t=s^{\prime },R_t=r|S_{t-1}=s,A_{t-1}=a\right\},$$

  (28)
• An agent policy, $\pi$, which determines the chosen action at a given state. Defined as a probability, $\pi \left(a|s\right)$ results in the probability of choosing action $a$ from state $s$.

Figure 4 shows a typical RL paradigm representation. In this case, policy $\pi$ depends on a set of parameters $\theta$ that represents the neural network weights to be discussed later.

The cumulative reward at a given time slot can be defined as in Equation (29):

$$G_t\dot{=}{\sum }_{i=0}^{T-t-1}{\gamma }^i{R}_{t+i+1},$$

(29)

where $T$ is the final time step and $\gamma$ is a discount rate that determines the worthiness of future rewards. Equation (29) helps to define the concept of the value of being at a state for a given policy given in Equation (30):

$${\nu }_{\pi }\left(s\right)\dot{=}{\mathbb{E}}_{\pi }\left[G_t|S_t=s\right],$$

(30)

and using Equation (28), Equation (30) becomes the Bellman equations for ${\nu }_{\pi }$, shown in Equation (31):

$${\nu }_{\pi }\left(s\right)={{\displaystyle \sum }}_a\pi (a|s){{\displaystyle \sum }}_{s^{\prime },r}p(s^{\prime },r|s,a)\left[r+\gamma {\nu }_{\pi }\left(s\prime \right)\right],$$

(31)

for all $s\in S$.

Solving a RL problem implies to find an optimal policy (${\pi }^{*}$) that solves the state-value function defined in Equation (32):

$${\nu }^{*}\left(s\right)\dot{=}\underset{\pi }{\max }{\nu }_{\pi }\left(s\right),$$

(32)

and derives from Equations (28), (29) and (32), the Bellman optimality equations as in Equation (33):

$${\nu }^{*}\left(s\right)\dot{=}\underset{a}{\max }{{\displaystyle \sum }}_{s^{\prime },r}p(s^{\prime },r|s,a)\left[r+\gamma {\nu }^{*}\left(s\prime \right)\right],$$

(33)

The solution of Equation (33) provides the best action $\left(a\right)$, in terms of future rewards, from a given state $\left(s\right)$. Once solved for every possible state, it gives the optimal policy,${\pi }^{*}$, because the probabilities $\pi \left(a|s\right)$ are known.

It is at this point that the whole family of reinforcement learning algorithms is created, trying to solve these optimality equations by different means. Resolution techniques based on dynamic programming (DP) may solve the problem, i.e., find an optimal solution, by iteratively finding the state-values, $\nu \left(s\right)$, but these methods suffer from the so-called curse of dimensionality, because the number of states grows exponentially with the number of state variables. Such a curse is tackled by Monte-Carlo (MC) methods by sampling values of the state-values through experience, by interaction with the model. Even with a partial knowledge of those state-value functions, good MC algorithms converge to acceptable solutions. Even more, if those MC methods are combined with DP ideas, such as update regularly the estimated values, a new family of algorithms arises, called temporal-difference (TD) learning, such as Sarsa $\left(\lambda \right)$, Q-Learning or TD $\left(\lambda \right)$, proving to be highly efficient methods for a lot of optimal control problems.

Even the improvement of new RL methods, large and complex problems may require an enormous amount of computational power, particularly when the number of states is large, during the learning phase. Under this scenario, the ground-breaking concept of deep reinforcement learning (DRL) [13,37] appears to change the rules of the game, scaling up RL to space state dimensions previously intractable. DRL deals efficiently with the curse of dimensionality by using neural networks as substituting parts of traditional value tables, obtaining approximations of the optimal value functions trained by their corresponding neural network backpropagation mechanisms. The emergence of specialized libraries as TensorFlow [38] did the rest, by allowing parallelization across multiple CPUs or GPUs and permitting in this way to train huge neural networks able to cope the structure of complex systems in affordable running times.

2.3.2. Policy Gradient Algorithms

The above-mentioned RL algorithms based the resolution of the Bellman optimality equations on the learned value of the selected actions. Instead, policy gradient methods base their learning on a parameterized policy that selects the actions without the knowledge of a value function. Generically, one can consider a set of parameters $\theta \in {ℝ}^d$ that usualy correspond to the weights of a neural network. By doing so, one can rephrase the policy function as ${\pi }_{\theta }\left(a|s\right)$.

At this point, Equation (30) may work as an objective function, $J\left(\theta \right)$. Effectively, one can define the objective as in Equation (34):

$$J\left(\theta \right)\dot{=}{\nu }_{\pi }{}_{\theta }\left(s_0\right)={\mathbb{E}}_{\theta }\left[G_0|s_0\right],$$

(34)

i.e., the expected cumulative reward from $t=0$. According to the policy gradient theorem [39], whenever the policy was differentiable with respect to $\theta$, the gradient of the cost function obeys the proportionality shown in Equation (35):

$${\nabla }_{\theta }J\left(\theta \right)={\mathbb{E}}_{\pi }\left[G_t\frac{{\nabla }_{\theta }\pi \left(A_t|S_t,\theta \right)}{\pi \left(A_t|S_t,\theta \right)}\right],$$

(35)

Considering that Equation (35) can be instantiated at each time slot and that parameters $\theta$ are time-dependent, one can apply any gradient descent algorithm to compute $\theta$ as in Equation (36):

$${\theta }_{t+1}\leftarrow {\theta }_t+\alpha G_t\frac{{\nabla }_{\theta }\pi \left(A_t|S_t,\theta \right)}{\pi \left(A_t|S_t,\theta \right)}={\theta }_t+\alpha G_t{\nabla }_{\theta }\ln \pi \left(A_t|S_t,\theta \right),$$

(36)

being $\alpha$ a learning rate constant. Equation (36) is the fundamental idea that supports a new family of RL algorithms called REINFORCE [40]. As noted, REINFORCE is a MC-like algorithm because it can be implemented by sampling the environment, getting from it the cumulative reward and the logarithm of the policy gradient, presenting good convergence properties for small enough values of the learning parameter. The existence of gradient descent optimizers based on neural networks, as well as the existing softmax layers did the rest to allow efficient REINFORCE implementations.

2.3.3. HYBUILD Control Model

The HYBUILD control is based on a REINFORCE algorithm with no baseline. HYBUILD system model operates at two differently slotted time scales. First, a finer slot is considered in order to numerically compute the HYBUILD system behavior (3 min are typically considered). This smaller time slot is only considered for inner model operations and it is not relevant for control purposes. Second, a larger slot ($T_s$) is used to manage the control system (15 and 30 min were considered). Within $T_s$ time slot, any action decided by the control system is invariant until reaching any subsystem limit. As an example, if during a given slot $T_s$ one decides to charge the heat pump/PCM tank subsystem, the charging process will not stop unless the maximum state of charge was reached. Similarly, the input system variables for the control system are considered invariant in $T_s$.

HYBUILD control model for the Mediterranean system may be defined for cooling or heating purposes, but the heating model can be considered as a subset of the cooling model because heating operations for the Mediterranean system are much simpler. Actually, heating mode bypasses the PCM tank and sorption subsystems, resulting in only one operating mode for the heat pump subsystem.

The state vector ($S_t$) is an 8-dimensional vector in cooling mode (7-dimensional in heating mode) with the following components:

• Thermal energy demand for cooling/heating in the current time slot ($T{E}_t^{dem}$).
• Thermal energy demand for domestic hot water (DHW) in the current time slot ($T{E}_t^{dhw}$).
• Ambient temperature ($T_{amb,t}$).
• Energy cost for electric demand in the current time slot ($C_t$).
• Direct normal irradiation, ($DN{I}_t$), as explained in Section 2.2.1 and Section 2.2.2.
• Charge level of the PCM tank subsystem, ($E_{PCM,t}$), as explained in Section 2.2.3. Not used in heating mode.
• Buffer tank top temperature, ($T_{buffer,top,t}$), as explained in Section 2.2.7.
• Battery state of charge in the DC-bus subsystem ($B_{S,t}$), as explained in Section 2.2.8. being $t$ the corresponding time and all of them were standard normalized according to their ranges.

Choosing thermal energy demand as input, instead of temperature set-points, allow to decouple the model from building thermal mass dynamics, providing more consistency to the Markovian assumption. In this sense, considering the control process as an MDP results is a valid assumption as long as the heating/cooling subsystem models, detailed in Section 2.2, are time-depending on only previous time slots. As a counter effect, an on-site control implementation will require to model the building dynamics based on the temperature set-points in order to predict the thermal demand. In this sense, the models used in this study are based on reinforcement learning that accurately provide the thermal demand for a particular building under different weather conditions and set-points.

The set of actions ($\mathcal{A}$) that guide the control can be defined as $\mathcal{A}=\left\{\mathcal{C},\mathcal{S},\mathcal{B}\right\}$, where $\mathcal{C}$ is the set of cooling/heating operating modes, $\mathcal{S}$ is the set of activation modes for the sorption subsystem and $\mathcal{B}$ is the set of battery modes in the DC-bus subsystem. As only the set $\mathcal{C}$ differs for the cooling and the heating models, one can differentiate the set of actions accordingly: ${\mathcal{A}}_{cool}=\left\{{\mathcal{C}}_{cool},\mathcal{S},\mathcal{B}\right\}$ and ${\mathcal{A}}_{heat}=\left\{{\mathcal{C}}_{heat},\mathcal{S},\mathcal{B}\right\}$.

According to the operating modes defined in Table 1,${\mathcal{C}}_{cool}=\left\{0,1,2,3,4\right\}$ and $\mathcal{S}=\left\{0,1\right\}$ because the sorption subsystem may be on or off. For the heating modes, as sorption and heat pump/PCM tank subsystems are bypassed, only one operating mode is considered, being ${\mathcal{C}}_{heat}=\left\{0,1\right\}$.

Concerning the actions related to the DC-bus subsystem, as detailed in Section 2.2.8, the high-level control may determine the $E_1$ and $E_2$ thresholds that define the area of DC-bus operation, as well as the maximum charging/discharging power when operating in charge/discharge areas. As the control model presented here only deals with discrete values, the DC-bus control operations were simplified according the following rules:

• Charging/discharging power is set to a fixed value, namely 3 kW.
• If from the high-level control the DC-bus is forced to operate in charging, buffer or discharging mode, the pair of values $\left(E_1,E_2\right)$ is set to three fixed levels: (75, 90), (10, 90) and (10, 25), respectively, as a percentage of the battery state of charge, $B_S$.

Following these assumptions,$\mathcal{B}=\left\{0,1,2\right\}$, which corresponds to charging, buffer and discharging modes, respectively.

Finally, considering that during cooling mode 2 (all cooling energy is supplied by the PCM tank) the sorption chiller is in mode 0, the set of possible actions are:

$$\begin{gathered} {\mathcal{A}}_{cool}=\left\{\right[1,0,0],[1,0,1],[1,0,2],[1,1,0],[1,1,1],[1,1,2], \\ [2,0,0],[2,0,1],[2,0,2], \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}[3,0,0],[3,0,1],[3,0,2],[3,1,0],[3,1,1],[3,1,2], \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}[4,0,0],[4,0,1],[4,0,2],[4,1,0],[4,1,1],[4,1,2\left]\right\} \end{gathered}$$

and $\left|{\mathcal{A}}_{cool}\right|$= 21.

In heating mode, considering that the sorption chiller is always off, it follows that:

$${\mathcal{A}}_{heat}=\left\{\right[1,0,0],[1,0,1],[1,0,2\left]\right\}$$

and $\left|{\mathcal{A}}_{heat}\right|$= 3.

It should be noted that all the cases where cooling/heating mode is 0 may be omitted because:

• If there is some energy demand, cooling/heating mode 0 is not an option.
• Otherwise, any cooling/heating mode will perform as mode 0 inside $T_S$.

In other words, mode 0 is adopted when energy demand is null.

For the purpose of this study, a policy gradient REINFORCE algorithm was implemented, with two three-layer fully-connected neural networks of sizes $N_{inp,heat}\times N_{hid,heat}\times N_{out,heat}$ and $N_{inp,cool}\times N_{hid,cool}\times N_{out,cool}$ for heating and cooling, respectively, with the following characteristics:

• $N_{inp,heat}$= 7 and $N_{inp,cool}$= 8 are the number of inputs, defined by the system state dimension. Their values are standard normalized with their corresponding ranges.
• $N_{hid,heat}$ and $N_{hid,cool}$ are the hidden layer sizes for heating and cooling modes, respectively. They use to be much larger than the size of inputs and outputs. Actually, the number of hidden layers, their size, the type activation functions, as well as other parameters will be adjusted in a future study by hyper-parameter setting analysis, being out of the scope of this paper. The values $N_{hid,heat}$= 100 and $N_{hid,cool}$= 1,000 were adopted here, with exponential linear unit activation functions and a dropout rate of 0.8.
• $N_{out,heat}$= 3 and $N_{out,cool}$= 21 are the number of outputs corresponding to the cardinality of the actions set. Outputs represent softmax of logits and the corresponding action is taken as a multinomial of the logarithm of outputs.
• Learning rate, $\alpha$= 0.0005.
• Discount rate, $\gamma$= 0.99.

The neural network was trained minimizing the cross entropy of the multinomial outputs using an Adam stochastic optimizer [41]. Under this scenario, one objective function was defined regarding an economic reward related to the cost associated to the system operation.

2.3.4. Minimum Cost Control Policy

In order to derive control policies focused on minimizing the cost of operation, the cumulative reward $G_t$ used in Equation (36) and in Equation (29) should be calculated considering the reward function $R_t$ defined in Equation (37):

$$R_t\dot{=}\left(E{E}_t^{fg}-0.5·E{E}_t^{tg}\right)·C_t+\left(T{E}_t^{dem}-T{E}_t^{hp}-T{E}_t^{pcm}\right)·Penalty,$$

(37)

where:

• $E{E}_t^{fg}$ is the electrical energy bought from the grid in slot $t$, either to feed the DC-bus or other equipment, such as the electric resistance of the DHW tank.
• $E{E}_t^{tg}$ is the electrical energy sold to the grid in slot $t$. A discount factor of 0.5 was considered.
• $T{E}_t^{hp}$ is the thermal energy provided by the heat pump subsystem for cooling/heating in slot $t$.
• $T{E}_t^{pcm}$ is the thermal energy provided by the PCM tank for cooling/heating in slot $t$.
• $Penalty$ is the cost assumed for a non-covered demand. A value much higher than the energy cost is used.
• $C_t$ and $T{E}_t^{dem}$ as detailed in Section 2.3.3.

Note that $T{E}_t^{dhw}$ is not part of the objective function because it is assumed that DHW requirements will always be fulfilled by the backup electric heater.

2.3.5. Rule-Based Control Policies

With the objective to evaluate the DRL control policy goodness, a simple rule-based control (RBC) policy for the cooling season was also implemented, which can be simplified for heating mode. The RBC policy is based on its own thresholds and can be described as follows:

• Battery mode—charging, buffer or discharging—is determined by two battery state of charge thresholds ($B_{min}^{th}$ and $B_{max}^{th}$) and the grid cost ($C_t$).
• Cooling mode 1 (PCM tank charging) is set if there is no cooling demand. Otherwise, cooling mode 2 (PCM tank discharging) is set if PCM energy ($E_{PCM,t}$) is larger than a threshold factor ($PC{M}_f^{th}$) times the cooling demand ($T{E}_t^{dem}$). Otherwise, cooling mode 3 (simultaneous PCM tank charging and cooling supply to the building) or 4 (cooling supply using the standard HP evaporator) is set according to the energy stored in the PCM tank in relation to the PCM energy threshold ($E_{PCM}^{th}$).
• Sorption chiller mode is set depending on the buffer tank temperature threshold ($B{T}^{th}$) in comparison to the buffer tank temperature at the top region ($T_{buffer,top,t}$).

The details on both cooling and heating RBC policies are shown in Appendix A. In both RBC policies, a hyper-parameter optimization was applied in order to determine the optimal thresholds. Hyperopt python library [42] was used employing an adaptive Tree Parzen Estimator algorithm with 400 runs over the same training test set.

2.3.6. Implementation Aspects

Figure 5 shows the structure designed for the implementation of the HYBUILD con-trol system. It is divided into three layers. Layer 3 is composed of the low-level controllers for each subsystem. It operates directly over the system components, including all sensors, actuators and low-level security protocols. Layer 2 is composed of the Supervisory Con-trol And Data Acquisition (SCADA) system. It monitors the system parameters, sends the state vector to layer 1 and executes the set of actions set by layer 1. Layer 1 is composed of the DRL control algorithm described in this paper. The communication between layers 1 and is done using MQTT(json) and the communication between layers 2 and 3 is performed using the OPC-UA communication protocol.

The HYBUILD control model was written in Python 3 [43]. Furthermore, Tensorflow libraries were used in control models [38]. The availability of a lite version of Tensorflow libraries makes suitable this implementation for light hardware or micro-controller environments that may be required for control scenarios in real time.

2.4. Network Trainizng

In this subsection, the data set used to train and test the network is described. The computations are performed with weather data for the reference building (assumed to be located in Athens), but it could be applied to any other location. The computing training time and its convergence issues are also presented in this subsection.

2.4.1. Training and Test Data

Cooling data set spans from day 120 to day 250 of the year, while heating data set spans from day 290 to day 365 and from day 1 to day 90. Such sets are shuffled and split into smaller subsets (batches). Each batch is composed of a fixed number of days ($\mathcal{T}$). Actually, its cardinality ($\left|\mathcal{T}\right|$) is a parameter. During the experimentation, batch sizes of 3 and 6 days were used, giving the last one better performance results. From the 130 days available for cooling, 18 days are taken for testing and the rest for training purposes. As mentioned in Section 2.3.3, control model inputs are: thermal demand for cooling/heating, thermal demand for DHW, ambient temperature, direct normal irradiation, cost of electricity, PCM state of charge (not used in heating mode), buffer tank top temperature and electric battery state of charge.

Ambient temperature and solar radiation are obtained from EnergyPlus weather data Europe WMO Region 6, Greece, Athens 167,160 (IWEC) [24]. Since the time slot for this data is one hour, data was linearly interpolated when $T_s$ was smaller.

As already mentioned in Section 2.1, the energy demand profile for cooling, heating and DHW were obtained within the HYBUILD project [23] activities. For the grid electricity price, a two-period tariff was assumed:

• 0.2 €/kWh from 13:00 to 23:00 h.
• 0.1 €/kWh for the rest of the day.

2.4.2. Training Times

Before presenting the results of system performance, it is worth mentioning a few aspects of the training process. Inside a batch (3 or 6 days), a reward defined by equation (37) is first computed, after which, gradients are computed and propagated. This process is repeated for all the sets in the training set, forming an iteration. After a small number of iterations, the trained model is applied to the test set in order to obtain the control system performance, always keeping the best model so far. Figure 6 shows the cumulative reward $G_0$(or cost) for the test and training sets as a function of the number of iterations at two different scales, showing the learning process. During the first iterations, the network rapidly finds better strategies than the random one established at the beginning. It is a common behavior to get stuck at a local minimum during a large number of iterations. Even though the discovered strategies are quite good, they are still far from the best ones found beyond 2000 iterations. From this point, the strategies are slightly improved until reaching overfitting, where no improvement is observed.

The following settings for the control system were considered:

• Time granularity for model computation: $\Delta t$= 3 min for cooling mode and $\Delta t$ = 15 s for heating mode. Taking longer time slots for the period when the heat pump is switched on would surpass in excess the heating demand in that time slot, due to the fact that the heat pump has higher coefficient of performance in heating mode.
• Time slot between control decisions: $T_s$= 30 min.
• Batch size of 6 days. Test set consists of 3 batches (18 days or 864 control slots).

Note that, using an Intel i5-6600 4-cores at 3.3 GHz CPU, each iteration takes approximately 15 s (for $T_s$= 30 min and $\Delta t$= 3 min) and, consequently, the learning plot shown in Figure 6 took almost two days of CPU computation.

2.5. Robustness Analysis

A robustness analysis was also carried out to evaluate the effect that the uncertainties in some parameters of the mathematical models (not experimentally validated) of the main system components might have on the results. First, the network was trained as described in the previous subsection using the reference values of all the parameters of the component models. Second, the reference values of some of the model parameters were randomly altered following a uniform distribution within a certain error range around the reference value, as shown in

Table 3. Set of parameters used to check the robustness of the model.

Variable	Symbol	Reference Value	Error Range	Units
Optical efficiency Fresnel	ηopt	Data from [22]	Ref·(1 ± 0.2·n)	-
PV efficiency	ηPV	0.16	Ref·(1 ± 0.25·n)	-
Maximum battery charging or discharging power	MaxB	3.0	Ref·(1 ± 0.2·n)	kW
Battery charging efficiency	ηB	0.9	Ref·(1 ± 0.11·n)	-
Sorption thermal efficiency	COPth	0.55	Ref·(1 ± 0.09·n)	-
Dry cooler electricity consumption	${\dot{W}}_{dc}$	Equation (10)	Ref·(1 ± 0.2·n)	kW
Heat pump cooling power	${\dot{Q}}_{evap}$	Data from [30]	Ref·(1 ± 0.2·n)	kW
Heat produced by the compressor	${\dot{Q}}_{comp}$	Data from [30]	Ref·(1 ± 0.2·n)	kW
Buffer tank thermal resistance	Rbuffer	430.3	Ref·(1 ± 0.13·n)	K/kW
RPW-HEX thermal resistance	$R_{PCM}$	424.5	Ref·(1 ± 0.18·n)	K/kW
DHW tank thermal resistance	RDHW	830.8	Ref·(1 ± 0.19·n)	K/kW

. An “error multiplying” factor (n) was used to define different levels of errors affecting the parameters of the model.

Next, the performance of the model trained using the reference values was tested for ten different independent data sets obtained at each error level (defined by the value of the error multiplying factor n). To check the robustness of the DRL approach, the network was also trained using new training data sets generated for each of the ten deviated models at each error level. The average of the relative deviations in the results obtained using the network trained with the reference model and using the network trained with each of the deviated models was used to quantify robustness of the DRL approach. Finally, to compare the DRL and the RBC approaches, the RBC was also applied for each of the deviated data sets mentioned above, using the same thresholds obtained for the model without error.

3. Results and Discussion

This section details the results obtained with the trained system and abovementioned settings and model parameters in both cooling and heating scenarios. System performance results obtained using the smart control are compared against conventional RBC mechanisms.

Figure 7 shows the performance of the trained network for the test set. The plots, from top to bottom, show:

• Cooling demand (‘Demand’) and global horizontal solar irradiation (‘GHI tilted’) on the tilted plane (PV surface). Green and orange areas show how the cooling demand was met: whether from the heat pump (‘From HP’) or from the PCM tank (‘From PCM’).
• The state of charge of the PCM tank (‘PCM SoC’), heat pump cooling mode (‘Cool. mode’) and mode of operation of the sorption chiller (‘Sorption act.’).
• The values of E1 and E2 thresholds of the DC-bus subsystem as detailed in Section 2.2.8. The state of charge of the battery is also shown (‘Battery SoC’), along with the cost of electricity (‘Grid cost’) as binary (0 corresponds to 0.1 €/kWh and 1 to 0.2 €/kWh).
• Domestic hot water demand (‘Demand DHW’) and top region temperature of the buffer tank (‘Buffer Tank top temp.’). Green and orange areas show how the DHW demand was met: whether from the heat pump (‘From elect’) or from the buffer tank (‘From BT’).
• Cumulative cost associated to the energy delivered to and taken from the power grid during valley (‘Ener. sold 0′ and ‘Ener. bought 0′, respectively) and peak (‘Ener. sold 1′ and ‘Ener. bought 1′, respectively) electricity tariff, along with the total cost according to the cumulative cost (‘Cost’) defined as ${\displaystyle \sum }_{i=0}^t{R}_i$. The total amount of electricity consumption is also plotted (‘Cumm. elec. energ.’).

From Figure 7, some aspects of the DRL control policy can be highlighted:

• The operating cost for the 18 days of the test set is 11.1 €. As seen below, it is far less than the RBC policy tested under the same scenario, indicating that the deep learning control approach is highly efficient.
• Cooling demand is always covered, either from the HP or the PCM tank, in order to avoid penalties.
• Cooling modes 1 (PCM tank charging) and 4 (operation of the HP with the standard evaporator) are never (or rarely) used.
• All energy storage modules (PCM tank, buffer tank and electric battery) are fully exploited by charging and discharging them as much as possible on a daily basis within the allowed thresholds.
• The sorption chiller is also activated on a daily basis to assist the operation of the HP, which is beneficial for the overall system performance.

As seen from the bottom plot, the cost associated with the amount of energy sold in tariff period 0 (low cost) does not exceed the cost associated with the amount of energy bought during the same period. Depending on national regulations, an energy retailer may not reward consumers for the surplus of energy supplied to the grid during a certain period. No substantial differences were observed when running the control with a smaller time slot ($T_s$= 15 min).

For comparison purpose, Figure 8 shows the performance of the system for the same test set using an RBC control policy. The same variables as in Figure 7 are shown. The following optimal thresholds were used in the simulations based on an RBC policy:

• Minimum and maximum battery thresholds: $B_{min}^{th}$= 0.01 and $B_{max}^{th}$= 0.94, respectively.
• Threshold factor for PCM tank discharging: $PC{M}_f^{th}$= 1.98.
• Buffer tank temperature threshold: $B{T}^{th}$= 76.7 °C.
• Threshold of the (normalized) amount of energy stored in the PCM tank: $E_{PCM}^{th}$= 0.19.

From Figure 8, the following aspects regarding the RBC policy can be highlighted:

• The operating cost for the 18 days of the test set is 23.5 €, which is more than double the cost obtained using an DRL policy.
• Cooling demand is always covered, either from the HP or the PCM tank.
• All cooling modes are used by the HP, with no clear predilection for a specific operating mode.
• Sorption chiller activation is much more irregular as compared with the DRL case.
• The full potential of the PCM tank is hardly exploited, while the buffer tank is charged and discharged as much as possible on a daily basis.
• Electric battery is reasonably well exploited, but the main difference with respect to the DRL policy is that it is not discharged when the electricity cost is high and electricity demand of the system is low.

Focusing on the DRL policy, a zoom view presented in Figure 9 shows that the battery is discharged at peak tariff periods by adjusting the E2 threshold, putting DC-bus in discharging mode. The control uses the PCM tank as a buffer and prevents its full discharge in order to ensure that the demand is met at all times and avoid penalties. Surprisingly, the energy required to meet the DHW demand is mostly supplied from the electric heater instead of the buffer tank. This could be explained by the fact that, from a cost point of view, it is better to use the heat stored in the buffer tank to drive the sorption module during periods of high cooling demand, which allows the heat pump to work with a higher efficiency leading to a lower electricity consumption and, therefore, to a lower operating cost.

In relation to the heating mode, Figure 10 plots the results of system performance using the deep learning control strategy. The following aspects are worth noting:

• The upper plot (first) shows how the heating demand is covered, whether by the heat pump (‘From HP’) or the buffer tank (‘From BT’).
• It can be observed, in the third plot, how the buffer tank temperature in the middle layer drops when heat is provided to the building from the buffer tank.
• The cumulative cost results negative (bottom plot), meaning that economic benefit is obtained from selling energy to the grid. This is achieved by charging/discharging the battery during the corresponding valley/peak tariff periods, as observed in the second plot.
• Bottom plot shows that the amount of energy sold in valley/peak tariff periods is larger than the energy bought during the same periods. As mentioned previously, an energy retailer may not reward energy reinjection when the amount of sold energy surpasses the bought energy. If this is the case, the cumulative cost will be zero instead of negative.

Table 4. Operating cost (€) for DRL and RBC control policies.

Operating Mode	Policy
	DRL	RBC
Cooling	11.1	23.5
Heating	−2.4	−0.1

shows the results for DRL and RBC policies over the same test set. Clearly, the DRL policy outperforms the tested RBC policy.

However, the comparison between the DRL and RBC policies makes it clear that the DRL policy is able to achieve considerably better results in cooling mode, while in the heating mode it is only slightly better than the RBC policy. This is not surprising given the fact that the system investigated in this study was designed and sized mainly for use in Mediterranean climate regions, where the cooling demand is significant. In addition, the complexity of the system control is mainly associated to the subsystem that provides cooling, where there is a higher potential for improvement through an adequate control strategy. Indeed, the control of the subsystem that provides heating and DHW is relatively simple and it already includes some basic control rules at low (component) system level, which means there is not much room for improvement.

With regards to the robustness analysis, the two curves plotted in Figure 11 show the results obtained using the RBC and DRL approaches, both of them optimized for the model without errors (reference model), for values of the error multiplying factor from 1 to 4. As explained in Section 2.5, each point on the two lines is an average of the behavior of both controls on ten independent instances of the model with errors. The green dots denote the average over the same ten instances that correspond to the DRL approach in the case when the network was retrained with the deviated values of model parameters. As expected, the results obtained using the retrained network are better than the ones obtained using the network trained with the reference values of model parameters. Nevertheless, it can be seen that the original model (trained using the reference model) does not deviate too much from the optimum value for error multiplying factors lower than, or equal to, 2. It is only for value of the multiplying factor around 3 or higher that the deviation between the results becomes relevant. This would demonstrate the robustness of the solution over a wide range of model errors, since considerable deviations from the theoretical model (up to 40%) would have little impact (less than 3%) on the behavior of the control. Even if this were the case, the difference between the system performance using an RBC and a DRL approach would still be clearly in favor of the DRL strategy.

Figure 12 shows the behavior of the two DRL models (the one trained using the reference model and the one trained with the deviated models) for each individual instance and for four different values of the error multiplying factor. It can be seen that, for values of the error multiplying factor up to 2, the error in the cost obtained with the model trained with reference values are below 5%, even though the cost has large variations as a result of different model parameters. This confirms that the DRL model is able to adapt to different types of deviations in the actual components’ behavior with respect to the mathematical model used in the simulations.

4. Conclusions and Future Work

This paper investigated a smart control based on a deep reinforcement learning control policy proposed for an innovative system developed within HYBUILD project. The main aim of the system is to reduce the energy demand for heating, cooling and domestic hot water of a standard single-family residential building by implementation of Fresnel collectors and PV panels combined with hybrid electrical and thermal storage components. The complexity of the system was a great challenge from the high-level control point of view, which was dealt with by applying deep learning techniques to optimize the operation of the overall system from a monetary point of view. To the best of the authors knowledge, this is the first study in which DRL has been applied to a complex TES system. The performance of the proposed control policy was compared with basic rule-based control policies for both cooling and heating modes. The results show that the deep learning control policy provides a proper system control that is able to efficiently manage the system and to obtain significant cost (and energy) savings with respect to a standard rule-based control. In addition, the results of the robustness analysis clearly showed that DRL model is able to adapt to any changes in the actual behavior of the system in a real test pilot plant, with deviations less than 3% in the average cost estimations for an error multiplying factor up to 2.

Immediate future work will consist of deploying the DRL control for a pilot plant in order to test its performance. Even the robustness analysis shows a good ability to deal with large mismatches between theoretical and real models, there are still big challenges before adopting this technology for the consumer market. Requiring accurate models for heating/cooling systems as well as for building thermal demand may be a time-consuming task, and more studies are required in order to determine the feasibility, in terms of time requirements, of self-training starting from a basic or general knowledge of the system.