Experimental, Analytical and Numerical Studies of Interfacial Bonding Properties between Silane-Coated Steel Fibres and Mortar
Abstract
:1. Introduction
2. Experiments
2.1. Materials
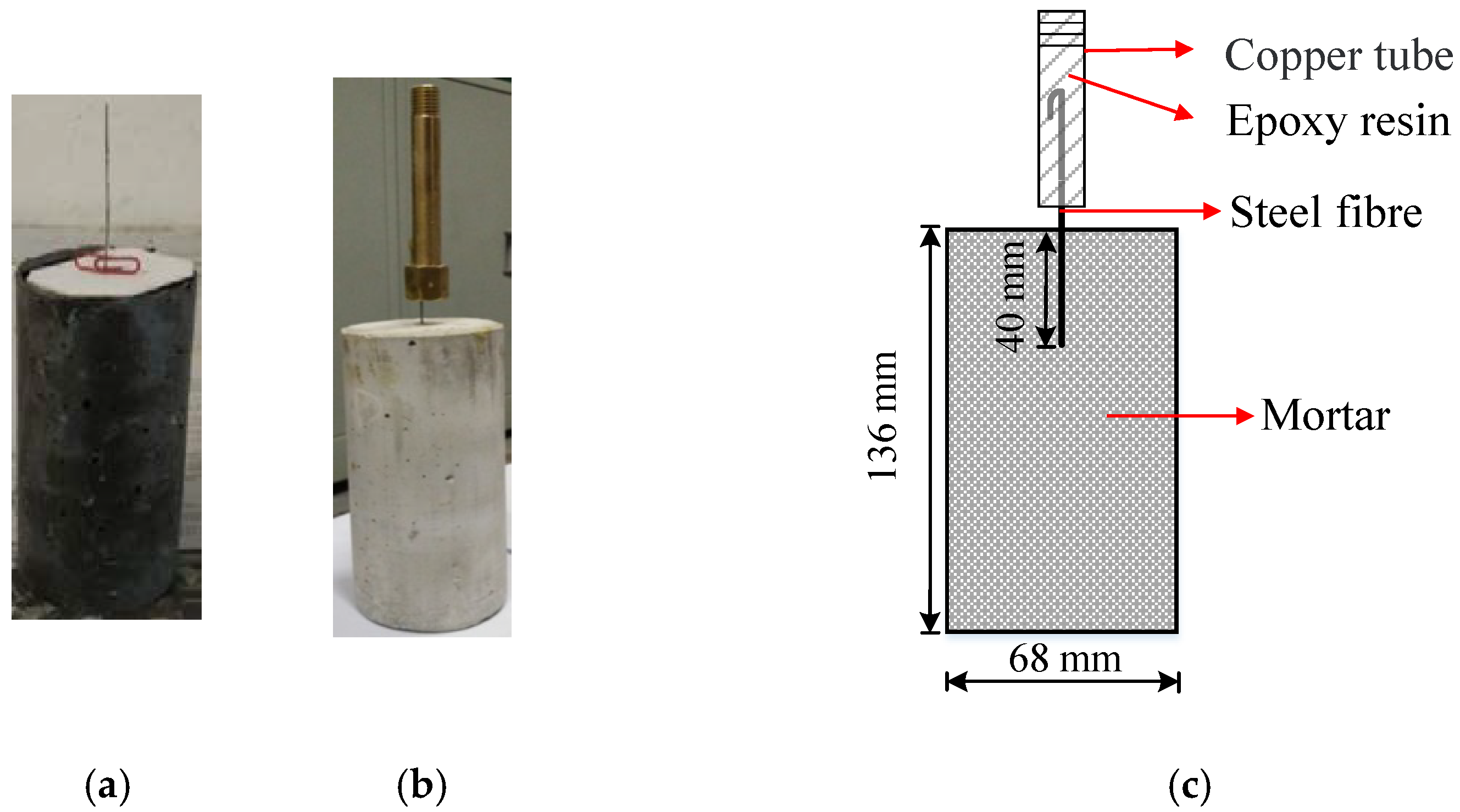
2.2. Coating Procedure and Specimen Fabrication
2.3. Single Fibre Pullout Tests
2.4. SEM Tests
3. Experimental Results and Discussion
3.1. Pullout Load-Displacement (P-Δ) Curves and the Bond-Slip Process
3.2. Parameters of Interfacial Bond Properties
3.3. The Effects of Silane Coatings on the Interfacial Properties
3.4. SEM Tests
3.4.1. Surface Observation of Steel Fibres
3.4.2. ITZ Observation
4. Analytical Solutions for the Full-Range Pullout Process
4.1. The Idealized Model and Assumptions
4.2. The Tri-Linear Bond-Slip Model
4.3. Analysis of the Full-Range Behaviour and Derivation of Analytical Solutions
4.3.1. Linear Elastic Stage (OA)
4.3.2. Elastic Softening Stage (ABC)
4.3.3. Softening Stage (CD)
4.3.4. Softening-Debonding Stage (DE)
4.3.5. Frictional Stage (EF)
4.4. Calibration of Control Parameters
5. Numerical Simulations
5.1. Modelling of the Single Fibre Pullout Tests
5.2. Direct Tensile Tests of SFRC Plates with Random Fibres
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Song, P.S.; Hwang, S. Mechanical properties of high-strength steel fiber-reinforced concrete. Constr. Build. Mater. 2004, 18, 669–673. [Google Scholar] [CrossRef]
- Redon, C.; Li, V.; Wu, C.; Hoshiro, H.; Saito, T.; Ogawa, A. Measuring and Modifying Interface Properties of PVA Fibers in ECC Matrix. J. Mater. Civ. Eng. 2001, 13, 399–406. [Google Scholar] [CrossRef]
- Vrijdaghs, R.; Prisco, M.D.; Vandewalle, L. Short-term and creep pull-out behavior of polypropylene macrofibers at varying embedded lengths and angles from a concrete matrix. Constr. Build. Mater. 2017, 147, 858–864. [Google Scholar] [CrossRef]
- Lee, A.T.; Michel, M.; Ferrier, E.; Benmokrane, B. Influence of curing conditions on mechanical behaviour of glued joints of carbon fiber-reinforced polymer composite/concrete. Constr. Build. Mater. 2019, 227, 116385. [Google Scholar] [CrossRef]
- Cheng, C.; He, J.; Zhang, J.; Yang, Y. Study on the time-dependent mechanical properties of glass fiber reinforced cement (GRC) with fly ash or slag. Constr. Build. Mater. 2019, 217, 128–136. [Google Scholar] [CrossRef]
- Dvorkin, L.; Dvorkin, O. Basics of Concrete Science; Stroi-Beton: St-Petersburg, Russia, 2006; ISBN 590319702-7. [Google Scholar]
- Liew, K.; Akbar, A. The recent progress of recycled steel fiber reinforced concrete. Constr. Build. Mater. 2020, 232, 117232. [Google Scholar] [CrossRef]
- Nataraja, M.C.; Dhang, N.; Gupta, A.P. Toughness characterization of steel fiber-reinforced concrete by JSCE approach. Cem. Concr. Res. 2000, 30, 593–597. [Google Scholar] [CrossRef]
- Zhang, J.; Stang, H.; Li, V. Experimental Study on Crack Bridging in FRC under Uniaxial Fatigue Tension. J. Mater. Civ. Eng. 2000, 12, 66–73. [Google Scholar] [CrossRef]
- Singh, S.P.; Kaushik, S.K. Fatigue strength of steel fiber reinforced concrete in flexure. Cem. Concr. Compos. 2003, 25, 779–786. [Google Scholar] [CrossRef]
- Li, V.C.; Stang, H.; Krenchel, H. Micromechanics of crack bridging in fiber-reinforced concrete. Mater. Struct. 1993, 26, 486–494. [Google Scholar] [CrossRef]
- Li, V.C.; Stang, H. Interface property characterization and strengthening mechanisms in fiber reinforced cement based composites. Adv. Cem. Based Mater. 1997, 6, 1–20. [Google Scholar] [CrossRef]
- Soetens, T.; Gysel, A.V.; Matthys, S.; Taerwe, L. A semi-analytical model to predict the pull-out behaviour of inclined hooked-end steel fibers. Constr. Build. Mater. 2013, 43, 253–265. [Google Scholar] [CrossRef]
- Deng, F.; Ding, X.; Chi, Y.; Xu, L.; Wang, L. The pull-out behavior of straight and hooked-end steel fiber from hybrid fiber reinforced cementitious composite: Experimental study and analytical modelling. Compos. Struct. 2018, 206, 693–712. [Google Scholar] [CrossRef]
- Khabaz, A. Performance evaluation of corrugated steel fiber in cementitious matrix. Constr. Build. Mater. 2016, 128, 373–383. [Google Scholar] [CrossRef]
- Ye, J.; Liu, G. Pullout Response of Ultra-High-Performance Concrete with Twisted Steel Fibers. Appl. Sci. 2019, 9, 658. [Google Scholar] [CrossRef] [Green Version]
- Won, J.P.; Lee, J.H.; Lee, S.J. Predicting pull-out behaviour based on the bond mechanism of arch-type steel fiber in cementitious composite. Compos. Struct. 2015, 134, 633–644. [Google Scholar] [CrossRef]
- Yoo, D.-Y.; Chun, B.; Kim, J.-J. Bond performance of abraded arch-type steel fibers in ultra-high-performance concrete. Cem. Concr. Compos. 2020, 109, 103538. [Google Scholar] [CrossRef]
- Hao, Y.; Hao, H. Pull-out behaviour of spiral-shaped steel fibers from normal-strength concrete matrix. Constr. Build. Mater. 2017, 139, 34–44. [Google Scholar] [CrossRef]
- He, Q.; Liu, C.; Yu, X. Improving steel fiber reinforced concrete pull-out strength with nanoscale iron oxide coating. Constr. Build. Mater. 2015, 79, 311–317. [Google Scholar] [CrossRef]
- Pi, Z.; Xiao, H.; Du, J.; Liu, M.; Li, H. Interfacial microstructure and bond strength of nano-SiO2-coated steel fibers in cement matrix. Cem. Concr. Compos. 2019, 103, 1–10. [Google Scholar] [CrossRef]
- Miller, H.D.; Akbarnezhad, A.; Mesgari, S.; Foster, S.J. Performance of oxygen/argon plasma-treated steel fibers in cement mortar. Cem. Concr. Compos. 2019, 97, 24–32. [Google Scholar] [CrossRef]
- Sun, M.; Wen, D.-J.; Wang, H.-W. Influence of corrosion on the interface between zinc phosphate steel fiber and cement. Mater. Corros. 2010, 63, 67–72. [Google Scholar] [CrossRef]
- Soulioti, D.; Barkoula, N.-M.; Koutsianopoulos, F.; Charalambakis, N.; Matikas, T. The effect of fibre chemical treatment on the steel fibre/cementitious matrix interface. Constr. Build. Mater. 2013, 40, 77–83. [Google Scholar] [CrossRef]
- Aggelis, D.; Soulioti, D.; Barkoula, N.; Paipetis, A.; Matikas, T. Influence of fiber chemical coating on the acoustic emission behavior of steel fiber reinforced concrete. Cem. Concr. Compos. 2012, 34, 62–67. [Google Scholar] [CrossRef]
- Pax, G.M.; Bouchet, J.; Michaud, V.; Månson, J.-A.E. Tailoring of the practical adhesion between polyethylene and galvanised steel. J. Adhes. Sci. Technol. 2006, 20, 1255–1272. [Google Scholar] [CrossRef]
- Alinejad, S.; Naderi, R.; Mahdavian, M. The effect of zinc cation on the anticorrosion behavior of an eco-friendly silane sol–gel coating applied on mild steel. Prog. Org. Coat. 2016, 101, 142–148. [Google Scholar] [CrossRef]
- Chen, M.A.; Zhang, X.M.; Huang, R.; Lu, X.B. Mechanism of adhesion promotion between aluminium sheet and polypropylene with maleic anhydride-grafted polypropylene by gamma-aminopropyltriethoxy silane. Surf. Interface Anal. 2008, 40, 1209–1218. [Google Scholar] [CrossRef]
- Underhill, R.S.; Fisher, G.C.; Farrell, S.P. Energy dispersive X-ray investigation of silane coupling agent modified nickel-manganese-gallium particle surfaces. Mater. Chem. Phys. 2012, 132, 253–257. [Google Scholar] [CrossRef]
- Kong, X.-M.; Liu, H.; Lu, Z.-B.; Wang, D.-M. The influence of silanes on hydration and strength development of cementitious systems. Cem. Concr. Res. 2015, 67, 168–178. [Google Scholar] [CrossRef]
- Felekoglu, B. A method for improving the early strength of pumice concrete blocks by using alky1 alkoxy silane (AAS). Constr. Build. Mater. 2012, 28, 305–310. [Google Scholar] [CrossRef]
- Cao, J.; Chung, D. Improving the dispersion of steel fibers in cement mortar by the addition of silane. Cem. Concr. Res. 2001, 31, 309–311. [Google Scholar] [CrossRef]
- Ma, Y.P. Study on Increasing of Interfacial Bond Strength between Cement Paste and Aggregate. J. Build. Mater. 1999, 2, 35–38. (In Chinese) [Google Scholar]
- Benzerzour, M.; Sebaibi, N.; Abriak, N.E.; Binetruy, C. Waste fiber–cement matrix bond characteristics improved by using silane-treated fibers. Constr. Build. Mater. 2012, 37, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Sebaibi, N.; Benzerzour, M.; Abriak, N.E.; Binetruy, C. Mechanical properties of concrete-reinforced fibers and powders with crushed thermoset composites: The influence of fiber/matrix interaction. Constr. Build. Mater. 2012, 29, 332–338. [Google Scholar] [CrossRef]
- Callens, M.G.; Gorbatikh, L.; Bertels, E.; Goderis, B.; Smet, M.; Verpoest, I. Tensile behaviour of stainless steel fiber/epoxy composites with modified adhesion. Compos. Part A Appl. Sci. Manuf. 2015, 69, 208–218. [Google Scholar] [CrossRef]
- Liu, T.; Wei, H.; Zhou, A.; Zou, D.; Jian, H. Multiscale investigation on tensile properties of ultra-high performance concrete with silane coupling agent modified steel fibers. Cem. Concr. Compos. 2020, 111, 103638. [Google Scholar] [CrossRef]
- Casagrande, C.A.; Cavalaro, S.H.P.; Repette, W.L. Ultra-high performance fiber-reinforced cementitious composite with steel microfibers functionalized with silane. Constr. Build. Mater. 2018, 178, 495–506. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.H.; Zhao, S.L.; Yang, S.Y.; Sun, B.; Shan, F.J. Preparation and performance of fluorozirconate-silane composite conversion film on cold-rolled steel surface. Electroplat. Finish. 2012, 31, 39–42. (In Chinese) [Google Scholar]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. JGJ/T 70-2009: Standard for Test Method of Basic Properties of Construction Mortar; Industry Standards of the People’s Republic of China; Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2009. (In Chinese) [Google Scholar]
- Leung, C.K.Y.; Shapiro, N. Optimal Steel Fiber Strength for Reinforcement of Cementitious Materials. J. Mater. Civ. Eng. 1999, 11, 116–123. [Google Scholar] [CrossRef]
- Arkles, B. Tailoring Surfaces with Silanes; Chemtech.: West Chester, PA, USA, 1977; Volume 7, pp. 766–778. [Google Scholar]
- Ren, F.; Yang, Z.; Chen, J.-F.; Chen, W. An analytical analysis of the full-range behaviour of grouted rockbolts based on a tri-linear bond-slip model. Constr. Build. Mater. 2010, 24, 361–370. [Google Scholar] [CrossRef]
- Zou, X.X.; Sneed, L.H.; D’Antino, T. Full range behavior of fber reinforced cementitious matrix (FRCM)-concrete joints using a trilinear bond-slip relationship. Compos. Struct. 2020, 239, 112024. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Onate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, Y.J.; Yang, Z.J.; Xu, S.L.; Chen, X.W. A discrete-continuum coupled finite element modelling approach for fibre reinforced concrete. Cem. Concr. Res. 2018, 106, 130–143. [Google Scholar] [CrossRef]
- Yang, Z.; Qsymah, A.; Peng, Y.; Margetts, L.; Sharma, R. 4D characterisation of damage and fracture mechanisms of ultra high performance fibre reinforced concrete by in-situ micro X-Ray computed tomography tests. Cem. Concr. Compos. 2020, 106, 103473. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, Z.; Pang, M.; Yao, Y.; Li, Q.M.; Marrow, T.J. Ex-situ micro X-ray computed tomography tests and image-based simulation of UHPFRC beams under bending. Cem. Concr. Compos. 2021, 123, 104216. [Google Scholar] [CrossRef]



























| Group No. | Coating Types | Pe (N) | Pmax (N) | Ps (N) | τmax (MPa) | τc (MPa) | τs (MPa) | G (J) |
|---|---|---|---|---|---|---|---|---|
| U | Untreated | 70.65 | 99.91 | 41.95 | 0.80 | 0.46 | 0.33 | 1.07 |
| Z1 | Z6011 | 546.88 (674%) | 673.96 (575%) | 158.95 (279%) | 5.37 (575%) | 4.10 (789%) | 1.27 (279%) | 3.71 (248%) |
| Z2 | Z6020 | 407.25 (476%) | 467.10 (368%) | 132.35 (215%) | 3.72 (368%) | 2.67 (478%) | 1.05 (215%) | 2.43 (128%) |
| Z3 | Z6030 | 126.11 (79%) | 141.22 (41%) | 83.22 (98%) | 1.12 (41%) | 0.46 (0.08%) | 0.66 (98%) | 2.02 (90%) |
| Z4 | Z6040 | 233.74 (231%) | 260.43 (161%) | 138.57 (230%) | 2.07 (161%) | 0.97 (110%) | 1.10 (230%) | 2.76 (159%) |
| ZZ1 | Z6011 + Zr(NO3)4 | 569.51 (706%) | 613.84 (514%) | 142.09 (239%) | 4.89 (514%) | 3.76 (714%) | 1.13 (239%) | 3.19 (200%) |
| ZZ2 | Z6020 + Zr(NO3)4 | 404.70 (473%) | 475.95 (376%) | 140.37 (235%) | 3.79 (376%) | 2.67 (479%) | 1.12 (235%) | 3.56 (200%) |
| ZZ3 | Z6030 + Zr(NO3)4 | 96.82 (37%) | 110.83 (11%) | 50.41 (20%) | 0.88 (11%) | 0.48 (4%) | 0.40 (20%) | 1.08 (2%) |
| ZZ4 | Z6040 + Zr(NO3)4 | 174.03 (146%) | 186.43 (87%) | 108.25 (158%) | 1.48 (87%) | 0.62 (35%) | 0.86 (158%) | 2.41 (126%) |
| ZH2 | Z6020 + H2ZrF6 | 522.34 (639%) | 587.41 (488%) | 156.05 (272%) | 4.68 (488%) | 3.43 (644%) | 1.24 (272%) | 3.52 (230%) |
| ID | δ1 (mm) | τf (MPa) | δf (mm) | τr (MPa) | k | a* (mm) | le (mm) | Analytical Pu (N) | Test PB (N) | |Pu − PB|/PB (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| U | 0.12 | 0.79 | 3.59 | 0.34 | 0.43 | 39.14 | 172.50 | 99.44 | 99.46 | 0.019 |
| Z1 | 0.69 | 5.06 | 3.61 | 1.26 | 0.25 | 33.64 | 164.89 | 631.74 | 631.68 | 0.009 |
| Z2 | 0.48 | 3.49 | 3.95 | 0.75 | 0.22 | 35.93 | 165.24 | 436.80 | 436.74 | 0.014 |
| Z3 | 0.13 | 1.10 | 1.75 | 0.70 | 0.63 | 38.57 | 152.69 | 137.48 | 137.42 | 0.043 |
| Z4 | 0.38 | 1.92 | 3.77 | 0.94 | 0.49 | 37.51 | 198.47 | 241.30 | 241.28 | 0.010 |
| ZZ1 | 0.55 | 4.75 | 3.83 | 1.18 | 0.25 | 35.26 | 152.10 | 593.69 | 593.73 | 0.007 |
| ZZ2 | 0.57 | 3.69 | 3.06 | 1.08 | 0.29 | 34.06 | 175.52 | 461.12 | 461.16 | 0.007 |
| ZZ3 | 0.19 | 0.87 | 5.49 | 0.23 | 0.26 | 38.91 | 208.48 | 109.66 | 109.63 | 0.024 |
| ZZ4 | 0.37 | 1.46 | 3.67 | 0.80 | 0.55 | 37.75 | 223.91 | 182.75 | 182.78 | 0.016 |
| ZH2 | 0.60 | 4.66 | 4.42 | 1.23 | 0.26 | 35.59 | 160.68 | 583.13 | 583.07 | 0.010 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, Y.; Zhang, H.; Zhang, X.; Ren, F.; Li, Y.; Yang, Z. Experimental, Analytical and Numerical Studies of Interfacial Bonding Properties between Silane-Coated Steel Fibres and Mortar. Buildings 2021, 11, 398. https://doi.org/10.3390/buildings11090398
Yao Y, Zhang H, Zhang X, Ren F, Li Y, Yang Z. Experimental, Analytical and Numerical Studies of Interfacial Bonding Properties between Silane-Coated Steel Fibres and Mortar. Buildings. 2021; 11(9):398. https://doi.org/10.3390/buildings11090398
Chicago/Turabian StyleYao, Yong, Hui Zhang, Xin Zhang, Feifan Ren, Yaqi Li, and Zhenjun Yang. 2021. "Experimental, Analytical and Numerical Studies of Interfacial Bonding Properties between Silane-Coated Steel Fibres and Mortar" Buildings 11, no. 9: 398. https://doi.org/10.3390/buildings11090398
APA StyleYao, Y., Zhang, H., Zhang, X., Ren, F., Li, Y., & Yang, Z. (2021). Experimental, Analytical and Numerical Studies of Interfacial Bonding Properties between Silane-Coated Steel Fibres and Mortar. Buildings, 11(9), 398. https://doi.org/10.3390/buildings11090398





