Continuous Reinforced Concrete Beams Strengthened with Fabric-Reinforced Cementitious Matrix: Experimental Investigation and Numerical Simulation
Abstract
:1. Introduction
2. Research Significance
3. Experimental Program
3.1. Test Matrix
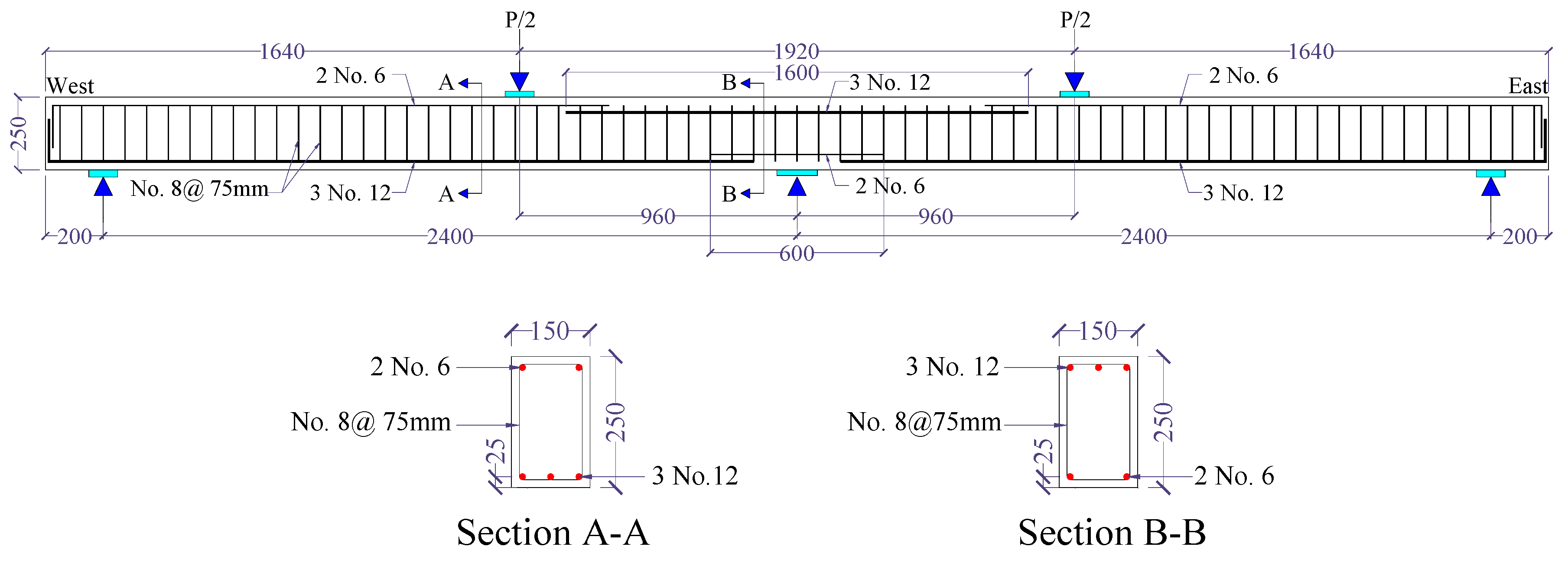
3.2. Test Specimens
3.3. Materials
3.4. FRCM Strengthening Methodology
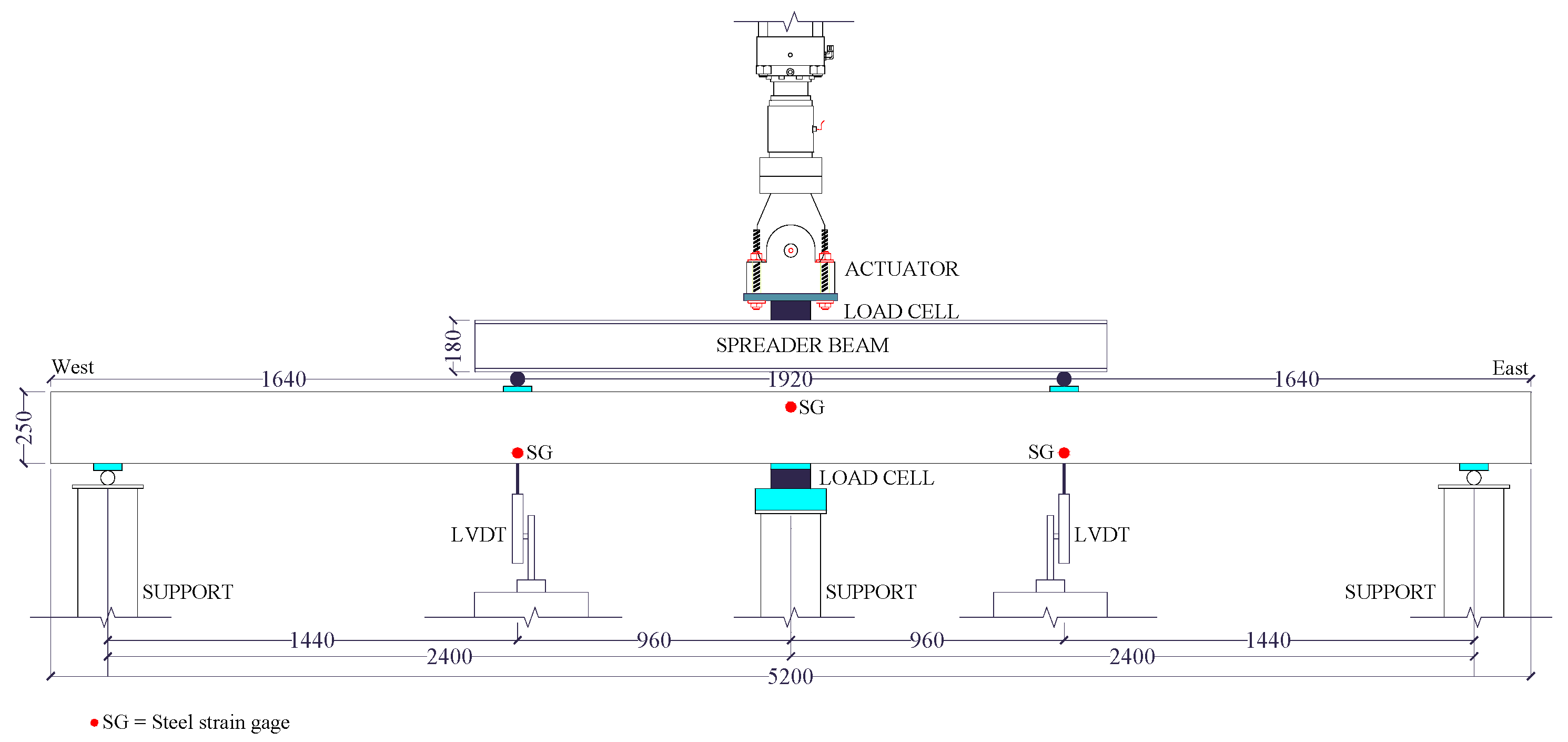
3.5. Test Set-Up and Instrumentation
4. Experimental Results
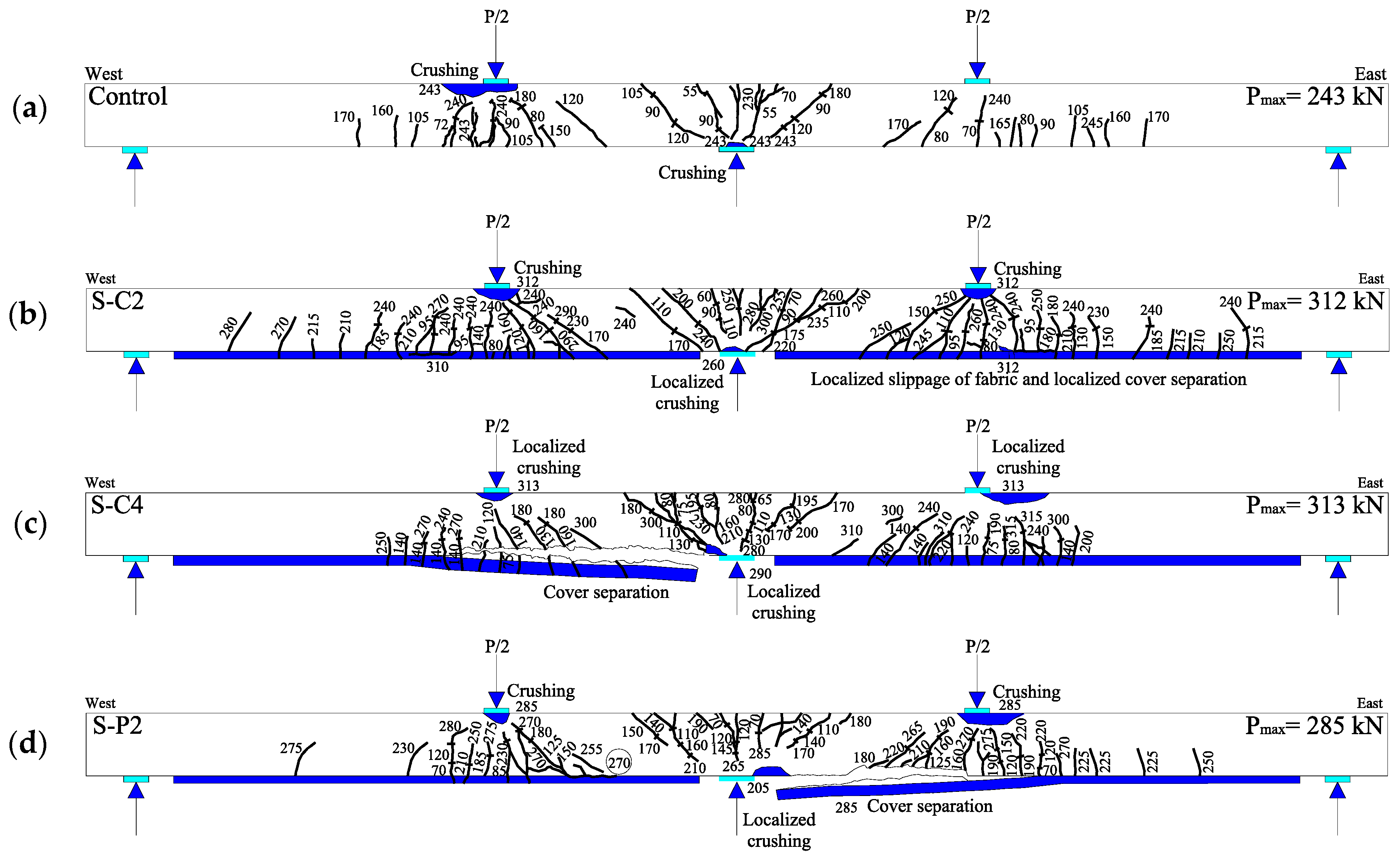
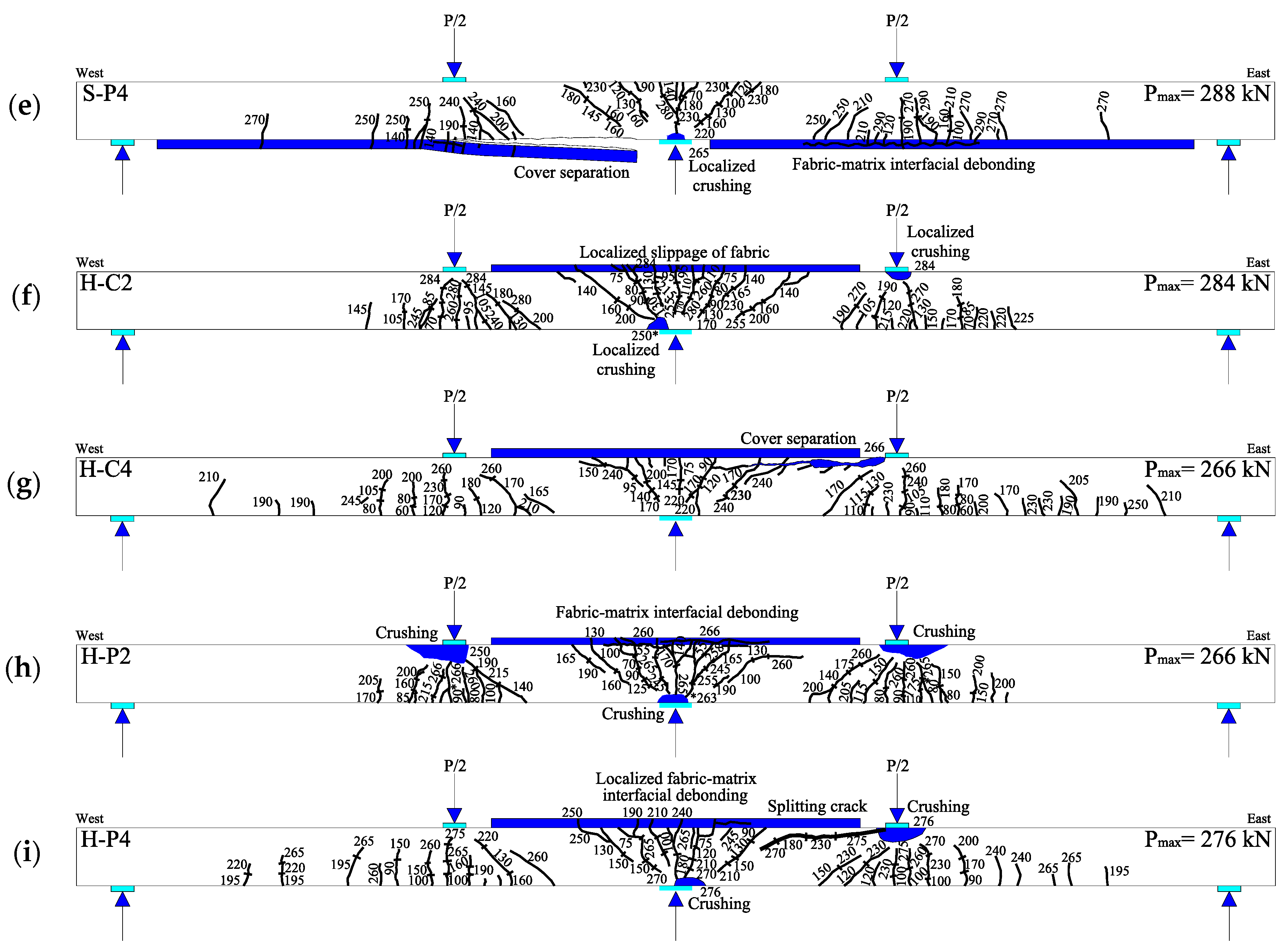
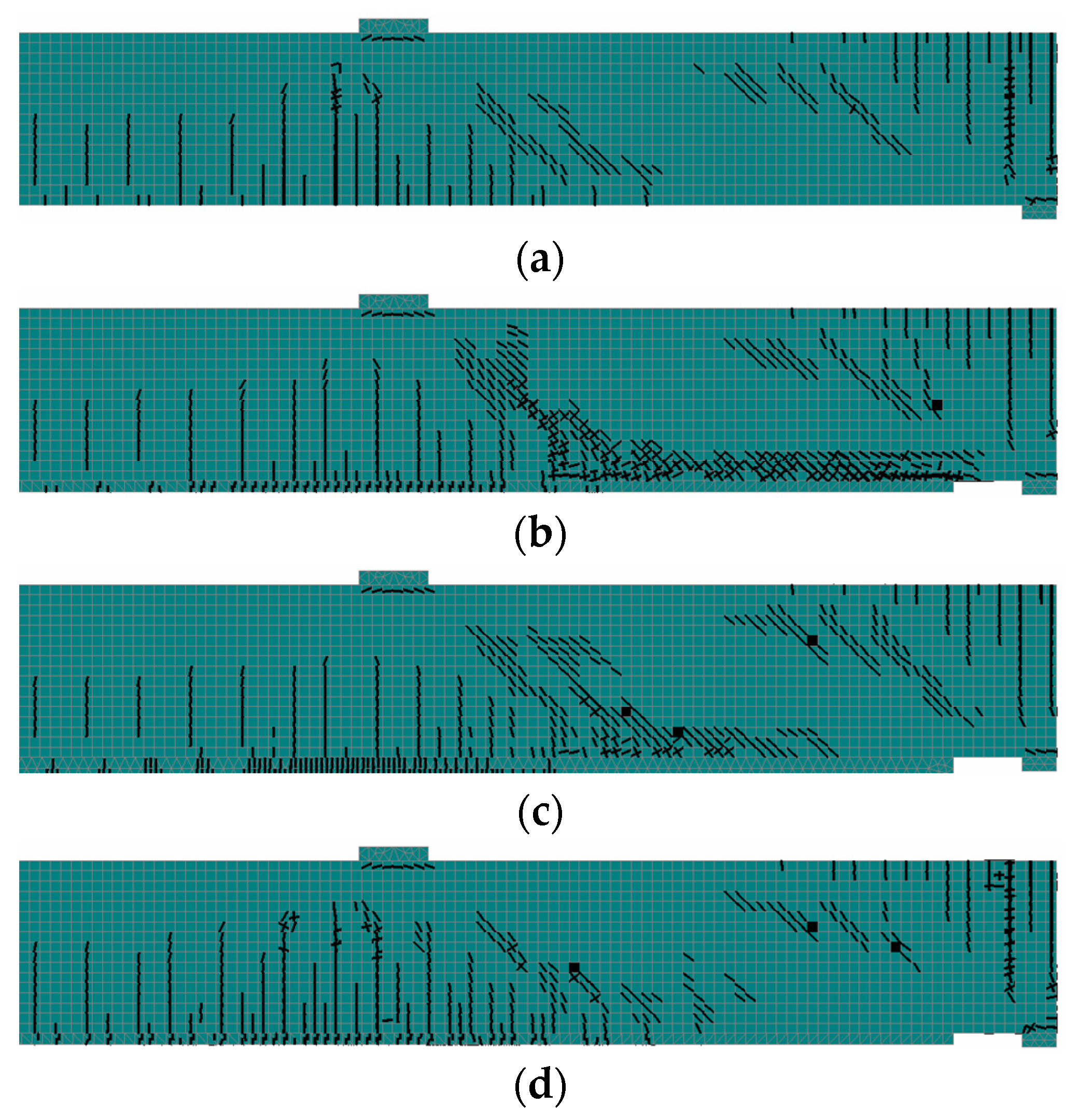
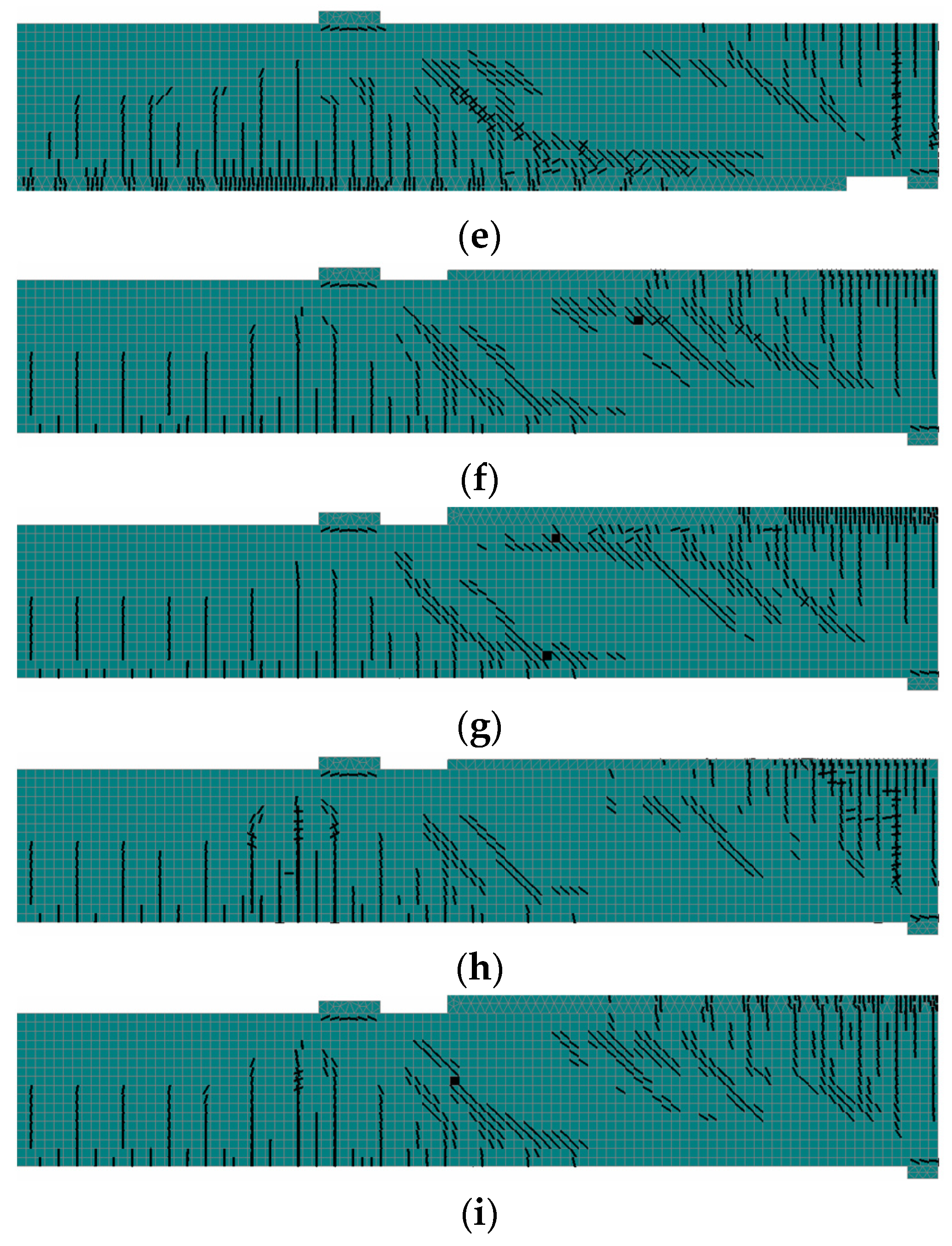
4.1. Crack Pattern and Failure Mode
4.2. Steel Strains
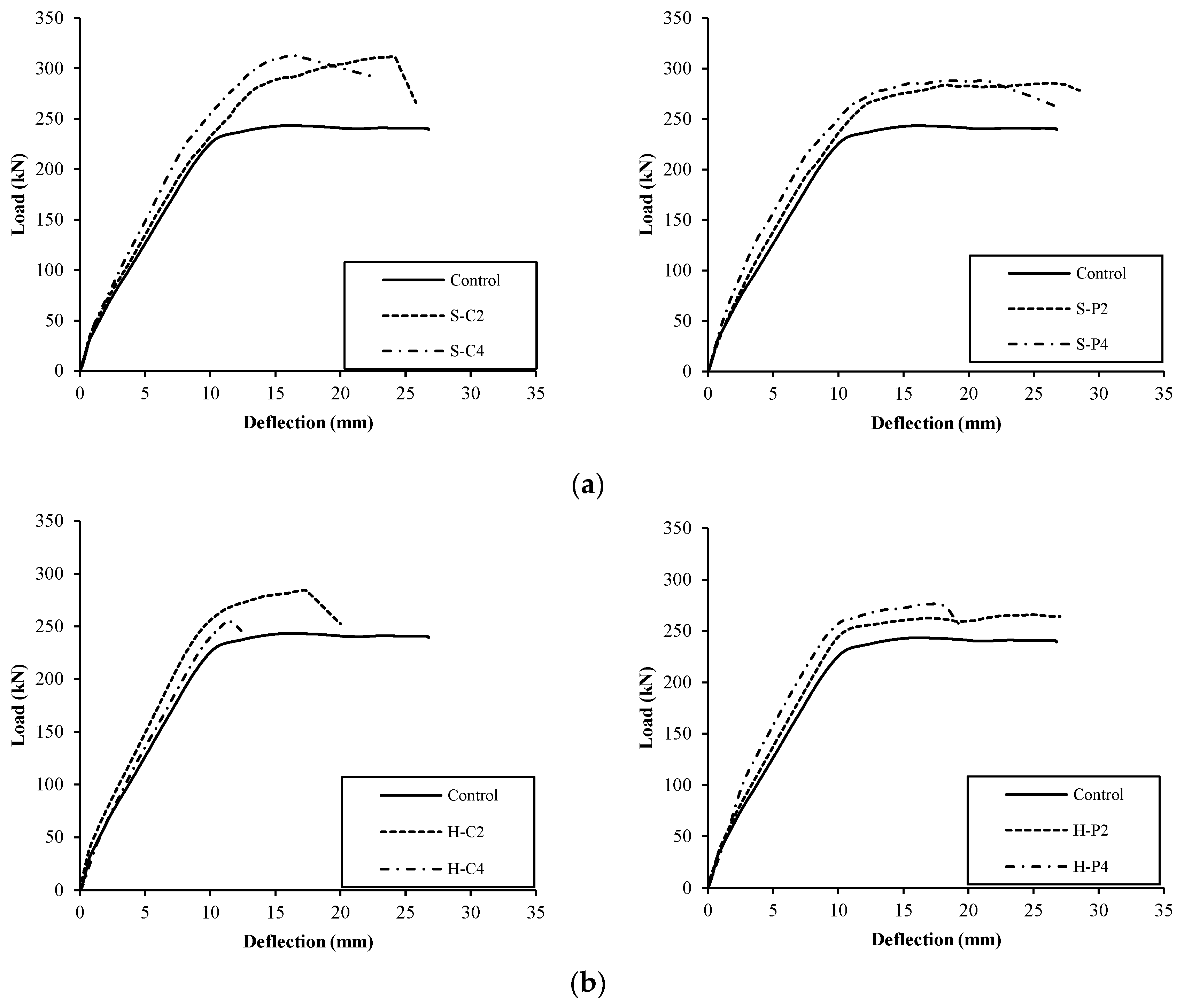
4.3. Load–Deflection Response
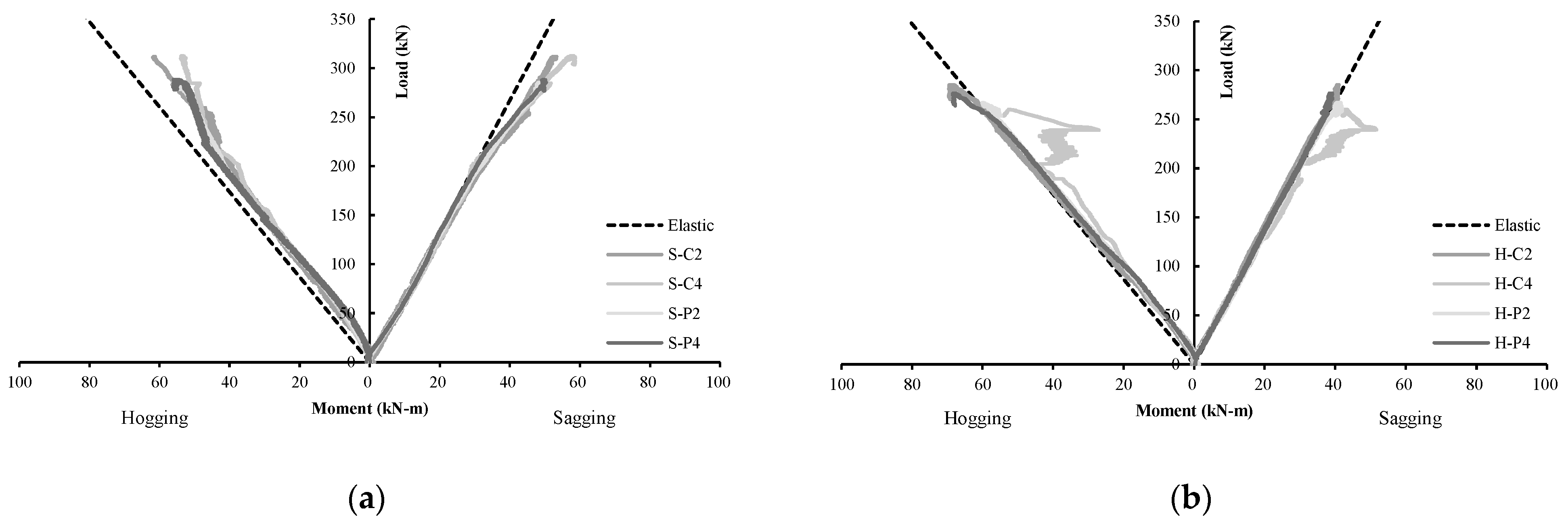
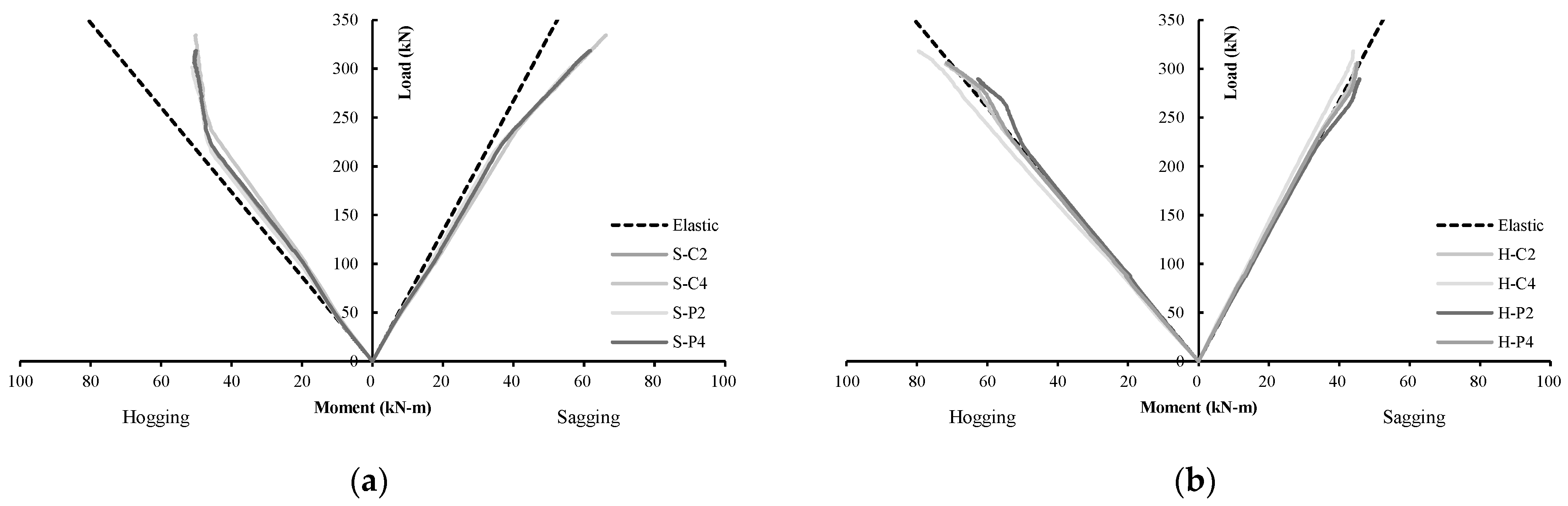
4.4. Moment Redistribution
5. Numerical Simulation
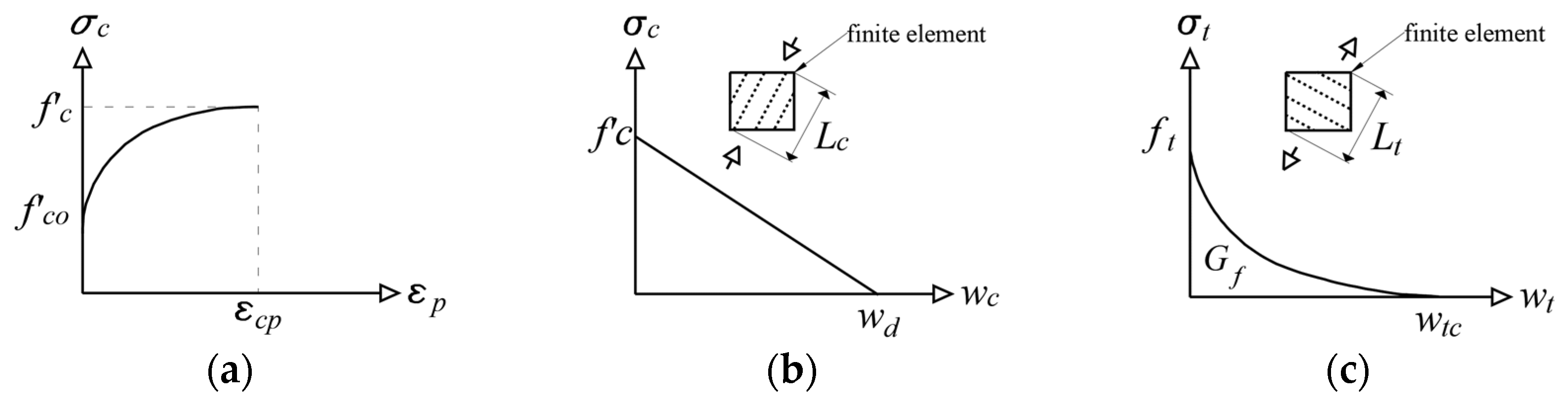
5.1. Material Constitutive Models
5.2. Bond-Slip Model at Fabric–Matrix Interface
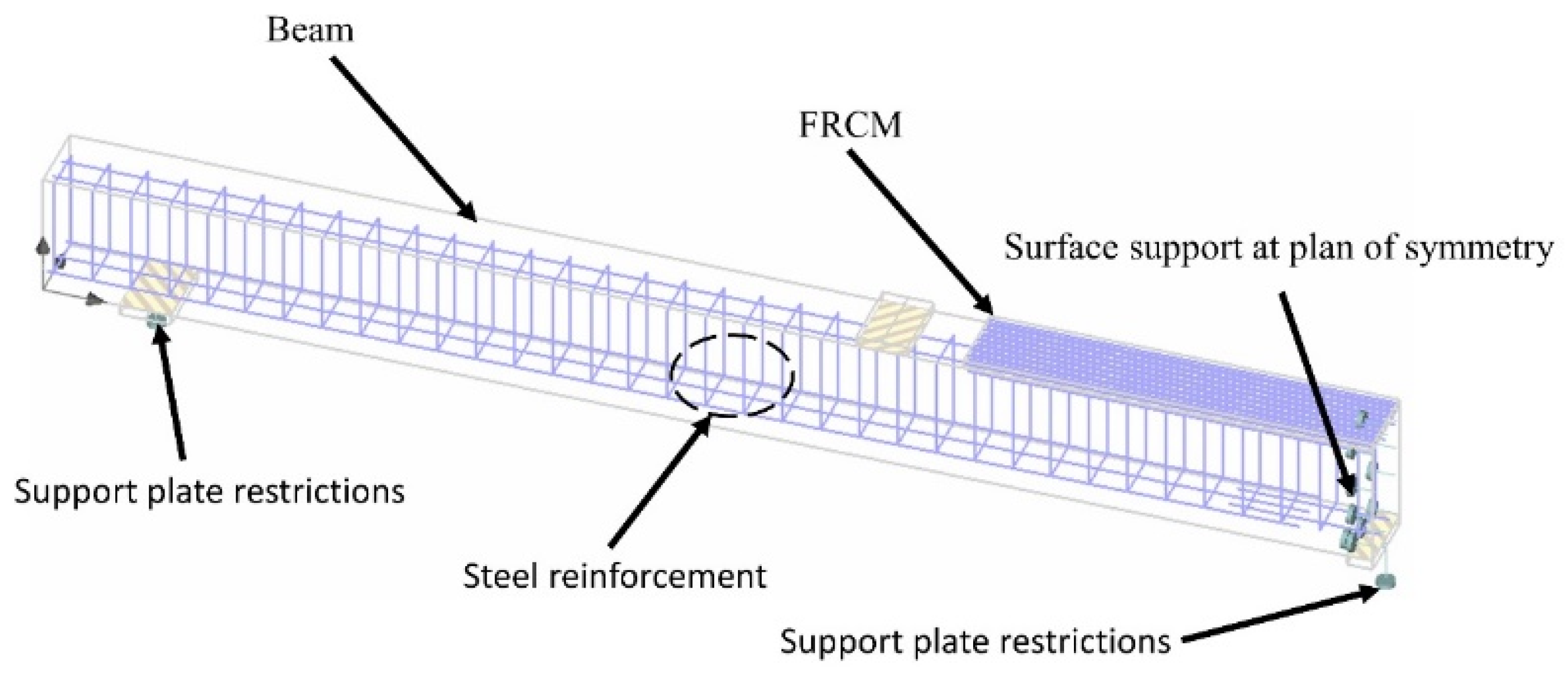
5.3. Element Types
5.4. Boundary Conditions and Loading
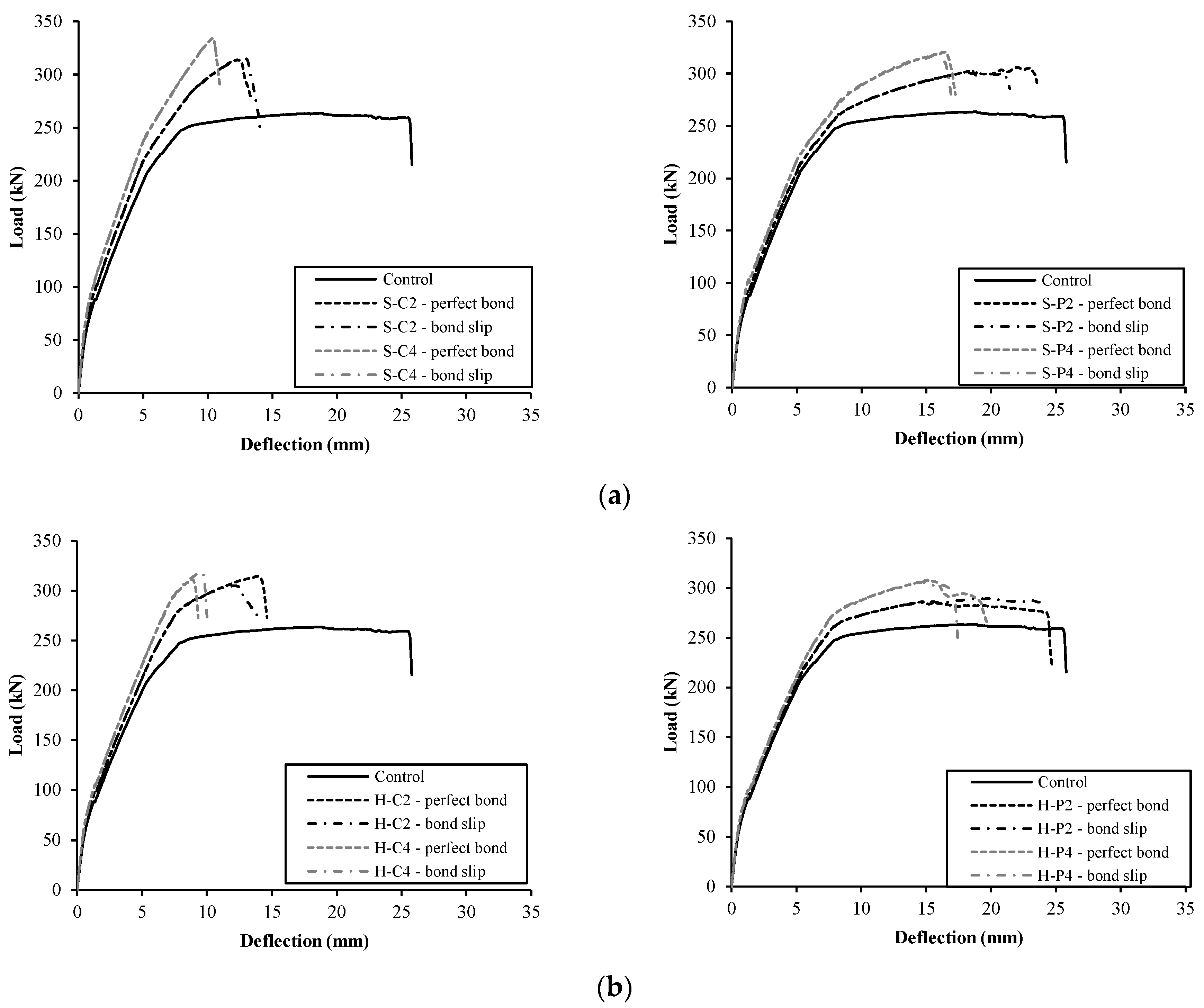
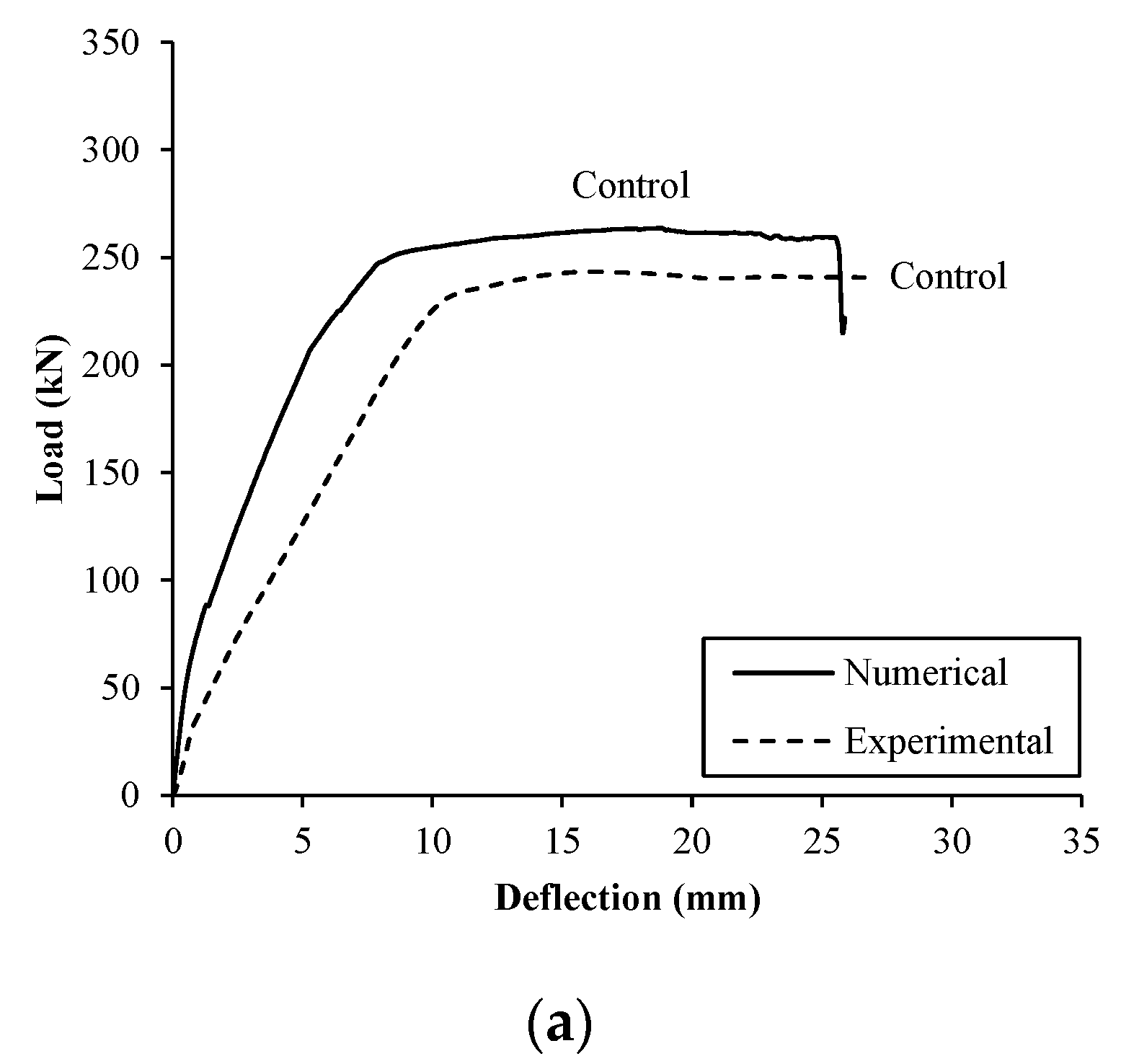
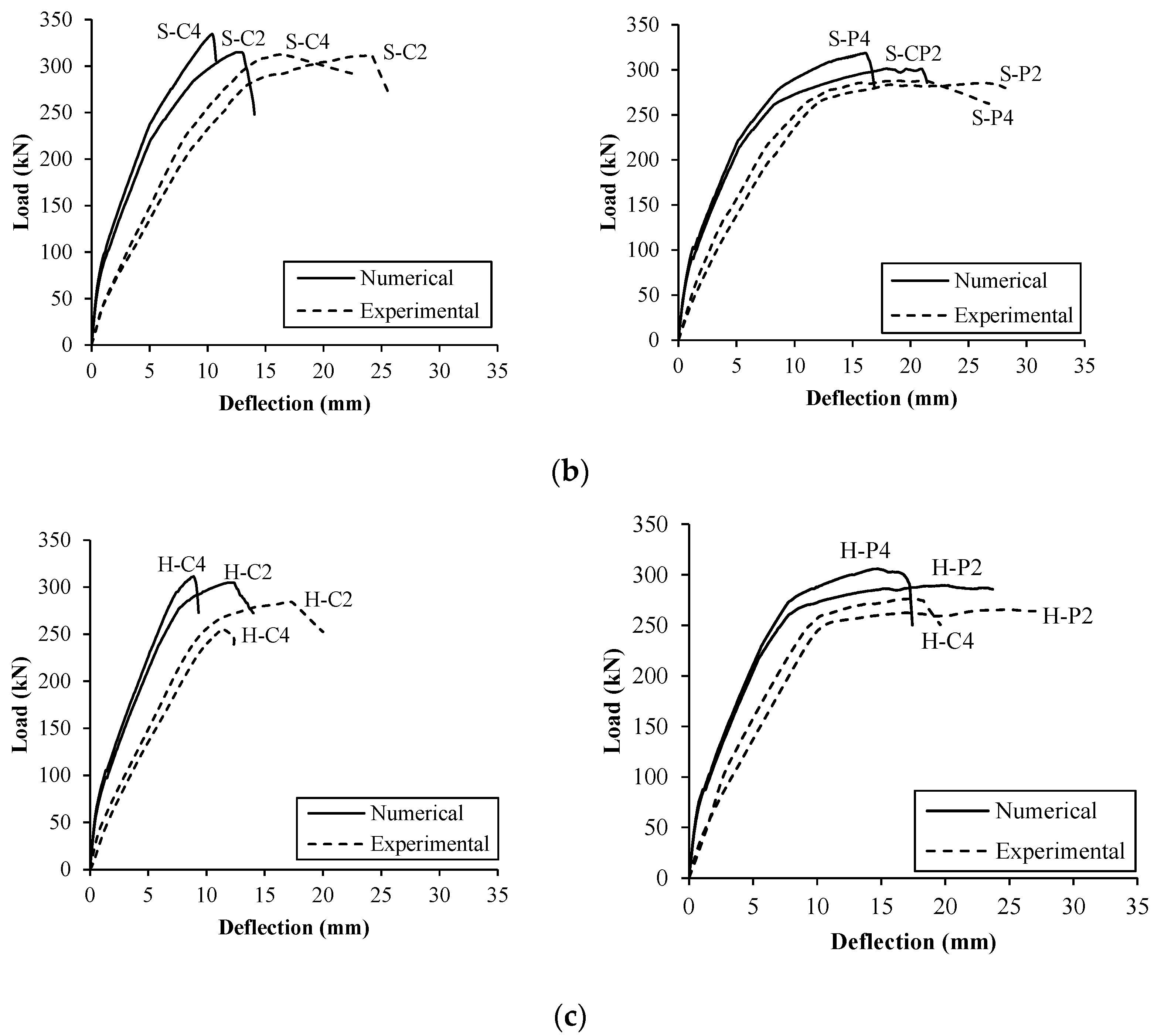
5.5. Numerical Results and Comparative Analysis
6. Discussion
7. Implications and Limitations
8. Conclusions
- Sagging strengthening with 2 layers of C-FRCM increased the load capacity by 28% while maintaining 77% and 90% of the original beam ductility and deflection capacity, respectively. The use of 2 layers of PBO-FRCM in the sagging region instead of C-FRCM increased the load capacity by 17% without compromising the original beam ductility and deflection capacity.
- Hogging strengthening with 2 layers of C-FRCM resulted in 17% increase in load capacity while maintaining 70% and 65% of the original beam ductility and deflection capacity, respectively. The use of 2 layers of PBO-FRCM in the hogging region instead of C-FRCM increased the load capacity by only 9% with no or insignificant reduction in the original beam ductility and deflection capacity.
- The use of 4 FRCM composite layers instead of 2 layers resulted in no or negligible additional increase in the load capacity but reduced the ductility and deflection capacity of the strengthened specimens.
- Specimens strengthened in the sagging regions exhibited up to 26% moment redistribution between the hogging and sagging regions. In contrast, insignificant moment redistribution was recorded for the specimens strengthened in the hogging region.
- The 3D numerical simulation models developed in the current study were capable of predicting the nonlinear response of the tested specimens. The inclusion of an interfacial bond-slip law at the fabric–matrix interface had an insignificant effect on the predicted response. Numerical findings were in agreement with those obtained from laboratory testing.
- The numerical models accurately predicted the load capacity of the tested specimens but tended to underestimate the deflection. The ratio of the predicted-to-measured load capacity was in the range of 1.01 to 1.12 with an average of 1.08, whereas the ratio of the predicted-to-measured deflection at ultimate load was on average 0.77.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- ACI Committee 549. Guide to Design and Construction of Externally Bonded Fabric-Reinforced and Steel-Reinforced Grout Systems for Repair and Strengthening of Concrete Structures; American Concrete Institute: Farmington Hills, MI, USA, 2020. [Google Scholar]
- Täljsten, B.; Blanksvärd, T. Mineral-based bonding of carbon FRP to strengthen concrete structures. J. Compos. Constr. 2007, 11, 120–128. [Google Scholar] [CrossRef] [Green Version]
- Hashemi, S.; Al-Mahaidi, R. Experimental and finite element analysis of flexural behavior of FRP-strengthened RC beams using cement-based adhesives. Constr. Build. Mater. 2012, 26, 268–273. [Google Scholar] [CrossRef]
- Elsanadedy, H.M.; Almusallam, T.H.; Alsayed, S.H.; Al-Salloum, Y.A. Flexural strengthening of RC beams using textile reinforced mortar–Experimental and numerical study. Compos. Struct. 2013, 97, 40–55. [Google Scholar] [CrossRef]
- D’Ambrisi, A.; Focacci, F. Flexural strengthening of RC beams with cement-based composites. J. Compos. Constr. 2011, 15, 707–720. [Google Scholar] [CrossRef]
- Jung, K.; Hong, K.; Han, S.; Park, J.; Kim, J. Prediction of flexural capacity of RC beams strengthened in flexure with FRP fabric and cementitious matrix. Int. J. Polym. Sci. 2015, 2015, 11. [Google Scholar] [CrossRef] [Green Version]
- El-Sherif, H.; Wakjira, T.G.; Ebead, U. Flexural strengthening of reinforced concrete beams using hybrid near-surface embedded/externally bonded fabric-reinforced cementitious matrix. Constr. Build. Mater. 2020, 238, 117748. [Google Scholar] [CrossRef]
- Jabr, A.; El-Ragaby, A.; Ghrib, F. Effect of the fiber type and axial stiffness of FRCM on the flexural strengthening of RC beams. Fibers 2017, 5, 2. [Google Scholar] [CrossRef]
- Ebead, U.; Shrestha, K.C.; Afzal, M.S.; El Refai, A.; Nanni, A. Effectiveness of fabric-reinforced cementitious matrix in strengthening reinforced concrete beams. J. Compos. Constr. 2017, 21, 994–1006. [Google Scholar] [CrossRef]
- Elghazy, M.; El Refai, A.; Ebead, U.; Nanni, A. Effect of corrosion damage on the flexural performance of RC beams strengthened with FRCM composites. J. Compos. Struct. Constr. 2017, 180, 04018039. [Google Scholar] [CrossRef]
- Elghazy, M.; El Refai, A.; Ebead, U.; Nani, A. Post-repair flexural performance of corrosion-damaged beams rehabilitated with fabric-reinforced cementitious matrix (FRCM). Constr. Build. Mater. 2018, 166, 732–744. [Google Scholar] [CrossRef]
- Elghazy, M.; El Refai, A.; Ebead, U.; Nanni, A. Corrosion-damaged RC beams repaired with fabric-reinforced cementitious matrix. J. Compos. Constr. 2018, 22, 04018039. [Google Scholar] [CrossRef]
- Hadad, H.A.; Erickson, B.; Nanni, A. Flexural analysis and design of FRCM-strengthened RC beams. Constr. Build. Mater. 2020, 244, 118371. [Google Scholar] [CrossRef]
- Escrig, C.; Gil, L.; Bernat-Maso, E. Experimental comparison of reinforced concrete beams strengthened against bending with different types of cementitious-matrix composite materials. Constr. Build. Mater. 2017, 137, 317–329. [Google Scholar] [CrossRef]
- Ombres, L. Flexural analysis of reinforced concrete beams strengthened with a cement based high strength composite material. Compos. Struct. 2011, 94, 143–155. [Google Scholar] [CrossRef]
- Schladitz, F.; Frenzel, M.; Ehlig, D.; Curbach, M. Bending load capacity of reinforced concrete slabs strengthened with textile reinforced concrete. Eng. Struct. 2012, 40, 317–326. [Google Scholar] [CrossRef]
- Babaeidarabad, S.; Loreto, G.; Nanni, A. Flexural strengthening of RC beams with an externally bonded fabric-reinforced cementitious matrix. J. Compos. Constr. 2014, 18, 04014009. [Google Scholar] [CrossRef]
- Loreto, G.; Leardini, L.; Arboleda, D.; Nanni, A. Performance of RC slab-type elements strengthened with fabric-reinforced cementitious-matrix composites. J. Compos. Constr. 2014, 18, A4013003. [Google Scholar] [CrossRef]
- El-Maaddawy, T.; El Refai, A. Innovative repair of severely corroded T-beams using fabric-reinforced cementitious matrix. J. Compos. Constr. 2016, 20, 04015073. [Google Scholar] [CrossRef]
- Aljazaeri, Z.R.; Janke, M.A.; Myers, J.J. A novel and effective anchorage system for enhancing the flexural capacity of RC beams strengthened with FRCM composites. Compos. Struct. 2019, 210, 20–28. [Google Scholar] [CrossRef]
- El-Refaie, S.; Ashour, A.; Garrity, S. Sagging and hogging strengthening of continuous reinforced concrete beams using carbon fiber-reinforced polymer sheets. ACI Struct. J. 2003, 100, 446–453. [Google Scholar]
- El-Maaddawy, T.; Alshawa, J.; El-Ariss, B. Strengthening of continuous concrete slab strips containing cutouts. ACI Struct. J. 2016, 113, 1243–1252. [Google Scholar] [CrossRef]
- Alkhalil, J.; El-Maaddawy, T. Nonlinear flexural response of continuous concrete slab strips strengthened with near-surface-mounted composites. J. Compos. Constr. 2017, 21, 04016071. [Google Scholar] [CrossRef]
- Alkhalil, J.; El-Maaddawy, T. Finite element modelling and testing of two-span concrete slab strips strengthened by externally-bonded composites and mechanical anchors. Eng. Struct. 2017, 147, 45–61. [Google Scholar] [CrossRef]
- Su, M.; Zeng, C.; Li, W.; Zhu, J.; Lin, W.; Ueda, T.; Xing, F. Flexural performance of corroded continuous RC beams rehabilitated by ICCP-SS. Compos. Struct. 2020, 232, 111556. [Google Scholar] [CrossRef]
- Feng, R.; Liu, Y.; Zhu, J.; Xing, F. Flexural behaviour of C-FRCM strengthened corroded RC continuous beams. Compos. Struct. 2020, 245, 112200. [Google Scholar] [CrossRef]
- ACI 318-19; Building Code Requirements for Structural Concrete—Commentary on Building Code Requirements for Structural Concrete (ACI 318R-19). American Concrete Institute (ACI): Farmington Hills, MI, USA, 2019.
- BS EN 12390-3; Testing Hardened Concrete—Compressive Strength of Test Specimens. British Standards: London, UK, 2009.
- ASTM C39/C39M-20; Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens. ASTM International: West Conshohocken, PA, USA, 2020.
- ASTM C496/C496M-17; Standard Test Method for Splitting Tensile Strength of Cylindrical Concrete Specimens. ASTM International: West Conshohocken, PA, USA, 2017.
- BS 4449:2005 +A2:2009; Steel for the Reinforcement of Concrete—Weldable Reinforcing Steel–Bar, Coil and Decoiled–Product Specification. British Standards: London, UK, 2009.
- ASTM C109/C109M-20b; Standard Test Method for Compressive Strength of Hydraulic Cement Mortars (Using 2-in. or [50 mm] Cube Specimens). ASTM International: West Conshohocken, PA, USA, 2020.
- ASTM C469/C469M-14; Standard Test Method for Static Modulus of Elasticity and Poisson’s Ratio of Concrete in Compression. ASTM International: West Conshohocken, PA, USA, 2014.
- S&P—A Simpson Strong-Tie Company. S&P ARMO-Mesh Reinforcement Made from Carbon Fiber. Available online: https://www.sp-reinforcement.ch/en-CH (accessed on 10 December 2019).
- Ruredil. Ruredil X Mesh Gold PBO (Poliparafenilenbenzobisoxazolo) Mesh in A Stabilized Inorganic Matrix for Flexural and Shear Strength Reinforcement of Concrete. Available online: http://english.ruredil.it/ (accessed on 10 December 2019).
- Emmons, P.H. Concrete Repair and Maintenance Illustrated: Problem Analysis; Repair Strategy; Techniques; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Yazdani, N.; Riad, M.; Salloum, R.; Carr, R. Effect of surface defects on FRP-concrete interface bond strength. J. Civ. Eng. Struct. 2018, 2, 17. [Google Scholar]
- Yazdani, N.; Beneberu, E.; Riad, M. Nondestructive evaluation of FRP-concrete interface bond due to surface defects. Adv. Civ. Eng. 2019, 2019, 10. [Google Scholar] [CrossRef]
- ATENA [Computer Software]. (n.d.). Červenka Consulting s.r.o., Prague, Czech Republic. Available online: https://www.cervenka.cz/products/atena/ (accessed on 27 November 2021).
- Menétrey, P.; Willam, K. Triaxial Failure criterion for concrete and its generalization. ACI Struct. J. 1992, 92, 311–318. [Google Scholar]
- Van Mier, J.G. Multiaxial strain-softening of concrete. Mater. Struct. 1986, 19, 190–200. [Google Scholar] [CrossRef]
- Zou, X.; Sneed, L.H.; D’Antino, T.; Carloni, C. Analytical Bond-Slip Model for Fiber-Reinforced Cementitious Matrix-Concrete Joints Based on Strain Measurements. J. Mater. Civ. Eng. 2019, 31, 04019247. [Google Scholar] [CrossRef]
- Abu Obaida, F.; El-Maaddawy, T.; El-Hassan, H. Bond behavior of carbon fabric-reinforced matrix composites: Geopolymeric matrix versus cementitious mortar. Buildings 2021, 11, 207. [Google Scholar] [CrossRef]
- Ibrahim, A.; Mahmood, M. Finite element modeling of reinforced concrete beams strengthened with FRP laminates. Eur. J. Sci. Res. 2009, 30, 526–541. [Google Scholar]
- Obaidat, Y.; Heyden, S.; Dahlblom, O. The effect of CFRP and CFRP/concrete interface models when modelling retrofitted RC beams with FEM. Compos. Struct. 2010, 92, 1391–1398. [Google Scholar] [CrossRef]
- Chin, S.; Shafiq, N.; Nuruddin, M. Strengthening of RC beams with large openings in shear by CFRP laminates: 2D nonlinear FE analysis. Int. J. Civ. Environ. Struct. Construct. Archit. Eng. 2012, 6, 153–158. [Google Scholar]
- Mansour, M.; El-Maaddawy, T. Testing and modeling of deep beams strengthened with NSM-CFRP reinforcement around cutouts. Case Stud. Constr. Mater. 2021, 15, e00670. [Google Scholar] [CrossRef]








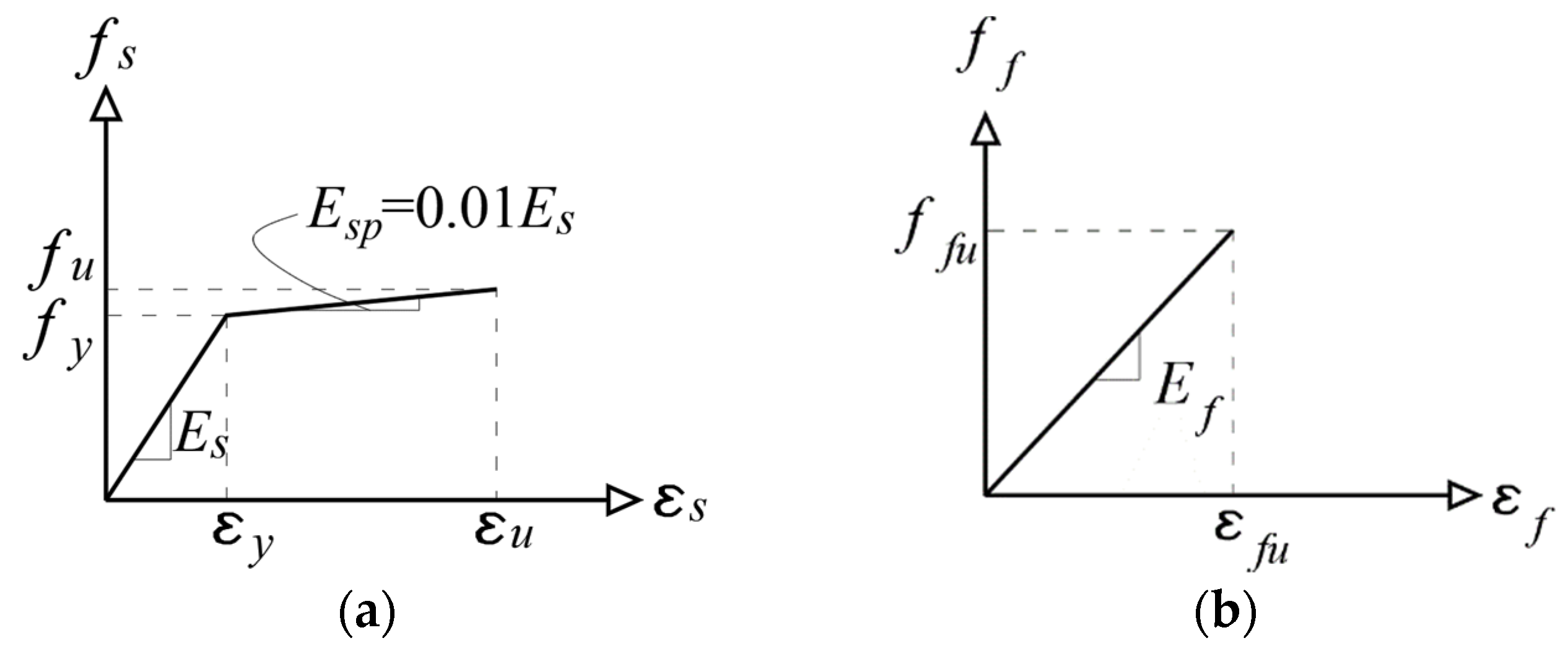
| Group | Strengthening Regime | Designation | ||
|---|---|---|---|---|
| Location | Fabric Type | No. of FRCM Layers | ||
| Control | - | - | - | Control |
| A | Sagging | Carbon | 2 | S-C2 |
| 4 | S-C4 | |||
| PBO | 2 | S-P2 | ||
| 4 | S-P4 | |||
| B | Hogging | Carbon | 2 | H-C2 |
| 4 | H-C4 | |||
| PBO | 2 | H-P2 | ||
| 4 | H-P4 | |||
| Property | Carbon | PBO |
|---|---|---|
| Weight per unit area (g/m2) | 281 | 88 |
| Tensile strength (MPa) | 4300 | 5800 |
| Modulus of elasticity (GPa) | 240 | 270 |
| Elongation at break (%) | 1.80 | 2.15 |
| Cross sectional area (mm2/mm) | 0.157 | 0.045 (0.012) 1 |
| Spacing between fabric bundles (mm) | 17 | 10 (17.5) 1 |
| Specimen | Loads (kN) | Deflection (mm) | Strength Gain (%) | Ductility Index 2 (Δf/Δy2) | Ductility Reduction 2 (%) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| At 1st Yield (Py1) | At 2nd Yield (Py2) | At Ultimate (Pu) | At 1st Yield (Δy1) | At 2nd Yield (Δy2) | At Peak Load (Δp) | At Failure 1 (Δf) | ||||
| Control | 190 | 230 | 243 | 7.8 | 10.4 | 16.2 | 26.8 | - | 2.6 | - |
| S-C2 | 190 | 260 | 312 | 7.5 | 11.9 | 24.0 | 24.0 | 28 | 2.0 | 23 |
| S-C4 | 180 | 280 | 313 | 6.2 | 11.9 | 16.5 | 16.5 | 29 | 1.4 | 46 |
| S-P2 | 190 | 260 | 285 | 7.3 | 11.7 | 26.1 | 28.8 | 17 | 2.5 | 4 |
| S-P4 | 180 | 260 | 288 | 6.0 | 11.7 | 21.2 | 21.2 | 19 | 1.8 | 31 |
| H-C2 | 230 | 250 | 284 | 8.4 | 9.5 | 17.3 | 17.3 | 17 | 1.8 | 31 |
| H-C4 3 | 230 | 230 | 256 | 9.3 | 9.3 | 11.4 | 11.4 | N/A | N/A | N/A |
| H-P2 | 230 | 255 | 266 | 9.2 | 11.1 | 25.0 | 27.0 | 9 | 2.4 | 8 |
| H-P4 | 250 | 250 | 276 | 9.4 | 9.4 | 17.5 | 17.5 | 14 | 1.9 | 27 |
| Specimen | Experimental Ultimate Moment, Mexp (kN-m) | Elastic Moment, Me (kN-m) | Moment Redistribution Ratio, β (%) | |||
|---|---|---|---|---|---|---|
| Sagging | Hogging | Sagging | Hogging | Sagging | Hogging | |
| Control | 39.7 | 50.7 | 36.4 | 56.1 | +9.1 | −9.6 |
| S-C2 | 53.1 | 61.1 | 46.7 | 71.9 | +13.7 | −15.0 |
| S-C4 | 57.9 | 53.5 | 46.8 | 72.0 | +23.7 | −25.7 |
| S-P2 | 48.1 | 56.8 | 42.7 | 65.8 | +12.7 | −13.7 |
| S-P4 | 49.5 | 55.8 | 43.2 | 66.4 | +14.6 | −16.0 |
| H-C2 | 40.0 | 70.4 | 42.7 | 65.7 | −6.3 | +7.2 |
| H-C4 | 39.9 | 58.3 | 38.9 | 59.9 | +2.6 | −2.7 |
| H-P2 | 41.4 | 60.1 | 40.3 | 61.9 | +2.8 | −2.9 |
| H-P4 | 39.1 | 68.5 | 41.7 | 64.1 | −6.2 | +6.9 |
| Parameter | Description | Value |
|---|---|---|
| fcu | Cube compressive strength | −40.0 MPa |
| f′c | Cylinder compressive strength | −29.0 MPa |
| ft | Tensile strength | 2.4 MPa |
| Ec | Elastic modulus | 2.5 × 104 MPa |
| μ | Poisson’s ratio | 0.2 |
| Gf | Specific fracture energy | 7.0 × 10−5 MN/m |
| wd | Critical compressive displacement | −5.0 × 10−4 m |
| εcp | Plastic strain at compressive strength | −1.0 × 10−3 |
| Parameter | Description | Value |
|---|---|---|
| fcu | Cube compressive strength | −45.0 MPa |
| f′c | Cylinder compressive strength | −35.0 MPa |
| ft | Tensile strength | 3.4 MPa |
| Ec | Elastic modulus | 2.8 × 104 MPa |
| μ | Poisson’s ratio | 0.2 |
| Gf | Specific fracture energy | 7.6 × 10−5 MN/m |
| wd | Critical compressive displacement | −5.0 × 10−4 m |
| εcp | Plastic strain at compressive strength | −1.1 × 10−3 |
| Parameter | Description | Value |
|---|---|---|
| fcu | Cube compressive strength | −35.0 MPa |
| f′c | Cylinder compressive strength | −28.0 MPa |
| ft | Tensile strength | 4.0 MPa |
| Ec | Elastic modulus | 9.0 × 103 MPa |
| μ | Poisson’s ratio | 0.2 |
| Gf | Specific fracture energy | 6.4 × 10−5 MN/m |
| wd | Critical compressive displacement | −5.0 × 10−4 m |
| εcp | Plastic strain at compressive strength | −9.2 × 10−4 |
| Specimen | Ultimate Load (kN) | Deflection at Ultimate Load (mm) | ||||
|---|---|---|---|---|---|---|
| Experimental (Pu) | Numerical 1 (PFE) | Ratio (PFE/Pu) | Experimental (Δp) | Numerical 1 (ΔFE) | Ratio (Δp/ΔFE) | |
| Control | 243 | 264 | 1.09 | 16.2 | 18.7 | 1.15 |
| S-C2 | 312 | 315 | 1.01 | 24 | 12.6 | 0.53 |
| S-C4 | 313 | 334 | 1.07 | 16.5 | 10.4 | 0.63 |
| S-P2 | 285 | 302 | 1.06 | 26.1 | 18 | 0.70 |
| S-P4 | 288 | 319 | 1.11 | 21.2 | 16.1 | 0.76 |
| H-C2 | 284 | 305 | 1.07 | 17.3 | 12.2 | 0.71 |
| H-C4 2 | 256 | 318 | N/A | 11.4 | 9.6 | N/A |
| H-P2 | 266 | 290 | 1.09 | 25 | 20.2 | 0.81 |
| H-P4 | 276 | 308 | 1.12 | 17.5 | 15.1 | 0.86 |
| Average | 1.08 | 0.77 | ||||
| Specimen | Numerical Ultimate Moment, MFE (kN-m) | Elastic Moment, Me (kN-m) | Moment RedistributionRatio, β (%) | |||
|---|---|---|---|---|---|---|
| Sagging | Hogging | Sagging | Hogging | Sagging | Hogging | |
| Control | 46 | 50 | 39 | 61 | +16.0 | −17.3 |
| S-C2 | 61 | 50 | 47 | 73 | +28.5 | −30.9 |
| S-C4 | 66 | 50 | 50 | 77 | +32.3 | −35.0 |
| S-P2 | 56 | 51 | 45 | 69 | +24.3 | −26.4 |
| S-P4 | 62 | 50 | 48 | 73 | +29.5 | −31.9 |
| H-C2 | 45 | 72 | 46 | 70 | −1.9 | +2.0 |
| H-C4 | 44 | 80 | 48 | 73 | −7.8 | +8.5 |
| H-P2 | 46 | 63 | 43 | 67 | +5.6 | −6.0 |
| H-P4 | 45 | 72 | 46 | 71 | −1.3 | +1.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khattak, N.; Mansour, M.; El-Maaddawy, T.; Ismail, N. Continuous Reinforced Concrete Beams Strengthened with Fabric-Reinforced Cementitious Matrix: Experimental Investigation and Numerical Simulation. Buildings 2022, 12, 27. https://doi.org/10.3390/buildings12010027
Khattak N, Mansour M, El-Maaddawy T, Ismail N. Continuous Reinforced Concrete Beams Strengthened with Fabric-Reinforced Cementitious Matrix: Experimental Investigation and Numerical Simulation. Buildings. 2022; 12(1):27. https://doi.org/10.3390/buildings12010027
Chicago/Turabian StyleKhattak, Nouman, Moustafa Mansour, Tamer El-Maaddawy, and Najif Ismail. 2022. "Continuous Reinforced Concrete Beams Strengthened with Fabric-Reinforced Cementitious Matrix: Experimental Investigation and Numerical Simulation" Buildings 12, no. 1: 27. https://doi.org/10.3390/buildings12010027
APA StyleKhattak, N., Mansour, M., El-Maaddawy, T., & Ismail, N. (2022). Continuous Reinforced Concrete Beams Strengthened with Fabric-Reinforced Cementitious Matrix: Experimental Investigation and Numerical Simulation. Buildings, 12(1), 27. https://doi.org/10.3390/buildings12010027








